Teoria Moderna del Portafoglio: la nascita dell'Asset Allocation

---

«A good portfolio is more than a long list of good stocks and bonds. It is a balanced whole, providing the investor with protections and opportunities with respect to a wide range of contingencies».

Harry Markowitz

Questo articolo fa parte del Percorso intermedio, pensato per chi possiede già le basi e vuole approfondire strategie di investimento e concetti teorici per una comprensione più approfondita della finanza. In fondo alla pagina, troverai il link al prossimo articolo del percorso.

L'Asset Allocation rappresenta uno dei concetti fondamentali nella gestione finanziaria e trova le sue radici nel lavoro pionieristico di Harry Markowitz.

Nel 1952, Markowitz pubblicò il suo rivoluzionario articolo intitolato Portfolio Selection, in cui gettava le basi per quella che sarebbe divenuta nota come la Modern Portfolio Theory (MPT), ovvero la Teoria Moderna del Portafoglio.

La Teoria Moderna del Portafoglio ha introdotto un approccio scientifico alla costruzione e alla gestione dei portafogli di investimento, enfatizzando l'importanza della diversificazione per ottimizzare il rapporto tra rischio e rendimento.

Markowitz fu il primo a proporre un modello quantitativo capace di superare la logica allora dominante, secondo cui l’investitore sceglieva semplicemente il titolo con il rendimento atteso più elevato: egli dimostrò che una simile regola conduce a portafogli non diversificati e quindi subottimali, poiché non sfruttano i benefici della combinazione di titoli con andamenti differenti.

Markowitz dimostrò che, attraverso una combinazione di strumenti finanziari non perfettamente correlati, è possibile ridurre la volatilità complessiva del portafoglio senza necessariamente sacrificare il rendimento atteso.

Questa teoria ha trasformato radicalmente il modo in cui gli investitori e i professionisti della finanza concepiscono la gestione del rischio e la creazione di valore nel lungo periodo.

Dal contributo originario di Markowitz, si è sviluppata una vera e propria architettura teorica che ha influenzato profondamente i modelli successivi come il Capital Asset Pricing Model (CAPM) e l’Arbitrage Pricing Theory (APT).

I principi della Teoria Moderna del Portafoglio continuano a costituire il nucleo concettuale delle strategie di Asset Allocation oggi impiegate da gestori, fondi pensione e investitori istituzionali.

Indice

1. La nascita della Modern Portfolio Theory
2. Rischio e rendimento di un portafoglio con due strumenti finanziari
3. Rischio e rendimento di un portafoglio con una quota priva di rischio
4. Rischio e rendimento di un portafoglio con più strumenti finanziari
5. Portafoglio tangente e indice di Sharpe: interpretazione e applicazioni
6. Estensioni e limiti della Modern Portfolio Theory

1. La nascita della Modern Portfolio Theory

Markowitz fu il primo studioso a formalizzare matematicamente la nozione di diversificazione degli investimenti, un concetto che da quel momento in poi cominciò a delinearsi come una strategia fondamentale nella gestione dei portafogli, anche se ci vorrà del tempo prima che la diversificazione diventi una prassi comune.

Attraverso il processo di Asset Allocation e grazie ai vantaggi offerti dalla diversificazione, è possibile ridurre il rischio complessivo di un portafoglio senza compromettere il rendimento atteso.

Questo principio rappresenta uno dei pilastri della Modern Portfolio Theory.

Markowitz definì il rischio come la varianza dei rendimenti. Scegliendo la giusta combinazione di strumenti finanziari e bilanciando opportunamente i loro pesi, è possibile identificare un portafoglio efficiente per ogni livello di rendimento atteso: quello che minimizza la varianza dei rendimenti, e quindi il rischio.

L'aspetto più rivoluzionario del lavoro di Markowitz fu il passaggio dall'analisi dei singoli titoli alla considerazione del portafoglio nel suo complesso: non è tanto il rischio intrinseco di un singolo strumento a essere determinante, quanto piuttosto il modo in cui quel singolo strumento contribuisce al rischio complessivo del portafoglio, misurato attraverso la varianza totale.

In altre parole, la covarianza tra un singolo strumento e gli altri componenti del portafoglio assume un ruolo cruciale nella determinazione del rischio complessivo.

Questa innovazione è di fondamentale importanza: la decisione di includere un determinato titolo non dipenderà più semplicemente dal confronto del suo rendimento e della sua varianza con quelli di altri titoli, quanto da quali altri strumenti l’investitore vorrà includere nel proprio portafoglio.

In questo articolo, applicheremo il processo di ottimizzazione sviluppato da Markowitz sia a esempi teorici che a casi pratici, utilizzando serie storiche dei rendimenti di strumenti finanziari reali, per mostrare concretamente come la Modern Portfolio Theory possa essere implementata nella gestione degli investimenti.

2. Rischio e rendimento di un portafoglio con due strumenti finanziari

«Diversifying sufficiently among uncorrelated risks can reduce portfolio risk toward zero. But financial engineers should know that's not true of a portfolio of correlated risks».

Harry Markowitz

Si suppone che l'investitore utilizzi interamente la propria disponibilità finanziaria per l'investimento.

Il rendimento di un portafoglio formato da due titoli, denominati a e b, è pari alla media ponderata dei rendimenti dei due titoli in base ai rispettivi pesi:

\begin{equation} r_p = x_ar_a + x_br_b \end{equation}

Dove:
r_p = Rendimento del portafoglio.
r_a = Rendimento del primo titolo.
r_b = Rendimento del secondo titolo.
x_a = Peso del primo titolo.
x_b = 1 – x_a = Peso del secondo titolo.

Il calcolo della varianza del portafoglio, che utilizziamo come misura del rischio, è invece più complesso.

Essa è data dalla seguente formula:

\begin{equation} σ_p^2 = x_a^2σ_a^2 + x_b^2σ_b^2 + 2x_ax_bσ_{ab} \end{equation}

Dove:
σ_p² = Varianza dei rendimenti del portafoglio.
σ_a² = Varianza dei rendimenti del primo titolo.
σ_b² = Varianza dei rendimenti del secondo titolo.
σ_ab = Covarianza tra i rendimenti del primo e del secondo titolo.

Per ottenere la deviazione standard del portafoglio (σ_p), è sufficiente estrarre la radice quadrata della varianza:

\begin{equation} \sigma_p=\sqrt{\sigma_p^2} \end{equation}

A differenza del rendimento atteso, la deviazione standard del portafoglio non è semplicemente una media ponderata delle deviazioni standard dei due titoli: il motivo è che entra in gioco la covarianza, cioè la misura di come i rendimenti dei due titoli si muovono insieme.

Se i rendimenti tendono a salire e scendere nello stesso momento, la covarianza sarà positiva; se invece tendono a muoversi in direzioni opposte, sarà negativa. Se non c’è relazione sistematica, sarà prossima a zero.

In termini più intuitivi, la covarianza (e la correlazione che ne deriva) stabilisce quanto la combinazione dei due titoli riesca a ridurre o meno il rischio complessivo. È questo il cuore dell’intuizione di Markowitz: non conta solo la volatilità di ciascun titolo, ma soprattutto come i titoli interagiscono fra loro.

Analisi dei casi estremi di correlazione

È particolarmente interessante analizzare i casi estremi in cui la correlazione lineare tra i due titoli assume i valori +1, −1 e 0, poiché questi scenari offrono intuizioni importanti sulla struttura del rischio del portafoglio.

Da questo punto in avanti, ogni riferimento alla correlazione indicherà sempre la correlazione lineare tra i rendimenti dei titoli.

Correlazione = +1.

La relazione grafica tra il rendimento atteso e la deviazione standard del portafoglio è la seguente:

 

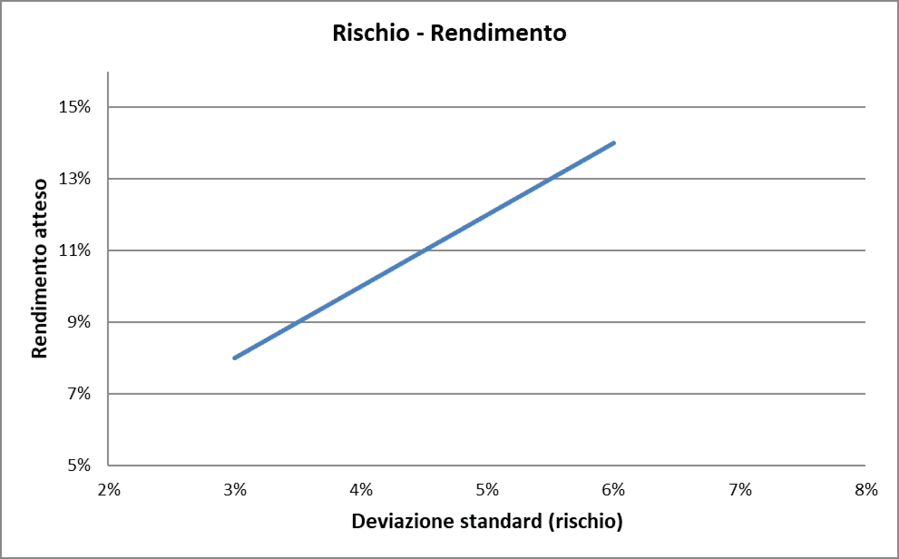
Rischio/Rendimento con correlazione = 1 (caso teorico)

La linea blu sul grafico rappresenta i livelli di rischio (misurati dalla deviazione standard) e rendimento atteso di un portafoglio composto da due titoli con una correlazione lineare perfettamente positiva, pari quindi a +1:

• Punto più in basso a sinistra. Questo punto sulla linea blu corrisponde a un portafoglio composto al 100% dal titolo a. In questo caso, la deviazione standard del portafoglio è del 3%, mentre il rendimento atteso è dell'8%.
• Punto più in alto a destra. Questo punto identifica un portafoglio composto al 100% dal titolo b. Qui, la deviazione standard è del 6% e il rendimento atteso è del 14%.
• Tutti i punti lungo la linea blu rappresentano combinazioni intermedie. Ad esempio, un portafoglio potrebbe essere composto per il 10% dal titolo a e per il 90% dal titolo b, o per il 20% dal titolo a e per l'80% dal titolo b, e così via.

In questo scenario estremo, la deviazione standard del portafoglio diventa una semplice media ponderata delle deviazioni standard dei titoli.

In altre parole, la diversificazione non produce alcun beneficio: detenere entrambi i titoli equivale, in termini di rischio, a possederne solo uno in proporzione ai pesi scelti.

CASO REALE (+1)

Nella realtà, è estremamente raro trovare due titoli con una correlazione dei rendimenti esattamente pari a +1. Solo titoli molto simili – ad esempio due fondi che replicano lo stesso indice, o due classi diverse dello stesso fondo – possono avvicinarsi a questo valore.

Facciamo un esempio: Fonditalia Equity Italy R e Interfund Equity Italy Acc, due fondi attivi appartenenti alla categoria degli "Azionari Italia". 

Analizzando i rendimenti giornalieri dal 30 maggio 2016 al 23 maggio 2017 (256 giorni di borsa), la correlazione risulta +0,9892, un valore molto vicino all'unità.

Questo risultato riflette una relazione quasi perfettamente lineare tra i rendimenti dei due fondi, il che li rende un caso di studio ideale per esaminare le dinamiche di un portafoglio con correlazione positiva molto alta.

La rappresentazione grafica della relazione tra il rendimento atteso e la deviazione standard del portafoglio, in funzione delle diverse combinazioni di peso tra i due titoli nel portafoglio, è la seguente:

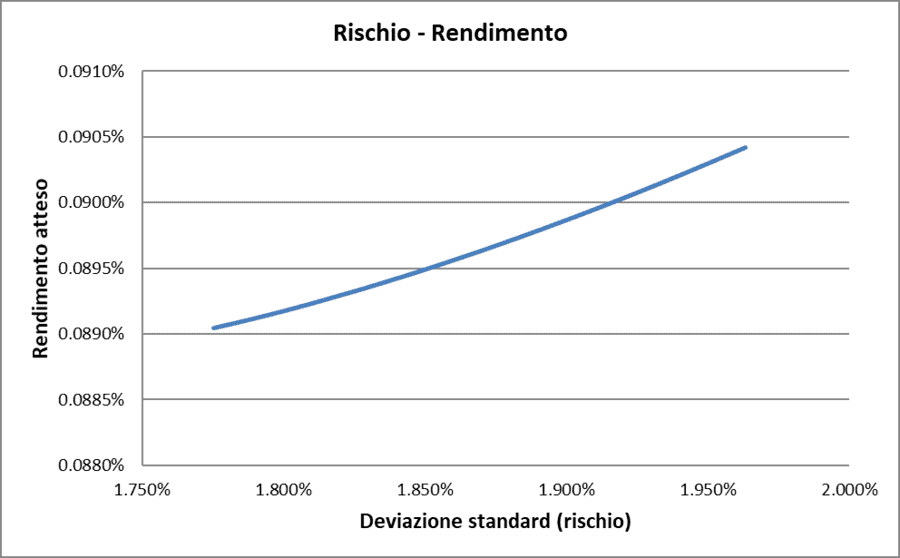
Rischio/Rendimento con correlazione = 1 (caso reale)

La curva risultante è leggermente arcuata, ma nel complesso quasi indistinguibile da una retta.

In pratica, detenere entrambi i fondi non ha ridotto il rischio: i loro rendimenti si muovono in modo troppo simile per offrire un beneficio di diversificazione.

Correlazione = −1. Quando la correlazione lineare tra i rendimenti di due titoli è pari a −1, la relazione grafica assume una configurazione particolare:

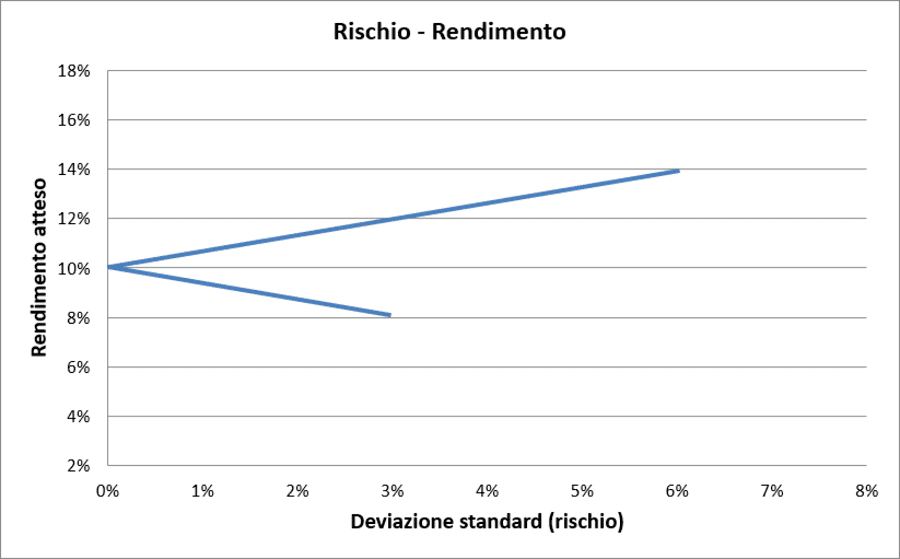
Rischio/Rendimento con correlazione = −1 (caso teorico)

In questo caso, esiste una combinazione di pesi che annulla completamente il rischio del portafoglio: grazie alla correlazione perfettamente negativa, gli alti rendimenti di un titolo coincidono sempre con i bassi rendimenti dell’altro, compensandosi esattamente.

Il risultato è straordinario: rischio zero con rendimento positivo. Questo rappresenta il massimo potenziale della diversificazione, anche se rimane un caso teorico quasi irrealizzabile nella pratica.

Anche se non si può eliminare completamente il rischio, una buona diversificazione può comunque migliorare sensibilmente il rapporto tra rendimento e rischio.

Un portafoglio ben diversificato è in grado di generare un rendimento atteso per unità di rischio (misurato come varianza o deviazione standard) superiore rispetto a quello che si otterrebbe investendo nei singoli strumenti finanziari presi singolarmente.

CASO REALE (−1)

Il portafoglio è stato costruito utilizzando i seguenti fondi: Fideuram Italia e UBI Pramerica – Obbligazioni Globali. Il primo fondo è classificato come azionario italiano; il secondo, come obbligazionario globale in euro. 

Nel periodo 30 maggio 2016 – 23 maggio 2017, la correlazione tra i rendimenti è stata −0,6015. Pur non essendo −1, questa correlazione negativa ha prodotto benefici tangibili: il rischio del portafoglio è risultato inferiore a quello di ciascun fondo singolarmente, e il rendimento atteso si è collocato in un intervallo intermedio, ma migliore rispetto al fondo con rendimento più basso.

La rappresentazione grafica della relazione tra il rendimento atteso e la deviazione standard del portafoglio, considerando le varie combinazioni di peso tra i due fondi, è la seguente:

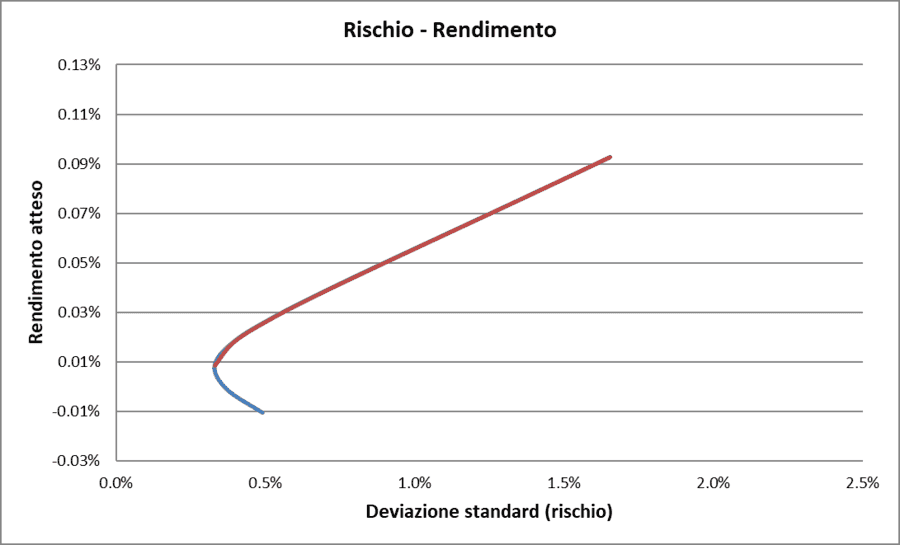
Rischio/Rendimento con correlazione = −1 (caso reale)

Da questa analisi emerge il concetto di portafoglio efficiente. La parte rossa della curva rappresenta la porzione di combinazioni tra pesi che, a parità di rischio, offrono il massimo rendimento possibile.

Questa regione, evidenziata in rosso, è chiamata frontiera efficiente.

Di conseguenza, un portafoglio efficiente non può essere migliorato né sul piano del rendimento atteso né su quello del rischio: portafogli con rendimenti più elevati comportano inevitabilmente una maggiore volatilità, mentre quelli con rischio inferiore offrono in cambio un rendimento atteso minore.

La scelta tra diversi portafogli efficienti dipende da fattori soggettivi, come la propensione individuale al rischio e le aspettative di rendimento dell'investitore.

Per ciascun investitore, il portafoglio efficiente corrisponde a un punto della frontiera efficiente che riflette il livello di rischio compatibile con la sua tolleranza personale.

Correlazione = 0. Quando la correlazione lineare tra i due titoli è nulla, i loro movimenti sono indipendenti. La rappresentazione grafica della relazione tra il rendimento atteso e la deviazione standard del portafoglio è la seguente:

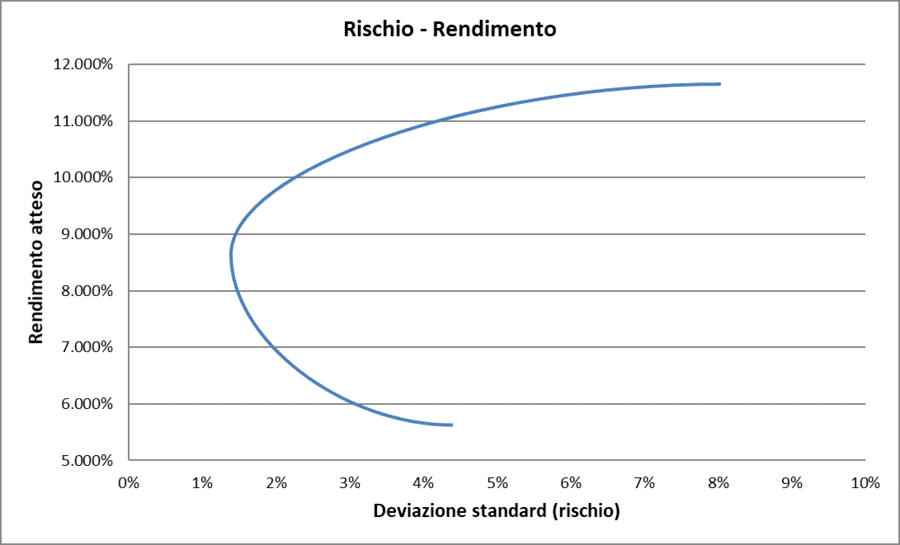
Rischio/Rendimento con correlazione = 0 (caso teorico)

La diversificazione in questo caso riduce il rischio complessivo, ma senza mai arrivare ad azzerarlo come nel caso di correlazione negativa.

CASO REALE (0)

Un portafoglio composto da BG Selection SICAV – Anima Italy Equities AX (azionario italiano) e Investec Global Strategy Fund – UK Alpha Fund F Acc USD (azionario Large Cap del Regno Unito denominato in dollari), analizzato nello stesso periodo, ha mostrato una correlazione pari a −0,0041, cioè praticamente nulla.

I due fondi hanno quindi operato in modo indipendente, con il risultato che il portafoglio ha beneficiato di una riduzione di rischio rispetto ai singoli strumenti, pur senza raggiungere i livelli ottenibili con correlazioni negative più forti.

La rappresentazione grafica è la seguente:

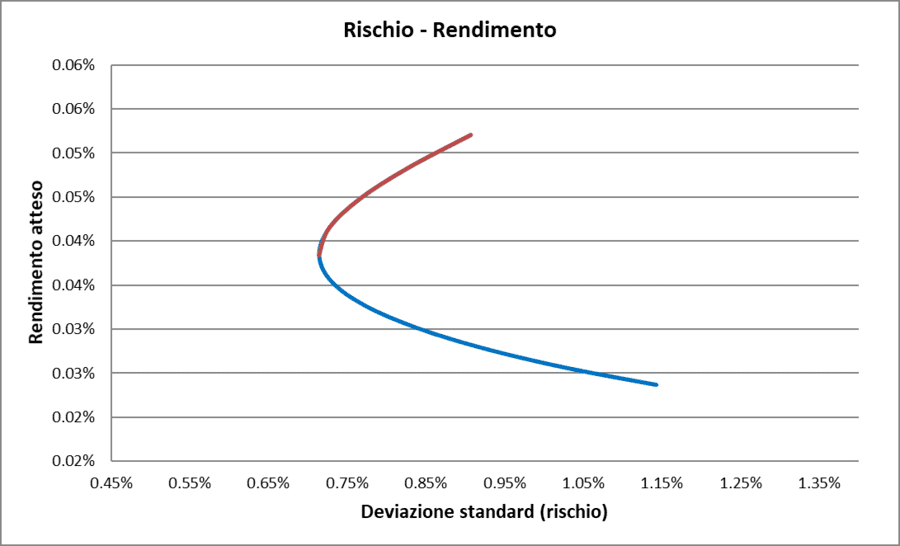
Rischio/Rendimento con correlazione = 0 (caso reale)

Anche in questo caso, la parte rossa della curva rappresenta la frontiera efficiente, ovvero l'insieme dei portafogli che offrono il miglior compromesso tra rischio e rendimento dei due fondi.

Per riassumere le diverse situazioni di correlazione, possiamo utilizzare un grafico che sintetizza in un'unica immagine tutte le relazioni precedentemente analizzate:

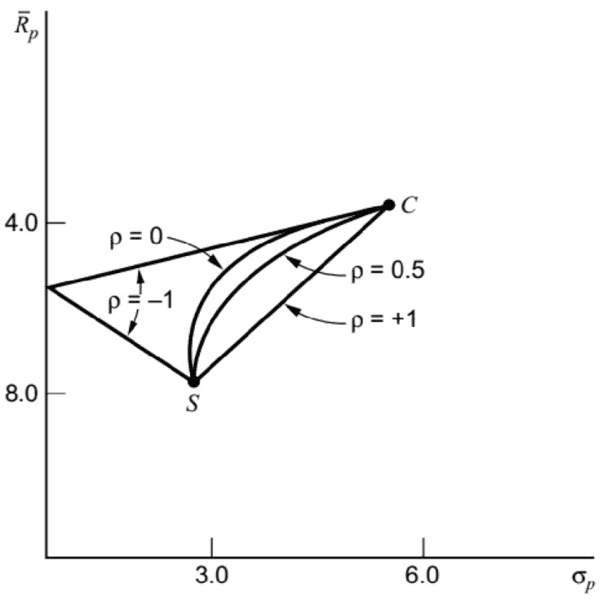
Rischio/rendimento (tutti i casi)

La regione compresa tra i punti C, S e il punto di intersezione con l’asse y rappresenta l'insieme dei portafogli ammissibili ottenibili dalla combinazione di due titoli, in funzione della correlazione tra i loro rendimenti.

Nella zona verde, che corrisponde a correlazioni comprese tra 0 e −1, la diversificazione produce i maggiori benefici: esistono combinazioni di portafoglio in cui il rischio si riduce in misura rilevante, fino a toccare un punto sull’asse delle ordinate in cui la varianza si annulla.

La fascia gialla, relativa a correlazioni intermedie (da 0 a +0,5), mostra come la diversificazione continui a essere vantaggiosa, anche se con un’efficacia via via minore.

La zona rossa, infine, rappresenta il caso di correlazioni elevate (da +0,5 a +1): in questo scenario, i rendimenti dei titoli si muovono in modo molto simile e i benefici della diversificazione si riducono progressivamente, fino ad annullarsi quando la correlazione raggiunge +1.

Solo una parte di questi portafogli è efficiente: quelli che si collocano lungo la frontiera efficiente, ossia le scelte ottimali per l’investitore che intende massimizzare il rendimento atteso per un dato livello di rischio o, viceversa, minimizzare il rischio a fronte di un determinato rendimento atteso.

3. Rischio e rendimento di un portafoglio con una quota priva di rischio

«Portfolio theory, as used by most financial planners, recommends that you diversify with a balance of stocks and bonds and cash that's suitable to your risk tolerance».

Harry Markowitz

Un investimento privo di rischio viene definito risk free. In realtà, nessun investimento è completamente esente da rischi: per quanto basso, ogni portafoglio e ogni strumento finanziario possiede un certo grado di rischio.

Nel mondo reale, si fa spesso riferimento ai titoli di Stato, ai Buoni Fruttiferi Postali, ai conti correnti con un massimale di 100.000 euro e ad altri strumenti simili come investimenti considerati privi di rischio.

Nella letteratura accademica, il titolo privo di rischio è generalmente rappresentato da un titolo di Stato a breve scadenza di un emittente considerato solvibile (ad esempio, i Treasury Bill statunitensi).

Questo perché il rischio di credito e il rischio di reinvestimento, pur non azzerabili, sono molto contenuti e quindi trascurabili nei modelli teorici.

Il rendimento atteso di un portafoglio rischioso, denominato r_pf, in cui non si investe l'intero capitale ma si riserva una parte a uno strumento privo di rischio (c), è calcolato come segue:

\begin{equation} r_{pf}=x_pr_p+\left(1-x_p\right)r_c=r_c + x_p\left(r_p-r_c\right) \end{equation}

Dove:
r_pf = Rendimento del portafoglio che include anche il titolo privo di rischio.
r_p = Rendimento del portafoglio rischioso.
r_c = Rendimento dello strumento privo di rischio.
x_p = Peso del portafoglio rischioso.

Il rendimento del portafoglio rischioso, in cui una parte del capitale è investita in uno strumento privo di rischio, non è altro che una media ponderata tra il rendimento del portafoglio rischioso e quello dello strumento privo di rischio.

Riorganizzando la formula, possiamo interpretare il risultato come il rendimento dello strumento privo di rischio, al quale si aggiunge il differenziale di rendimento tra il portafoglio rischioso e il rendimento privo di rischio (r_p − r_c), moltiplicato per il peso del portafoglio rischioso (x_p).

Questa interpretazione è particolarmente interessante: il differenziale tra il rendimento del portafoglio rischioso e quello privo di rischio è chiamato premio per il rischio o rendimento in eccesso. 

Si tratta della remunerazione aggiuntiva che un investitore si attende di ricevere per sopportare la volatilità del portafoglio rischioso invece di detenere esclusivamente attività prive di rischio.

Per quanto riguarda la varianza del portafoglio, considerando che lo strumento privo di rischio ha varianza (σ_c²) e covarianza con il portafoglio rischioso (σ_pc) pari a zero, la formula si semplifica così:

\begin{equation} σ_{pf}^2 = x_p^2σ_p^2 + (1 - x_p)σ_c^2 + 2x_p(1 - x_p)σ_{pc} = x_p^2σ_p^2 \end{equation}

Per calcolare la deviazione standard del portafoglio (σ_pf), sarà sufficiente estrarre la radice quadrata della varianza:

\begin{equation} \sigma_{pf}=\sqrt{x_p^2σ_p^2}=x_pσ_p \end{equation}

La varianza del nuovo portafoglio dipende quindi soltanto dalla parte investita nel portafoglio rischioso.

Ne consegue che il rischio cresce in modo proporzionale al peso attribuito alla componente rischiosa: se x_p = 0, l’investitore detiene solo attività prive di rischio; se x_p = 1, l’investitore detiene esclusivamente il portafoglio rischioso; se x_p > 1, l’investitore sta utilizzando leva finanziaria, cioè si espone a un rischio superiore al portafoglio rischioso originario.

Graficamente:

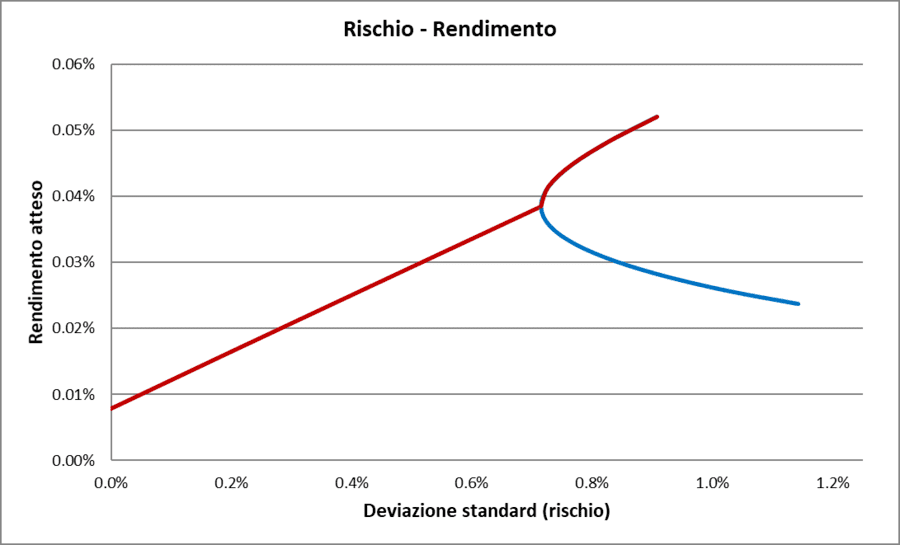
Rischio/Rendimento con investimento privo di rischio

La parte rossa della curva rappresenta la frontiera efficiente.

La retta sul grafico rappresenta tutte le possibili combinazioni di rischio e rendimento di un portafoglio composto dai fondi BG Selection SICAV – Anima Italy Equities AX (60% della parte rischiosa) e Investec Global Strategy Fund – UK Alpha Fund F Acc USD (40% della parte rischiosa), insieme a un investimento privo di rischio. L'analisi si basa sullo stesso periodo di riferimento.

I pesi assegnati ai due fondi, rispettivamente 60% e 40%, non sono casuali: individuano il portafoglio efficiente col minor rischio.

La curva, invece, rappresenta le possibili combinazioni di rischio e rendimento nel caso in cui l'intero capitale sia investito esclusivamente nel portafoglio rischioso, senza alcuna allocazione a uno strumento privo di rischio.

4. Rischio e rendimento di un portafoglio con più strumenti finanziari

«The investor does (or should) consider expected return a desirable thing and variance of return an undesirable thing».

Harry Markowitz

Dopo aver analizzato i portafogli di due titoli, passiamo ora alla formulazione generale per un portafoglio di N titoli: il rendimento atteso rimane una media ponderata dei rendimenti attesi dei singoli titoli:

\begin{equation}
E(r_p) = \sum_{i=1}^{N} x_i E(r_i)
\end{equation}

Dove:
N = Numero di titoli nel portafoglio.
xᵢ = Peso del titolo i nel portafoglio.
E(rᵢ) = Rendimento atteso del titolo i.

La formula della varianza invece si estende includendo tutte le covarianze tra le coppie di titoli:

\begin{equation}
\sigma_p^2 = \sum_{i=1}^{N} x_i^2 \sigma_i^2 + \sum_{i=1}^{N} \sum_{\substack{j=1 \ j \neq i}}^{N} x_i x_j \sigma_{ij}
\end{equation}

La prima parte dell’equazione rappresenta la componente di rischio legata alla volatilità dei singoli titoli, ponderata per il quadrato del loro peso. La seconda parte invece tiene conto di tutte le covarianze, moltiplicate per i pesi dei due titoli coinvolti.

È proprio quest’ultima componente a determinare l’efficacia della diversificazione: se le covarianze sono basse o negative, la varianza complessiva del portafoglio scende.

Vediamo il nostro solito caso pratico: il portafoglio seguente è stato costruito utilizzando i seguenti tre fondi: Fonditalia Equity Italy R, Investec Global Strategy Fund – UK Alpha Fund F Acc USD e UBI Pramerica – Obbligazioni Globali. Il periodo di analisi è invariato.

Questi fondi sono stati già analizzati in precedenza, e la loro combinazione offre un'interessante opportunità per esplorare le dinamiche di un portafoglio diversificato con più di due strumenti finanziari.

Le correlazioni tra i rendimenti dei fondi sono le seguenti:

• 0,477 tra Fonditalia e Investec.
• −0,3563 tra Fonditalia e UBI.
• −0,3387 tra Investec e UBI.

Questi valori indicano che i fondi hanno una relazione non perfettamente lineare tra di loro, con una correlazione positiva e due negative. Ciò implica che la diversificazione attraverso questi fondi può offrire benefici in termini di riduzione del rischio complessivo del portafoglio.

La rappresentazione grafica della relazione tra il rendimento atteso e la deviazione standard del portafoglio, considerando le diverse combinazioni di peso tra i tre fondi, è la seguente:

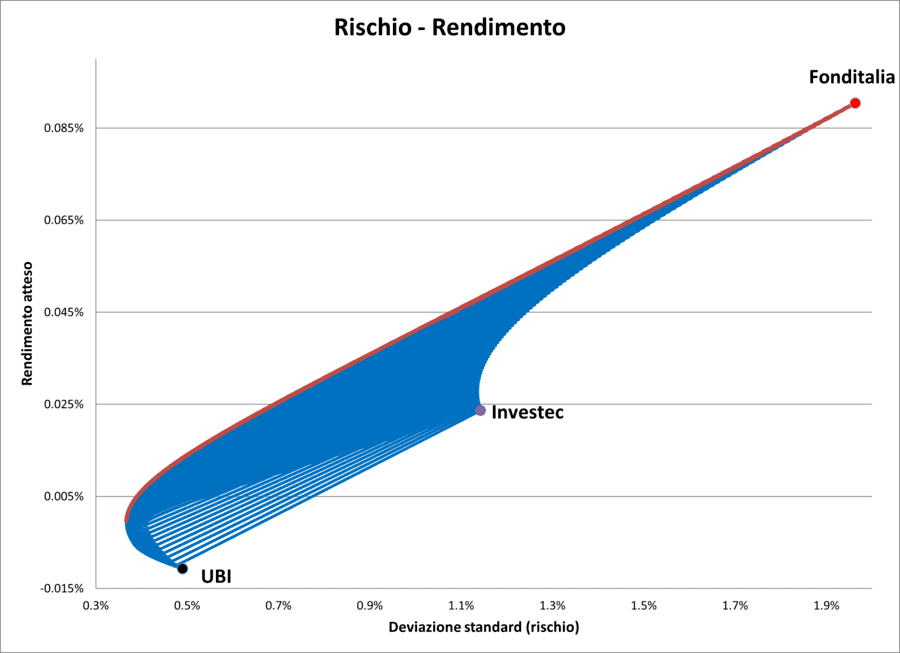
Rischio/Rendimento (caso reale con 3 fondi)

In questo caso, il grafico non presenta una semplice curva, ma un'area composta da una moltitudine di punti, ciascuno dei quali rappresenta una combinazione specifica di rischio-rendimento.

Il bordo superiore di quest’area, colorato di rosso, individua la frontiera efficiente: i portafogli che offrono il massimo rendimento atteso per ciascun livello di rischio.

Il grafico è stato creato considerando un totale di 5.151 punti (combinazioni di rischio e rendimento atteso), ottenuti calcolando la volatilità e il rendimento per tutte le possibili combinazioni di pesi tra i tre fondi analizzati.

Il gap tra i pesi è stato del solo 1%, il che ha permesso di considerare una vasta gamma di possibili combinazioni, come ad esempio 0-0-100%, 1-0-99%, 1-1-98%, e così via.

Di questi 5.151 punti, 675 si trovano sulla frontiera efficiente e individuano i portafogli che offrono il massimo rendimento possibile per ciascun livello di rischio.

Il grafico evidenzia anche i livelli di rischio e rendimento atteso generati dai portafogli composti al 100% da ciascuno dei tre fondi individualmente.

È interessante notare che solo uno di questi portafogli, quello composto interamente da Fonditalia, si trova sulla frontiera efficiente: precisamente nel punto associato al massimo rendimento e al maggior rischio.

Questo suggerisce che, se questi tre fondi costituissero l'intero universo investibile, un investitore con elevata propensione al rischio sceglierebbe teoricamente il portafoglio costituito al 100% da Fonditalia.

Tuttavia, la maggior parte degli investitori si collocherebbe lungo la frontiera efficiente, dove è possibile ottenere combinazioni più equilibrate tra rischio e rendimento.

Gli altri due fondi (UBI e Investec), presi singolarmente, non rappresentano soluzioni efficienti, perché esistono combinazioni che, a parità di rischio, offrono rendimenti superiori.

L'esempio mostra in modo chiaro il principio di dominanza: un portafoglio inefficiente è sempre dominato da un portafoglio efficiente, che offre un rendimento superiore a parità di rischio, oppure un rischio inferiore a parità di rendimento.

Un aspetto essenziale di questo approccio è che, all’aumentare del numero di titoli inclusi nel portafoglio, il rischio legato a eventi specifici dei singoli strumenti (rischio specifico o diversificabile) tende a ridursi progressivamente, mentre rimane soltanto il rischio connesso all’andamento generale del mercato (rischio sistematico o non diversificabile).

In termini grafici, l’inserimento di titoli con correlazioni basse o negative sposta la frontiera efficiente verso sinistra (minor rischio) o verso l’alto (maggior rendimento). Superata una certa soglia, però, l’effetto marginale della diversificazione diventa sempre più limitato: l’aggiunta di ulteriori strumenti produce riduzioni di rischio via via meno rilevanti.

Ne consegue una conclusione importante: la diversificazione non elimina mai completamente il rischio, ma consente di ridurre quello specifico fino a isolare soltanto il rischio sistematico, che è inevitabile e non può essere annullato.

5. Portafoglio tangente e indice di Sharpe: interpretazione e applicazioni

«The best investors do not target return; they focus first on risk, and only then decide whether the projected return justifies taking each particular risk».

Seth Klarman

Abbiamo visto come il rendimento di un portafoglio rischioso che includa anche una quota in attività prive di rischio possa essere espresso come una media ponderata dei rendimenti di queste due componenti.

Graficamente, questa relazione corrisponde a una retta che rappresenta tutte le possibili combinazioni di rischio e rendimento ottenibili da un portafoglio misto.

Riprendiamo ora il concetto introducendo alcune differenze:

• Il portafoglio è composto da tre fondi, anziché due.
• La retta non interseca più la frontiera efficiente nel punto di minima volatilità, ma le è tangente.
• Si assume che la retta intersechi l’asse delle ordinate al livello di rendimento dell'investimento privo di rischio.

Il punto di tangenza tra la retta e la frontiera efficiente individua il cosiddetto portafoglio tangente, che rappresenta l’unico portafoglio efficiente in grado di offrire, in combinazione con l’attività priva di rischio, il miglior rapporto tra rendimento e rischio.

In altre parole, una volta identificato, il portafoglio tangente diventa l’unico portafoglio rischioso che meriti di essere detenuto: qualunque combinazione ottimale di rischio e rendimento può essere costruita mescolando questo portafoglio con il titolo privo di rischio.

La pendenza della retta che passa per il portafoglio tangente è nota come Indice di Sharpe, ed è calcolata come:

\begin{equation} Indice\ di\ Sharpe=\frac{Rendimento\ in\ eccesso\ del\ portafoglio}{Volatilità\ del\ portafoglio} \end{equation}

Più precisamente:

\begin{equation} Indice\ di\ Sharpe=\frac{r_p-r_f}{\sigma_p} \end{equation}

Dove:
r_p = Rendimento del portafoglio.
r_f = Tasso di rendimento a rischio zero.
σ_p = Volatilità del portafoglio.

L’Indice di Sharpe misura quanta “ricompensa” in termini di rendimento extra si ottiene per ogni unità di rischio assunta. È una metrica chiave della performance, ancora oggi ampiamente utilizzata dai gestori professionali per confrontare portafogli o fondi di investimento.

Questo indice viene massimizzato quando il portafoglio efficiente scelto è proprio il portafoglio tangente. Tutti gli altri portafogli rischiosi lungo la frontiera efficiente (e naturalmente anche quelli inefficienti) si troveranno al di sotto della retta tangente.

Il coefficiente angolare di questa retta rappresenta l'Indice di Sharpe, indicando che il portafoglio tangente è quello che offre il rendimento più elevato per unità di volatilità rispetto a qualsiasi altro portafoglio disponibile.

Questo concetto può essere rappresentato graficamente come segue:

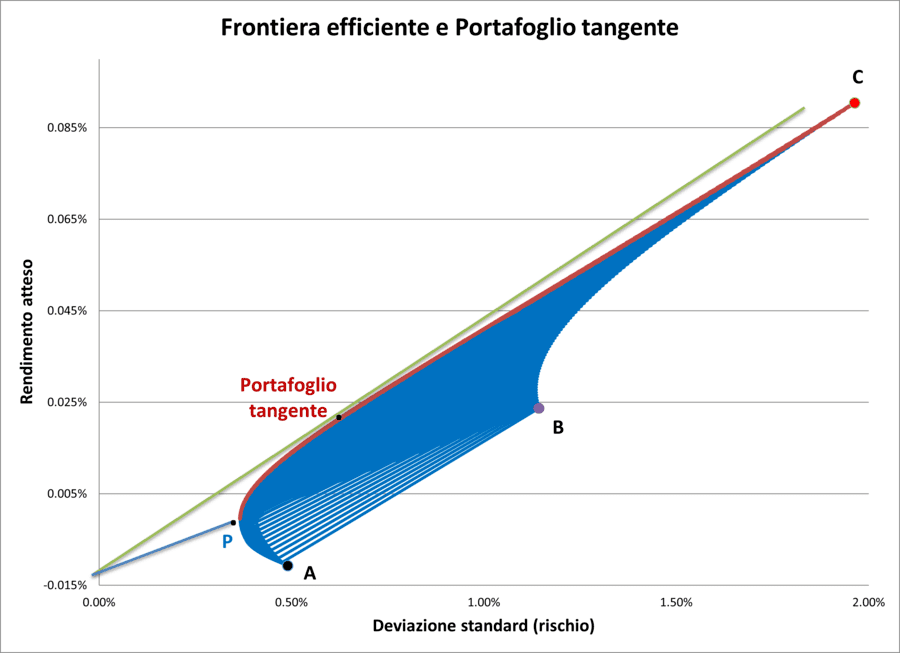
Portafoglio tangente

Il portafoglio tangente è quindi considerato il miglior portafoglio in senso assoluto, poiché massimizza il rendimento per unità di rischio.

Questo concetto è fondamentale nel Capital Asset Pricing Model (CAPM), che deriva direttamente dalla Modern Portfolio Theory.

Nel CAPM, l’insieme delle opportunità efficienti non è più rappresentato da una curva, ma dalla Capital Market Line (CML): una retta che parte dal tasso risk-free e passa per il portafoglio tangente.

Quando si introduce un investimento privo di rischio, il portafoglio tangente diventa l'unico portafoglio rischioso efficiente. In altre parole, la frontiera efficiente si riduce a una linea retta, detta appunto Capital Market Line, lungo la quale ogni combinazione di rendimento e rischio ottimale può essere ottenuta bilanciando il portafoglio tangente con il titolo privo di rischio.

Di conseguenza, la scelta dell’investitore non riguarda più quale portafoglio efficiente selezionare, ma soltanto la proporzione di capitale da destinare al portafoglio tangente e quella da riservare all’investimento privo di rischio.

La propensione individuale al rischio continua a essere determinante:

• Gli investitori più aggressivi allocano una quota maggiore del proprio capitale nel portafoglio tangente, arrivando anche a ricorrere alla leva finanziaria (x_p > 1).
• Gli investitori più prudenti si collocano invece in prossimità dell’asse delle ordinate, mantenendo gran parte del capitale nell’attività priva di rischio.

In entrambe le situazioni, il portafoglio tangente costituisce il fulcro della strategia: è l’unico portafoglio rischioso che permette di massimizzare l’efficienza rischio/rendimento e di costruire qualsiasi combinazione ottimale in funzione delle preferenze dell’investitore.

6. Estensioni e limiti della Modern Portfolio Theory

«As a model of a complex system becomes more complete, it becomes less understandable».

John M. Dutton & William H. Starbuck

La Modern Portfolio Theory ha avuto un impatto straordinario sulla finanza moderna, diventando la pietra angolare dell’asset allocation e delle strategie di gestione del rischio.

Tuttavia, come ogni modello, essa si fonda su ipotesi semplificative che ne limitano l’applicabilità diretta al mondo reale.

Tra le assunzioni più rilevanti ricordiamo:

• Distribuzione normale dei rendimenti: la MPT presuppone che i rendimenti siano distribuiti normalmente, il che implica simmetria e assenza di code pesanti. In realtà, i mercati mostrano spesso fenomeni di skewness (asimmetria) e kurtosis (code grasse), che amplificano la probabilità di eventi estremi.

• Razionalità e avversione al rischio: il modello assume che tutti gli investitori siano pienamente razionali e si muovano unicamente per massimizzare rendimento atteso e minimizzare varianza. La finanza comportamentale ha dimostrato come i bias cognitivi e le emozioni influenzino fortemente le decisioni.

• Mercati perfettamente efficienti: la teoria ipotizza assenza di costi di transazione, tasse, asimmetrie informative e restrizioni alla vendita allo scoperto. Queste condizioni si verificano raramente nella realtà.

• Stabilità delle correlazioni: la MPT assume che correlazioni e varianze possano essere stimate in modo stabile a partire dai dati storici. In realtà, queste grandezze variano nel tempo e tendono a mutare proprio nei momenti di maggiore stress di mercato, quando la diversificazione servirebbe di più.

Di conseguenza, la Modern Portfolio Theory fornisce una rappresentazione elegante e matematica del problema della scelta di portafoglio, ma la sua applicazione pratica richiede adattamenti e correzioni.

Proprio da queste esigenze sono nate diverse estensioni che hanno cercato di superarne i limiti:

• Capital Asset Pricing Model (CAPM): elaborato da Sharpe, Treynor, Lintner e Mossin, introduce il concetto di portafoglio di mercato come benchmark unico, collegando rischio sistematico e rendimento atteso attraverso il coefficiente β. Il CAPM traduce la frontiera efficiente in una relazione lineare tra rischio e rendimento, formalizzata nella Security Market Line.
• Arbitrage Pricing Theory (APT): proposta da Stephen Ross, supera l’idea di un unico fattore di rischio (il mercato) introducendo un approccio multifattoriale. Secondo l’APT, il rendimento atteso di un titolo è funzione di diversi fattori sistematici, come inflazione, tassi di interesse o variabili macroeconomiche.
• Modelli multifattoriali e Factor Investing: sviluppi più recenti hanno reso operative le intuizioni dell’APT attraverso strategie di investimento basate su fattori come dimensione (Small vs Large cap), valore (value), momentum e qualità (quality). Questi approcci hanno trovato ampia applicazione nella costruzione di ETF fattoriali e smart beta portfolios.

Oggi, la Modern Portfolio Theory continua a rappresentare il punto di partenza per la costruzione dei portafogli, ma viene affiancata da altri strumenti che ne compensano le limitazioni.

Tra questi si annoverano i modelli a volatilità condizionata, come GARCH ed EWMA, che permettono di catturare la variabilità dinamica del rischio, gli stress test e gli scenari di crisi per gestire i rischi di coda, le tecniche di robust optimization per ridurre la dipendenza dalle stime storiche e, non da ultimo, l’integrazione di considerazioni comportamentali che rendono i portafogli più coerenti con le reali preferenze degli investitori.

La Modern Portfolio Theory ha rivoluzionato la finanza introducendo un metodo razionale e quantitativo per affrontare il problema della scelta di portafoglio.

Pur con i suoi limiti, essa rimane il fondamento concettuale da cui hanno preso vita il CAPM, l’APT e il Factor Investing, oltre a ispirare le pratiche moderne di gestione del rischio.

Il messaggio di fondo rimane invariato: non conta la valutazione isolata di un titolo, ma il suo contributo al portafoglio complessivo. Questa intuizione, formulata da Markowitz oltre settant’anni fa, continua a guidare la costruzione dei portafogli ancora oggi.

---

Per chi volesse approfondire direttamente dalle parole di Harry Markowitz, è disponibile su YouTube un’interessante intervista in lingua inglese: IFA.tv - An Hour with Harry Markowitz, Father of Modern Portfolio Theory.

Il Percorso intermedio continua con l'articolo Capital Asset Pricing Model (CAPM).