Modelli GARCH univariati e multivariati
- Information
- Investimenti 17153 hits
- Prima pubblicazione: 20 Febbraio 2019
«Fragility is the quality of things that are vulnerable to volatility».
Nassim Nicholas Taleb
In questo articolo eseguiremo l'analisi di alcuni modelli GARCH univariati e multivariati in R.
Ci avvarremo di alcuni packages molto utili: tra gli altri, i più importanti sono rugarch, rmgarch e parma, tutti sviluppati e mantenuti da Alexios Ghalanos.
Partiremo con la simulazione di un modello GARCH(1,1) per poi passare all'applicazione di un ARMA-GARCH su una serie storica reale e, successivamente, su un portafoglio composto da 5 fondi, che sarà ottimizzato in modo da giungere alla definizione di un portafoglio efficiente.
Indice
- Dall’analisi del passato ai possibili scenari futuri: problemi ed implicazioni
- Stima del rendimento e della varianza attesa
- Modelli GARCH e ARMA-GARCH univariati
- Modelli GARCH multivariati
- Frontiera efficiente e portafoglio ottimale
Dall’ analisi del passato ai possibili scenari futuri: problemi ed implicazioni
I dati che abbiamo a disposizione sono le serie storiche dei prezzi di uno o più strumenti finanziari. Questi dati sono di solito costituiti da una serie di valori numerici associati a delle date. La loro frequenza, ovvero il lasso di tempo che intercorre tra un valore e l’altro, può andare dallo spazio di un minuto fino ad uno o più anni. Un esempio di serie storica è il seguente:
Data NAV
................... ............
06/06/2016 14,1610
07/06/2016 14,4210
08/06/2016 14,3690
09/06/2016 14,2600
10/06/2016 13,7930
................... ............
La particolarità di una serie storica è quella per cui i valori associati a ciascuna data (NAV nell’esempio) possono essere conosciuti con certezza soltanto a posteriori, cioè quando non sono più utilizzabili operativamente ma soltanto per scopi didattico-informativi. In altre parole, il NAV associato alla data del 06/06/2016 non poteva essere diffuso prima dell’orario di chiusura borsistica del 6 giugno 2016; nel caso dei fondi il NAV può essere reso noto il giorno seguente o addirittura due o più giorni dopo.
Per sfruttare i risultati di un’analisi a livello operativo i dati passati non sono quindi di grande aiuto. Certo, possono essere utilizzati come stima grezza di quelli futuri ma, per ottenere esiti migliori, occorrerà sostituirli con stime generate da procedure più raffinate.
Proprio dalla bontà della stima dei valori attesi (essenzialmente rendimenti e volatilità o altre misure del rischio) dipende gran parte dell’efficacia dei risultati che vogliamo ottenere. Gli errori nelle stime si ripercuotono infatti sui pesi dei fondi in portafoglio e fanno sì che, ad esempio, un ipotetico portafoglio efficiente o di varianza minima non sia più tale. Questo avviene non soltanto utilizzando direttamente i parametri calcolati su dati passati ma anche stimando in modo errato quelli futuri.
L’obiettivo sarà quindi quello di stimare con la massima precisioni i parametri necessari ai calcoli di ottimizzazione dei pesi dei fondi in portafoglio anche se, inevitabilmente, degli errori saranno presenti.
Per cercare di mitigare le conseguenze di questi errori saranno anche imposte restrizioni sui pesi di ciascun fondo e non saranno ammesse posizioni corte. Questi due vincoli vengono applicati nei Portafogli modello di Dedalo Invest. In particolare, le posizioni corte o short selling (vendite allo scoperto) sono ammesse solo per gli ETF ma non per la grande maggioranza dei fondi a gestione attiva.
Stima del rendimento e della varianza attesa
I modelli di rischio che analizzeremo si basano su alcune tesi che possono essere considerate come veri e propri dati di fatto, ovvero fatti stilizzati, ormai universalmente accettati in quanto avvalorati da innumerevoli analisi empiriche.
In particolare:
- I modelli di rischio che assumono che le perdite (rendimenti negativi) siano delle variabili casuali indipendenti e identicamente distribuite (i.i.d.) non sono adeguati a rappresentare tutti i possibili scenari configurabili sui mercati
- I modelli di rischio che si basano sulla distribuzione normale dei rendimenti sottostimano la frequenza di eventi estremi (perdite)
- I modelli di rischio dovrebbero poter contemplare diversi livelli di volatilità. In altre parole, dovrebbero sapersi adattare all’alternarsi di momenti ad alta e a bassa volatilità sui mercati
- Il modello impiegato dovrebbe essere sufficientemente flessibile da permettere di prendere in considerazione i co-movimenti dei rendimenti negativi tra i fondi presenti in portafoglio
Tutte le analisi che seguiranno sono state effettuate con l’ausilio di R. R è un ambiente di sviluppo utilizzato principalmente per l’analisi statistica di dati. R è anche un linguaggio di programmazione ed è un software disponibile in modo gratuito, essendo distribuito con la licenza GNU GPL.
Modelli GARCH e ARMA-GARCH univariati
Le serie storiche economiche e, in particolare, quelle dei rendimenti di prodotti finanziari, mostrano spesso periodi con alta o bassa concentrazione di volatilità. Per queste tipologie di serie storiche una volatilità che cambia nel tempo è molto più frequente di una volatilità costante.
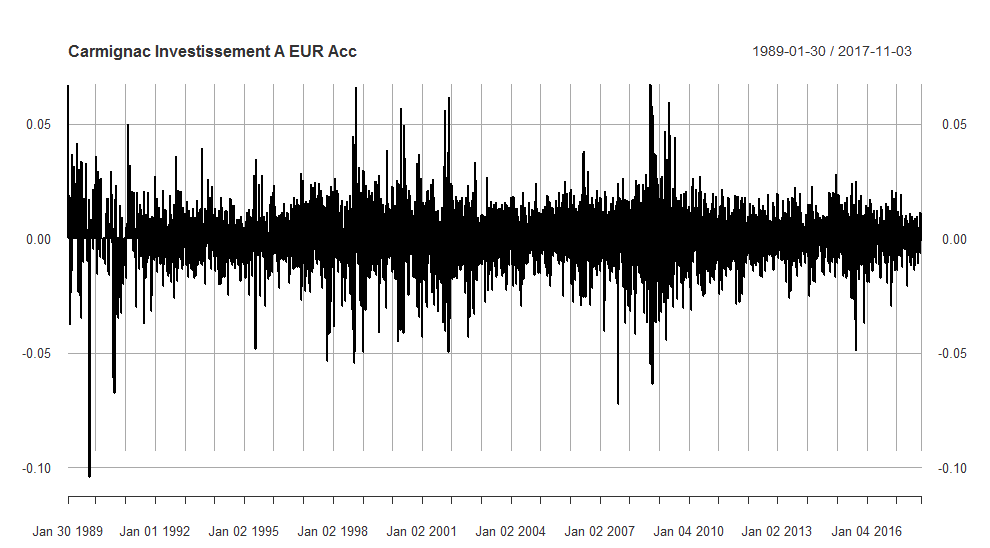
Rendimenti giornalieri del fondo Carmignac Investissement A EUR Acc
Questo grafico rappresenta i rendimenti giornalieri del fondo “Carmignac Investissement A EUR Acc” dal 26 gennaio 1989 al 3 novembre 2017. Si possono osservare dei raggruppamenti di volatilità, definiti in letteratura volatility clustering, ovvero periodi con fluttuazioni dei rendimenti elevati che si alternano a periodi con fluttuazioni più basse.
Questo fenomeno era peraltro già stato osservato da Mandelbrot nel 1963: «large changes tend to be followed by large changes - of either sign - and small changes tend to be followed by small changes».
I modelli GARCH si basano sui modelli ARCH. ARCH è l’acronimo di Auto-Regressive Conditional Heteroskedasticity ed un modello ARCH è quindi un modello Auto-Regressivo a Eteroschedasticità Condizionata. Il modello ARCH è stato presentato per la prima volta nel 1982 da Robert Franklin Engle, che vincerà il premio Nobel per l’economia nel 2003 insieme a Clive Granger proprio per lo sviluppo di "metodi di analisi delle serie storiche economiche con volatilità variabile nel tempo".
L’eteroschedasticità è una caratteristica presente in alcune variabili casuali, quali ad esempio le serie storiche dei rendimenti di strumenti finanziari, nelle quali alcuni gruppi o sottoinsiemi di variabili casuali mostrano una varianza diversa dalle altre. Quando l’eteroschedasticità è correlata serialmente, ovvero condizionata a periodi di elevata o modesta varianza, definiamo una serie storica “ad eteroschedasticità condizionata”.
Il modello ARCH più semplice è l’ARCH(1) e può essere sviluppato nel modo seguente:
Dove 
è un white noise con media uguale a zero e varianza pari a 1, e 
è pari a:
e 
sono i parametri del modello. 
è quindi un modello ARCH(1) e, sostituendo la radice quadrata della seconda equazione alla prima equazione, otteniamo:
Le condizioni richieste sono 
e 
in modo che la quantità sotto radice sia sempre positiva. Inoltre, deve essere 
affinché 
sia stazionario ed abbia una varianza finita. La varianza della serie storica è quindi una combinazione lineare della varianza degli elementi precedenti della serie stessa. Si può osservare che spesso una serie storica che è già stata adattata ad un modello lineare produce dei residui white noise. Tuttavia, analizzando il quadrato degli stessi ed il relativo correlogramma, è possibile ipotizzare la possibilità di applicare un ARCH(1).
Il modello può essere esteso a ritardi di ordine maggiore. Un processo ARCH(p) è dato da:
Se un ARCH è un processo AR applicato alla varianza invece che ai rendimenti, ci potremmo chiedere se sia possibile applicargli anche un modello MA o addirittura un ARMA: la risposta è fornita dai modelli GARCH (Generalized AutoRegressive Conditional Heteroskedastic). Un GARCH(p, q) assume la forma seguente:
Dove 
è un white noise con media uguale a zero e varianza pari a 1, e 
è pari a:
e 
sono i parametri del modello. 
è quindi un modello GARCH di ordine p e q e viene indicato con GARCH(p, q). Il termine che abbiamo aggiunto può essere paragonato a quello di un MA, infatti il valore di 
è dipendente dai precedenti 
valori. Il vantaggio del GARCH è che riesce ad approssimare modelli ARCH di ordine più elevato con l’ausilio di un numero di parametri minore.
Affinché il processo sia stazionario dovranno valere le seguenti condizioni: 
, 
per i = 1, ..., p e 
per j = 1, ..., q.
Procediamo con la simulazione di un modello GARCH e, successivamente, con l’applicazione di un modello ARMA-GARCH ad una serie storica reale. Il package di R che utilizzeremo, laddove non diversamente specificato, sarà “rugarch”.
Simulazione di un GARCH(1,1)
Proviamo a simulare in R il seguente modello GARCH(1, 1):
assegnando i seguenti valori ai parametri del modello: 
= 0,3; 
= 0,4 e 
= 0,5.
set.seed(10)a0 = 0.3a1 = 0.4b1 = 0.5w = rnorm(15000)epsilon = rep(0, 15000)sigmasquared = rep(0, 15000)for (i in 2:15000) {sigmasquared[i] = a0 + a1 * (epsilon[i-1]^2) + b1 * sigmasquared[i-1]epsilon[i] = w[i]*sqrt(sigmasquared[i])}
Un modello GARCH(1, 1) è stato generato attraverso 15.000 campionamenti effettuati sulla base dei precedenti parametri. I correlogrammi di epsilon e del quadrato di epsilon sono i seguenti:
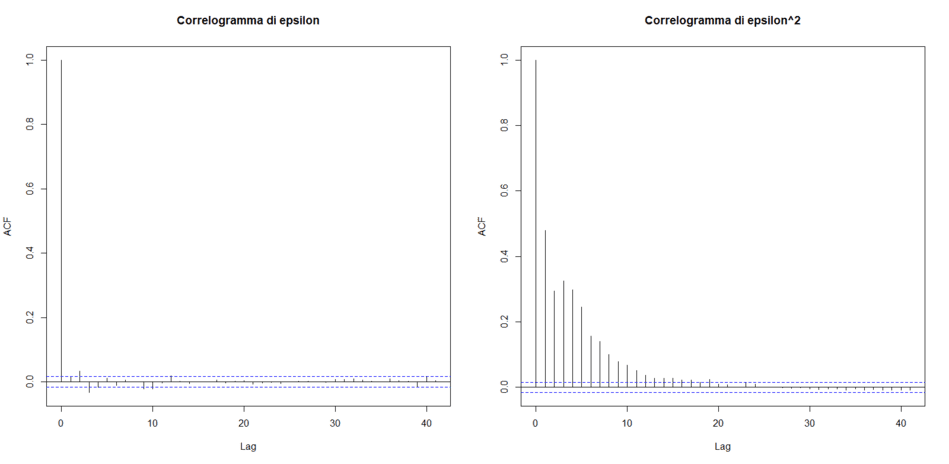
Correlogrammi di epsilon e di epsilon al quadrato
La serie storica degli epsilon è white noise ma quella degli epsilon al quadrato presenta autocorrelazioni fin oltre al decimo lag. Siamo in presenza di una serie storica a eteroschedasticità condizionata.
Possiamo ora provare a modellare un GARCH sulla serie storica simulata per vedere se si riescono a recuperare i parametri 
, 
e 
. Carichiamo in memoria il package rugarch ed assegniamo alla variabile uspec le specifiche che serviranno per l’adattamento del modello, che viene eseguito con la funzione ugarchfit.
Essa ci permette di ottenere una grande quantità di informazioni sul modello; in questo contesto ci interessano soltanto i parametri che sono stati stimati e che vengono restituiti alla variabile coefficienti:
library(rugarch)
uspec = ugarchspec(variance.model = list(model = "sGARCH", garchOrder = c(1, 1)))
fit = ugarchfit(spec = uspec, data = eps)
coefficienti = coef(fit)
show(coefficienti)
mu ar1 ma1 omega alpha1 beta1
-0.01347529 0.64393934 -0.63285958 0.28845665 0.41318712 0.50130763
corrisponde al valore stimato omega, 
ad alpha1 e 
a beta1. Come era da aspettarsi, i valori ottenuti sono molto vicini a quelli utilizzati nella costruzione della serie storica (0,3 0,4 e 0,5).
Possiamo infine utilizzare il comando confint per produrre gli intervalli di confidenza dei parametri:
intconf = confint(fit)
show(intconf)
2.5 % 97.5 %
omega 0.25909547 0.317817835
alpha1 0.38640744 0.439966806
beta1 0.47630057 0.526314695
I parametri effettivi rientrano nei rispettivi intervalli di confidenza.
Il metodo appena esplorato non è l’unico disponibile per simulare i modelli GARCH. Il package rugarch, ad esempio, ci permette di effettuare questo tipo di operazioni con estrema semplicità. A questo scopo si utilizza ugarchspec, al quale forniamo tutte le specifiche del modello GARCH che desideriamo simulare. Il risultato lo assegniamo all’oggetto specsim:
specsim = ugarchspec(variance.model = list(model = "sGARCH", garchOrder = c(1, 1)), mean.model = list(armaOrder = c(0, 0),include.mean=FALSE), distribution.model = 'norm', fixed.pars = list(omega=0.3, alpha1=0.4, beta1=0.5))
L’argomento variance.model contiene le informazioni sul modello scelto, uno standard ARMA(0,0)-GARCH(1,1) che segue la distribuzione normale. L’argomento fixed.pars ci permette di impostare i valori di omega, alpha1 e beta1 rispettivamente a 0,3, 0,4 e 0,5 (che ricordiamo corrispondere ad 
, 
e 
). A questo punto entra in gioco la funzione ugarchpath nel modo seguente:
pathsim = ugarchpath(specsim, n.sim = 15000, n.start = 1, m.sim = 10)
specsim è l’oggetto poco sopra definito; n.sim rappresenta la lunghezza della simulazione (che impostiamo a 15.000, così come avevamo fatto in precedenza); ad n.start viene associato il numero di burn-in samples, che possiamo descrivere come i campionamenti scartati prima di iniziare a registrare i dati; m.sim è infine il numero di campionamenti totali realizzati.
È palese la maggior semplicità nell’impostazione delle opzioni desiderate seguendo questo procedimento rispetto al precedente. Si stimano quindi i parametri per verificare che siano coerenti con quelli effettivi che avevamo impostato:
returnsim = pathsim@path$seriesSim
uspec = ugarchspec(variance.model = list(model = "sGARCH", garchOrder = c(1, 1)))
fitsim = ugarchfit(spec = uspec, data = returnsim)
coefficienti = coef(fitsim)
intconf = confint(fitsim)
show(coefficienti)
mu ar1 ma1 omega alpha1 beta1
0.00683009 -0.23778145 0.24921049 0.29642553 0.41197658 0.50316376
show(intconf)
2.5 % 97.5 %
omega 0.26660456 0.32624650
alpha1 0.38505132 0.43890183
beta1 0.47842605 0.52790146
A returnsim assegniamo i rendimenti simulati. uspec è l’oggetto che contiene le specifiche del modello che vogliamo stimare con ugarchspec mentre fitsim contiene l’esito della procedura di stima. In particolare, a noi interessano adesso i parametri stimati ed i loro intervalli di confidenza al 95%: omega, alpha1 e beta1.
Come era lecito attendersi, i loro valori sono molto prossimi a quelli che avevamo utilizzato per creare la simulazione ed i valori dei parametri effettivi (0,3, 0,4 e 0,5) rientrano nei rispettivi intervalli di confidenza.
Un’interessante funzione è quella che permette di stimare automaticamente i più appropriati parametri p e q in un modello GARCH(p,q). La funzione utilizzata si chiama garchAuto e, ad oggi, non sembra essere disponibile in nessun package di R ma deve essere definita direttamente dall’utente all’interno di uno script. Per la precisione, questa funzione permette di ottenere i più appropriati parametri m, n, p e q di un modello ARMA(m,n)-GARCH(p,q) ma, volendo limitarsi a p e q, è sufficiente vincolare a 0 o a 1 i parametri ARMA m ed n.
Il modello più adeguato sarà quello che presenterà il valore più basso dell’AIC (Akaike Information Criterion). Il listato della funzione garchAuto è abbastanza lungo e non viene inserito in questo contesto per motivi di spazio. La funzione, come era lecito attendersi, ci suggerisce un GARCH(1,1) come miglior modello applicato alla serie storica fornita in input.
Applicazione di un ARMA-GARCH ad una serie storica reale
Proviamo ad adattare un modello ARMA-GARCH al fondo Carmignac Investissement A EUR Acc, cui abbiamo accennato all’inizio del paragrafo. Si tratta di un fondo gestito attivamente appartenente alla categoria degli “Azionari internazionali”. Utilizziamo la serie storica dei rendimenti dal 3 gennaio 2000 al 3 novembre 2017.
Per prima cosa, identifichiamo i parametri m, n, p e q che meglio adattano un modello ARMA-GARCH ai rendimenti del Carmignac. Utilizziamo la funzione garchAuto vista in precedenza, vincolando i valori m ed n ad essere compresi tra 0 e 2 ed i valori p e q ad essere compresi tra 1 e 2. I due migliori modelli in base all’AIC sono l’ARMA(0,1)-GARCH(1,1) e l’ARMA(2,0)-GARCH(1,1). Alcuni modelli (ad esempio (1,2,1,1) non compaiono in quanto la funzione garchAuto ha restituito il messaggio “Bad model”, senza fornire ulteriori informazioni:
> autofit = garchAuto(asset_returns, cores=1, trace=TRUE)
Analyzing (0,0,1,1) with norm distribution done.Good model. AIC = -6.467257
Analyzing (0,0,1,2) with norm distribution done.Good model. AIC = -6.466786
Analyzing (0,0,2,1) with norm distribution done.Good model. AIC = -6.466804
Analyzing (0,0,2,2) with norm distribution done.Good model. AIC = -6.466773
Analyzing (0,1,1,1) with norm distribution done.Good model. AIC = -6.476503
Analyzing (0,1,1,2) with norm distribution done.Good model. AIC = -6.476104
Analyzing (0,1,2,1) with norm distribution done.Good model. AIC = -6.476332
Analyzing (0,1,2,2) with norm distribution done.Good model. AIC = -6.476258
Analyzing (0,2,1,1) with norm distribution done.Good model. AIC = -6.476521
Analyzing (0,2,1,2) with norm distribution done.Good model. AIC = -6.47611
Analyzing (0,2,2,1) with norm distribution done.Good model. AIC = -6.476328
Analyzing (0,2,2,2) with norm distribution done.Good model. AIC = -6.476242
Analyzing (1,0,1,1) with norm distribution done.Good model. AIC = -6.476459
Analyzing (1,0,1,2) with norm distribution done.Good model. AIC = -6.476058
Analyzing (1,0,2,1) with norm distribution done.Good model. AIC = -6.476289
Analyzing (1,0,2,2) with norm distribution done.Good model. AIC = -6.476221
Analyzing (1,1,1,1) with norm distribution done.Good model. AIC = -6.476086
Analyzing (1,1,1,2) with norm distribution done.Good model. AIC = -6.475687
Analyzing (1,1,2,1) with norm distribution done.Good model. AIC = -6.475916
Analyzing (1,1,2,2) with norm distribution done.Good model. AIC = -6.475844
Analyzing (2,0,1,1) with norm distribution done.Good model. AIC = -6.476547
Analyzing (2,0,1,2) with norm distribution done.Good model. AIC = -6.476135
Analyzing (2,0,2,1) with norm distribution done.Good model. AIC = -6.476348
Analyzing (2,0,2,2) with norm distribution done.Good model. AIC = -6.476259Le specifiche del modello da ottimizzare vengono definite con ugarchspec, al quale forniamo gli argomenti che vogliamo usare. Iniziamo a modellare la serie dei rendimenti con un’ARMA(2,0)-GARCH(1,1):
spec = ugarchspec(variance.model = list(model = "sGARCH", garchOrder = c(1, 1)), mean.model = list(armaOrder = c(2, 0)), distribution.model = 'norm')
I valori n, m, p e q, che abbiamo scelto essere 2, 0, 1 e 1 sono definiti nell’argomento variance.model (in garchOrder inseriamo p e q ed in armaOrder m ed n). In variance.model scegliamo poi il modello GARCH che vogliamo utilizzare: optiamo per “sGARCH”, ovvero un GARCH standard.
È possibile inoltre scegliere la distribuzione condizionata da utilizzare per i termini di errore (detti anche innovazioni): abbiamo scelto la distribuzione normale ma molte altre opzioni sono disponibili.
Per stimare il modello utilizziamo la funzione ugarchfit, alla quale forniamo come argomenti le specifiche del modello definite con ugarchspec ed inserite nell’oggetto spec, la serie storica dei rendimenti ed il solver da utilizzare:
fit = ugarchfit(spec = spec, data = asset_returns, solver = 'hybrid')L’oggetto fit è molto complesso e non può essere analizzato in dettaglio in questo contesto. Ci limitiamo a far notare che la sua struttura può essere esaminata con str(fit), ricevendo in output 2 slots chiamati fit e model che, al loro interno, contengono tutta una serie di oggetti di R come vettori, matrici o liste.
Esistono molti metodi per visualizzare specifiche informazioni contenute nell’oggetto fit quali, ad esempio, coef, confint, vcov e così via, ma si può anche semplicemente mandare in esecuzione il nome dell’oggetto (fit) ed ottenere un lungo elenco di importanti informazioni, alcune delle quali saranno qui di seguito esaminate.
Partiamo dai parametri ottimali stimati, indicati con ar1, ar2, alpha1 ed alpha2:
Optimal Parameters
------------------------------------
Estimate Std. Error t value Pr(>|t|)
mu 0.000486 0.000137 3.55162 0.000383
ar1 0.103163 0.015564 6.62840 0.000000
ar2 -0.014137 0.015460 -0.91446 0.360475
omega 0.000001 0.000001 1.66264 0.096384
alpha1 0.064912 0.009924 6.54089 0.000000
beta1 0.924944 0.010666 86.71694 0.000000
L’analisi dei t values e delle probabilità associate ci permette di concludere che i parametri stimati sono tutti significativi oltre ogni ragionevole intervallo di confidenza, con la sola eccezione di ar2. Ricordiamo che omega è 
nella formula del GARCH di inizio paragrafo.
Il risultato ottenuto ci fa comunque sospettare che il modello stimato non sia il migliore in assoluto e che, forse, uno alternativo che si limiti al solo ar1 potrebbe essere preso in considerazione. Da notare che beta1 è pari a 0,924944: questo implica una forte persistenza dei raggruppamenti di volatilità (tra l’altro beta1 è anche il paramentro più significativo).
Continuiamo l’analisi del nostro oggetto fit con la disamina dei residui: i residui standardizzati si ottengono dividendo i residui ordinari per la loro deviazione standard condizionata stimata e sono quelli che vengono utilizzati per la verifica del modello in quanto, se questo è buono, né i residui stessi né i loro quadrati devono mostrare autocorrelazione.
Vediamo l’output relativo ai residui standardizzati e ai residui standardizzati al quadrato:
Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
statistic p-value
Lag[1] 4.349e-05 0.9947
Lag[2*(p+q)+(p+q)-1][5] 1.147e+00 0.9999
Lag[4*(p+q)+(p+q)-1][9] 2.961e+00 0.8965
d.o.f=2
H0 : No serial correlation
Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
statistic p-value
Lag[1] 0.4678 0.4940
Lag[2*(p+q)+(p+q)-1][5] 1.5529 0.7269
Lag[4*(p+q)+(p+q)-1][9] 2.8819 0.7783
d.o.f=2
Per entrambi, più sono alti i p-values e minore è la probabilità di presenza di correlazione seriale (almeno per i ritardi testati). Nel nostro caso i p-values sono estremamente elevati, il che ci lascia pensare che non dovremmo riscontrare un’autocorrelazione significativa. L’analisi dei correlogrammi ce lo conferma:
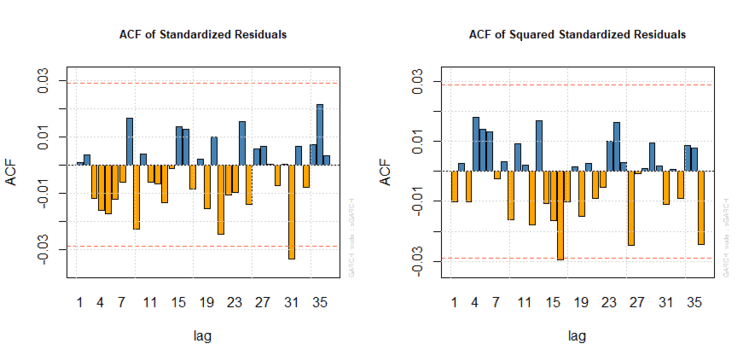
Correlogrammi dei residui di un’ARMA(2,0)-GARCH(1,1)
Le bande superiori ed inferiori dei correlogrammi fino al trentacinquesimo lag, pari a 0,03 e -0,03, vengono raggiunte complessivamente solo in un paio di occasioni.
Verifichiamo infine le informazioni contenute nella sezione “Information Criteria”:
Information Criteria
------------------------------------
Akaike -6.4757
Bayes -6.4673
Shibata -6.4757
Hannan-Quinn -6.4728
Limitiamoci al primo e forse più conosciuto criterio (Akaike Information Criterion o AIC): otteniamo un valore pari a -6,4757 che utilizzeremo come livello di confronto con altri modelli ARMA-GARCH.
È interessante notare una leggera discrepanza rispetto al valore che ci era stato restituito dalla funzione garchAuto, dove l’AIC del modello ARMA(2,0)-GARCH(1,1) era risultato pari a -6,476547. La differenza sembra minima ma i valori dell’AIC e degli altri Information Criteria sono stati normalizzati dividendo per n = 4607. Senza questo passaggio i valori dei diversi criteri non sarebbero così vicini.
Il risultato ottenuto è buono ma la speranza è quella di trovare un modello migliore. Proviamo quindi a vedere se un ARMA(0,1)-GARCH(1,1) sia in grado di migliorare le stime.
Ripetiamo la procedura seguita in precedenza (senza riportare l’analogo codice in R) e giungiamo all’analisi dell’oggetto fit, iniziando dai parametri ottimali stimati, indicati adesso con ma1, alpha1 ed alpha2.
Optimal Parameters
------------------------------------
Estimate Std. Error t value Pr(>|t|)
mu 0.000489 0.000138 3.5559 0.000377
ma1 0.102593 0.015458 6.6367 0.000000
omega 0.000001 0.000001 1.6802 0.092911
alpha1 0.065009 0.009827 6.6154 0.000000
beta1 0.924952 0.010541 87.7443 0.000000I parametri stimati sono tutti significativi oltre ogni ragionevole intervallo di confidenza. È un primo indizio che ci porta a pensare che questo modello possa essere migliore del precedente.
Continuiamo quindi l’analisi dell’oggetto fit con la disamina dei residui standardizzati e dei residui standardizzati al quadrato:
Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
statistic p-value
Lag[1] 0.0008037 0.9774
Lag[2*(p+q)+(p+q)-1][2] 0.0020852 1.0000
Lag[4*(p+q)+(p+q)-1][5] 1.2125991 0.9101
d.o.f=1
H0 : No serial correlation
Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
statistic p-value
Lag[1] 0.4803 0.4883
Lag[2*(p+q)+(p+q)-1][5] 1.5672 0.7234
Lag[4*(p+q)+(p+q)-1][9] 2.9029 0.7749
d.o.f=2
I p-values sono estremamente elevati; come nel caso precedente non dovremmo riscontrare un’autocorrelazione significativa neppure nei rispettivi correlogrammi, come dimostrato graficamente:
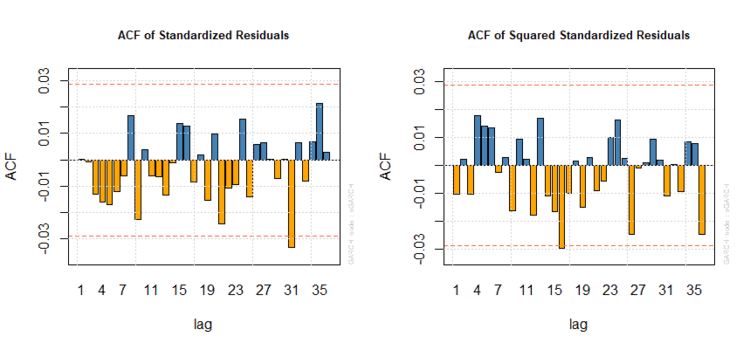
Correlogrammi dei residui di un’ARMA(0,1)-GARCH(1,1)
Per finire, diamo un’occhiata alle informazioni fornite nella sezione “Information Criteria”:
Information Criteria
------------------------------------
Akaike -6.4762
Bayes -6.4692
Shibata -6.4762
Hannan-Quinn -6.4737
L’Akaike Information Criterion è più basso di quello del modello testato in precedenza. Otteniamo pertanto un’ulteriore conferma che l’ARMA(0,1)-GARCH(1,1) è migliore dell’ARMA(2,0)-GARCH(1,1). Questa differenza è ancora più pronunciata a favore dell’ARMA(0,1)-GARCH(1,1) in base al Bayesian Information Criterion (-6,4692 contro -6,4673) e all’Hannan–Quinn Information Criterion (-6,4737 contro -6,4728). Lo Shibata Information Criterion propone invece gli stessi valori dell’AIC.
Quando avevamo specificato l’oggetto ugarchspec era stata scelta la distribuzione normale come distribuzione condizionata da utilizzare per i termini di errore.
Esistono due strumenti per verificare la bontà di questa scelta: il primo è l’Adjusted Pearson Goodness-of-Fit Test, di cui riportiamo l’output disponibile visualizzando l’oggetto fit:
Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
group statistic p-value(g-1)
1 20 87.1 1.076e-10
2 30 115.1 3.338e-12
3 40 135.0 1.687e-12
4 50 142.5 4.602e-11
Questo test confronta la distribuzione empirica dei residui standardizzati con la distribuzione teorica della normale. I p-values sono estremamente piccoli: si rifiuta perciò l’ipotesi nulla in base alla quale i residui standardizzati white noise seguono la normale.
Il secondo strumento è l’analisi grafica di due importanti grafici: il primo misura le differenze tra la distribuzione empirica e teorica dei residui standardizzati mentre il secondo è un Q-Q Plot di questi ultimi:
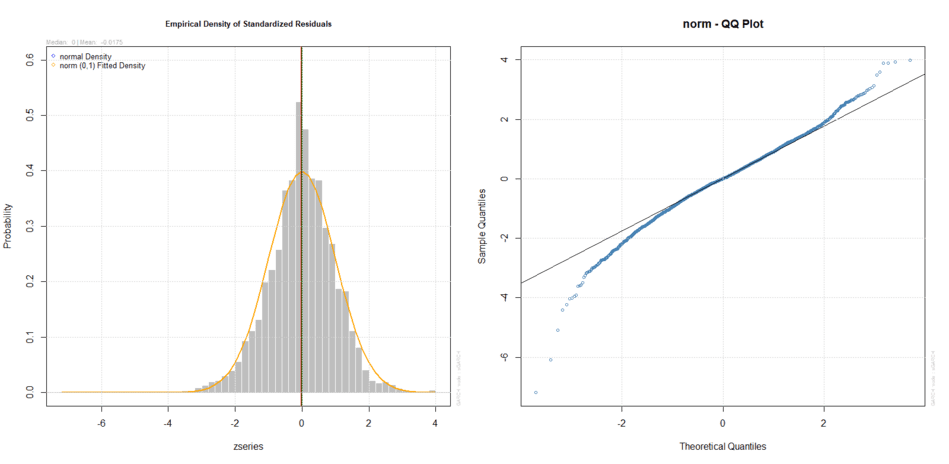
Densità empirica e teorica e Q-Q Plot dei residui standardizzati (normale)
I grafici confermano in modo evidente che i residui standardizzati non seguono la distribuzione normale. Ci aspettavamo un risultato del genere, tra l’altro già anticipato precedentemente.
Ripetiamo dunque la nostra analisi del modello ARMA(0,1)-GARCH(1,1) specificando stavolta che i residui seguono la distribuzione t di Student:
t_spec = ugarchspec(variance.model = list(model = "sGARCH", garchOrder = c(1, 1)), mean.model = list(armaOrder = c(0, 1)), distribution.model = 'std')
t_fit = ugarchfit(spec = t_spec, data = asset_returns, solver = 'hybrid')
I risultati principali dell’output dell’oggetto t_fit sono i seguenti:
Optimal Parameters
------------------------------------
Estimate Std. Error t value Pr(>|t|)
mu 0.000617 0.000132 4.6799 0.000003
ma1 0.090933 0.015063 6.0368 0.000000
omega 0.000001 0.000000 2.8960 0.003779
alpha1 0.064724 0.005871 11.0237 0.000000
beta1 0.925349 0.006387 144.8730 0.000000
shape 7.670371 0.790575 9.7023 0.000000
Information Criteria
------------------------------------
Akaike -6.5098
Bayes -6.5014
Shibata -6.5098
Hannan-Quinn -6.5069
Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
statistic p-value
Lag[1] 0.5535 0.4569
Lag[2*(p+q)+(p+q)-1][2] 0.5619 0.9477
Lag[4*(p+q)+(p+q)-1][5] 1.8417 0.7564
d.o.f=1
H0 : No serial correlation
Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
statistic p-value
Lag[1] 0.3932 0.5306
Lag[2*(p+q)+(p+q)-1][5] 1.5116 0.7370
Lag[4*(p+q)+(p+q)-1][9] 2.8371 0.7855
d.o.f=2
Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
group statistic p-value(g-1)
1 20 65.26 5.540e-07
2 30 72.76 1.260e-05
3 40 81.42 8.043e-05
4 50 99.52 2.693e-05
Come nel caso precedente i parametri sono tutti significativi e sia i residui standardizzati che quelli al quadrato non danno segni di presenza di autocorrelazione. Stavolta però il valore dell’AIC è diminuito sostanzialmente: è un indizio importante a favore del nuovo modello.
A questo riguardo notiamo che i p-values dell’Adjusted Pearson Goodness-of-Fit Test sono più grandi di diversi ordini di grandezza rispetto a prima: ciononostante non sono grandi abbastanza da permetterci di non rifiutare l’ipotesi nulla in base alla quale i residui standardizzati white noise seguono la t di Student.
Questo risultato è comunque da imputarsi alla grandezza del campione utilizzato, che rende tale esito probabile anche quando le discrepanze sono trascurabili da un punto di vista pratico.
L’analisi grafica permette di percepire le differenze in modo più immediato:
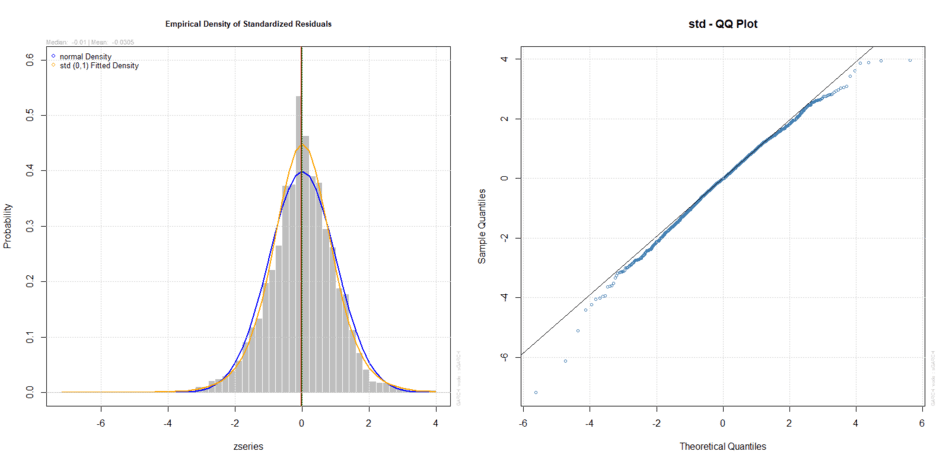
Densità empirica e teorica e Q-Q Plot dei residui standardizzati (t di Student)
Indubbiamente la t di Student non è la risposta definitiva ma il risultato è più che soddisfacente. In particolare il Q-Q Plot segue una linea decisamente più dritta rispetto a quella seguita dalla distribuzione normale e, tutto sommato, l’utilizzo della distribuzione t di Student invece della normale sembra giustificato.
Forecast
Una volta stimato il nostro modello ARMA(0,1)-GARCH(1,1) possiamo usarlo per fare previsioni. Utilizziamo l’oggetto fit come primo argomento della funzione ugarchforecast:
forc = ugarchforecast(fit, data = NULL, n.ahead = 50, n.roll = 0, out.sample = 0)
L’argomento data è NULL in quanto la serie storica dei rendimenti è già contenuta in t_fit. n.ahead è l’ampiezza della previsione mentre n.roll indica il numero di rolling forecast da generare oltre al primo.
Assegnando a n.roll un valore maggiore di 0 si dovrà fare attenzione ad inserire l’argomento out.sample nella funzione ugarchfit, attribuendogli un valore almeno pari a quello di n.roll.
I grafici dei forecast della nostra serie storica e della volatilità (Sigma) sono i seguenti:
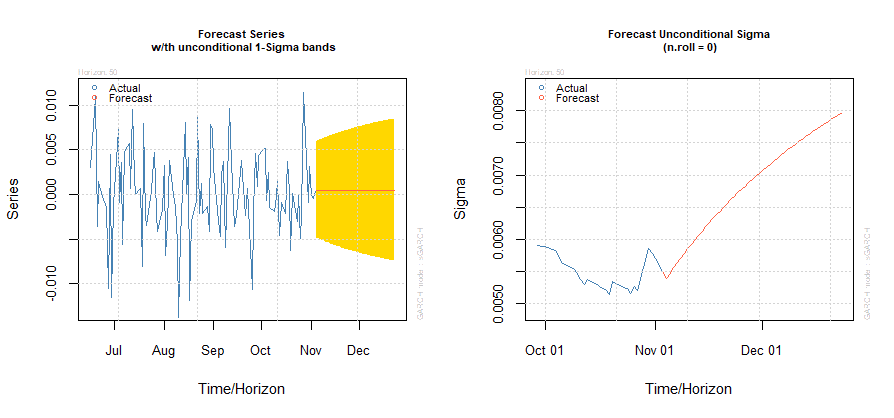
Forecast della serie storica e della volatilità
Rolling forecast
Una volta stimato il modello previsionale può essere interessante verificare la bontà delle previsioni stesse. Quello di cui abbiamo bisogno è una serie di osservazioni da comparare con i valori previsionali.
La funzione ugarchroll ci permette di effettuare una stima rolling del modello, con la quale saranno fatte previsioni del GARCH condizionato e, opzionalmente, sarà calcolato il Value at Risk (VaR, in italiano si traduce in Valore a Rischio) a prestabiliti livelli di confidenza. Il forecast è limitato ad un solo valore futuro (n.ahead = 1).
Naturalmente, una procedura coerente con la realtà deve permettere la stima del modello senza utilizzare tutte le osservazioni disponibili, onde evitare il fenomeno distorsivo che viene definito Look-Ahead Bias: una sbirciata nel futuro, ovvero l’utilizzo di dati o informazioni che non sarebbero stati disponibili al momento della stima del modello.
Per questo motivo, sarà importante definire con l’argomento forecast.length il numero di periodi (a partire dall’ultimo) o il periodo a partire dal quale la serie storica deve essere utilizzata per previsioni out of sample (impostando l’argomento n.start). Vediamo come funziona ugarchroll concretamente:
forcrolling = ugarchroll(spec = t_spec, data = asset_returns, n.ahead = 1, forecast.length = 500, n.start = NULL, refit.every = 50, refit.window = c("recursive"), window.size = NULL, solver = "hybrid", calculate.VaR = TRUE, VaR.alpha = c(0.01, 0.05), cluster = NULL, keep.coef = TRUE)
Il modello GARCH è definito dall’argomento spec e la serie storica dei rendimenti è contenuta in asset_returns. forecast.length e n.start sono già stati introdotti mentre refit.every individua il numero di periodi che devono trascorrere affinché il modello venga ri-stimato. refit.window può assumere due valori: recursive quando la nuova stima viene basata su tutti i dati disponibili fino a quel momento, moving se invece vengono utilizzati solo gli ultimi x dati (dove x viene definito con l’argomento window.size).
Infine calculate.VaR deve essere impostato su TRUE se si vuole ottenere una previsione del VaR durante la stima mentre VaR.alpha è il livello (o i livelli) di confidenza desiderati.
L’oggetto forcrolling contiene tutte le informazioni relative alla procedura effettuata.
Una prima analisi dei risultati può essere effettuando visualizzando l’oggetto stesso attraverso il comando show(forcrolling):
> show(forcrolling)
*-------------------------------------*
* GARCH Roll *
*-------------------------------------*
No.Refits : 10
Refit Horizon : 50
No.Forecasts : 500
GARCH Model : sGARCH(1,1)
Distribution : std
Forecast Density:
Mu Sigma Skew Shape Shape(GIG) Realized
2015-12-01 0.0005 0.0077 0 8.1097 0 0.0050
2015-12-02 0.0011 0.0075 0 8.1097 0 -0.0019
2015-12-03 0.0004 0.0074 0 8.1097 0 -0.0369
2015-12-04 -0.0031 0.0121 0 8.1097 0 0.0041
2015-12-07 0.0014 0.0118 0 8.1097 0 0.0007
2015-12-08 0.0006 0.0114 0 8.1097 0 -0.0022
..........................
Mu Sigma Skew Shape Shape(GIG) Realized
2017-10-27 0.0004 0.0054 0 7.7037 0 0.0114
2017-10-30 0.0016 0.0060 0 7.7037 0 -0.0009
2017-10-31 0.0004 0.0059 0 7.7037 0 0.0031
2017-11-01 0.0009 0.0058 0 7.7037 0 0.0000
2017-11-02 0.0005 0.0057 0 7.7037 0 -0.0004
2017-11-03 0.0005 0.0056 0 7.7037 0 0.0018
Il modello è stato ricalcolato 10 volte, avendo lasciato 500 osservazioni out of sample ed avendo impostato un ricalcolo ogni 50 osservazioni.
Il modello applicato è un GARCH(1,1) e la distribuzione dei rendimenti è la t di Student (std). Le “Forecast Density” sono quindi visualizzate subito dopo (prime ed ultime 6 date del periodo di 500 osservazioni che è stato stimato).
I dati che possiamo ottenere per ciascuna di esse sono Mu, Sigma, Skew, Shape, Shape (GIG) e Realized. Da notare che Shape indica i gradi di libertà, ovvero il parametro che descrive completamente la funzione t di Student. Realized individua invece il rendimento effettivo del giorno a cui è associato.
Per visualizzare l’intera serie con i 500 valori stimati si può fare nuovamente ricorso ad un’analisi più approfondita degli oggetti restituiti attraverso il comando slotNames:
> str(forcrolling@forecast)
List of 2
$ VaR :'data.frame': 500 obs. of 3 variables:
..$ alpha(1%): num [1:500] -0.0187 -0.0178 -0.0181 -0.0335 -0.0282 ...
..$ alpha(5%): num [1:500] -0.0118 -0.011 -0.0115 -0.0227 -0.0176 ...
..$ realized : num [1:500] 0.004982 -0.001907 -0.036938 0.004058 0.000685 ...
$ density:'data.frame': 500 obs. of 6 variables:
..$ Mu : num [1:500] 0.000517 0.00115 0.000376 -0.003149 0.001432 ...
..$ Sigma : num [1:500] 0.00767 0.00755 0.00739 0.01212 0.01183 ...
..$ Skew : num [1:500] 0 0 0 0 0 0 0 0 0 0 ...
..$ Shape : num [1:500] 8.11 8.11 8.11 8.11 8.11 ...
..$ Shape(GIG): num [1:500] 0 0 0 0 0 0 0 0 0 0 ...
..$ Realized : num [1:500] 0.004982 -0.001907 -0.036938 0.004058 0.000685 ...
Gli oggetti ottenuti contengono 500 valori perché 500 sono le osservazioni out of sample. Possiamo infine accedere ad ognuna di tali serie di 500 valori (ad esempio al VaR con alpha del 5%) nel modo seguente:
var_5_percento = forcrolling@forecast$VaR[,alpha(5%)"]Il vettore var_5_percento contiene quindi la serie di 500 VaR stimati con alpha pari al 5%.
L’esito della procedura di forecast può essere ulteriormente analizzato attraverso la funzione report.
Esistono due tipi di “report” ma ci concentreremo solo sul “VaR” report, ottenibile nel modo seguente:
> report(forcrolling, type = "VaR", VaR.alpha = 0.05, conf.level = 0.95)
VaR Backtest Report
===========================================
Model: sGARCH-std
Backtest Length: 500
Data:
==========================================
alpha: 5%
Expected Exceed: 25
Actual VaR Exceed: 23
Actual %: 4.6%
Unconditional Coverage (Kupiec)
Null-Hypothesis: Correct Exceedances
LR.uc Statistic: 0.173
LR.uc Critical: 3.841
LR.uc p-value: 0.678
Reject Null: NO
Conditional Coverage (Christoffersen)
Null-Hypothesis: Correct Exceedances and Independence of Failures
LR.cc Statistic: 0.177
LR.cc Critical: 5.991
LR.cc p-value: 0.915
Reject Null: NO
Scopriamo così che, rispetto al forecast prodotto, ci saremmo dovuti aspettare 25 violazioni del VaR con un alpha fissato al 5% mentre se ne sono realizzate soltanto 23 (quindi una percentuale effettiva del 4,6%).
Ci vengono poi fornite informazioni sul test non condizionato di Kupiec (non viene rifiutata l’ipotesi nulla che prevede un corretto numero di violazioni del VaR) e su quello condizionato di Christoffersen (non viene rifiutata l’ipotesi nulla che prevede un corretto numero di violazioni del VaR e l’indipendenza delle stesse).
La percentuale di violazioni delle soglie previste dal VaR poteva anche essere calcolata per mezzo delle seguenti linee di codice:
rendimenti = forcrolling@forecast$VaR[, "realized"]
superamenti = rendimenti < var_5_percento
violazioni = sum(superamenti)
violazperc = violazioni / 500
show(violazperc)
[1] 0.046
Otteniamo di nuovo il 4,6% di violazioni rispetto ad un valore atteso del 5%.
Visualizziamo infine alcuni dei risultati ottenuti con l’ausilio dei seguenti grafici:
plot(forcrolling, which = 'all')
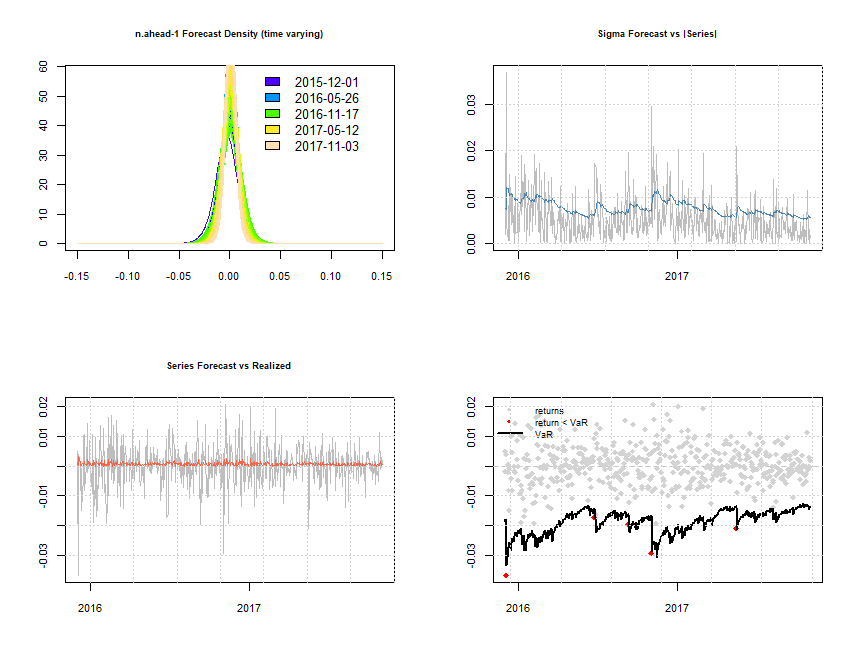
Forecast rolling
Partendo dal primo grafico in alto a sinistra e procedendo in senso orario abbiamo: la densità delle previsioni ad un periodo effettuate (i colori misurano le variazioni delle densità nel tempo); le previsioni di Sigma ed i valori effettivi; VaR/rendimenti e violazioni realizzate (alpha = 1%); previsioni dei rendimenti e valori effettivi.
Ulteriori miglioramenti al modello potrebbero essere possibili adattando altri modelli GARCH alla serie storica dei rendimenti del fondo Carmignac. Ad esempio i modelli fGARCH includono una serie di sotto-modelli tendenti a modellare la volatilità in modo asimmetrico, dando un’importanza diversa alla volatilità originata da rendimenti negativi rispetto a quella derivante da rendimenti positivi.
La modellistica GARCH univariata che si è sviluppata negli anni è imponente e il package rugarch è uno strumento molto potente per la ricerca e i backtest di molti di questi modelli.
Modelli GARCH multivariati
I modelli GARCH multivariati sono stati sviluppati a partire dalla fine degli anni ’80 del secolo scorso e rappresentano un’estensione in ambito multivariato dei modelli GARCH univariati.
La loro importanza è cresciuta costantemente ed una delle principali loro applicazioni è quella di modellare le complesse relazioni e dipendenze tra serie storiche finanziarie in un’ottica di gestione del rischio e di ottimizzazione di un portafoglio finanziario.
Due tra i principali modelli multivariati sono il GARCH DCC (a Correlazione Condizionata Dinamica) ed il Generalized Orthogonal GARCH (GO-GARCH). Il package di R che utilizzeremo si chiama rmgarch.
In linea con il paragrafo sui modelli GARCH univariati non ci soffermeremo sulle tecniche multivariate finalizzate a modellare i rendimenti attesi. Tra queste, nell’analisi dei modelli GARCH multivariati utilizzeremo principalmente il Vector AR (VAR). Il package rmgarch fa comunque uso anche di modelli a varianza costante e di AR univariati in alcune fasi della stima dei modelli.
Il VAR è stato introdotto nel 1980 da Christopher Sims (che avrebbe poi vinto il premio Nobel per l’economia nel 2011 insieme a Thomas Sargent) e rappresenta la naturale estensione dei modelli autoregressivi univariati a serie storiche multivariate.
Il VAR è un modello che cerca di catturare l’interdipendenza lineare tra molteplici serie storiche: ogni variabile è contraddistinta da un’equazione che ne spiega l’evoluzione in base ai suoi valori passati (a determinati ritardi), a quelli delle altre variabili del modello e ad un termine di errore.
I modelli GARCH multivariati presentano alcune difficoltà difficili da superare. La prima è la dimensionalità: un processo k-dimensionale comporta il calcolo di k(k+1)/2 varianze e covarianze (già con un valore di n = 10 il numero di varianze e covarianze è pari a 55), che mutano in funzione del trascorrere del tempo (per la precisione k varianze e k(k-1)/2 covarianze).
La seconda difficoltà è che tutte queste varianze e covarianze sono latenti e non vengono osservate in modo diretto. Considerando che molte parametrizzazioni dell’evoluzione delle matrici di varianza covarianza (dette anche di volatilità) utilizzano un grande numero di parametri, ci si rende subito conto che lavorare con modelli multivariati di più di 10 serie storiche diventa difficile, in alcuni casi proibitivo.
Per finire, è necessario che la matrice di volatilità multivariata di un buon processo di stima sia definita positiva in ogni momento, dato che le proprietà di questo particolare sottoinsieme di matrici sono necessarie nelle applicazioni pratiche.
Scomponiamo una serie storica multivariata di rendimenti:
Dove 
è il valore atteso condizionato di 
dato 
, ovvero la componente prevedibile di 
, che rappresenta l’informazione disponibile al tempo t-1. 
rappresenta invece l’innovazione ed è la parte non prevedibile in quanto non autocorrelata.
Possiamo scrivere 
come:
Dove 
è una sequenza di vettori casuali indipendenti e identicamente distribuiti tali che E(
) = 0 e Cov(
) = 
è la matrice radice quadrata di 
, la matrice di volatilità.
rappresenta la decomposizione spettrale di 
, dove è la matrice diagonale degli autovalori di 
e 
è la matrice ortonormale degli autovettori. Se 
non è normalmente distribuito si ipotizza che 
sia finito per tutti gli i. Una distribuzione comunemente usata per 
è la t di Student multivariata standardizzata.
La modellizzazione della volatilità consiste generalmente di due insiemi di equazioni. Il primo controlla l’evoluzione temporale della media condizionata 
mentre il secondo descrive la dipendenza dinamica della matrice di volatilità 
. È quindi consuetudine riferirsi a questi due insiemi di equazioni come equazioni della media e della volatilità.
Il modello relativo a 
è relativamente semplice dato che 
può essere un vettore costante o seguire un VAR. Più complicato è il modello che descrive 
, di cui ci occuperemo con l’ausilio dei due modelli introdotti precedentemente: GARCH DCC e GO-GARCH.
Dynamic Conditional Correlation model (DCC GARCH)
è la matrice di volatilità di 
dato 
. La matrice di correlazione condizionata è:
dove 
è la matrice diagonale delle k volatilità al tempo t modellate dal processo GARCH univariato:
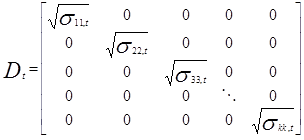
Gli elementi contenuti in 
non devono essere necessariamente stimati da processi GARCH(p,q) standard ma da qualsiasi processo GARCH con errori normalmente distribuiti e che soddisfino le condizioni di stazionarietà e non negatività. Anche il numero di lags non deve essere lo stesso per tutte le serie univariate.
Ci sono k(k-1)/2 elementi in 
. Il vantaggio dei modelli DCC è che le matrici di correlazione sono più facili da maneggiare di quelle di covarianza. L’idea dei modelli DCC è quella di dividere il processo in due fasi: la prima serve a calcolare le volatilità 
per i = 1, ..., k; la seconda, a modellare le dipendenze dinamiche delle matrici di correlazione 
.
Ipotizziamo che 
sia il vettore marginale standardizzato delle innovazioni, dove 
. 
è allora la matrice di volatilità di 
. Il modello DCC proposto da Engle è definito come:
dove 
è la matrice di covarianza non condizionata di 
, 
sono numeri reali non negativi che devono soddisfare la condizione 0 < 
+ 
< 1 e 
= diag{
} dove 
sono gli (i,i)esimi elementi di Q.
Si può notare come l’equazione di 
sia simile a quella di un processo GARCH(1,1). Q è una matrice definita positiva e 
è una matrice di normalizzazione. La dipendenza dinamica delle correlazioni è controllata dalla prima delle due equazioni del modello attraverso i due parametri 
e 
, il che rende il modello DCC molto parsimonioso: 
e 
controllano l’evoluzione nel tempo di tutte le correlazioni condizionate indipendentemente dal numero di serie storiche k coinvolte.
Questa caratteristica rappresenta nello stesso tempo un vantaggio, dato che i modelli sono relativamente semplici da stimare, e una debolezza del modello stesso, dato che è difficile giustificare da un punto di vista teorico che tutte le correlazioni si sviluppano nel medesimo modo a prescindere dalla tipologia delle serie storiche dei rendimenti coinvolte.
Riassumendo, per costruire un modello DCC la procedura è la seguente:
- Si utilizza un modello VAR(p) per stimare la media condizionata
delle serie storiche dei rendimenti mentre 
sono i residui. - Si applicano modelli di volatilità univariati, quali ad esempio i modelli GARCH, ad ogni componente della serie
. Definiamo 
le serie delle volatilità e le assumiamo essere una stima di 
, ovvero 
. - Si standardizzano le innovazioni tramite
e si adatta un modello DCC a 
.
La distribuzione condizionata di 
può essere sia una normale standard multivariata che una t di Student standard multivariata con 
gradi di libertà.
Applichiamo un modello DCC con l’ausilio del package rmgarch ad un portafoglio composto da 5 fondi: Carmignac Investissement A EUR Acc, Candriam Bonds - Euro Government Investment Grade C EUR Acc, Eurizon Bilanciato Euro Multimanager, Henderson Horizon Fund - Euroland A2 EUR Acc e Nordea-1 Global Bond BP.
L’intervallo di tempo analizzato va dall’01/01/2000 al 31/10/2017 (4.604 periodi).
spec = ugarchspec(mean.model = list(armaOrder = c(0, 0)), variance.model = list(garchOrder = c(1,1), model = 'sGARCH'), distribution.model = 'norm')
mspec = multispec(replicate(numerofondi, spec))
dcc.garch11.var.spec = dccspec(uspec = mspec, VAR = TRUE, robust = TRUE, lag = 1, lag.max = NULL, dccOrder = c(1,1), distribution = "mvnorm")
dcc.fit.var = dccfit(dcc.garch11.var.spec, data = asset_returns, solver = "solnp")
La prima fase consiste nel creare 5 modelli GARCH(1,1) univariati, uno per ogni serie storica, le cui specifiche vengono inserite nell’oggetto mspec.
La seconda fase consta nell’applicazione di un modello VAR(1) + GARCH(1,1) per le correlazioni condizionate sulla base dei parametri stimati nella prima fase. Vale la pena notare come, nel nostro caso, sia stata scelta la versione robusta del VAR.
Analizziamo quindi l’oggetto dcc.garch11.var.spec:
> show(dcc.garch11.var.spec)
*------------------------------*
* DCC GARCH Spec *
*------------------------------*
Model : DCC(1,1)
Estimation : 2-step
Distribution : mvnorm
No. Parameters : 57
No. Series : 5
Le informazioni che ci fornisce sono le seguenti: modello scelto DCC(1,1); stima effettuata in due fasi; distribuzione normale multivariata; 57 parametri stimati partendo da 5 serie storiche.
Vediamo come può essere analizzata la funzione dccfit. Innanzitutto attraverso il comando slotNames:
> slotNames(dcc.fit.var)
[1] "mfit" "model"
I due slots sono mfit e model. L’oggetto dcc.fit.var è ricchissimo di informazioni che possono essere visualizzate in vari modi. La funzione
> str(dcc.fit.var)
fornisce un output strutturato a partire dai due slots e suddiviso rispettivamente in liste di 17 e 21 elementi, di cui elenchiamo soltanto i nomi:
> names(dcc.fit.var@mfit)
[1] "coef" "matcoef" "garchnames" "dccnames"
[5] "cvar" "scores" "R" "H"
[9] "Q" "stdresid" "llh" "log.likelihoods"
[13] "timer" "convergence" "Nbar" "Qbar"
[17] "plik"
> names(dcc.fit.var@model)
[1] "modelinc" "modeldesc" "modeldata" "varmodel"
[5] "pars" "start.pars" "fixed.pars" "maxgarchOrder"
[9] "maxdccOrder" "pos.matrix" "pidx" "DCC"
[13] "varcoef" "mu" "residuals" "sigma"
[17] "mpars" "ipars" "midx" "eidx"
[21] "umodel"
Analizzare questi elementi è semplice. Ad esempio, per accedere a “modelinc” basta eseguire il seguente comando:
dcc.fit.var@model$modelinc
Esiste poi tutta una serie di funzioni per estrarre informazioni dall’oggetto dcc.fit.var: coef, likelihood, rshape, rskew, fitted, sigma, residuals, plot, infocriteria, rcor, rcov, show, nisurface. Lanciando la funzione show(dcc.fit.var) si ottiene il seguente report:
*---------------------------------*
* DCC GARCH Fit *
*---------------------------------*
Distribution : mvnorm
Model : DCC(1,1)
No. Parameters : 57
[VAR GARCH DCC UncQ] : [30+15+2+10]
No. Series : 5
No. Obs. : 4604
Log-Likelihood : 92685.29
Av.Log-Likelihood : 20.13
Optimal Parameters
-----------------------------------
Estimate Std. Error t value Pr(>|t|)
[Carmignac Investissement A EUR Acc].omega 0.000001 0.000002 0.521749 0.601845
[Carmignac Investissement A EUR Acc].alpha1 0.065816 0.028701 2.293181 0.021838
[Carmignac Investissement A EUR Acc].beta1 0.923347 0.031332 29.469598 0.000000
[Candriam Bonds - Euro Govern... .omega 0.000000 0.000001 0.024999 0.980056
[Candriam Bonds - Euro Govern... .alpha1 0.045916 0.048253 0.951562 0.341319
[Candriam Bonds - Euro Govern... .beta1 0.950166 0.041582 22.850668 0.000000
[Eurizon Bilanciato Euro Multi... .omega 0.000000 0.000019 0.005401 0.995691
[Eurizon Bilanciato Euro Multi... .alpha1 0.063795 0.509783 0.125142 0.900411
[Eurizon Bilanciato Euro Multi... .beta1 0.934891 0.438041 2.134252 0.032822
[Henderson Horizon Fund - Euro... .omega 0.000003 0.000002 1.535015 0.124780
[Henderson Horizon Fund - Euro... .alpha1 0.116459 0.023226 5.014206 0.000001
[Henderson Horizon Fund - Euro... .beta1 0.864934 0.025779 33.551410 0.000000
[Nordea-1 Global Bond BP].omega 0.000000 0.000000 0.228189 0.819499
[Nordea-1 Global Bond BP].alpha1 0.042233 0.004708 8.970124 0.000000
[Nordea-1 Global Bond BP].beta1 0.955074 0.003603 265.094234 0.000000
[Joint]dcca1 0.016951 0.000761 22.269953 0.000000
[Joint]dccb1 0.976512 0.004001 244.076891 0.000000
Information Criteria
---------------------
Akaike -40.238
Bayes -40.159
Shibata -40.238
Hannan-Quinn -40.210
Nel primo blocco troviamo alcune nuove informazioni. In particolare, scopriamo che i 57 parametri stimati dal modello sono stati nella maggior parte richiesti per la stima del VAR (30) e del GARCH univariato (15) mentre soltanto due parametri sono stati richiesti per il DCC (chiamati 
e 
nel modello teorico visto in precedenza).
Il secondo blocco di informazioni ci fornisce i valori stimati dei 15+2 parametri relativi al GARCH univariato e al DCC accompagnati dai relativi standard error, t-value e p-value. Delle 5 serie storiche stimate col GARCH univariato 3 hanno entrambi i valori alpha1 e beta1 significativi mentre 2 hanno almeno uno dei due parametri significativi. I parametri alpha1 e beta1 del DCC sono entrambi significativi. Tutto sommato il modello applicato sembra buono.
Il terzo blocco contiene i valori dei test di verifica delle informazioni di Akaike (AIC), Bayes (BIC), Shibata e Hannan-Quinn. Per finire, possiamo visualizzare alcuni interessanti risultati.
La prima serie di grafici è relativa alle medie condizionate fittate (fitted) di ciascun fondo, stimate nella prima fase del processo DCC:
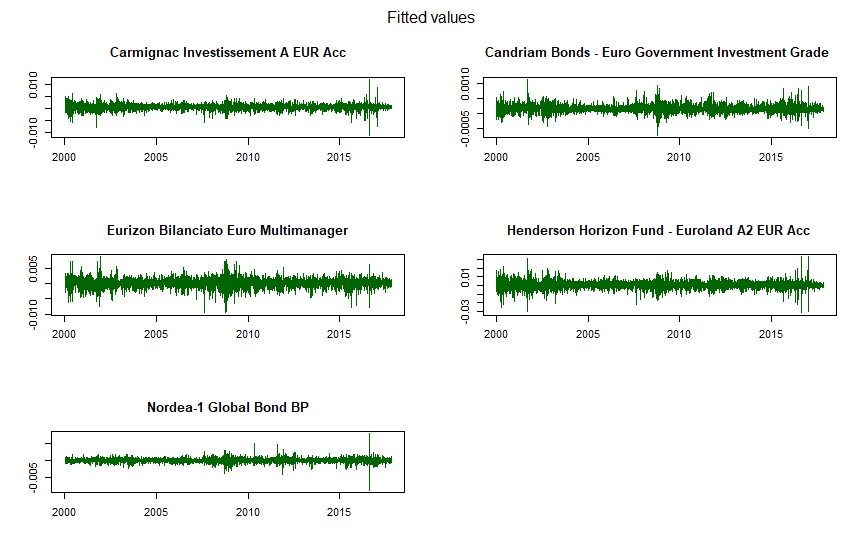
DCC GARCH: medie condizionate fittate di ciascun fondo
I grafici seguenti rappresentano invece le varianze condizionate fittate col GARCH di ciascun fondo:
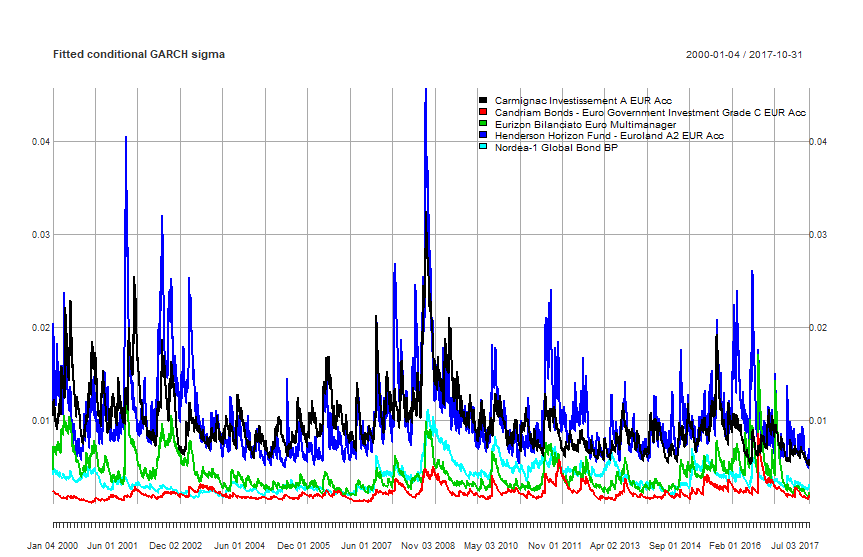
DCC GARCH: varianze condizionate fittate di ciascun fondo
Può essere interessante poi visualizzare i grafici dell’evoluzione delle covarianze e delle correlazioni condizionate tra le varie coppie di fondi in portafoglio (un portafoglio di 5 fondi implica 15 varianze/covarianze e correlazioni). Questi valori sono stati stimati nella seconda fase del processo DCC.
Per motivi di spazio mostriamo soltanto i grafici relativi alle correlazioni:
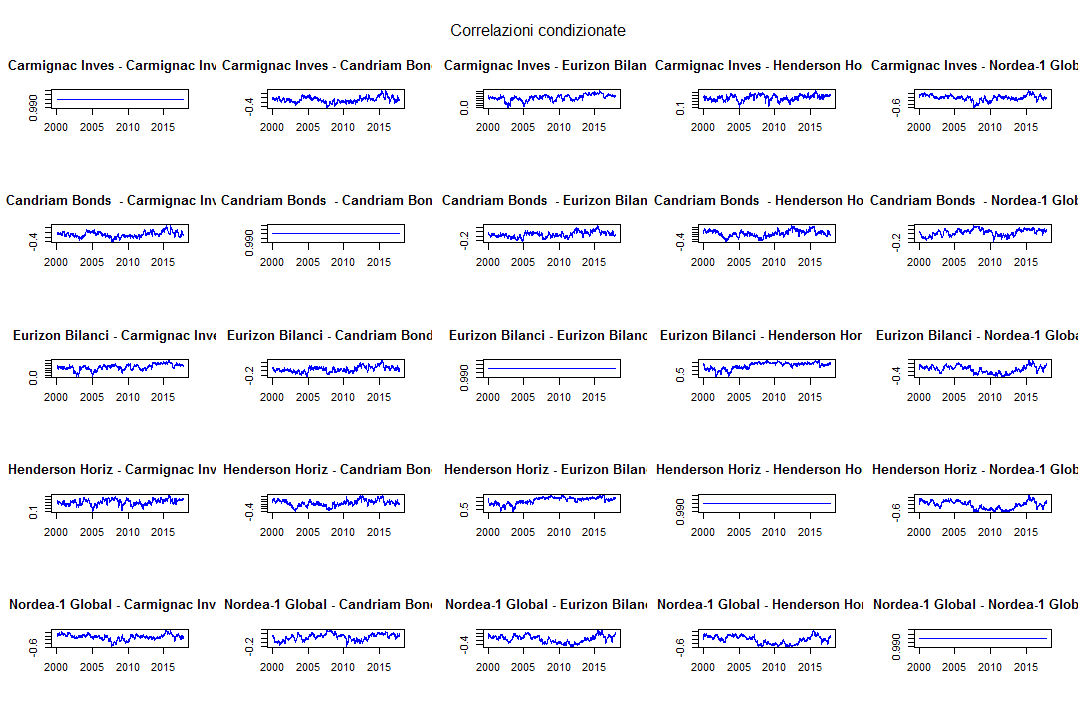
DCC GARCH: correlazioni condizionate
Come era prevedibile i grafici sulla diagonale rappresentano le autocorrelazioni di ciascun fondo ed appaiono quindi come rette orizzontali (la correlazione di una serie storica con se stessa è sempre 1).
Forecast
rmgarch ci mette a disposizione anche una funzione per produrre un forecast generato dal modello DCC-GARCH: dccforecast. Vediamone l’uso:
dcc.for = dccforecast(dcc.fit.var, n.ahead = 255, n.roll = 0)
forecastmean = fitted(dcc.for)
forecastvariancecovariance = rcov(dcc.for)
dcc.fit.var è l’oggetto creato ed analizzato precedentemente.
n.ahead è l’orizzonte temporale del forecast e n.roll rappresenta il numero di rolling forecast da creare oltre al primo.
forecastmean è un oggetto di dimensione 255 x 5 e contiene i 255 rendimenti attesi di ciascuno dei 5 fondi.
forecastvariancecovariance è invece un oggetto di dimensione 5 x 5 x 255 e contiene le 255 varianze/covarianze attese dei 5 fondi.
Calcoliamo quindi i valori medi dei 255 periodi futuri di ciascun oggetto che, essendo valori giornalieri, andiamo poi ad annualizzare:
forecastmean = t(forecastmean[255,,])
forecastvariancecovariance = apply(simplify2array(forecastvariancecovariance), c(1,2), mean)
forecastmean_yearly = forecastmean * 252
forecastvariancecovariance_yearly = forecastvariancecovariance * sqrt(252)
Queste quantità sono molto importanti in quanto saranno utilizzate successivamente per il calcolo della frontiera efficiente e del portafoglio ottimale.
Come per l’oggetto dcc.fit.var, analizziamo poi gli slots dell’oggetto dcc.for con la funzione slotNames:
> slotNames(dcc.for)
[1] "mforecast" "model"
I due slots sono mforecast e model. Visualizziamo adesso la struttura dell’oggetto dcc.for:
> str(dcc.for)
L’output è strutturato a partire dai due slots e suddiviso rispettivamente in liste di 5 e 24 elementi, di cui elenchiamo soltanto i nomi:
> names(dcc.for@mforecast)
[1] "H" "R" "Q" "Rbar" "mu"
> names(dcc.for@model)
[1] "modelinc" "modeldesc" "modeldata" "varmodel"
[5] "pars" "start.pars" "fixed.pars" "maxgarchOrder"
[9] "maxdccOrder" "pos.matrix" "pidx" "DCC"
[13] "varcoef" "mu" "residuals" "sigma"
[17] "mpars" "ipars" "midx" "eidx"
[21] "umodel" "n.roll" "n.ahead" "H"
Come sempre si può accedere ad ognuno di questi elementi, ad esempio a “modelinc”, eseguendo il seguente comando:
> dcc.for@model$modelincLe funzioni per estrarre informazioni dall’oggetto dcc.for sono: rshape, rskew, fitted, sigma, plot, rcor, rcov e show. Lanciando la funzione show(dcc.for) si ottiene il seguente output:
*---------------------------------*
* DCC GARCH Forecast *
*---------------------------------*
Distribution : mvnorm
Model : DCC(1,1)
Horizon : 255
Roll Steps : 0
-----------------------------------
0-roll forecast:
First 2 Correlation Forecasts
, , 1
[,1] [,2] [,3] [,4] [,5]
[1,] 1.000000 -0.13777 0.4847 0.52930 -0.009542
[2,] -0.137770 1.00000 0.1261 -0.09374 0.411835
[3,] 0.484705 0.12611 1.0000 0.76307 0.228155
[4,] 0.529302 -0.09374 0.7631 1.00000 0.024695
[5,] -0.009542 0.41184 0.2282 0.02470 1.000000
, , 2
[,1] [,2] [,3] [,4] [,5]
[1,] 1.000000 -0.13748 0.4842 0.52859 -0.009754
[2,] -0.137483 1.00000 0.1260 -0.09347 0.410785
[3,] 0.484217 0.12601 1.0000 0.76270 0.226062
[4,] 0.528591 -0.09347 0.7627 1.00000 0.023152
[5,] -0.009754 0.41078 0.2261 0.02315 1.000000
. . . . .
Last 2 Correlation Forecasts
, , 1
[,1] [,2] [,3] [,4] [,5]
[1,] 1.00000 -0.10219 0.42428 0.44132 -0.03577
[2,] -0.10219 1.00000 0.11322 -0.06073 0.28171
[3,] 0.42428 0.11322 1.00000 0.71672 -0.03117
[4,] 0.44132 -0.06073 0.71672 1.00000 -0.16644
[5,] -0.03577 0.28171 -0.03117 -0.16644 1.00000
, , 2
[,1] [,2] [,3] [,4] [,5]
[1,] 1.00000 -0.10213 0.42419 0.44119 -0.03581
[2,] -0.10213 1.00000 0.11320 -0.06068 0.28151
[3,] 0.42419 0.11320 1.00000 0.71665 -0.03157
[4,] 0.44119 -0.06068 0.71665 1.00000 -0.16673
[5,] -0.03581 0.28151 -0.03157 -0.16673 1.00000
Le informazioni fornite sono le seguenti: distribuzione utilizzata (normale multivariata), modello DCC applicato (1,1), orizzonte temporale del forecast (255 periodi), numero di forecast rolling creati oltre al primo (fissato a zero nella funzione dccforecast) e forecast delle prime e delle ultime 2 matrici di correlazione.
Anche in questo caso è interessante visualizzare i grafici dei principali risultati dell’analisi. Iniziamo dal forecast delle medie condizionate:
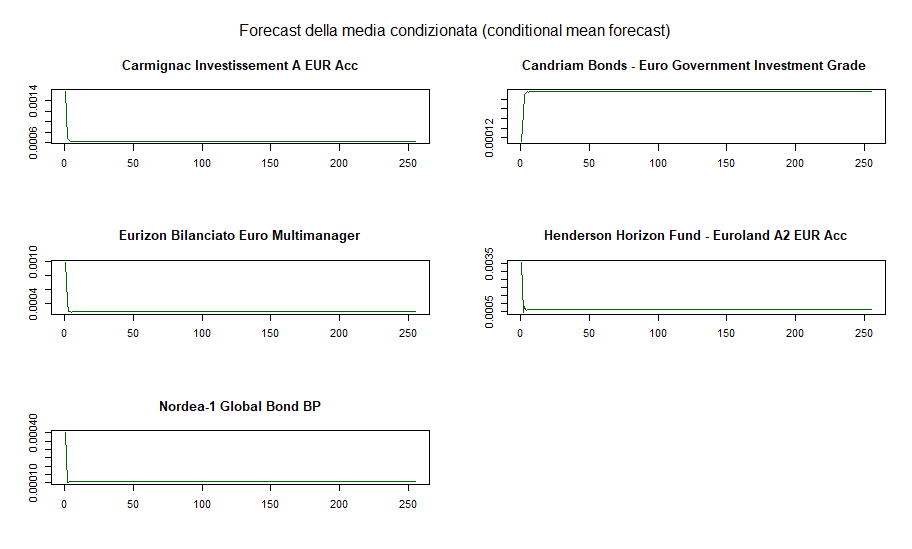
DCC GARCH: forecast della media condizionata di ciascun fondo
Le medie condizionate tendono ad assumere un valore costante molto rapidamente. Quelli che seguono sono invece gli andamenti dei forecast delle varianze condizionate:
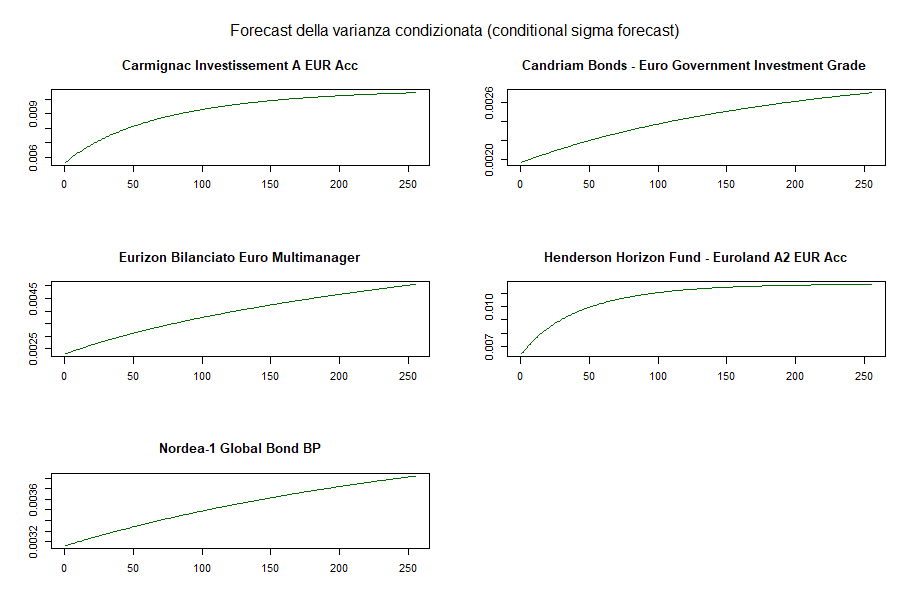
DCC GARCH: forecast della varianza condizionata di ciascun fondo
Possiamo infine vedere i grafici delle correlazioni condizionate (omettiamo anche in questo caso i grafici delle covarianze condizionate):
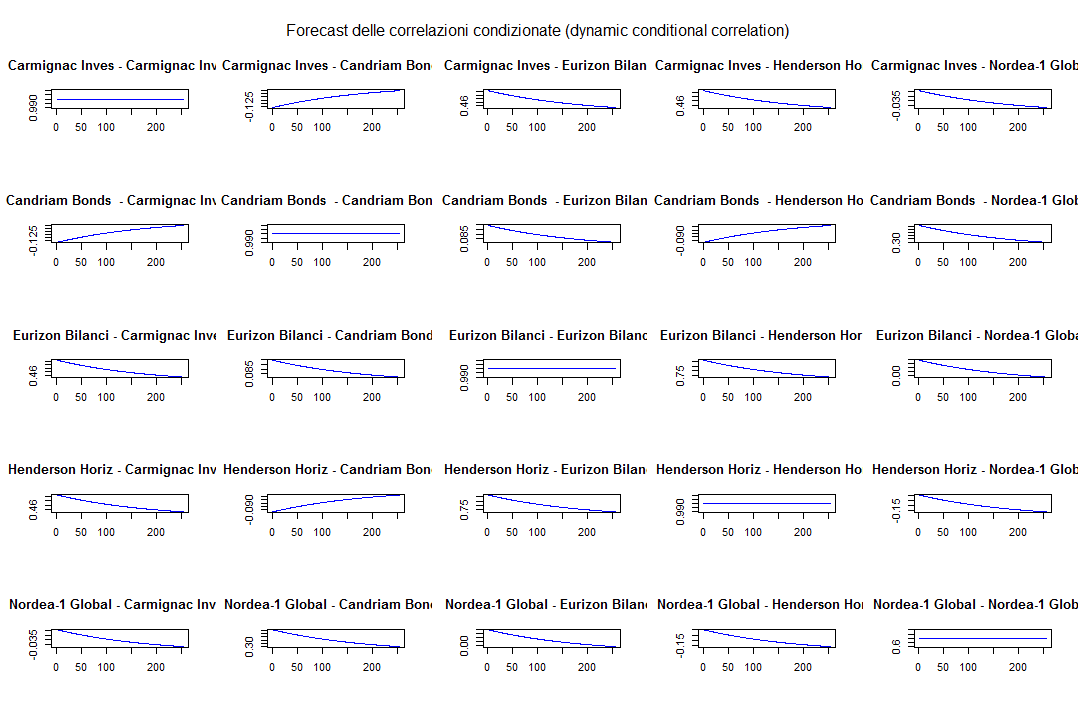
DCC GARCH: forecast delle correlazioni condizionate
Rolling forecast
Come nel caso univariato è utile verificare la bontà delle previsioni del modello multivariato scelto, comparando una serie di osservazioni con i valori previsionali.
La funzione che ci viene in aiuto si chiama dccroll. Il forecast è limitato ad un solo valore futuro (n.ahead = 1).
È bene ribadire che per la stima del modello non dovranno essere utilizzate tutte le osservazioni disponibili, onde evitare di cadere nella trappola del Look-Ahead Bias:
dcc.for.rolling = dccroll(spec = dcc.garch11.var.spec, data = asset_returns, n.ahead = 1, forecast.length = 500, n.start = NULL, refit.every = 50, refit.window = c("recursive"), window.size = NULL, solver = "solnp", cluster = NULL)
Gli argomenti della funzione sono stati già analizzati nel rolling forecast del GARCH univariato. Analizziamo quindi le informazioni principali dell’oggetto che abbiamo creato tramite il comando show(dcc.for.rolling):
*---------------------------------------------------*
* DCC GARCH Roll *
*---------------------------------------------------*
Distribution : mvnorm
Simulation Horizon : 500
Refits : 10
Window : recursive
No.Assets : 5
Optimal Parameters Across Rolls (First 2, Last 2)
---------------------------------------------------
roll-1 roll-2 roll-9 roll-10
[Carmignac Investissement A EUR Acc].omega 0.0000 0.0000 0.0000 0.0000
[Carmignac Investissement A EUR Acc].alpha1 0.0684 0.0647 0.0635 0.0634
[Carmignac Investissement A EUR Acc].beta1 0.9188 0.9224 0.9244 0.9251
[Candriam Bonds - Euro Govern... .omega 0.0000 0.0000 0.0000 0.0000
[Candriam Bonds - Euro Govern... .alpha1 0.0540 0.0506 0.0477 0.0473
[Candriam Bonds - Euro Govern... .beta1 0.9419 0.9452 0.9484 0.9489
[Eurizon Bilanciato Euro Mult... .omega 0.0000 0.0000 0.0000 0.0000
[Eurizon Bilanciato Euro Mult... .alpha1 0.0924 0.0918 0.0638 0.0656
[Eurizon Bilanciato Euro Mult... .beta1 0.8921 0.8935 0.9312 0.9301
[Henderson Horizon Fund - Eur... .omega 0.0000 0.0000 0.0000 0.0000
[Henderson Horizon Fund - Eur... .alpha1 0.0945 0.0935 0.0949 0.0943
[Henderson Horizon Fund - Eur... .beta1 0.8909 0.8927 0.8887 0.8891
[Nordea-1 Global Bond BP] .omega 0.0000 0.0000 0.0000 0.0000
[Nordea-1 Global Bond BP] .alpha1 0.0408 0.0415 0.0403 0.0410
[Nordea-1 Global Bond BP] .beta1 0.9567 0.9563 0.9568 0.9564
[Joint]dcca1 0.0151 0.0146 0.0174 0.0177
[Joint]dccb1 0.9811 0.9817 0.9764 0.9758
Il modello è stato ricalcolato 10 volte, avendo lasciato 500 osservazioni out of sample ed avendo impostato un ricalcolo ogni 50 osservazioni.
L’output ci fornisce quindi le serie dei 15 parametri ottimali stimati nella prima fase del DCC e dei 2 parametri ottimali stimati nella seconda fase del DCC; le serie visualizzate sono quelle ottenute dai primi e dagli ultimi due ricalcoli del forecast.
L’oggetto dcc.for.rolling è composto da due slots:
> slotNames(dcc.for.rolling)
[1] "mforecast" "model"
Non analizziamo in dettaglio questi due slots, che sono comunque ricchissimi di preziose informazioni, e ci limitiamo ad elencare i principali metodi che permettono di ricavare in modo immediato alcuni importanti elementi: coef restituisce i parametri stimati in tutti e 10 i rolling; fitted i forecast delle medie condizionate; sigma i forecast delle varianze condizionate; rcor i forecast delle correlazioni dinamiche condizionate e rcov i forecast delle covarianze dinamiche condizionate.
Per finire, è possibile visualizzare i forecast delle medie e delle varianze condizionate in un unico grafico:
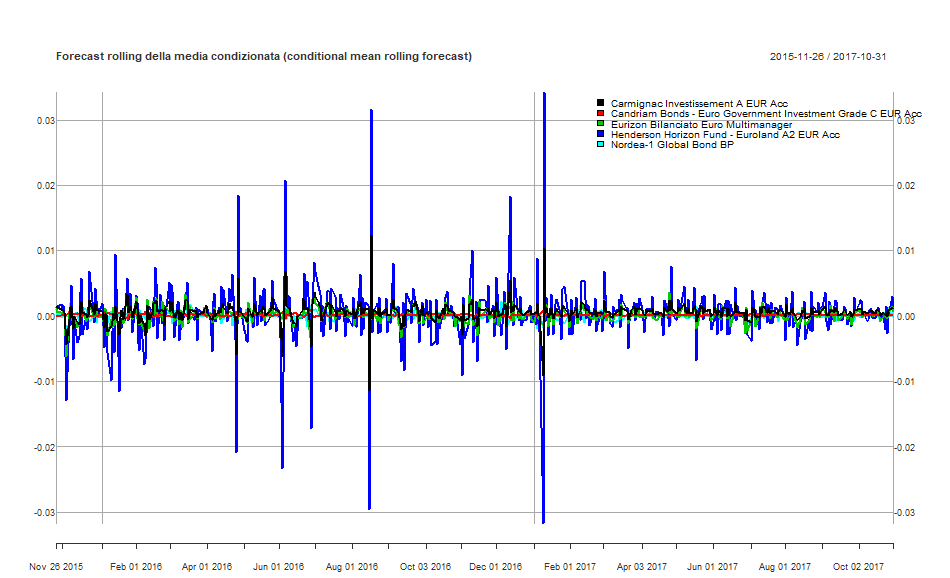
DCC GARCH: forecast rolling della media condizionata di ciascun fondo
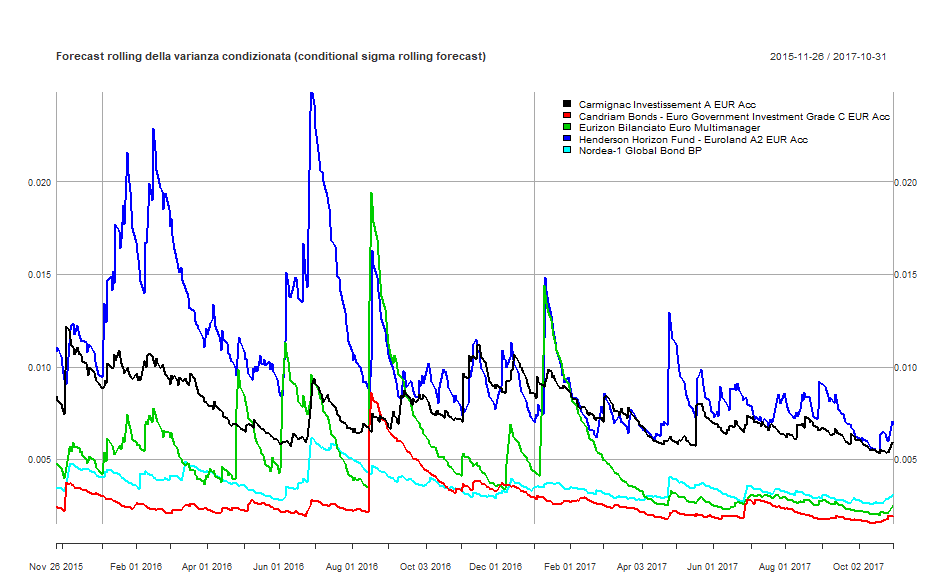
DCC GARCH: forecast rolling della varianza condizionata di ciascun fondo
Prima di passare alla stima della frontiera efficiente vale la pena menzionare un’ultima funzione fornita dal package rmgarch: fmoments.
fmoments è un metodo alternativo per generare n matrici di stima dei momenti futuri a partire dal nostro insieme di serie storiche dei rendimenti e dal modello GARCH multivariato scelto:
fmomentsparma = fmoments(spec = dcc.garch11.var.spec, Data = asset_returns, n.ahead = 1, roll = 50, solver = "solnp", fit.control = list(eval.se = FALSE))
Il primo argomento che deve essere fornito è l’insieme di specifiche che contraddistinguono il modello di stima. L’abbiamo definito in precedenza: dcc.garch11.var.spec. Questo oggetto contiene tutte le informazioni necessarie per stimare un modello multivariato DCC.
Il secondo argomento è la matrice dei rendimenti, contenuta in asset_returns. roll, se diverso da zero, permette di adattare il modello utilizzando (n - roll) periodi ottenendo in output un rolling forecast dei momenti a (n + roll) periodi. Gli altri argomenti sono stati analizzati in precedenza.
Il risultato viene assegnato all’oggetto fmomentsparma che, come sempre, si può visualizzare con il comando show(dcc.garch11.var.spec). fmomentsparma contiene i 50 rolling forecast dei momenti di ordine primo (rendimenti attesi) di ciascuno dei 5 titoli che compongono il nostro portafoglio e dei momenti di ordine secondo (varianze/covarianze attese) tra gli stessi titoli.
I momenti di ordine terzo e quarto (skewness e curtosi) sono nulli in quanto abbiamo ipotizzato una distribuzione normale multivariata.
L’estrazione di queste informazioni si può fare semplicemente utilizzando i metodi fitted e rcov:
fittedparma = fitted(fmomentsparma)
rcovparma = rcov(fmomentsparma)
Il passo successivo sarà la stima della frontiera efficiente e la determinazione del portafoglio ottimale, che saranno effettuate sulla base dei forecast dei momenti di ordine primo e secondo assegnati rispettivamente alle variabili forecastmean e forecastvariancecovariance.
Generalized Orthogonal GARCH model (GO-GARCH)
La procedura di stima in due fasi del modello GO-GARCH che utilizzeremo è stata proposta per la prima volta da Roy van Der Weide e sviluppata grazie all’utilizzo di una tecnica chiamata Independent Componenet Analysis (ICA) da Simon Broda e Marc Paolella.
Chiamiamo d il numero di titoli il cui vettore associato dei rendimenti è 
, con t 
{1, ... , }. Le innovazioni 
sono delle combinazioni lineari di d fattori 
non osservabili:
A è una matrice invertibile e costante nel tempo. Si ipotizza che i fattori non osservabili siano indipendenti e che abbiano una varianza unitaria incondizionata. Di conseguenza la matrice di covarianza incondizionata dei rendimenti è data da:
Ipotizzando un processo GARCH(1,1) per ogni fattore {
} dove 
e
con 
e 
vettore d x 1 con i k-esimi elementi pari a 1 e gli altri valori uguali a 0. La covarianza condizionata dei rendimenti diventa allora:
Dove 
.
Per mezzo di una decomposizione polare la matrice A può essere univocamente fattorizzata in una matrice definita positiva simmetrica 
e una matrice ortogonale U:
rappresenta la matrice positiva definita simmetrica radice quadrata della matrice di covarianza incondizionata 
tale che
dal momento che UU’ = I. Si deve notare che, dal momento che i fattori 
non sono osservabili, il loro ordine non è identificabile. Di conseguenza l’ordine delle colonne di U può essere scelto arbitrariamente in modo da rendere il determinante positivo e la matrice U una matrice di rotazione scomponibile come prodotto di 
matrici di rotazione elementari 
, dove ogni 
rappresenta una rotazione di angolo 
nel piano attraversato da una coppia di assi in 
. Pertanto U può essere completamente parametrizzata in termini degli angoli di Eulero. Ad esempio, nel caso di d = 2
Gli angoli 
possono essere limitati all’intervallo 
dal momento che i segni e l’ordine dei fattori non possono essere identificati.
Ipotizzando una struttura GARCH(1,1) per ogni fattore otteniamo un modello GO-GARCH contenente 
parametri.
Le difficoltà associate ad una stima congiunta di un vettore di parametri di questa dimensione rende desiderabile la scelta di una procedura in due fasi dove si stima in un primo momento la matrice A, riducendo il problema a un insieme di d problemi univariati.
d(d + 1)/2 parametri in 
possono essere stimati dalla covarianza non condizionata del campione; in particolare utilizzando lo stimatore “shrinkage” di Ledoit e Wolf che garantisce maggiore efficienza e un 
definito positivo.
I d(d – 1)/2 parametri in U, invece, vengono stimati per mezzo di un’analisi delle componenti indipendenti (ICA), i cui dettagli possono essere trovati nella monografia di Hyvärinen et al. e in un paper a supporto del package rmgarch di Ghalanos.
Applichiamo un modello GO-GARCH con l’ausilio del package rmgarch allo stesso portafoglio analizzato in precedenza e composto dai seguenti 5 fondi: Carmignac Investissement A EUR Acc, Candriam Bonds - Euro Government Investment Grade C EUR Acc, Eurizon Bilanciato Euro Multimanager, Henderson Horizon Fund - Euroland A2 EUR Acc e Nordea-1 Global Bond BP.
Come nel caso precedente l’intervallo di tempo analizzato va dall’01/01/2000 al 31/10/2017 (4.604 periodi).
ggspec = gogarchspec(mean.model = list(model = "VAR", robust = TRUE, lag = 1, lag.max = NULL, lag.criterion = "AIC", robust.control = list("gamma" = 0.25, "delta" = 0.01, "nc" = 10, "ns" = 500)), variance.model = list(model = "sGARCH", garchOrder = c(1,1)), distribution.model = "mvnorm", ica = "fastica")
I principali argomenti della funzione gogarchspec sono:
mean.model: il modello per la stima del rendimento atteso. Come nel modello DCC, anche in questo caso viene scelto il VAR nella sua versione robusta. Le altre due opzioni disponibili sono “AR” e “constant”.variance.model: modello univariato di stima della varianza dei fattori indipendenti del modello GO-GARCH.distribution.model: oltre alla distribuzione normale multivariata “mvnorm” si possono scegliere la distribuzione multivariata Normale Inversa Gaussiana (“manig”) o la GHYP di Schmidt (“magh”).ica: algoritmo utilizzato per l’estrazione delle componenti indipendenti. Le opzioni disponibili sono “fastica” e “radical”.
Analizziamo l’oggetto gg.spec:
> show(ggspec)
*------------------------------*
* GO-GARCH Spec *
*------------------------------*
Mean Model : VAR
(Lag) : 1
(Robust) : TRUE
GARCH Model : sGARCH
Distribution : mvnorm
ICA Method : fastica
Vengono fornite le seguenti informazioni: modello scelto per i rendimenti attesi VAR (1 lag, versione robusta); standard GARCH come modello univariato scelto per modellare la volatilità; distribuzione normale multivariata; fastica algoritmo utilizzato per l’estrazione delle componenti indipendenti.
Per stimare il modello utilizziamo la funzione gogarchfit, alla quale forniamo come argomenti le specifiche del modello definite con gogarchspec ed inserite nell’oggetto ggspec, la serie storica dei rendimenti, il solver da utilizzare e un ulteriore argomento (fit.control) che impone il vincolo di stazionarietà della varianza durante l’ottimizzazione:
gogarch.fit.var = gogarchfit(ggspec, data = asset_returns, solver = "solnp", fit.control = list(stationarity = 1))
Analogamente a quanto visto nel modello DCC, anche l’oggetto gogarch.fit.var può essere analizzato con le funzioni slotNames e str e si possono utilizzare numerosi metodi quali as.matrix, coef, convolution, fitted, residuals, likelihood, nisurface, gportmoments, rcoskew, rcokurt, rcov, rcor, betacovar, betacoskew, betacokurt e show per estrarne specifiche informazioni.
Forecast
La funzione per produrre un forecast generato dal modello GO-GARCH è gogarchforecast:
gg.for = gogarchforecast(gogarch.fit.var, n.ahead = 255, n.roll = 0)
Gli argomenti sono del tutto analoghi a quelli del precedente modello DCC e non verranno quindi nuovamente analizzati.
Estraiamo ed annualizziamo i rendimenti attesi e i forecast delle varianze/covarianze che saranno utilizzati successivamente per ottenere la frontiera efficiente ed il portafoglio ottimale (dopo averli trasformati in matrici 1xn e nxn):
forecastmean = fitted(gg.for)
forecastvariancecovariance = rcov(gg.for)
forecastmean = t(forecastmean[255,,])
forecastvariancecovariance = ap-ply(simplify2array(forecastvariancecovariance), c(1,2), mean)
forecastmean_yearly = forecastmean * 252
forecastvariancecovariance_yearly = forecastvariancecovariance * sqrt(252)
Rolling forecast
Ci interessa adesso verificare la bontà delle previsioni del modello GO-GARCH comparando una serie di osservazioni con i valori previsionali per mezzo della funzione gogarchroll.
Gli argomenti sono del tutto analoghi a quelli del modello DCC, a cui rimandiamo per maggiori informazioni:
gg.for.rolling = gogarchroll(spec = ggspec, data = asset_returns, n.ahead = 1, forecast.length = 500, n.start = NULL, refit.every = 50, refit.window = c("recursive"), window.size = NULL, solver = "solnp", cluster = NULL)
show(gg.for.rolling)
*---------------------------------------------------*
* GO-GARCH Roll *
*---------------------------------------------------*
Distribution : mvnorm
Simulation Horizon : 500
Refits : 10
Window : recursive
No.Assets : 5
Visualizziamo quindi i forecast delle medie e delle varianze condizionate:
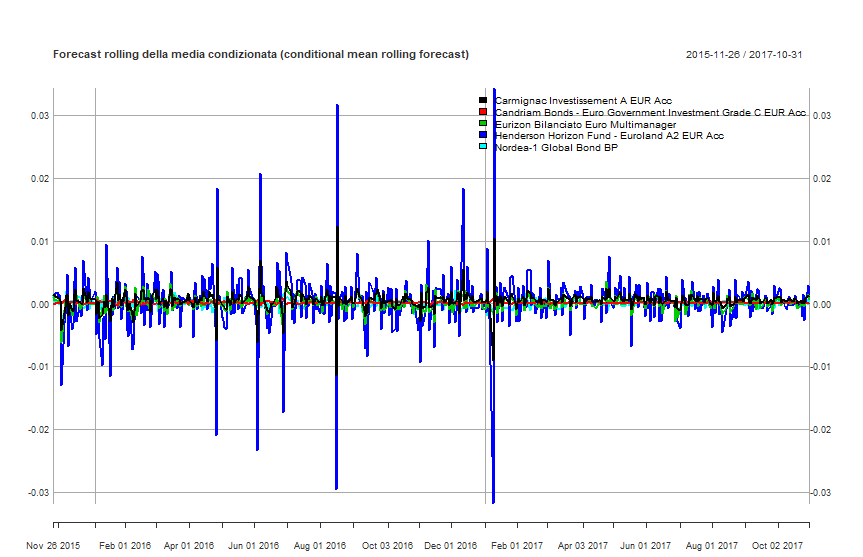
GO-GARCH: forecast rolling della media condizionata di ciascun fondo
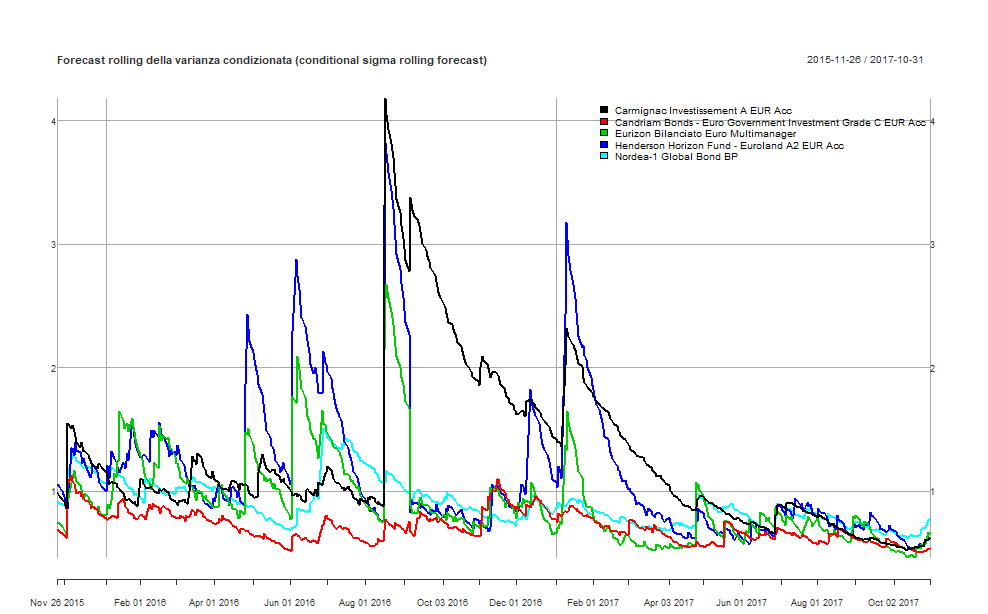
GO-GARCH: forecast rolling della varianza condizionata di ciascun fondo
Ai fini di ottenere la frontiera efficiente ed il portafoglio ottimale si può utilizzare anche la funzione fmoments, disponibile anche per il modello GO-GARCH, che permette l’estrazione dei momenti di ordine primo e secondo con i metodi fitted e rcov:
gogarchfmomentsparma = fmoments(spec = ggspec, Data = asset_returns, n.ahead = 1, roll = 50, solver = "solnp", fit.control = list(eval.se = FALSE))
ggfittedparma = fitted(gogarchfmomentsparma)
ggrcovparma = rcov(gogarchfmomentsparma)
Le stime dei rendimenti attesi e delle varianze/covarianze attese saranno fondamentali per la successiva stima della frontiera efficiente e determinazione del portafoglio ottimale anche se, a questo fine, utilizzeremo le quantità precedentemente calcolate ed assegnate alle variabili forecastmean_yearly e forecastvariancecovariance_yearly.
Al termine di questa fase confronteremo le frontiere efficienti generate dai modelli DCC GARCH e GO-GARCH.
Frontiera efficiente e portafoglio ottimale
Le informazioni ottenute ci permettono di poter effettuare una prima stima della frontiera efficiente. L’obiettivo è ovviamente quello di ricavarne il portafoglio ottimale. Vale la pena ricordare ancora una volta che la stima della frontiera efficiente viene effettuata sulla base dei rendimenti attesi e delle matrici di varianza/covarianza stimate dinamicamente dal modello GARCH multivariato scelto.
Il package di R che utilizzeremo si chiama parma (Portfolio Allocation and Risk Management Applications) e contiene una serie di metodi e modelli unici nel loro genere per l’allocazione ottimale di capitali nei portafogli finanziari.
La prima frontiera efficiente ed il primo portafoglio ottimale che otterremo si baseranno sui momenti generati dal modello multivariato DCC GARCH. La stessa procedura sarà poi replicata con lo scopo, stavolta, di ottenere la frontiera efficiente ed il portafoglio ottimale originati dai momenti prodotti dal GO-GARCH.
Il punto di partenza è la definizione di un oggetto per mezzo della funzione parmaspec con tutte le specifiche del modello e del metodo di ottimizzazione:
parmaspecmult = parmaspec(S = forecastvariancecovariance_yearly, forecast =
forecastmean_yearly, risk = "EV", riskType = "minrisk", target = mean(forecastmean_yearly), targetType = 'equality', LB = rep(0.02, 5), UB = rep(0.4, 5), budget = 1, asset.names = nomifondi)
Gli argomenti sono i seguenti:
S= matrici della varianza/covarianza attesaforecast= matrice dei rendimenti attesirisk= misura di rischio utilizzata nella procedura di ottimizzazione. Nel caso in esame si tratta dell’EV (Mean Variance)riskType= tipo di ottimizzazione da usare: si può scegliere se minimizzare il rischio dati determinati vincoli (minrisk), se ottimizzare il rapporto rischio/rendimento (optimal) o se massimizzare il rendimento nel rispetto di un limite massimo di rischio e di eventuali altri vincoli (maxreward)target= il rendimento a cui miriamo, argomento richiesto quandoriskType = minrisk, come nel nostro casotargetType= specificazione del target come rigida uguaglianza o disuguaglianzaLB= peso minimo di ciascun titolo in portafoglioUB= peso massimo di ciascun titolo in portafoglioBudget= vincolo d’investimento. Se uguale ad 1 significa pieno investimento
La struttura completa dell’oggetto parmaspecmult può essere visualizzata con il comando str(parmaspecmult) mentre con show(parmaspecmult) si ottiene un output riassuntivo delle principali specifiche che lo caratterizzano:
+---------------------------------+
| PARMA Specification |
+---------------------------------+
No.Assets : 5
Problem : QP,SOCP
Input : Covariance
Risk Measure : EV
Objective : minrisk
Come sappiamo il nostro portafoglio è composto da 5 fondi (No.Assets).
Problem individua le possibili modalità di risoluzione del nostro problema: QP (Quadratic), o SOCP (Second Order Cone Programming).
Differenti tipologie di problemi possono essere affrontate con altre modalità di risoluzione quali LP (Linear), NLP (Non-Linear), GNLP (Global Non-Linear), MILP (Mixed Integer Linear), MIQP (Mixed Integer Quadratic) e MINLP (Mixed Integer Non-Linear).
Abbiamo inserito in input la matrice di varianza/covarianza (input: Covariance); la misura di rischio scelta è l’EV e l’obiettivo, identificato con l’argomento riskType, è quello di minimizzare il rischio.
Una volta definito, il problema deve essere risolto. parmasolve è la funzione che ci permette di raggiungere questo risultato, ottenendo i pesi ottimali del portafoglio.
Gli argomenti di questa funzione sono essenzialmente l’oggetto con le specifiche del modello che abbiamo appena creato e il tipo di modalità di risoluzione del problema.
Creiamo due oggetti parmasolve, uno generato con la modalità QP ed uno con quella SOCP:
parmasolveQP = parmasolve(parmaspecmult, type = 'QP')
parmasolveSOCP = parmasolve(parmaspecmult, type = 'SOCP')
Come sempre si possono visualizzare la struttura degli oggetti creati con il comando str() o le informazioni principali in essi contenute con il comando show():
+---------------------------------+
| PARMA Portfolio |
+---------------------------------+
No.Assets : 5
Problem : QP
Risk Measure : EV
Objective : minrisk
Risk : 0.000224
Reward : 0.0886452
Optimal_Weights
1 0.4000
2 0.2858
3 0.1414
4 0.1028
5 0.0700
Le nuove informazioni sono il rischio atteso, il rendimento atteso ed i pesi ottimali.
Il listato seguente ci permette di ricavare le stesse informazioni e di visualizzarle, insieme al rendimento e al rischio atteso, in un modo più comprensibile:
Peso = cbind(parmasolveQP@solution$weights, parmasolveSOCP@solution$weights)
Rendimento_atteso = cbind(parmasolveQP@solution$reward, parmasol-veSOCP@solution$reward)
Rischio_atteso = cbind(parmasolveQP@solution$risk, parmasolveSOCP@solution$risk)
Nomi_fondi = parmasolveQP@model$asset.names
outputtitle = cbind('','QP', 'SOCP')
outputrendimento = cbind('Rendimento atteso', Rendimento_atteso)
outputrischio = cbind('Rischio atteso', Rischio_atteso)
outputfinale = rbind(outputtitle, outputrendimento, outputrischio)
show(outputweights)
Fondo Peso QP Peso SOCP
1 Carmignac Investissement A EUR Acc 0.2858282 0.28564717
2 Candriam Bonds - Euro Government Investment Grade C EUR Acc 0.4000000 0.39999998
3 Eurizon Bilanciato Euro Multimanager 0.1413750 0.14127776
4 Henderson Horizon Fund - Euroland A2 EUR Acc 0.1027887 0.10300599
5 Nordea-1 Global Bond BP 0.0700081 0.07007909
> show(outputfinale)
QP SOCP
Rendimento atteso 0.0886452 0.0886443
Rischio atteso 0.0002240 0.0002240
Innanzitutto, si osserva che i risultati ottenuti con le due diverse modalità di risoluzione del problema sono molto simili. In questo caso la scelta dell’uno o dell’altro metodo dovrà quindi basarsi esclusivamente sulla velocità di calcolo.
Il portafoglio ottimale è dunque quello formato dai 5 fondi pesati nel modo suggerito nella precedente tabella.
È importante osservare che il rendimento ed il rischio atteso sono stimati in base ad un orizzonte temporale impostato a 255 periodi, come specificato nell’oggetto dcc.for dal quale abbiamo ricavato i forecast dei rendimenti attesi e delle matrici di varianza/covarianza stimate, poi annualizzate.
Per finire, si può notare che nessun fondo è pesato meno del 2% o più del 40%, percentuali che rappresentano i limiti minimo e massimo dei pesi di ciascun fondo, stabiliti dai vincoli specificati negli argomenti LB e UB della funzione parmaspec.
Il package parma dispone di un’altra funzione molto interessante: parmafrontier. Essa permette di ricavare la frontiera efficiente a partire da un oggetto di specifiche come quello che abbiamo poco sopra creato.
Naturalmente, se i calcoli sono corretti, la frontiera efficiente dovrà contenere il portafoglio ottimale appena ottenuto:
Frontiera_efficiente_QP = parmafrontier(parmaspecmultfrontier, n.points = 100, type = 'QP')
Frontiera_efficiente_SOCP = parmafrontier(parmaspecmultfrontier, n.points = 100, type = 'SOCP')
Creiamo due oggetti contenenti 100 punti appartenenti alla frontiera efficiente, uno ottenuto col metodo di risoluzione QP ed uno con il SOCP. Più in dettaglio, gli oggetti appena creati sono delle matrici di 100 righe e 7 colonne. In 5 di queste colonne sono presenti i pesi di ciascun fondo e nelle rimanenti 2 il rischio e il rendimento atteso.
Visualizziamo quindi in un grafico le due frontieri efficienti ed il punto dove si situa il portafoglio ottimale, ricavato per mezzo dei metodi parmarisk e parmareward.
Il grafico e le linee di codice che lo generano sono le seguenti:
risk_QP = Frontiera_efficiente_QP[, 'EV']
return_QP = Frontiera_efficiente_QP[, 'reward']
risk_SOCP = Frontiera_efficiente_SOCP[, 'EV']
return_SOCP = Frontiera_efficiente_SOCP[, 'reward']
plot(risk_QP, return_QP, type = 'p', col = 'steelblue', xlab = 'Rischio atteso (EV)', ylab = 'Rendimento atteso', main = 'Frontiera efficiente', ylim=c(0.035, 0.15), xlim=c(0,0.001))
lines(risk_SOCP, return_SOCP, col = 'tomato3')
points(parmarisk(parmasolveQP), parmareward(parmasolveQP), col = 'yellow', pch = 6, lwd = 3)
legend('topleft', c('Frontiera efficiente QP', 'Frontiera efficiente SOCP', paste('Portafoglio ottimale parmasolve (', round(parmarisk(parmasolveQP)/parmareward(parmasolveQP), 4), ')', sep = '')), col = c('steelblue', 'tomato1', 'yellow'), pch = c(1, -1, 4, 6), lwd = c(1, 1, 3, 3),
lty = c(0, 1, 0, 0), bty = 'n', cex = 0.9)
grid()
mtext(paste('parma package', sep = ''), side = 4, adj = 0, padj = -0.6, col = 'grey50', cex = 0.7)
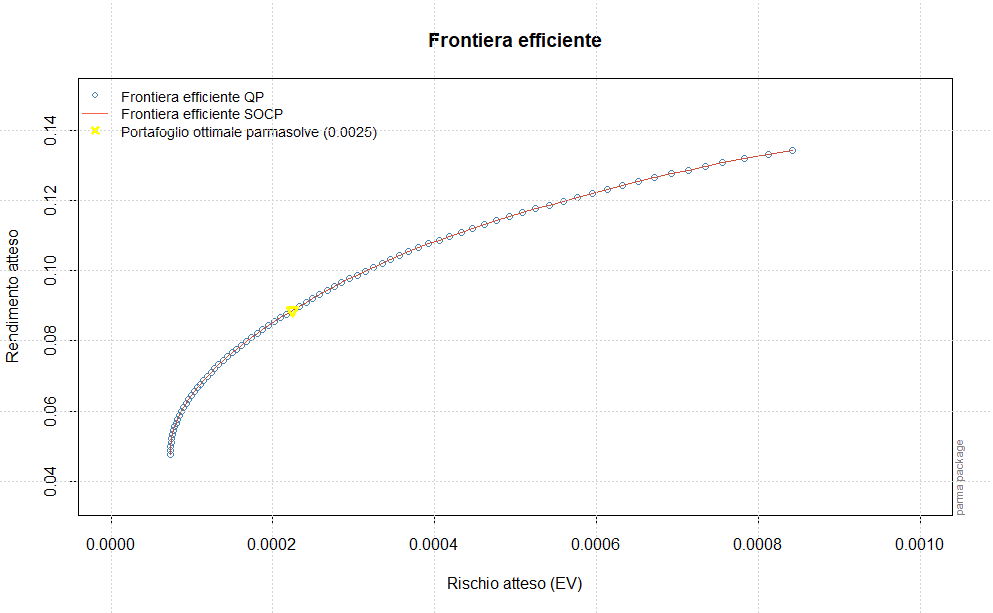
DCC GARCH: Frontiera efficiente vincolata
Le due frontiere efficienti e i due portafogli ottimali coincidono.
Il grafico dimostra come la risoluzione del problema di ottimizzazione tramite le modalità QP e SOCP sia efficiente e permetta di ottenere in modo rapido e diretto il portafoglio ottimale, senza doverlo ricavare dalla frontiera efficiente.
Si può osservare come la frontiera efficiente sia composta da meno dei 100 punti richiesti dalla funzione parmasolve. Il motivo è da ricercarsi nel fatto che i calcoli per ottenere la frontiera sono terminati prima del raggiungimento dei 100 punti previsti (per la precisione 79).
Avendo impostato un vincolo sui pesi di ciascun fondo (2% - 40%) il solver implementato nel package parma ha estrapolato una frontiera composta da meno punti rispetto a quelli richiesti. In generale non bisogna dimenticarci che più un problema viene vincolato e più le sue soluzioni sono limitate.
A riprova di quanto affermato possiamo risolvere lo stesso problema ma, questa volta, senza vincoli sui pesi di ciascun fondo:
show(outputweights_nv)
Fondo Peso QP Peso SOCP
1 Carmignac Investissement A EUR Acc 0.2856105 0.28523695
2 Candriam Bonds - Euro Government Investment Grade C EUR Acc 0.5870860 0.58707724
3 Eurizon Bilanciato Euro Multimanager 0.0000000 0.00000023
4 Henderson Horizon Fund - Euroland A2 EUR Acc 0.1273031 0.12769545
5 Nordea-1 Global Bond BP 0.0000000 0.00000010
> show(outputfinale_nv)
QP SOCP
Rendimento atteso 0.0886452 0.0886443
Rischio atteso 0.0002108 0.0002108
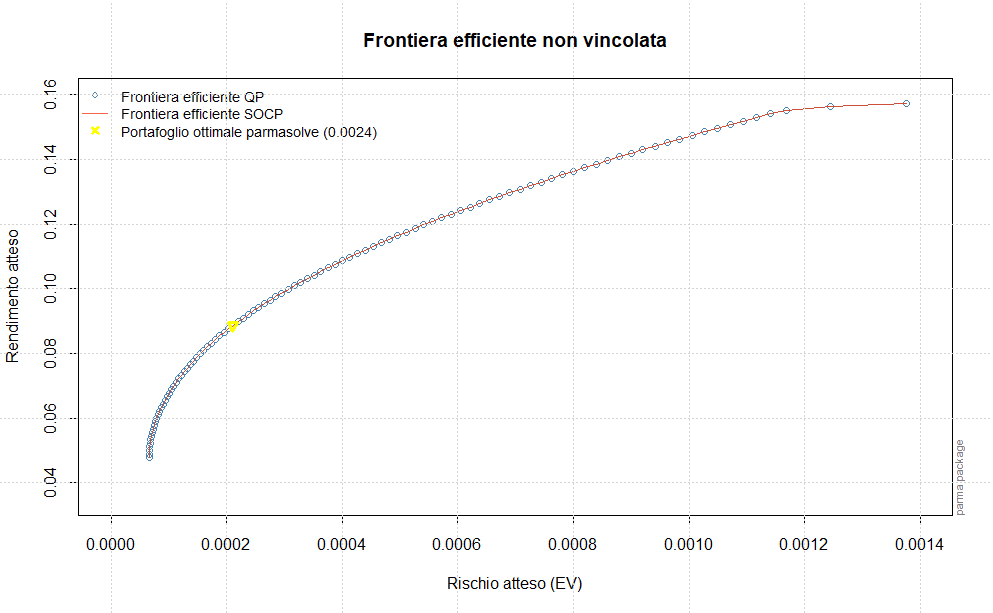
DCC GARCH: Frontiera efficiente vincolata
In questo caso il solver è riuscito ad estrapolare tutti i 100 punti richiesti. Disponendo di più opzioni (assenza di vincoli) è lecito aspettarsi che questa frontiera efficiente domini quella vincolata e che il portafoglio ottimale non vincolato sia preferibile a quello vincolato.
Unendo i due precedenti grafici queste differenze sono più evidenti:
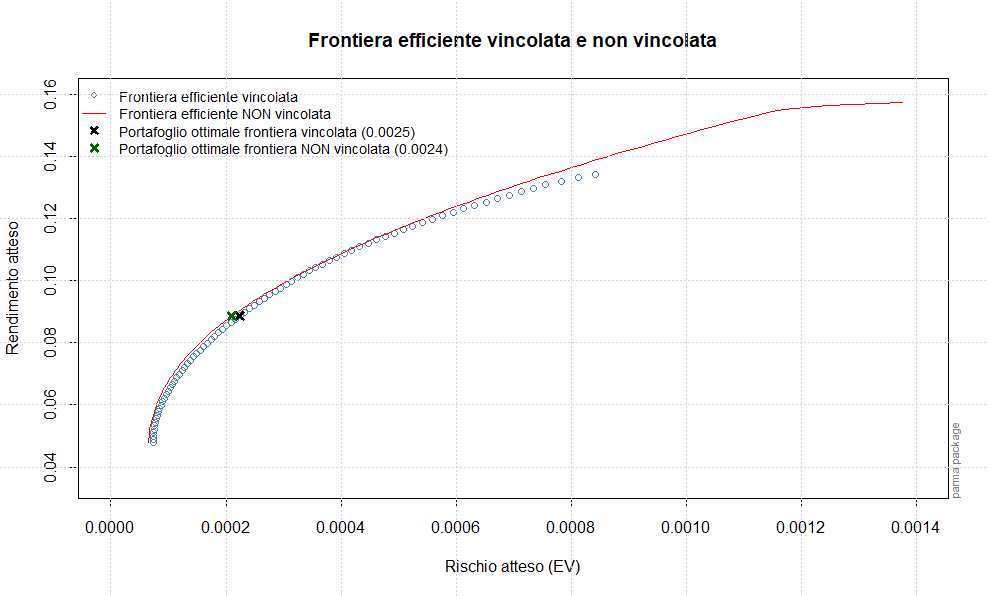
DCC GARCH: Frontiera efficiente vincolata e non vincolata
Per quale motivo dovremmo quindi introdurre dei vincoli nei pesi dei fondi in portafoglio? Perché con i vincoli si possono ottenere portafogli maggiormente diversificati. È infatti pacifico che le ottimizzazioni non vincolate producano spesso dei portafogli fortemente concentrati e la concentrazione è un fattore di rischio da prendere seriamente in considerazione. Se avessimo la certezza che il nostro modello e le nostre stime fossero corrette, molti vincoli perderebbero di significato.
Purtroppo, questa certezza non esiste e la diversificazione è spesso una misura di sicurezza in più per difendersi da eventi non previsti o non prevedibili. La diversificazione ha quindi un ruolo fondamentale in un processo di investimento, spesso anche da un punto di vista meramente psicologico.
A questo punto si ripete l’intera procedura utilizzando però i rendimenti attesi e le matrici di varianza/covarianza generate dal modello GO-GARCH.
Non visualizzeremo il codice utilizzato in quanto del tutto simile al precedente. I risultati della procedura di ottimizzazione sono i seguenti:
Fondo Peso QP Peso SOCP
1 Carmignac Investissement A EUR Acc 0.27912407 0.27880702
2 Candriam Bonds - Euro Government Investment Grade C EUR Acc 0.40000000 0.39999993
3 Eurizon Bilanciato Euro Multimanager 0.03319499 0.03357096
4 Henderson Horizon Fund - Euroland A2 EUR Acc 0.14643803 0.14664163
5 Nordea-1 Global Bond BP 0.14124291 0.14099043
QP SOCP
Rendimento atteso 0.0886452 0.0886443
Rischio atteso 0.0002005 0.0002005
Vediamo quindi il grafico delle due frontiere efficienti (ancora una volta ricavate coi metodi di risoluzione QP e SOCP) ed il punto in cui si trova il portafoglio ottimale, ricordando che abbiamo applicato un vincolo minimo e massimo sui pesi di ciascun fondo in portafoglio (2% - 40%):
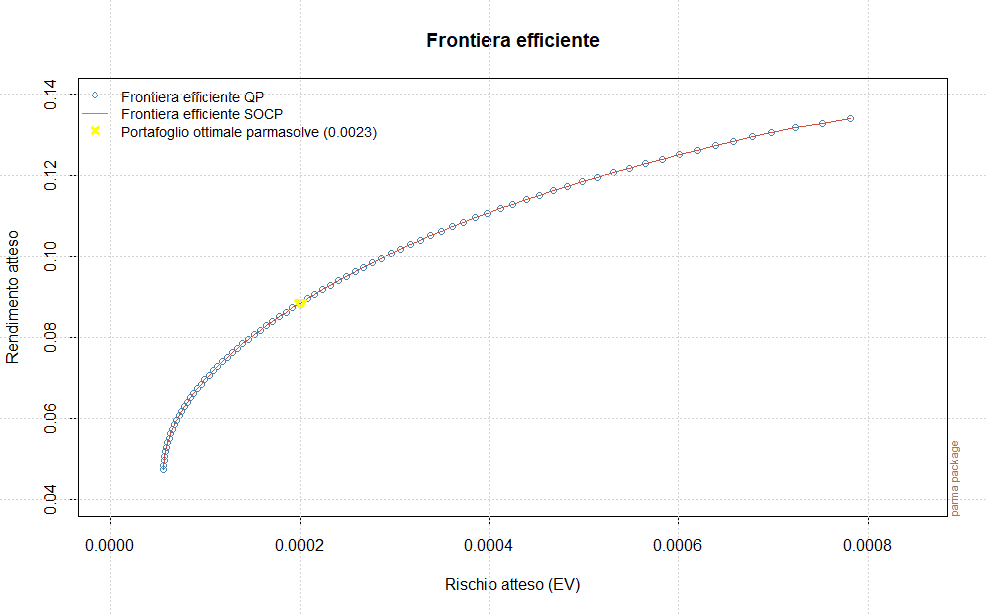
GO-GARCH: Frontiera efficiente vincolata
Come abbiamo visto in precedenza eliminando i vincoli si ottiene una frontiera che domina quella vincolata. I risultati della procedura di ottimizzazione non vincolata sono i seguenti:
Fondo Peso QP Peso SOCP
1 Carmignac Investissement A EUR Acc 0.27685234 0.27652209
2 Candriam Bonds - Euro Government Investment Grade C EUR Acc 0.58636773 0.58636247
3 Eurizon Bilanciato Euro Multimanager 0.00000000 0.00000016
4 Henderson Horizon Fund - Euroland A2 EUR Acc 0.13677993 0.13712500
5 Nordea-1 Global Bond BP 0.00000000 0.00000026
QP SOCP
Rendimento atteso 0.0886452 0.0886443
Rischio atteso 0.0001913 0.0001913
Visualizziamo subito le due frontiere in un unico grafico:
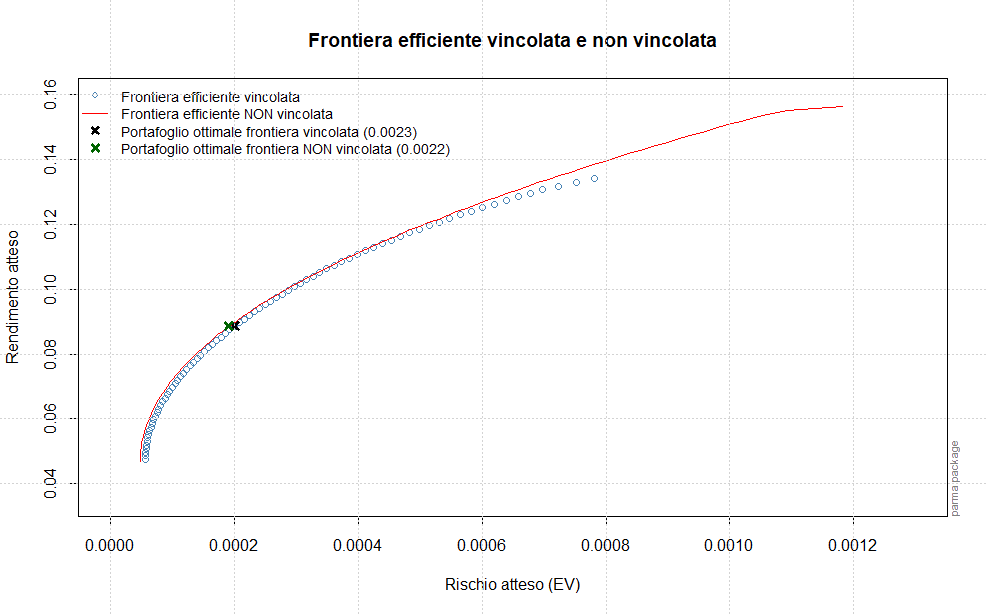
GO-GARCH: Frontiera efficiente vincolata e non vincolata
I portafogli ottimali, sia vincolati che non vincolati, a cui siamo giunti attraverso i modelli DCC GARCH e GO-GARCH sono abbastanza simili.
Le differenze maggiori si riscontrano in quelli vincolati e sarebbe interessante verificare in fase di backtest (out of sample) quale sia il modello che ottiene i risultati migliori.
Nell'articolo relativo ai Portafogli modello si possono trovare molte altre informazioni relative alle procedure di stima dei portafogli efficienti e ai loro backtest.
I modelli GARCH, in particolare, vengono utilizzati nella determinazione dei Portafogli modello di Dedalo Invest costituiti da un'unica tipologia di fondi: portafogli azionari, obbligazionari o bilanciati.
REGISTRATI
SOTTOSCRIVI
