Capital Asset Pricing Model (CAPM)
- Information
- Investimenti
- Prima pubblicazione: 11 Dicembre 2018 Stampa
«All models are wrong, but some are useful».
George E. P. Box
Questo articolo fa parte del Percorso intermedio, pensato per chi possiede già le basi e vuole approfondire strategie di investimento e concetti teorici per una comprensione più approfondita della finanza. In fondo alla pagina, troverai il link al prossimo articolo del percorso.
Uno dei principali ostacoli nell'applicazione pratica della Teoria Moderna del Portafoglio risiede nella necessità di stimare con precisione i rendimenti, le volatilità e le correlazioni attese tra i vari strumenti finanziari inclusi nel portafoglio.
Queste stime, spesso complesse e soggette a un elevato margine di incertezza, sono il fondamento per la costruzione della frontiera efficiente e la determinazione del portafoglio ottimale.
In risposta a queste complicazioni, il Capital Asset Pricing Model (CAPM) si propone come un modello di equilibrio che semplifica notevolmente il processo decisionale degli investitori.
La sua bellezza risiede nell'offrire un ponte logico e quantificabile tra il rischio di un investimento e il suo rendimento atteso, eliminando la necessità di effettuare stime dettagliate per ogni singolo titolo.
Il CAPM, infatti, identifica il portafoglio efficiente con il cosiddetto "portafoglio di mercato", un concetto teorico che rappresenta l'insieme di tutti gli strumenti finanziari disponibili, ponderati per la loro capitalizzazione di mercato.
Questa innovativa prospettiva, oltre a ridurre la complessità dei calcoli, offre anche un approccio più intuitivo e strutturato alla gestione del rischio e alla diversificazione degli investimenti.
In questo articolo, esploreremo in modo semplice e con esempi pratici i concetti fondamentali del CAPM: dal ruolo del beta alla distinzione tra rischio diversificabile e non, fino alla sua applicazione nella valutazione della performance di un investimento.
Indice
- Le ipotesi fondamentali del CAPM
- Il Portafoglio di Mercato e la Capital Market Line (CML)
- Rischio sistematico e rischio specifico
- Il beta: la misura del rischio sistematico
- La Security Market Line (SML)
- L'alfa: la misura della sovraperformance
- Limiti, evidenza empirica e impieghi pratici del CAPM
- La critica di Richard Roll
1. Le ipotesi fondamentali del CAPM
«Truly important and significant hypotheses will be found to have ‘assumptions’ that are wildly inaccurate descriptive representations of reality, and, in general, the more significant the theory, the more unrealistic the assumptions».
Milton Friedman
Il CAPM è un modello introdotto da William Sharpe nel 1964. In maniera indipendente, anche altri economisti svilupparono questa idea: Jack Treynor, John Lintner e Jan Mossin.
Per questo importante lavoro, William Sharpe ha ricevuto nel 1990 il Premio Nobel per l’economia (condiviso con Harry Markowitz e Merton Miller).
Per tutti e tre, la motivazione del premio fu il «contributo pionieristico apportato alla teoria dell’economia finanziaria». Sharpe, in particolare, è stato premiato per aver «sviluppato una teoria generale per la determinazione del prezzo delle attività finanziarie».
Il CAPM, come ogni modello economico, si basa su una serie di ipotesi semplificatrici che non trovano pieno riscontro nel mondo reale.
La validità di un modello, però, non si misura dal realismo delle sue premesse, ma dalla sua capacità di descrivere e predire i fenomeni finanziari in modo utile.
I postulati del CAPM sono i seguenti:
- Non esistono costi di transazione. Non vengono, cioè, sostenute commissioni o altri costi quando si comprano o si vendono titoli.
- Ogni titolo è infinitamente divisibile e può essere frazionato a piacimento.
- Non si pagano imposte. Gli investitori sono indifferenti tra plusvalenze e dividendi, poiché entrambi – nel modello – non sono tassati.
- Gli investitori non possono influenzare il prezzo di un titolo in modo individuale attraverso le proprie vendite o i propri acquisti. È l’insieme delle azioni dei singoli che fa aumentare o diminuire il prezzo dei titoli.
- Gli investitori agiscono soltanto in base ai rendimenti attesi e alla volatilità attesa dei loro portafogli. Inoltre, le loro aspettative (su rendimenti, volatilità e correlazioni) e il relativo orizzonte temporale sono omogenei. Di conseguenza, dato che le informazioni sono pubblicamente e istantaneamente disponibili a tutti, ogni investitore giungerà alla stessa identica frontiera efficiente.
- Le posizioni corte (vendite allo scoperto) sono illimitatamente ammesse (un investitore può vendere titoli che non possiede, senza limiti).
- Gli investitori possono prendere o dare in prestito denaro in quantità illimitata al tasso di interesse privo di rischio (risk-free).
- Ogni bene è perfettamente liquido e negoziabile, inclusi beni come il capitale umano.
In base a queste ipotesi, la teoria conduce al cosiddetto teorema di separazione a due fondi (two-fund separation theorem): tutti gli investitori deterranno lo stesso portafoglio di attività rischiose – il portafoglio di mercato – e si distingueranno soltanto per la combinazione con l’attività priva di rischio (risk-free).
In altre parole, ogni portafoglio efficiente è ottenibile come una combinazione lineare di due soli fondi: il risk-free e il portafoglio di mercato.
2. Il Portafoglio di Mercato e la Capital Market Line (CML)

Accettare i precedenti postulati significa ammettere che ogni investitore razionale inviduerà lo stesso portafoglio di attività rischiose come ottimale.
Questo portafoglio non è altro che il portafoglio tangente che avevamo già incontrato nella Teoria Moderna del Portafoglio.
Abbandonando l’esempio semplificato di un portafoglio con pochi titoli e allargando l’orizzonte alla miriade di attività rischiose negoziabili, la domanda che sorge spontanea è: come facciamo a individuare la composizione del portafoglio tangente nel mondo reale?
La risposta è una diretta conseguenza logica delle ipotesi del modello: se tutti gli investitori detengono lo stesso portafoglio di attività rischiose, e se la somma di questi portafogli deve coincidere con l'insieme di tutte le attività rischiose esistenti (cioè il portafoglio di mercato), allora quel portafoglio condiviso non può che avere la stessa composizione del portafoglio di mercato.
Di conseguenza, il portafoglio di mercato è l'unico portafoglio rischioso che risulti efficiente.
Ogni investitore, per raggiungere il proprio livello di rischio/rendimento desiderato, non farà altro che combinare questo portafoglio con l'attività priva di rischio (ad esempio, prestando o prendendo in prestito denaro).
Questa relazione è rappresentata graficamente dalla Capital Market Line (CML):
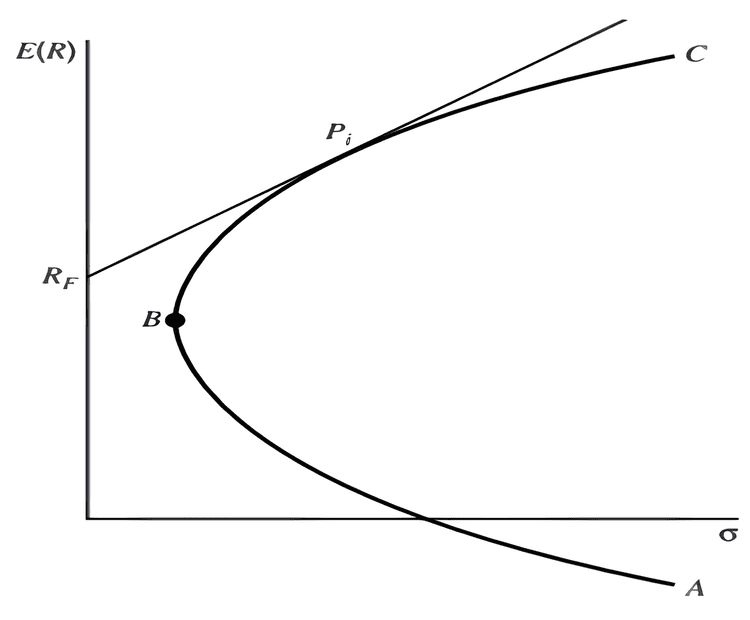
Capital Market Line con possibilità di prestare e di prendere in prestito denaro da investire nel portafoglio di mercato
La CML si origina dall’asse Y nel punto RF (il rendimento di un investimento senza rischio) e passa per il portafoglio di mercato (punto Pi). Tutti i portafogli efficienti si trovano su questa linea.
La pendenza della Capital Market Line ha un significato economico importante: rappresenta il compenso che il mercato richiede per ogni unità addizionale di rischio assunto.
In formule, è pari a:
\begin{equation}
\text{Pendenza}_{\text{CML}} = \frac{E[R_{M}] - R_{f}}{\sigma_{M}}
\end{equation}
- Al numeratore troviamo il premio per il rischio di mercato: la differenza tra il rendimento atteso del portafoglio di mercato e il tasso privo di rischio.
- Al denominatore c’è la deviazione standard del portafoglio di mercato, cioè la misura della sua rischiosità complessiva.
Il rapporto tra queste due grandezze indica quante unità di rendimento extra l’investitore ottiene, in media, per ogni unità di rischio accettata (deviazione standard). Per questo viene chiamato prezzo di mercato del rischio.
In altre parole, se la pendenza è pari, ad esempio, a 0,5, significa che per ogni 1% di rischio aggiuntivo (in termini di deviazione standard), l’investitore può attendersi un rendimento extra dello 0,5% rispetto al tasso privo di rischio.
Ipotizzando che un investitore allochi una percentuale x dei propri impieghi nel portafoglio di mercato ed una percentuale (1 – x) in un titolo privo di rischio, egli si troverà in un punto della Capital Market Line compreso tra Rf e Pi, in funzione di x.
Possiamo calcolare il rendimento atteso e la volatilità di questo specifico portafoglio nel modo seguente:
\begin{equation} E[R_{xCML}]=(1-x) R_f+x(E[R_{Mkt}]-R_f ) \end{equation}
\begin{equation} SD[R_{xCML}]=xSD[R_{Mkt}] \end{equation}
- Al diminuire di x avremo che E[RxCML] tenderà a Rf mentre SD(RxCML) tenderà a 0.
- All’aumentare di x, invece, E[RxCML] tenderà a E[RMkt] mentre SD(RxCML) tenderà a SD(RMkt).
Si noti che x può assumere anche valori maggiori di 1: è il caso in cui l’investitore si indebita per aumentare l’investimento nel portafoglio di mercato.
Facciamo un esempio numerico semplice. Supponiamo che:
- Il tasso privo di rischio (Rf) sia del 2%.
- Il rendimento atteso del portafoglio di mercato (E[RMkt]) sia del 10%.
- La volatilità del portafoglio di mercato (SD(RMkt)) sia del 15%.
Un investitore prudente decide di investire il 60% nel portafoglio di mercato (x = 0,6) e il 40% nell'attività priva di rischio.
- Il suo rendimento atteso sarà: (40% × 2%) + (60% × 10%) = 0,8% + 6% = 6,8%.
- La sua volatilità sarà: 60% × 15% = 9%.
Un investitore più aggressivo decide di prendere a prestito denaro al tasso del 2% per investire il 120% del proprio capitale nel portafoglio di mercato (x = 1,20). In questo caso, (1 − x) sarà pari a −0,20.
- Il suo rendimento atteso sarà: (−20% × 2%) + (120% × 10%) = −0,4% + 12% = 11,6%.
- La sua volatilità sarà: 120% × 15% = 18%.
Come si può vedere, la CML definisce il miglior trade-off rischio/rendimento possibile, ma solo per portafogli efficienti e perfettamente diversificati.
I portafogli non efficienti, cioè quelli che non offrono il massimo rendimento possibile dato un certo livello di rischio (o, viceversa, il minimo rischio dato un certo rendimento), si collocheranno al di sotto della CML: per lo stesso grado di rischio forniranno un rendimento atteso inferiore rispetto ai portafogli sulla CML.
Questo avviene perché includono ancora una quota di rischio specifico non diversificato, che il mercato non remunera, come approfondiremo nel prossimo capitolo.
3. Rischio sistematico e rischio specifico

«Some investments do have higher expected returns than others. Which ones? Well, by and large they're the ones that will do the worst in bad times».
William F. Sharpe
Un titolo finanziario è rischioso perché il suo valore futuro è incerto.
L'origine di questa incertezza può essere scomposta in due categorie:
- Rischio specifico (o diversificabile): legato a fattori unici di una singola azienda o di un settore ristretto. Alcuni esempi di questi fattori possono essere il successo di un nuovo prodotto, uno sciopero dei dipendenti, un cambio di management o una nuova regolamentazione settoriale. Questi eventi influenzano una o poche aziende, ma non l'intero mercato.
- Rischio sistematico (o di mercato): legato a fattori macroeconomici che influenzano l'intera economia e, di conseguenza, la quasi totalità dei titoli. Tra gli esempi, troviamo una recessione globale, una variazione inattesa dell'inflazione, un aumento dei tassi di interesse o un'instabilità geopolitica.
Il primo tipo di rischio, essendo specifico per ogni azienda, può essere quasi completamente eliminato attraverso la diversificazione.
In un portafoglio con molti titoli, le buone notizie di un'azienda (che ne fanno salire il prezzo) tenderanno a essere compensate dalle cattive notizie di un'altra (che ne fanno scendere il prezzo).
Con un numero sufficiente di titoli, l'impatto del rischio specifico sul portafoglio complessivo tende ad annullarsi.
Il rischio sistematico, invece, non può essere eliminato con la diversificazione. Qualsiasi portafoglio di azioni, non importa quanto diversificato, sarà sempre esposto agli andamenti generali dell'economia.
Ecco perché, nella Teoria Moderna del Portafoglio, eravamo giunti alla conclusione che solitamente un portafoglio costituito da più titoli è meno volatile di un singolo titolo, a parità di rendimento atteso: il titolo singolo, l’azienda singola, incorpora sia il rischio specifico che quello sistematico; un portafoglio ben diversificato soltanto il rischio sistematico.
Da un punto di vista grafico, possiamo rappresentare la relazione che esiste tra questi due tipi di rischio e il numero di titoli presenti in portafoglio nel modo seguente:
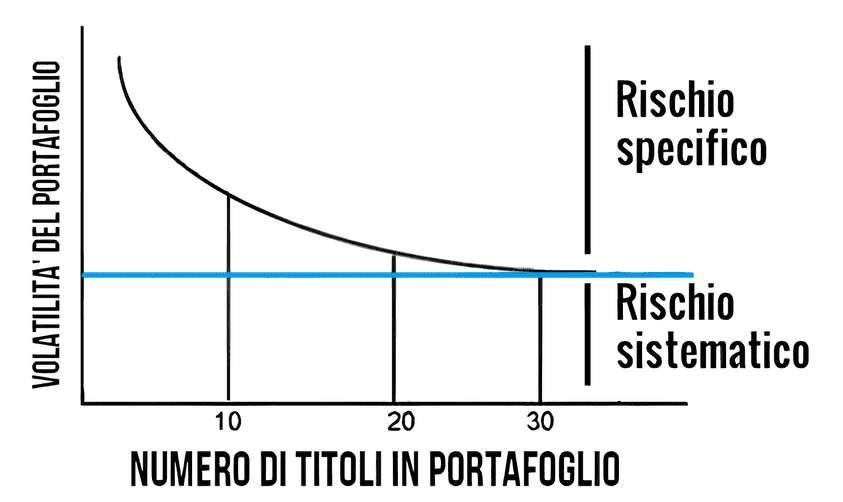
Rischio specifico e rischio sistematico
Una delle conclusioni più importanti del CAPM è che il mercato remunera gli investitori solo per l'assunzione del rischio sistematico. Il rischio specifico, infatti, può essere eliminato "gratuitamente" attraverso la diversificazione.
Per quale motivo un investitore dovrebbe aspettarsi un rendimento extra per un rischio che potrebbe facilmente evitare?
Questa intuizione è fondamentale: la volatilità (deviazione standard) di un singolo titolo non è una buona misura del rischio che il mercato prezza, perché include anche il rischio specifico.
Serve una misura che isoli unicamente il rischio sistematico.
4. Il beta: la misura del rischio sistematico
La misura che isola il rischio sistematico è il beta (β). Il beta di un titolo quantifica la sua sensibilità ai movimenti del portafoglio di mercato.
Matematicamente, è definito come:
\begin{equation}
\beta_i = \frac{\text{Cov}(R_i, R_{\text{Mkt}})}{\text{Var}(R_{\text{Mkt}})}
\end{equation}
Dove:
Ri = rendimento del titolo i.
RMkt = rendimento del portafoglio di mercato.
Cov(Ri, RMkt) = covarianza tra il rendimento del titolo i e il rendimento del portafoglio di mercato.
Var(RMkt) = varianza del rendimento del portafoglio di mercato.
In parole semplici, il beta misura quanto il rendimento di un'attività tende a variare in linea con quello del mercato, in rapporto alla variazione complessiva del mercato stesso:
- β = 1: il titolo ha lo stesso rischio sistematico del mercato. Tende a muoversi in linea con esso.
- β > 1: il titolo è più volatile del mercato (più rischioso). Tende ad amplificare i movimenti del mercato, sia al rialzo che al ribasso. Alcuni esempi tipici sono le azioni di società tecnologiche o di settori fortemente influenzati dal ciclo economico, come l'automotive o i semiconduttori.
- β < 1 (ma > 0): il titolo è meno volatile del mercato (meno rischioso). Tende a smorzarne i movimenti, sia positivi che negativi. È il caso, ad esempio, delle azioni di società attive nei servizi pubblici o nella produzione di beni di prima necessità.
- β = 0: il titolo non ha correlazione con i movimenti del mercato. È il caso dell'attività priva di rischio.
- β < 0: il titolo tende a muoversi in direzione opposta al mercato. È una condizione poco comune tra le azioni, ma può essere osservata in alcune attività non azionarie, come l’oro in fasi di forte avversione al rischio.
Il beta del portafoglio di mercato, per definizione, è uguale a 1. Il beta di un qualsiasi altro portafoglio, invece, è dato dalla media ponderata dei beta dei singoli titoli che lo compongono.
5. La Security Market Line (SML)
Se il beta è la misura corretta del rischio, allora il rendimento atteso di qualsiasi titolo o portafoglio dovrebbe essere linearmente proporzionale al suo beta.
Questa relazione è formalizzata dalla celebre equazione del CAPM:
\begin{equation} R_i=R_f + β_i(R_{Mkt}-R_f) \end{equation}
Dove:
Ri è il rendimento atteso dell'investimento i.
Rf è il tasso di rendimento privo di rischio.
βi è il beta dell'investimento i.
RMkt − Rf è il premio per il rischio di mercato, ovvero l'extra rendimento che gli investitori si aspettano di ottenere per investire nel portafoglio di mercato anziché nell'attività priva di rischio.
Questa equazione rappresenta una delle più importanti scoperte nel settore della finanza e può essere rappresentata graficamente dalla Security Market Line (SML):
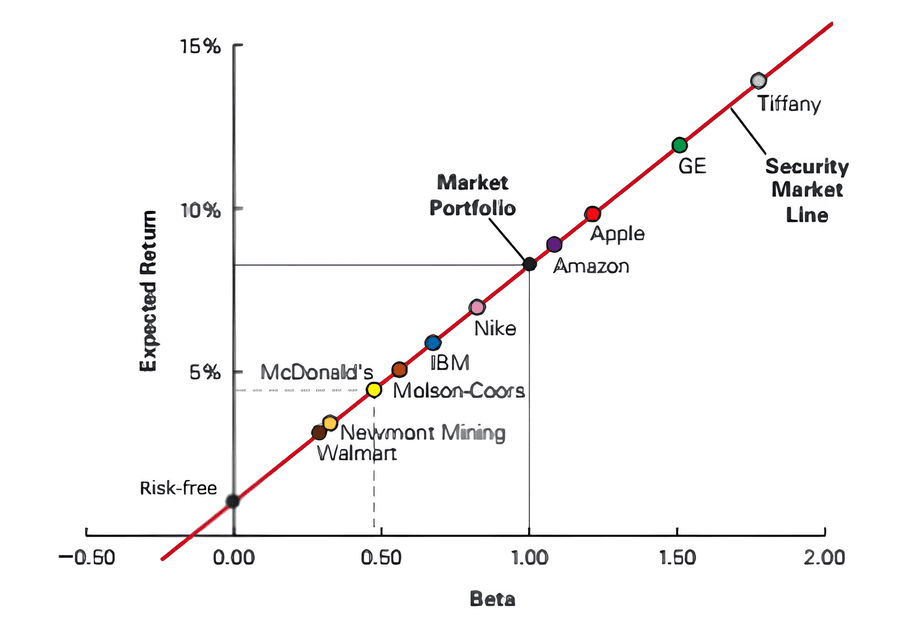
Immagine del grafico della Security Market Line, con l'asse Y che rappresenta il Rendimento Atteso e l'asse X il beta (β). La linea parte da Rf (beta=0) e passa per RMkt (beta=1)
A differenza della CML, che vale solo per i portafogli efficienti, la SML descrive il rendimento atteso di qualsiasi titolo o portafoglio, efficiente o meno, in un mercato in equilibrio. Tutti i titoli, in equilibrio, devono trovarsi su questa linea.
Riprendiamo l'esempio numerico precedente (Rf = 2%, RMkt = 10%): il premio per il rischio di mercato è 10% − 2% = 8%.
Ora calcoliamo il rendimento atteso richiesto dal mercato per tre titoli con beta diversi:
- Azione A (difensiva, β = 0,5): RA = 2% + 0,5 × 8% = 2% + 4% = 6%.
- Azione B (con rischio pari al mercato, β = 1): RB = 2% + 1 × 8% = 2% + 8% = 10%.
- Azione C (aggressiva, β = 1,5): RC = 2% + 1,5 × 8% = 2% + 12% = 14%.
La SML ci dice quale dovrebbe essere il rendimento di un titolo per compensare adeguatamente il suo rischio sistematico.
Bisogna fare attenzione a non credere che, invariabilmente, i titoli con un beta più alto abbiano sempre dei rendimenti più alti dei titoli con un beta più basso. Questo dovrebbe essere vero solo in media e nel lungo termine: se aziende più rischiose producessero costantemente rendimenti superiori, paradossalmente, inizierebbero a essere percepite come meno rischiose.
Il CAPM, d'altronde, è un modello di equilibrio che descrive le tendenze di lungo periodo.
La Security Market Line (SML) descrive la relazione lineare tra rischio sistematico (beta) e rendimento atteso, valida per qualsiasi titolo o portafoglio.
È il “gemello concettuale” della Capital Market Line (CML): mentre la CML distingue tra prezzo del tempo (il tasso privo di rischio, dato dall'intercetta della CML con l'asse verticale) e prezzo del rischio (la pendenza della CML), la SML mostra come tale compenso si traduca nel rendimento richiesto per ogni singolo titolo in funzione del suo beta.
Se un titolo si colloca esattamente sulla SML, significa che il mercato lo sta valutando in modo coerente; se invece se ne discosta, nasce quello scarto che chiamiamo alfa, oggetto del prossimo capitolo.
6. L'alfa: la misura della sovraperformance
Il CAPM è un modello di equilibrio ma, nella realtà, i mercati possono trovarsi temporaneamente in disequilibrio: notizie inattese o nuove informazioni possono far sì che il rendimento atteso percepito di un titolo si discosti da quello teorico previsto dalla SML.
Questa differenza è chiamata alfa (α):
\begin{equation} α_i = E[R_i] -r_i \end{equation}
Dove E[Ri] è il rendimento richiesto calcolato con la formula della SML.
- Se α > 0, il titolo ha un rendimento atteso superiore a quello giustificato dal suo rischio sistematico. Secondo il modello, è sottovalutato e rappresenterebbe un'opportunità di acquisto.
- Se α < 0, il titolo ha un rendimento atteso inferiore a quello giustificato dal suo rischio. È sopravvalutato e andrebbe venduto.
- Se α = 0, il titolo è correttamente prezzato e si trova sulla SML.
Torniamo all'esempio dell'Azione C (β = 1,5), per cui il CAPM richiede un rendimento del 14%:
- Se un analista stima che l'azione renderà il 16%, il suo alfa è: α = 16% − 14% = 2% (segnale di acquisto).
- Se un altro analista stima un rendimento dell'11%, il suo alfa è: α = 11% − 14% = −3% (segnale di vendita).
In un mercato efficiente, le opportunità di alfa positivo dovrebbero scomparire molto rapidamente: non appena le informazioni diventano pubbliche, gli investitori agiscono per trarne profitto.
La ricerca di alfa è, in essenza, l'obiettivo della gestione attiva.
Nei fondi comuni di investimento e nelle Sicav, l'alfa è spesso usato come misura della performance del gestore: un alfa positivo e persistente indica l'abilità di selezionare titoli che hanno sovraperformato rispetto al rischio assunto.
Il concetto di alfa non è privo di insidie. La sua interpretazione dipende interamente dal benchmark di riferimento: se il portafoglio usato come proxy del mercato non coincide con il vero portafoglio di mercato – quello teorico che includerebbe tutte le attività rischiose dell’economia – oppure non è efficiente, allora gli alfa calcolati ex post rischiano di essere fuorvianti.
In tal caso, uno scostamento positivo o negativo dalla Security Market Line potrebbe riflettere non una reale abilità (o incapacità) del gestore ma, più semplicemente, un difetto del benchmark utilizzato.
Questo problema è stato messo in evidenza da Richard Roll nel 1977 e rappresenta una delle critiche più forti al CAPM: non possiamo sapere se stiamo misurando davvero l’efficienza del mercato o solo l’adeguatezza del proxy che abbiamo scelto per rappresentarlo.
Nell'ottavo capitolo analizzeremo più nel dettaglio questa critica e le sue implicazioni.
7. Limiti, evidenza empirica e impieghi pratici del CAPM
Il CAPM è stato oggetto di numerose critiche, soprattutto a causa delle sue ipotesi semplificatrici, difficilmente riscontrabili nel mondo reale.
La più rilevante è l’impossibilità di osservare direttamente il vero portafoglio di mercato, che in teoria dovrebbe comprendere non solo tutte le azioni, ma anche obbligazioni, immobili, materie prime, capitale umano e ogni altra forma di ricchezza.
Nella pratica, si utilizzano proxy come l’indice S&P 500 o altri indici azionari ampi: si tratta però di approssimazioni che possono distorcere i risultati e compromettere l’interpretazione delle misure di rischio e rendimento.
Fin dai primi test, la relazione lineare prevista dal CAPM tra beta e rendimento atteso ha mostrato delle deviazioni.
Black, Jensen e Scholes hanno osservato che i titoli a beta elevato tendono a rendere meno del previsto, mentre quelli a beta basso più del previsto, con un’intercetta della SML diversa da zero. Da qui hanno proposto una versione alternativa, il CAPM a zero-beta, che elimina l’ipotesi secondo cui gli investitori possono prestare e prendere in prestito somme illimitate allo stesso tasso privo di rischio.
Fama e MacBeth hanno introdotto un metodo in due stadi per stimare i premi al rischio, mostrando che la linearità tra beta e rendimenti medi non è sempre confermata, soprattutto in campioni più ampi e su archi temporali lunghi.
Fama e French hanno evidenziato come altri fattori oltre al beta – in particolare la dimensione dell’impresa (Size) e il rapporto valore contabile/prezzo di mercato (Value) – spieghino in modo più sistematico il rendimento medio delle azioni.
Questa scoperta ha portato allo sviluppo dei modelli multifattoriali, oggi molto utilizzati nella ricerca accademica e nella pratica.
Prima ancora, l’Arbitrage Pricing Theory (APT) aveva mostrato che il beta di mercato da solo non è sufficiente a spiegare i rendimenti: in un contesto realistico sono molteplici i fattori macroeconomici e finanziari che possono influenzare i prezzi delle attività.
Nonostante i suoi limiti teorici ed empirici, il CAPM rimane uno strumento fondamentale per almeno tre motivi:
- Semplicità e chiarezza concettuale: fornisce un quadro intuitivo della relazione tra rischio e rendimento, distinguendo tra rischio diversificabile e rischio di mercato.
- Stima del costo del capitale: è molto utilizzato dalle aziende per stimare il costo del capitale proprio (cost of equity), un parametro centrale nelle decisioni di investimento e valutazione dei progetti.
- Valutazione della performance: tramite la SML e l’alfa, offre un benchmark di riferimento per giudicare l’operato dei gestori, pur con la cautela di considerare l’adeguatezza del benchmark scelto.
Sebbene non rappresenti una descrizione perfetta della realtà, il CAPM ha rivoluzionato la teoria finanziaria e continua a essere un punto di partenza indispensabile per lo studio dei modelli di equilibrio nei mercati finanziari.
Nello stesso tempo, i limiti empirici e teorici hanno aperto la strada a modelli più sofisticati – come il CAPM a zero-beta, l’Arbitrage Pricing Theory (APT) e i modelli multifattoriali – e alla critica di Roll, che vedremo nel prossimo capitolo.
8. La critica di Richard Roll

La critica di Richard Roll al CAPM, formulata nel 1977, è considerata una delle più incisive nella storia della finanza.
La critica non è, come molte altre, una semplice obiezione empirica: si tratta di un’osservazione logico-matematica che mette in discussione la stessa possibilità di testare il modello.
In breve, Roll sostiene che se non possiamo osservare il vero portafoglio di mercato, allora non possiamo nemmeno verificare fino in fondo se il modello funziona davvero.
Secondo Roll, affermare che i rendimenti attesi dei titoli dipendono linearmente dal loro beta (come previsto dalla SML) equivale ad affermare che il vero portafoglio di mercato è efficiente.
Non sono due proposizioni separate, ma due modi diversi di dire esattamente la stessa cosa.
Da questa equivalenza deriva che ogni test empirico del CAPM è congiunto: non stiamo verificando solo se il modello è valido, ma anche se l’indice che usiamo come sostituto del mercato è davvero rappresentativo. In pratica, non è possibile separare le due cose.
Quando utilizziamo un indice azionario (come l’S&P 500) come sostituto del portafoglio di mercato, stiamo in realtà testando contemporaneamente il CAPM e l’ipotesi che quell’indice sia un buon proxy dell’intero universo degli asset rischiosi.
Questo porta a due importanti conseguenze:
- Se il proxy è incompleto (ad esempio, contiene solo azioni domestiche), possiamo “rigettare” il CAPM non perché il modello sia errato, ma perché il portafoglio utilizzato non rappresenta davvero il mercato.
- In ogni campione di dati storici, esistono portafogli che risultano efficienti ex post. Calcolando i beta rispetto a uno di questi, la relazione lineare della SML sembrerebbe sempre confermata, anche se il vero portafoglio di mercato non fosse in realtà efficiente.
Il messaggio della critica di Roll è chiaro: non potendo osservare il vero portafoglio di mercato, non possiamo mai testare in modo non ambiguo il CAPM. Qualunque test si basi su un indice o su un sottoinsieme di attività è inevitabilmente vulnerabile alla seguente obiezione: stai testando il modello o l'indice che approssima il mercato?
Questa critica ha conseguenze concrete, soprattutto quando si utilizza l’alfa per valutare la bravura di un gestore.
Se il benchmark adottato non è un portafoglio efficiente, allora gli alfa ex post diventano difficili da interpretare: lo scostamento dalla SML potrebbe riflettere soltanto l’inefficienza del proxy utilizzato, e non la reale capacità del gestore di generare valore.
La critica di Richard Roll ha un peso enorme sul piano teorico: senza poter osservare il vero portafoglio di mercato, il CAPM non è testabile in senso stretto.
Qualsiasi verifica empirica si riduce, di fatto, a un test congiunto: non è mai possibile stabilire con certezza se si stia confermando (o smentendo) il modello teorico oppure la validità dell’indice scelto come proxy del mercato.
Se da un punto di vista logico-matematico questa osservazione è difficilmente confutabile, sul piano operativo il quadro cambia.
Negli ultimi decenni sono nati indici estremamente ampi e diversificati – globali, multi-settoriali e multi-asset – che si avvicinano molto più di quanto accadeva ai tempi di Roll al concetto teorico di portafoglio di mercato.
Utilizzare questi proxy non risolve del tutto il problema logico, ma riduce di molto la distanza pratica tra modello e realtà.
Molte critiche emerse nel tempo – dall’Arbitrage Pricing Theory ai modelli multifattoriali come quello di Fama-French – hanno aggiunto complessità al quadro, ma non sempre maggiore capacità esplicativa.
Spesso questi modelli poggiano su relazioni statistiche fragili, dove la correlazione osservata non implica necessariamente causalità.
Gli studi più recenti di Marcos López de Prado hanno rafforzato questa prospettiva, mostrando quanto sia facile scambiare regolarità econometriche del tutto casuali per leggi economiche.
A ciò si aggiunge un’evidenza empirica ormai difficilmente contestabile: la gestione attiva, nel lungo termine, non riesce a mantenere la promessa di battere i benchmark di riferimento.
I report periodici (come lo SPIVA di S&P Global) documentano che la grande maggioranza dei gestori attivi sottoperforma rispetto agli indici nel medio-lungo periodo: è chiaro che non possiamo attribuire questa sistematica “sconfitta” sempre e soltanto a benchmark inadeguati.
Più semplicemente, il concetto stesso di generare alfa in modo sistematico appare irrealistico.
In questo senso, il capitolo della valutazione dei gestori basata sull’alfa può considerarsi chiuso: non si riesce a sovraperformare il mercato in modo continuativo.
A maggior ragione, il CAPM rimane ancora oggi un punto di riferimento sia teorico che pratico.
Non sarà mai un modello perfetto, né può essere dimostrato empiricamente senza ambiguità: continua, però, a rappresentare la base concettuale su cui poggiano l’investimento passivo, la costruzione degli indici e, in ultima analisi, la filosofia di investimento dei portafogli pigri (Lazy portfolios).
Nonostante i suoi limiti, è la sua forza intuitiva a renderlo ancora oggi un modello vivo e rilevante.
Il Percorso intermedio continua con l'articolo:


