6. Preferenze di rischio, parte I: il modello dell’utilità attesa tra teoria e realtà

«Arriva sempre un momento in cui non c’è altro da fare che rischiare».

José Saramago

Il tema delle preferenze di rischio riveste un'importanza centrale nell'analisi economica e, più in generale, nella comprensione del comportamento umano.

Molte delle decisioni che affrontiamo ogni giorno, sia a livello individuale che collettivo, implicano infatti un certo grado di incertezza sugli esiti.

Capire in che modo le persone valutano e prendono decisioni in situazioni rischiose è fondamentale per interpretare numerosi fenomeni economici e per progettare politiche pubbliche efficaci.

In ambito finanziario, si parla spesso di "propensione al rischio" o di "avversione al rischio" per indicare quanto rischio un individuo è disposto ad assumersi quando investe. La scelta del portafoglio deve quindi essere coerente con il suo profilo di rischio, per evitare che un’eccessiva volatilità provochi un livello di stress tale da portarlo a disinvestire in modo prematuro.

La propensione o l'avversione al rischio rappresenta uno specifico aspetto delle più ampie "preferenze di rischio", che descrivono l’insieme degli atteggiamenti di una persona nei confronti dell’incertezza, spaziando dall’avversione fino alla ricerca del rischio.

In questa prospettiva, le preferenze di rischio costituiscono la base per comprendere il comportamento decisionale in condizioni di incertezza.

Indice

1. La natura delle scelte rischiose: esempi dalla vita quotidiana
2. L’avversione al rischio nel modello dell’utilità attesa: un approccio razionale
3. Misurazione delle preferenze di rischio: quantificare l’avversione
4. Critiche e limiti del modello dell’utilità attesa: dalla teoria al comportamento reale
5. Evidenza dal mercato delle assicurazioni: il caso delle franchigie
6. Conclusioni

1. La natura delle scelte rischiose: esempi dalla vita quotidiana

Numerose decisioni quotidiane comportano un elemento di rischio o di incertezza.

Un esempio tipico è la scelta del percorso di studi: lo studente che seleziona una facoltà universitaria lo fa anche nella speranza che tale scelta gli offra in futuro valide opportunità professionali, pur senza alcuna garanzia.

Anche l’acquisto di una casa, o la decisione se affittare o acquistare, dipende spesso dalle previsioni sull’andamento del mercato immobiliare: se si acquista e i prezzi calano, si subisce una perdita; se, invece, si sceglie l’affitto e i prezzi salgono, si può arrivare a rimpiangere di non aver comprato.

Un altro caso emblematico riguarda poi gli agricoltori, che devono scegliere quali colture piantare o quali fertilizzanti impiegare, tenendo conto di variabili ambientali incerte, come le condizioni climatiche future.

La costruzione di un portafoglio finanziario è forse il più classico degli esempi: i rendimenti dipendono da fattori esterni e incontrollabili, che avranno un impatto sull’andamento dei mercati azionari e obbligazionari.

Perfino decisioni più semplici, come indossare il casco quando si va in bicicletta, implicano una valutazione del rischio: non si può mai sapere in anticipo se quella scelta si rivelerà vantaggiosa.

Oltre alle decisioni che comportano un’esposizione al rischio, esistono anche strategie per limitarlo.

Una di queste è la stipula di assicurazioni, come la Kasko in ambito automobilistico: a differenza della RCA, che è obbligatoria e copre esclusivamente i danni causati a terzi, la Kasko è facoltativa e tutela anche contro i danni subiti dal proprio veicolo. Sebbene il premio da pagare sia più elevato, questa forma di assicurazione consente di proteggersi da perdite potenzialmente molto ingenti.

Un’altra forma di gestione del rischio consiste nell’evitare del tutto comportamenti o situazioni percepite come pericolose. Si può, ad esempio, scegliere di non sottoscrivere un investimento troppo volatile o di rinunciare a un’attività considerata eccessivamente incerta.

Anche questo approccio rappresenta una forma di mitigazione del rischio, poiché consente di limitare l’esposizione a eventi sfavorevoli e ridurre l’incertezza che accompagna molte decisioni quotidiane.

2. L’avversione al rischio nel modello dell’utilità attesa: un approccio razionale

Nel pensiero economico classico, il principale strumento per analizzare le decisioni in condizioni di rischio è il modello dell’utilità attesa.

Le origini del modello dell’utilità attesa risalgono al XVIII secolo, quando Nicolaus Bernoulli introdusse questo concetto nel 1738 per risolvere il cosiddetto paradosso di San Pietroburgo.

Secondo Bernoulli, le persone non valutano le scelte rischiose solo in base al valore monetario atteso, ma in funzione dell’utilità soggettiva che attribuiscono agli esiti.

Questo principio, rivoluzionario per l’epoca, fu poi ripreso e formalizzato nel XX secolo da von Neumann e Morgenstern nel loro classico Theory of Games and Economic Behavior del 1944, che pose le basi teoriche della teoria dei giochi.

Nato come modello normativo – cioè volto a descrivere come gli individui dovrebbero comportarsi se agissero in modo pienamente razionale – il modello dell'utilità attesa è stato progressivamente utilizzato anche come modello descrittivo del comportamento reale.

Secondo questo approccio, le persone valutano le scelte rischiose considerando tutti gli esiti possibili e le probabilità associate a ciascuno di essi. L’innovazione di questo modello è che gli individui non si limitano a guardare il valore monetario degli esiti, ma attribuiscono importanza all’utilità soggettiva, cioè alla “soddisfazione” che ciascun esito produce.

L’utilità attesa di una scommessa (indicata con G) si calcola come media ponderata delle utilità dei diversi esiti, pesate in base alle loro probabilità.

Formalmente, per una scommessa che offre un esito x con probabilità p e un esito y con probabilità (1 − p), l’utilità attesa EU(G) è data da:

\begin{equation} EU(G) = p \cdot u(x) + (1 - p) \cdot u(y) \end{equation}

dove u(·) è la funzione di utilità individuale, che trasforma la ricchezza o il consumo in un livello di soddisfazione.

Consideriamo una semplice lotteria: 50% di probabilità di vincere 1.000 € e 50% di probabilità di vincere 0 €.

L’utilità attesa sarà:

\begin{equation} EU(G) = 0{,}5 \cdot u(1000\,€) + 0{,}5 \cdot u(0\,€) \end{equation}

Per confronto, il valore monetario atteso (Expected Monetary Value, EMV) della stessa scommessa è:

\begin{equation} EMV(G) = 0{,}5 \cdot 1000\,€ + 0{,}5 \cdot 0\,€ = 500\,€ \end{equation}

Il concetto chiave per spiegare l’avversione al rischio nel modello dell’utilità attesa è la concavità della funzione di utilità, che implica una utilità marginale decrescente della ricchezza: man mano che la ricchezza aumenta, ogni euro aggiuntivo genera un beneficio sempre minore.

Questa idea, oggi fondamentale nella teoria economica, è uno dei pilastri della cosiddetta rivoluzione marginalista del 1870. Tra i protagonisti di questo cambiamento vi fu William S. Jevons (1835–1882) che, ispirandosi all’utilitarismo di Jeremy Bentham – secondo cui piaceri e dolori sono misurabili – introdusse il concetto di “grado finale di utilità”, oggi noto come utilità marginale.

Secondo Jevons, il valore soggettivo di un bene diminuisce all’aumentare della quantità già posseduta. In pratica, 10 euro valgono molto di più per chi ha poco che per chi è già ricco: per una persona affamata, 10 euro possono fare una grossa differenza; per un milionario, il loro impatto è trascurabile.

Graficamente, una funzione di utilità concava mostra che la retta che unisce due punti della curva si trova al di sotto della curva stessa. Questo riflette il fatto che l’utilità di un esito certo equivalente al valore atteso è superiore all’utilità attesa della scommessa.

Formalmente, per una funzione di utilità concava u(·) e per ogni x, y e p ∈ (0, 1), si ha:

\begin{equation} u(p \cdot x + (1 - p) \cdot y) \geq p \cdot u(x) + (1 - p) \cdot u(y) \end{equation}

Se la funzione è due volte derivabile, la concavità si esprime come u′′(⋅) < 0:

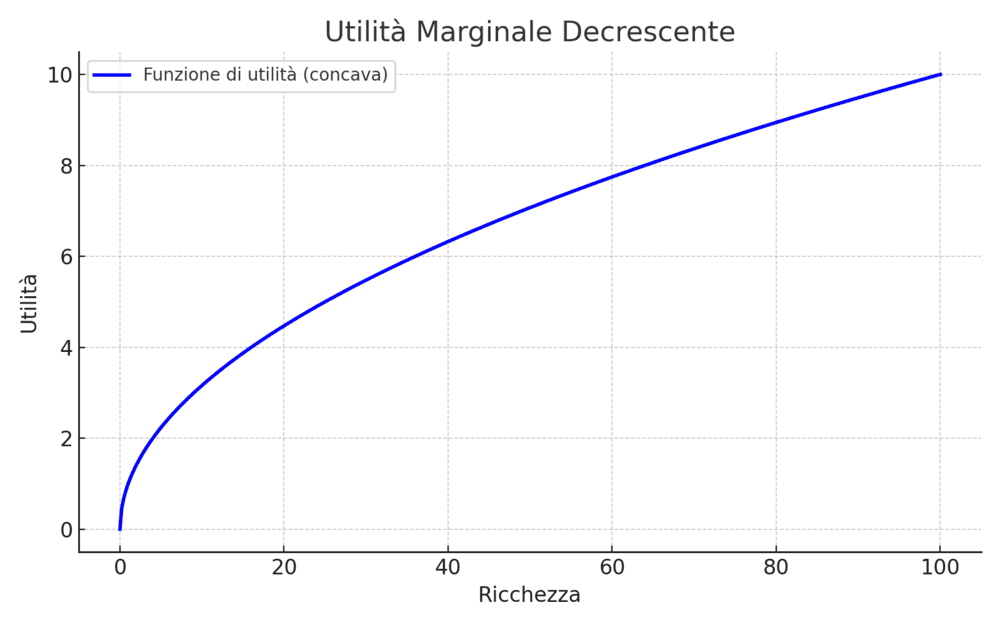
Il grafico mostra la relazione tra ricchezza (asse orizzontale) e utilità (asse verticale), secondo una funzione concava che esprime il principio dell’utilità marginale decrescente.

Ad esempio, di fronte a una scommessa con il 50% di probabilità di vincere 100 € e il 50% di probabilità di vincere 0 € (valore atteso: 50 €), una persona avversa al rischio potrebbe preferire ricevere non soltanto 50 €, ma anche 40 € con certezza.

Questo accade perché la “perdita” di utilità nel passare da 50 a 0 € è percepita come più pesante del “guadagno” derivante dal passaggio da 50 a 100 €.

Nel modello dell’utilità attesa, un individuo:

• È avverso al rischio se preferisce ricevere con certezza EMV(G) anziché partecipare alla scommessa G.
• È neutrale al rischio se è indifferente tra G e EMV(G), il che avviene se la funzione di utilità è lineare.
• È propenso al rischio se preferisce G rispetto a ricevere con certezza EMV(G).

Oltre alla concavità della funzione di utilità, esistono altri fattori che contribuiscono all’avversione al rischio, tra cui:

• L’avversione alle perdite (loss aversion).
• Il timore di cadere al di sotto di standard minimi di benessere (es. perdere la casa o non poter mangiare).
• L’ansia e lo stress legati all’incertezza.
• La difficoltà nel pianificare in presenza di esiti imprevedibili.

Nella sua versione più semplice, però, il modello dell’utilità attesa astrae da questi aspetti e si concentra sulla forma della funzione di utilità come principale determinante del comportamento in presenza di rischio.

3. Misurazione delle preferenze di rischio: quantificare l’avversione

«Chi non ha in sé la misura non la troverà mai».

Henri-Frédéric Amiel

Per misurare il grado di avversione al rischio di un individuo, gli economisti ricorrono a diversi strumenti analitici.

Tra le misure più comuni vi sono:

Coefficiente di Avversione Assoluta al Rischio (CARA):

\begin{equation} r(x) = -\frac{u''(x)}{u'(x)} \end{equation}

Coefficiente di Avversione Relativa al Rischio (CRRA):

\begin{equation} \gamma(x) = -x \cdot \frac{u''(x)}{u'(x)} = x \cdot r(x) \end{equation}

Il termine u′(x), che rappresenta l’utilità marginale (cioè il beneficio ottenuto da un euro in più), è incluso in queste formule per una ragione precisa: serve a rendere le misure invarianti rispetto a trasformazioni lineari positive della funzione di utilità.

In altre parole, ciò che conta non è il valore assoluto dell’utilità, ma l’ordine delle preferenze e la forma della funzione.

Infatti, in economia l’utilità è una grandezza ordinale, non cardinale: ciò che rileva è quali alternative un individuo preferisce, non quanto intensamente le preferisce in termini numerici.

Se prendiamo una funzione di utilità e moltiplichiamo tutti i suoi valori per 2 (o aggiungiamo una costante), le preferenze dell’individuo non cambiano: continuerà a preferire ciò che preferiva prima, perché l’ordine degli esiti resta lo stesso.

Ecco perché nelle misure di avversione al rischio si usa un rapporto: il numeratore (la derivata seconda) indica quanto è concava la funzione, mentre il denominatore (la derivata prima) indica quanto cresce.

Moltiplicando tutta la funzione per 2, entrambi questi termini raddoppiano e il loro rapporto – cioè la misura dell’avversione al rischio – rimane identico. Questo garantisce che la misura rifletta le preferenze effettive della persona, e non il modo arbitrario in cui abbiamo rappresentato l’utilità.

Ad esempio, supponiamo che una persona assegni queste utilità: u(0 €) = 0; u(100 €) = 10 e u(200 €) = 18. Ora, moltiplichiamo tutti i valori per 2: u(0 €) = 0; u(100 €) = 20 e u(200 €) = 36.

Le preferenze non sono cambiate: la persona preferisce ancora 200 € a 100 €, e 100 € a 0 €. Tuttavia, se le misure di avversione al rischio dipendessero direttamente dai valori numerici della funzione di utilità, esse cambierebbero quando applichiamo una trasformazione lineare (come raddoppiare tutti i valori), pur senza alcuna variazione nel comportamento dell’individuo.

L’uso del rapporto tra derivata seconda e derivata prima – come avviene nelle misure CARA e CRRA – serve proprio a evitare questo problema: rende la misura invariante rispetto alla scala numerica utilizzata per rappresentare l’utilità.

Il ruolo di γ (gamma) nel modello dell’utilità attesa

Nel contesto delle funzioni di utilità CRRA, il parametro γ (gamma) rappresenta il grado di avversione relativa al rischio. Valori più elevati di γ indicano una maggiore avversione.

Una forma comune di funzione CRRA è:

\begin{equation} u(x) = \frac{x^{1 - \gamma}}{1 - \gamma}, \quad \text{per } \gamma \neq 1 \end{equation}

\begin{equation} u(x) = \ln(x), \quad \text{per } \gamma = 1 \end{equation}

Dove x rappresenta la ricchezza o il consumo, e u(x) l’utilità percepita. La forma logaritmica si applica nel caso limite in cui γ=1, poiché in quel caso la formula generale non è definita.

Le caratteristiche di questa funzione sono intuitive:

• Se γ = 0, la funzione è lineare → nessuna avversione al rischio.
• Se γ > 0, la funzione è concava → avversione al rischio. Più γ è alto, più la funzione si appiattisce → maggiore è l'avversione al rischio.
• Se γ < 0, la funzione è convessa → amante del rischio, ovvero preferisce opzioni rischiose anche quando il valore certo sarebbe pari o superiore (caso raro).

Misurazione sperimentale dell’avversione al rischio

L’avversione al rischio può essere misurata in contesti controllati, come gli esperimenti in laboratorio, o attraverso l’osservazione di comportamenti reali.

In laboratorio, un metodo molto usato è la determinazione del valore certo equivalente (certainty equivalent, CE) di una scommessa: la somma sicura che rende l’individuo indifferente tra riceverla o affrontare la scommessa.

Conoscendo il CE e la funzione di utilità adottata, è possibile stimare il parametro γ.

Ad esempio, una scommessa equa con il 50% di probabilità di ottenere 40.000 € e il 50% di ottenere 80.000 € ha un valore atteso di 60.000 €. Se il soggetto preferisce ricevere 55.000 € con certezza, ciò implica:

\begin{equation} u(55{.}000\,€) = 0{,}5 \cdot u(40{.}000\,€) + 0{,}5 \cdot u(80{.}000\,€) \end{equation}

Da questa equazione si può dedurre γ.

Un CE più basso (ad esempio 50.000 €) indicherebbe una maggiore avversione al rischio, e quindi un valore di γ più elevato.

Inferenza sul campo

Nel mondo reale, le preferenze di rischio possono essere inferite osservando comportamenti concreti, come le scelte assicurative.

Ad esempio, analizzando le decisioni tra polizze con diverse combinazioni di franchigia e premio, è possibile stimare un intervallo plausibile per γ. Approfondiremo questo punto più avanti.

Le preferenze manifestate attraverso queste scelte rivelano implicitamente quanto rischio l’individuo è disposto a tollerare.

4. Critiche e limiti del modello dell’utilità attesa: dalla teoria al comportamento reale

Nonostante la sua ampia diffusione e il suo valore analitico, il modello dell’utilità attesa presenta limiti evidenti nel descrivere accuratamente alcuni comportamenti osservati nella realtà.

Una delle critiche più incisive riguarda l’incoerenza tra l’avversione al rischio osservata nelle piccole scommesse e quella mostrata in decisioni che coinvolgono somme molto più elevate.

Numerosi esperimenti hanno mostrato che, quando si tratta di importi modesti, le persone tendono a rifiutare scommesse con valore atteso positivo.

Ad esempio, molti rifiutano una scommessa equa 50/50 che comporta la possibilità di perdere 10 euro o vincerne 11, anche se il guadagno atteso è positivo (+0,50 euro).

Se interpretiamo questo comportamento attraverso il modello dell’utilità attesa, otteniamo un coefficiente di avversione al rischio γ molto elevato, spesso superiore a 10, 20 o addirittura 30.

Consideriamo un altro caso: una persona con una ricchezza di 25.000 euro rifiuta una scommessa 50/50 che offre la possibilità di vincere 120 euro o di perderne 100.

Secondo il modello, questa scelta implica un γ superiore a 15. Tuttavia, quando si analizzano decisioni su scala più ampia – che coinvolgono importi vicini alla ricchezza complessiva dell’individuo – le stesse persone si comportano in modo molto meno avverso al rischio, con valori impliciti di γ molto più bassi (tipicamente tra 0 e 2, raramente oltre 5).

Studi empirici, come quello di Chetty e Szeidl del 2006, confermano questi valori analizzando scelte reali in ambito assicurativo e previdenziale.

Il problema nasce dal fatto che il modello dell’utilità attesa utilizza un solo parametro, γ, per rappresentare l’avversione al rischio. Questo parametro dovrebbe essere costante, indipendentemente dalla dimensione della scommessa.

Ma ciò crea una contraddizione: se γ è alto per giustificare il rifiuto di piccole scommesse, allora il modello impone che lo stesso individuo debba rifiutare anche opportunità di guadagno molto elevato – con rischio minimo – su larga scala, un comportamento decisamente irrazionale.

Al contrario, se γ è basso per giustificare l’accettazione di grandi scommesse, allora la stessa persona dovrebbe accettare anche scommesse modeste con valore atteso positivo.

In entrambi i casi, il modello risulta incoerente.

Questa incongruenza è stata formalizzata da Matthew Rabin nel suo celebre Calibration Theorem. Rabin dimostra che, anche sotto ipotesi molto deboli (come una funzione di utilità debolmente concava), il rifiuto sistematico di piccole scommesse con valore atteso positivo conduce a previsioni assurde su scala più ampia.

Ad esempio, se un individuo rifiuta sempre una scommessa 50/50 tra perdere 10 euro e guadagnarne 11, allora – seguendo la logica del modello – dovrebbe anche rifiutare una scommessa tra perdere 100 e vincere una somma arbitrariamente grande: il rifiuto iniziale implica infatti che l’utilità marginale del denaro decresca in modo estremamente rapido, fino a livelli irrealistici.

Il Calibration Theorem mette dunque in luce un limite strutturale del modello dell’utilità attesa: la sua incapacità di rappresentare in modo coerente le preferenze di rischio su scale diverse.

Pur restando uno strumento fondamentale dell’analisi economica, il modello si rivela inadeguato quando si cerca di applicarlo al comportamento reale in presenza di rischio.

L'incoerenza del modello può essere visualizzata graficamente confrontando la forma della funzione di utilità necessaria a spiegare le scelte su piccola scala con quella che descrive le decisioni su larga scala.

Inoltre, un’analisi empirica dei valori impliciti di γ mostra una chiara tendenza decrescente all’aumentare dell’entità delle scommesse, evidenziando la difficoltà del modello nel mantenere coerenza tra le scale:

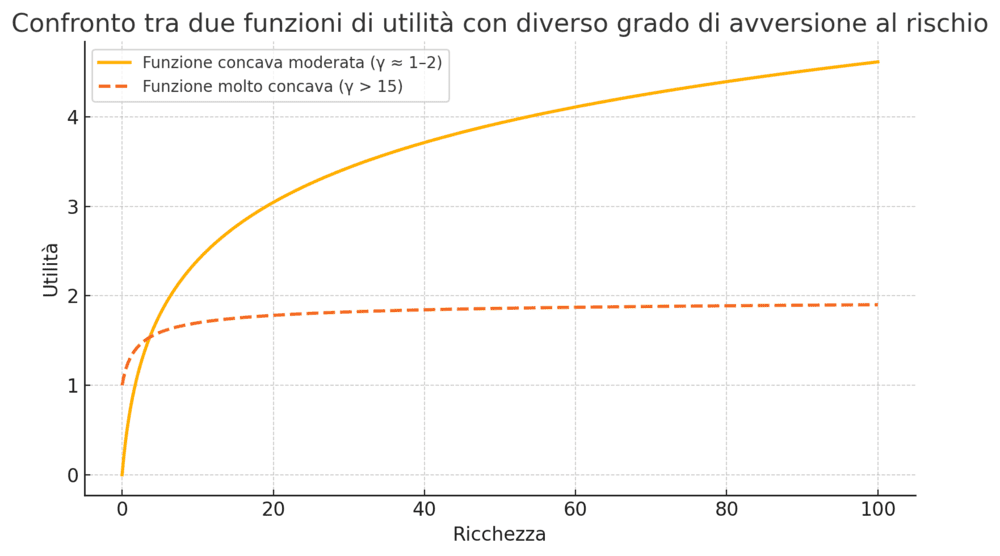
La curva continua rappresenta una funzione di utilità moderatamente concava (es. γ ≅ 1–2), coerente con scelte realistiche su larga scala. La curva tratteggiata mostra invece una funzione molto più concava, necessaria a giustificare il rifiuto di scommesse piccole ma con valore atteso positivo (es. −10/+11). Questo grado di concavità implicherebbe un’avversione irrealistica per importi più elevati, evidenziando l’incoerenza del modello con il comportamento reale.

5. Evidenza dal mercato delle assicurazioni: il caso delle franchigie

Le decisioni assicurative nella vita reale offrono un’interessante opportunità per osservare concretamente le preferenze di rischio.

Un contributo fondamentale in questo ambito è lo studio di Justin Sydnor del 2010: (Over)insuring Modest Risks.

L’analisi si concentra sulle scelte relative alla franchigia nelle polizze assicurative sulla casa. La franchigia è l’importo che l’assicurato deve coprire di tasca propria in caso di danno, prima che intervenga la copertura della compagnia.

In generale, franchigie più basse (ad esempio, 250 dollari) implicano premi assicurativi annui più alti rispetto a franchigie più elevate (come 1.000 dollari).

Scegliere una franchigia bassa significa quindi pagare un premio maggiore ogni anno, in cambio di una riduzione del rischio di dover affrontare un esborso più alto in caso di sinistro.

Sydnor ha analizzato un ampio database di 50.000 polizze standard, esaminando sia le opzioni di franchigia offerte sia le scelte effettivamente fatte dagli assicurati.

Le opzioni a disposizione prevedevano quattro livelli di franchigia. I dati hanno mostrato che la maggioranza degli assicurati ha scelto franchigie basse, in particolare da 250 o 500 dollari, mentre in pochissimi hanno optato per l’alternativa più elevata da 1.000 dollari, anche tra i clienti di lunga data, presumibilmente più consapevoli della bassa probabilità di sinistro.

Si tratta di una scelta poco razionale dato che, ad esempio, per ridurre la franchigia da 1.000 a 500 dollari, i clienti pagano circa 100 dollari in più all’anno. Ma con un tasso di sinistri inferiore al 5%, il beneficio atteso di questa scelta, cioè il risparmio potenziale sulla franchigia, è di circa 25 dollari (il 5% di 500 dollari).

Pagare 100 dollari per ottenere un beneficio atteso di 25 dollari riflette un livello di avversione al rischio molto elevato.

Questo comportamento può essere formalizzato attraverso la seguente funzione di utilità attesa:

\begin{equation} V(W, P, D, \pi) = \pi \cdot u(W - P - D) + (1 - \pi) \cdot u(W - P) \end{equation}

Dove:

W = ricchezza dell’individuo.
P = premio assicurativo annuale.
D = franchigia.
π = probabilità di un sinistro.

Analizzando quale combinazione di premio e franchigia (P_j, D_j) viene scelta tra le opzioni disponibili, è possibile inferire limiti al parametro γ di avversione al rischio, assumendo una funzione di utilità CRRA.

I risultati sono sorprendenti: le scelte di franchigie basse implicano valori di γ spesso superiori a 100, anche per individui con ricchezze moderate (ad esempio, 50.000 dollari). Parliamo di livelli molto più alti di quelli compatibili con il comportamento previsto dal modello standard in contesti realistici.

Queste evidenze confermano quanto osservato anche in laboratorio su scala ridotta. Quando le decisioni riguardano importi modesti, le persone mostrano una forte avversione al rischio, un comportamento difficilmente giustificabile con il modello dell’utilità attesa che, in teoria, prevederebbe una quasi neutralità, dato l’esiguo impatto sul benessere complessivo.

Sono state avanzate alcune spiegazioni alternative per questa tendenza alla sovrassicurazione, tra cui:

• Una percezione soggettiva esagerata della probabilità di sinistro.
• Vincoli di liquidità che rendono problematico sostenere un esborso improvviso.
• Influenze di marketing.

Secondo Sydnor, tuttavia, nessuna di queste spiegazioni è da sola sufficiente a giustificare l’intensità dell’avversione al rischio osservata.

6. Conclusioni

Il modello dell’utilità attesa costituisce un quadro teorico elegante per analizzare le scelte in condizioni di rischio, basandosi sul principio dell’utilità marginale decrescente.

L’osservazione dei comportamenti reali – sia in scommesse di piccola entità che in decisioni assicurative quotidiane – mette però in luce delle importanti discrepanze tra la teoria e ciò che accade nella pratica.

La teoria classica fatica a spiegare perché le persone tendano a mostrare una forte avversione al rischio in presenza di perdite modeste, pur mostrando una minore sensibilità al rischio quando sono coinvolti importi molto più alti.

Questa incoerenza suggerisce che altri fattori influenzano il comportamento decisionale in condizioni di incertezza.

Nel prossimo articolo esamineremo approcci alternativi, con particolare attenzione ai contributi della finanza comportamentale.

I modelli che analizzeremo cercano di fornire una rappresentazione più ricca e realistica delle preferenze di rischio, incorporando elementi psicologici, percettivi e contestuali che il paradigma dell’utilità attesa tradizionale tende a trascurare.