Le misure di rischio

«I must tell you I take terrible risks. Because my playing is very clear, when I make a mistake you hear it».

Vladimir Horowitz

Il rischio di un investimento finanziario riguarda il carattere non deterministico dei suoi rendimenti futuri. In ambito operativo, tale rischio viene spesso approssimato e misurato attraverso la variabilità dei rendimenti osservati.

Quando l’esito di un investimento è noto con certezza in anticipo, il rischio è nullo.

Anche se nella realtà l’assenza totale di rischio non esiste, alcuni investimenti vengono considerati senza rischio (risk-free). Non ci si deve stupire, però, che anche il loro rendimento reale sia vicino a zero o, comunque, molto contenuto.

In senso stretto, in teoria economica e statistica si distingue tra rischio e incertezza:

• Si parla di rischio quando gli esiti possibili sono noti e sono note (o stimabili) anche le probabilità associate, come nel caso del lancio di un dado non truccato.
• Si parla invece di incertezza quando mancano informazioni affidabili anche sulle probabilità degli esiti.

Nel contesto finanziario non esistono esiti deterministici e le distribuzioni dei rendimenti non sono note con certezza; inoltre, esse presentano spesso caratteristiche come asimmetrie e code grasse.

Ciò non implica, però, una condizione di incertezza assoluta. Pur in assenza di una conoscenza perfetta del processo generatore dei rendimenti, è possibile stimarne alcune proprietà statistiche e ragionare in termini probabilistici.

Per questo motivo, nel linguaggio della finanza il termine rischio viene comunemente utilizzato in senso ampio per indicare la variabilità e l’imprevedibilità dei rendimenti, anche quando le probabilità non sono note in modo esatto.

Uno degli assiomi alla base della finanza è quello di avversione al rischio. In base a questo principio, un investitore:

• A parità di rendimento, sceglierà sempre il portafoglio meno rischioso.
• Accetta un livello di rischio più elevato solo in cambio di un rendimento atteso superiore.

L’avversione al rischio è una caratteristica intrinseca del comportamento umano: in ogni contesto, l’incertezza rappresenta una fonte di disagio e, quando non può essere eliminata, si cerca quantomeno di mitigarla.

La difficoltà, nel mondo finanziario, nasce dal fatto che rischio e rendimento si muovono sempre nella stessa direzione: a un livello di rischio più basso corrisponde, di norma, un rendimento atteso inferiore.

Questa regola, salvo inefficienze temporanee, è sempre valida per singoli strumenti finanziari.

Nella costruzione di un portafoglio esistono però situazioni in cui la combinazione di asset con determinate caratteristiche consente di aumentare il rendimento atteso a parità di rischio, o persino insieme a una sua riduzione.

Dobbiamo questa intuizione a Harry Markowitz, che nel 1952 pose le basi alla Teoria Moderna del Portafoglio (Modern Portfolio Theory).

L’avversione al rischio non deve essere confusa con la propensione al rischio: la propensione al rischio è una variabile soggettiva e indica la capacità dell’investitore di tollerare investimenti che possono registrare perdite o presentare rendimenti variabili.

Un’analisi puramente descrittiva del rischio può essere utile sul piano concettuale, ma non è sufficiente. Per essere realmente operativa, la nozione di rischio deve essere quantificata.

In particolare, il rischio di un portafoglio finanziario deve poter essere misurato.

Indice

1. Varianza e deviazione standard
2. Semi-varianza e semi-deviazione standard
3. Indice di Sharpe
4. Maximum drawdown (massima perdita cumulata)
5. Ulcer index
6. Value at Risk (VaR)
7. Conditional Value at Risk (CVaR)
8. Misure "di coda" e asimmetria: skewness e kurtosis
9. Tracking error

1. Varianza e deviazione standard

La misura di rischio più utilizzata è la variabilità dei rendimenti rispetto al loro valore medio, quantificata attraverso la varianza e la deviazione standard:

\begin{equation}
\text{Varianza} = \sigma^2 = \frac{1}{n}\sum_{i=1}^{n}\left(r_i - \bar{r}\right)^2
\end{equation}

\begin{equation}
\text{Deviazione standard} = \sigma = \sqrt{\frac{1}{n}\sum_{i=1}^{n}\left(r_i - \bar{r}\right)^2}
\end{equation}

Dove:
\(r_i\) = Rendimento del periodo i.
\(\bar{r}\) = Rendimento medio.
\(n\) = Numero di osservazioni.

Tra le due misure si preferisce in genere la deviazione standard, poiché risulta più immediata da interpretare: è espressa nella stessa unità di misura dei rendimenti osservati.

Un valore elevato indica una forte dispersione dei rendimenti attorno alla media e, di conseguenza, un rischio maggiore.

La deviazione standard può essere annualizzata moltiplicando il valore ottenuto dalla precedente formula per \(\sqrt{t}\), dove \(t\) rappresenta il numero di osservazioni in un anno (4 nel caso di rendimenti trimestrali, 12 nel caso di rendimenti mensili, 252 per i giornalieri e così via).

La validità di questa trasformazione richiede che i rendimenti non presentino autocorrelazione e che la loro varianza sia costante nel tempo.

Si tratta di un’ipotesi piuttosto forte, soprattutto nelle misurazioni di lungo termine e, nella pratica, spesso non verificata per quanto riguarda la costanza della varianza nel tempo: alcuni modelli statistici di stima, come i modelli GARCH, rilassano esplicitamente questo assunto.

La deviazione standard annualizzata dei rendimenti prende il nome di volatilità.

Un limite importante di questa misura è il trattamento simmetrico del rischio: vengono considerati rilevanti sia i movimenti bruschi al ribasso, che preoccupano l’investitore, sia quelli al rialzo, che invece risultano favorevoli.

Per affrontare questo aspetto sono state sviluppate misure alternative che si concentrano esclusivamente sulle perdite.

2. Semi-varianza e semi-deviazione standard

Poiché una forte variabilità dei rendimenti al di sopra della media è un esito favorevole per l’investitore, in alcuni contesti viene adottata una misura di rischio alternativa: la semi-varianza. La semi-deviazione standard non è altro che la radice quadrata della semi-varianza.

La semi-varianza si calcola utilizzando soltanto i rendimenti al di sotto del rendimento medio.

La formula di calcolo è analoga a quella della varianza e della deviazione standard, con l’unica differenza che i valori \(r_i\) inclusi sono solo quelli al di sotto di \(\bar{r}\):

\begin{equation}
\sigma_{\text{semi}} = \sqrt{\frac{1}{n}\sum_{r_i < \bar{r}}\left(r_i - \bar{r}\right)^2}
\end{equation}

Queste misure rientrano nel più ampio concetto di downside risk (rischio di ribasso), che concentra l'attenzione esclusivamente sugli esiti sfavorevoli.

Un’evoluzione rilevante consiste nel sostituire la media storica con un rendimento minimo accettabile (MAR, Minimum Acceptable Return).

In questo caso, la semi-deviazione standard viene calcolata considerando solo i rendimenti che scendono sotto una soglia prefissata, come ad esempio lo zero o il tasso d’inflazione.

La semi-deviazione standard compare al denominatore dell’indice di Sortino, un indicatore di performance corretta per il rischio che penalizza esclusivamente le variazioni negative dei rendimenti.

Questa misura di rischio ha una sua logica ma, nella pratica, non viene molto utilizzata: in presenza di una distribuzione simmetrica dei rendimenti, i risultati coincidono con quelli ottenuti tramite varianza o deviazione standard, poiché la semi-varianza risulta proporzionale alla varianza.

In un portafoglio ben diversificato, l’ipotesi di simmetria dei rendimenti è generalmente plausibile. In tali casi, il ricorso alla semi-varianza o alla semi-deviazione standard come misura aggiuntiva di rischio non fornisce informazioni ulteriori rispetto a quelle già offerte dagli indicatori tradizionali.

3. Indice di Sharpe

L’indice di Sharpe (Sharpe ratio) è un indicatore che valuta la performance di un portafoglio corretta per il rischio.

La sua formula è:

\begin{equation}SR=\frac{r_p-r_f}{\sigma_p} \end{equation}

Dove:
\(r_p\) = Rendimento del portafoglio.
\(r_f\) = Tasso di rendimento a rischio zero.
\(\sigma_p\) = Volatilità del portafoglio.

Un valore elevato dell’indice di Sharpe rende un portafoglio particolarmente interessante, poiché indica un buon equilibrio tra rischio e rendimento. L’indice può infatti essere interpretato come il rendimento ottenuto per ogni unità di rischio assunta.

Affidarsi esclusivamente all’indice di Sharpe per la scelta di un portafoglio non è però consigliabile. Considerato isolatamente, questo indicatore non consente di caratterizzare in modo univoco il rischio dell’investimento: uno stesso valore può infatti derivare sia da rendimenti e volatilità entrambi elevati, sia da una combinazione di valori entrambi contenuti.

Un’ulteriore criticità si verifica in presenza di rendimenti negativi, dove si produce un risultato controintuitivo. In tali casi, selezionare il portafoglio con l’indice di Sharpe più alto può portare a decisioni in contrasto con il principio di razionalità dell’investitore.

Si consideri, ad esempio, la scelta tra due portafogli. Il portafoglio A presenta un extra-rendimento rispetto al tasso privo di rischio pari al −5% e una deviazione standard del 10%. Il portafoglio B offre invece un extra-rendimento del −10% e una deviazione standard del 30%.

L’indice di Sharpe del portafoglio A è −0,50 mentre quello del portafoglio B è −0,33. Seguendo rigidamente il criterio dell’indice di Sharpe, si dovrebbe preferire il portafoglio B, poiché caratterizzato da un valore più elevato.

Eppure, questa scelta è irrazionale: come faccio a preferire il portafoglio che ha performato peggio sia in termini di rendimento che di volatilità?

Secondo alcune interpretazioni, la preferenza per il portafoglio più volatile potrebbe comunque essere coerente: se l’obiettivo è tornare rapidamente a rendimenti positivi, un livello di rischio più elevato aumenterebbe le probabilità di successo.

Altri autori ritengono invece questa lettura forzata e sostengono che, in presenza di rendimenti negativi, il criterio di selezione debba essere modificato, privilegiando il portafoglio con l’indice di Sharpe più elevato in valore assoluto: nell’esempio proposto, ciò porterebbe a scegliere il portafoglio A.

Questo dibattito resta in larga parte teorico e risulta rilevante soprattutto nell’analisi delle performance passate. Se l’obiettivo è selezionare un portafoglio in un’ottica prospettica, extra-rendimento e volatilità non sono osservabili, ma devono essere stimati.

Qualora tali stime indichino un extra-rendimento atteso negativo, la scelta è a senso unico: l’investimento più razionale è quello privo di rischio, che garantisce il rendimento \(r_f\).

In una simile situazione, evitare attività rischiose rappresenta la decisione più coerente. L’investimento a rischio zero offre infatti un rendimento atteso superiore e, al tempo stesso, assicura una volatilità nulla.

4. Maximum drawdown (massima perdita cumulata)

Tra le misure di rischio più direttamente percepibili dall’investitore, il maximum drawdown occupa una posizione di rilievo.

Un drawdown quantifica la perdita percentuale subita passando da un punto di massimo (picco) al successivo punto di minimo, prima che venga raggiunto un nuovo massimo.

Il maximum drawdown è il valore più elevato, in valore assoluto, tra tutti i drawdown osservati in un determinato periodo di tempo.

A differenza della volatilità, che è una misura statistica di natura aggregata, il drawdown risponde a una domanda molto precisa: nel momento peggiore osservato in passato, quale sarebbe stata la perdita acquistando sui massimi e vendendo sui minimi?

Nel grafico seguente, viene visualizzato il maximum drawdown di un portafoglio, calcolato sulla base del suo rendimento cumulato:

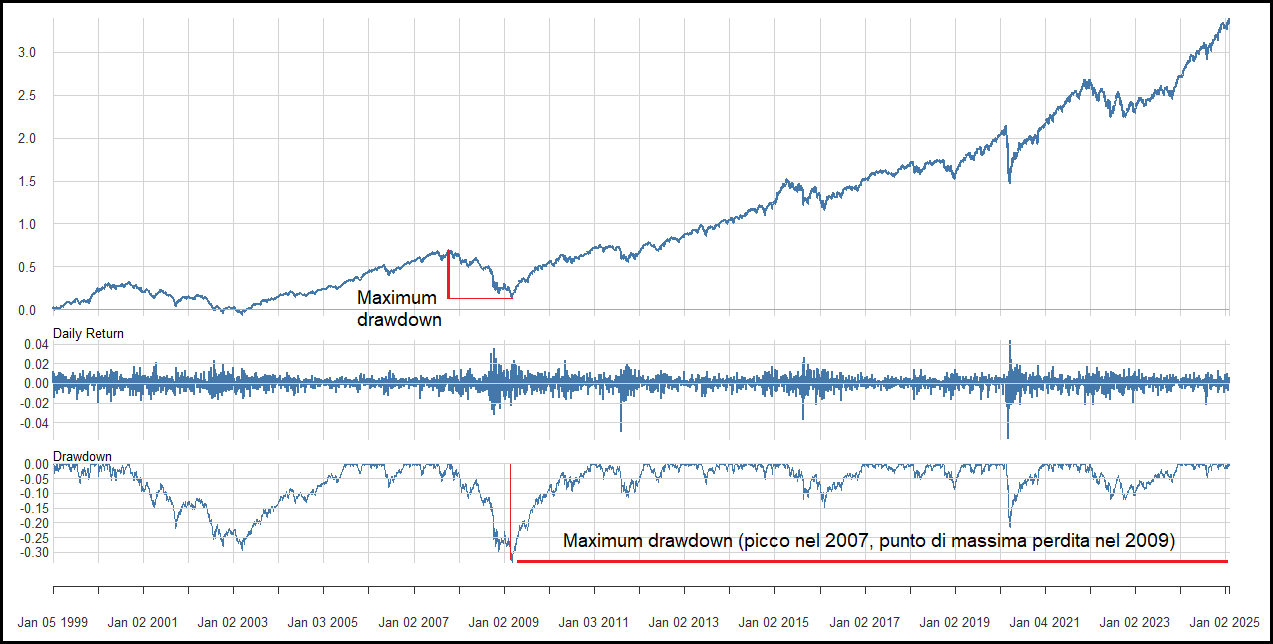
Nella parte superiore è riportato il rendimento cumulato, mentre in quella inferiore sono rappresentati i drawdown registrati nel periodo tra il 1999 e il 2024.

Il maximum drawdown è quello più profondo, ovvero quello con la distanza massima tra il massimo rendimento cumulato e il successivo minimo prima del raggiungimento di un nuovo massimo.

Nel grafico, è quello indicato in rosso e corrisponde a una perdita di poco superiore al 30%, toccata approssimativamente nel marzo 2009. Si tratta, quindi, della perdita percentuale massima subita da un investitore che avesse acquistato sul picco e venduto nel successivo punto di massima flessione.

Vediamo un esempio numerico. Si consideri un fondo che parte da un valore iniziale di 100 euro:

1. sale a 120 euro (picco);
2. scende a 90 euro;
3. risale a 110 euro (non supera il picco precedente);
4. scende a 80 euro (nuovo minimo);
5. risale a 130 euro (nuovo picco).

Il calcolo del maximum drawdown non dipende dall’ultimo movimento osservato, ma dalla massima distanza registrata rispetto al picco precedente più elevato:

• Primo calo: da 120 a 90 euro, con una perdita del 25%.
• Il valore scende successivamente fino a 80 euro, ma il picco di riferimento resta 120 euro, poiché 110 euro non costituiva un nuovo massimo storico.
• Calo massimo: da 120 a 80 euro, pari a una perdita del 33,3%.

Il maximum drawdown risulta quindi pari al −33,3%. È importante notare che un portafoglio può presentare una volatilità contenuta e, al tempo stesso, un maximum drawdown elevato quando le perdite, pur essendo singolarmente modeste, si accumulano in modo persistente nel tempo.

Pur offrendo una descrizione immediata delle perdite storicamente sperimentate, il maximum drawdown coglie solo l’episodio peggiore e non fornisce indicazioni sulla persistenza delle fasi di sottoperformance.

Per incorporare anche la dimensione temporale delle perdite, è stato introdotto l’Ulcer index.

5. Ulcer index

Accanto al maximum drawdown, un indicatore meno diffuso ma concettualmente importante è l’Ulcer index (UI), introdotto da Martin e McCann nel 1989.

Il nome richiama il disagio (“ulcer”) sperimentato sia dal gestore sia dall’investitore durante fasi prolungate di sottoperformance.

L’Ulcer index è affine alle misure basate sul drawdown, ma si distingue per il fatto di incorporare esplicitamente la durata delle perdite, oltre alla loro profondità.

In particolare, per ogni periodo viene considerato il drawdown rispetto al precedente massimo, e tale scostamento viene elevato al quadrato. In questo modo, drawdown profondi e persistenti nel tempo ricevono un peso maggiore.

L’Ulcer index è definito come:

\begin{equation}
\text{UI} = \sqrt{\frac{1}{n}\sum_{i=1}^{n} D_i^2}
\end{equation}

dove:
\(D_i\) è il drawdown registrato nel periodo \(i\) rispetto al precedente massimo.
\(n\) è il numero totale di osservazioni.

A differenza del maximum drawdown, che cattura solo l’episodio peggiore, l’Ulcer Index tiene conto dell’intero percorso dei rendimenti, penalizzando in modo particolare le fasi in cui il portafoglio impiega molto tempo a recuperare i livelli precedenti.

Per questo motivo, l’indicatore è sensibile sia alla profondità sia alla durata delle perdite.

L’Ulcer index risulta quindi particolarmente informativo in contesti in cui la tolleranza dell’investitore alle fasi prolungate di sottoperformance è un aspetto rilevante.

L’Ulcer index dipende dalla frequenza dei dati utilizzati e, come tutte le misure di drawdown, riflette esclusivamente il comportamento storico del portafoglio.

Sebbene le misure basate sul drawdown forniscano informazioni rilevanti sul profilo delle perdite storiche, esse non consentono di valutare la probabilità di eventi futuri, motivando l’introduzione di misure di rischio di natura probabilistica.

6. Value at Risk (VaR)

Il Value at Risk può essere definito come l’ammontare della perdita che, con un dato livello di confidenza, ci si attende di non superare su un portafoglio in un determinato periodo di tempo.

Il VaR è caratterizzato da due parametri:

• Il livello di confidenza α.
• L’orizzonte temporale di riferimento su cui viene calcolato.

Questi parametri possono essere scelti liberamente dall’analista oppure imposti da un’autorità di vigilanza, come avviene nel caso degli accordi internazionali di Basilea II.

In assenza di vincoli regolamentari, l’orizzonte temporale dovrebbe riflettere il periodo durante il quale l’investitore prevede di detenere il portafoglio, oppure il tempo necessario per liquidarlo.

Esistono diverse metodologie di calcolo del VaR, ognuna con pregi e difetti:

1. Metodo parametrico (varianza–covarianza): assume che i rendimenti seguano una distribuzione normale, la classica “curva a campana”.
2. Simulazione storica: non richiede ipotesi teoriche sulla distribuzione dei rendimenti; utilizza i dati storici, li ordina dal peggiore al migliore e seleziona il percentile desiderato.
3. Simulazione Monte Carlo: genera migliaia di scenari futuri tramite un modello statistico e ricava il VaR dalla distribuzione simulata.

Il metodo parametrico è il più semplice da implementare, ma risulta molto sensibile all’ipotesi di normalità dei rendimenti. La simulazione storica è spesso più facile da interpretare, mentre l’approccio Monte Carlo è potenzialmente molto solido, pur introducendo un maggiore “rischio di modello”.

Vediamo un semplice esempio numerico relativo al metodo parametrico. Consideriamo un portafoglio bilanciato 60/40 (60% azioni e 40% obbligazioni) del valore di 100.000 euro.

Assumiamo un rendimento atteso annuo pari al 5% e una volatilità del 10%. Si assume inoltre che i rendimenti seguano una distribuzione normale.

In una distribuzione normale, il 5° percentile si colloca circa a 1,65 deviazioni standard sotto la media. Il VaR annuale al 95% può quindi essere approssimato come:

\begin{equation}
\text{VaR}_{95\%}^{(1\,\text{anno})} \approx 1{,}65 \times 10\% - 5\% = 11{,}5\%
\end{equation}

Ne consegue che, con una probabilità del 95%, il portafoglio non subirà una perdita superiore all’11,5% nel corso dell’anno successivo. In termini monetari, ciò equivale a:

\begin{equation}
100.000\,\text{€} \times 11{,}5\% = 11.500\,\text{€}
\end{equation}

Il VaR a un anno con livello di confidenza del 95% è quindi pari a 11.500 euro. Questo significa che esiste una probabilità del 5% di registrare, nell’arco di un anno, una perdita superiore a tale importo.

Il VaR non va confuso con una perdita massima: il portafoglio potrebbe subire perdite superiori al VaR, seppure con una probabilità minore di quella utilizzata nel calcolo del VaR.

Uno dei limiti principali di questa misura risiede proprio nel fatto che non fornisce informazioni sull’ammontare medio delle perdite oltre la soglia del VaR: in altre parole, indica con quale probabilità la “diga” tiene, ma non quanta acqua entri nel caso in cui ceda.

Il VaR può infine essere convertito su orizzonti temporali diversi applicando la regola della radice quadrata del tempo: ad esempio, partendo da un VaR giornaliero, moltiplicandolo per \(\sqrt{21}\) si ottiene il VaR mensile (un mese borsistico conta in media 21 sedute).

Analogamente, un VaR mensile moltiplicato per \(\sqrt{12}\) fornisce una stima del VaR annuale.

Come già accennato, il VaR non fornisce informazioni sull’entità media delle perdite che si verificano oltre la soglia considerata; questo aspetto viene affrontato dal Conditional Value at Risk.

7. Conditional Value at Risk (CVaR)

Il Conditional Value at Risk (CVaR), noto anche come Expected Shortfall (ES) o Expected Tail Loss (ETL), permette di superare alcuni dei limiti del Value at Risk.

Il CVaR misura il valore atteso della perdita che si registrerà qualora questa ecceda il VaR calcolato al livello di confidenza α.

Se il VaR risponde alla domanda qual è la soglia di perdita associata a un dato livello di confidenza?, il CVaR affronta una questione diversa: se gli eventi peggiori si verificano, quanto si perde mediamente?

In termini assoluti di perdita, il CVaR è sempre superiore al VaR e fornisce quindi un’informazione più completa sulla rischiosità di un portafoglio.

Analogamente al VaR, anche il CVaR dipende da due parametri: il livello di confidenza α e l’orizzonte temporale considerato.

Riprendendo l’esempio precedente, con un VaR annuale pari a 11.500 euro a un livello di confidenza del 95%, ci si può chiedere cosa accada nel restante 5% dei casi peggiori:

• Scenario A: le perdite in quel 5% di casi sono tutte concentrate intorno a valori leggermente superiori al VaR, ad esempio intorno a 12.000 euro.
• Scenario B: le perdite nello stesso 5% variano in modo importante, arrivando anche a 25.000 o 30.000 euro, come può accadere in presenza di forti crolli di mercato.

Dal punto di vista del VaR, i due scenari risultano indistinguibili, poiché la soglia di rischio rimane pari a 11.500 euro. Il CVaR, invece, prende in considerazione la severità delle perdite oltre tale soglia e ne calcola la media:

• Nello Scenario A, il CVaR potrebbe attestarsi intorno a 12.200 euro.
• Nello Scenario B, il CVaR potrebbe salire anche fino a circa 18.000 euro.

La differenza è evidente: il CVaR dello Scenario B segnala un rischio molto più alto, che il VaR non è in grado di catturare.

L’informazione fornita dal CVaR è particolarmente rilevante perché descrive la profondità delle perdite in presenza di eventi estremi, legati alle cosiddette code grasse (fat tails).

Due portafogli possono infatti presentare lo stesso VaR ma valori di CVaR differenti, rendendo più rischioso quello caratterizzato da un CVaR più elevato.

Un ulteriore punto di forza del CVaR riguarda una proprietà matematica nota come sub-additività, che il VaR non sempre soddisfa.

In virtù di tale proprietà, il CVaR di un portafoglio diversificato è sempre minore o uguale alla somma dei CVaR dei singoli strumenti che lo compongono.

Il VaR, in alcune configurazioni statistiche, può invece suggerire paradossalmente che la diversificazione aumenti il rischio complessivo, in contrasto con l’intuizione e con il buon senso finanziario.

Così come nel caso del VaR, il Conditional Value at Risk non rappresenta una perdita massima: perdite superiori al CVaR sono possibili, sebbene associate a probabilità più basse.

8. Misure "di coda" e asimmetria: skewness e kurtosis

Volatilità e VaR parametrico tendono a sottostimare il comportamento dei rendimenti nelle code della distribuzione.

Per questo motivo, accanto alle principali misure di rischio già introdotte, è utile considerare anche ulteriori indicatori:

• Skewness (asimmetria): indica se i rendimenti estremi sono distribuiti in modo simmetrico attorno alla media. Una skewness negativa, tipica dei mercati azionari, segnala che i crolli improvvisi tendono a essere più frequenti e più intensi rispetto ai rialzi di pari rapidità. Dal punto di vista di un investitore prudente, gli asset caratterizzati da un’asimmetria negativa pronunciata risultano quindi meno desiderabili.
• Kurtosis (curtosi): misura la probabilità che si verifichino eventi estremi. Una distribuzione con elevata curtosi, detta leptocurtica, presenta le cosiddette code grasse: eventi che, sotto l’ipotesi di normalità, sarebbero ritenuti altamente improbabili si manifestano invece con una frequenza tutt’altro che trascurabile, come mostrano episodi quali il crollo del 1987 o la crisi finanziaria del 2008.

Trascurare questi due parametri significa sottostimare il rischio associato a eventi estremi e, nei casi più gravi, del rischio di rovina.

Skewness e kurtosis non sono misure di rischio in senso stretto, ma forniscono informazioni sulla struttura della distribuzione dei rendimenti.

Il loro ruolo è quindi complementare rispetto a indicatori come volatilità, VaR e CVaR: aiutano a interpretare correttamente le ipotesi sottostanti a tali misure.

In presenza di forte asimmetria o di elevata curtosi, l’uso di modelli basati sull’ipotesi di normalità può risultare particolarmente fuorviante, portando a una sottostima sistematica della probabilità e della severità degli eventi estremi.

Per questo motivo, l’analisi di skewness e kurtosis è spesso utilizzata come valutazione preliminare, utile per giudicare l’adeguatezza delle misure di rischio adottate.

Finora il rischio è stato analizzato in termini assoluti, ossia con riferimento alle perdite potenziali di un portafoglio considerato isolatamente; in molti contesti operativi, tuttavia, l’attenzione si sposta sullo scostamento rispetto a un indice di riferimento, dando origine a misure di rischio di natura relativa.

9. Tracking error

Per chi investe in fondi a gestione attiva che puntano a superare un indice di riferimento (benchmark), una misura di rischio particolarmente rilevante è il tracking error volatility, spesso indicato semplicemente come tracking error.

Questo indicatore misura la deviazione standard della differenza tra i rendimenti del portafoglio e quelli del benchmark.

Il tracking error quantifica quanto la gestione si discosti dall’andamento dell’indice di riferimento, ossia dalla “traiettoria media” del mercato. In questo senso, esso cattura il grado di discrezionalità del gestore rispetto al benchmark.

Un tracking error contenuto suggerisce una gestione molto vicina a quella passiva, con scostamenti limitati rispetto all’indice. Al contrario, valori elevati indicano che il gestore sta assumendo posizioni sensibilmente diverse dal benchmark, effettuando scelte attive più marcate.

In questo contesto, il rischio consiste nella possibilità di ottenere risultati potenzialmente molto diversi da quelli del mercato, in senso positivo o negativo, come conseguenza di decisioni di investimento che si discostano dalla media.

Il tracking error risulta perciò particolarmente informativo quando l’obiettivo dell’investimento è la sovraperformance rispetto al mercato.