Piano di Accumulo del Capitale a rate costanti (PAC Cost averaging)
- Information
- PAC
- Prima pubblicazione: 07 Marzo 2016
«La semplicità è la suprema sofisticazione».
Leonardo da Vinci
L'ebook dell'articolo in formato PDF può essere scaricato dagli utenti BASIC (registrazione gratuita): una volta effettuato il log in, basterà selezionare l'opzione "Download" dal menu utente in alto a destra.
Questo articolo fa parte del Percorso per principianti, pensato per chi desidera apprendere le basi della finanza personale e degli investimenti. In fondo alla pagina, troverai il link al prossimo articolo del percorso.
Il Cost Averaging (CA) è una strategia di investimento molto utilizzata dagli investitori da oltre 70 anni. Ancora oggi, è al centro dell'attenzione degli studiosi di finanza e del mondo accademico, che su di esso continuano ad esprimere giudizi molto contrastanti.
In italiano, il Cost Averaging viene quasi sempre identificato con un Piano di Accumulo del Capitale a rate costanti o, più semplicemente, PAC.
Il PAC a rate costanti non è tuttavia l'unico: la più conosciuta modalità alternativa è il Value Averaging.
Questo articolo, suddiviso in 18 capitoli, ha i seguenti obiettivi:
- Approfondire lo studio dei PAC a rate costanti con una metodologia di analisi nuova, supportata da numerosi grafici, backtest su serie storiche reali e simulazioni col metodo Monte Carlo.
- Introdurre e backtestare alcuni interventi discrezioniali sui PAC a rate costanti: i disinvestimenti anticipati e i versamenti aggiuntivi.
- Confrontare tra di loro i piani di accumulo in base alle seguenti variabili: periodicità dei versamenti, commissioni, maxi-rata iniziale e giorno d'investimento della rata.
- Mettere in luce i pro ed i contro dei PAC a rate costanti rispetto agli investimenti in un'unica soluzione (PIC).
- Analizzare e commentare i principali articoli scientifici sul Cost Averaging.
Si consiglia la lettura dei capitoli nell'ordine proposto. Dall’indice è comunque possibile accedere direttamente a ciascuno di essi.
I backtest dei Piani di Accumulo del Capitale a rate costanti (Cost Averaging) su singoli fondi possono essere effettuati nella sezione Analisi PAC di Dedalo Invest.
Indice
- Introduzione
- Funzionamento di un Piano di Accumulo del Capitale a rate costanti
- Backtest e analisi di un Piano di Accumulo del Capitale a rate costanti
- Simulazione di migliaia di PAC su un unico fondo
- Simulazioni su un fondo dal trend discendente
- Rendimento e volatilità interna
- Simulazioni non parametriche col metodo Monte Carlo
- Simulazioni parametriche col metodo Monte Carlo
- Quando le cose vanno male: il PAC peggiore (serie storiche reali)
- Confronto tra PAC a rate costanti e PIC
- I disinvestimenti anticipati e i versamenti aggiuntivi
- Confronto tra PAC mensili e di altre periodicità
- La maxi-rata iniziale
- Le commissioni di transazione e d’ingresso
- La scelta del giorno d’investimento della rata
- Letteratura sul Cost Averaging
- Conclusioni
- Bibliografia
1. Introduzione

«Fai in modo che il tuo discorso sia migliore del tuo silenzio o taci».
Dionisio I di Siracusa
Il Piano di Accumulo del Capitale (PAC) è una modalità di investimento che prevede una serie di versamenti periodici finalizzati alla costruzione del capitale nel tempo.
Il piano di accumulo ha la peculiarità di diversificare temporalmente gli acquisti e permettere un investimento graduale sui mercati finanziari.
Come lo stesso nome sottintende, l’investitore non dispone necessariamente del capitale iniziale, ma lo accumula nel tempo grazie al risparmio periodico di una parte di reddito, che viene destinata all’acquisto di quote di uno strumento finanziario: di solito, un fondo a gestione attiva o passiva.
La rateizzazione del capitale differenzia il Piano di Accumulo del Capitale dal semplice investimento in un’unica soluzione (PIC, Piano di Investimento di Capitale).
Come vedremo nel capitolo 16, in certi contesti, quando si parla di PAC, si implica la disponibilità di tutto il capitale fin dall’inizio dell’investimento. In questi casi, la scelta di suddividere l’investimento in più rate periodiche sarebbe motivata esclusivamente da considerazioni di tipo strategico.
In questo articolo, faremo riferimento essenzialmente a piani di accumulo azionari. Tuttavia, essendo una modalità di investimento, un PAC potrebbe essere sviluppato con qualsiasi tipo di strumento finanziario (fondi azionari, obbligazionari, bilanciati, monetari, azioni di singole società e così via).
L’analisi dei Piani di Accumulo del Capitale che verrà svolta nei capitoli successivi si avvarrà sia di backtest con serie storiche reali, sia di simulazioni parametriche e non parametriche effettuate con il metodo Monte Carlo.
I risultati ottenuti ci aiuteranno a rispondere alle seguenti domande:
- Quali sono i rendimenti medi generati dai Piani di Accumulo del Capitale in funzione della loro durata?
- Per quanto tempo devo investire per minimizzare la probabilità di incorrere in un rendimento negativo?
- In caso di rendimento negativo, quanto tempo devo aspettare affinché la perdita venga riassorbita?
- Quale forbice di rendimento posso aspettarmi da un Piano di Accumulo del Capitale costruito su un determinato fondo?
- Come posso evitare di perdere tutto o buona parte del guadagno costruito in tanti anni di versamenti, a causa di un crollo improvviso dei mercati finanziari?
- È conveniente effettuare dei versamenti aggiuntivi quando il mercato sta attraversando una fase negativa?
- Quali sono le differenze nelle performance di un Piano di Accumulo del Capitale con versamenti delle rate a periodicità mensile, bimestrale, trimestrale, quadrimestrale, semestrale o addirittura annuale?
- Che differenza di rendimento esiste, mediamente, tra un PAC e un PIC di pari durata? Quale dei due è più rischioso?
- Qual è il reale impatto delle commissioni di transazione e di quelle d’ingresso su un Piano di Accumulo del Capitale?
- Qual è il miglior giorno del mese per investire in un Piano di Accumulo del Capitale?
2. Funzionamento di un Piano di Accumulo del Capitale a rate costanti

«Il poco è poco, ma se aggiungi il poco al poco e lo fai di frequente, presto il poco diventerà molto».
Esiodo
Le principali tipologie di piano di accumulo sono il Cost Averaging (detto anche Dollar Cost Averaging o Unit Cost Averaging) e il Value Averaging.
In un piano di accumulo Cost Averaging, la rata è costante; in uno Value Averaging, i versamenti sono variabili e hanno l’obiettivo di riallineare il valore corrente del sottostante a quello di un target che cresce nel tempo.
I vantaggi principali di un PAC a rate costanti sono i seguenti:
- Trasformazione di piccoli versamenti periodici in un grande capitale: un piano di accumulo permette di costruire un capitale nel tempo a partire da piccoli risparmi periodici. Il valore del capitale al termine del piano di accumulo varierà in funzione della durata dell’investimento, dell’entità e della frequenza dei versamenti e dell’andamento del sottostante.
- Mediazione del prezzo di acquisto e riduzione dei rischi: con un piano di accumulo, è possibile mediare nel tempo i prezzi di carico delle posizioni. In alcune occasioni, si acquisterà a quotazioni di mercato basse e in altre elevate ma, rappresentando ciascun versamento una quota minima del capitale che verrà complessivamente impiegato, il prezzo medio di carico si collocherà raramente su un livello troppo elevato. Nei piani di accumulo, il prezzo medio di carico delle quote acquistate è pari alla media armonica dei prezzi di acquisto (approfondiremo questa proprietà in seguito). La maggior parte degli autori, infine, ritiene che i piani di accumulo siano meno rischiosi di un investimento in un’unica soluzione.
- Soluzione al problema del timing d’ingresso: è molto diffusa l’opinione che i piani di accumulo abbiano l’importante vantaggio di eliminare il rischio di sbagliare il momento giusto per entrare in Borsa:
Si elimina completamente anche il rischio di sbagliare il momento giusto per entrare in Borsa.
Investire, settembre 2006
L’ultimo dei vantaggi elencati non è formulato correttamente: un PAC, infatti, mitiga il rischio rispetto a un investimento in un’unica soluzione, ma non esclude la possibilità di sbagliare il momento giusto per entrare in borsa.
Il momento si può sbagliare in pieno (basti pensare a un piano di accumulo decennale iniziato a marzo 1999, che approfondiremo nel capitolo 9): il minor rischio del piano di accumulo è determinato dalla diversificazione temporale degli acquisti e non dal timing d’ingresso.
Il timing d’ingresso determina per forza di cose quello di fine investimento ed è quest’ultimo che definisce il valore finale del capitale investito, pari al numero di quote accumulate moltiplicato per il prezzo finale delle quote.
Per ottenere un rendimento positivo, è necessario che il valore finale delle quote sia superiore alla somma investita complessivamente (numero delle rate × valore della rata):
Rendimento del PAC (in euro o altra valuta) = NAV finale × Numero Quote − Numero Rate × Importo rata
Nella parte destra di questa uguaglianza troviamo quattro quantità: il NAV finale (il prezzo finale delle quote), il numero delle quote accumulate, il numero delle rate e l’importo di ciascuna rata.
- Gli ultimi 2 valori sono costanti e vengono impostati all’inizio dell’investimento. Salvo cambi di strategia in corsa – generalmente sconsigliabili – non vengono mai modificati.
- Il numero di quote dipende dall’andamento del NAV durante la vita del piano di accumulo: è un valore che non possiamo ovviamente influenzare o prevedere con esattezza. Tuttavia, il numero di quote ha delle caratteristiche che lo rendono abbastanza stabile nel tempo:
- È sempre crescente: in un PAC Cost Averaging senza interventi discrezionali, compreremo un certo numero di quote a intervalli regolari, senza mai effettuare vendite.
- È legato all’andamento del NAV da una relazione inversa: cresce maggiormente quando i prezzi scendono (e viceversa). In un mercato crescente, il suo incremento marginale è decrescente.
- Il NAV finale dipende dalla quotazione del sottostante nel momento in cui il piano di accumulo giunge al termine. Questa è la variabile chiave e la conosceremo soltanto a fine investimento, quando sarà troppo tardi per intervenire nel caso in cui le cose non fossero andate per il verso giusto. È una variabile sulla quale non abbiamo alcun controllo. Se ci si vuole attivare per limitare i danni che potrebbero essere causati da un'improvvisa discesa del NAV, bisogna farlo prima, in tempo utile. Nel capitolo 11, analizzeremo una modalità operativa con questo specifico scopo: i disinvestimenti anticipati.
I piani di accumulo a rate costanti hanno un’interessante proprietà: il prezzo medio di carico delle quote è pari alla media armonica dei prezzi di acquisto.
La media armonica è il reciproco della media aritmetica dei reciproci: dato un insieme di n osservazioni x1, x2, …, xn, la media armonica H è pari a:
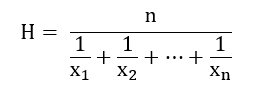
Vediamo un esempio.
Ipotizziamo il versamento di 5 rate costanti sul fondo XYZ. I prezzi delle quote sono: 51,88; 53,11; 49,99; 53,41 e 56,29. Applicando la formula della media armonica, il prezzo medio di carico sarà:
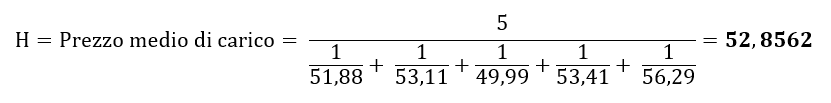
Verifichiamo la correttezza della formula sviluppando il calcolo di un piano di accumulo vero e proprio. Ipotizziamo 5 versamenti da 1.000 euro ciascuno:
| Piano di accumulo a rate costanti | ||||||
|---|---|---|---|---|---|---|
| N° rata | Data | NAV | Rata | Quote acquistate | Quote totali | Pagamenti totali |
| 1 | 1986-11-17 | 51,88 | 1.000 | 19,2753 | 19,2753 | 1.000 |
| 2 | 1986-12-15 | 53,11 | 1.000 | 18,8288 | 38,1041 | 2.000 |
| 3 | 1987-01-15 | 49,99 | 1.000 | 20,0040 | 58,1081 | 3.000 |
| 4 | 1987-02-16 | 53,41 | 1.000 | 18,7231 | 76,8312 | 4.000 |
| 5 | 1987-03-17 | 56,29 | 1.000 | 17,7651 | 94,5963 | 5.000 |
Prezzo medio di carico: 5.000 / 94,5963 = 52,8562
Il prezzo medio di carico è esattamente lo stesso. La media armonica giunge allo stesso risultato senza la necessità di conoscere il valore della rata e senza dover calcolare il numero di quote acquistate ogni volta che si effettua un versamento.
La funzione per il calcolo della media armonica è disponibile e facilmente utilizzabile in tutti i software per la produzione e gestione di fogli elettronici.
3. Backtest e analisi di un Piano di Accumulo del Capitale a rate costanti

«Prima di iniziare, pianifica attentamente».
Marco Tullio Cicerone
Analizzeremo uno specifico Piano di Accumulo del Capitale Cost Averaging su una serie storica reale, appartenente a un fondo azionario a gestione attiva: Raiffeisen Azionario Globale VT (ISIN: AT0000785266). Il fondo appartiene alla categoria Azionari Internazionali Large Cap Blend ed è un fondo ad accumulazione.
La scelta di questo fondo e di uno specifico piano di accumulo (il primo tra i piani trentennali che possono essere simulati sulla serie storica disponibile) è riconducibile alla lunghezza della serie storica (oltre 33 anni).
Sarebbe stato preferibile scegliere un ETF della stessa categoria: gli ETF sono dei fondi a gestione passiva, in generale molto più economici ed efficienti di quelli a gestione attiva.
Ai fini della nostra analisi, abbiamo tuttavia preferito il Raiffeisen a causa della limitatezza delle serie storiche degli ETF, che sono degli strumenti finanziari relativamente nuovi.
In un certo senso, è meglio così: le performance conseguite saranno con molta probabilità inferiori a quelle di un ipotetico fondo a gestione passiva della stessa categoria. I valori ottenuti nelle nostre analisi potranno essere considerati, quindi, prudenziali.
Partiamo con la visualizzazione del grafico dei NAV del fondo Raiffeisen Azionario Globale VT, nel periodo compreso tra il 15 novembre 1986 e il 15 novembre 2016:
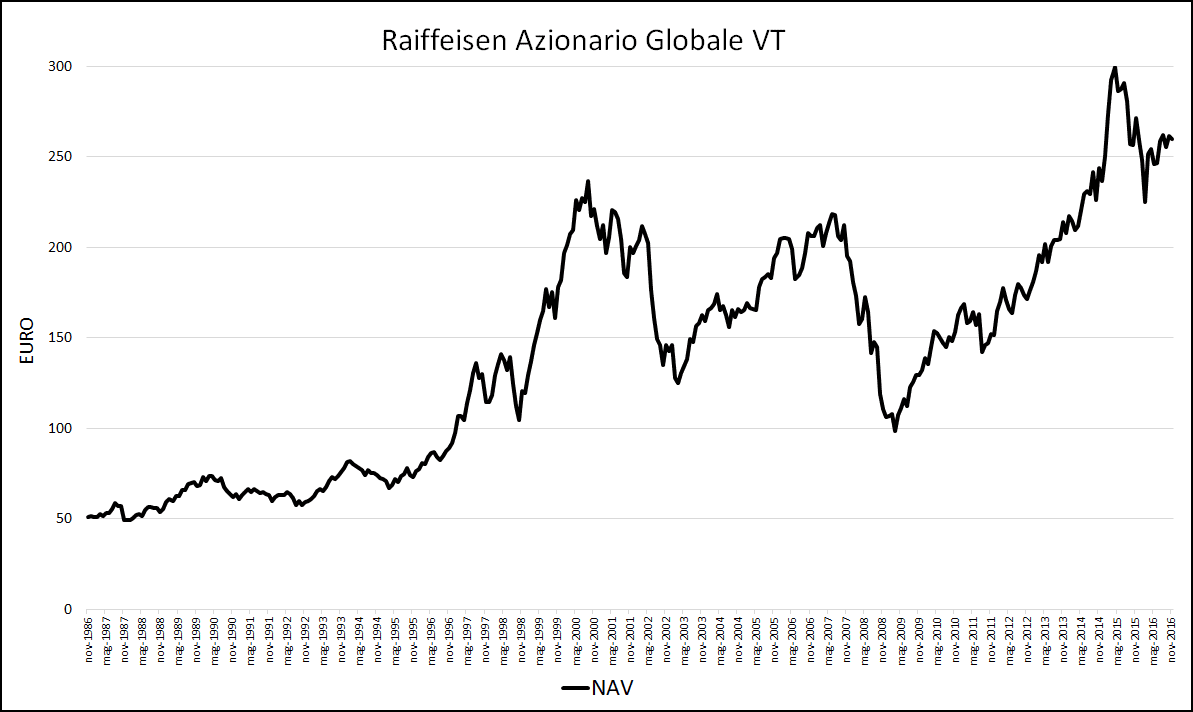
Fig. 1 – Grafico del NAV (Raiffeisen Azionario Globale VT)
Il trend del fondo è molto simile a quello del mercato azionario globale. La riprova ce la fornisce l’indice MSCI World, il cui grafico nello stesso periodo è il seguente:
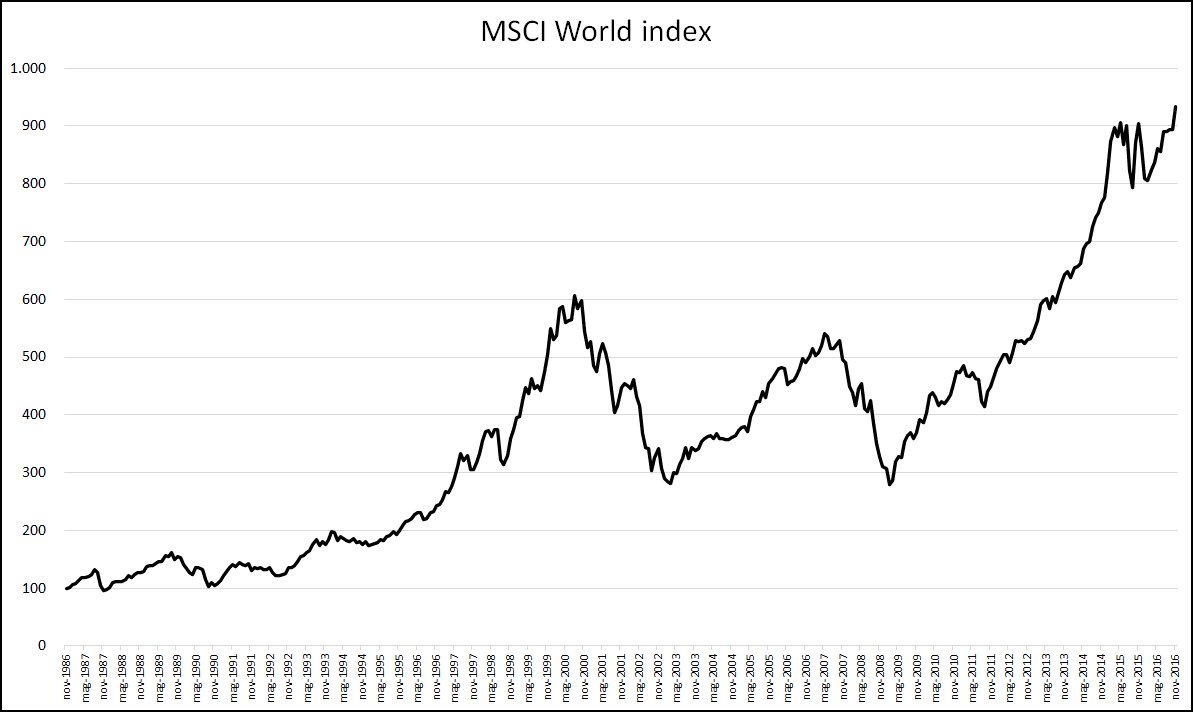
Fig. 2 – Grafico dell’indice MSCI World Gross (USD)
Le due più importanti crisi dell’ultimo ventennio sono ben visibili: la dotcom, esplosa nel 2000 e terminata nel 2003 e la più violenta crisi dei subprime, iniziata verso la fine del 2007 e durata fino ai primi mesi del 2009.
I grafici successivi entreranno nel merito del piano di accumulo Cost Averaging e si focalizzeranno sulle grandezze principali che lo contraddistinguono: pagamenti cumulati, valore corrente, numero cumulato di quote.
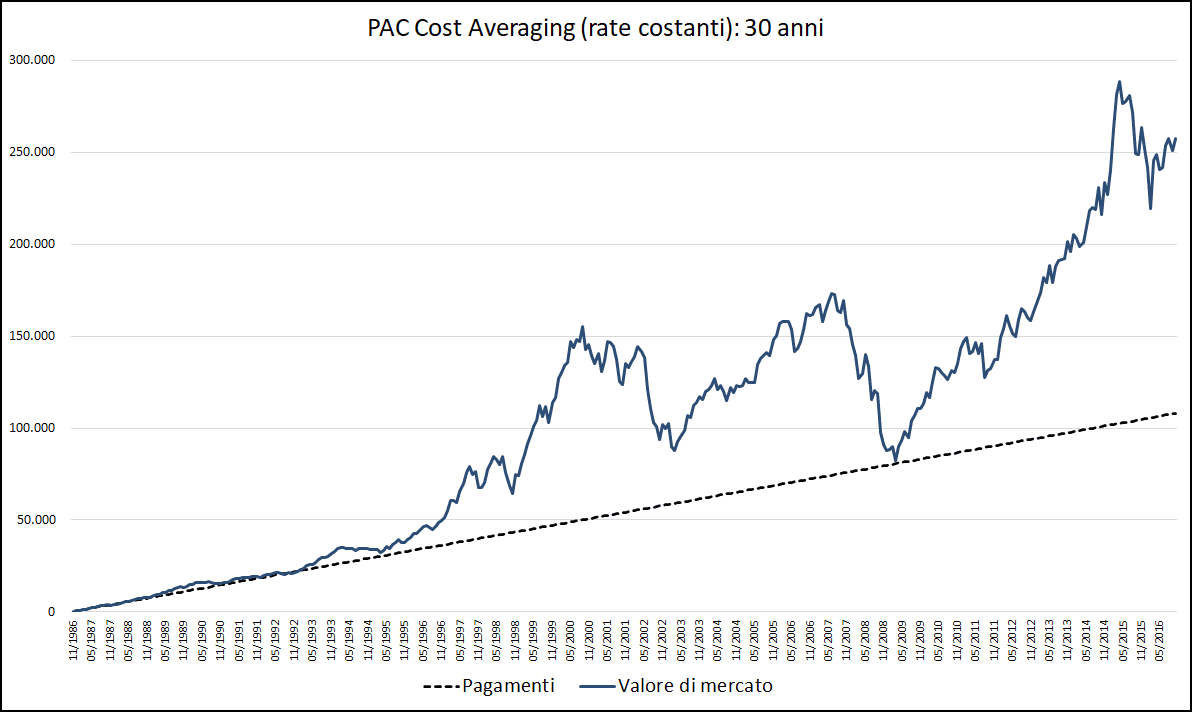
Fig. 3 – PAC Cost Averaging. Rata: 300 euro. Durata: 30 anni
Questo è il grafico di un piano di accumulo Cost Averaging costituito da 360 rate mensili dell’importo di 300 euro ciascuna. Per semplicità, non sono stati considerati i costi di transazione (saranno inseriti in seguito).
La linea nera tratteggiata misura il totale dei pagamenti effettuati. La crescita è costante: alla fine del PAC, saranno stati versati complessivamente 108.000 euro (360 rate da 300 euro ciascuna).
La linea blu rappresenta il valore corrente (o valore di mercato) delle quote accumulate: il grafico segue approssimativamente l’andamento del NAV del fondo.
Il valore corrente, una volta versata l’ultima rata, corrisponde alla somma finale generata dal piano di accumulo: 257.517,32 euro.
L’investimento si è concluso con il rendimento del 138,44%, pari al 5,26% annualizzato. Sono state sottoscritte complessivamente 984,0549 quote: la linea fucsia misura il numero cumulato di quote per rata versata.
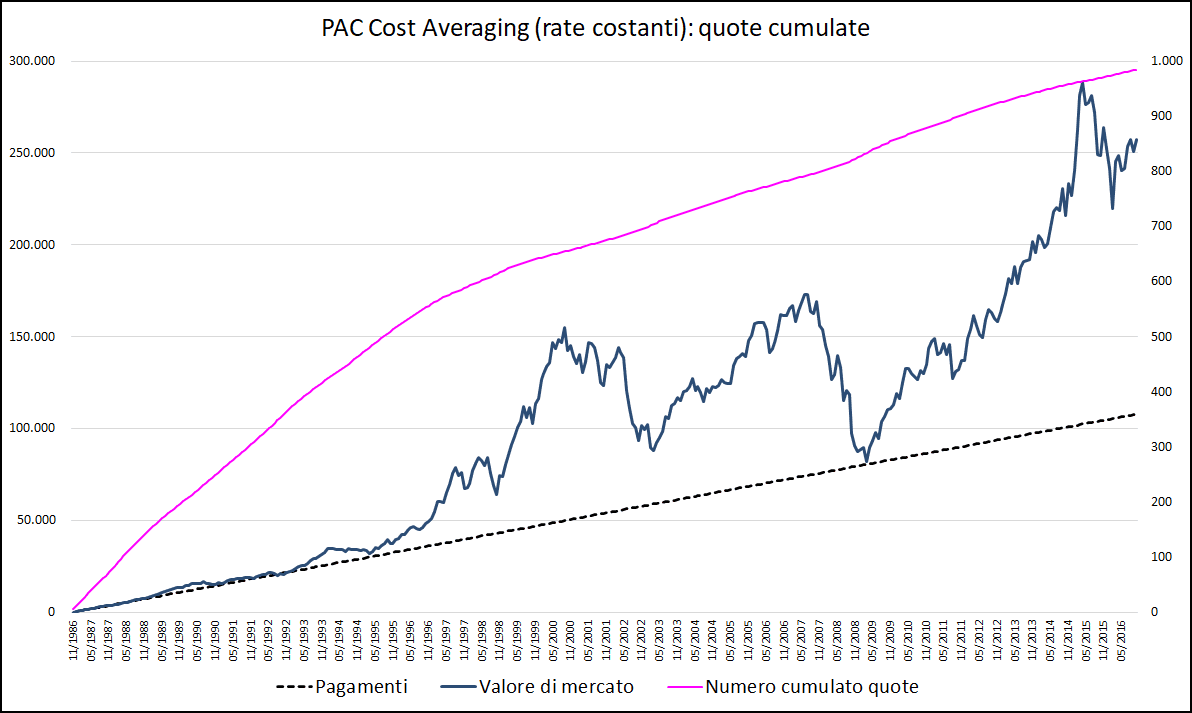
Fig. 4 – PAC Cost Averaging. Rata: 300 euro. Durata: 30 anni (con andamento cumulato quote)
Il numero cumulato di quote sottoscritte è una quantità sempre crescente ma, dato che il sottostante segue un trend positivo di lungo termine, l’incremento marginale si riduce con il passare del tempo: i prezzi delle quote salgono e con la stessa somma di denaro se ne comprano sempre di meno.
Un orizzonte temporale trentennale è particolarmente adatto agli investimenti azionari: è molto lungo e c’è tutto il tempo per recuperare eventuali perdite o, come in questo caso, per non andare in rosso nonostante le due gravi crisi ricordate in precedenza, sopraggiunte dopo circa 14 e 22 anni dall’inizio del piano di accumulo.
Non sempre, però, gli investitori possono permettersi investimenti così lunghi. Vediamo il grafico di un piano di accumulo decennale sullo stesso fondo, costruito con i dati dei primi 10 anni della serie storica disponibile:
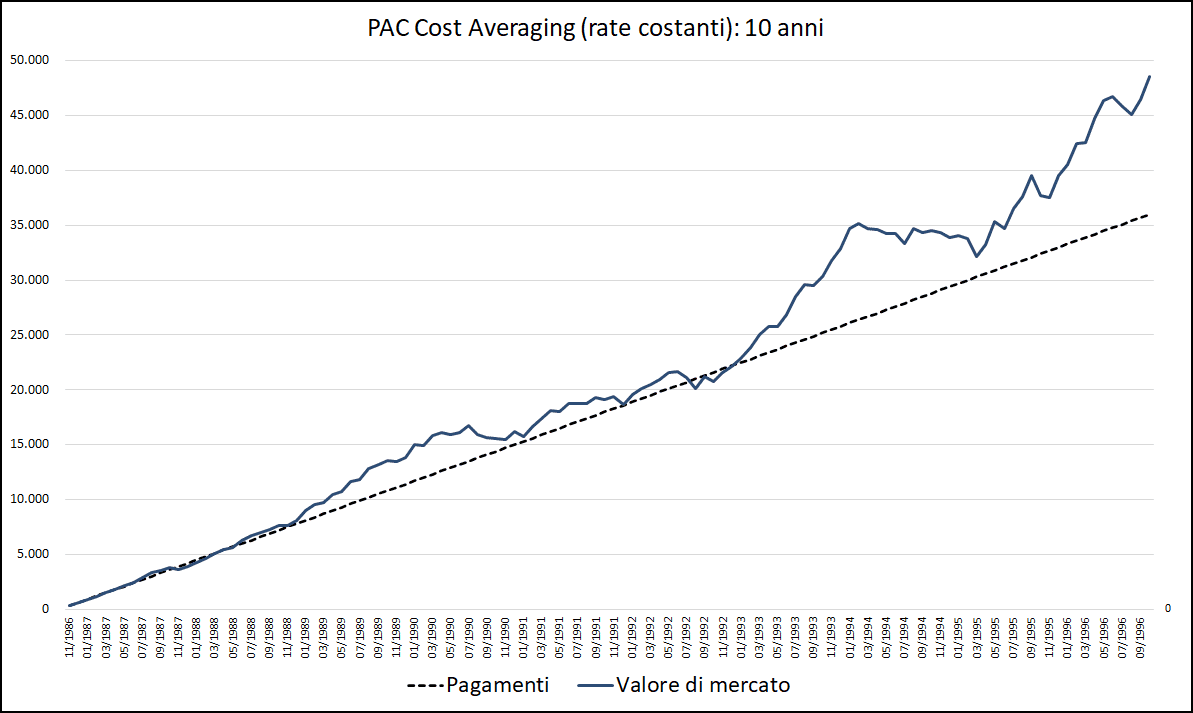
Fig. 5 – PAC Cost Averaging. Rata: 300 euro. Durata: 10 anni
Il valore corrente è sempre stato superiore a quello dei pagamenti effettuati, salvo brevi periodi nei primi anni dell’investimento e intorno al 1992.
Si è trattato di un buon piano di accumulo, che ha messo al riparo l’investitore dallo stress psicologico di eventuali crisi finanziarie: i momenti in cui il rendimento è stato negativo sono stati pochissimi, con perdite molto contenute.
Scendere sotto i 10 anni, aumenta il rischio di un investimento azionario: la probabilità di chiudere un investimento con un rendimento negativo è tanto maggiore quanto minore è la durata del piano di accumulo.
Analizziamo il PAC biennale:
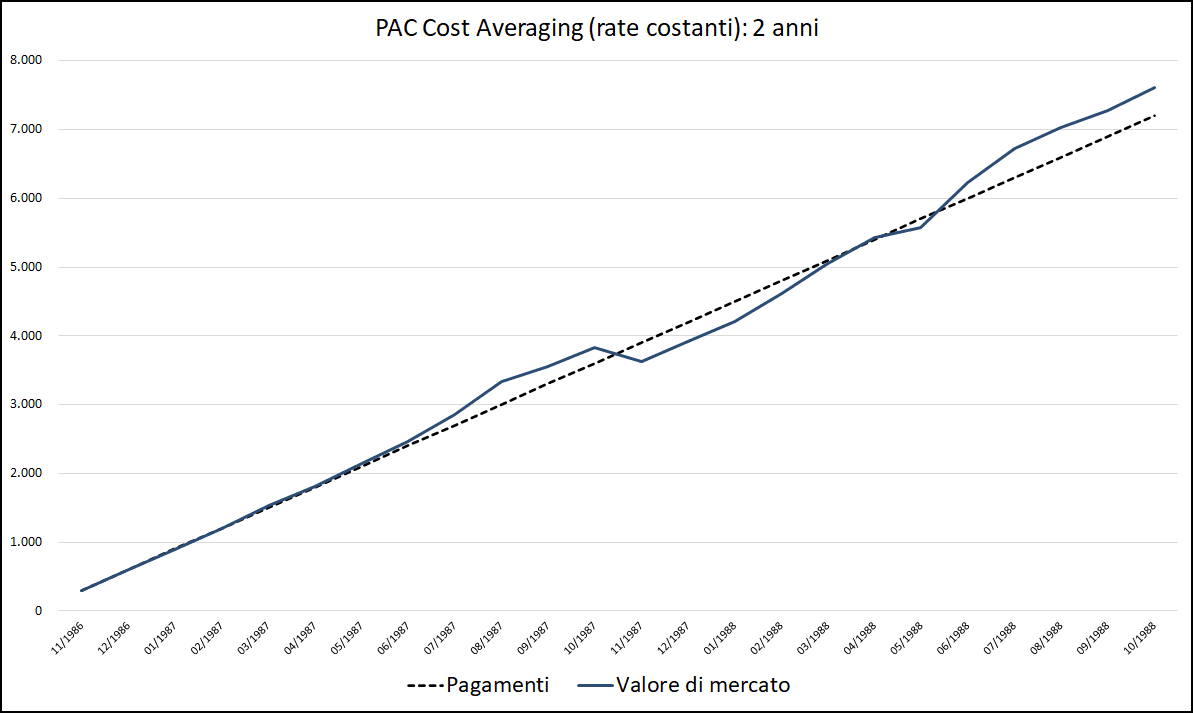
Fig. 6 – PAC Cost Averaging. Rata: 300 euro. Durata: 2 anni
Di nuovo, il valore corrente del piano di accumulo oscilla intorno alla linea tratteggiata dei pagamenti. La volatilità è molto ridotta: 2 anni sono pochi e questo piano di accumulo avrebbe attraversato periodi con rendimenti leggermente negativi, per poi concludersi positivamente.
Un piano di accumulo Cost Averaging iniziato a novembre 1986 sarebbe stato particolarmente vantaggioso dato che, indipendentemente dalla sua durata, avrebbe generato un rendimento positivo o appena negativo.
Vedremo nel prossimo capitolo quali siano i rischi dei PAC di breve durata.
Invece di un fondo dal trend positivo, avremmo potuto sceglierne uno dalle prestazioni inferiori. Prendiamo l’Aberdeen Japanese Equity Fund A Acc JPY (ISIN: LU0011963674), appartenente alla categoria Azionari Giappone: è un fondo di lunghezza simile al Raiffeisen, ma dalla performance decisamente peggiore.
Questo è il grafico del NAV:
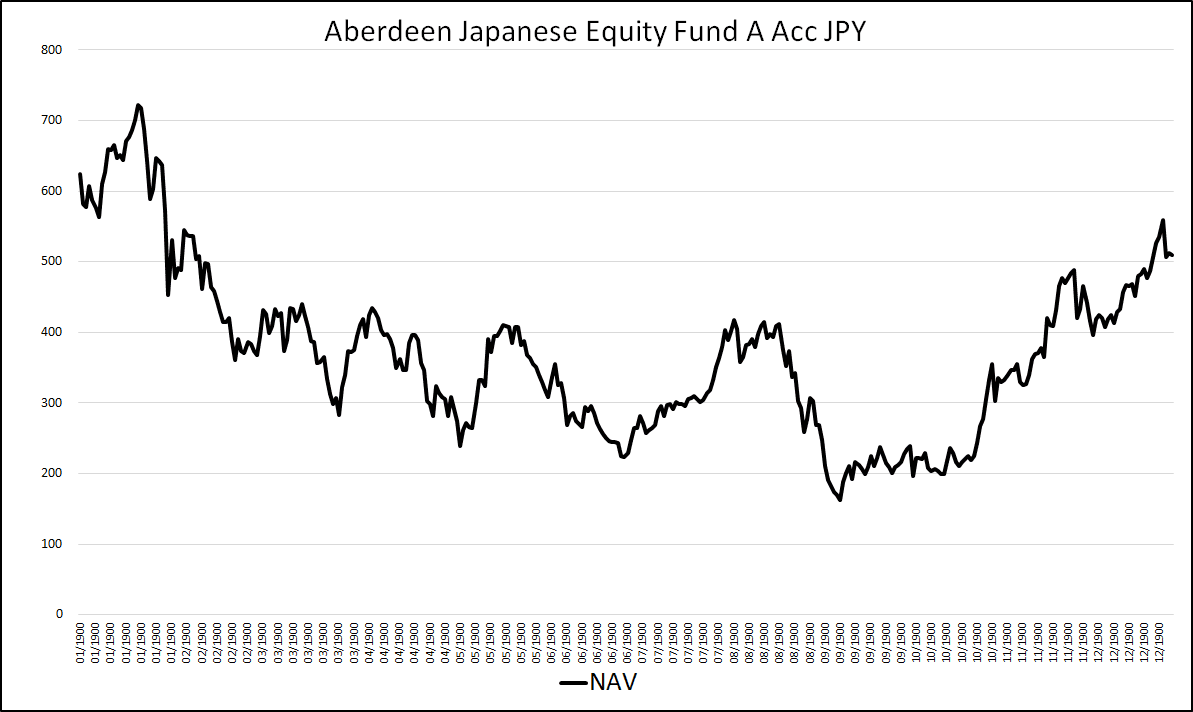
Fig. 7 – Grafico del NAV (Aberdeen Japanese Equity Fund A Acc JPY)
Il mercato azionario giapponese, dopo il massimo assoluto raggiunto sul finire degli anni ‘80, è entrato in una fase di depressione durata oltre due decenni. Anch’esso è stato vittima della crisi dei subprime, che l’ha trascinato fino ai minimi di inizio 2009, prima di tornare a crescere in modo convincente soltanto nel 2012.
I valori di inizio 1990 non sono stati più raggiunti.
Chi avesse investito in un’unica soluzione nel mercato azionario giapponese a partire dal 1990 avrebbe molto difficilmente realizzato un rendimento positivo. Con un piano di accumulo, la probabilità di successo sarebbe stata maggiore.
Partiamo con l’analisi di un PAC trentennale:
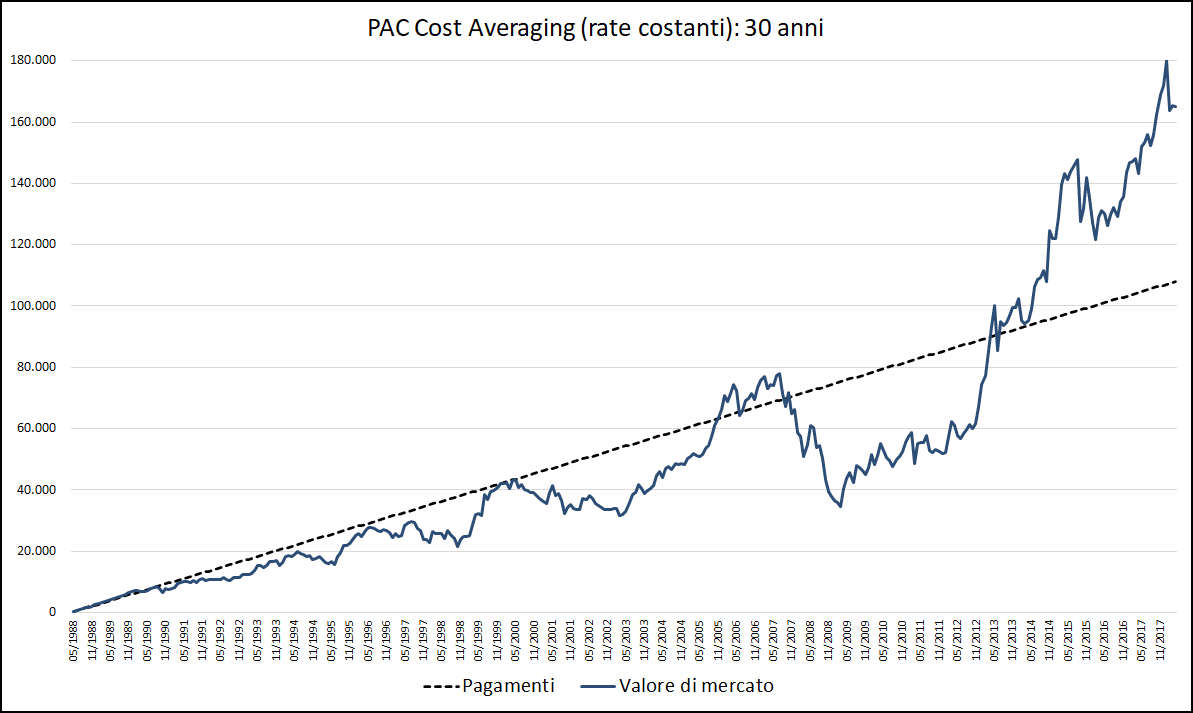
Fig. 8 – PAC Cost Averaging. Rata: 300 euro. Durata: 30 anni (Aberdeen Japanese Equity Fund A Acc JPY)
Il rendimento è stato del 52,96%: il valore finale dell’investimento è risultato essere 165.193 euro a fronte di una somma cumulata di pagamenti di 108.000 euro. Un bel successo, considerando l’andamento del NAV del fondo.
Tuttavia, analizzando il grafico è possibile osservare come il rendimento di questo piano di accumulo sia stato prevalentemente negativo per circa 25 anni: un periodo lunghissimo, difficile da superare anche per gli investitori più disciplinati.
Vediamo come sarebbero andate le cose con un piano di accumulo decennale:
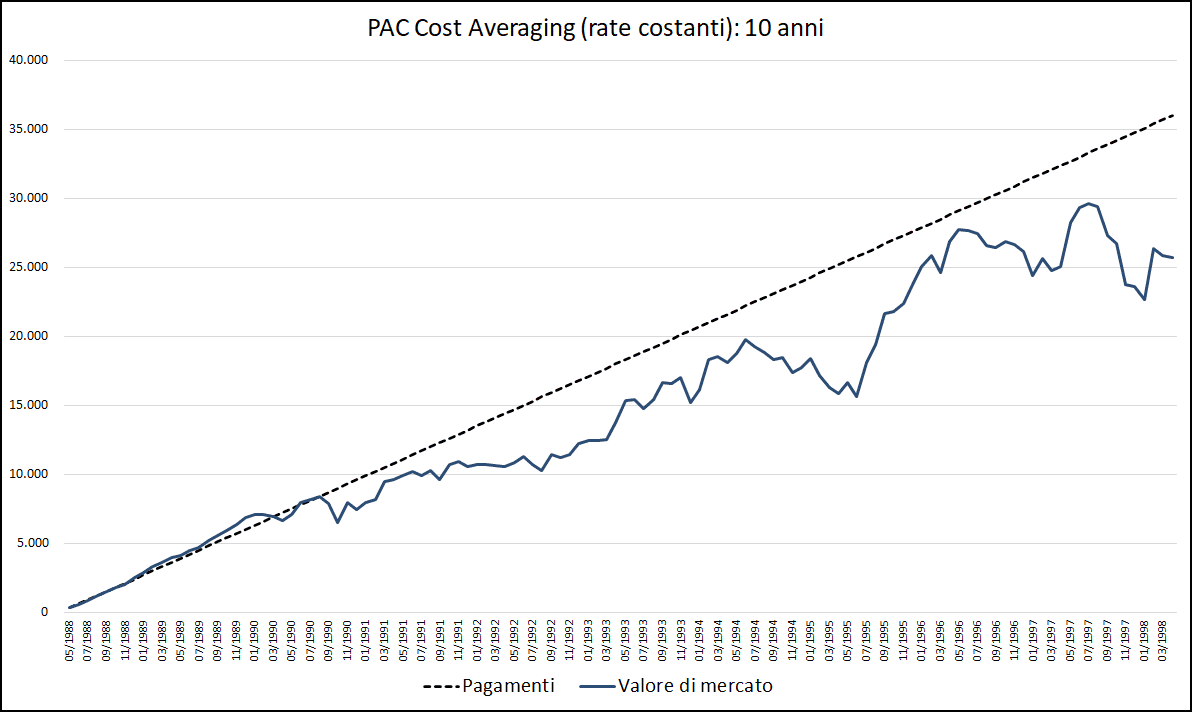
Fig. 9 – PAC Cost Averaging. Rata: 300 euro. Durata: 10 anni (Aberdeen Japanese Equity Fund A Acc JPY)
Per quasi tutta la vita del PAC, il rendimento sarebbe stato negativo, con una performance finale intorno al −30%: un classico esempio di investimento che per tutta la sua durata avrebbe stressato psicologicamente lo sfortunato sottoscrittore.
Riducendo la lunghezza del piano di accumulo a soli due anni, l’andamento del valore di mercato sarebbe stato il seguente:
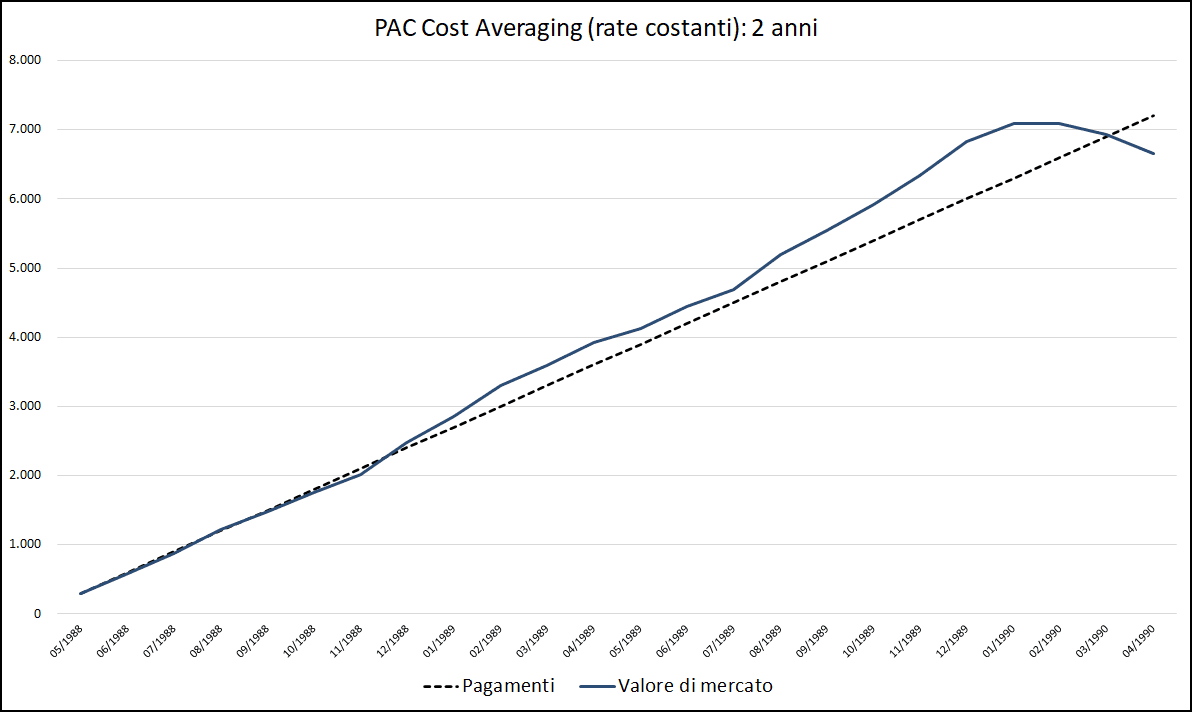
Fig. 10 – PAC Cost Averaging. Rata: 300 euro. Durata: 2 anni (Aberdeen Japanese Equity Fund A Acc JPY)
Il destino sarebbe stato beffardo: l’investimento, dopo essere quasi sempre stato in terreno positivo e aver toccato il 12,50% a gennaio 1990, avrebbe subito un brusco calo, generando un pessimo rendimento finale: −7,50%.
I risultati di questi pochi piani di accumulo costruiti sui fondi Raiffeisen e Aberdeen sono stati disomogenei, sia nel breve che nel lungo termine. Possiamo però fare già qualche considerazione: un Piano di Accumulo del Capitale a rate costanti permette di diversificare temporalmente l’investimento, comprando quote di fondi in modo graduale.
La diversificazione temporale è assente in un investimento in un’unica soluzione (PIC), dato che l’intera somma viene impiegata nello stesso momento.
Come è noto, esiste un altro tipo di diversificazione: quella orizzontale (o spaziale), finalizzata a suddividere il capitale in più strumenti finanziari.
Dato che con un piano di accumulo si investe spesso in un singolo strumento finanziario, è importante che se ne scelga uno ben diversificato: i fondi svolgono benissimo questo compito, ma non tutti i fondi sono uguali.
Il fondo Raiffeisen, il primo analizzato, è un azionario globale; il secondo, l’Aberdeen, è un azionario giapponese. Il primo permette di investire in azioni di tutto il mondo; il secondo soltanto in azioni giapponesi. Il primo è più diversificato del secondo e questa maggiore diversificazione ha permesso di ottenere una performance decisamente migliore, dal momento che il mercato azionario globale è cresciuto molto più di quello giapponese nel periodo analizzato.
Sarebbe potuto accadere il contrario?
Certamente: avremmo potuto scegliere un fondo azionario di un’area geografica o di un settore con delle performance migliori di quelle del mercato globale.
In generale, però, ogni investimento limitato a una specifica area geografica è meno diversificato di uno globale. Alcune aree otterranno dei rendimenti migliori di quelli del mercato globale; altre, peggiori: dato che è impossibile conoscere a priori quale area geografica o quale settore performerà sopra alla media, la scelta di concentrare l'investimento in una specifica area geografica sarà inevitabilmente più rischiosa rispetto a quella di diversificare a livello globale.
Un'ultima considerazione: i piani di accumulo hanno generalmente durate lunghe o molto lunghe. Se si decide di non diversificare al massimo, ci si assume il rischio di vanificare uno sforzo di 15, 20 o addirittura più anni, non a causa dell'andamento del mercato, quanto della scelta dell'area geografica o del settore sbagliato.
Vale la pena prendersi un rischio del genere?
4. Simulazione di migliaia di PAC su un unico fondo

«I nostri obiettivi possono essere raggiunti solamente attraverso una buona pianificazione, nella quale dobbiamo assolutamente credere e in base alla quale dobbiamo agire».
Pablo Picasso
Generalizziamo l’analisi e concentriamoci su tutti i possibili Piani di Accumulo del Capitale Cost Averaging che sarebbe stato possibile costruire sul fondo Raiffeisen Azionario Globale VT.
Oltre ai piani di accumulo biennali, decennali e trentennali, saranno simulati anche quelli delle seguenti durate: 3, 4, 5, 6, 7, 8, 9, 15, 20 e 25 anni.
Nei backtest verranno considerate anche le commissioni di transazione, dette anche diritti fissi.
Le analisi seguenti sono state condotte utilizzando il servizio di Analisi PAC disponibile su Dedalo Invest.
Abbiamo utilizzato i seguenti parametri:
- Importo rata: 300 euro.
- Giorno di pagamento della rata: 15 del mese (o primo giorno feriale successivo, nel caso in cui il 15 sia un sabato, una domenica o un altro giorno festivo).
- Data di inizio e fine analisi: novembre 1986 - novembre 2021.
- Numero di rate della maxirata: 1 (maxirata non presente).
- Applicazione commissioni: nessuna commissione percentuale (casella non selezionata, quindi i valori presenti nei campi “Commissioni (%)” e “% prima rata” non saranno applicati).
- Diritti fissi: 9 euro, applicati una sola volta all’inizio di ciascun PAC.
- Diritti fissi rata: 0,95 euro, applicati ogni volta che viene versata una rata (a partire dalla seconda di ciascun PAC).
- Periodicità rata: 1 (rata mensile).
- Rendimento medio annualizzato: presente (casella selezionata).
- Più uno: non presente (casella non selezionata). Selezionando questa checkbox i calcoli vengono effettuati un periodo successivo al versamento dell’ultima rata. Questo parametro sarà approfondito nel capitolo 12.
- Disinvestimenti anticipati e Versamenti aggiuntivi: non selezionati.
Vediamo la tabella di output dell’analisi:
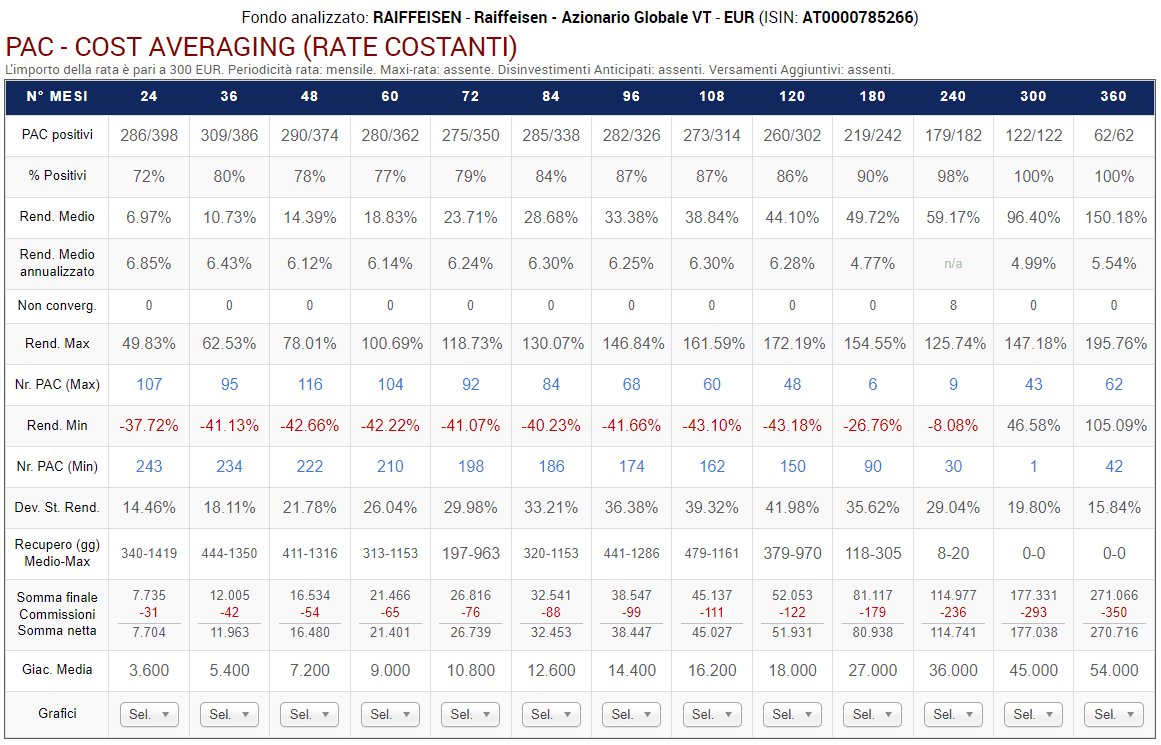
Fig. 11 – Raiffeisen: PAC Cost Averaging. Rata: 300 euro
Ogni colonna corrisponde a una specifica lunghezza in mesi dei piani di accumulo, come da intestazione della tabella. La tabella dovrà leggersi, quindi, verticalmente.
Sono stati analizzati i piani a 24 rate (2 anni), 36 rate (3 anni), 48 rate (4 anni), 60 rate (5 anni), 72 rate (6 anni), 84 rate (7 anni), 96 rate (8 anni), 108 rate (9 anni), 120 rate (10 anni), 180 rate (15 anni), 240 rate (20 anni), 300 rate (25 anni) e 360 rate (30 anni).
I backtest sono rolling. Questo significa che, ad esempio, sono state effettuate 398 simulazioni a 2 anni. La prima copre il periodo novembre 1986 – ottobre 1988; la seconda, dicembre 1986 – novembre 1988; la 398°, dicembre 2019 – novembre 2021.
Le prime due righe della tabella riportano il numero di PAC positivi sul totale e la percentuale corrispondente. Ad esempio, i piani di accumulo più brevi vantano una percentuale positiva del 72% (286 PAC positivi su 398).
La percentuale di PAC positivi tende a incrementarsi col crescere della lunghezza dei piani di accumulo: una conferma che – per aumentare la probabilità di chiudere positivamente un investimento azionario – si debba utilizzare un orizzonte temporale il più lungo possibile (i piani della durata di 25 e di 30 anni sono risultati tutti positivi).
Il rendimento medio e il rendimento medio annualizzato sono un’informazione estremamente importante: mentre i piani di accumulo più corti hanno ottenuto un rendimento medio del 6,97% e del 6,85% medio annualizzato, quelli di durata trentennale (che sono 62), hanno generato, rispettivamente, il 150,18% e il 5,54%.
La riga successiva indica il numero di PAC nei quali il calcolo del rendimento annualizzato non ha generato un risultato valido: quando si ha a che fare con una serie di cash flow, non esiste una formula matematica che ci consenta di ottenere il risultato voluto.
Per calcolare il rendimento annualizzato deve essere utilizzata una procedura iterativa, conosciuta come metodo di Newton (o delle tangenti), che permette di determinare il risultato tramite successive approssimazioni.
Purtroppo, in certe occasioni la procedura non converge verso un valore specifico, e il numero di volte che questo succede è riportato nella riga “Non converg.” della tabella: dato che non è stato possibile far convergere 8 procedure di calcolo nei PAC a 240 rate, non è stato nemmeno visualizzato il rendimento annualizzato medio dei piani di questa durata.
Dalla sesta alla nona riga della tabella troviamo i rendimenti massimi e minimi dei piani di accumulo e il numero di piano corrispondente.
Prendiamo ad esempio i PAC di durata quinquennale (60 rate): il migliore ha generato un rendimento del 100,69%; il peggiore, del −42,22%. La differenza tra questi due valori è enorme ed è un primo indicatore della variabilità dei rendimenti dei piani di accumulo per durata.
Il rendimento minimo è una misura molto importante: rappresenta il caso peggiore tra tutti quelli backtestati. Oscilla intorno al −40% nei PAC delle durate fino a 10 anni: in quelli più lunghi inizia a migliorare, fino a essere abbondantemente positivo nei piani di accumulo di 25 e 30 anni.
Selezionando i numeri corrispondenti, si possono visualizzare i grafici dei rendimenti per rata versata dei PAC che hanno ottenuto il rendimento massimo o minimo. Ad esempio, cliccando sul numero 48 nella colonna dei piani di accumulo decennali, sarà visualizzato il seguente grafico (il miglior PAC è stato il 48° dei 302 analizzati):
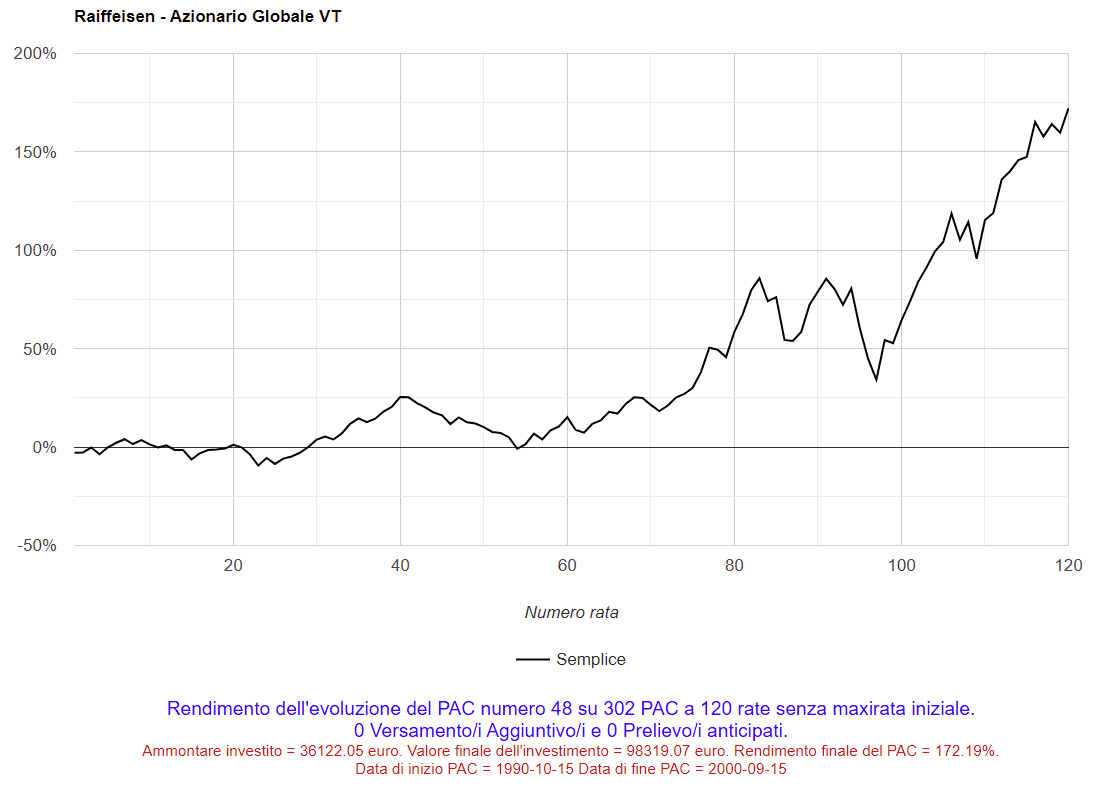
Fig. 12 – Raiffeisen: PAC Cost Averaging. Miglior PAC
Nell’asse delle ascisse troviamo il numero di rata versata; in quello delle ordinate il rendimento del piano di accumulo dopo il versamento di ognuna di esse.
Il rendimento finale è stato del 172,19% ma, nei primi 5 anni (60 rate), è oscillato intorno allo zero: sembrava un PAC non degno di nota. Nei 5 anni successivi, e in particolare negli ultimi 2, il rendimento è iniziato a crescere in maniera vertiginosa fino a toccare il suo massimo proprio in concomitanza dell’ultima rata.
Sotto al grafico, vengono riportate delle informazioni addizionali: questo piano di accumulo è iniziato il 15 ottobre 1990 ed è terminato il 15 settembre 2000. Nel 2000 i mercati azionari mondiali hanno segnato dei massimi assoluti (fino a quel momento): di lì a poco però, in seguito allo scoppio della bolla dei titoli legati a Internet, sarebbe iniziata la crisi finanziaria dotcom, che avrebbe provocato un lungo mercato orso durato fino a marzo 2003.
In altre occasioni, le cose sono andate in modo diverso: cliccando sul numero 150 nella colonna dei piani di accumulo decennali, sarà visualizzato il seguente grafico (il peggior PAC è stato il 150° dei 278 analizzati):
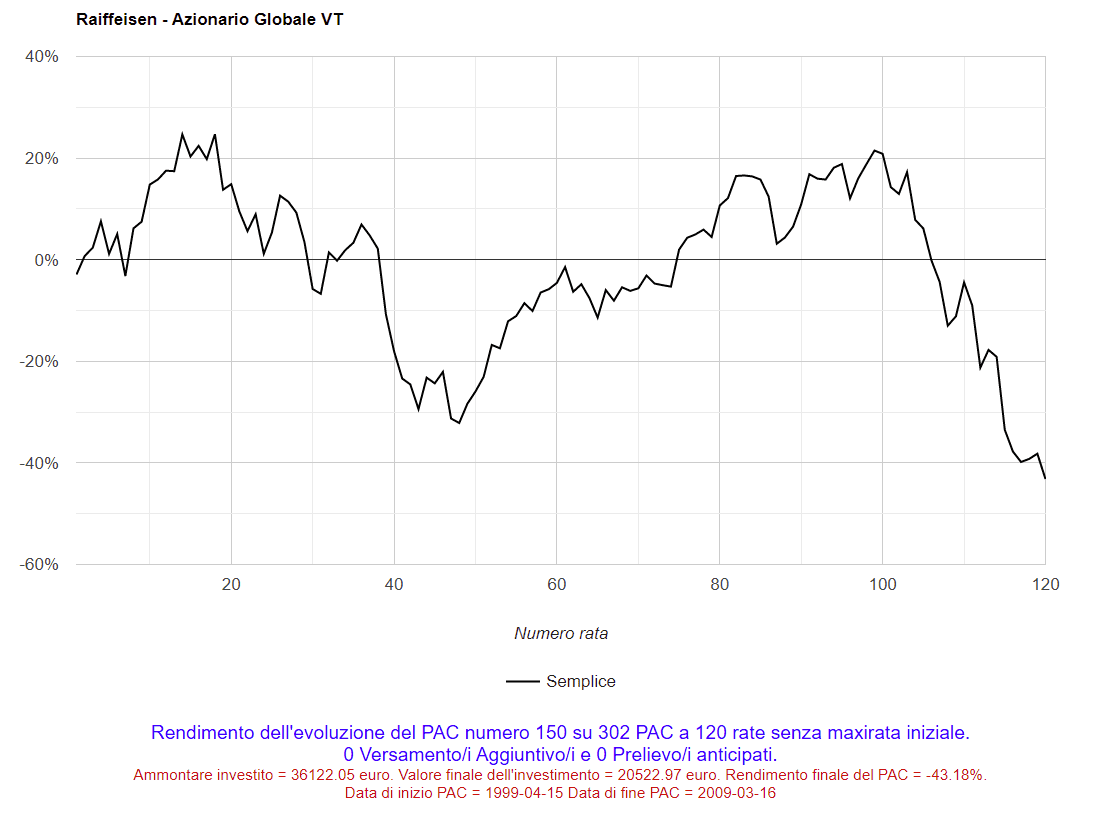
Fig. 13 – Raiffeisen: PAC Cost Averaging. Peggior PAC
Il rendimento finale è stato del −43,18%. Eppure, soltanto una ventina di rate prima del termine, il rendimento era addirittura superiore al 20%. Qualcosa di grave deve essere successo in quegli ultimi, drammatici, mesi: la crisi dei subprime.
Nelle informazioni sotto al grafico, si può osservare come questo piano di accumulo si sia sviluppato dal 15 aprile 1999 al 16 marzo 2009: esattamente nel momento più acuto della crisi, quando i mercati hanno toccato i valori minimi.
Il rendimento per rata di questo PAC è stato altalenante: il piano è iniziato ad aprile 1999, quando i mercati erano in forte crescita (sprint finale della bolla dotcom, scoppiata l’anno successivo). C’è stata quindi una lunga fase di decrescita, seguita da un recupero durato quasi 5 anni e dalla violenta crisi dei subprime.
L’andamento dei mercati finanziari non può essere previsto: l’investitore nel miglior PAC avrebbe avuto una grande dose di fortuna; quello nel peggior PAC, di sfortuna.
Nel commentare il terzo dei vantaggi generalmente associati ai piani di accumulo (soluzione al problema del timing d’ingresso), avevamo detto che il momento di ingresso sul mercato si può sbagliare in pieno, mentre il minor rischio rispetto a un investimento in un’unica soluzione è determinato dalla diversificazione temporale degli acquisti e non dal timing d’ingresso.
È un po’ quello che abbiamo riscontrato analizzando il migliore e il peggior PAC:
- Momento di ingresso sul mercato: iniziando un piano di accumulo decennale il 15 ottobre 1990, avremmo ottenuto un rendimento del 172,19%; iniziandolo il 15 aprile 1999, del −43,18%. Iniziandolo in qualsiasi altro momento, nell’intervallo temporale analizzato, avremmo ottenuto un rendimento all’interno di questa forbice. Il momento di ingresso determina quello di fine dell’investimento e influenza pesantemente il risultato finale.
- Minor rischio rispetto a un investimento in un’unica soluzione: l’investimento decennale in un’unica soluzione iniziato il 15 ottobre 1990 avrebbe generato un rendimento del 272,68%; quello iniziato il 15 aprile 1999, del −35,34%. In questo caso, l'ipotetico minor rischio dei piani di accumulo non si sarebbe concretizzato: investendo in un’unica soluzione, il rendimento peggiore sarebbe stato più alto (in assoluto, sarebbe stato pari al −38,76%, ottenuto dal 167° PIC). Selezionando una diversa durata, avremmo potuto ottenere il risultato opposto, ma avremmo distorto l’analisi scegliendo a posteriori una durata conveniente alla tesi da dimostrare (Look-back Bias). Il rischio, comunque, si misura anche con altre grandezze, come la dispersione dei rendimenti attorno al valore medio: analizzeremo tra un attimo le differenze tra PIC e PAC da questo punto di vista.
La tabella di output dell’Analisi PAC mostra, nella decima riga, proprio la deviazione standard dei rendimenti per ciascuna durata.
Il valore della deviazione standard è crescente e compreso tra il 14,46% dei piani di accumulo biennali e il 41,98% di quelli decennali. Nei PAC di durata più lunga la deviazione standard inizia a scendere, fino ad arrivare al 15,84% nei piani trentennali.
Con il crescere della durata, la deviazione standard è calcolata su un numero di valori sempre minore: si deve perciò fare attenzione nel confrontare le deviazioni standard tra durate diverse.
Nella riga 11, vengono visualizzati il periodo di recupero medio e quello massimo dei piani di accumulo che hanno generato un rendimento negativo.
Il periodo di recupero misura il numero di giorni che sono trascorsi, a partire dalla fine di un PAC dal rendimento negativo, prima che quest’ultimo valore sia tornato positivo.
Ad esempio, immaginiamo che un piano di accumulo quinquennale abbia realizzato un rendimento del −12%. Si ipotizza che le quote in portafoglio non siano state liquidate.
Il PAC a questo punto si è trasformato in un PIC e, dal momento in cui è stata versata l’ultima rata, abbiamo iniziato a conteggiare i giorni in cui il valore delle quote, ai prezzi correnti, ha continuato a generare un rendimento negativo. Il primo giorno in cui il rendimento è diventato positivo, il conteggio è stato interrotto: il numero di giorni trascorsi rappresenta il periodo di recupero di quel PAC.
Nei piani di accumulo di durata uguale o inferiore a 10 anni, il periodo di recupero medio è compreso tra 197 e 479 giorni borsistici. Quello massimo oscilla invece tra 963 e 1.419 giorni.
Nelle durate superiori, il periodo di recupero diminuisce drasticamente: 118 e 305 giorni sono il periodo medio e massimo dei piani di 15 anni; solo 8 e 20 giorni in quelli ventennali. I piani di 25 e 30 anni di durata non hanno registrato nemmeno un rendimento negativo e i loro periodi di recupero sono ovviamente pari a 0.
Il periodo di recupero può essere interpretato come un indicatore di rischio. Se è molto lungo, significa che un investimento non andato a buon fine richiederà un periodo di tempo molto esteso prima che la perdita venga riassorbita. Più questo periodo è lungo, più è alta la probabilità che un investitore non abbia la pazienza di aspettare tutto quel tempo e lo liquidi in perdita (qualora non lo avesse già fatto al termine del PAC).
Gli investimenti azionari, soprattutto di breve termine, sono considerati molto rischiosi perché, tra le altre cose, possono avere dei periodi di recupero molto lunghi: il più esteso periodo di recupero dei PAC biennali backtestati è stato pari a 1.419 giorni borsistici, che corrispondono a quasi 6 anni.
Il periodo di recupero conferma il minor rischio dei piani di accumulo rispetto agli investimenti in un’unica soluzione: questi ultimi hanno dei periodi di recupero molto più lunghi di quelli dei PAC (anche più del doppio). Ad esempio, il periodo di recupero più lungo di un investimento biennale in un’unica soluzione è stato di ben 3.136 giorni borsistici (oltre 12 anni).
Nel decimo capitolo sarà svolta un’ampia analisi degli investimenti in un’unica soluzione e delle principali differenze con i piani di accumulo Cost Averaging.
La dodicesima riga della tabella riporta la somma finale che sarebbe stata ottenuta, mediamente, dai piani di accumulo di ciascuna durata. La somma finale viene suddivisa in tre quantità:
- Somma finale: ammontare in euro generato dal PAC al lordo delle commissioni di transazione.
- Commissioni: ammontare corrispondente alle commissioni di transazione pagate complessivamente nel PAC.
- Somma netta: differenza tra le due quantità precedenti.
La somma finale corrisponde sempre al montante del PAC, dato che nel Cost Averaging tutta la liquidità a disposizione viene utilizzata. Nei PAC Value Averaging, montante del PAC e liquidità disponibile sono spesso diversi tra loro.
La somma finale è direttamente proporzionale al rendimento medio. La somma netta mediamente generata dai piani di accumulo trentennali è stata pari a 270.716 euro: circa 13.000 euro in più della somma ottenuta dallo specifico piano trentennale analizzato nel capitolo precedente (si tratta del primo dei 62 PAC backtestati nella presente analisi). Evidentemente, quel piano di accumulo aveva performato sotto la media.
La tredicesima riga della tabella individua la giacenza media: si tratta della cifra mediamente investita in un piano di accumulo. Tutti i piani della stessa durata hanno la medesima giacenza media.
Nei piani trentennali, la giacenza media è stata di 54.000 euro. Complessivamente, un investitore avrebbe investito 300 euro (importo rata) × 360 (rate) = 108.000 euro ma, in media, il capitale investito sarebbe stato pari alla metà.
La quattordicesima riga della tabella (“Grafici”) permette, infine, di visualizzare il grafico di qualsiasi piano di accumulo analizzato. Ad esempio, potremmo essere curiosi di vedere l’andamento del rendimento per rata versata del 302° PAC di 24 rate (numero scelto casualmente): sarebbe stato sufficiente selezionare 302 nel menu a tendina della prima colonna per visualizzarlo:
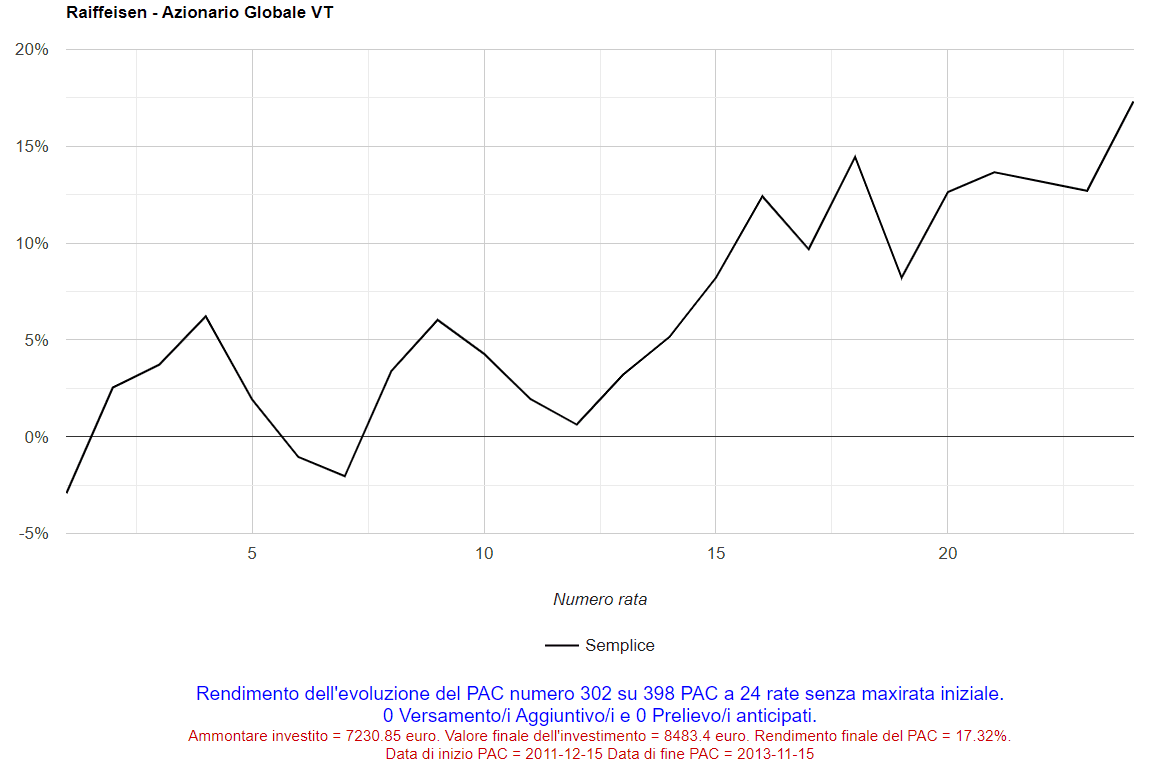
Fig. 14 – Raiffeisen: 302° PAC Cost Averaging della durata di 24 rate
Si tratta del piano di accumulo iniziato il 15 dicembre 2011 e terminato il 15 novembre 2013, che ha ottenuto un rendimento del 17,32%.
Alternativamente, avremmo potuto visualizzare il primo dei 62 PAC trentennali: proprio quello analizzato nel capitolo precedente:
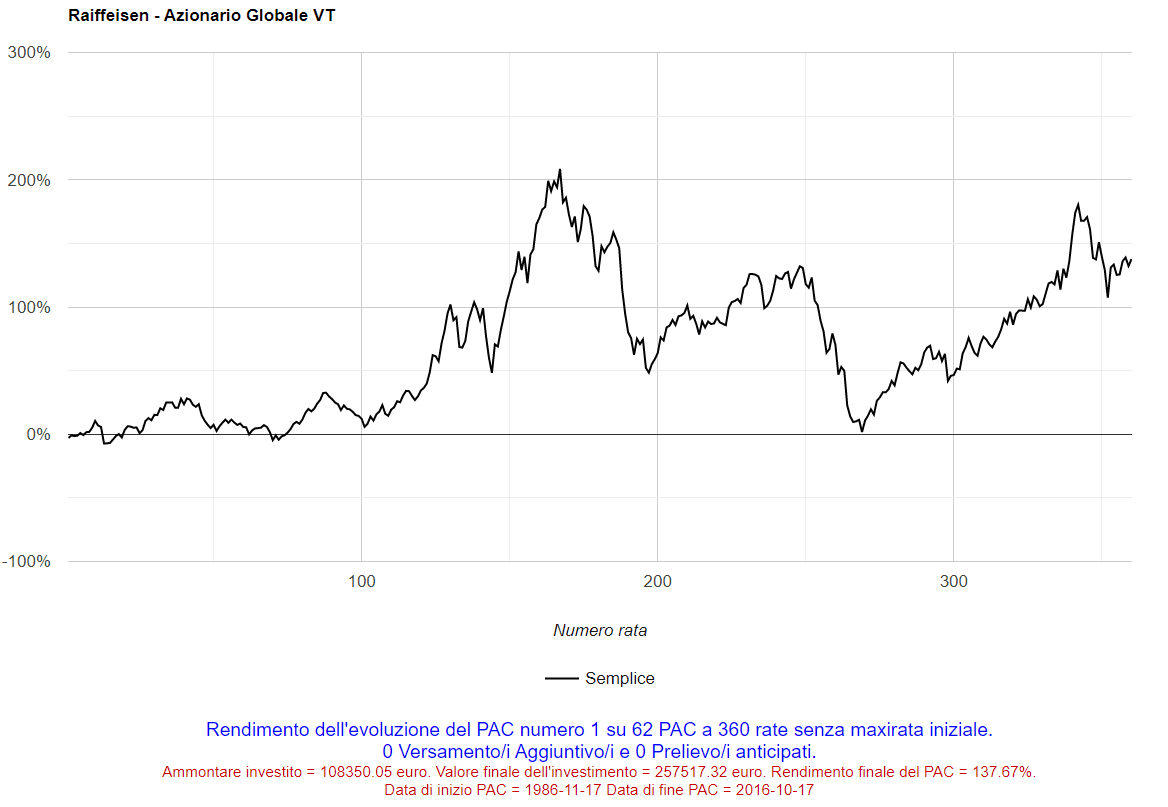
Fig. 15 – Raiffeisen: 1° PAC Cost Averaging della durata di 360 rate
Le informazioni sotto al grafico confermano che il suo valore finale è stato pari a 257.517,32 euro. Ci si potrebbe chiedere perché l’ammontare investito sia stato di 108.350,05 euro invece che di 108.000 euro esatti. I 350,05 euro in più identificano le commissioni di transazione (diritti fissi) pagate per la costruzione del PAC: 9 euro contestualmente alla prima rata e 0,95 euro per ognuna delle 359 rate successive (9 + 0,95 × 359 = 9 + 341,05 = 350,05).
Le commissioni hanno abbassato il rendimento finale dal 138,44% (risultato dell’analisi del capitolo precedente) al 137,67%: la differenza, in un piano di accumulo di questa lunghezza, è trascurabile.
Nell’Analisi PAC, le commissioni di transazione possono essere personalizzate a piacimento. Nel form iniziale, inoltre, potrebbero essere incluse anche commissioni d’ingresso percentuali, applicate su tutta la somma investita.
I campi da utilizzare per la personalizzazione delle commissioni di ingresso sono:
- “Applicazione commissioni”: checkbox che deve essere selezionata, altrimenti le commissioni, anche se specificate, non saranno applicate.
- “Commissioni (%)”: percentuale di commissioni applicate sul valore totale del PAC (numero di rate × ammontare rata).
- “% prima rata”: percentuale dell’ammontare commissionale che viene addebitato al momento del versamento della prima rata (di solito in presenza di una maxi-rata iniziale).
Al giorno d’oggi, le commissioni d’ingresso non vengono utilizzate frequentemente, ma non sono affatto sparite. Alcune banche continuano a farle pagare alla sottoscrizione di molti fondi a gestione attiva.
Applicando un 2% di commissione al piano di accumulo trentennale precedente, il grafico e i risultati dell’investimento sarebbero cambiati nel modo seguente:
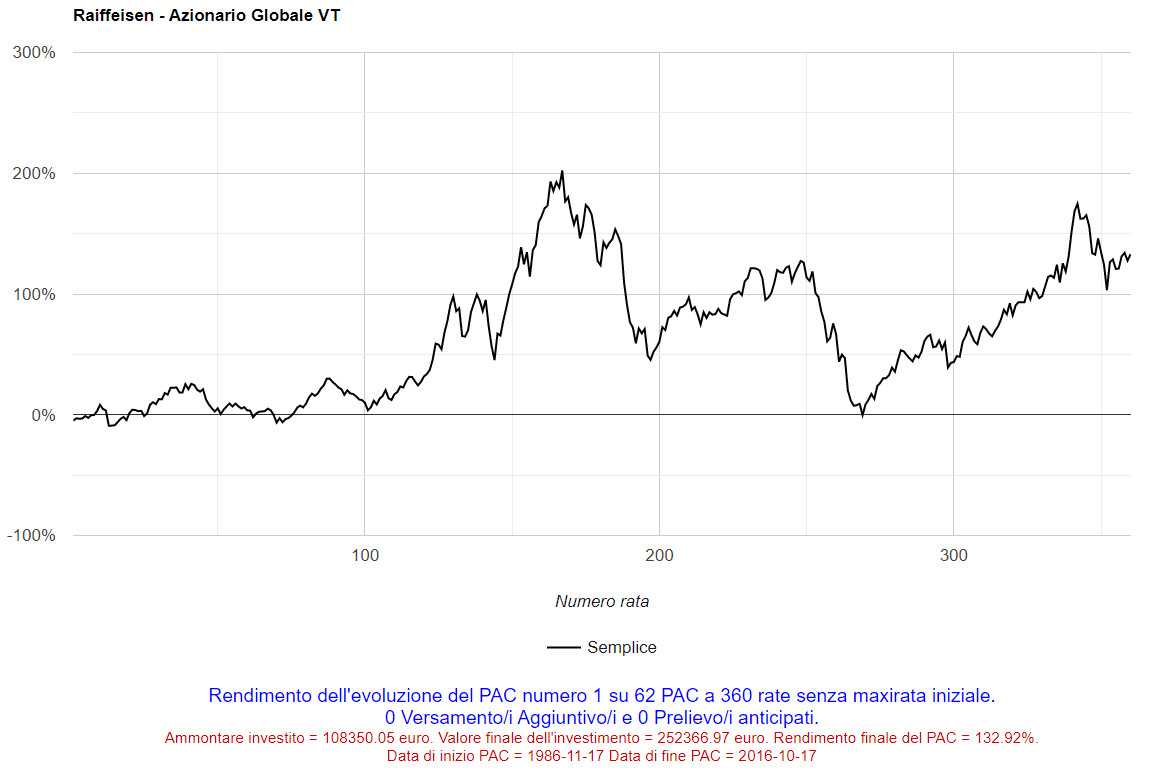
Fig. 16 – Raiffeisen: 1° PAC Cost Averaging della durata di 360 rate. Commissioni: 2%
Il grafico è molto simile al precedente ma, dalle informazioni addizionali, si può verificare come il rendimento finale sia sceso al 132,92% e la somma finale a 252.366,97 euro.
Le commissioni di transazione e d’ingresso verranno approfondite nel capitolo 14.
Nello stesso menu a tendina utilizzato per la visualizzazione di specifici grafici, si può optare per l’andamento medio per rata di tutti i piani di accumulo di una certa durata.
Vediamo quello dei PAC ventennali:
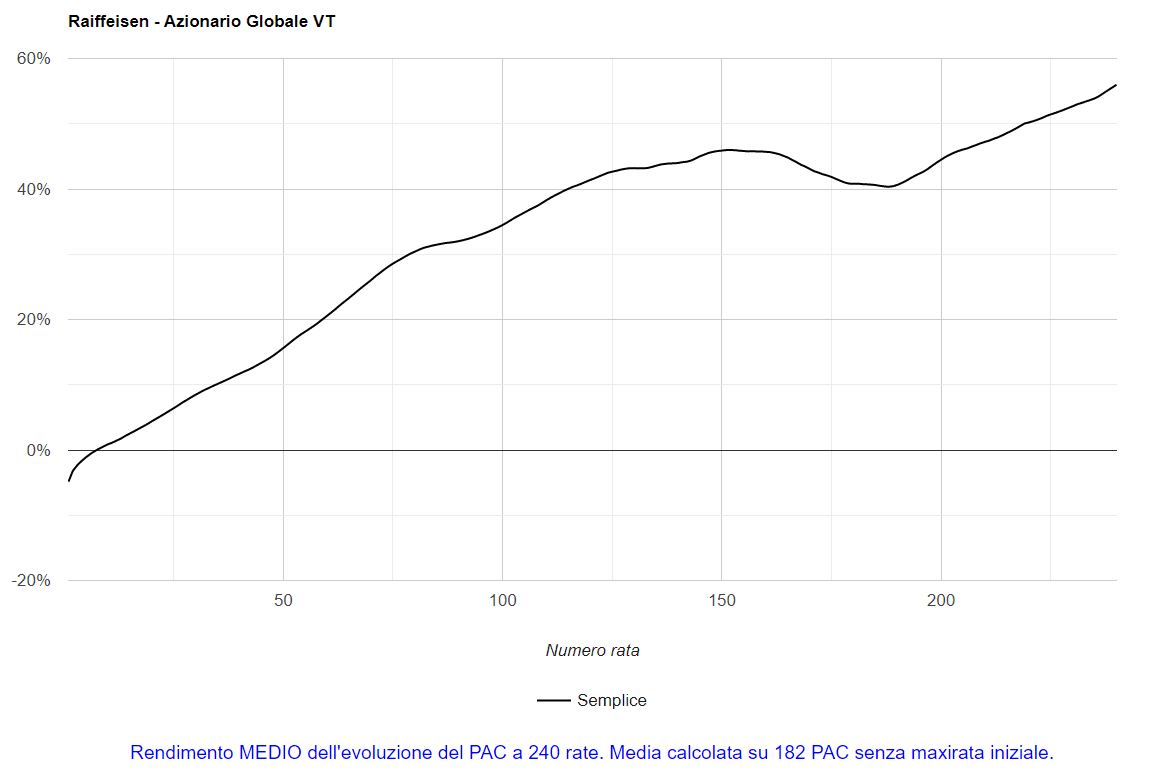
Fig. 17 – Raiffeisen: media dei PAC Cost Averaging della durata di 240 rate
Questa curva, molto liscia, rappresenta il sogno di ogni investitore (nonostante la fase di decrescita): un andamento senza le classiche spigolosità generate da crisi finanziarie improvvise e violente, che sono la fonte di gran parte dello stress psicologico di un investitore. Purtroppo, questo morbido andamento non sarebbe stato accessibile a nessuno: una media è utile ai fini analitici, ma non può essere utilizzata operativamente.
Il grafico, forse unico nel suo genere, rinforza le convinzioni ormai diffuse in materia di piani di accumulo azionari: il rendimento, seppure con alti e bassi, cresce con il passare del tempo e tende a essere negativo nelle prime fasi dell’investimento.
Perché questa partenza in apnea?
A causa dei diritti fissi che vengono generalmente pagati all’inizio di un Piano di Accumulo (quantificati in 9 euro) e, in misura minore, a ogni versamento (0,95 euro nella nostra analisi).
Nello specifico, oltre al primo versamento di 300 euro, l’investitore avrebbe pagato anche 9 euro di diritti fissi: sono pochi ma, percentualmente, si tratta del 3% (che infatti è il valore negativo del primo rendimento del grafico).
Le commissioni fisse sulle rate successive hanno un peso decisamente minore: meno dello 0,32%, ovvero 0,95 euro su 300.
Se oltre ai diritti fissi avessimo applicato anche le commissioni d’ingresso, l’impatto negativo sarebbe stato ben più importante (il 2% di 108.000 euro è pari a 2.160 euro, che sarebbero stati spalmati sulle 360 rate, con un aggravio di 6 euro per ciascuna di esse).
Quando si investe in un Piano di Accumulo del Capitale è impossibile conoscere la traiettoria che verrà seguita dal rendimento: il caso, la fortuna, fanno spesso la differenza. Tuttavia, la probabilità di realizzare un rendimento positivo cresce contestualmente alla durata del piano di accumulo.
Un’ulteriore caratteristica dell’Analisi PAC è quella di visualizzare graficamente i rendimenti finali di tutti i piani di accumulo di una certa durata. Per far questo, è sufficiente cliccare sul numero di mesi di ciascuna durata.
Ad esempio, cliccando su 120, ottengo il seguente grafico:
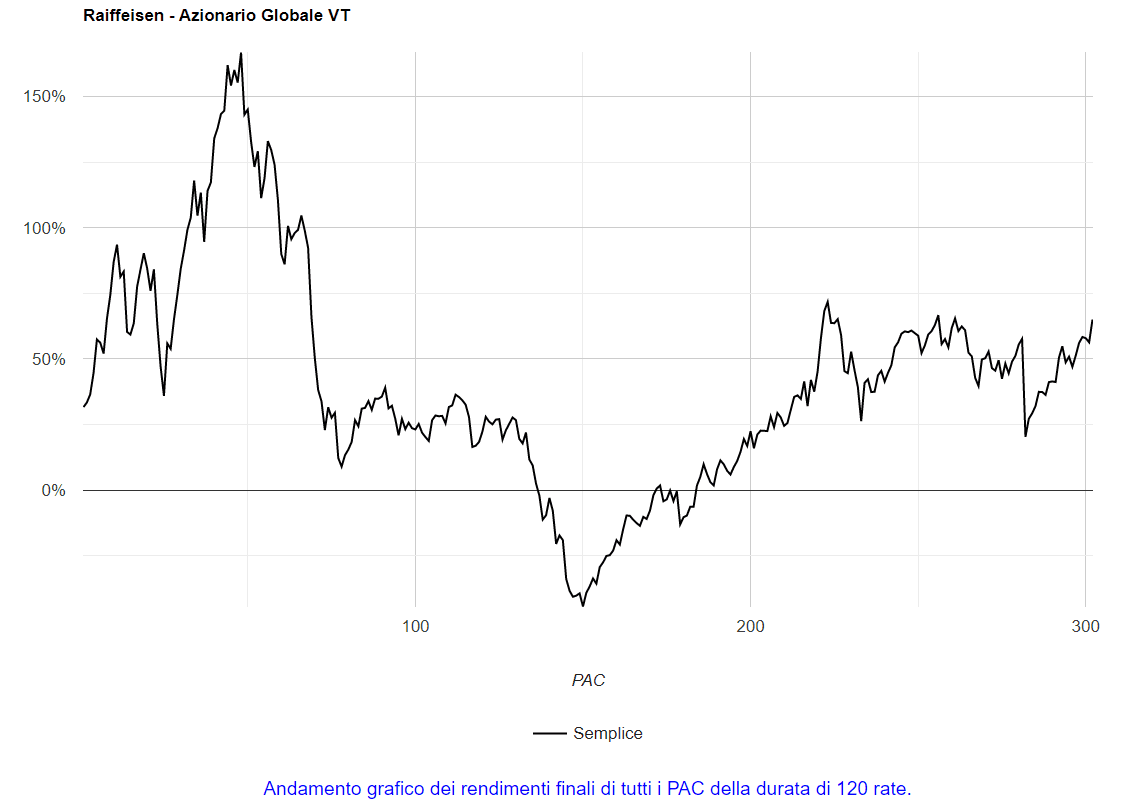
Fig. 18 – Raiffeisen: rendimenti di tutti i PAC Cost Averaging della durata di 120 rate
I piani di accumulo sono stati 302 e tutti i rendimenti finali sono mostrati in questo grafico.
Come ci aveva informato la prima riga della tabella (“PAC positivi”), 257 PAC su 302 hanno ottenuto un rendimento positivo. Il grafico conferma che il 48° PAC della serie è stato il migliore e il 150° il peggiore.
Sarebbe stata necessaria una po’ di sfortuna per portare a casa un rendimento negativo in un piano di accumulo di 120 rate. Una buona dose di fortuna sarebbe invece servita per ottenere un rendimento superiore al 100%.
La maggior parte dei PAC avrebbe invece realizzato un rendimento compreso tra il 20% e il 60%: il grafico conferma visivamente come il rendimento medio di questi piani di accumulo sia stato del 41,22%.
Se si vogliono visualizzare, invece, i rendimenti di tutti i 398 piani di accumulo di 24 rate, si dovrà cliccare su 24 (intestazione della prima colonna):
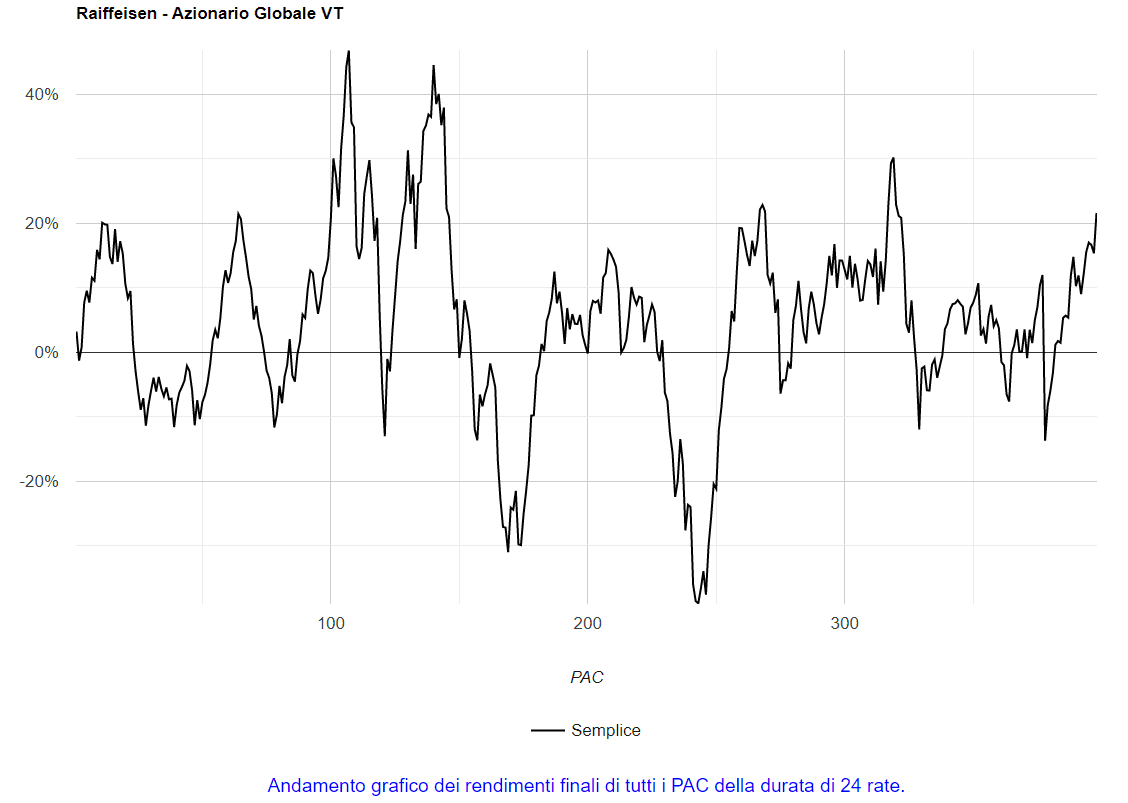
Fig. 19 – Raiffeisen: rendimenti di tutti i PAC Cost Averaging della durata di 24 rate
Se è vero che il 71% dei PAC hanno generato un risultato positivo, è altrettanto evidente la maggior variabilità dei rendimenti di questi piani di accumulo: la minor durata aumenta il rischio; rendimenti positivi e negativi si alternano a breve distanza.
Ancora più di prima, l’esito dell’investimento sarà governato dal caso.
5. Simulazioni su un fondo dal trend discendente

«It doesn't take many observations to think you've spotted a trend, and it's probably not a trend at all».
Daniel Kahneman
Sulla falsariga dell’analisi di un singolo piano di accumulo, procediamo con il backtest di un fondo dal trend negativo: l’Aberdeen Japanese Equity Fund A Acc JPY (ISIN: LU0011963674), appartenente alla categoria “Azionari Giappone”.
Lanciando l’Analisi PAC si ottengono i seguenti risultati:
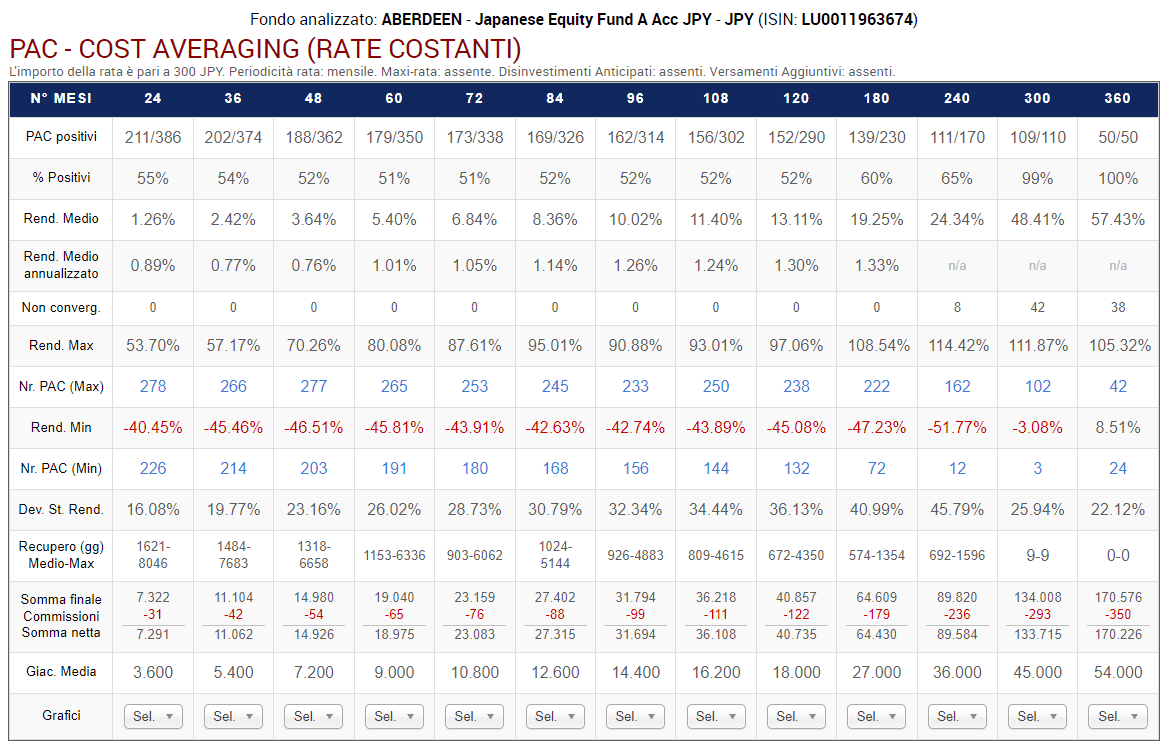
Fig. 20 – Aberdeen: PAC Cost Averaging. Rata: 300 euro
Rispetto a prima, lo scenario è completamente diverso.
La percentuale di PAC positivi di durata compresa tra 2 e 20 anni è scesa drasticamente. Se nel fondo Raiffeisen oscillava tra il 72% e il 98%, adesso varia tra il 55% e il 65%. I livelli precedenti vengono mantenuti soltanto nelle durate più lunghe: 25 e 30 anni (nei soli piani di 25 anni di durata questa percentuale è scesa dal 100% al 99%).
Rimane valido il principio seguente: per aumentare la probabilità di chiudere positivamente un investimento azionario, l'orizzonte temporale deve essere il più lungo possibile. Con un trend discendente, i tempi si allungano ulteriormente.
I rendimenti medi e medi annualizzati sono anch’essi scesi in maniera eclatante: si mantengono positivi, ma di poco, soprattutto nelle brevi durate. Nel capitolo 10, saranno approfondite le differenze tra piani di accumulo e PIC: rispetto al PIC, in questo specifico caso il piano di accumulo avrebbe minimizzato il rischio e aumentato i rendimenti a partire dalla durata di 15 anni (180 mesi).
I rendimenti massimi e minimi sono peggiorati. La cosa curiosa è che, mentre la diminuzione è sensibile per i rendimenti massimi, quelli minimi diminuiscono di pochissimi punti percentuali (se non addirittura di decimali) in quasi tutte le durate fino a 10 anni.
In quelle superiori, invece, c’è un vero e proprio crollo: dal −26,76% al −47,23% nei piani di 15 anni, dal −8,08% al −51,77% in quelli di 20 anni, dal 46,58% al −3,08% in quelli di 25 anni e dal 105,09% al 8,51% in quelli trentennali:
- Una nota positiva è non aver riscontrato valori negativi estremi, nell’ordine del −60/70% o addirittura peggio (li troveremo nei PIC).
- Una nota negativa è il segno meno che, oltre a essere più frequente, appare adesso anche su durate lunghissime (25 anni).
Non visualizziamo i grafici del PAC migliore e di quello peggiore perché, fondamentalmente, non offrono nessuna ulteriore informazione rispetto a quelli visti in precedenza. Anche la deviazione standard dei rendimenti non offre nuovi spunti.
I periodi di recupero medi crescono notevolmente. Nei piani di accumulo più brevi, il periodo di recupero medio si attesta intorno ai 1.500 giorni borsistici (6 anni circa) per poi scendere a 574-809 giorni (poco più di 2-3 anni) nei piani compresi tra 9 e 20 anni di durata. L’unico PAC negativo di 25 anni ha invece avuto un periodo di recupero brevissimo (9 giorni).
I periodi di recupero massimi prendono letteralmente il volo: sono superiori ai 6.000 giorni nei PAC di 2-6 anni di durata; compresi tra 4.350 e 5.144 giorni in quelli di 7-10 anni; intorno ai 1.500 giorni nei piani di 15 e 20 anni di durata; si azzerano in quelli di 25-30 anni.
Sono periodi lunghissimi, motivati dal trend discendente di lungo termine del fondo, che in alcuni casi non ha permesso il recupero – o lo ha fatto in tempi estremamente lunghi – dei piani di accumulo dal rendimento negativo.
In finanza, purtroppo non esistono certezze: si possono solo dare consigli che, nel migliore dei casi, siano associati a una buona probabilità di successo. Queste probabilità vengono di solito calcolate o modellate in base a quello che ci dice la storia: quando siamo in presenza di un outlier – un evento molto raro – anche un suggerimento molto sensato potrebbe portare a un risultato disastroso.
Capita di leggere, anche in ottimi libri di finanza personale, che in caso di performance negativa la cosa migliore sia non disinvestire e aspettare fino a quando il rendimento dell’investimento torni positivo. È un consiglio logico, corretto da un punto di vista probabilistico: da mettere in pratica se l’investitore ha ascoltato anche altri suggerimenti, tra i quali quello di investire in uno strumento finanziario molto diversificato.
Concentrando il rischio, aumentano le probabilità di rimanere bloccati per molti anni in un investimento dal rendimento negativo.
Le somme finali mediamente generate sono state, in linea con i rendimenti medi, molto inferiori a quelle del fondo Raiffeisen. La giacenza media è invece rimasta immutata, dal momento che dipende solo dall’importo della rata.
Avevamo già visto che l’ultima riga della tabella permette di visualizzare il grafico di qualsiasi piano di accumulo analizzato, incluso quello del rendimento medio per rata di tutti i piani di una certa durata.
Ecco quello dei PAC ventennali:
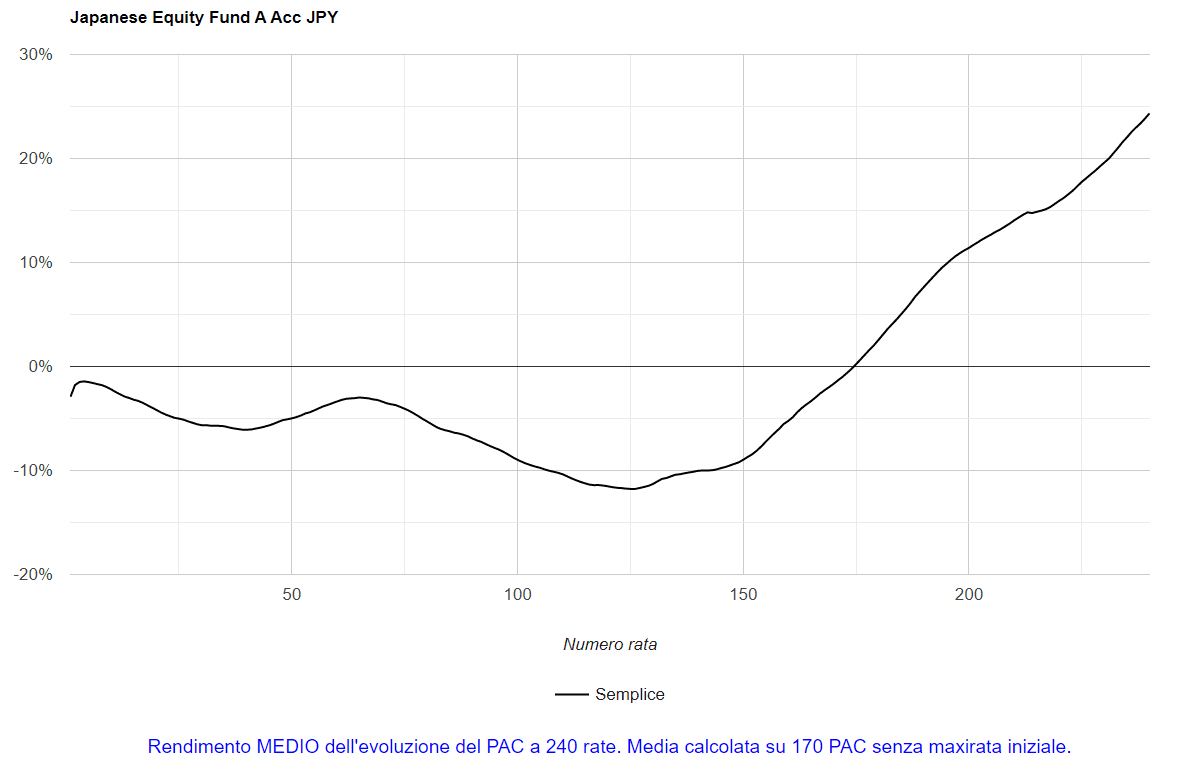
Fig. 21 – Aberdeen: media dei PAC Cost Averaging della durata di 240 rate
La curva è molto liscia. Il risultato finale è stato mediamente positivo ma, per gran parte della vita dei piani di accumulo, il rendimento ha stazionato in territorio negativo.
In linea con quanto fatto in precedenza, cliccando su 120 nell’intestazione della tabella visualizziamo i rendimenti finali di tutti i piani di accumulo decennali:
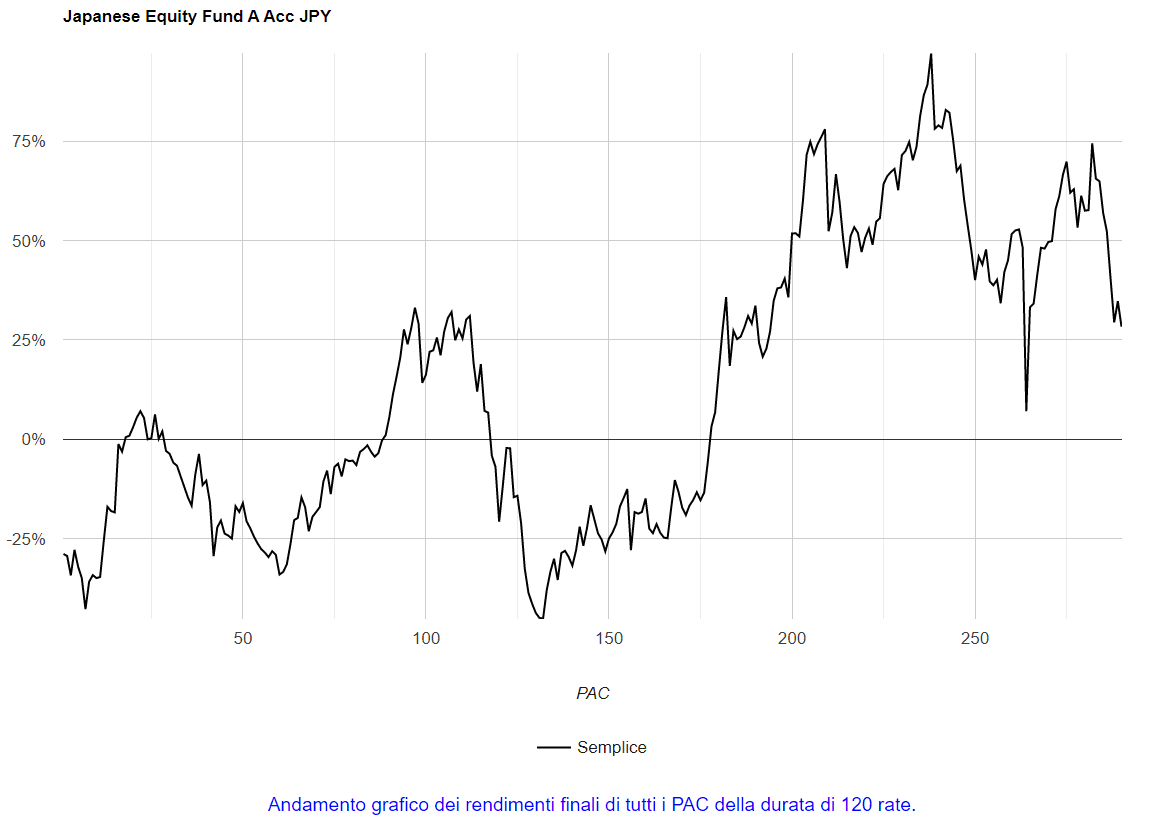
Fig. 22 – Aberdeen: rendimenti di tutti i PAC Cost Averaging della durata di 120 rate
I piani di accumulo sono stati 290: soltanto 152 i positivi (52%).
La tabella precedente (Fig. 20) individuava il 132° PAC come il peggiore e il 238° come il migliore della serie. Effettivamente, nel grafico si nota come il minimo assoluto sia in linea col valore 132 sull’asse delle ascisse, mentre il massimo assoluto lo sia con il 238.
La maggior parte dei PAC ha realizzato un rendimento compreso tra il −30% e il 60%: la fascia è ampia, ma il valore medio si inquadra più o meno nel suo punto intermedio, essendo stato pari al 13,11%.
Visualizziamo adesso i rendimenti dei 386 piani di accumulo di 24 rate:
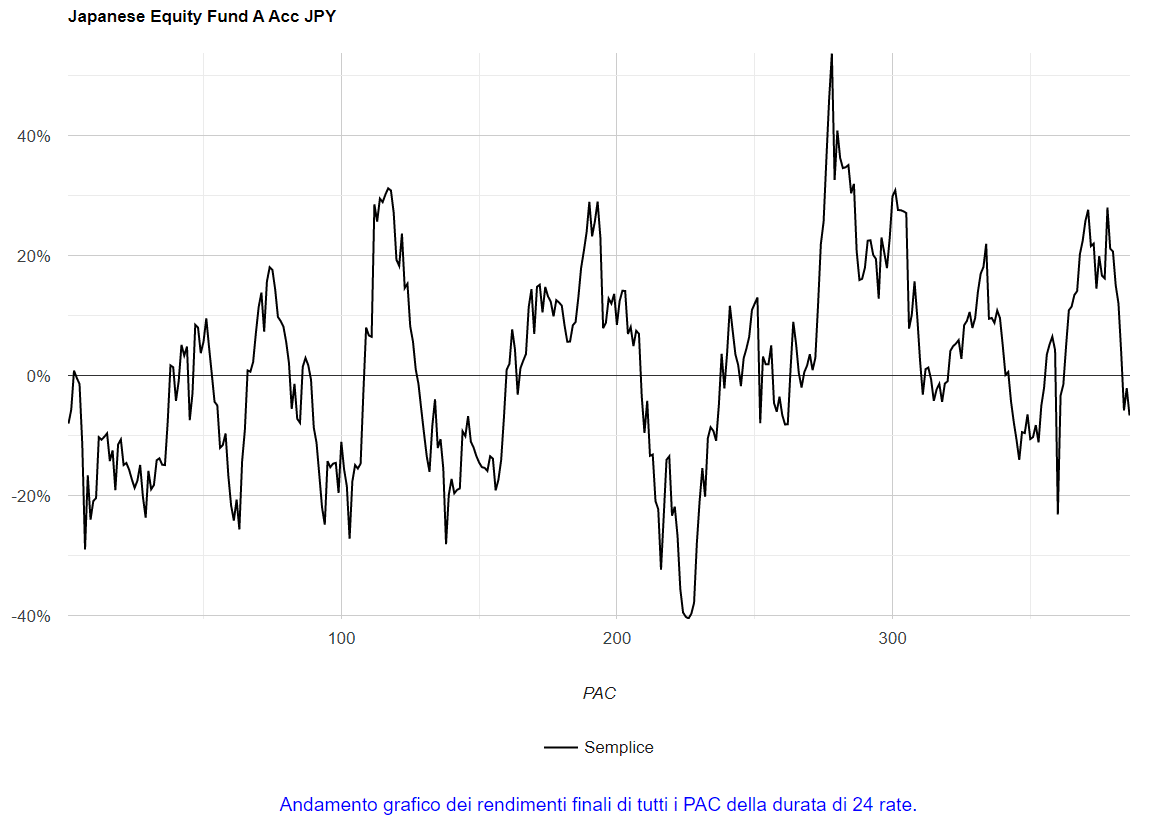
Fig. 23 – Aberdeen: rendimenti di tutti i PAC Cost Averaging della durata di 24 rate
Il grafico mostra una situazione di estrema confusione, con rendimenti positivi e negativi che si alternano a breve distanza. Il 55% dei PAC ha ottenuto un rendimento positivo.
Si distinguono il minimo e il massimo assoluto, posizionati a una distanza relativamente breve (226° e 278° piano di accumulo).
Nel prossimo capitolo sposteremo il focus dell’analisi sulle performance realizzate durante la vita dei PAC. In particolare, ci concentreremo sulla volatilità interna.
6. Rendimento e volatilità interna

«One cannot reflect in streaming water. Only those who know internal peace can give it to others».
Lao Tzu
L’ultima tabella generata dall’Analisi PAC è denominata “Rendimento e Volatilità interna”.
Nelle analisi precedenti (Fig. 11 e 20), tra le altre cose erano stati calcolati i rendimenti finali e le deviazioni standard dei rendimenti finali dei piani di accumulo: tutte informazioni importanti, ma che non gettano alcuna luce sull’andamento del rendimento durante la vita dei PAC.
Uno dei rischi principali di un investitore è ottenere un rendimento finale inferiore alle attese. L’investitore si assume però anche un altro rischio, spesso sottovalutato: quello della variabilità del rendimento durante la costruzione del piano di accumulo. In altre parole, il rischio di non riuscire a portare a termine l’investimento: molte volte, gli investitori gettano la spugna prima.
Occasionalmente, questo può essere dovuto a una necessità inaspettata e imprevedibile di liquidità, che costringe a monetizzare prima del tempo. Nella maggior parte dei casi, però, il disinvestimento è legato a fattori psicologici: una crisi finanziaria improvvisa, l’eccessiva volatilità dello strumento utilizzato, la convinzione di aver trovato un’alternativa migliore, il rendimento corrente sopra alle attese e così via.
Tra i tanti, lo stress psicologico è senz’altro uno dei motivi principali che inducono a interrompere l’investimento. I piani di accumulo non fanno eccezione.
È indubbio che lo stress possa derivare dall’eccessiva volatilità del sottostante: proveremo perciò a misurare la variabilità del rendimento durante la vita dei PAC.
In questo contesto, faremo riferimento al rendimento del controvalore investito, misurato a intervalli periodici (in concomitanza con il versamento di ciascuna rata); questa grandezza differisce dal rendimento del fondo, dal momento che ogni volta che viene versata una rata si ha una mediazione del prezzo medio di carico delle quote acquistate.
Gli investitori sono più sensibili alle variazioni del controvalore investito che non a quelle del fondo sottostante. Nei PIC queste due grandezze combaciano; nei PAC, no.
Per un miglior confronto tra la rischiosità dei PAC e dei PIC, calcoleremo anche nei PIC il rendimento in concomitanza del versamento di ciascuna rata del PAC di pari durata.
In questo modo, sarà possibile confrontare queste due tipologie di investimento non soltanto in base alle loro performance finali, ma anche rispetto alla volatilità interna dei loro rendimenti durante l’investimento.
Un esempio aiuterà a capire meglio questa differenza. Nella seguente tabella troviamo il primo piano di accumulo di 24 rate mensili che è stato simulato sul fondo Raiffeisen (il piano che va dal 17/11/1986 al 17/10/1988). Per semplicità, non sono state conteggiate le commissioni di transazione.
Nelle ultime due colonne sulla destra sono stati inseriti anche i calcoli del PIC relativi allo stesso periodo. La somma investita nel PIC, anche se non influisce sui rendimenti, è stata quantificata in 7.200 euro, lo stesso importo di quanto versato complessivamente nel PAC (24 rate da 300 euro ciascuna):
| Volatilità interna | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PAC | PIC | ||||||||||
| N° rata | Data | NAV | Rata | P med. carico | Q.te acq. | Q.te tot. | Pagam. totali | Valore di mercato | Rend. Int. PAC | Rend. Int. PIC | Valore di mercato |
| 1 | 1986-11-17 | 51,1115 | 300 | 51,11 | 5,8695 | 5,8695 | 300 | 300,00 | 0,00% | 0,00% | 7.200,00 |
| 2 | 1986-12-15 | 51,8515 | 300 | 51,48 | 5,7858 | 11,6553 | 600 | 604,34 | 0,72% | 1,45% | 7.304,24 |
| 3 | 1987-01-15 | 51,3224 | 300 | 51,43 | 5,8454 | 17,5007 | 900 | 898,18 | −0,20% | 0,41% | 7.229,71 |
| 4 | 1987-02-16 | 51,3347 | 300 | 51,40 | 5,8440 | 23,3447 | 1.200 | 1.198,39 | −0,13% | 0,44% | 7.231,44 |
| 5 | 1987-03-16 | 52,5680 | 300 | 51,63 | 5,7069 | 29,0516 | 1.500 | 1.527,18 | 1,81% | 2,85% | 7.405,17 |
| 6 | 1987-04-15 | 51,7063 | 300 | 51,64 | 5,8020 | 34,8536 | 1.800 | 1.802,15 | 0,12% | 1,16% | 7.283,79 |
| 7 | 1987-05-15 | 53,0464 | 300 | 51,84 | 5,6554 | 40,5090 | 2.100 | 2.148,86 | 2,33% | 3,79% | 7.472,57 |
| 8 | 1987-06-15 | 53,3433 | 300 | 52,02 | 5,6239 | 46,1329 | 2.400 | 2.460,88 | 2,54% | 4,37% | 7.514,39 |
| 9 | 1987-07-15 | 55,3824 | 300 | 52,38 | 5,4169 | 51,5498 | 2.700 | 2.854,95 | 5,74% | 8,36% | 7.801,64 |
| 10 | 1987-08-17 | 58,8509 | 300 | 52,96 | 5,0976 | 56,6475 | 3.000 | 3.333,75 | 11,13% | 15,14% | 8.290,24 |
| 11 | 1987-09-15 | 57,3281 | 300 | 53,33 | 5,2330 | 61,8805 | 3.300 | 3.547,49 | 7,50% | 12,16% | 8.075,72 |
| 12 | 1987-10-15 | 56,9431 | 300 | 53,61 | 5,2684 | 67,1489 | 3.600 | 3.823,67 | 6,21% | 11,41% | 8.021,49 |
| 13 | 1987-11-16 | 49,6415 | 300 | 53,28 | 6,0433 | 73,1922 | 3.900 | 3.633,37 | −6,84% | −2,88% | 6.992,92 |
| 14 | 1987-12-15 | 49,4576 | 300 | 52,99 | 6,0658 | 79,2580 | 4.200 | 3.919,91 | −6,67% | −3,24% | 6.967,02 |
| 15 | 1988-01-15 | 49,3676 | 300 | 52,73 | 6,0769 | 85,3349 | 4.500 | 4.212,78 | −6,38% | −3,41% | 6.954,34 |
| 16 | 1988-02-15 | 50,6231 | 300 | 52,60 | 5,9261 | 91,2611 | 4.800 | 4.619,92 | −3,75% | −0,96% | 7.131,20 |
| 17 | 1988-03-15 | 52,0752 | 300 | 52,57 | 5,7609 | 97,0220 | 5.100 | 5.052,44 | −0,93% | 1,89% | 7.335,75 |
| 18 | 1988-04-15 | 52,9181 | 300 | 52,58 | 5,6691 | 102,6911 | 5.400 | 5.434,22 | 0,63% | 3,53% | 7.454,49 |
| 19 | 1988-05-16 | 51,4290 | 300 | 52,52 | 5,8333 | 108,5244 | 5.700 | 5.581,30 | −2,08% | 0,62% | 7.244,73 |
| 20 | 1988-06-15 | 54,6956 | 300 | 52,63 | 5,4849 | 114,0093 | 6.000 | 6.235,81 | 3,93% | 7,01% | 7.704,89 |
| 21 | 1988-07-15 | 56,3775 | 300 | 52,79 | 5,3213 | 119,3305 | 6.300 | 6.727,56 | 6,79% | 10,30% | 7.941,81 |
| 22 | 1988-08-15 | 56,3642 | 300 | 52,95 | 5,3225 | 124,6531 | 6.600 | 7.025,97 | 6,45% | 10,28% | 7.939,94 |
| 23 | 1988-09-15 | 56,0129 | 300 | 53,07 | 5,3559 | 130,0090 | 6.900 | 7.282,18 | 5,54% | 9,59% | 7.890,45 |
| 24 | 1988-10-17 | 56,2786 | 300 | 53,20 | 5,3306 | 135,3396 | 7.200 | 7.616,72 | 5,79% | 10,11% | 7.927,88 |
| Media Rendimenti interni | 1,68% | 4,35% | |||||||||
| Volatilità Interna (SD Rendimenti Interni) | 4,65% | 5,29% | |||||||||
| Rendimento Interno Max | 11,13% | 15,14% | |||||||||
| Rendimento Interno Min | −6,84% | −3,41% | |||||||||
Fig. 24 – Raiffeisen: Rendimento e Volatilità Interna del primo PAC di 24 rate (Cost Averaging) e del corrispondente PIC
Le due colonne relative al PIC ne fotografano il valore di mercato e il rendimento in corrispondenza di ciascuna data di versamento delle rate del PAC.
Sono state calcolate le seguenti grandezze (i valori sono riportati sotto alla tabella):
- Media dei 24 rendimenti interni del PAC e del PIC: la media dei rendimenti interni del PIC è stata molto più alta. Gli ultimi valori della serie – quelli in corrispondenza della rata numero 24 – sono i rendimenti finali del PAC (5,79%) e del PIC (10,11%).
- Volatilità interna del PAC e del PIC: si tratta della deviazione standard dei 24 rendimenti interni e misura la variabilità dei rendimenti per rata. Più è alta, maggiore è l’impatto emotivo sull’investitore, a causa delle elevate fluttuazioni del rendimento. La volatilità interna del PAC è stata inferiore a quella del PIC. La volatilità interna può essere interpretata come una misura di rischio: insieme a molte altre, sarà utilizzata nel confronto tra la rischiosità dei PAC e dei PIC.
- Rendimento interno massimo e minimo del PAC e del PIC: incidentalmente, potrebbero coincidere col rendimento finale di un PAC o di un PIC. Molto più probabilmente, si posizioneranno al di sopra o al di sotto.
Gli stessi risultati della tabella si possono ottenere lanciando un’Analisi PAC sul fondo Raiffeisen (300 euro di rata, diritti fissi uguali a 0), selezionando come data di inizio quella predefinita (16/10/1986) e come data finale l’01/11/1988 (in realtà qualsiasi data compresa tra il 18 ottobre 1988 e il 14/11/1988 può andare bene, avendo selezionato il 15 come giorno del mese in cui le rate vengono versate).
La selezione di queste date permette di isolare il primo piano di accumulo di 24 rate disponibile sul fondo Raiffeisen: esattamente lo stesso PAC esaminato nella tabella precedente.
Lanciando l’analisi otteniamo il seguente risultato:
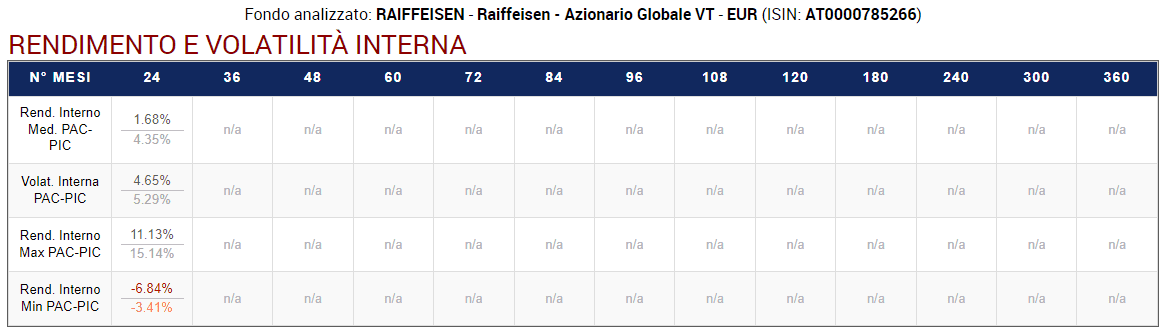
Fig. 25 – Raiffeisen: Rendimento e Volatilità Interna del primo PAC di 24 rate (Cost Averaging) e del corrispondente PIC
I valori sono uguali a quelli ottenuti prima.
In ogni riga della tabella, le quantità in alto sono relative ai PAC; quelle in basso, ai PIC (il colore è meno pronunciato).
Come riprova, vediamo quali sarebbero stati i risultati nelle tabelle principali dell’Analisi PAC e PIC:
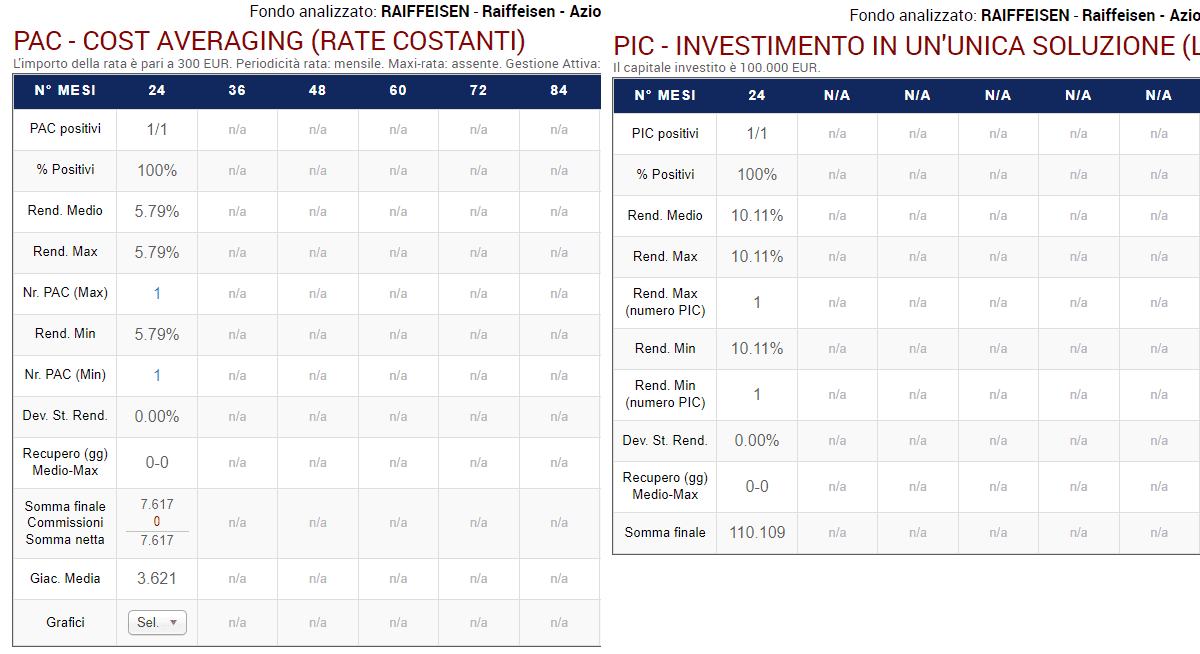
Fig. 26 – Raiffeisen: primo PAC Cost Averaging di 24 rate e corrispondente PIC
I rendimenti degli unici PAC e PIC backtestati sono proprio quelli dell’ultima riga delle colonne “Rendimento Interno PAC” e “Rendimento Interno PIC” della tabella precedente (Fig. 24): 5,79% e 10,11%.
La somma finale del PAC è 7.617 euro, proprio come l’ultima quantità della colonna “Valore di mercato” nella sezione dei PAC. La somma finale del PIC è diversa, dato che vengono sempre simulati investimenti di 100.000 euro.
Quando si effettuano i backtest utilizzando tutta la serie storica disponibile, vengono visualizzati i risultati medi di tutti i PAC e di tutti i PIC backtestati per ogni durata.
Vediamoli (abbiamo reintrodotto le commissioni di transazione):
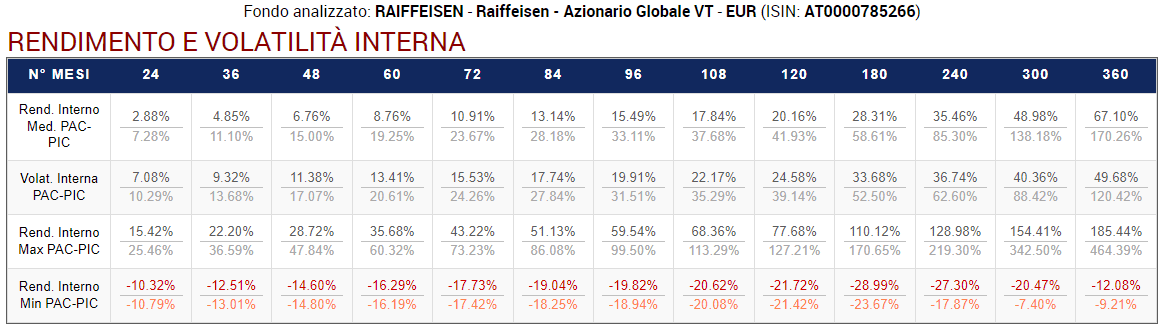
Fig. 27 – Raiffeisen: Rendimento e Volatilità Interna di tutti i PAC (Cost Averaging) e dei corrispondenti PIC
- Media dei rendimenti interni: il fondo Raiffeisen ha seguito un trend crescente e la media dei rendimenti interni dei PIC è risultata sempre nettamente superiore a quella dei PAC. Quando il mercato sale, prima si investe meglio è.
- Volatilità Interna: quella dei PAC è nettamente inferiore a quella dei PIC, su ogni durata. Si verifica il classico trade-off rischio rendimento: i PIC generano rendimenti più alti, ma la loro volatilità è maggiore.
- Media dei rendimenti interni massimi: quella dei PIC è molto più alta rispetto a quella dei PAC.
- Media dei rendimenti interni minimi: molto simili fino alla durata decennale. Sulle durate maggiori, quella dei PIC è superiore.
Dei risultati molto diversi sarebbero stati ottenuti su una serie storica dal trend discendente. Vediamo i risultati del backtest sul fondo Aberdeen: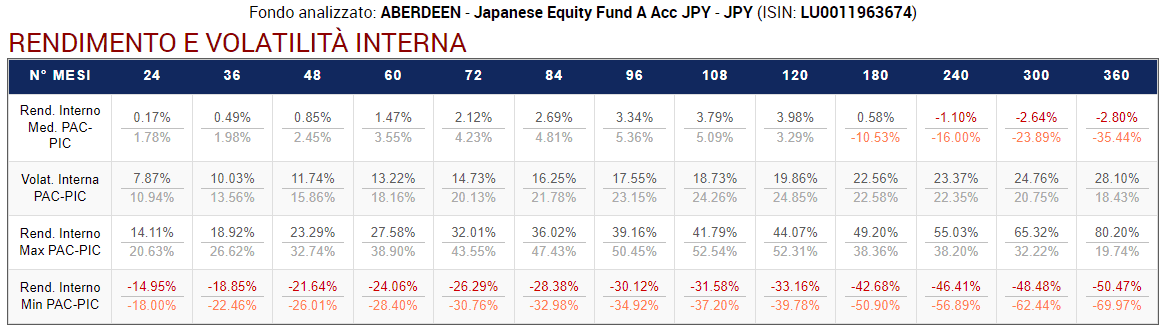
Fig. 28 – Aberdeen: Rendimento e Volatilità Interna di tutti i PAC (Cost Averaging) e dei corrispondenti PIC
Lo scenario è cambiato. Buona parte delle medie dei rendimenti interni, di quelli massimi e tutte quelle dei rendimenti minimi interni sono adesso a favore dei PAC.
La volatilità interna è favorevole ai PAC nelle durate fino a 180 mesi. In quelli di durata superiore sono i PIC ad avere la meglio.
In generale, la diversa rischiosità tra un PAC e un PIC si può quantificare analizzando le differenze tra le volatilità interne, ma anche quelle tra i rendimenti interni minimi:
- Volatilità interna: molto maggiore quella dei PIC su quasi tutte le durate del fondo Raiffeisen; nell’Aberdeen è ancora una volta maggiore quella dei PIC su gran parte delle durate.
- Media dei rendimenti interni minimi: simile nel fondo Raiffeisen su durate uguali o inferiori a 10 anni e migliore nei PIC su durate superiori; a favore dei PAC su tutte le durate nel fondo Aberdeen.
Tirando le somme, i piani di accumulo sembrano essere meno rischiosi degli investimenti in un’unica soluzione: non soltanto prendendo in considerazione i rendimenti finali, ma anche quelli interni.
Come sempre, le conclusioni sui backtest di singoli fondi non possono essere automaticamente generalizzate. Per far questo, ci avvarremo delle simulazioni col metodo Monte Carlo.
Queste informazioni potrebbero essere utili ad altri scopi?
Non possiamo escluderlo, dato che non sono informazioni interpretabili in modo univoco. Ad esempio, dal momento che i rendimenti interni massimi vengono raggiunti, talvolta, un po’ prima del completamento dei piani di accumulo, potrebbe essere sensato intervenire preventivamente liquidando una parte delle quote detenute per mettersi al riparo da ipotetici crolli dei rendimenti nell’ultima fase dell’investimento.
Approfondiremo questa strategia nel capitolo 11.
7. Simulazioni non parametriche col metodo Monte Carlo
«We don’t have to be smarter than the rest, we have to be more disciplined than the rest».
Warren Buffett
Abbiamo fin qui analizzato due serie storiche dei rendimenti. Si tratta di serie storiche profondamente diverse, sulle quali sono stati complessivamente backtestati migliaia di piani di accumulo di varie durate.
Quando si indaga una strategia di investimento, è sempre auspicabile espandere il più possibile l’analisi, in modo da comprendere tutti gli eventuali scenari futuri. Purtroppo, una copertura esaustiva è impossibile.
Quello che possiamo fare, però, è simulare un grandissimo numero di serie storiche, in modo da aumentare la probabilità che quella reale venga compresa nei backtest.
Per far questo, utilizzeremo un procedimento pensato proprio con questa finalità: il metodo Monte Carlo.
Utilizzeremo R, un ambiente che è nello stesso tempo un software statistico e un linguaggio di programmazione. Con l’aiuto di R, potremo simulare un’ampia gamma di possibili scenari e analizzare il comportamento delle nostre strategie di investimento al verificarsi di ognuno di essi.
In massima sintesi, il metodo Monte Carlo si basa sulla generazione di serie di numeri che seguono la distribuzione di probabilità desiderata (che ovviamente si dovrà avvicinare il più possibile a quella del fenomeno da studiare). Queste simulazioni sono dette parametriche.
La generazione di scenari ipotetici può avvenire anche per mezzo di simulazioni non parametriche, ovvero che non necessitano di modelli statistici basati su distribuzioni di probabilità: ci concentreremo inizialmente su queste.
Svilupperemo delle serie storiche alternative a quella già analizzata, permutando l’ordine in cui i rendimenti si sono presentati.
Le nostre serie storiche di partenza sono composte da 360 rendimenti mensili: quelli del primo PAC simulato sul fondo Raiffeisen Azionario Globale VT e sul fondo Aberdeen Japanese Equity Fund A Acc JPY. Questi 360 valori saranno rimescolati in modo casuale per 1.000.000 di volte, generando traiettorie anche molto diverse da quella iniziale. A partire da ognuna di queste 1.000.000 di serie storiche dei rendimenti, sarà ricostruita la rispettiva serie dei prezzi, sulla quale saranno simulate le tipologie di Piani di Accumulo del Capitale Cost Averaging.
Partiamo dal fondo Raiffeisen. Le rate dei piani di accumulo sono pari a 300 euro. I risultati medi ottenuti sono contenuti nella seguente tabella:
| Raiffeisen – 1.000.000 simulazioni NON parametriche | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. tot. | St. Dev. | Somma finale | Rend. Max | Rend. Min | % Pos. | Mediana | Skew. | Kurt. | Vol. Interna |
| PAC | 360 | CA | 166,93% | 69,47% | 288.284 | 872,47% | −10,57% | 99,9997% | 156,73% | 0,981 | 1,765 | 8,44% |
| PAC | 300 | CA | 128,89% | 72,18% | 206.001 | 817,86% | −43,93% | 99,6166% | 117,55% | 1,066 | 2,070 | 7,56% |
| PAC | 240 | CA | 94,91% | 64,63% | 140.334 | 771,70% | −61,09% | 97,5797% | 84,27% | 1,118 | 2,289 | 6,77% |
| PAC | 180 | CA | 65,23% | 52,42% | 89.225 | 636,09% | −57,58% | 93,3702% | 56,95% | 1,074 | 2,116 | 6,06% |
| PAC | 120 | CA | 39,79% | 38,44% | 50.325 | 386,09% | −61,05% | 86,7803% | 34,47% | 0,910 | 1,484 | 5,42% |
| PAC | 60 | CA | 18,04% | 23,54% | 21.247 | 194,21% | −57,26% | 77,0658% | 15,72% | 0,612 | 0,672 | 4,79% |
| PAC | 36 | CA | 10,35% | 17,05% | 11.918 | 137,21% | −51,37% | 71,4826% | 9,21% | 0,415 | 0,304 | 4,49% |
| PAC | 24 | CA | 6,65% | 13,34% | 7.679 | 103,25% | −45,37% | 67,9678% | 6,04% | 0,282 | 0,156 | 4,26% |
Fig. 29 – Tabella riassuntiva dei risultati di 1.000.000 di simulazioni Monte Carlo con tecniche non parametriche di Piani di Accumulo del Capitale Cost Averaging (a partire dai rendimenti del fondo Raiffeisen)
I rendimenti aumentano con il crescere delle durate dei PAC: è normale, dato che la serie di rendimenti del fondo Raiffeisen era crescente.
La deviazione standard dei rendimenti segue lo stesso andamento: fin qui nessuna sorpresa, salvo notare che quella dei piani della durata di 25 anni è superiore a quella dei trentennali. Con molta probabilità, è un risultato casuale.
Le somme finali sono in linea con i rendimenti: come avevamo visto in precedenza, queste due misure si muovono all’unisono.
I rendimenti max e min ci danno un’idea dell’enorme forbice di valori che è possibile ottenere permutando i rendimenti. Si va dal −10,57% all'872,47%. È importante ricordare che questo pur grande divario non esaurisce tutti gli ipotetici scenari futuri: una copertura completa è irrealizzabile.
Per avere una copertura maggiore (anche se non esaustiva) ci torneranno utili le simulazioni Monte Carlo parametriche, che analizzeremo nel prossimo capitolo.
% Positivi: è la percentuale di piani di accumulo che hanno ottenuto un rendimento finale positivo. I risultati confermano che più un PAC è lungo e più alta è la probabilità di chiuderlo positivamente (siamo ben oltre il 90% già a partire dai piani di durata di 15 anni).
Mediana: è il valore assunto dalle unità statistiche che si trovano nel mezzo della distribuzione. Rispetto alla media, la mediana non è influenzata dalla presenza di outlier, cioè di dati anomali (nel nostro caso, gli outlier sono rendimenti eccezionalmente alti o bassi). Il rendimento mediano si posiziona al di sotto di quello medio su ogni durata.
Skewness: è una misura dell’asimmetria della distribuzione di probabilità della variabile casuale rispetto alla sua media. Quando è positiva, significa che la distribuzione ha una coda destra più lunga (e viceversa). La skewness della distribuzione normale è pari a zero, essendo perfettamente simmetrica.
La distribuzione dei rendimenti dei piani di accumulo di ciascuna durata ha una skewness positiva: in particolare, dai 10 anni in su la skewness si assesta intorno a 1. Ci dobbiamo perciò aspettare una coda destra lunga e possiamo verificarlo visualizzando gli istogrammi della distribuzione delle frequenze dei rendimenti del milione di piani di accumulo Cost Averaging trentennali:
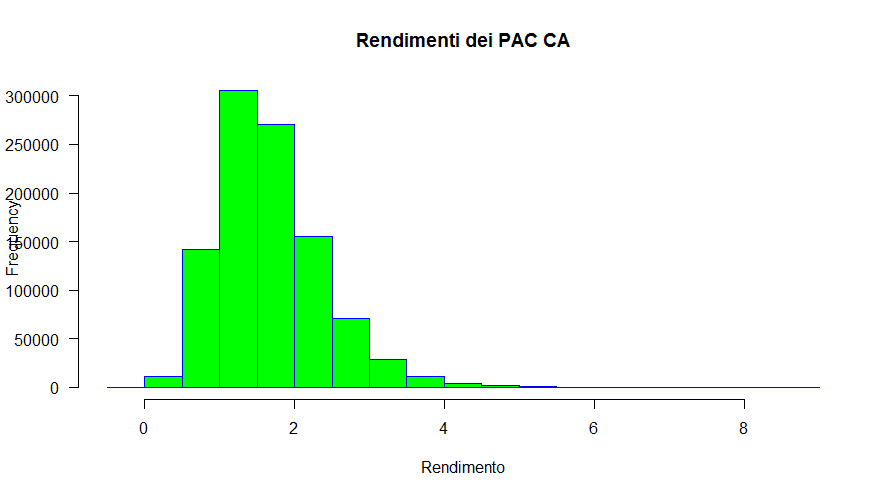
Fig. 30 – Distribuzione delle frequenze dei rendimenti di 1.000.000 di simulazioni Monte Carlo con tecniche non parametriche di Piani di Accumulo del Capitale Cost Averaging (a partire dai rendimenti del fondo Raiffeisen)
La coda lunga destra è ben visibile. Sulla sinistra la coda è molto più breve, dal momento che si è verificato un solo rendimento negativo e i piani che hanno generato un rendimento inferiore al 50% sono stati molto pochi.
Kurtosis (curtosi): è una misura dello spessore delle code di una distribuzione di probabilità. Il coefficiente di curtosi di una distribuzione normale è pari a 3 e di solito – come faremo anche noi – si tende a misurare l’eccesso di curtosi rispetto a questo valore; se il coefficiente è negativo, significa che il suo valore è minore di 3.
Un coefficiente pari a zero descrive una distribuzione mesocurtica (come la normale); un coefficiente positivo descrive una distribuzione leptocurtica (code più spesse della normale); un coefficiente negativo descrive invece una distribuzione platicurtica (code meno spesse della normale).
La kurtosis dei PAC trentennali è positiva. Anche quelle di tutte le altre durate sono positive: con il diminuire di queste ultime, si avvicinano sempre più a zero.
L’ultima grandezza della tabella è la volatilità interna dei piani di accumulo: la misura che abbiamo approfondito nel capitolo precedente.
Passiamo adesso alle simulazioni Monte Carlo non parametriche sviluppate a partire dai rendimenti del fondo Aberdeen.
Vediamo i risultati:
| Aberdeen – 1.000.000 simulazioni NON parametriche | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. tot. | St. Dev. | Somma finale | Rend. Max | Rend. Min | % Pos. | Mediana | Skew. | Kurt. | Vol. Interna |
| PAC | 360 | CA | 1,75% | 34,22% | 109.890 | 404,80% | −72,18% | 44,5304% | −4,30% | 1,259 | 2,964 | 6,20% |
| PAC | 300 | CA | 4,26% | 38,71% | 93.830 | 440,28% | −77,75% | 46,7184% | −2,87% | 1,307 | 3,132 | 6,17% |
| PAC | 240 | CA | 5,61% | 40,55% | 76.041 | 517,67% | −77,10% | 47,7654% | −2,02% | 1,366 | 3,488 | 6,10% |
| PAC | 180 | CA | 6,00% | 39,30% | 57.242 | 550,07% | −76,75% | 48,5837% | −1,24% | 1,334 | 3,354 | 6,00% |
| PAC | 120 | CA | 5,14% | 34,52% | 37.852 | 374,03% | −74,49% | 49,0793% | −0,73% | 1,183 | 2,571 | 5,85% |
| PAC | 60 | CA | 3,03% | 25,19% | 18.546 | 255,84% | −63,86% | 49,5317% | −0,28% | 0,859 | 1,378 | 5,60% |
| PAC | 36 | CA | 1,96% | 19,52% | 11.012 | 166,28% | −56,61% | 49,8385% | −0,08% | 0,666 | 0,826 | 5,40% |
| PAC | 24 | CA | 1,30% | 15,77% | 7.294 | 124,29% | −52,86% | 49,9306% | −0,03% | 0,531 | 0,573 | 5,21% |
Fig. 31 – Tabella riassuntiva dei risultati di 1.000.000 di simulazioni Monte Carlo con tecniche non parametriche di Piani di Accumulo del Capitale Cost Averaging (a partire dai rendimenti del fondo Aberdeen)
Il rendimento totale, seppur ancora leggermente positivo, è diminuito drasticamente (gli effetti sono visibili anche sulla somma finale). La deviazione standard è diminuita soltanto nei piani di durata maggiore o uguale a 10 anni.
I rendimenti massimi sono aumentati nei PAC brevi (fino a 5 anni), mentre si sono ridotti in quelli più lunghi. Non si tratta di un errore: la serie storica dei rendimenti del fondo Aberdeen tende a decrescere ma, tra i 360 rendimenti che la compongono, ce ne sono anche di positivi: questi ultimi, pur essendo meno frequenti, contengono dei valori superiori a quelli del Raiffeisen.
Lanciando tantissime simulazioni, che utilizzano soltanto 24, 36 o 60 dei 360 rendimenti disponibili, ce ne saranno alcune composte in prevalenza dai rendimenti positivi più alti: la simulazione che genera il rendimento finale maggiore è proprio quella riportata nella tabella, per ogni durata.
Il discorso vale ovviamente anche dal lato negativo: esistono dei rendimenti inferiori a quelli del fondo Raiffeisen che, concentrati nei PAC corti, generano dei rendimenti minimi più bassi.
Nelle durate più lunghe (soprattutto nei piani trentennali), il calo è molto più drastico.
La percentuale di PAC positivi subisce una diminuzione notevole, tanto più ampia quanto maggiore è la durata dei piani di accumulo.
Come nel caso del fondo Raiffeisen, il rendimento mediano si posiziona sulla sinistra di quello medio, essendo inferiore a quest’ultimo in tutti i piani analizzati.
Aumentano sia i valori della skewness che quelli della kurtosis: abbiamo cioè distribuzioni delle frequenze dei rendimenti leptocurtiche, con le code destre più lunghe.
Verifichiamole visualizzando la distribuzione delle frequenze dei rendimenti dei piani di accumulo trentennali:
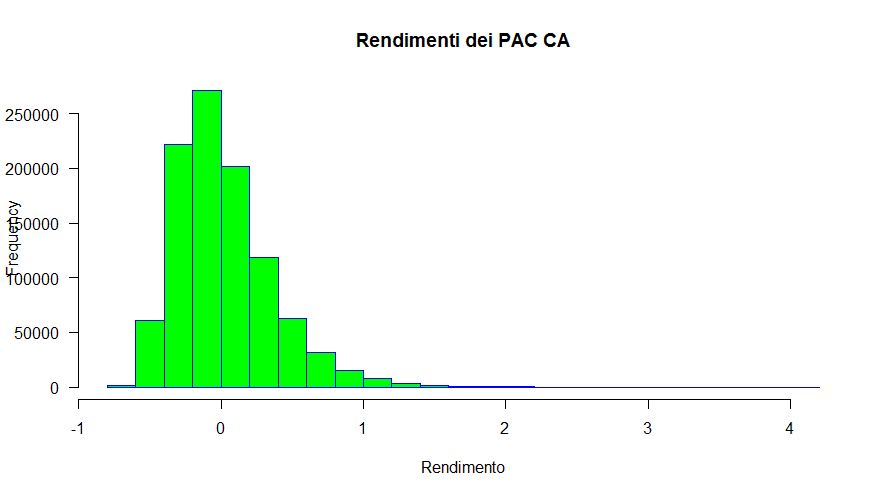
Fig. 32 – Distribuzione delle frequenze dei rendimenti di 1.000.000 di simulazioni Monte Carlo con tecniche non parametriche di Piani di Accumulo del Capitale Cost Averaging (a partire dai rendimenti del fondo Aberdeen)
La coda destra è evidente; le code spesse lo sono un po’ meno, anche se è difficile da valutare con un semplice colpo d'occhio.
Dagli istogrammi si nota come oltre la metà dei rendimenti ottenuti siano negativi ma, dato che il limite minimo del rendimento è il −100% (perdita totale del capitale investito), la coda sinistra è più corta della destra (il rendimento più alto è stato del 404,80%).
L’ultima grandezza della tabella è la volatilità interna. Rispetto a prima, è più elevata nei piani di accumulo di durata inferiore o uguale a 10 anni ed è minore in quelli più lunghi.
8. Simulazioni parametriche col metodo Monte Carlo
«If you don’t know where you are going, you’ll end up someplace else».
Yogi Berra
Continuiamo la nostra analisi con le simulazioni parametriche col metodo Monte Carlo.
Nei nostri test simuleremo 1.000.000 di serie storiche di rendimenti mensili che seguono la distribuzione normale con:
- Media pari a 0,5% e deviazione standard del 5%: simulazione di rendimenti azionari in un mercato crescente.
- Media pari a 0 e deviazione standard del 5%: simulazione di rendimenti azionari in un mercato laterale.
- Media pari a −0,50% e deviazione standard del 5%: simulazione di rendimenti azionari in un mercato in decrescita.
Questi valori sono mensili e, seppur arbitrari, non dovrebbero essere troppo lontani dalla realtà. A partire da queste serie “sintetiche” di rendimenti abbiamo ricostruito quelle dei prezzi (per semplicità al primo della serie è stato assegnato il valore 100).
Sulle serie dei prezzi sono stati quindi simulati i Piani di Accumulo del Capitale a rate costanti.
La scelta della distribuzione normale che, come è noto, è solo un’approssimazione della reale (ma sconosciuta) distribuzione dei rendimenti finanziari (che è leptocurtica, ovvero possiede code più spesse), non deve preoccupare più di tanto: non stiamo ottimizzando un modello econometrico che abbia l’obiettivo di stimare i prezzi futuri nel modo più esatto possibile.
Quello che vogliamo fare, invece, è costruire un insieme di scenari sui quali saranno backtestati gli andamenti dei piani di accumulo Cost Averaging.
Le simulazioni sono state nuovamente realizzate in linguaggio R.
Questa è la prima tabella di risultati:
| Media 0,50%, Volatilità 5% – 1.000.000 simulazioni | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. tot. | St. Dev. | Somma finale | Rend. Max | Rend. Min | % Pos. | Mediana | Skew. | Kurt. | Vol. Interna |
| PAC | 360 | CA | 178,88% | 213,76% | 301.192 | 8.302,62% | −78,29% | 90,7078% | 120,04% | 3,304 | 24,790 | 9,24% |
| PAC | 300 | CA | 131,21% | 152,84% | 208.085 | 5.375,91% | −78,57% | 88,6097% | 91,61% | 2,763 | 17,163 | 8,15% |
| PAC | 240 | CA | 92,57% | 106,94% | 138.650 | 2.118,47% | −73,94% | 85,9795% | 66,86% | 2,167 | 9,389 | 7,23% |
| PAC | 180 | CA | 61,57% | 73,69% | 87.246 | 1.321,23% | −76,47% | 82,3635% | 45,74% | 1,761 | 6,216 | 6,46% |
| PAC | 120 | CA | 36,56% | 47,84% | 49.162 | 783,23% | −64,88% | 77,6258% | 27,99% | 1,294 | 3,200 | 5,79% |
| PAC | 60 | CA | 16,31% | 27,01% | 20.936 | 280,36% | −60,00% | 70,5220% | 12,87% | 0,833 | 1,305 | 5,16% |
| PAC | 36 | CA | 9,29% | 19,09% | 11.804 | 165,10% | −49,68% | 66,2324% | 7,45% | 0,612 | 0,695 | 4,86% |
| PAC | 24 | CA | 5,98% | 14,78% | 7.630 | 105,80% | −43,66% | 63,4346% | 4,84% | 0,477 | 0,413 | 4,64% |
Fig. 33 – Tabella riassuntiva dei risultati di 1.000.000 di simulazioni Monte Carlo con tecniche parametriche di Piani di Accumulo del Capitale Cost Averaging (media 0,50% e deviazione standard 5%)
Questo set di backtest è in qualche modo confrontabile con quello delle simulazioni non parametriche con serie storica iniziale appartenente al fondo Raiffeisen.
Le simulazioni parametriche hanno però maggiore libertà di movimento in fase di creazione delle serie storiche dei rendimenti. Questa maggiore libertà si traduce in una forbice di valori molto più ampia.
Il rendimento medio e la somma finale generata dai piani di accumulo è tanto maggiore quanto più lunga è la durata.
La volatilità è molto più alta di quella delle simulazioni non parametriche, soprattutto nei piani dalla durata di almeno 10 anni.
I rendimenti massimi e minimi si posizionano su valori molto più estremi dei precedenti, mentre le percentuali dei positivi, rispetto alle simulazioni non parametriche, sono diminuite.
I rendimenti mediani si confermano più bassi di quelli medi.
La skewness e la kurtosis sono invece sensibilmente aumentati, come gli istogrammi della distribuzione delle frequenze ci dimostrano:
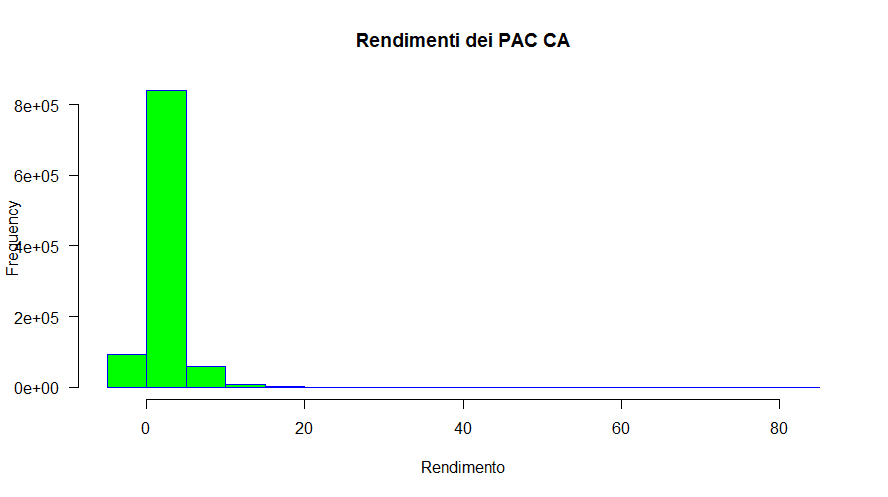
Fig. 34 – Distribuzione delle frequenze dei rendimenti di 1.000.000 di simulazioni Monte Carlo con tecniche parametriche di Piani di Accumulo del Capitale Cost Averaging (media 0,50% e deviazione standard 5%)
Meno del 10% dei piani di accumulo simulati hanno ottenuto dei rendimenti negativi. La stragrande maggioranza dei rendimenti è compresa tra 0 e 500% e una piccola parte ha ottenuto rendimenti superiori.
Il grafico evidenzia la coda lunga destra (il rendimento massimo è stato addirittura dell’8.302,62%). Lo spessore delle code è meno vistoso, ma questo fenomeno non è di facile percezione in questa tipologia di grafici.
La volatilità interna è leggermente aumentata su tutte le durate. Sarà interessante confrontarla con quella dei PIC nel decimo capitolo.
Il passo successivo è stata la simulazione di 1.000.000 di serie storiche di rendimenti con la media pari a zero (stessa deviazione standard).
Vediamo la tabella dei risultati:
| Media 0%, Volatilità 5% – 1.000.000 simulazioni | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. tot. | St. Dev. | Somma finale | Rend. Max | Rend. Min | % Pos. | Mediana | Skew. | Kurt. | Vol. Interna |
| PAC | 360 | CA | −0,03% | 61,45% | 107.964 | 1.391,10% | −87,15% | 37,2814% | −15,74% | 2,723 | 15,951 | 5,14% |
| PAC | 300 | CA | 0,06% | 55,12% | 90.054 | 1.225,02% | −86,42% | 38,4021% | −13,35% | 2,350 | 11,479 | 5,10% |
| PAC | 240 | CA | −0,03% | 48,20% | 71.981 | 821,16% | −83,70% | 39,5399% | −10,91% | 1,991 | 8,096 | 5,05% |
| PAC | 180 | CA | 0,05% | 40,89% | 54.029 | 635,58% | −79,56% | 41,0010% | −8,25% | 1,619 | 5,177 | 4,99% |
| PAC | 120 | CA | −0,04% | 32,64% | 35.987 | 384,58% | −73,10% | 42,5948% | −5,70% | 1,233 | 2,880 | 4,91% |
| PAC | 60 | CA | −0,02% | 22,50% | 17.997 | 194,21% | −63,75% | 44,7909% | −2,82% | 0,819 | 1,266 | 4,78% |
| PAC | 36 | CA | −0,01% | 17,14% | 10.799 | 120,35% | −52,87% | 46,1338% | −1,64% | 0,599 | 0,664 | 4,64% |
| PAC | 24 | CA | −0,00% | 13,79% | 7.200 | 101,91% | −46,76% | 46,8694% | −1,06% | 0,472 | 0,405 | 4,51% |
Fig. 35 – Tabella riassuntiva dei risultati di 1.000.000 di simulazioni Monte Carlo con tecniche parametriche di Piani di Accumulo del Capitale Cost Averaging (media 0% e deviazione standard 5%)
Come era da aspettarsi, il rendimento medio è stato nullo. La deviazione standard dei rendimenti è diminuita molto così come, ovviamente, la somma finale.
Anche tutte le altre misure sono peggiorate: i rendimenti massimi e minimi, la percentuale di PAC positivi, il rendimento mediano, la skewness e la kurtosis.
La volatilità interna è diminuita soprattutto nei PAC dalla durata maggiore o uguale a 10 anni.
Il dato più curioso è quello relativo alla percentuale di PAC positivi: è infatti più alta nei piani di accumulo corti che in quelli lunghi.
Questa è la distribuzione delle frequenze dei rendimenti dei piani di accumulo trentennali:
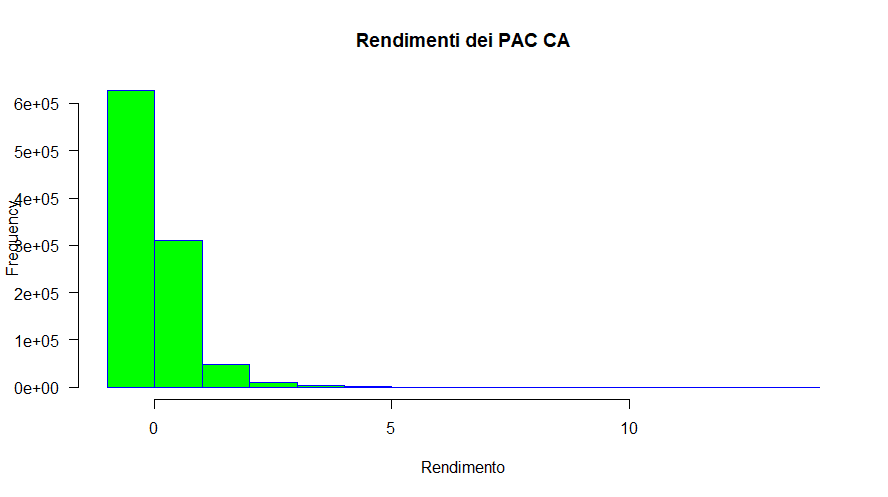
Fig. 36 – Distribuzione delle frequenze dei rendimenti di 1.000.000 di simulazioni Monte Carlo con tecniche parametriche di Piani di Accumulo del Capitale Cost Averaging (media 0% e deviazione standard 5%)
Lanciamo le ultime simulazioni parametriche col metodo Monte Carlo. Poniamo il valore medio pari al −0,50%.
I risultati saranno pessimi, molto peggiori di quelli appena analizzati. Non entreremo in commenti dettagliati, perché i numeri parlano da soli.
Ecco la tabella dei risultati:
| Media −0,50%, Volatilità 5% – 1.000.000 simulazioni | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. tot. | St. Dev. | Somma finale | Rend. Max | Rend. Min | % Pos. | Mediana | Skew. | Kurt. | Vol. Interna |
| PAC | 360 | CA | −53,57% | 21,89% | 50.148 | 441,55% | −90,80% | 2,7802% | −58,59% | 2,123 | 9,418 | 3,55% |
| PAC | 300 | CA | −48,16% | 22,93% | 46.656 | 392,98% | −89,84% | 3,9405% | −53,21% | 1,923 | 7,596 | 3,70% |
| PAC | 240 | CA | −41,72% | 23,75% | 41.963 | 311,86% | −87,31% | 5,6937% | −46,65% | 1,717 | 5,938 | 3,88% |
| PAC | 180 | CA | −33,95% | 23,92% | 35.669 | 316,15% | −84,29% | 8,5051% | −38,52% | 1,468 | 4,238 | 4,07% |
| PAC | 120 | CA | −24,64% | 22,78% | 27.131 | 325,90% | −80,40% | 13,0857% | −28,37% | 1,170 | 2,697 | 4,27% |
| PAC | 60 | CA | −13,41% | 18,80% | 15.587 | 162,56% | −68,28% | 21,3283% | −15,67% | 0,798 | 1,222 | 4,45% |
| PAC | 36 | CA | −8,28% | 15,42% | 9.906 | 113,01% | −57,73% | 27,0185% | −9,73% | 0,592 | 0,641 | 4,45% |
| PAC | 24 | CA | −5,57% | 12,89% | 6.799 | 87,25% | −48,43% | 30,9257% | −6,54% | 0,469 | 0,400 | 4,38% |
Fig. 37 – Tabella riassuntiva dei risultati di 1.000.000 di simulazioni Monte Carlo con tecniche parametriche di Piani di Accumulo del Capitale Cost Averaging (media -0,50% e deviazione standard 5%)
Come sempre, visualizziamo anche la distribuzione delle frequenze dei rendimenti dei piani di accumulo trentennali.
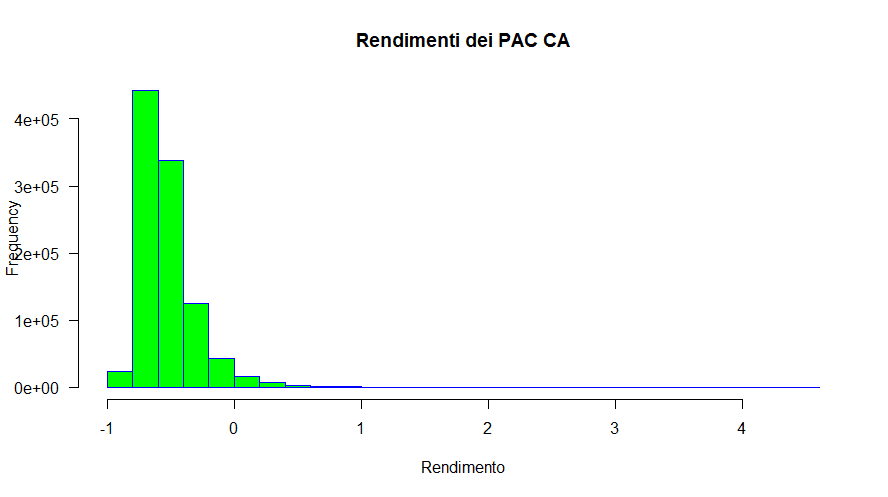
Fig. 38 – Distribuzione delle frequenze dei rendimenti di 1.000.000 di simulazioni Monte Carlo con tecniche parametriche di Piani di Accumulo del Capitale Cost Averaging (media -0,50% e deviazione standard 5%)
L’obiettivo di questa serie di simulazioni è stato quello di osservare il comportamento di un piano di accumulo sul più alto numero di scenari che potrebbero verificarsi in un investimento reale.
La copertura non è esaustiva e non potrà mai esserlo: l’importante è farsi un’idea più precisa di ciò che potrebbe accadere, anche nei casi più estremi.
Il rendimento è la grandezza alla quale gli investitori sono maggiormente interessati: in fin dei conti, ciò che conta di più è incrementare il capitale impiegato in un piano di accumulo.
In fase di analisi, ci sono però altre misure fondamentali: la volatilità è sicuramente quella più importante; forse è anche la più sottovalutata.
Quando il rendimento finale è negativo, gli effetti indesiderati sono due: la perdita di una parte del capitale e la perdita di tempo prezioso. Il capitale può tornare a crescere, il tempo a disposizione dell’investitore può solo diminuire.
Purtroppo, non esistono investimenti o strategie di investimento che permettano un incremento del capitale senza rischio.
Il cosiddetto risk-free offre dei rendimenti bassi: se si vuole ottenere un rendimento più alto, è inevitabile assumersi un rischio altrettanto alto.
9. Quando le cose vanno male: il PAC peggiore (serie storiche reali)

«You get recessions, you have stock market declines. If you don't understand that's going to happen, then you're not ready, you won't do well in the markets».
Peter Lynch
Dopo aver analizzato le performance dei piani di accumulo in alcuni contesti ipotetici, vediamo quali risultati sarebbero stati prodotti in uno degli scenari reali peggiori degli ultimi 80 anni: un piano di accumulo conclusosi a marzo 2009.
Marzo 2009 è stato il bottom, il punto di minimo assoluto raggiunto dai mercati azionari in seguito alla gravissima crisi dei subprime.
Alcuni investitori, molto sfortunati, avevano investito in piani di accumulo a rate costanti destinati a esaurirsi proprio in quel mese: vedremo quali sarebbero state le perdite conseguite.
I backtest che abbiamo eseguito sono facilmente riproducibili con l’Analisi PAC, scegliendo un fondo azionario dalla serie storica molto lunga con i seguenti parametri:
- Data di fine analisi: 1° aprile 2009, in modo che l’effettivo termine del PAC sia avvenuto nel giorno scelto del mese di marzo (in base al campo “Giorno PAC” del form).
- Data di inizio analisi: 1° aprile di X anni prima.
In questo modo, l’analisi dei PAC della durata desiderata inizierà ad aprile dell’anno 2009 meno X e terminerà a marzo 2009.
Nelle colonne dei risultati delle analisi, dovrà apparire un solo piano di accumulo della durata scelta: i risultati saranno relativi a quel singolo PAC.
In conformità alle analisi precedenti, abbiamo seguito questa procedura con i fondi Raiffeisen e Aberdeen. Sono state applicate commissioni di 9 euro a inizio PAC e di 0,95 euro al versamento di ogni rata.
Le durate dei piani di accumulo backtestati vanno da 24 a 240 mesi (da 2 a 20 anni): la lunghezza delle serie storiche dei fondi non ha permesso di andare oltre.
Per completezza, abbiamo anche riportato i risultati dell’analisi di un PIC di pari durata.
Ecco la tabella:
| PAC e PIC peggiori | |||||
|---|---|---|---|---|---|
| N° Rate | Tipologia | RAIFFEISEN | ABERDEEN | ||
| Rendimento | Somma finale | Rendimento | Somma finale | ||
| 240 | PAC Cost Averaging | −8,08% | 66.398 | −51,77% | 34.840 |
| 240 | PIC | 57,35% | n/a | −74,84% | n/a |
| 180 | PAC Cost Averaging | −26,76% | 39.682 | −47,23% | 28.592 |
| 180 | PIC | 24,38% | n/a | −59,77% | n/a |
| 120 | PAC Cost Averaging | −43,18% | 20.523 | −45,08% | 19.839 |
| 120 | PIC | −35,34% | n/a | −49,73% | n/a |
| 108 | PAC Cost Averaging | −43,10% | 18.497 | −43,89% | 18.243 |
| 108 | PIC | −52,93% | n/a | −56,52% | n/a |
| 96 | PAC Cost Averaging | −41,66% | 16.860 | −42,74% | 16.549 |
| 96 | PIC | −52,02% | n/a | −50,33% | n/a |
| 84 | PAC Cost Averaging | −40,23% | 15.114 | −42,63% | 14.507 |
| 84 | PIC | −52,46% | n/a | −41,88% | n/a |
| 72 | PAC Cost Averaging | −41,07% | 12.773 | −43,91% | 12.158 |
| 72 | PIC | −24,53% | n/a | −25,27% | n/a |
| 60 | PAC Cost Averaging | −42,22% | 10.438 | −45,62% | 9.823 |
| 60 | PIC | −43,34% | n/a | −43,45% | n/a |
| 48 | PAC Cost Averaging | −42,66% | 8.287 | −46,05% | 7.797 |
| 48 | PIC | −40,53% | n/a | −45,12% | n/a |
| 36 | PAC Cost Averaging | −41,13% | 6.383 | −44,31% | 6.038 |
| 36 | PIC | −51,78% | n/a | −59,95% | n/a |
| 24 | PAC Cost Averaging | −36,34% | 4.603 | −37,84% | 4.495 |
| 24 | PIC | −52,58% | n/a | −58,26% | n/a |
Fig. 39 – Tabella riassuntiva dei risultati dei peggiori PAC Cost Averaging (disinvestimento a marzo 2009) dei fondi Raiffeisen ed Aberdeen
Le performance di questi PAC sono state disastrose.
Il fondo Aberdeen ha generato i rendimenti peggiori su tutte le durate. Le differenze con il fondo Raiffeisen sono importanti soltanto nei piani di accumulo di 15 e 20 anni: nei piani di accumulo più corti i rendimenti variano in media soltanto di un paio di punti percentuali.
I PIC hanno ottenuto delle performance molto eterogenee:
- Raiffeisen: i rendimenti sono stati peggiori di quelli dei PAC nelle durate inferiori a 10 anni ma nettamente superiori in quelle dai 10 anni in su.
- Aberdeen: i rendimenti sono stati peggiori di quelli del PAC in tutte le durate, con l’eccezione dei PIC a 6 anni. Il motivo per cui il periodo di 6 anni sembra essere sempre favorevole al PIC è del tutto casuale: 6 anni prima di marzo 2009 – marzo 2003 – c'è stato un altro bottom, quello che ha segnato la fine della crisi finanziaria Gli acquisti in un’unica soluzione in quel periodo sarebbero avvenuti a prezzi molto bassi, permettendo di limitare i danni sugli investimenti liquidati esattamente 6 anni dopo. A parte questo, il periodo di 6 anni non ha niente di speciale e non deve assolutamente essere scelto come periodo “meno rischioso” per gli investimenti in un’unica soluzione.
È impressionante il rendimento negativo dell’investimento ventennale in un’unica soluzione sul fondo Aberdeen: −74,84%. Questa terribile percentuale è il frutto di due fattori: il trend decrescente del mercato azionario giapponese e il timing di fine investimento.
Analizziamo graficamente i rendimenti dei “PAC peggiori” per durata e dei corrispondenti PIC:
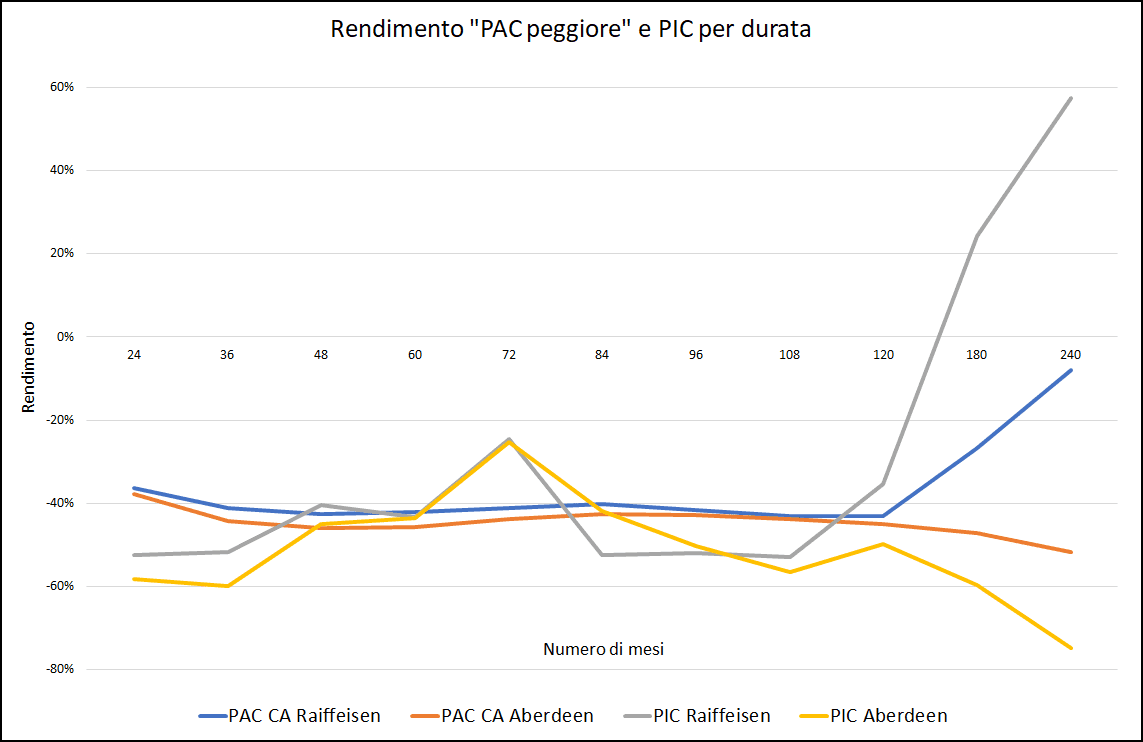
Fig. 40 – Grafico dei rendimenti dei “PAC peggiori” Cost Averaging per durata (disinvestimento marzo 2009) e dei corrispondenti PIC sui fondi Raiffeisen e Aberdeen
Le differenze nei rendimenti dei PAC sui fondi Raiffeisen e Aberdeen sono minime nelle durate uguali o inferiori a 10 anni. In quelle di 15 e 20 anni assumono proporzioni rilevanti, a vantaggio dei piani costruiti sul fondo Raiffeisen.
Anche i PIC seguono un andamento abbastanza simile fino alla durata di 9/10 anni. Al di sopra, prendono direzioni diametralmente opposte: l’investimento sul fondo Raiffeisen entra in territorio positivo; quello sul fondo Aberdeen sprofonda a livelli intorno al −60% e −75%.
In generale, i grafici dei rendimenti dei PIC presentano delle oscillazioni molto più marcate di quelle dei PAC: una conferma della loro maggior volatilità/rischiosità.
Come si sarebbero dovuti comportare, a marzo 2009, gli sfortunatissimi investitori in questi PAC?
Chi aveva necessità di liquidare la somma investita in concomitanza della fine del piano di accumulo, non avrebbe potuto far altro che incassare la pesante perdita.
Per gli altri, la soluzione migliore sarebbe stata quella di non disinvestire: il PAC si sarebbe trasformato in un PIC e le quote accumulate sarebbero state mantenute in portafoglio almeno fin quando il rendimento fosse tornato positivo.
Quanto tempo sarebbe stato necessario?
Nelle tabelle di output dell’Analisi dei PAC (e dei PIC), viene visualizzato il tempo di recupero medio e massimo degli investimenti in perdita.
Non è detto che il periodo di recupero più lungo per ogni durata sia necessariamente associato al PAC o al PIC con il rendimento più basso, ma è sufficiente a darci un’idea di quanti giorni borsistici sarebbero occorsi nel caso peggiore: un valore indirettamente proporzionale alla durata dei piani di accumulo.
In generale, a parità di durata, il periodo di recupero di un piano di accumulo Cost Averaging è sempre inferiore a quello di un investimento in un’unica soluzione.
Il periodo di recupero è un importante indicatore di rischio, spesso sottovalutato o ignorato (e molto difficile da reperire).
Che cosa è possibile fare per evitare di perdere gran parte del capitale accumulato, nel caso in cui si verifichi una crisi finanziaria proprio nella parte finale dell’investimento?
Una possibile risposta è l’utilizzo dei disinvestimenti anticipati: si tratta della vendita di una parte delle quote sottoscritte al verificarsi di determinate condizioni.
I disinvestimenti anticipati verranno approfonditi nell’undicesimo capitolo.
10. Confronto tra PAC a rate costanti e PIC
«Be yourself; everyone else is already taken».
Oscar Wilde
Abbiamo già confrontato in diverse occasioni i Piani di Accumulo del Capitale con i PIC, gli investimenti in un’unica soluzione.
L’Analisi PAC consente di effettuare anche l’analisi dei PIC nel periodo temporale scelto e ne visualizza i risultati in una tabella separata.
L’analisi dei PIC è – esattamente come quella dei PAC – di tipo rolling su tutte le durate considerate: nei fondi che dispongono di serie storiche molto lunghe, come il Raiffeisen e l’Aberdeen più volte utilizzati, con una singola analisi si backtestano centinaia di PAC/PIC per durata.
Vediamo la tabella di output dell’analisi PIC sul fondo Raiffeisen:
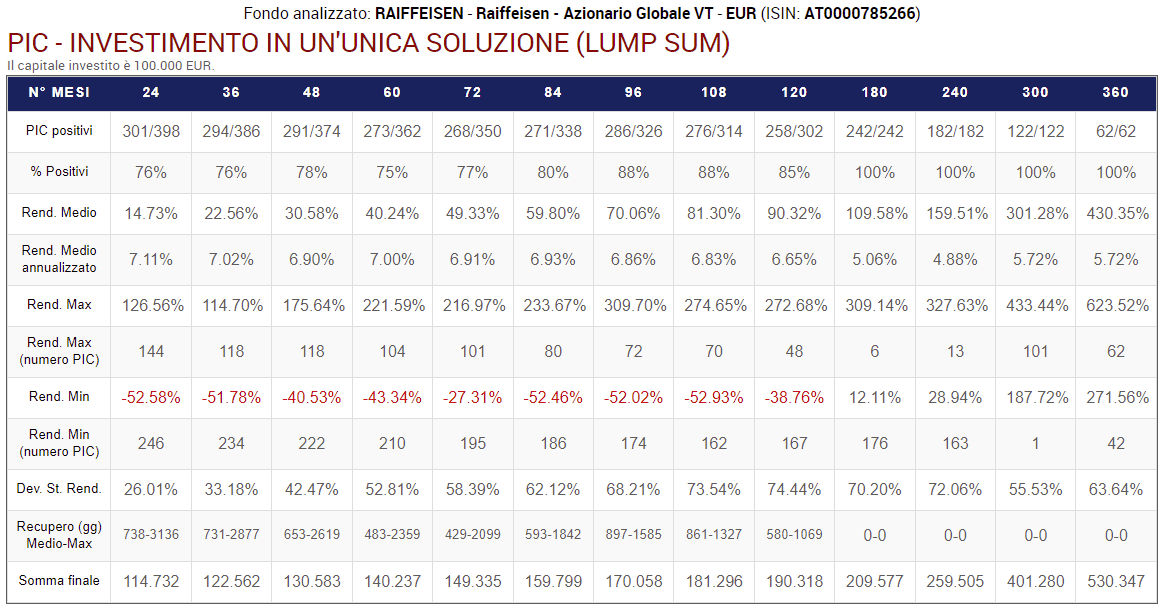
Fig. 41 – Raiffeisen: PIC. Capitale investito: 100.000 euro
La struttura è molto simile a quella dell’Analisi PAC. Ci limiteremo a formulare alcune considerazioni:
- I rendimenti medi e medi annualizzati dei PIC sono più alti di quelli dei piani di accumulo (il confronto è con i dati della Fig. 11). Dal momento che il mercato azionario globale è costantemente cresciuto negli ultimi 35 anni, è normale che un investimento effettuato in un’unica soluzione all’inizio di ciascun periodo di analisi abbia generato un rendimento più elevato di un investimento dilazionato nel tempo.
- I 242 PIC della durata di 15 anni sono risultati tutti positivi. Il 90% dei piani di accumulo di pari durata era stato positivo (per avere il 100% di PAC positivi erano serviti almeno 25 anni).
- I rendimenti massimi sono tutti più elevati mentre quelli minimi sono più bassi nei PIC a 2, 3, 5, 7, 8 e 9 anni di durata.
- Le deviazioni standard dei rendimenti dei PIC sono tutte maggiori. È un altro indizio a favore della minor rischiosità dei piani di accumulo rispetto agli investimenti in un’unica soluzione: minor rischiosità che, almeno per ogni singolo fondo, può adesso essere misurata con precisione.
- Un ulteriore indizio ci viene fornito dal periodo di recupero. Sia i periodi di recupero medi che quelli massimi dei PIC sono molto più lunghi di quelli dei PAC. In caso di un investimento andato male, l’attesa necessaria per riportarne il valore in territorio positivo è molto maggiore nei PIC.
- Le somme finali, infine, consistono in una media per durata dei valori finali dei PIC, ipotizzando un capitale iniziale di ogni investimento pari a 100.000 euro.
Vediamo le performance dei PIC sul fondo Aberdeen:
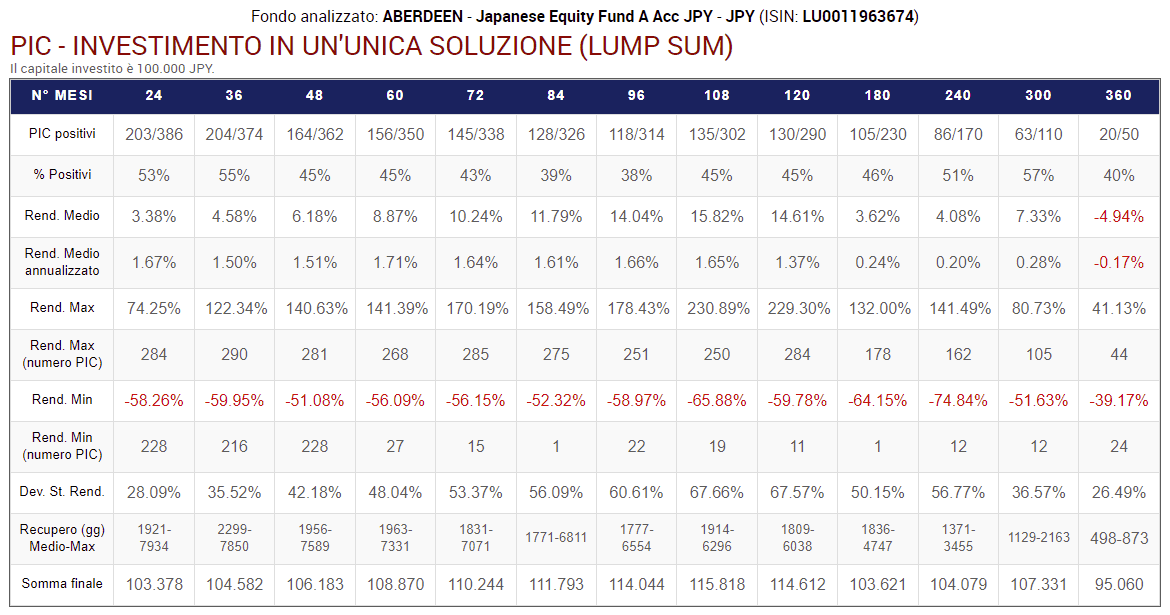
Fig. 42 – Aberdeen: PIC. Capitale investito: 100.000 euro
La tabella con cui effettuiamo il confronto è quella della Fig. 20:
- La percentuale di PIC positivi è molto inferiore a quella dei PAC positivi. L’unica eccezione è nella durata triennale: la differenza è solo dell’1% e, molto probabilmente, è causale. È impressionante il dato relativo alla durata trentennale: mentre il 100% dei piani di accumulo si sono conclusi positivamente, soltanto il 40% dei PIC è riuscito a fare altrettanto.
- Il rendimento medio e medio annualizzato sono a favore dei PIC fino a 10 anni di durata. In quelle superiori, il PAC ha performato meglio anche da questo punto di vista.
- I rendimenti massimi dei PIC sono decisamente superiori per tutte le durate comprese tra 2 e 20 anni. Quelle di 25 e 30 anni, invece, premiano i piani di accumulo.
- I rendimenti minimi sono tutti pesantemente in rosso e oscillano intorno al −60% su tutte le durate fino a 15 anni. Il peggior PIC ventennale registra una perdita che sfiora il −75%, mentre quelli di 25 e 30 anni fanno un po' meglio di quest'ultimo (−51,63% e −39,17%).
- Rispetto a quelle dei PAC, nei PIC le deviazioni standard dei rendimenti sono molto più elevate: avevamo ottenuto lo stesso risultato sul fondo Raiffeisen. All’aumentare delle durate le distanze si assottigliano (i PIC trentennali sono appena più volatili dei piani di accumulo di pari durata).
- I periodi di recupero sono molto più lunghi di quelli dei PAC.
Simulazioni Monte Carlo
Diamo adesso un’occhiata alle simulazioni col metodo Monte Carlo, effettuate sulla base di rendimenti generati sinteticamente a partire dalla distribuzione normale con media mensile dello 0,50%, 0% e −0,50% e deviazione standard pari al 5%.
In questa e in tutte le prossime simulazioni Monte Carlo abbiamo simulato l’investimento di 100.000 euro per ogni durata.
La prima tabella è la seguente:
| Media 0,50%, Volatilità 5% – 1.000.000 simulazioni | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. tot. | St. Dev. | Somma finale | Rend. Max | Rend. Min | % Pos. | Mediana | Skew. | Kurt. | Vol. Interna |
| PIC | 360 | Puro | 499,58% | 718,50% | 599.581 | 34.821,57% | −96,24% | 92,2486% | 283,65% | 5,112 | 61,006 | 16,37% |
| PIC | 300 | Puro | 345,14% | 466,34% | 445.143 | 19.488,19% | −93,83% | 90,3005% | 207,73% | 4,300 | 44,578 | 13,09% |
| PIC | 240 | Puro | 229,39% | 293,76% | 329.386 | 8.054,39% | −93,86% | 87,7140% | 145,36% | 3,236 | 21,501 | 10,53% |
| PIC | 180 | Puro | 144,25% | 182,58% | 244.253 | 4.410,86% | −92,78% | 84,2003% | 95,54% | 2,623 | 14,069 | 8,56% |
| PIC | 120 | Puro | 80,98% | 105,77% | 180.976 | 1.844,31% | −88,28% | 79,3139% | 56,35% | 1,919 | 7,127 | 7,04% |
| PIC | 60 | Puro | 34,28% | 53,21% | 134.277 | 627,71% | −80,49% | 71,8759% | 24,92% | 1,227 | 2,778 | 5,85% |
| PIC | 36 | Puro | 19,10% | 35,81% | 119.098 | 353,45% | −73,27% | 67,2845% | 14,21% | 0,898 | 1,455 | 5,44% |
| PIC | 24 | Puro | 12,17% | 27,15% | 112.168 | 218,45% | −67,61% | 64,2327% | 9,13% | 0,712 | 0,904 | 5,24% |
Fig. 43 – Tabella riassuntiva dei risultati di 1.000.000 di simulazioni Monte Carlo con tecniche parametriche di Piani di Accumulo del Capitale Cost Averaging (media 0,50% e deviazione standard 5%)
Sono state effettuate un milione di simulazioni parametriche (media mensile dello 0,50%): il rendimento medio e la deviazione standard sono molto più elevati di quelli dei piani di accumulo simulati sulla serie storica reale del fondo Raiffeisen o sulle serie storiche sintetiche generate col metodo Monte Carlo.
I rendimenti minimi sono impressionanti. I valori sono terribili, tanto peggiori quanto più lunghe sono le durate. Bisogna fare attenzione a leggere correttamente questi dati: sono i casi estremi di un milione di simulazioni, eventi dalla bassissima probabilità di verificarsi ma che, su numeri così grandi, fanno la loro comparsa.
I rendimenti minimi oscillano tra il −67,61% dei piani di accumulo biennali e il −96,24% di quelli trentennali. Risultati incredibili in uno scenario di crescita (media dello 0,50% mensile).
Questa è la distribuzione delle frequenze del milione di rendimenti trentennali che abbiamo simulato:
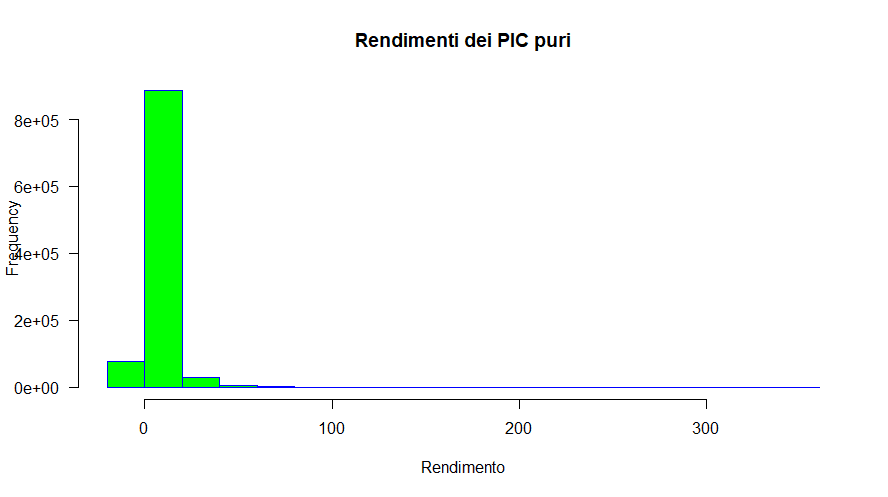
Fig. 44 – Distribuzione delle frequenze dei rendimenti di 1.000.000 di simulazioni Monte Carlo con tecniche parametriche dei PIC (media 0,50% e deviazione standard 5%)
I rendimenti negativi sono stati una piccola parte del totale: il 7,75%, come si può ricavare per differenza dalla tabella precedente. Tra questi, è compreso anche il minimo assoluto del −96,24%.
Gli outlier valgono ovviamente in entrambe le direzioni: la stessa piccolissima probabilità che ha generato il rendimento minimo ha reso possibile anche quello massimo, pari al 34.821,57%. Un valore straordinariamente alto, che nella realtà è pressoché impossibile che si possa verificare (sulle durate inferiori i rendimenti massimi sono meno elevati, ma pur sempre altissimi).
Continuando con l’analisi della tabella, i rendimenti mediani si confermano minori di quelli medi, mentre la skewness e la kurtosis sono positive: tanto maggiori quanto più lunghe sono le durate dei piani di accumulo backtestati.
Infine, la volatilità interna: è molto più elevata di quella dei piani di accumulo di pari lunghezza, dato che le oscillazioni del controvalore dell’investimento sono maggiori rispetto a quella dei PAC.
Vediamo la tabella dei risultati di un milione di simulazioni col metodo Monte Carlo sulla base di rendimenti generati a partire da una distribuzione normale con media dello 0% (deviazione standard sempre pari al 5%):
| Media 0%, Volatilità 5% – 1.000.000 simulazioni | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. tot. | St. Dev. | Somma finale | Rend. Max | Rend. Min | % Pos. | Mediana | Skew. | Kurt. | Vol. Interna |
| PIC | 360 | Puro | 0,03% | 120,21% | 100.030 | 6.147,78% | −98,99% | 31,8557% | −36,18% | 5,204 | 65,958 | 5,36% |
| PIC | 300 | Puro | 0,12% | 105,53% | 100.122 | 5.452,18% | −99,03% | 33,2788% | −31,18% | 4,252 | 44,320 | 5,30% |
| PIC | 240 | Puro | −0,06% | 90,32% | 99.936 | 2.423,50% | −98,55% | 34,9805% | −25,81% | 3,403 | 24,550 | 5,24% |
| PIC | 180 | Puro | 0,11% | 75,12% | 100.112 | 1.622,17% | −97,45% | 37,0375% | −19,82% | 2,629 | 13,842 | 5,18% |
| PIC | 120 | Puro | −0,16% | 58,72% | 99.844 | 1.106,04% | −93,94% | 39,2025% | −13,93% | 1,916 | 6,896 | 5,11% |
| PIC | 60 | Puro | −0,01% | 39,86% | 99.994 | 504,67% | −86,53% | 42,4702% | −7,05% | 1,238 | 2,827 | 5,04% |
| PIC | 36 | Puro | 0,01% | 30,22% | 100.009 | 272,14% | −78,96% | 44,2680% | −4,18% | 0,901 | 1,455 | 5,00% |
| PIC | 24 | Puro | −0,01% | 24,29% | 99.986 | 210,03% | −68,56% | 45,4339% | −2,72% | 0,703 | 0,878 | 4,97% |
Fig. 45 – Tabella riassuntiva dei risultati di 1.000.000 di simulazioni Monte Carlo con tecniche parametriche di Piani di Accumulo del Capitale Cost Averaging (media 0% e deviazione standard 5%)
Il rendimento totale si azzera e la deviazione standard diminuisce, così come pure i rendimenti massimi e minimi.
La percentuale di PIC positivi è molto più bassa e si è invertito l’ordine: è più probabile che un rendimento positivo sia generato da un PIC corto che da uno lungo.
I rendimenti mediani sono negativi, mentre i valori della skewness e della kurtosis sono rimasti sugli stessi livelli.
La volatilità interna è scesa molto, ma si mantiene superiore a quella dei piani di accumulo di pari durata (stessa media dello 0%).
Questa è la distribuzione delle frequenze dei rendimenti dei piani trentennali:
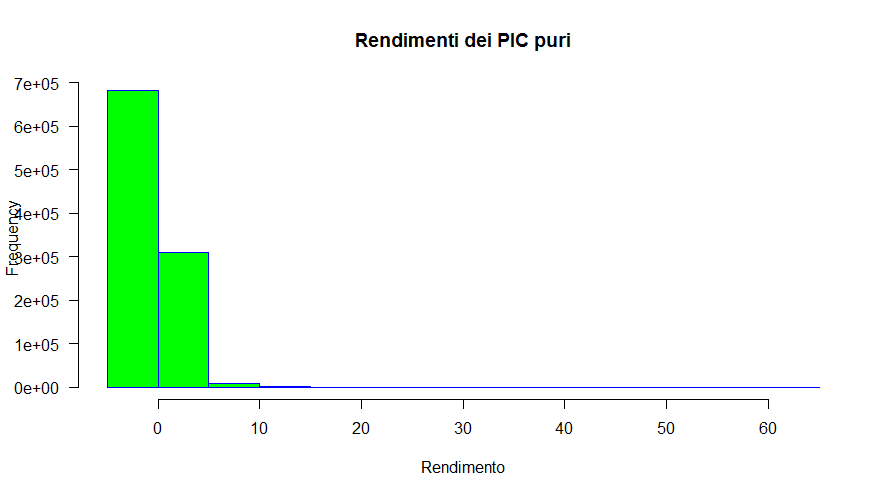
Fig. 46 – Distribuzione delle frequenze dei rendimenti di 1.000.000 di simulazioni Monte Carlo con tecniche parametriche dei PIC (media 0% e deviazione standard 5%)
Il rettangolo sulla sinistra contiene tutti i rendimenti negativi, che sono ben più della metà.
Per finire, presentiamo la tabella dei risultati di un milione di simulazioni col metodo Monte Carlo sulla base di rendimenti generati sinteticamente a partire dalla distribuzione normale con media del −0,50% (deviazione standard sempre pari al 5%):
| Media −0,50%, Volatilità 5% – 1.000.000 simulazioni | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. tot. | St. Dev. | Somma finale | Rend. Max | Rend. Min | % Pos. | Mediana | Skew. | Kurt. | Vol. Interna |
| PIC | 360 | Puro | −83,44% | 20,10% | 16.558 | 903,33% | −99,86% | 0,9114% | −89,50% | 5,127 | 59,316 | 2,75% |
| PIC | 300 | Puro | −77,67% | 23,68% | 22.333 | 852,22% | −99,65% | 1,5181% | −84,70% | 4,310 | 42,582 | 2,96% |
| PIC | 240 | Puro | −69,87% | 27,39% | 30.132 | 744,83% | −99,60% | 2,6654% | −77,71% | 3,381 | 23,806 | 3,22% |
| PIC | 180 | Puro | −59,23% | 30,84% | 40.774 | 786,74% | −98,86% | 4,7376% | −67,49% | 2,682 | 14,966 | 3,54% |
| PIC | 120 | Puro | −44,88% | 32,63% | 55.118 | 570,82% | −97,01% | 8,7303% | −52,52% | 1,961 | 7,531 | 3,93% |
| PIC | 60 | Puro | −25,58% | 29,81% | 74.423 | 311,83% | −91,95% | 16,9481% | −30,82% | 1,243 | 2,865 | 4,40% |
| PIC | 36 | Puro | −16,12% | 25,49% | 83.881 | 214,50% | −82,82% | 23,1140% | −19,63% | 0,900 | 1,438 | 4,62% |
| PIC | 24 | Puro | −10,93% | 21,78% | 89.069 | 192,00% | −71,07% | 27,5692% | −13,37% | 0,714 | 0,913 | 4,72% |
Fig. 47 – Tabella riassuntiva dei risultati di 1.000.000 di simulazioni Monte Carlo con tecniche parametriche di Piani di Accumulo del Capitale Cost Averaging (media -0,50% e deviazione standard 5%)
I numeri sono angoscianti. La durata dei PIC è la variabile che governa la percentuale dei positivi: più è lunga, più è alta la probabilità di terminare l’investimento con un rendimento negativo.
Questa è la distribuzione delle frequenze dei rendimenti dei piani trentennali:
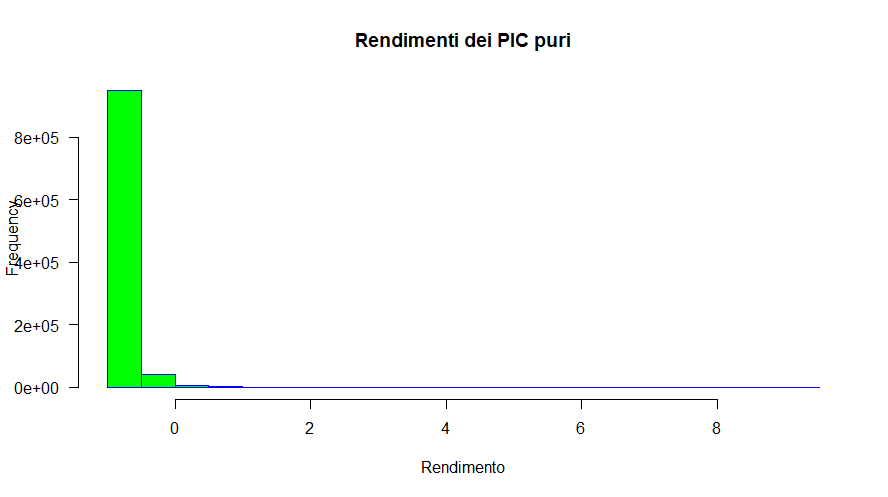
Fig. 48 – Distribuzione delle frequenze dei rendimenti di 1.000.000 di simulazioni Monte Carlo con tecniche parametriche dei PIC (media -0,50% e deviazione standard 5%)
La stragrande maggioranza di rendimenti è pesantemente negativa e sono visibili a malapena i rettangoli dei pochissimi piani di accumulo conclusisi positivamente (lo 0,911%).
Un dato interessante ci viene fornito dalla volatilità interna: stavolta, la volatilità interna dei PIC è inferiore a quella dei PAC a partire dalla durata quinquennale. È difficile però parlare di minor rischiosità dei PIC in un contesto dove sia il numero che la portata delle simulazioni negative sono maggiori.
Il raffronto tra le performance dei Piani di Accumulo di Capitale (PAC) e dei Piani di Investimento di Capitale (PIC) ci permette di individuare i vantaggi e i limiti di ciascuno.
Sono due modalità di investimento molto diverse, ma non si escludono necessariamente l’una con l’altra: qualora ci siano le condizioni e l’investitore sia dotato di una disponibilità finanziaria sufficiente, possono essere portate avanti in modo sinergico.
L’investimento in un un’unica soluzione ha un rendimento atteso e una volatilità superiori a quello dei piani di accumulo. Siamo in presenza del più classico dei trade-off della finanza:
- Se si punta a un rendimento alto, ci si deve assumere un livello di rischio maggiore.
- Se si vuole rischiare di meno, ci si deve accontentare di un rendimento inferiore.
11. I disinvestimenti anticipati e i Versamenti aggiuntivi

«Management is, above all, a practice where art, science, and craft meet».
Henry Mintzberg
Quando si investe sui mercati finanziari, il pericolo più grande è costituito dalle crisi finanziarie.
Le crisi causano brusche cadute nei prezzi degli strumenti finanziari e, molto spesso, tendono anche ad aumentare la correlazione lineare tra gli asset di diversa tipologia (ad esempio, azionari e obbligazionari).
Limitandoci ai mercati azionari, che costituiscono il sottostante della maggior parte dei piani di accumulo del capitale, i pericoli principali sono due:
- Quando la discesa dei prezzi avviene poco prima della fine di un PAC, non c’è più tempo per recuperare. L’investimento si concluderà inevitabilmente con un rendimento negativo. Si può decidere di non disinvestire, soprattutto se non si ha bisogno di liquidità, trasformando il PAC in un PIC nella speranza che i mercati tornino a crescere e il rendimento in territorio positivo. Abbiamo visto nei capitoli precedenti come i tempi di recupero medi e massimi siano grandezze che, sulla base del passato, possano essere stimati con una certa precisione.
- Le crisi finanziarie più intense generano panico. Il panico è all’origine del panic-selling: la liquidazione anticipata degli strumenti finanziari. Durante le fasi di panic-selling, vengono quasi sempre generate delle perdite finanziarie. Il panic-selling manda all’aria i piani degli investitori, anche di quelli che avevano un orizzonte temporale molto lungo. Il panic-selling colpisce soprattutto un investitore in un PIC: più raramente quello in un PAC, dove i meno esperti potrebbero essere indotti a sospendere i versamenti delle rate (soluzione molto inopportuna, dato che in un piano di accumulo le crisi permettono di acquistare un maggior numero di quote del sottostante, a parità di ammontare versato).
Per arginare il primo di questi due pericoli si può ricorrere ai disinvestimenti anticipati. Per sfruttare il secondo, anziché subirne passivamente gli effetti, si possono attuare dei versamenti aggiuntivi.
11.1 I disinvestimenti anticipati

«Quando il mare è calmo, chiunque può far da timoniere».
Publilio Siro
I disinvestimenti anticipati consistono nella vendita di una parte delle quote accumulate in uno o più momenti precedenti al completamento di un Piano di Accumulo del Capitale.
I disinvestimenti anticipati hanno lo scopo di minimizzare il rischio che, nell’ultima parte di vita del piano di accumulo, una crisi finanziaria generi una discesa rapida e considerevole del valore delle quote, facendo diminuire il rendimento finale o, peggio ancora, trasformando un rendimento positivo in uno negativo.
Si vuole cioè evitare l’erosione parziale o totale del guadagno conseguito fino a quel momento.
Non si tratta, quindi, di una variante strategica finalizzata a incrementare il rendimento. Al contrario, i disinvestimenti anticipati sono una misura che gli investitori potrebbero applicare per limitare il rischio di perdere quanto accumulato.
In questo capitolo, verranno analizzati i disinvestimenti anticipati su fondi azionari o bilanciati. Nulla vieta, comunque, di effettuarli anche ad altre tipologie di fondi, facendo attenzione a selezionare i parametri più appropriati (saranno approfonditi in seguito).
I disinvestimenti anticipati hanno anche un grosso inconveniente: quando il valore delle quote continua a salire, il rendimento finale del PAC sarà peggiore.
I mercati azionari, storicamente, hanno sempre seguito un trend di crescita nel lungo termine. Di conseguenza, in media, i disinvestimenti anticipati faranno diminuire il rendimento finale dei piani di accumulo.
In alcuni casi, però, i disinvestimenti anticipati possono salvare l’investitore da un vero e proprio crollo del rendimento: quando vengono effettuati prima di una crisi finanziaria che si sviluppa in prossimità della fine del piano di accumulo.
Succede raramente, ma in quei pochi casi l’impatto può essere molto positivo.
I disinvestimenti anticipati possono essere interpretati come un’assicurazione contro una crisi finanziaria. La maggior parte delle volte, il prezzo pagato per assicurarsi sarà un costo in più: non si verificherà l’evento assicurato e, con il senno di poi, avremmo risparmiato evitando di pagare il premio assicurativo.
Se l’evento assicurato si dovesse verificare (crisi e perdita di rendimento), i disinvestimenti anticipati permetterebbero però di limitare i danni: l’assicurazione – ovvero la liquidazione anticipata di una parte del capitale investito – avrebbe dato i suoi frutti.
Non potendo sapere in anticipo se si verificherà una crisi finanziaria, la scelta di attuare i disinvestimenti anticipati sarà soggettiva e legata ad alcune variabili come la durata del piano di accumulo, la propensione al rischio e la necessità più o meno inderogabile di disinvestire il capitale una volta completato il PAC.
I disinvestimenti anticipati offrono un supporto psicologico all’investitore: sono un modo per vivere con più tranquillità le ultime fasi dell’investimento in un piano di accumulo.
L’Analisi PAC permette di backtestare la performance dei Piani di Accumulo del Capitale sui quali siano stati effettuati dei disinvestimenti anticipati: per l’effettuazione di backtest su larga scala servono alcune regole precise.
Nel form relativo all’Analisi PAC, 6 parametri sono dedicati esclusivamente ai disinvestimenti anticipati: con l’eccezione della “% Prelievo”, ognuno di essi individua una condizione necessaria ma non sufficiente alla loro attivazione:
- Livello soglia del Filtro VIX: valore minimo del VIX (End of Day).
- % Completamento PAC: percentuale del numero di rate versate rispetto a quelle totali (la maxirata, se presente, conta quanto il numero di rate che la compongono).
- Rendimento minimo: rendimento percentuale minimo che il PAC deve aver raggiunto.
- % Prelievo: percentuale di quote prelevate.
- Numero massimo di prelievi: numero massimo di prelievi effettuabili durante la vita di un PAC.
- Intervallo rate: numero minimo di rate da versare prima di eseguire un nuovo prelievo.
Sopra a questi 6 parametri esiste la checkbox “Disinvestimenti anticipati”, che deve essere selezionata per includere i disinvestimenti anticipati nell’Analisi PAC.
Questi parametri possono essere modificati dinamicamente ma, la cosa da evitare assolutamente, è quella di effettuare tanti backtest per trovare la combinazione che avrebbe prodotto i risultati migliori.
Seguendo questa strada, non si fa altro che overfittare i parametri: ottimizzarli su valori che avrebbero massimizzato le performance passate, ma che quasi sicuramente non produrrebbero buoni risultati in futuro.
I parametri devono essere selezionati sulla base del buon senso:
- Livello soglia del Filtro VIX: il valore predefinito è 24. È un valore scelto guardando al passato (in particolare comparando visivamente i grafici del VIX e dello S&P 500), ma non è stato overfittato. Il livello soglia del Filtro VIX ha lo scopo di delimitare un periodo di bassa o medio/bassa volatilità, in cui i disinvestimenti anticipati non vengono applicati, da uno di medio/alta o alta volatilità, in cui i disinvestimenti anticipati possono essere attivati.
- % Completamento PAC: il valore predefinito è il 90%, ma è consigliabile che venga scelto anche in funzione della durata del PAC. Il 90% di completamento in un PAC trentennale corrisponde a 27 anni, 3 anni prima del completamento; in un PAC decennale equivale a 9 anni, un solo anno prima del termine. Impostando una “% Completamento PAC” alta, aumenta il rischio che un’eventuale crisi sia già avvenuta al momento di prendere in considerazione i disinvestimenti anticipati; impostando una percentuale bassa, sarà più grande l’impatto negativo sul rendimento finale nel caso in cui la crisi non si verifichi o sia di proporzioni limitate.
- Rendimento minimo: in linea di massima, si tende a disinvestire una parte delle quote quando il rendimento del PAC è positivo: il valore predefinito è il 10%. In caso di rendimento inferiore – a maggior ragione se negativo – è presumibile che l’investitore preferisca non disinvestire, nella speranza che nell’ultima parte di vita del piano di accumulo si verifichi una crescita del mercato al posto di una crisi finanziaria. È un parametro che, come tutti gli altri, può essere personalizzato.
- % Prelievo: dovrà essere impostata a un livello che sia compatibile con la propria propensione al rischio. In generale, più si vuole essere prudenti e maggiore sarà la percentuale prelevata. Questo parametro dovrà essere coerente con la “% completamento PAC”: sarebbe poco sensato prelevare il 10% una volta completato il 90% del PAC o viceversa. La percentuale predefinita è l’85%.
- Numero massimo di prelievi: si può decidere di utilizzare i disinvestimenti anticipati una o più volte durante la vita di un piano di accumulo. Il valore predefinito è 3 ma difficilmente, anche in un piano di accumulo molto lungo, i disinvestimenti anticipati verranno azionati più di una volta.
- Intervallo rate: una volta eseguito un prelievo, non avrebbe molto senso eseguirne un altro a distanza ravvicinata. Il valore predefinito è di 12 rate e, come tutti gli altri, può essere modificato in base alle preferenze dell’investitore.
Il “Livello soglia del Filtro VIX” è l’interruttore principale, la condizione che deve essere innanzitutto verificata per poter azionare un Disinvestimento anticipato. Come è noto, il filtro VIX ha una correlazione lineare negativa con lo S&P 500: per questo motivo, il VIX che supera una certa soglia può essere considerato il primo indizio di un’imminente crisi finanziaria. Purtroppo (o forse sarebbe meglio dire per fortuna!), non sempre è così: potrebbe trattarsi di un falso segnale.
Al posto del VIX potrebbe essere utilizzato un altro indicatore trend following o di momentum. Ognuno è libero di utilizzare, a livello operativo, quello che preferisce o di cui si fida di più.
Suggeriamo l’utilizzo del filtro VIX soprattutto con fondi azionari o bilanciati; potrebbe perciò non essere opportuno applicare i disinvestimenti anticipati a certi fondi obbligazionari, come i monetari o i governativi.
Gli obbligazionari high yield e corporate sono invece abbastanza correlati col mercato azionario e potrebbero essere backtestati con una certa significatività.
Non è tuttavia da escludere che una violenta crisi finanziaria possa aumentare, seppure momentaneamente, la correlazione tra il mercato azionario e quello obbligazionario. In questo senso, avrebbe una certa logica l’utilizzo del filtro VIX con tutti i fondi obbligazionari.
Effettuiamo il primo backtest sul fondo Raiffeisen, senza modificare i parametri predefiniti dei disinvestimenti anticipati.
I risultati ottenuti sono i seguenti:
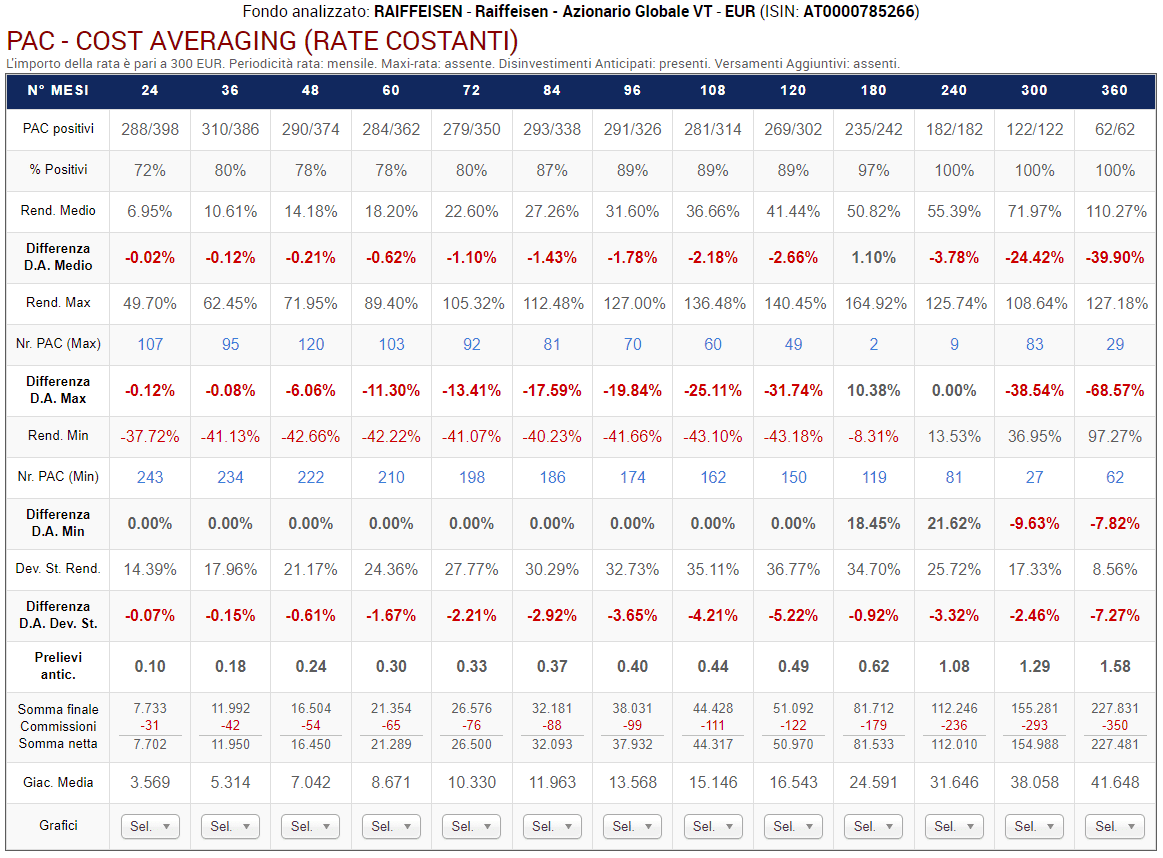
Fig. 49 – Raiffeisen: Disinvestimenti anticipati. VIX = 24; % Completamento PAC = 90%; Rendimento minimo = 10%; % Prelievo = 85%; Numero massimo di prelievi = 3; Intervallo rate = 12. PAC Cost Averaging. Rata: 300 euro
Commentiamo soltanto le misure di output specifiche dei disinvestimenti anticipati (righe in grassetto, a eccezione della giacenza media):
- Differenza D.A. Medio: è la differenza tra il rendimento medio dei PAC con o senza disinvestimenti anticipati. Se questa grandezza è negativa, come per la maggior parte delle durate (l'unica eccezione è la durata di 15 anni), significa che i disinvestimenti anticipati hanno avuto un impatto negativo. I piani di accumulo più lunghi (25 e 30 anni) generano dei valori particolarmente pessimi: interrompendo investimenti in essere da moltissimi anni, si blocca l'effetto benefico della capitalizzazione composta che, quando i mercati continuano a crescere, ha un impatto tanto più positivo quando più tempo è passato. Nello stesso tempo, sono stati backtestati soltanto 62 PAC di 30 anni e 122 di 25 anni: forse, servirebbero più simulazioni per tirare delle conclusioni più precise. Questi risultati dimostrano che, in molti casi, i disinvestimenti anticipati hanno peggiorato il rendimento finale del PAC (è stata pagata la polizza assicurativa ma l’evento assicurato – una forte decrescita dei rendimenti – non si è verificata).
- Differenza D.A. Max: è la differenza tra il rendimento massimo dei PAC con o senza disinvestimenti anticipati. Se il valore è negativo, significa che i disinvestimenti anticipati hanno avuto un impatto negativo, come in effetti è nuovamente avvenuto per la maggior parte delle durate (le uniche eccezioni sono le durate di 15 e 20 anni).
- Differenza D.A. Min: è la differenza tra il rendimento minimo dei PAC con o senza disinvestimenti anticipati. Se il valore è negativo, significa che i disinvestimenti anticipati hanno avuto un impatto negativo. Il rendimento minimo è rimasto invariato in tutte le durate uguali o inferiori a 10 anni; è migliorato in quelle di 15 e 20 anni ed è diminuito nelle durate di 25 e 30 anni.
- Differenza D.A. Dev. St.: è la differenza tra la deviazione standard dei rendimenti calcolati con e senza disinvestimenti anticipati. Stavolta, se il valore è negativo significa che i disinvestimenti anticipati hanno avuto un impatto positivo (e viceversa). La deviazione standard è diminuita in tutte le durate.
- Prelievi antic.: è il numero medio dei prelievi anticipati azionati su ciascun PAC. Il numero cresce con l’aumentare della durata dei PAC ed è compreso tra 0,10 nei PAC biennali (un prelievo anticipato ogni 10 PAC) e 1,58 in quelli trentennali. Come avevamo anticipato, i disinvestimenti anticipati vengono difficilmente azionata più di una volta per PAC, almeno lasciando i parametri sui valori predefiniti.
- Giac. Media: questa grandezza è diminuita. È una conseguenza inevitabile quando si applicano dei prelievi anticipati.
Cliccando sul numero del PAC migliore della riga “Nr. PAC (Max)”, sul numero di quello peggiore della riga “Nr. PAC (Min)” o su un qualsiasi PAC scelto in base al suo numero dal menu a tendina della riga “Grafici”, si può visualizzare graficamente l’andamento del rendimento per rata versata di quel PAC.
Selezioniamo il numero 49 (miglior PAC decennale):
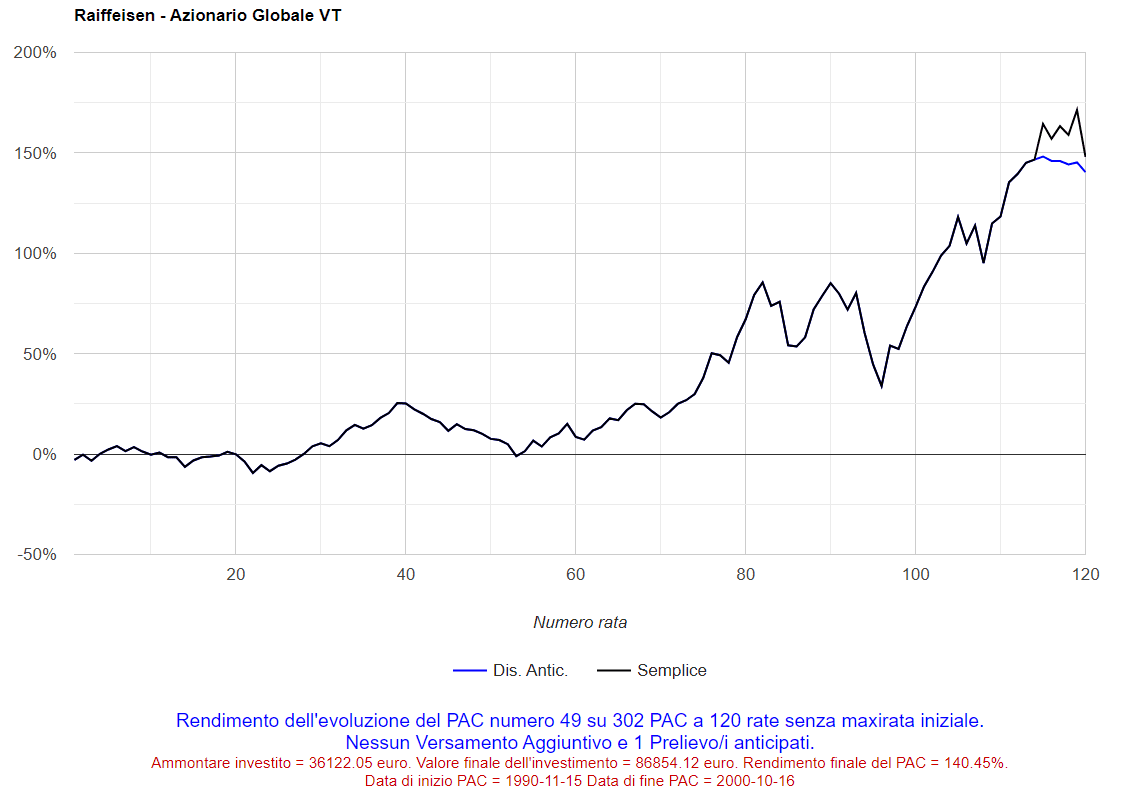
Fig. 50 – Raiffeisen: PAC Cost Averaging. Disinvestimenti anticipati: Miglior PAC
L’effetto dei disinvestimenti anticipati è visibile nella parte finale del PAC: la linea blu mostra l’andamento del rendimento con i disinvestimenti anticipati; la linea nera, senza.
Alla fine, la differenza di rendimento non è poi molta. È comunque già intuibile il principale effetto dei disinvestimenti anticipati: proteggere il rendimento ottenuto fino alla fine del piano di accumulo. L'impatto si manifesta con la curva del rendimento per rata (linea blu) poco inclinata verso l’alto o verso il basso.
Prendiamo adesso un grafico favorevole ai disinvestimenti anticipati; si tratta del 30° piano di accumulo ventennale:
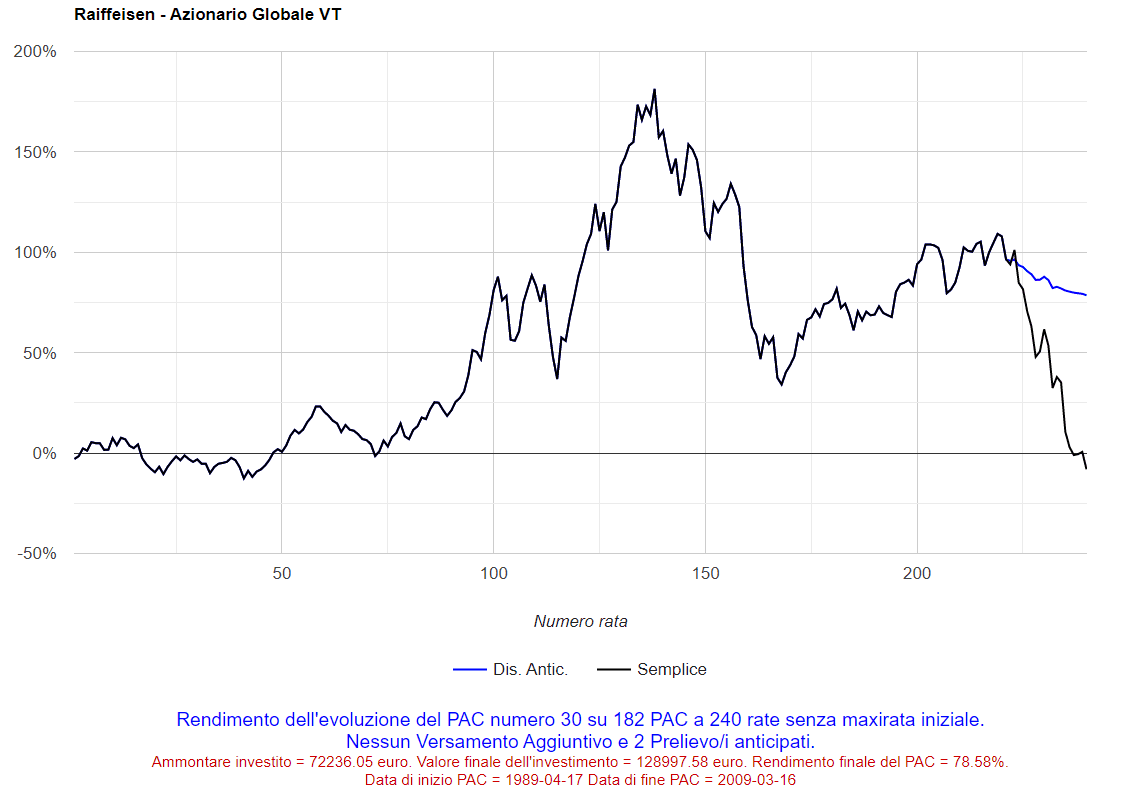
Fig. 51 – Raiffeisen: PAC Cost Averaging. Disinvestimenti anticipati: 30° PAC ventennale
Si tratta del piano di accumulo conclusosi a marzo 2009. Non è una data casuale: si tratta proprio del minimo raggiunto dai mercati azionari in seguito alla crisi subprime.
Senza disinvestimenti anticipati il rendimento finale sarebbe stato del −8,08%; con i disinvestimenti anticipati è stato del 78,58%. La differenza è abissale.
Di nuovo, il grafico ci mostra come i disinvestimenti anticipati, una volta attivati, tendano a proteggere il rendimento conseguito, che procede con una linea poco inclinata.
Una cosa interessante da notare è la seguente: quelli che, in precedenza – senza disinvestimenti anticipati – erano i PAC peggiori (come il 30° PAC ventennale, visualizzato nella Fig. 51), adesso non lo sono più e vengono rimpiazzati da un altro PAC.
Nel nostro backtest, il peggior PAC ventennale è adesso diventato l’81°: un PAC dove i disinvestimenti anticipati hanno purtroppo peggiorato le cose:
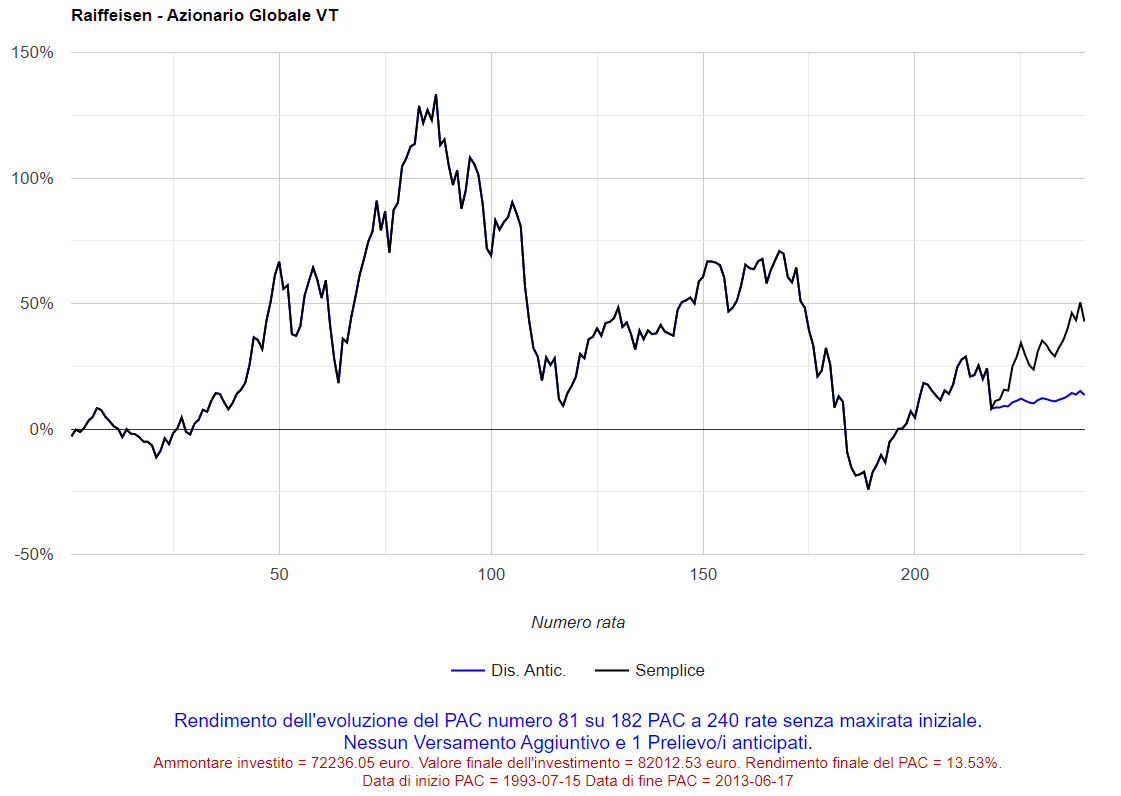
Fig. 52 – Raiffeisen: PAC Cost Averaging. Disinvestimenti anticipati: 81° PAC ventennale
I disinvestimenti anticipati sono stati attivati da un falso segnale e il rendimento finale, pari al 13,53%, è stato inferiore a quello che avremmo ottenuto senza intervenire (42,76%).
Il valore che troviamo nella riga della “Differenza D.A. Min” è 21,62%, che misura proprio la differenza tra il peggior PAC con i disinvestimenti anticipati (13,53%) e il peggior PAC senza i disinvestimenti anticipati (−8,08%).
Per vedere i rendimenti di tutti i piani di accumulo di una certa durata, con e senza disinvestimenti anticipati, si può cliccare sul numero dei mesi della prima riga della tabella.
Ad esempio, cliccando su 240 si ottiene il seguente grafico:
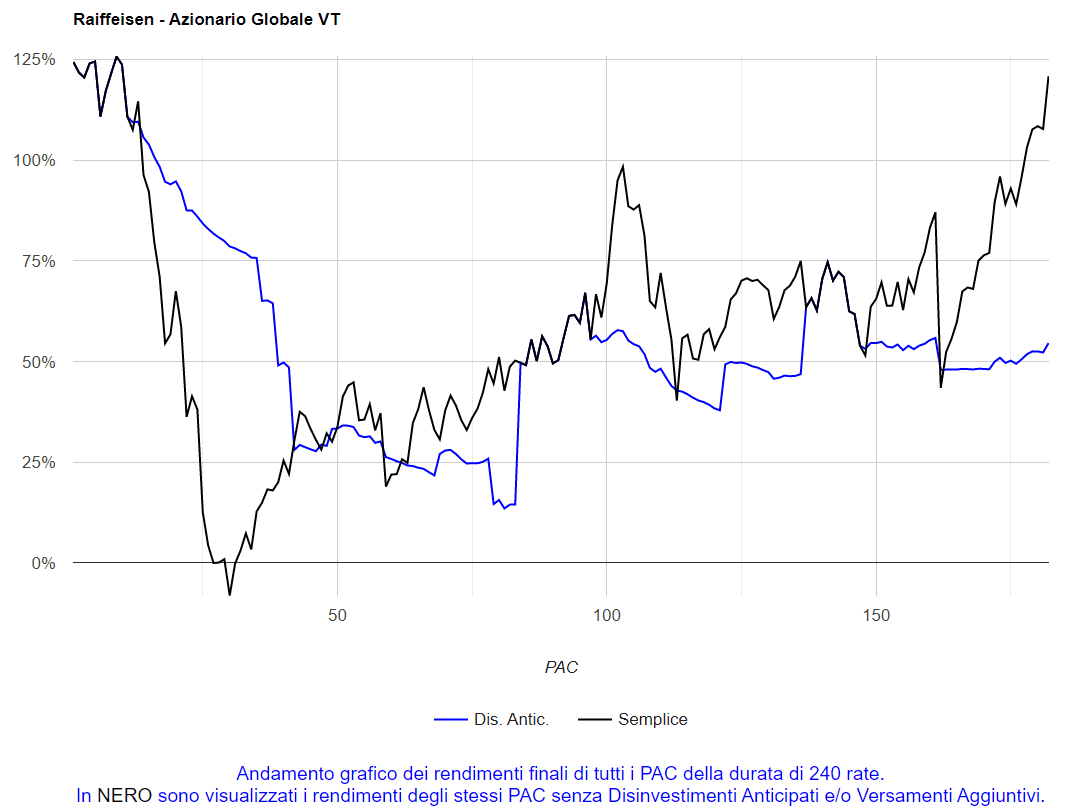
Fig. 53 – Raiffeisen: PAC Cost Averaging. Disinvestimenti anticipati: tutti i PAC ventennali (prelievo del 90%)
I disinvestimenti anticipati hanno svolto un lavoro eccellente nei PAC compresi tra il 15° e il 40° (quelli terminati tra dicembre 2007 e gennaio 2010); successivamente, sono stati attivati da falsi segnali e hanno quasi sempre peggiorato il rendimento finale.
In quest’ultimo grafico, si può notare come il peggior PAC senza disinvestimenti anticipati sarebbe stato il 30° (il 9° il migliore), mentre con i disinvestimenti anticipati l’81° (il 9° è risultato ancora una volta il migliore).
Vediamo le performance di tutti i piani di accumulo ventennali, cambiando soltanto un parametro: la percentuale di completamento PAC, che abbassiamo dal 90% al 75%:
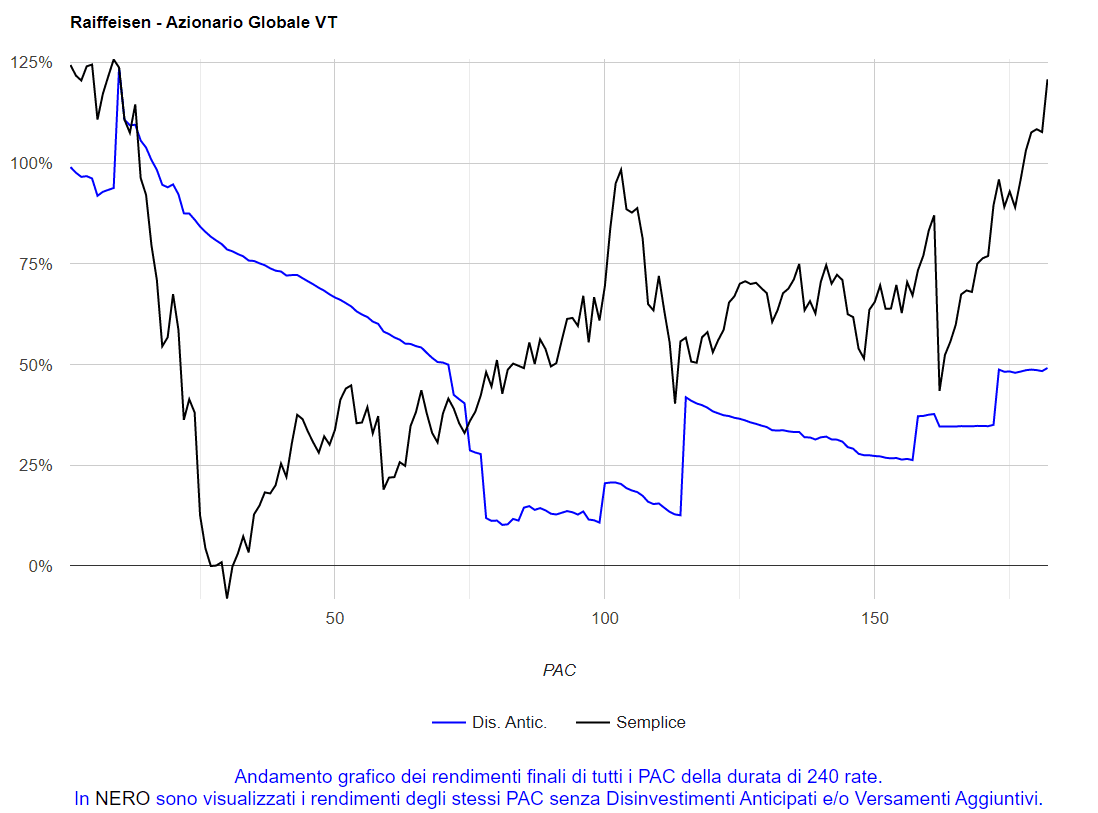
Fig. 54 – Raiffeisen: PAC Cost Averaging. Disinvestimenti anticipati: tutti i PAC ventennali (prelievo del 75%)
I disinvestimenti anticipati avrebbero offerto un contributo positivo nei piani di accumulo compresi tra il 15° e il 75° e uno negativo in tutti gli altri.
Quelli che seguono sono invece i risultati dell’Analisi PAC Cost Averaging con disinvestimenti anticipati sul fondo Aberdeen, già utilizzato in precedenza.
Tutti i parametri sono stati lasciati sui valori predefiniti:
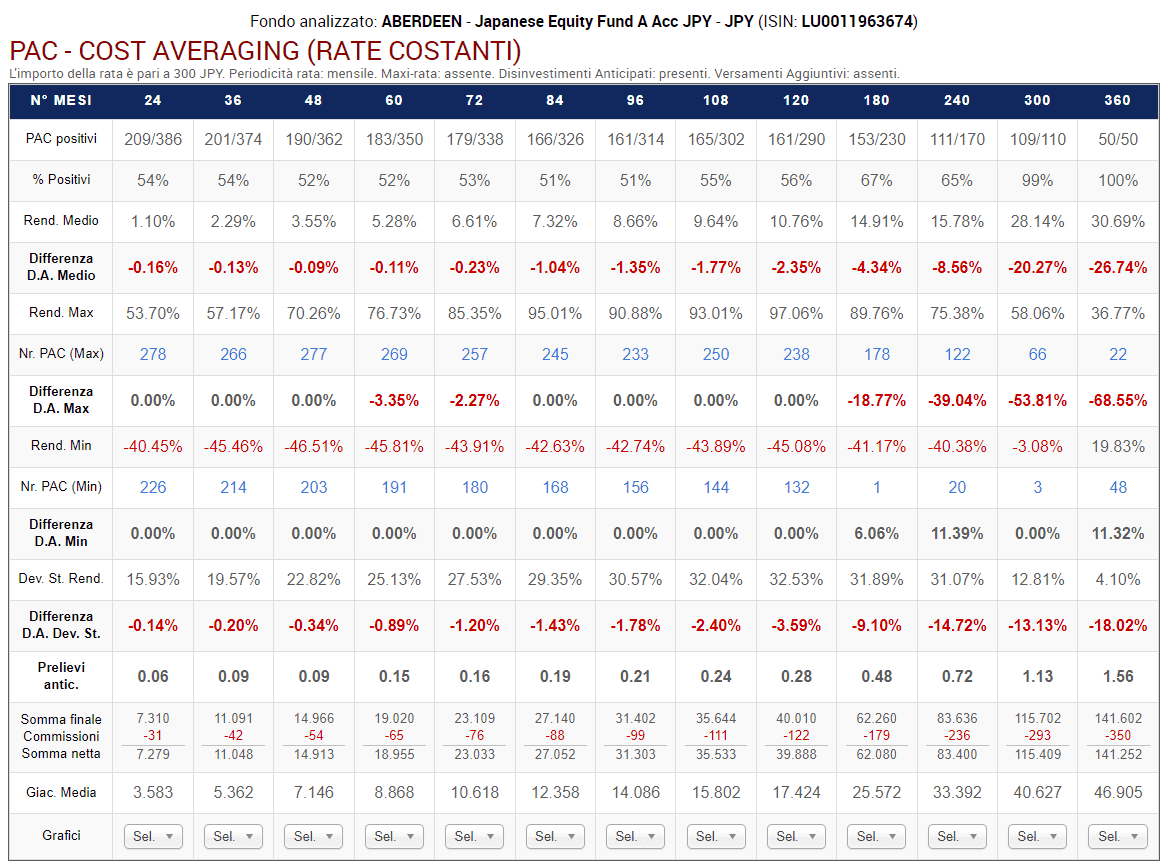
Fig. 55 – Aberdeen: Disinvestimenti anticipati. VIX = 24; % Completamento PAC = 90%; Rendimento minimo = 10%; % Prelievo = 85%; Numero massimo di prelievi = 3; Intervallo rate = 12. PAC Cost Averaging. Rata: 300 euro
Le differenze dei rendimenti medi con e senza disinvestimenti anticipati sono tutte negative, anche se abbastanza contenute (salvo quelle relative ai piani di accumulo della durata dai 15 anni in su).
Anche le differenze dei rendimenti massimi con e senza disinvestimenti anticipati sono tutte nulle o negative. Quelle dei rendimenti minimi sono invece quasi tutte nulle, con l’eccezione dei PAC della durata di 15, 20 e 30 anni.
Le differenze delle deviazioni standard dei rendimenti con o senza disinvestimenti anticipati sono invece tutte negative.
I prelievi anticipati, in media, sono stati meno di quelli del fondo precedente: dato il trend decrescente di lungo termine dell’Aberdeen, le occasioni per l’attivazione dei disinvestimenti anticipati sono diminuite.
Scorciando la percentuale di completamento PAC dal 90% al 75%, i risultati migliorano: abbiamo una differenza positiva nei rendimenti medi e, soprattutto, molte differenze positive nei rendimenti minimi.
Tra le note sfavorevoli troviamo le differenze tra i rendimenti massimi con o senza disinvestimenti anticipati, che sono negative già a partire dalla durata di 4 anni (sono nulle quelle di 2 e 3 anni).
Si impongono un paio di riflessioni sulle analisi condotte. Sono osservazioni che, data la loro importanza, vale la pena ripetere:
- Le conseguenze peggiori dovute all'attivazione di disinvestimenti anticipati si sono verificati nei piani di accumulo più lunghi (25 e soprattutto 30 anni). È una conseguenza legata anche alla mancanza di crisi finanziarie durature tra aprile 2018 e maggio 2022, il periodo in cui si sono conclusi i 50 PAC trentennali backtestati.
- I disinvestimenti anticipati sono finalizzati alla diminuzione del rischio, non alla massimizzazione del rendimento: il loro merito principale è quello di mettere in salvo gran parte del rendimento nel caso in cui si dovesse verificare una crisi finanziaria nell’ultima parte della vita di un PAC. I disinvestimenti anticipati hanno tuttavia un prezzo: la perdita di rendimento in tutti quei casi in cui vengano attivati senza che il trend subisca un’inversione significativa. La migliore dimostrazione di questo punto è il grafico seguente, che mostra tutti i rendimenti dei PAC ventennali del fondo Aberdeen in presenza di disinvestimenti anticipati (percentuale di completamento PAC del 75%):
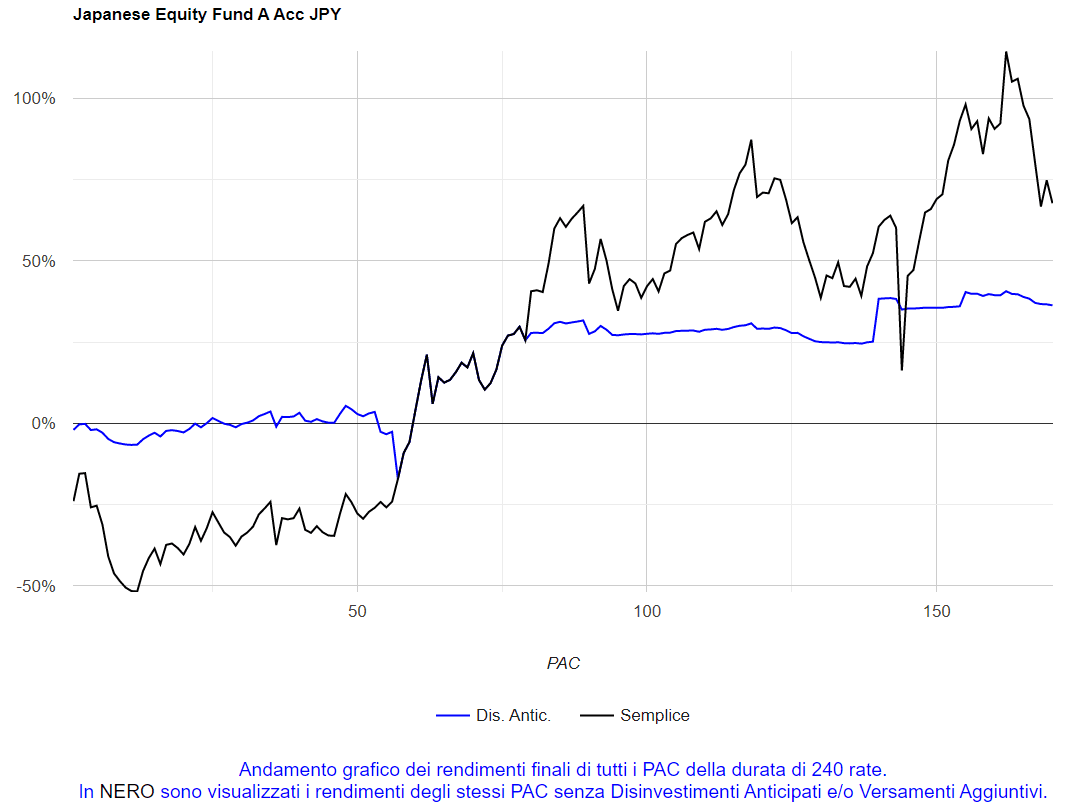
Fig. 56 – Aberdeen: PAC Cost Averaging. Disinvestimenti anticipati: tutti i PAC ventennali (prelievo del 75%)
Nei primi 60 PAC i disinvestimenti anticipati svolgono un lavoro egregio, permettendo di concludere tutti i piani di accumulo con rendimenti vicini allo 0%, invece che pesantemente negativi.
Seguono una ventina di PAC in cui i disinvestimenti anticipati non vengono attivati, dopo di che in tutti i piani seguenti (un centinaio) i rendimenti finali peggiorano, stabilizzandosi intorno al 30%.
Se si vogliono evitare i rendimenti negativi della parte sinistra del grafico, si deve essere disposti a rinunciare a quelli positivi della parte destra.
Un ultimo interessante grafico da visualizzare è quello del rendimento medio per rata dei piani di accumulo. Visualizzeremo quelli di 5, 10, 20 e 30 anni di durata:
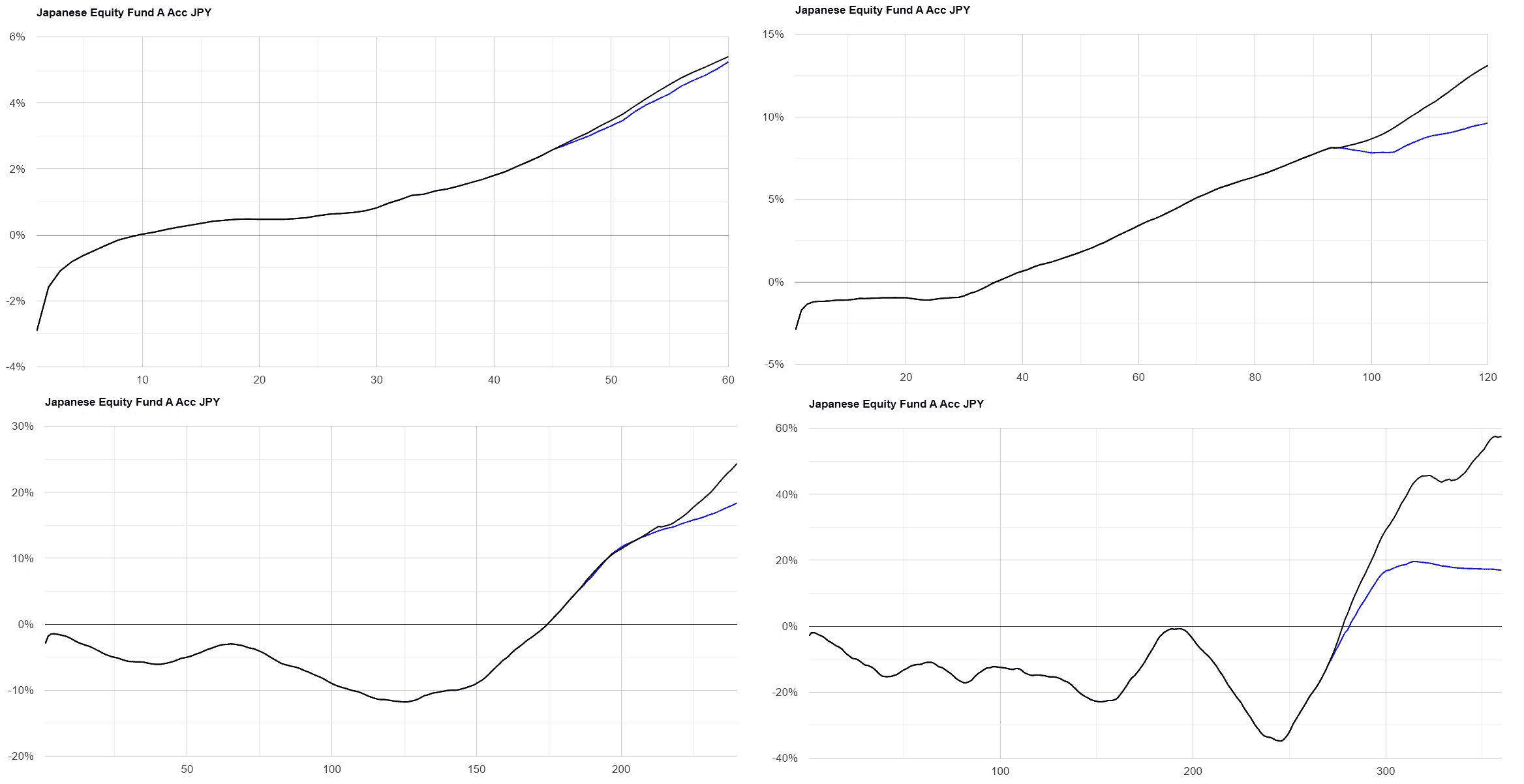
Fig. 57 – Aberdeen: PAC Cost Averaging. Disinvestimenti anticipati: rendimento medio per rata versata. Durata PAC: 5, 10, 20 e 30 anni
Dal momento che abbiamo selezionato una percentuale di completamento PAC del 75%, le differenze tra i rendimenti con o senza disinvestimenti anticipati si vedono soltanto nell’ultimo quarto di vita dei piani di accumulo.
Trattandosi di rendimenti medi per rata le differenze sono esigue (escludendo la durata trentennale) ma, a livello di singolo PAC, i gap sono talvolta molto ampi.
Quelli mostrati sono soltanto alcuni esempi dei molteplici effetti che possono essere generati dalla presenza dei disinvestimenti anticipati in un piano di accumulo.
Per qualche investitore, la soglia del VIX fissata a 24 potrebbe non essere giusta: in generale, scegliendo valori più alti i disinvestimenti anticipati saranno azionati con meno frequenza; scegliendo valori più bassi, il loro impiego aumenterà (inevitabilmente cresceranno anche i falsi segnali).
Alcuni investitori potrebbero preferire percentuali di prelievo più o meno alte, o l’utilizzo dei disinvestimenti anticipati già molto prima del 75% o del 90% di completamento del PAC.
Ogni combinazione dei valori assegnati a questi parametri produrrà uno scenario diverso: nessuna è giusta o sbagliata in termini assoluti ma, di nuovo, si consiglia di utilizzare grandezze ispirate da ragionamenti logici o macroeconomici e non da mere ottimizzazioni sulla base di molteplici backtest su questo o quel fondo.
I disinvestimenti anticipati hanno la finalità di supportare l’investitore da un punto di vista psicologico: il Piano di Accumulo del Capitale è una modalità di investimento che offre maggiore tranquillità di un investimento in un’unica soluzione ma, dopo molti anni di versamenti e con l’avvicinarsi dell’orizzonte temporale, è inevitabile il sopraggiungere di uno stato di inquietudine dovuto al timore che un’improvvisa crisi finanziaria vanifichi anni di risparmi.
11.2 I Versamenti aggiuntivi

«Thinking is easy, acting is difficult, and to put one's thoughts into action is the most difficult thing in the world».
Johann Wolfgang von Goethe
Durante la vita di un Piano di Accumulo del Capitale, può essere opportuno effettuare pagamenti più consistenti della tipica rata standard. Molto spesso, questi versamenti sono discrezionali, frutto di una reazione ai movimenti del mercato invece che di una pianificazione dell'investitore effettuata all’inizio del PAC.
Una delle leggi economiche più importanti è quella della domanda: per la maggior parte dei beni, la domanda è legata da una relazione inversa al prezzo. Quando il prezzo sale, la domanda diminuisce; quando il prezzo scende, la domanda aumenta.
Nel mercato azionario le cose sono un po’ più complicate e questa relazione non è automatica, soprattutto durante le bolle speculative e le crisi finanziarie.
Proprio quando avvengono le crisi e i prezzi scendono bruscamente, alcuni investitori approfittano dell’occasione e incrementano le loro posizioni: il rischio, soprattutto per i meno esperti, è quello di reagire in modo confuso e utilizzare la liquidità disponibile in modo poco efficiente o addirittura controproducente.
Durante una crisi finanziaria, nessuno è in grado di sapere quando la discesa dei prezzi sia giunta al termine. Se questa informazione fosse disponibile, chiunque sarebbe disposto a investire tutta la liquidità residua proprio in quel momento, sicuro di poter sfruttare la successiva risalita dei prezzi.
Quello che invece accade è che molti investitori con un portafoglio di titoli già in essere (molto probabilmente in perdita), mediano al ribasso il prezzo medio di carico con ulteriori acquisti, spesso di una certa consistenza.
La mediazione al ribasso è una pratica pericolosissima se perseguita su azioni di singole società, ma molto sensata se effettuata su fondi a gestione passiva che replicano indici importanti (World index, S&P 500, EuroStoxx ecc.).
Il vero problema della mediazione al ribasso sorge quando i prezzi continuano a scendere. Se per l’investitore col portafoglio già in essere può essere un guaio (soprattutto avendo terminato la liquidità), per quello in un piano di accumulo l’ulteriore discesa permetterà di acquistare un maggior numero di quote. Inoltre, è l'occasione per incrementare gli acquisti effettuando dei versamenti aggiuntivi.
Definiamo versamenti aggiuntivi quei versamenti che non sono pianificabili temporalmente in un PAC a rate costanti.
Approfondiremo i versamenti aggiuntivi azionati da regole ben precise, definite all’inizio dell’investimento. Operando in questo modo, sarà possibile backtestare i piani di accumulo che li includono.
L’Analisi PAC è predisposta per la simulazione di piani di accumulo con versamenti aggiuntivi: nella tabella di output, oltre alle solite misure statistiche troveremo le differenze tra il rendimento medio, massimo, minimo e la deviazione standard dei piani di accumulo con e senza versamenti aggiuntivi.
Nel form dell’Analisi PAC, 7 parametri sono dedicati esclusivamente ai versamenti aggiuntivi:
- Numero rate aggiuntivo: consistenza di ogni versamento aggiuntivo espressa in numero di rate standard. Ad esempio, se la rata standard è di 300 euro, inserendo in questo campo un valore pari a 8 avremo dei versamenti aggiuntivi di 2.400 euro.
- % di Perdita richiesta: quando un PAC raggiunge questa percentuale di perdita in termini assoluti, scatta l’investimento di un versamento aggiuntivo. Ad esempio, se si seleziona una percentuale di perdita richiesta del 10% (il valore deve essere inserito in valore assoluto), il primo versamento aggiuntivo sarà effettuato quando il rendimento del PAC scenderà al −10%; il secondo versamento avverrà quando il rendimento del PAC raggiungerà il −20%; il terzo al −30% e così via, fino al raggiungimento del numero massimo di versamenti aggiuntivi.
- % di completamento PAC: percentuale del numero di rate versate rispetto a quelle totali (la maxirata, se presente, conta il numero di rate che la compongono).
- Numero massimo di versamenti aggiuntivi: numero massimo di versamenti aggiuntivi effettuabili in un singolo PAC.
- Rate residue: numero minimo di rate che, dopo un versamento aggiuntivo, dovranno ancora essere versate prima della conclusione effettiva del PAC.
- Drawdown: selezionando questa opzione, i versamenti aggiuntivi saranno effettuati in base a percentuali progressive di drawdown, ovvero a partire dal rendimento massimo realizzato dal PAC fino a quel momento. La percentuale di perdita richiesta sarà riportata al valore iniziale ogni volta che il PAC realizzerà un nuovo rendimento massimo.
- Durata massima: quando si effettua un versamento aggiuntivo, la durata del PAC viene automaticamente ridotta del numero di rate standard che lo compongono. Selezionando questa opzione, invece, il piano di accumulo non viene accorciato: l’investimento continuerà fino al termine inizialmente stabilito.
Un versamento aggiuntivo può essere effettuato in qualsiasi momento, non necessariamente in concomitanza del pagamento di una rata standard.
Non è possibile eseguire più di un versamento aggiuntivo tra una rata standard e la successiva.
Se, nello spazio di un giorno, si verifica una diminuzione di rendimento pari ad almeno il doppio della percentuale di perdita richiesta per far scattare l’aggiuntivo, non verrà effettuato un versamento aggiuntivo doppio. Un ulteriore aggiuntivo sarà però versato, insieme alla rata standard successiva, se il doppio della percentuale di perdita richiesta persistesse fino a quel momento.
Ad esempio, ipotizziamo che il rendimento scenda in un giorno dal −8% al −22% e che si sia stata impostata una “% di Perdita richiesta” pari al 10%. Il giorno in cui viene toccato il −22% sarà effettuato un solo versamento aggiuntivo (e non 2).
Se il rendimento fosse ancora al di sotto del −20% al momento del pagamento della rata standard successiva allora, insieme a questa, verrebbe effettuato anche un altro versamento aggiuntivo.
Affinché un versamento possa aver luogo, deve verificarsi anche un'altra condizione: il PAC dovrà avere un numero di rate mancanti almeno pari a quelle del versamento aggiuntivo sommato al numero minimo di rate residue (specificate nel parametro omonimo).
Ipotizziamo di aver impostato un numero minimo di rate residue pari a 4 e un versamento aggiuntivo pari a 8 rate. Ipotizziamo inoltre che manchino 10 rate al termine del PAC e si siano verificate tutte le altre condizioni richieste: il versamento aggiuntivo non verrà effettuato, perché una volta eseguito rimarrebbero soltanto 2 rate, mentre tra le varie condizioni avevamo stabilito anche quella di avere un numero minimo di rate residue pari a 4.
Il versamento aggiuntivo avrebbe avuto luogo se:
- Fossero mancate 12 o più rate al termine del PAC.
- La consistenza del versamento aggiuntivo fosse stata di 6 rate (o meno).
- Il numero di rate residue fosse stato minore o uguale a 2.
Un paio di esempi aiuteranno invece a capire meglio la differenza tra l’attivazione dei versamenti aggiuntivi in base a una perdita in termini assoluti o di drawdown.
Esempio 1. Versamento aggiuntivo sulla base di percentuali di perdita in termini assoluti: la checkbox “Drawdown” non è selezionata.
Ipotizziamo una percentuale di perdita richiesta del 10%: un versamento aggiuntivo sarà effettuato ogni volta che il PAC raggiungerà, solo la prima volta, un rendimento pari al −10% o un suo multiplo.
Esempio 2. Versamento aggiuntivo sulla base di percentuali di perdita in termini di drawdown: la checkbox “Drawdown” è selezionata.
Ipotizziamo una percentuale di perdita richiesta del 10%: un versamento aggiuntivo sarà effettuato ogni volta che il rendimento del PAC diminuirà del −10% o di un suo multiplo rispetto al rendimento massimo realizzato fino a quel momento.
Supponiamo che un PAC raggiunga un rendimento del 4,37%: il primo versamento aggiuntivo avverrà nel momento in cui il rendimento dovesse scendere al 4,37% − 10% = −5,63%; il secondo versamento aggiuntivo al 4,37% − 20% = −15,63% e così via.
Attenzione: ogni volta che il piano di accumulo realizza un nuovo rendimento massimo (supponiamo che il mercato torni a salire e, dopo aver effettuato il primo aggiuntivo, il rendimento raggiunga il 7,82%), il versamento aggiuntivo successivo si verificherà nel momento in cui il rendimento del PAC diminuirà del −10% dal nuovo massimo: nel nostro esempio, la percentuale sarà adesso del 7,82% − 10% (e non −20% o altri multipli) = −2,18%.
Altri due esempi, infine, aiuteranno a capire come un PAC venga accorciato (o meno), in base al parametro “Durata massima”.
Esempio 1. Durata massima assente (checkbox non selezionata): ipotizziamo un piano di accumulo di 60 rate mensili, in cui sono stati eseguiti 3 versamenti aggiuntivi, ognuno dei quali pari a 5 rate.
La durata effettiva del PAC sarà di soli 45 mesi e 45 saranno le rate standard versate ma, in 3 occasioni, sarà stato versato un importo pari a 5 rate, per un totale di 15: i fondi necessari vengono stornati dal valore totale delle rate (60 x importo singola rata).
Il PAC si esaurisce, perciò, dopo 45 mesi; l’ammontare totale versato sarà pari all’equivalente di 60 rate standard.
Esempio 2. Durata massima presente (checkbox selezionata): ipotizziamo, di nuovo, un piano di accumulo di 60 rate mensili, in cui sono stati eseguiti 3 versamenti aggiuntivi, ognuno dei quali pari a 5 rate.
La durata effettiva del PAC sarà di 60 mesi e 60 saranno le rate standard versate ma, in 3 occasioni, sarà stato versato un importo pari a 5 rate, per un totale di 15: stavolta, i fondi necessari non vengono stornati dal valore totale delle rate (60 x importo singola rata).
Il PAC si esaurisce, perciò, dopo 60 mesi (il suo termine naturale); l’ammontare totale versato sarà pari all’equivalente di 75 rate standard.
Per includere i versamenti aggiuntivi nell’Analisi PAC, deve essere selezionata l’omonima checkbox.
Le stesse considerazioni riservate ai disinvestimenti anticipati sono valide anche per i versamenti aggiuntivi: i 7 parametri che abbiamo analizzato possono essere modificati dinamicamente dagli utenti, ma la cosa da evitare assolutamente è effettuare numerosi backtest per ottimizzare i parametri in modo che i backtest producano i risultati migliori.
Questo modo di procedere comporterebbe l’overfitting dei parametri: un’ottimizzazione che avrebbe massimizzato le performance passate, ma che quasi sicuramente non produrrebbe buoni risultati in futuro.
Passiamo ai backtest. Partiamo con i valori predefiniti dei parametri e vediamo quali sono i risultati dell’analisi con versamenti aggiuntivi sul fondo Raiffeisen:
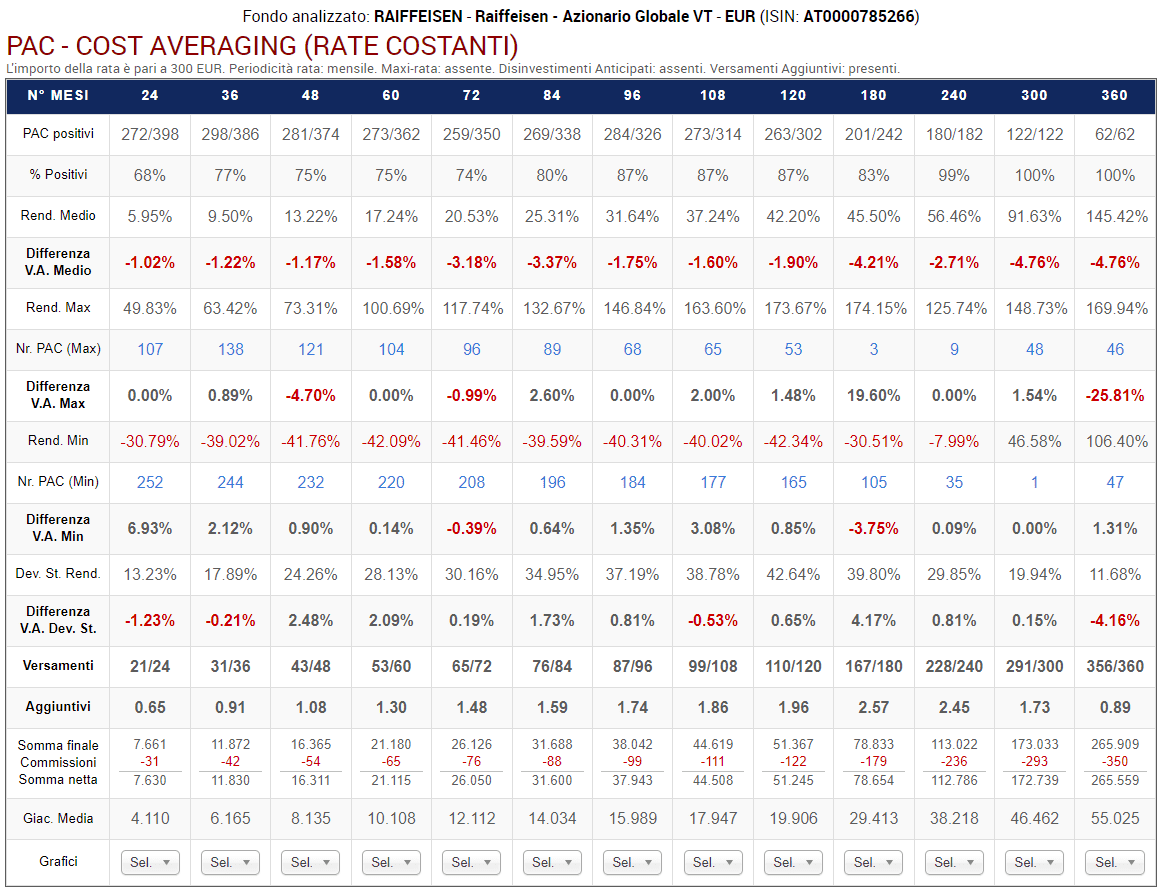
Fig. 58 – Raiffeisen: Versamenti aggiuntivi. Nr. rate aggiuntivo = 5; % Perdita richiesta = 10%; % Completamento PAC = 5%; Nr. massimo di Versamenti aggiuntivi = 10; Rate residue = 1; Drawdown e Durata massima non selezionati. Rata: 300 euro
La “Differenza V.A. Medio”, ovvero quella tra i rendimenti medi con o senza i versamenti aggiuntivi è negativa su tutte le durate.
Le differenze tra i rendimenti massimi e minimi con o senza i versamenti aggiuntivi sono invece tendenzialmente positive. Dato che la differenza tra i rendimenti medi era negativa, si tratta di un risultato strano: se non è frutto di un errore ci deve essere un motivo che possa spiegarlo.
In effetti, non è un errore: semplicemente, non abbiamo selezionato l’opzione “Durata massima”. Tutti i piani di accumulo sui quali sono stati eseguiti dei versamenti aggiuntivi hanno avuto, in realtà, una durata più breve: sono stati mediamente completati con parecchi mesi di anticipo rispetto alla loro scadenza naturale.
Il confronto non è perciò corretto: in un contesto di trend al rialzo del sottostante (come nel caso del fondo Raiffeisen), un tempo di investimento mediamente più lungo permette dei rendimenti medi maggiori.
Per questo motivo, sarà sempre meglio selezionare l’opzione “Durata massima”. Questa scelta è anche più logica: è plausibile che un piano di accumulo Cost Averaging venga sviluppato in modo automatico; i versamenti aggiuntivi saranno invece eseguiti manualmente quando si verificano le giuste condizioni.
Lanciamo nuovamente l’analisi con la checkbox “Durata massima” selezionata:
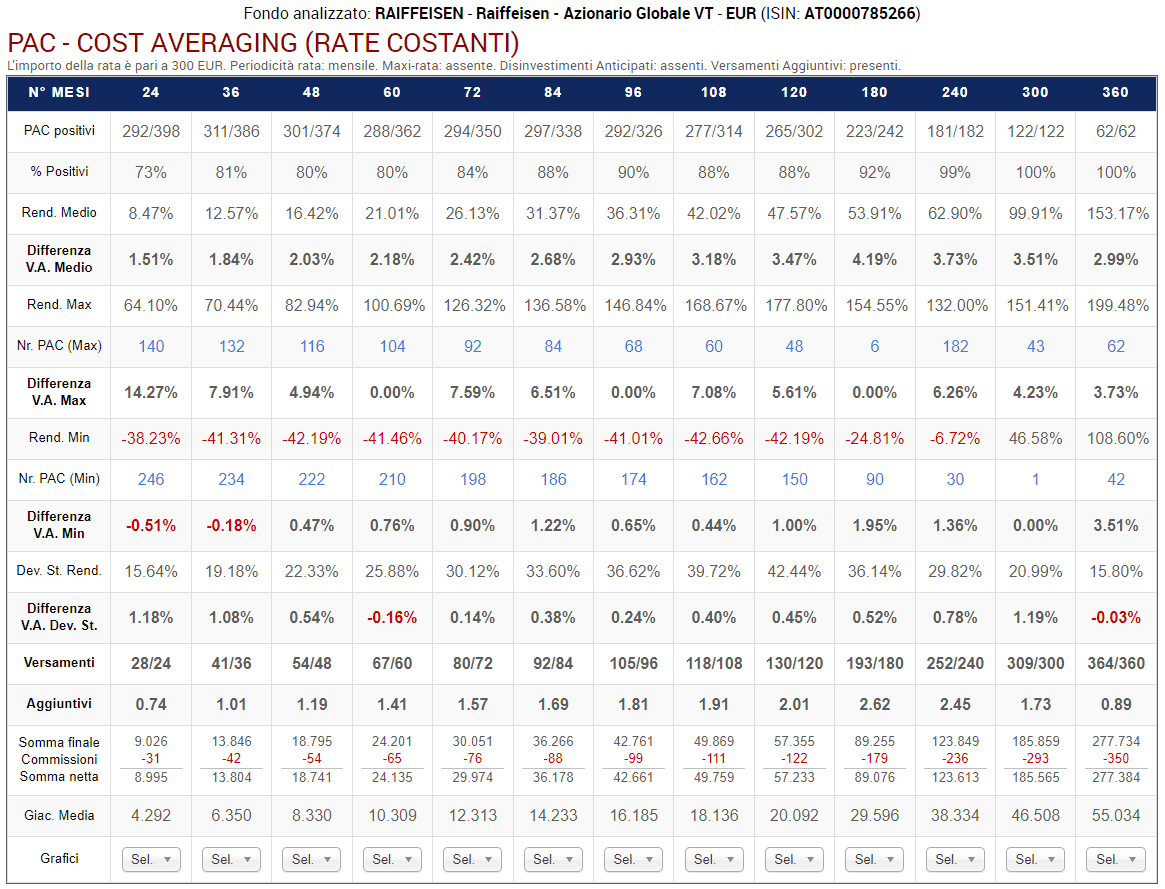
Fig. 59 – Raiffeisen: Versamenti aggiuntivi. Nr. rate aggiuntivo = 5; % Perdita richiesta = 10%; % Completamento PAC = 5%; Nr. massimo di Versamenti aggiuntivi = 10; Rate residue = 1; Drawdown non selezionato. Durata massima selezionata. Rata: 300 euro
I risultati sono molto diversi dai precedenti:
- Differenza V.A. Medio: tutti i valori sono positivi e crescono con l’aumentare della durata dei PAC (fino a 15 anni; poi iniziano a diminuire). Le differenze non sono enormi, ma la positività di tutti i valori lascia pensare che i versamenti aggiuntivi siano una variante strategica vantaggiosa. Verificheremo se, aumentandone la consistenza, si riesca a migliorare questi risultati.
- Differenza V.A. Max: anche in questo caso tutte le differenze sono nulle o positive. È il segnale che i versamenti aggiuntivi tendono a migliorare o a lasciare invariati i rendimenti massimi dei piani di accumulo. In altre parole, apportano benefici senza alcuna controindicazione (se non quella di richiedere extra-liquidità). Particolarmente rilevanti sono gli incrementi di rendimento dei PAC brevi: in quelli biennali si registra il 14,27%; in quelli triennali il 7,91%. Nei PAC lunghi le differenze sono inferiori.
- Differenza V.A. Min: tutti i valori sono positivi, con l’eccezione dei piani di accumulo biennali (−0,51%) e triennali (−0,18%). Le differenze, sia positive che negative, sono molto piccole: era importante verificare che, a fronte degli incrementi di rendimento sui PAC migliori, non ci fosse un contraccolpo significativo su quelli peggiori.
- Differenza V.A. Dev. St.: l’analisi della differenza tra le deviazioni standard dei rendimenti dei PAC con o senza versamenti aggiuntivi è confortante. La deviazione standard è cresciuta molto poco su quasi tutte le durate, con le uniche eccezioni dei piani di accumulo quinquennali (−0,16%) e trentennali (−0,03%). La poca variabilità in più non sembra inficiare gli ottimi risultati conseguiti in termini di rendimento.
- Versamenti: numero di versamenti realmente effettuati, in media, per durata. Ad esempio, le rate versate dei PAC biennali sono state, in media, 28. Dato che abbiamo impostato la composizione di ogni versamento aggiuntivo a 5 rate, possiamo intuire che in ogni PAC è stato effettuato, sempre in media, meno di un aggiuntivo. Il dato esatto viene fornito nella riga successiva.
- Aggiuntivi: numero di versamenti aggiuntivi effettuati, in media, per durata. Il numero degli aggiuntivi aumenta col crescere della durata dei PAC, per poi tornare a diminuire nei piani della durata di 20 o più anni. Questo strano comportamento non è il frutto di un errore: più i PAC sono lunghi e meno backtest vengono effettuati; in un mercato crescente, non si sono probabilmente presentate troppe occasioni in cui il rendimento di questi PAC sia sceso sotto alla soglia di perdita minima richiesta.
- Giac. Media: a differenza dei disinvestimenti anticipati, che avevano fatto diminuire la giacenza media dei PAC, i versamenti aggiuntivi la fanno crescere: è la logica conseguenza dell’investimento di extra-liquidità rispetto a quella normalmente necessaria a completare un piano di accumulo.
I versamenti aggiuntivi, laddove non diminuiscano la lunghezza dei piani di accumulo e vengano sfruttati come un puro apporto di extra-liquidità, dimostrano di essere una soluzione tattica efficiente.
Vediamo come cambia il grafico del rendimento per rata di uno specifico piano di accumulo con i versamenti aggiuntivi attivati. Il PAC visualizzato è il 140° di quelli biennali: si tratta del miglior PAC, quello che ha generato il rendimento più alto:
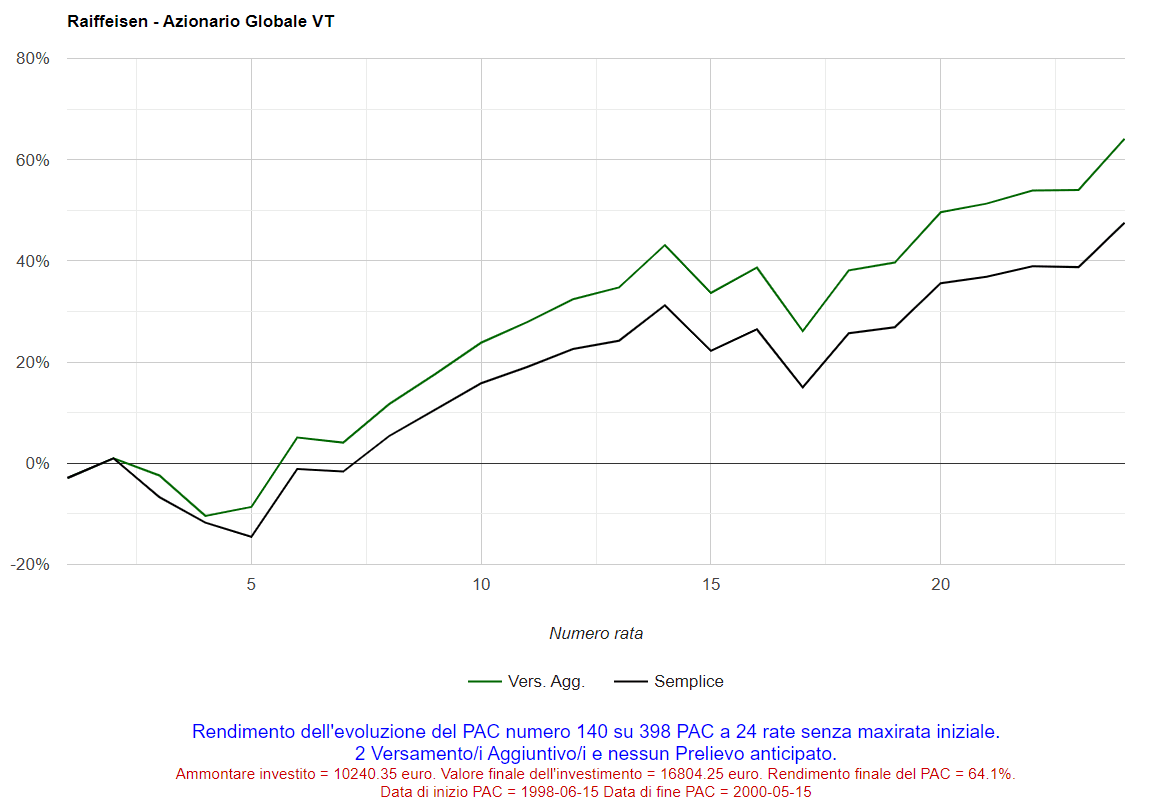
Fig. 60 – Raiffeisen: PAC Cost Averaging con versamenti aggiuntivi. PAC nr. 140 biennale (Nr. Rate aggiuntivo = 5)
In questo piano di accumulo sono stati eseguiti 2 versamenti aggiuntivi.
La linea verde traccia il rendimento per rata del piano di accumulo con i versamenti aggiuntivi attivati. La linea nera traccia il rendimento del PAC semplice, ovvero senza alcun intervento discrezionale.
Il primo versamento aggiuntivo è avvenuto subito dopo l’inizio del PAC e ha permesso di incrementare il rendimento fin da subito. Il vantaggio è cresciuto col passare del tempo, aiutato anche dal secondo aggiuntivo.
Analizziamo adesso il 90° PAC della durata di 15 anni. Stavolta, si tratta del peggior PAC:
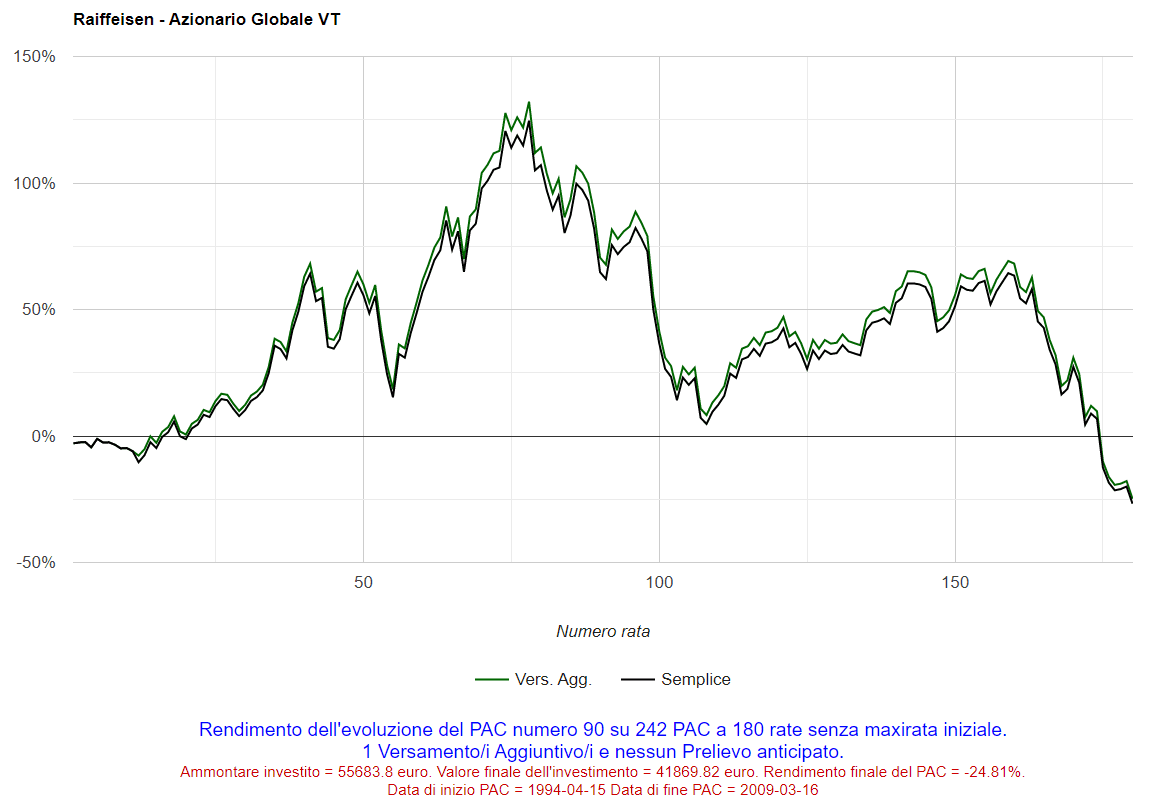
Fig. 61 – Raiffeisen: PAC Cost Averaging con versamenti aggiuntivi. PAC nr. 140 biennale (Nr. Rate aggiuntivo = 5)
È stato eseguito un solo versamento aggiuntivo, anche in questo caso quasi subito dopo l’inizio dell’investimento.
Il vantaggio conseguito in termini di rendimento si è mantenuto per tutta la durata residua del PAC, nonostante la rapida discesa finale.
Possiamo constatare come i versamenti aggiuntivi funzionino in maniera radicalmente diversa dai disinvestimenti anticipati: mentre i primi permettono di sfruttare eventuale extra-liquidità per incrementare il rendimento, con i disinvestimenti anticipati si interviene soltanto verso la fine del PAC, con esiti contrastanti: una grande differenza positiva nei casi in cui la crisi finanziaria si verifichi, oppure una piccola/media differenza negativa tutte le volte in cui la crisi non si concretizza.
Il prossimo grafico rappresenta i rendimenti finali, con o senza versamenti aggiuntivi, di tutti i piani di accumulo della durata di 15 anni:
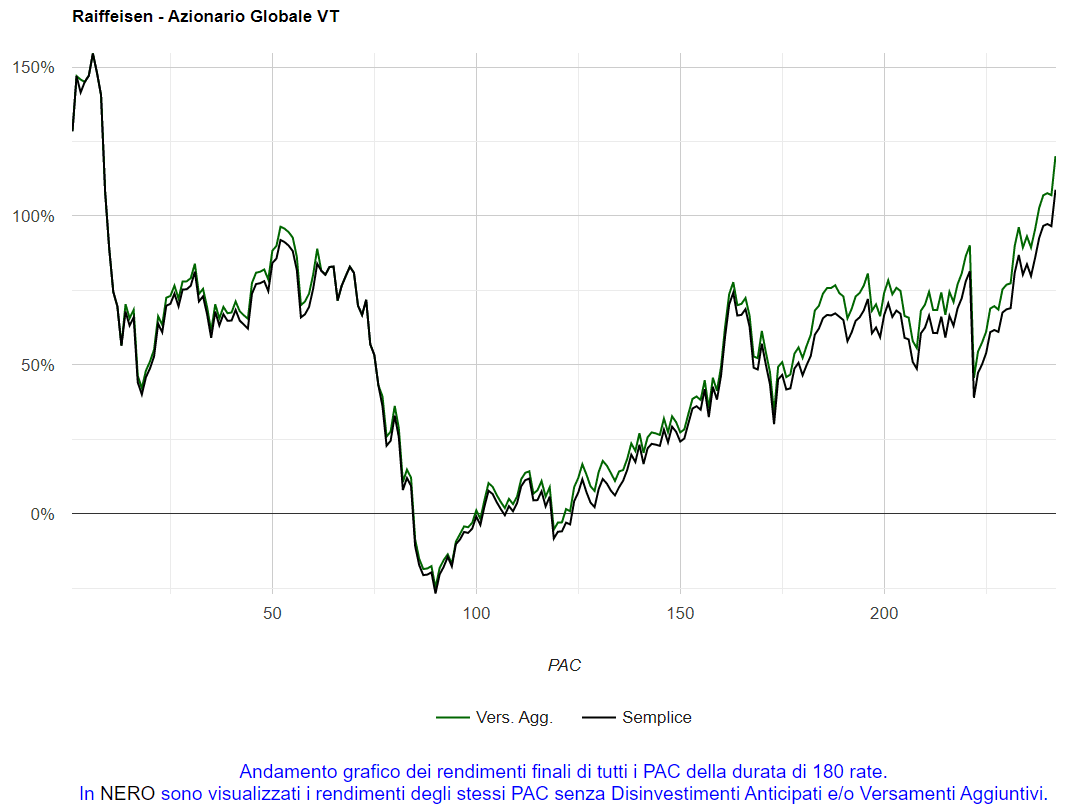
Fig. 62 – Raiffeisen: PAC Cost Averaging con versamenti aggiuntivi. Tutti i PAC della durata di 15 anni (V.A. pari a 5 rate standard)
L’andamento è molto simile, ma si denota una piccola superiorità dei PAC con versamenti aggiuntivi.
Questa superiorità è ancora più evidente nel grafico dei rendimenti medi per rata di tutti i piani di accumulo della durata di 15 anni:
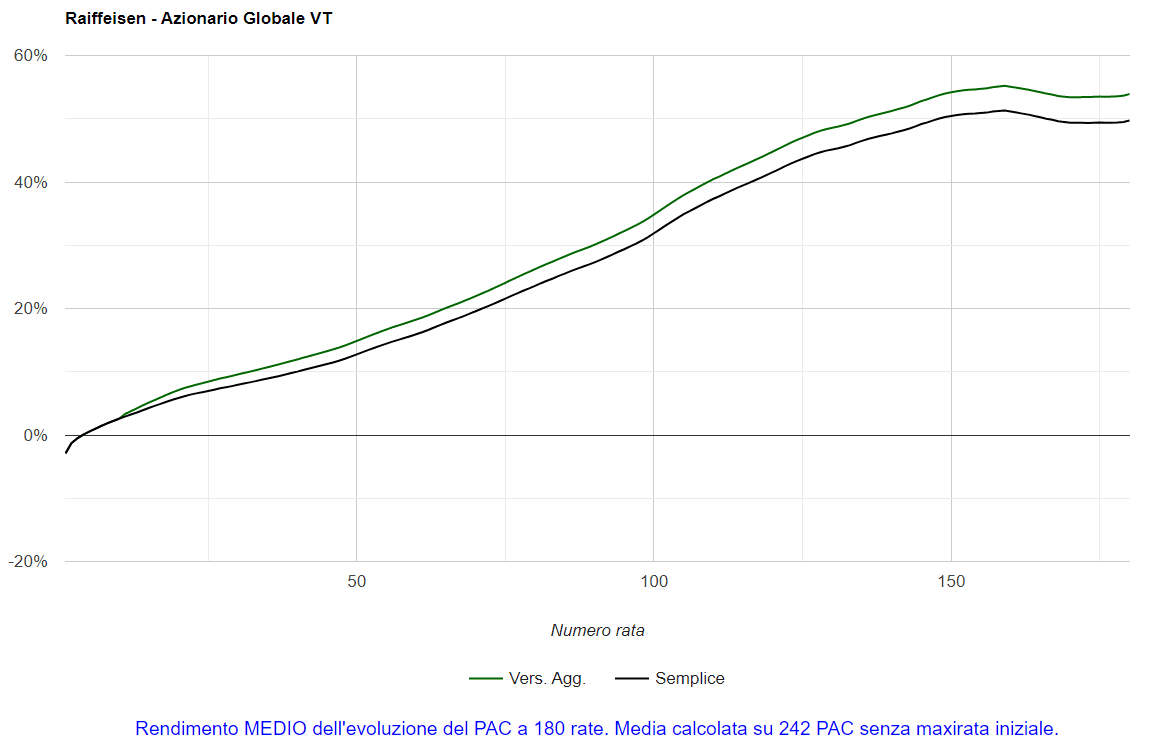
Fig. 63 – Raiffeisen: PAC Cost Averaging con versamenti aggiuntivi. Rendimento medio per rata dei PAC della durata di 15 anni (V.A. pari a 5 rate standard)
I versamenti aggiuntivi avvengono generalmente nella prima fase di vita dei piani di accumulo: essendo attivati da una perdita del 10% (e successivi incrementi della stessa ampiezza) la loro probabilità di realizzarsi decresce con l’aumentare del loro numero: il primo avverrà nella gran parte dei PAC, perché è molto probabile che tutti o quasi raggiungano una perdita del −10%; il secondo è già molto meno probabile, perché la perdita richiesta sarà adesso del −20%; il terzo sarà ancora più improbabile e così via. Un numero sempre minore di piani di accumulo raggiungerà rendimenti del −20%, −30%, −40% ecc.
Gli investitori che preferiscono essere più attivi, intervenendo con versamenti aggiuntivi più frequenti, hanno la possibilità di farlo selezionando la checkbox “Drawdown”: il parametro che favorisce un maggior numero di esecuzioni è la percentuale di perdita richiesta, che viene riportata al valore di partenza ogni volta che il PAC realizza un nuovo rendimento massimo.
I risultati dell’analisi con la checkbox “Drawdown” selezionata sono i seguenti:
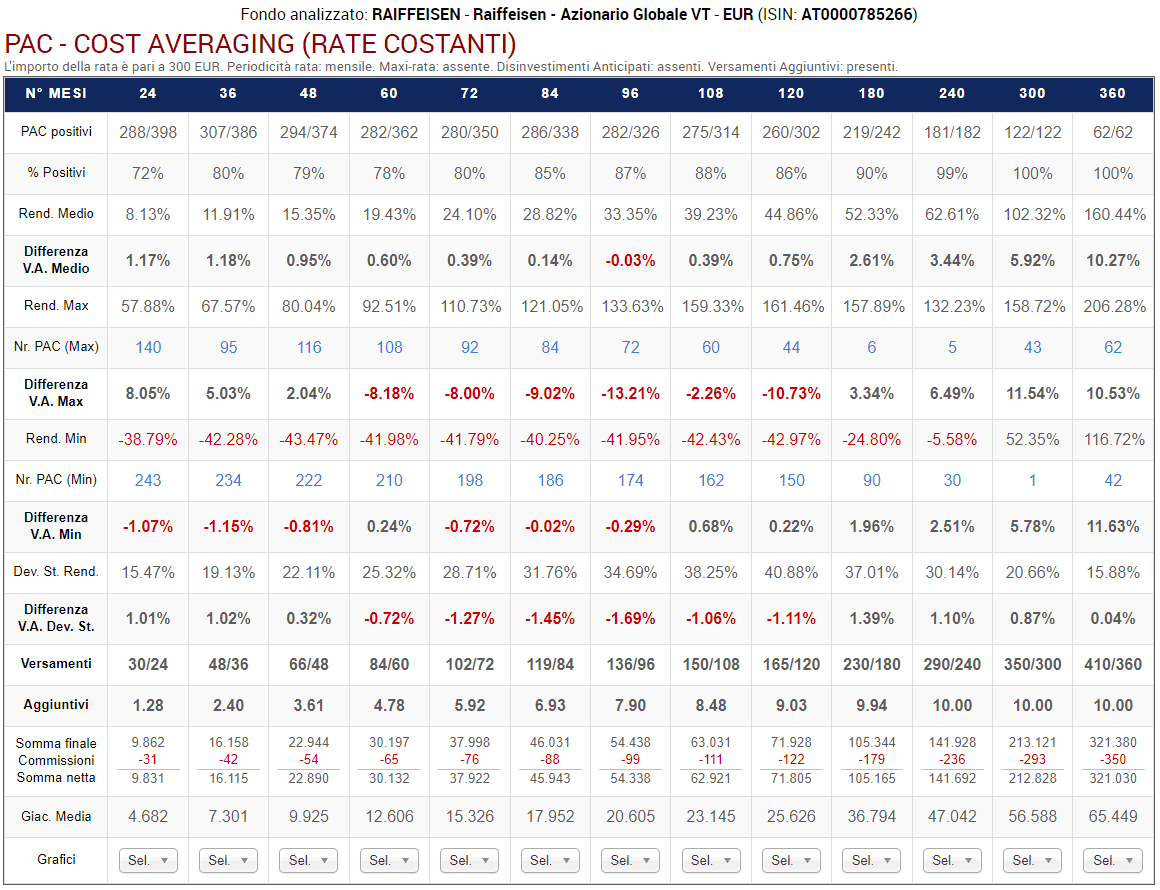
Fig. 64 – Raiffeisen: Versamenti aggiuntivi. Nr. rate aggiuntivo = 5; % Perdita richiesta = 10%; % Completamento PAC = 5%; Nr. massimo di Versamenti aggiuntivi = 10; Rate residue = 1; Drawdown selezionato. Durata massima selezionata. Rata: 300 euro
Tutti i confronti seguenti sono eseguiti rispetto alla precedente analisi (parametro “Drawdown” non selezionato, fig. 59).
I risultati sono molto diversi:
- Differenza V.A. Medio: tutti i valori sono positivi, con l’eccezione dei PAC di durata di 8 anni (−0,03%). Le differenze sono piccole fino ai 15 anni di durata, ma crescono in modo deciso in quelle più lunghe. Si tratta di incrementi più contenuti di quelli della tabella precedente fino ai ventennali; sono superiori nei PAC di 25 e 30 anni.
- Differenza V.A. Max: negativa nelle durate comprese tra 5 e 10 anni; positiva in tutte le altre. Fino ai 10 anni, i valori sono inferiori rispetto all’analisi precedente; dai 15 anni in su, sono superiori.
- Differenza V.A. Min: si ripete lo schema precedente. Valori appena inferiori a prima fino agli 8 anni e superiori dai 9 anni in poi.
- Differenza V.A. Dev. St.: i valori sono tutti inferiori ai precedenti, con l’eccezione delle durate più lunghe (15 anni e oltre) e quelle più brevi (fino a 4 anni). Il maggior numero di versamenti aggiuntivi ha quindi il pregio di diminuire – in molti casi – le oscillazioni nei rendimenti finali dei piani di accumulo.
- Versamenti: sono aumentati in maniera decisa. La riga seguente ci permetterà di quantificare con esattezza l’incremento nel numero dei versamenti aggiuntivi.
- Aggiuntivi: il numero medio di versamenti aggiuntivi è cresciuto in tutte le durate. In tutti i piani di accumulo di 20 o più anni è stato raggiunto il numero massimo, impostato a 10.
Si deve fare attenzione a non lasciarsi ingannare dal numero medio di versamenti aggiuntivi: se, ad esempio, è pari a 4,78 come nel caso dei piani quinquennali, non è detto che la liquidità corrispondente a 5 versamenti aggiuntivi sia sempre sufficiente. Essendo un valore medio, molti dei PAC backtestati avranno richiesto una liquidità maggiore, pari a 6, 7, 8 o più versamenti aggiuntivi.
Addirittura, potrebbe darsi che il limite massimo di 10 sia stato raggiunto anche in qualche PAC di questa durata: lanciando una serie di backtest con un massimale superiore, i risultati medi ottenuti dai piani quinquennali potrebbero quindi modificarsi.
Verifichiamo l’impatto dei versamenti aggiuntivi anche sul fondo Aberdeen che, come sappiamo, ha seguito un trend di decrescita di lungo termine.
La durata massima è stata selezionata; il parametro drawdown no:
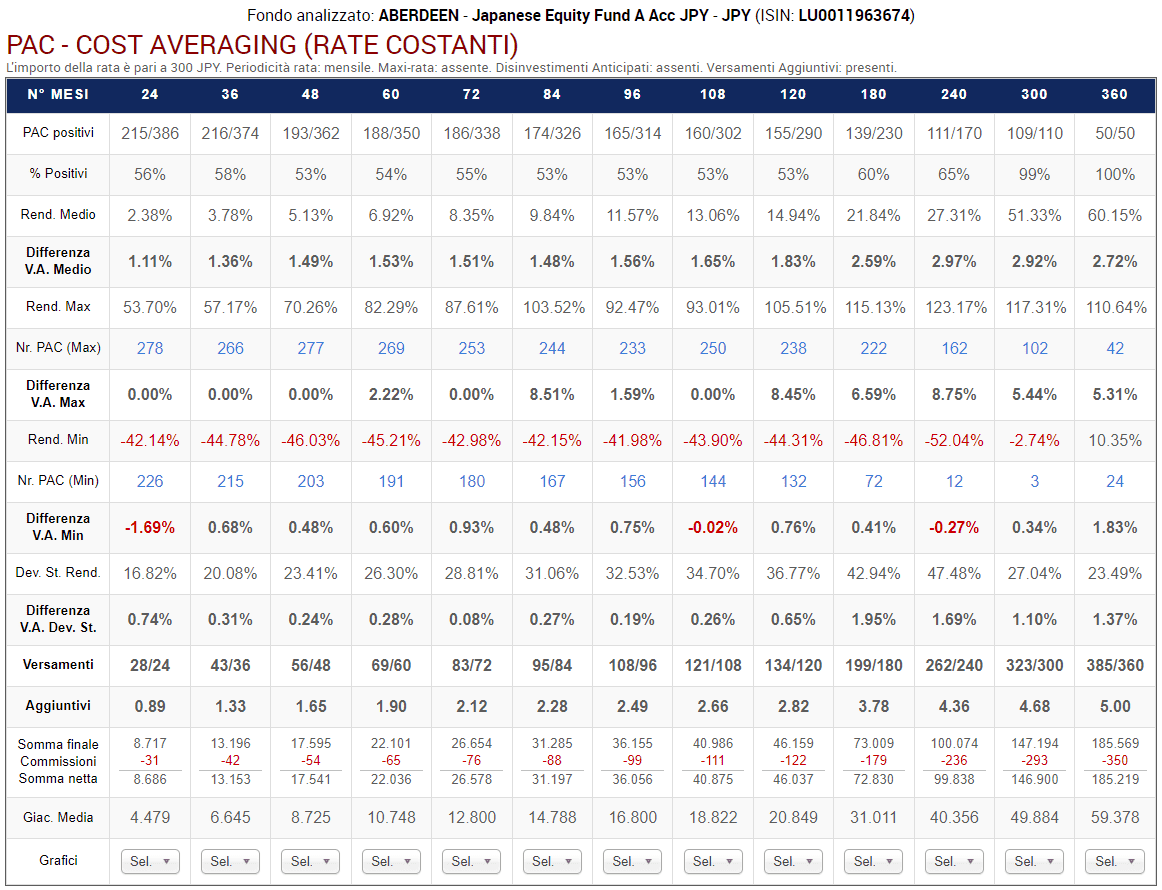
Fig. 65 – Aberdeen: Versamenti aggiuntivi. Nr. rate aggiuntivo = 5; % Perdita richiesta = 10%; % Completamento PAC = 5%; Nr. massimo di Versamenti aggiuntivi = 10; Rate residue = 1; Drawdown non selezionato. Durata massima selezionata. Rata: 300 euro
Le performance sono incoraggianti.
La differenza tra i rendimenti medi con e senza versamenti aggiuntivi è a favore dei primi su tutte le durate, con incrementi che vanno dall'1,11% al 2,97%. Niente di sconvolgente, ma sono pur sempre dei valori non trascurabili.
La differenza tra i rendimenti massimi è, su tutte le durate, nulla o a favore dei piani di accumulo con versamenti aggiuntivi. Quella tra i rendimenti minimi è invece negativa in soli 3 casi (2, 9 e 20 anni).
La deviazione standard è aumentata su tutte le durate, ma gli incrementi non sono molto rilevanti: tutti inferiori all’1%, con le sole eccezioni dei piani di durata uguale o superiore a 15 anni.
Il numero di versamenti aggiuntivi è cresciuto sensibilmente. Il risultato non deve sorprendere: il trend negativo del fondo Aberdeen ha favorito il raggiungimento di rendimenti tali da azionare gli aggiuntivi anche 2, 3 o più volte nell’arco della vita di un singolo PAC.
Aggiungendo l’opzione “Drawdown”, tutte le differenze di rendimento diminuiscono: le performance sono leggermente peggiori di prima.
I backtest sui fondi Raiffeisen e Aberdeen sembrano dimostrare la bontà dei versamenti aggiuntivi. I miglioramenti in termini di rendimento e deviazione standard rispetto a un PAC senza interventi discrezionali sono relativamente modesti, ma bisogna considerare che si applicano a somme maggiori, comprensive dell’extra-liquidità investita.
I rendimenti dei piani di accumulo con versamenti aggiuntivi sono in realtà leggermente distorti: non tengono conto del fatto che l’extra-liquidità – che viene impiegata in base alle regole impostate nei parametri dell’analisi – deve essere sempre a disposizione dell’investitore, in quanto non può apparire dal nulla soltanto nel momento del bisogno.
Si tratta di una critica sviluppata soprattutto nei confronti dei piani di accumulo Value Averaging, ma che può applicarsi anche al Cost Averaging con versamenti aggiuntivi.
Questa critica verrà approfondita nell’analisi del Value Averaging: una strategia che permetterà di gestire l’investimento di extra-liquidità in modo più strutturato.
11.3 Sinergia tra disinvestimenti anticipati e versamenti aggiuntivi

«Talent perceives differences; genius, unity».
William Butler Yeats
Un investitore può decidere di unire i vantaggi dei disinvestimenti anticipati a quelli dei versamenti aggiuntivi: sono infatti due varianti strategiche che agiscono in maniera molto diversa su un Piano di Accumulo del Capitale.
L’Analisi PAC permette di effettuare i backtest di un piano di accumulo che sfrutti queste due varianti in modo sinergico fornendo, oltre alle solite misure statistiche, le differenze tra il rendimento medio, massimo, minimo e la deviazione standard dei piani di accumulo con o senza disinvestimenti anticipati e versamenti aggiuntivi.
I parametri che possono essere personalizzati sono quelli analizzati in precedenza (6 per i disinvestimenti anticipati e 7 per i versamenti aggiuntivi).
In linea con le scelte del capitolo precedente, nei parametri dei disinvestimenti anticipati abbiamo selezionato la checkbox "Durata massima".
Lanciando un’analisi del fondo Raiffeisen con entrambe le strategie si ottengono i risultati seguenti:
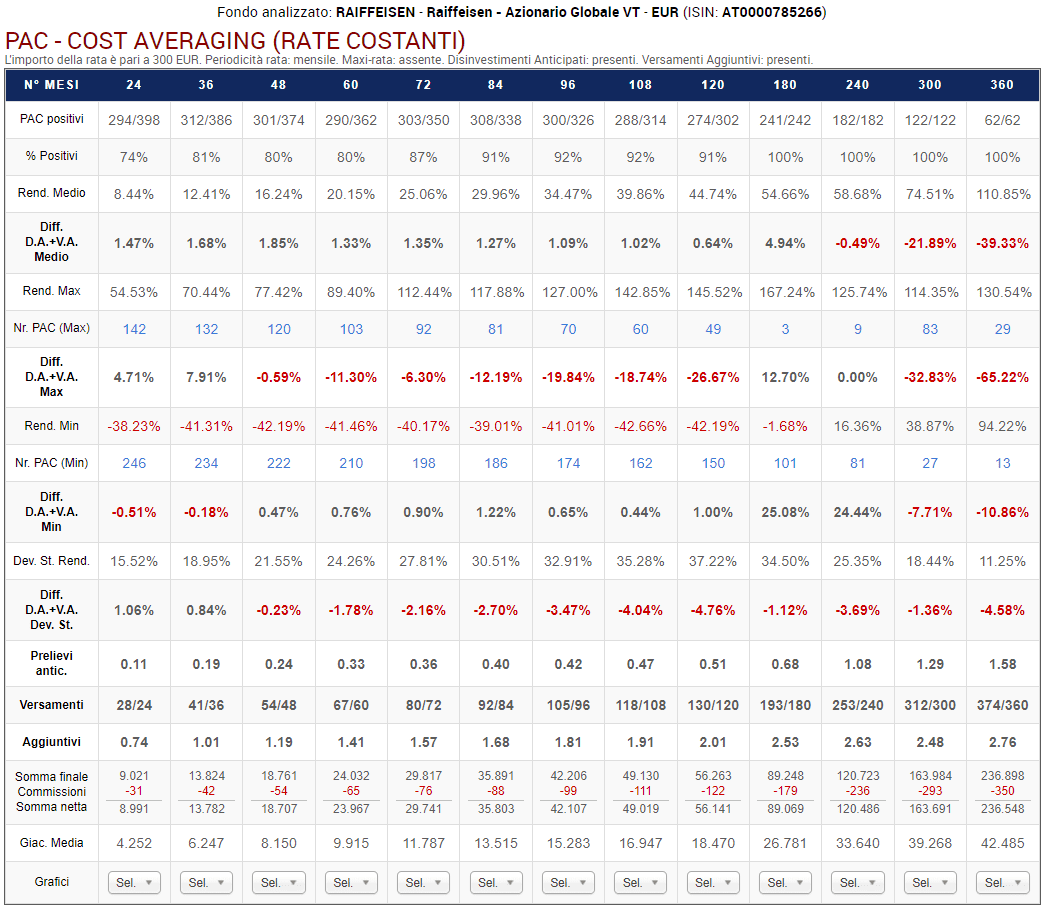
Fig. 66 – Raiffeisen: Disinvestimenti anticipati e Versamenti aggiuntivi. Parametri di default (Durata massima selezionata nei versamenti aggiuntivi). Rata: 300 euro
I pro e i contro dei disinvestimenti anticipati e dei versamenti aggiuntivi si sommano e producono dei risultati interessanti:
- Differenza D.A. + V.A. Medio: positivi per tutte le durate inferiori o uguali a 15 anni; negativi per quelle superiori.
- Differenza D.A. + V.A. Max: in linea di massima sono valori negativi, ma con notevoli eccezioni: i piani di accumulo della durata di 2 anni (4,71%), 3 anni (7,91%), 15 anni (12,70%) e 20 anni (differenza nulla).
- Differenza D.A. + V.A. Min: stavolta i valori sono tendenzialmente positivi, con l’eccezione delle durate più brevi (2 e 3 anni) e più lunghe (25 e 30 anni).
- Differenza D.A. + V.A. Dev. St.: la maggior parte dei valori sono negativi, segno di un impatto tendenzialmente positivo sulla variabilità dei rendimenti dei piani di accumulo.
Durante le simulazioni, lanciando l’analisi di un piano di accumulo con disinvestimenti anticipati e versamenti aggiuntivi, vengono effettuate 4 serie di backtest:
- PAC semplice: si effettuano le analisi dei piani di accumulo senza alcun intervento discrezionale.
- PAC con disinvestimenti anticipati: si effettuano le analisi dei piani di accumulo con i soli disinvestimenti anticipati.
- PAC con versamenti aggiuntivi: si effettuano le analisi dei piani di accumulo con i soli versamenti aggiuntivi.
- PAC con disinvestimenti anticipati e versamenti aggiuntivi: si effettuano le analisi dei piani di accumulo con i disinvestimenti anticipati e i versamenti aggiuntivi.
Questo tipo di analisi dura un po' di più: il vantaggio è quello di poter tracciare tutti i rendimenti dei piani di accumulo di una specifica durata.
Ad esempio, cliccando su 180 nella riga delle intestazioni della colonna, verranno visualizzati i rendimenti delle 4 tipologie di analisi:
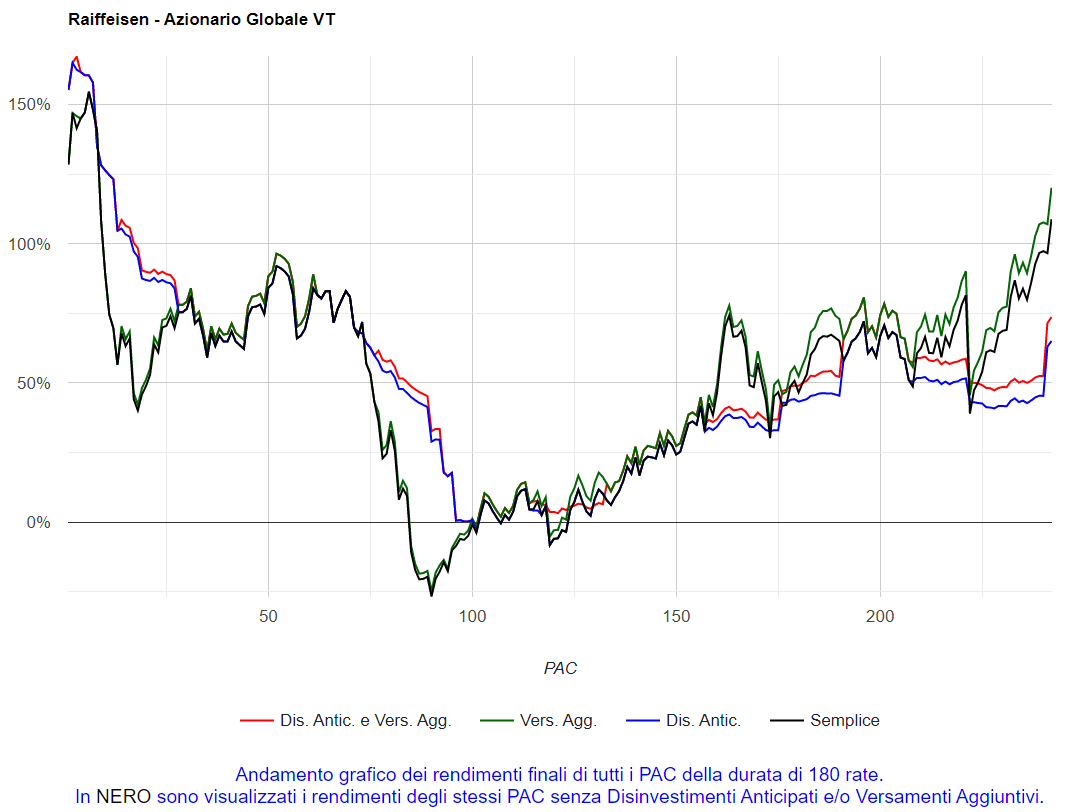
Fig. 67 – Raiffeisen: PAC Cost Averaging con disinvestimenti anticipati e versamenti aggiuntivi. Tutti i PAC della durata di 15 anni (V.A. con durata massima selezionata e drawdown non selezionato)
In nero vengono visualizzati i rendimenti finali dei PAC senza alcun intervento discrezionale; in blu quelli dei PAC con i soli disinvestimenti anticipati; in verde quelli con i soli versamenti aggiuntivi e in rosso i rendimenti finali dei PAC con disinvestimenti anticipati e versamenti aggiuntivi.
La variante strategica che ha il maggior impatto in caso di utilizzazione sinergica è quella dei disinvestimenti anticipati. La linea rossa è infatti molto più vicina alla blu che non alla verde o alla nera. Tuttavia, si può apprezzare anche l’apporto benefico dei versamenti aggiuntivi: la linea rossa si posiziona quasi sempre al di sopra di quella blu.
Dal grafico si risale con facilità ai piani di accumulo che hanno tratto vantaggio dai disinvestimenti anticipati e/o dai versamenti aggiuntivi. Il numero 89, ad esempio, evidenzia l’importanza di entrambi:
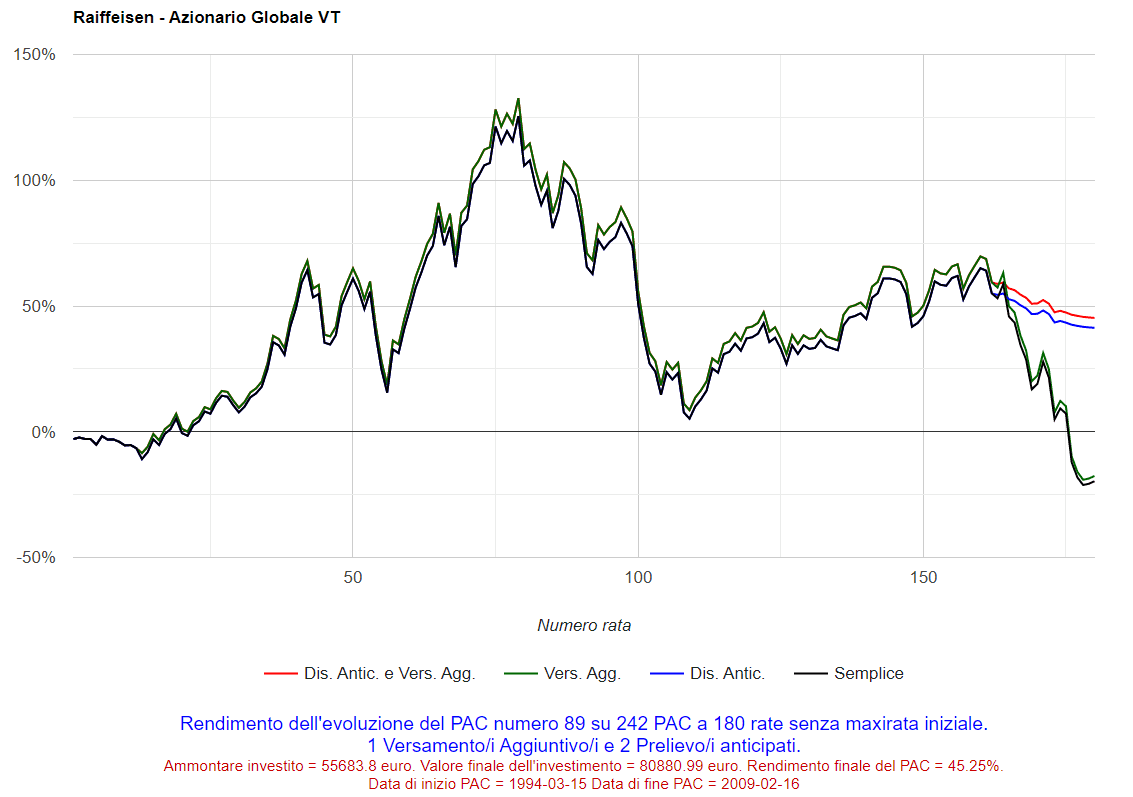
Fig. 68 – Raiffeisen: PAC Cost Averaging della durata di 15 anni con disinvestimenti anticipati e versamenti aggiuntivi. PAC nr. 89 (Drawdown non selezionato)
Alla fine, anche la sola implementazione dei versamenti aggiuntivi sarebbe stata positiva.
Ovviamente, i disinvestimenti anticipati hanno il merito di preservare gran parte del rendimento: sono stati utilizzati addirittura due volte in questo specifico PAC, con pieno successo. L’utilizzo sinergico di entrambe le strategie ha prodotto il risultato migliore.
Non sempre le cose vanno nel verso giusto.
Il PAC seguente, il 189° dei 242 della durata di 15 anni, ha beneficiato dei versamenti aggiuntivi, ma i disinvestimenti anticipati non hanno evitato alcun crollo dei rendimenti, dal momento che il mercato è tornato in breve tempo a salire:
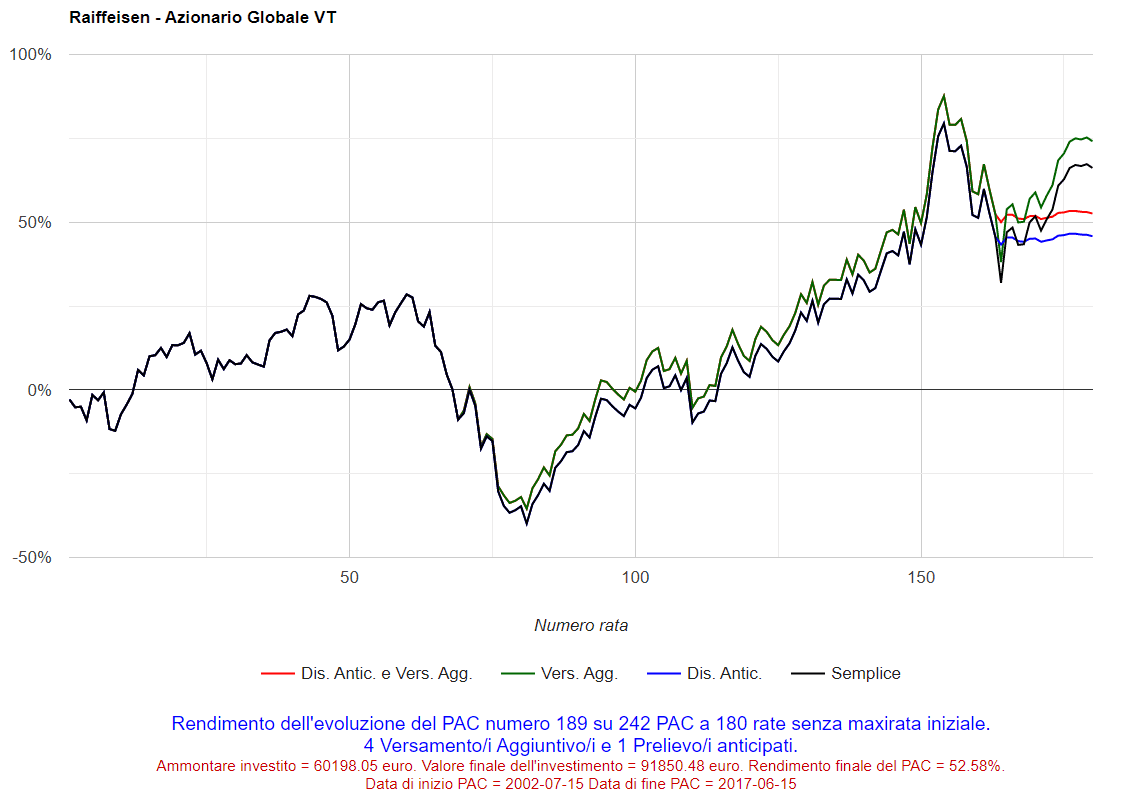
Fig. 69 – Raiffeisen: PAC Cost Averaging della durata di 15 anni con disinvestimenti anticipati e versamenti aggiuntivi. PAC nr. 188 (Drawdown non selezionato)
In questo PAC, iniziato a giugno 2002 e terminato a maggio 2017, sono stati effettuati 4 versamenti aggiuntivi e un prelievo anticipato.
Il grafico seguente è invece quello dei rendimenti medi per rata:
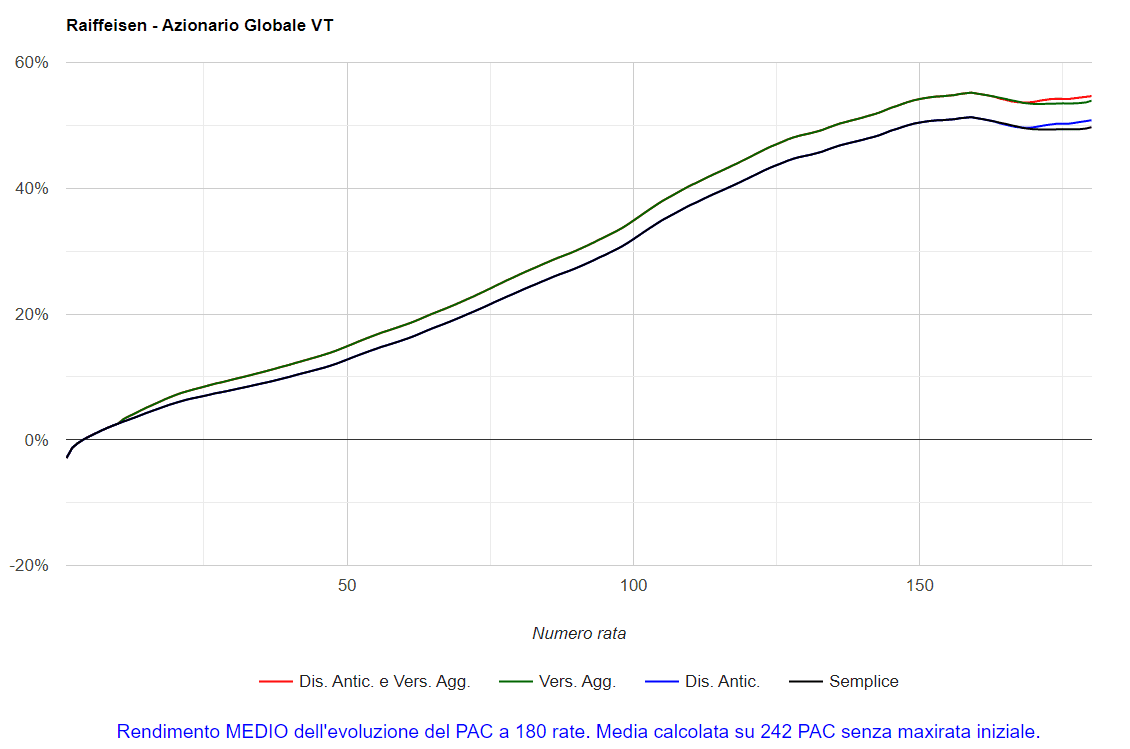
Fig. 70 – Raiffeisen: PAC Cost Averaging della durata di 15 anni con disinvestimenti anticipati e versamenti aggiuntivi. Rendimento medio per rata dei 218 PAC (Drawdown non selezionato)
Per un piano di accumulo il cui sottostante cresce nel tempo, i versamenti aggiuntivi avranno con molta probabilità effetti benèfici:
- Il rendimento sarà mediamente più alto.
- Quando la “Durata massima” viene selezionata, il rendimento sarà calcolato su un capitale maggiore di quello dei PAC semplici.
Anche i disinvestimenti anticipati, in media, hanno aumentato il rendimento finale dei piani di accumulo (la linea blu). In sinergia con i versamenti aggiuntivi, il beneficio è stato ancora maggiore (linea rossa).
La differenza tra il rendimento finale della linea rossa (54,66%) e di quella nera (49,72%) è pari al 4,94%, che nella tabella dei risultati era proprio il valore relativo alla “Diff. D.A. + V.A. Medio” dei piani di accumulo di 180 rate.
I disinvestimenti anticipati e i versamenti aggiuntivi sono due modalità di intervento discrezionale sui Piani di Accumulo del Capitale. La loro implementazione può essere simulata nell’Analisi PAC, con la possibilità di personalizzare tutti i parametri disponibili.
I disinvestimenti anticipati e i versamenti aggiuntivi non sono ovviamente gli unici modi in cui un investitore può intervenire attivamente su un piano di accumulo. Ci potrebbero essere altre modalità altrettanto valide.
Ogni intervento discrezionale dovrebbe comunque seguire delle regole ben precise, rigorosamente pianificate all’inizio dell’investimento. L’improvvisazione e la reazione ai movimenti inattesi dei mercati finanziari non sono consigliabili: è molto difficile che procurino dei vantaggi nel lungo termine.
Quando si verificano le crisi finanziarie, la volatilità cresce improvvisamente e il nervosismo dei mercati causa stress e preoccupazione: molti investitori tendono a reagire subito, con l’illusione che essersi attivati in prima persona sia un rimedio valido.
Uno degli errori più comuni è quello di sospendere il versamento delle rate o, peggio ancora, di liquidare quanto investito, magari per riprendere posizione sui mercati “quando la crisi sarà passata”.
La sospensione dei versamenti è oltremodo sbagliata, dal momento che il pagamento delle rate in tempi di crisi permette di acquistare più quote con la stessa somma: i piani di accumulo sfruttano i trend al ribasso del sottostante e una parte degli ottimi rendimenti finali vengono costruiti proprio in questi momenti.
Il disinvestimento dopo una crisi finanziaria è ancora più inopportuno: ormai è tardi, non si fa altro che monetizzare una perdita, probabilmente ingente.
Il disinvestimento ha senso se effettuato prima della crisi, proprio come i disinvestimenti anticipati si prefiggono di fare, ma sono interventi che comportano dei rischi: a volte il risultato è eccellente; altre volte si paga un prezzo corrispondente al minor rendimento, quando il sottostante continua a salire.
Intervenire attivamente su un piano di accumulo non è semplice: se siamo consci delle possibili ripercussioni, positive e negative, di un intervento discrezionale (possibilmente backtestandolo come abbiamo fatto con i disinvestimenti anticipati e i versamenti aggiuntivi), se si ha chiaro il rischio che ci si sta assumendo e, soprattutto, se abbiamo pianificato quel tipo di intervento prima, allora può essere corretto farlo.
Se invece ci muoviamo a caso, in preda al panico, seguendo l’istinto o un’idea appena balenata (per quanto brillante possa sembrare), allora il consiglio è quello di fermarsi: molto probabilmente, è meglio continuare con i soli versamenti periodici, rinunciando a ogni intervento discrezionale.
12. Confronto tra PAC mensili e di altre periodicità

«All we have to decide is what to do with the time that is given us».
J. R. R. Tolkien
Quando si pensa a un Piano di Accumulo del Capitale, si fa di solito riferimento a un PAC le cui rate vengono versate con frequenza mensile.
La periodicità mensile è quella più utilizzata perché ha diversi vantaggi:
- Permette la massima distribuzione del capitale nel tempo, ovvero la più ampia diversificazione temporale.
- Favorisce una disciplina finanziaria nell’investitore, che ogni mese risparmia e investe una somma stabilita.
- Le piattaforme d’investimento che permettono l’esecuzione automatica di Piani di Accumulo a rate costanti prevedono talvolta la sola periodicità mensile.
Il principale svantaggio è quello di non ottimizzare le commissioni di transazione, dette anche diritti fissi. Ogni volta che l’investitore versa una rata, paga una somma fissa o percentuale: per minimizzarla, sarebbe opportuno diminuire la frequenza delle rate.
A parte quella mensile, la periodicità più comunemente utilizzata è la trimestrale. Altre frequenze disponibili sono la bimestrale, quadrimestrale, semestrale e annuale.
L’Analisi PAC permette il backtest di piani di accumulo Cost Averaging con queste periodicità.
La frequenza desiderata viene selezionata grazie al parametro “Periodicità rata”. L’unità di misura è il mese: il valore predefinito è 1, al quale corrisponde la frequenza mensile.
Per selezionare periodicità superiori si devono scegliere le seguenti grandezze:
- 2 → periodicità bimestrale.
- 3 → periodicità trimestrale.
- 4 → periodicità quadrimestrale.
- 6 → periodicità semestrale.
- 12 → periodicità annuale.
In caso di analisi con periodicità superiore al mese, un altro parametro importante è il “Più uno”. Se la checkbox non viene selezionata, tutte le misure statistiche vengono calcolate al momento del versamento dell’ultima rata; se viene selezionata, un periodo successivo a questo.
Un esempio aiuterà a capire meglio perché questa differenza è importante.
Ipotizziamo di aver iniziato un piano di accumulo il 15 gennaio 2010. Se lanciamo un’analisi, i risultati dei PAC mensili della durata di 24 rate (2 anni) saranno calcolati al 15 dicembre 2011, ovvero al momento del versamento della 24° rata. Per la precisione, il periodo trascorso è pari a 23 mesi.
Perché si dovrebbero considerare 23 mesi invece di 24?
La risposta è che, tecnicamente, il piano di accumulo è terminato con il versamento dell’ultima rata. È stato completato in quel momento e, da lì in poi, si è di fatto trasformato in un PIC: le quote accumulate fino a quel momento rimarranno invariate, salvo eventuali vendite o acquisti successivi.
I backtest eseguiti finora sono stati realizzati calcolando le performance dei PAC nel modo appena descritto. Esistono però dei casi in cui sia preferibile calcolarle un periodo successivo a quello del versamento dell’ultima rata.
I più comuni sono due:
- Piani di accumulo di periodicità superiore al mese: nell’esempio precedente, il versamento dell’ultima rata di un PAC bimestrale di 2 anni di durata (quindi composto da 12 rate) sarebbe avvenuto il 15 novembre 2011. Soltanto 22 mesi dopo il versamento della prima rata. L’ultimo versamento di un PAC trimestrale sarebbe invece avvenuto il 15 ottobre 2011: 21 mesi dopo l’inizio del piano. E così via fino a un PAC annuale, composto da due soli versamenti: il primo, il 15 gennaio 2010 e il secondo, il 15 gennaio 2011. Soltanto 12 mesi dopo. Anche se, tecnicamente, i piani di accumulo si completano con il versamento dell’ultima rata, con periodicità superiori al mese si vengono a creare delle distorsioni nel calcolo delle performance.
- Quando si vuol fare un confronto tra le performance di PAC di uguale durata, ma con frequenze di versamento delle rate diverse: in questo caso, le distorsioni che si verrebbero a creare falserebbero le conclusioni.
Selezionando la checkbox “Più uno”, stabiliamo come momento finale della vita di un PAC quello corrispondente a un periodo successivo al versamento dell’ultima rata, indipendentemente dalla frequenza.
Tornando all’esempio precedente, in un PAC mensile questo momento sarà il 15 gennaio 2012 invece del 15 dicembre 2011: esattamente un mese dopo il versamento della 24° e ultima rata. In un PAC bimestrale, il momento scelto sarà, di nuovo, il 15 gennaio 2012: due mesi dopo il versamento della dodicesima e ultima rata. La stessa cosa varrà per i piani di accumulo trimestrali, quadrimestrali, semestrali e annuali. In quest’ultimo caso, il momento scelto sarà ancora il 15 gennaio 2012, ovvero un anno dopo il versamento della seconda e ultima rata.
Nei piani di accumulo di durata superiore ai 2 anni, sarà applicato lo stesso principio di calcolo.
Procedendo in questo modo, potremo confrontare tra loro le performance dei PAC con diverse frequenze di versamento delle rate.
In un piano di accumulo costruito su un fondo dal trend crescente, i rendimenti medi calcolati con il parametro “Più uno” selezionato saranno più elevati: il periodo di investimento sarà mediamente superiore di 1-12 mesi, a seconda della periodicità scelta.
Tutti i backtest che seguono saranno effettuati con il parametro “Più uno” selezionato.
Partiamo dall’analisi dei piani di accumulo con versamenti mensili:
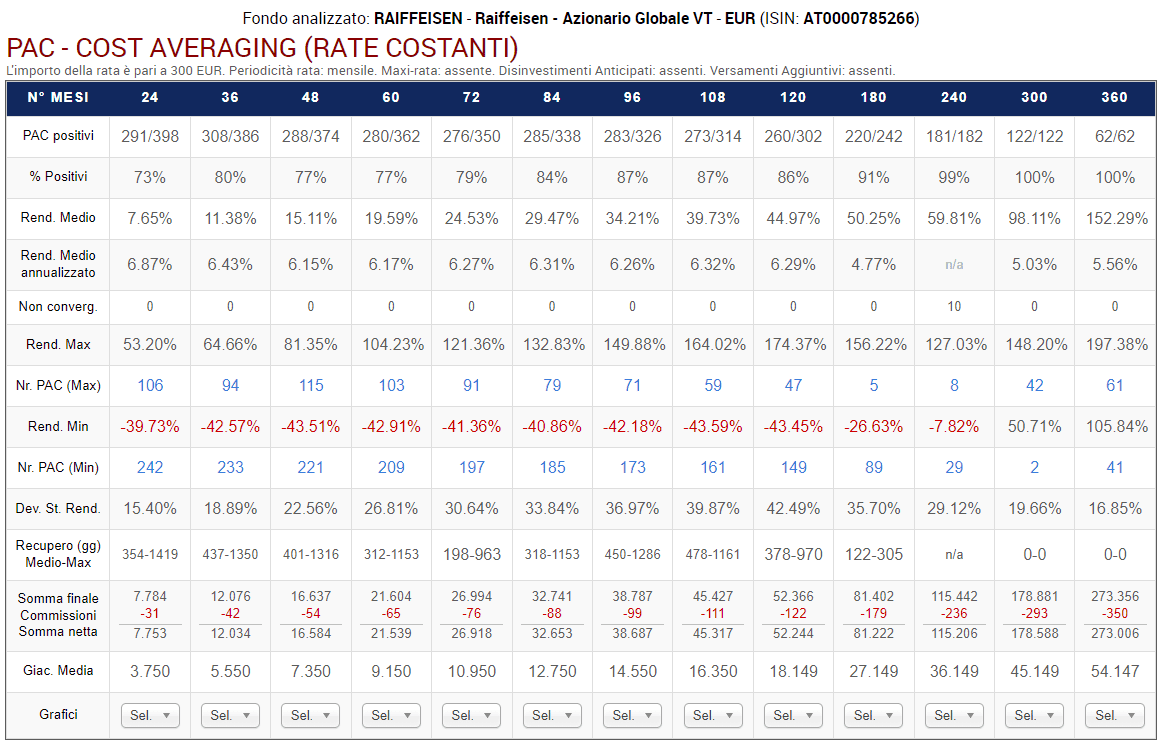
Fig. 71 – Raiffeisen: PAC Cost Averaging. Rata: 300 euro. Frequenza versamenti: mensile. “Più uno” selezionato
I risultati della tabella sono simili ma leggermente migliori a quelli della Fig. 11.
Il mese in più si ripercuote anche sulle giacenze medie, che sono maggiori di quelle ottenute senza l’opzione “Più uno”.
Quando si versa una rata, indipendentemente dalla frequenza, si ipotizza che il pagamento venga effettuato al tempo 0.
In un asse temporale dove l’unità di misura è il mese, abbiamo i seguenti piani dei versamenti (PAC della durata di 24 rate):
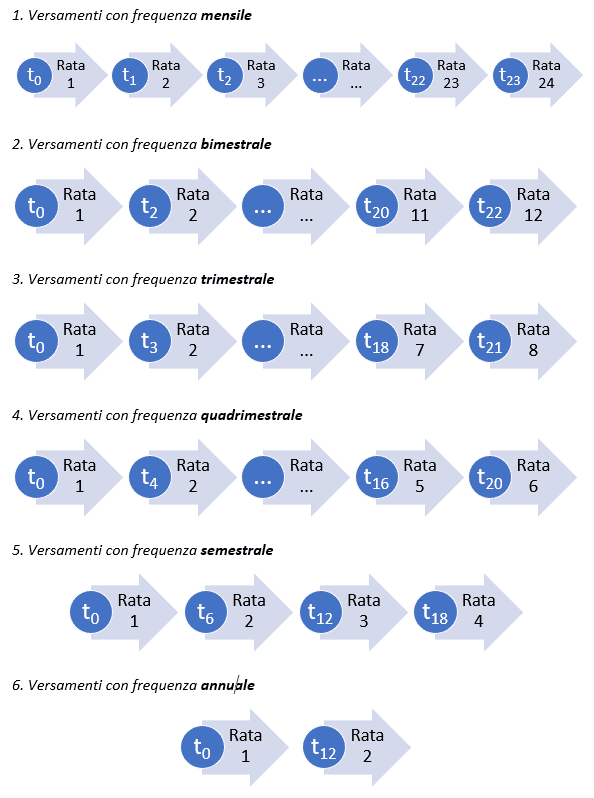
La prima rata viene sempre versata all’inizio del primo periodo, al tempo 0 (t0). Nella realtà, t0 corrisponde ovviamente a una data precisa (ipotizziamo il 15 gennaio 2010).
Per rendere omogenei i confronti, minore è la frequenza delle rate, maggiore sarà l’importo versato a t0: 300 euro se la frequenza è mensile; 600 euro se è bimestrale; 900 euro se è trimestrale; 1.200 euro se è quadrimestrale; 1.800 euro se è semestrale e 3.600 euro se è annuale.
Di conseguenza, la giacenza media di ciascun PAC aumenterà col diminuire della frequenza delle rate.
Un’altra interpretazione sarebbe stata possibile: quella di determinare l’inizio di un PAC un periodo prima del versamento della rata: ad esempio, un PAC mensile la cui prima rata sarebbe stata versata il 15 gennaio 2010, avrebbe avuto in realtà inizio il 15 dicembre 2009.
Se il PAC fosse stato trimestrale, la prima rata sarebbe stata versata il 15 marzo 2010.
Da un punto di vista logico questa interpretazione è altrettanto valida: decido di iniziare un piano di accumulo il 15 dicembre 2009 e sfrutto il mese, il trimestre, il semestre o l’anno successivo per accantonare il capitale da versare alla fine del periodo.
In pratica, si sceglie tuttavia di far iniziare l’investimento nel momento in cui si versa la prima rata per vari motivi:
- È una prassi ormai consolidata, utilizzata in ogni analisi finanziaria.
- È più semplice programmare gli algoritmi di calcolo.
- Non è detto che l’investitore abbia davvero bisogno di quel periodo di tempo per accantonare la somma da impiegare: potrebbe averla già disponibile.
- È più facile confrontare i piani di accumulo con altre metodologie di investimento, ad esempio i PIC (investimenti in un’unica soluzione).
Vediamo quali sono le performance dei piani di accumulo con versamento delle rate bimestrale:
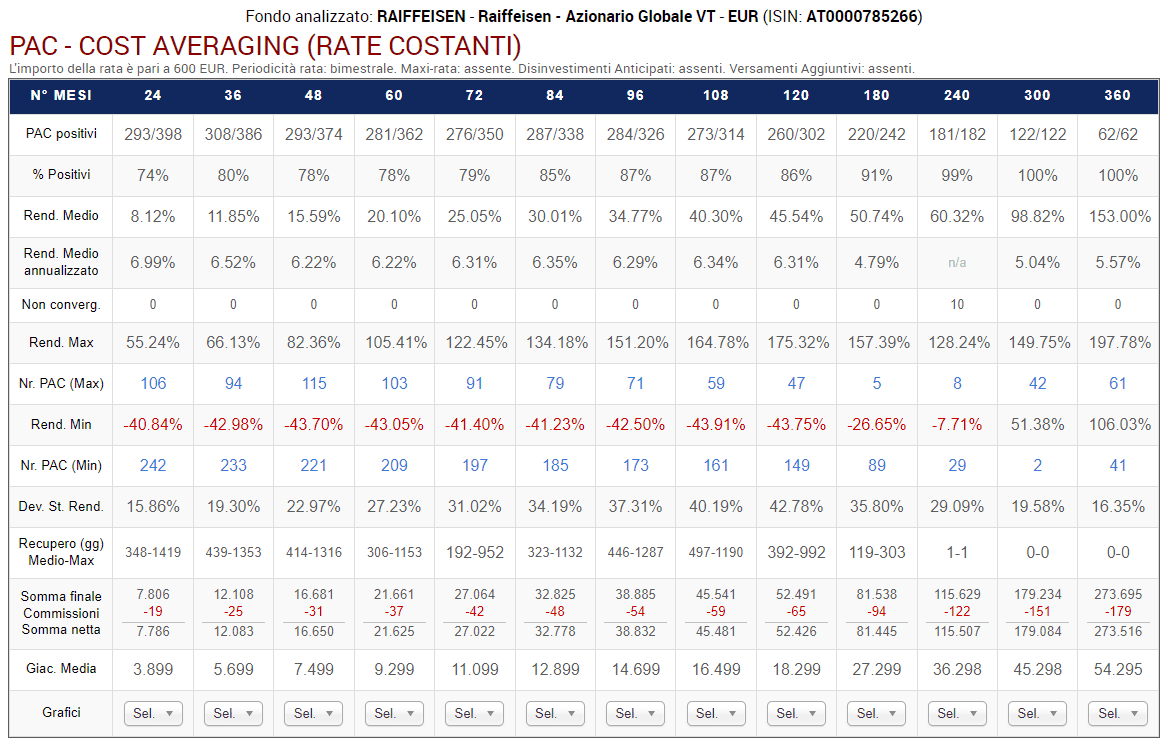
Fig. 72 – Raiffeisen: PAC Cost Averaging. Rata: 600 euro. Frequenza versamenti: bimestrale. “Più uno” selezionato
I risultati sono leggermente migliori:
- Il numero e la percentuale di PAC positivi sono maggiori o uguali a prima. Ad esempio, i piani di accumulo positivi della durata di 24 mesi sono adesso 293; in precedenza, erano 291.
- Il rendimento medio e medio annualizzato sono più alti. L’incremento del rendimento medio oscilla intorno allo 0,40-0,70%, su tutte le durate. Il pagamento di minori commissioni di transazione contribuisce positivamente in questo senso, per quanto le differenze siano sempre meno significative con l'aumentare della lunghezza dei PAC.
- I rendimenti massimi sono tutti più alti. I rendimenti minimi sono invece inferiori nelle durate fino a 15 anni.
- La giacenza media è più alta.
- La deviazione standard dei rendimenti è leggermente più elevata nelle durate fino a 15 anni. Versare una cifra doppia la metà delle volte non causa, perciò, un grosso peggioramento nella variabilità dei rendimenti finali dei PAC.
Passiamo ai piani di accumulo con versamento delle rate trimestrale:
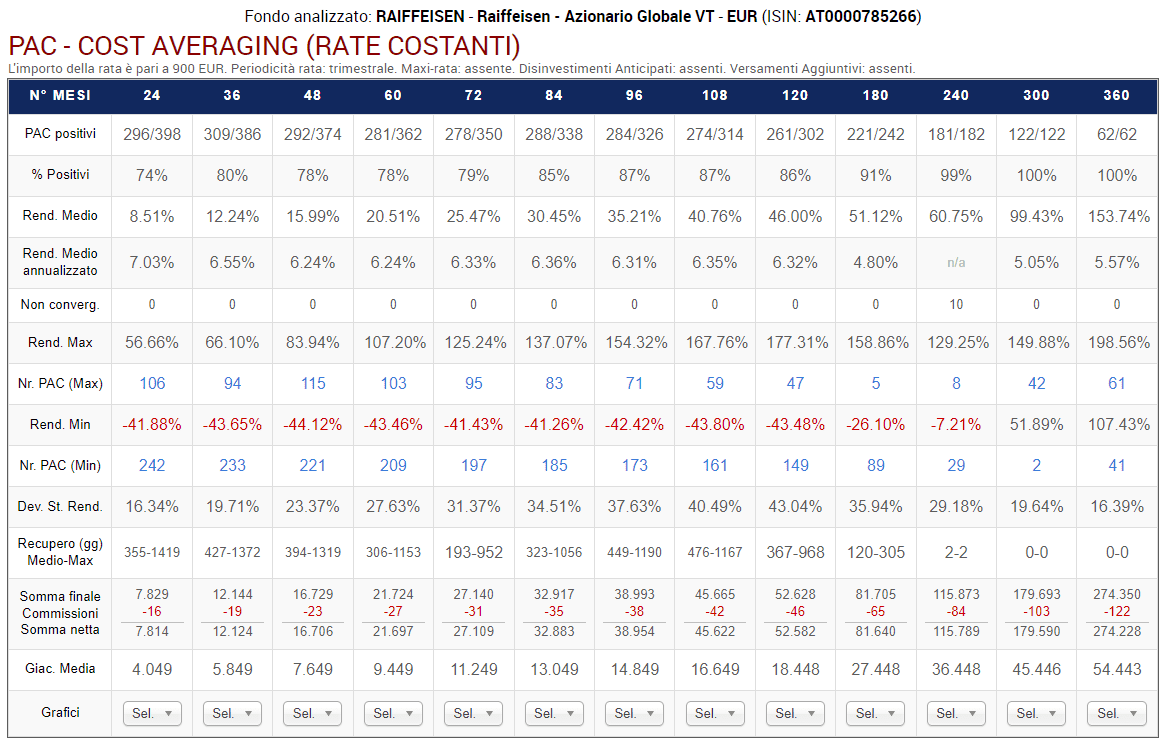
Fig. 73 – Raiffeisen: PAC Cost Averaging. Rata: 900 euro. Frequenza versamenti: trimestrale. “Più uno” selezionato
Escludendo l’ulteriore piccolo incremento di volatilità, i risultati continuano a migliorare:
- Il numero e la percentuale di PAC positivi sul totale sono ancora una volta maggiori o uguali a quelli precedenti.
- Il rendimento medio e medio annualizzato sono più alti. L’incremento del rendimento medio, rispetto ai PAC con versamento bimestrale, è compreso tra mezzo e un punto percentuale.
- I rendimenti massimi sono più alti. I rendimenti minimi sono inferiori nelle durate fino a 7 anni: dagli 8 anni in su, invece, migliorano.
- La giacenza media continua a crescere.
- La deviazione standard dei rendimenti continua debolmente a crescere.
Sembra configurarsi un pattern costante: con il diminuire della frequenza nei versamenti delle rate, i rendimenti e la volatilità crescono in modo contenuto.
Visualizziamo adesso le performance dei piani di accumulo quadrimestrali, semestrali e annuali.
Partiamo con i quadrimestrali:
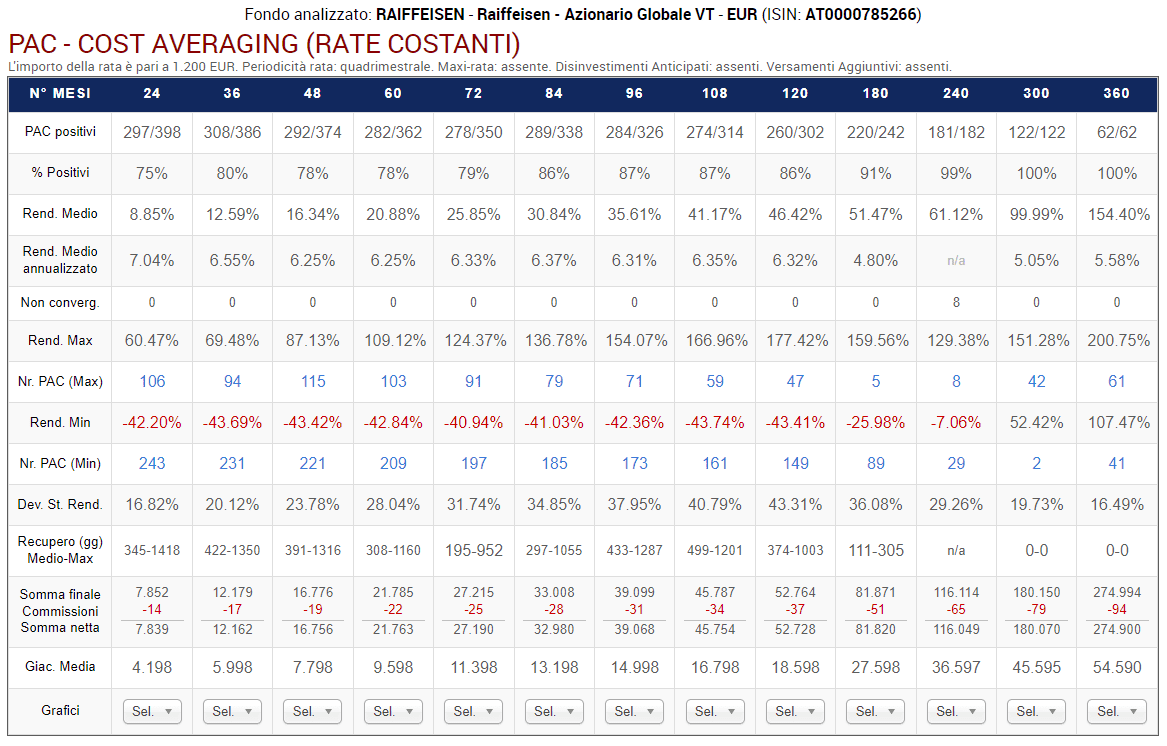
Fig. 74 – Raiffeisen: PAC Cost Averaging. Rata: 1.200 euro. Frequenza versamenti: quadrimestrale. “Più uno” selezionato
Continuiamo con i semestrali:
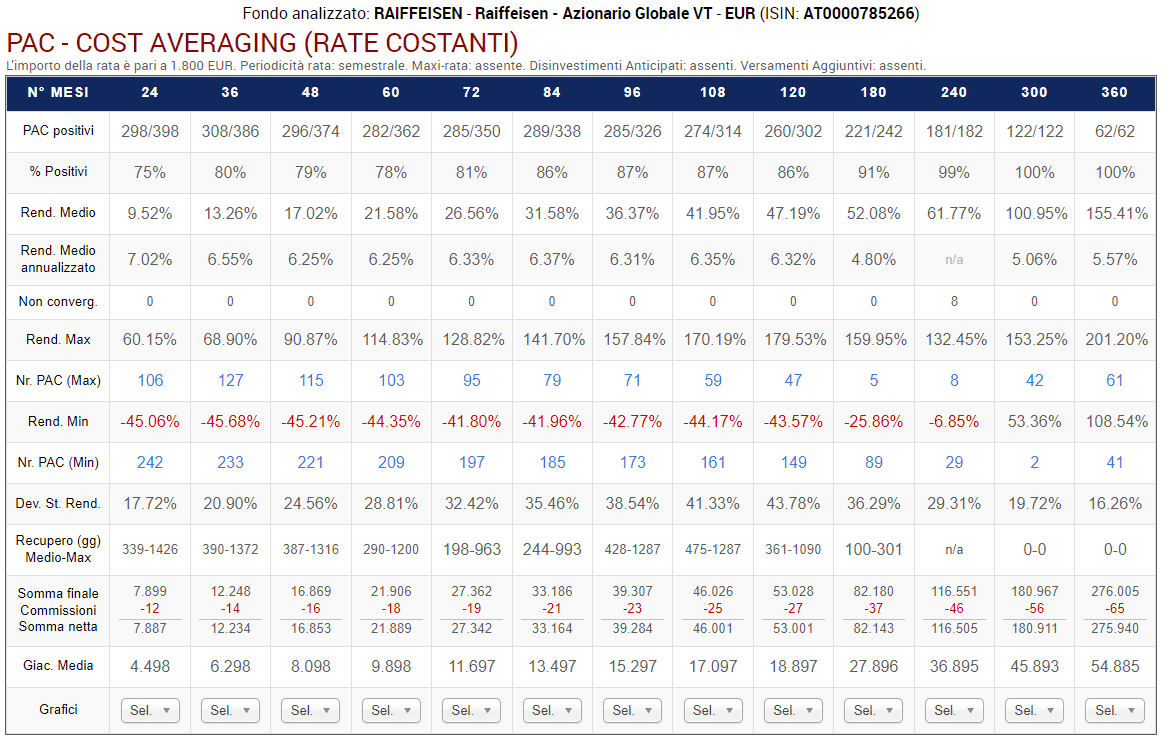
Fig. 75 – Raiffeisen: PAC Cost Averaging. Rata: 1.800 euro. Frequenza versamenti: semestrale. “Più uno” selezionato
Terminiamo con i piani di accumulo dalle rate di periodicità annuale:
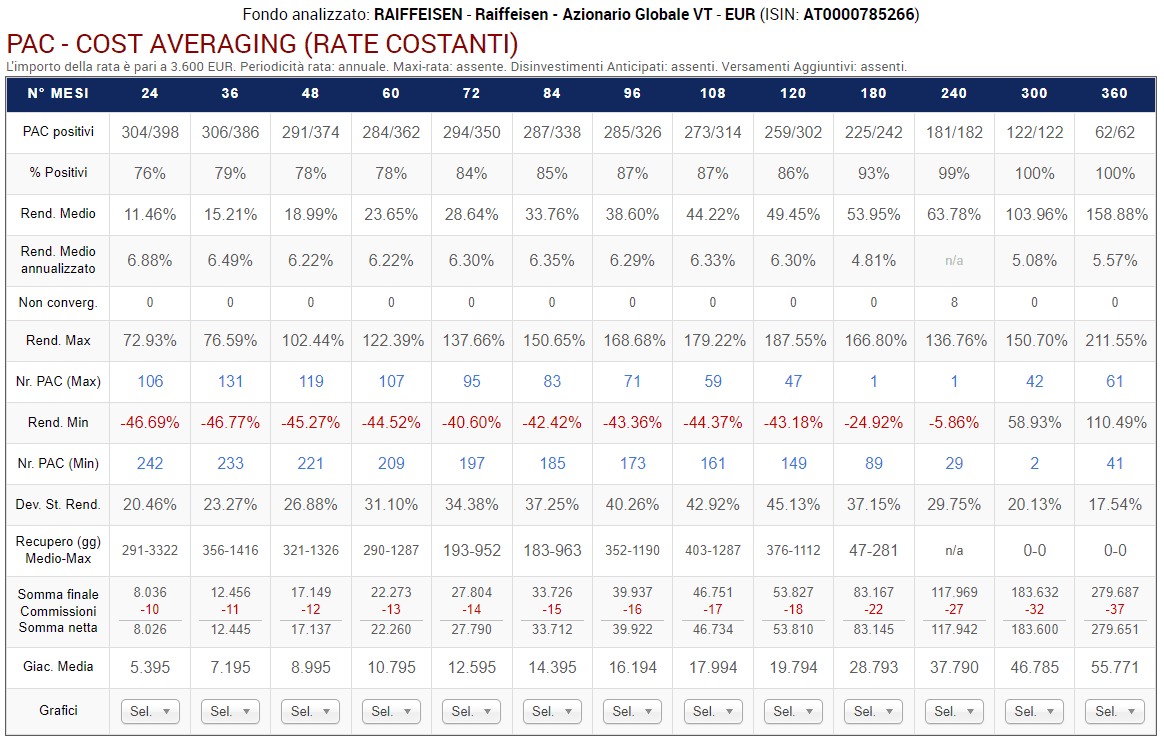
Fig. 76 – Raiffeisen: PAC Cost Averaging. Rata: 3.600 euro. Frequenza versamenti: annuale. “Più uno” selezionato
Le considerazioni precedenti sembrano essere confermate: meno frequenti sono le rate, migliori sono i risultati in termini di rendimento medio e massimo. Le percentuali di PAC positivi sono più alte. Peggiorano invece i rendimenti minimi e le deviazioni standard dei rendimenti.
Che effetti produce la diversa frequenza nei versamenti delle rate in un piano di accumulo il cui sottostante non segue un trend crescente?
Per rispondere a questa domanda effettuiamo i backtest anche sul fondo Aberdeen.
Ci limiteremo a visualizzare le performance dei piani mensili, trimestrali e annuali.
Partiamo dai primi:
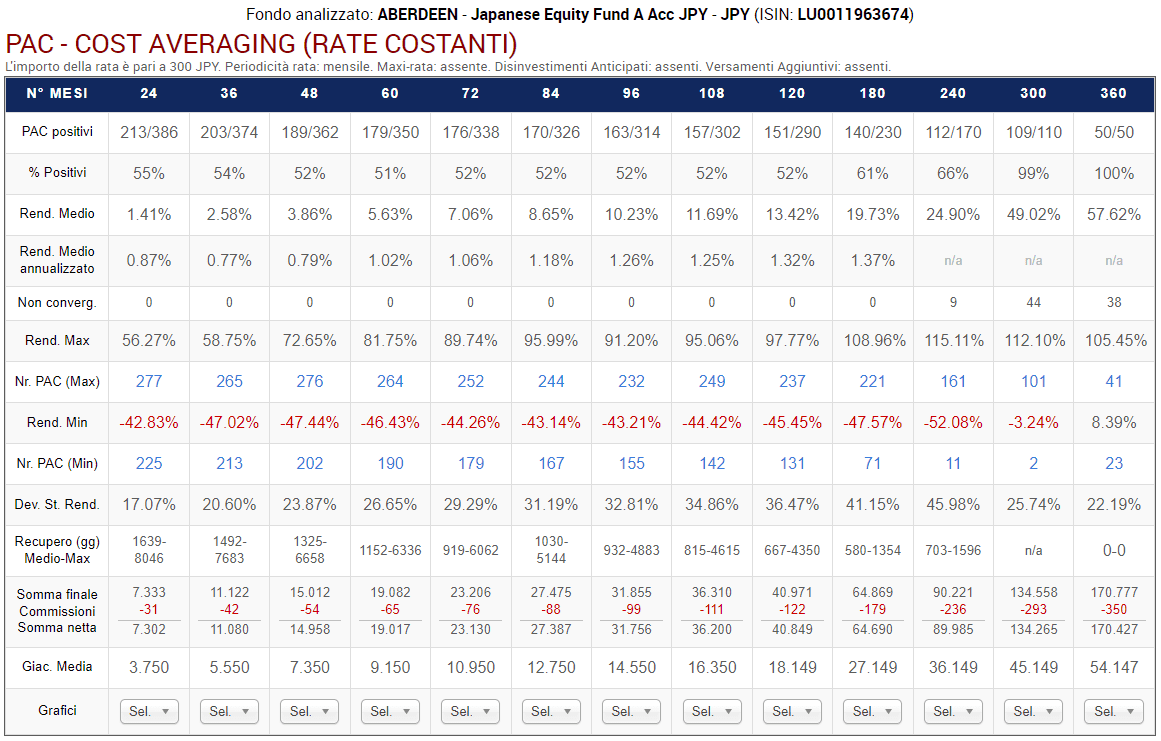
Fig. 77 – Aberdeen: PAC Cost Averaging. Rata: 300 euro. Frequenza versamenti: mensile. “Più uno” selezionato
Continuiamo con i trimestrali:
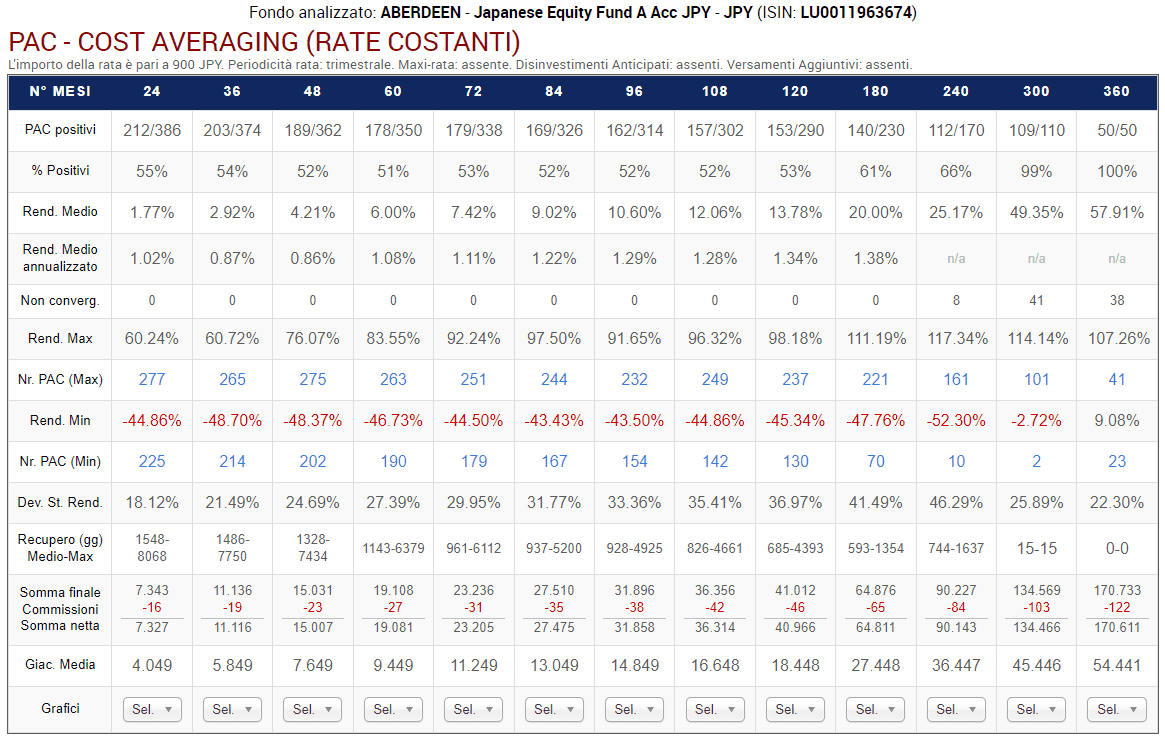
Fig. 78 – Aberdeen: PAC Cost Averaging. Rata: 900 euro. Frequenza versamenti: trimestrale. “Più uno” selezionato
E, per finire, i piani di accumulo con versamenti annuali:
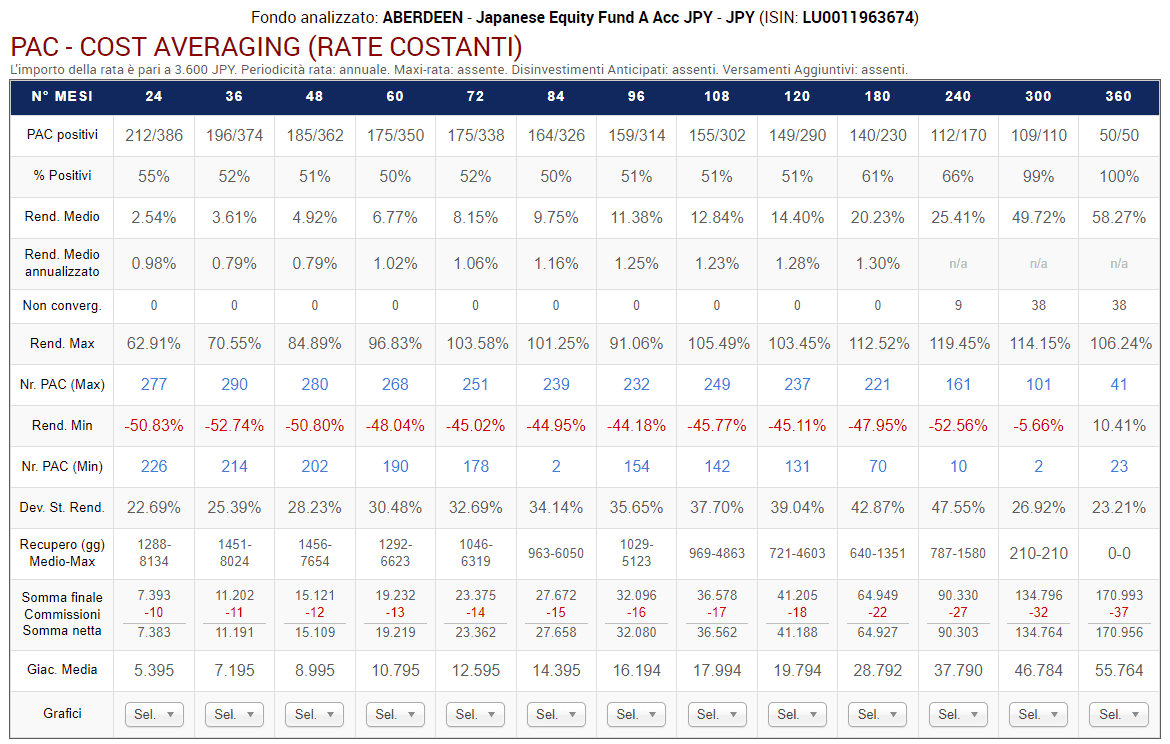
Fig. 79 – Aberdeen: PAC Cost Averaging. Rata: 3.600 euro. Frequenza versamenti: annuale. “Più uno” selezionato
Le cose, stavolta, sono un po’ cambiate:
- Il numero e la percentuale di PAC positivi tendono a essere superiori nei piani di accumulo mensili. Ad esempio, i PAC quinquennali positivi sono 179 se i versamenti sono mensili; 178 se sono trimestrali e 175 se sono annuali. Le differenze tra i primi due sono abbastanza esigue, mentre i piani annuali performano peggio fino alla durata decennale. I piani maggiori o uguali a 15 anni hanno invece la stessa percentuale di PAC positivi.
- Il rendimento medio è più alto nei dei piani di accumulo trimestrali e annuali, a parità di durata dei PAC.
- Rendimenti massimi e minimi: in generale, seguono il trend precedente. Salvo qualche eccezione, minore è la frequenza di versamento delle rate, più alti sono i rendimenti massimi e più bassi quelli minimi.
- Giacenza media: meno frequenti sono le rate, più è alta la giacenza media.
- La deviazione standard è maggiore nei PAC trimestrali e soprattutto annuali.
La scelta di optare per piani di accumulo con versamenti meno frequenti di quelli mensili è sensata: comporta dei vantaggi, ma ha anche alcuni limiti.
Le differenze nelle performance non sono elevate e, in linea generale, si può affermare che le frequenze di versamento minori permettono di ottenere dei rendimenti più elevati, anche se leggermente più volatili.
È consigliabile che l’investitore non basi la sua scelta solo sulla performance; meglio dare la precedenza ad altre variabili:
- Semplicità: disponibilità di piani di accumulo automatizzati.
- Facilità nel risparmio delle rate: accantonare l’importo relativamente piccolo di una rata mensile è più agevole che farlo con importi più consistenti, da versare magari annualmente.
- Tranquillità: selezionare la frequenza che permette di affrontare l’investimento con la fiducia necessaria a portarlo a termine, senza eccessivo stress psicologico.
13. La maxi-rata iniziale

«Even the largest avalanche is triggered by small things».
Vernor Vinge
Un Piano di Accumulo del Capitale con maxi-rata iniziale prevede il versamento di una prima rata più consistente, seguita da rate standard periodiche dell’importo stabilito.
La maxi-rata iniziale è costituita generalmente da un importo corrispondente a 12 rate standard. Nulla impedisce, però, di impostarla a un numero più basso o più alto di rate.
In presenza di maxi-rata iniziale, la periodicità più utilizzata è quella mensile.
La durata complessiva del piano di accumulo viene di solito accorciata di un numero di rate pari a quelle che costituiscono la maxi-rata (meno una).
Ad esempio, se si decide di costruire un piano di accumulo quinquennale, con frequenza mensile delle rate (quindi 60 in totale) e inclusivo di una maxi-rata composta da 12 rate standard, l’effettiva durata del PAC sarà pari a 49 mesi: 60 − (12 − 1) = 60 − 11 = 49.
Si dovrà fare molta attenzione a non confrontare un piano di accumulo quinquennale con maxi-rata con uno senza maxi-rata: le performance ottenute, oltre a differire a causa della presenza della maxi-rata, saranno diverse anche per via della minore durata effettiva del piano con la maxi-rata.
Un piano quinquennale mensile con una maxi-rata di 12 rate standard, avendo una durata effettiva di 49 mesi, dovrebbe quindi essere confrontato con uno di pari lunghezza.
Nell’Analisi PAC, la maxi-rata può essere compresa tra 2 e 12 rate standard e può essere applicata soltanto a piani di accumulo mensili.
I risultati dei backtest dei piani di accumulo con maxi-rata di 12 rate standard sono i seguenti:
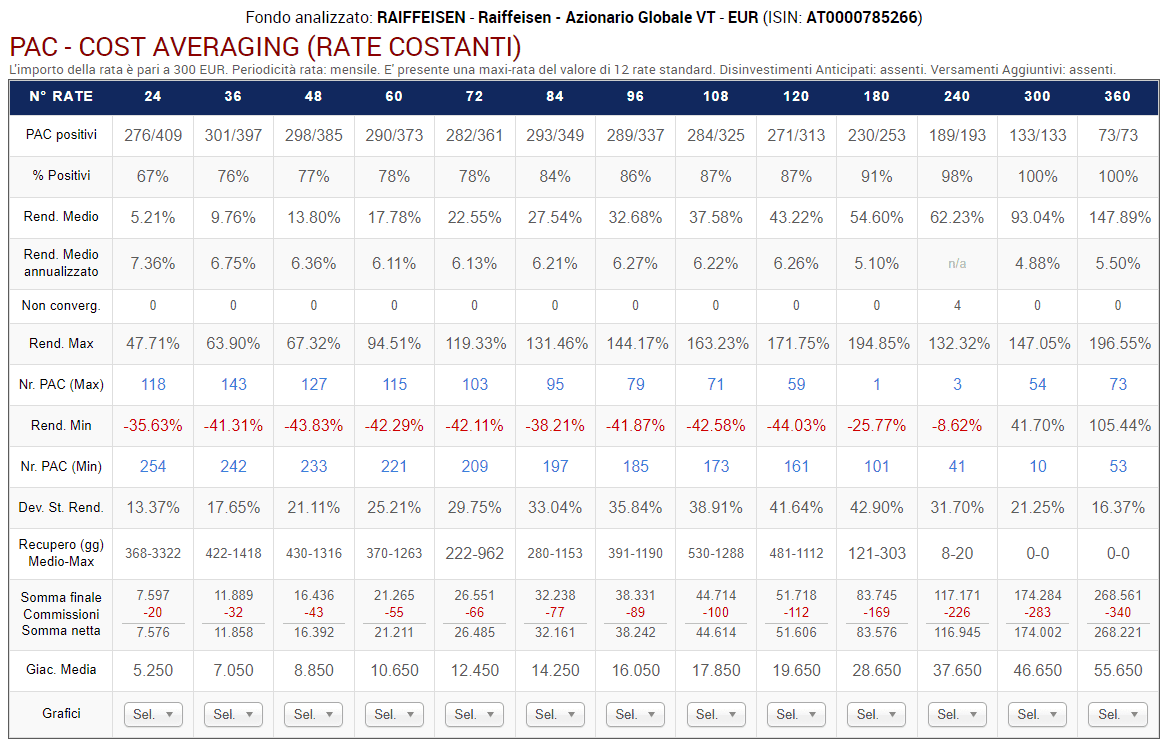
Fig. 80 – Raiffeisen: PAC Cost Averaging. Rata: 300 euro. Maxi-rata pari a 12 rate standard
Rispetto alla stessa analisi senza maxi-rata iniziale (Fig. 11), il numero di PAC simulati per ogni durata è aumentato di 11 unità. Il motivo è che la durata di ciascuno di essi è diminuita proprio di 11 mesi: in un contesto di backtest rolling mensile, è stato possibile simulare 11 piani in più per ogni durata.
Le performance di questi backtest sono il risultato della somma di due effetti generati dalla maxi-rata iniziale:
- Con un mercato sottostante crescente, la maxi-rata iniziale ha un impatto mediamente positivo sul rendimento finale, dal momento che permette di concentrare un buon numero di rate standard all’inizio dell’investimento.
- La minor durata complessiva del piano di accumulo con maxi-rata ha un impatto mediamente negativo sul rendimento finale.
La maxi-rata iniziale produce un aumento della giacenza media, mentre la deviazione standard dei rendimenti non subisce grossi cambiamenti.
Perché in alcuni piani di accumulo è prevista la maxi-rata iniziale? Come si giustifica la sua applicazione?
I motivi principali – uno più nobile e uno meno – sono i seguenti:
- La maxi-rata sfrutta il beneficio derivante dalla concentrazione delle rate all’inizio dell’investimento (punto 1. precedente)
- Alcune banche applicano delle commissioni d’ingresso sui piani di accumulo. Queste commissioni vengono calcolate sul capitale versato in totale dall’investitore (numero di rate del PAC × importo della rata). Spesso, se è presente la maxi-rata, una buona parte della commissione grava proprio sulla prima rata del piano (questo punto sarà sviluppato nel capitolo successivo).
In definitiva, dal momento che quando si investe l’aspettativa è che i mercati seguano un trend crescente, l’utilizzo della maxi-rata iniziale è una buona soluzione, soprattutto se all’inizio del PAC si dispone di una somma più cospicua delle singole rate standard.
Si dovrà fare però molta attenzione a non ritrovarsi con una maxi-rata su cui gravano pesanti commissioni.
14. Le commissioni di transazione e d’ingresso
«Kind words do not cost much. Yet they accomplish much».
Blaise Pascal
L’investitore in un Piano di Accumulo del Capitale a rate costanti deve far fronte a due tipologie di commissioni:
- Commissioni di transazione (dette anche diritti fissi).
- Commissioni di ingresso.
Le prime sono di solito inevitabili. Investendo in un piano di accumulo si dovrà pagare una commissione fissa o percentuale ogni volta che si versa una rata.
La commissione sulla prima rata potrebbe essere più elevata delle altre.
Ovviamente ogni banca applica delle commissioni diverse. Nei nostri backtest abbiamo sempre applicato:
- Una commissione fissa sulla prima rata di 9 euro (“Diritti fissi”).
- Una commissione fissa su tutte le altre rate pari a 0,95 euro (“Diritti fissi rata”).
Potrebbe accadere che alcune piattaforme di investimento offrano la possibilità di costruire un piano di accumulo senza applicare alcuna commissione di transazione. Si tratta di casi eccezionali e, probabilmente, sono offerte riservate a un sottoinsieme di prodotti finanziari (ad esempio, agli ETF) o sono promozioni limitate nel tempo.
Laddove fossero disponibili, sarebbe ovviamente il caso di approfittarne, ma senza esagerare: 1 o 2 euro di commissioni di transazione in più non sono un problema e se, per risparmiarle, si devono aprire altri conti o addirittura rinunciare all'automatizzazione dei pagamenti, il gioco non vale la candela.
Le commissioni di ingresso, invece, vengono sempre applicate percentualmente sul valore totale investito, pari al numero delle rate per il valore di ogni singola rata (di solito la percentuale applicata arriva fino al 5%).
Questa tipologia di commissioni deve essere evitata. È un costo che non ha più ragione di esistere e, se presente, deve essere negoziato e, possibilmente, azzerato.
Il seguente esempio permetterà di capire il modo in cui le commissioni di transazione e di ingresso vengono applicate in un piano di accumulo.
Supponiamo di costruire un PAC di 120 rate mensili da 300 euro ciascuna sul fondo azionario XYZ, con maxi-rata iniziale di 12 rate. Verranno applicate delle commissioni di ingresso dell’1,5%, con addebito del 30% sulla prima rata.
Saranno altresì applicate commissioni di transazione di 9 euro (prima rata) e 0,95 euro (rate successive).
L’ammontare del versamento iniziale è pari a 12 rate mensili, ovvero 3.600 euro. Al momento dell’apertura del PAC saranno quindi addebitati 3.609 euro sul conto dell’investitore: 3.600 euro di versamento iniziale e 9 euro di diritti fissi.
A questo punto, vengono conteggiate le commissioni d’ingresso: il 30% graverà sul primo versamento (la maxi-rata iniziale); il 70% verrà distribuito sulle restanti 108 rate.
La prima cosa da fare per calcolare le commissioni d’ingresso è determinare l’importo complessivo del PAC. Nel nostro esempio, è pari a 36.000 euro. Si ottiene come segue: 3.600 euro (importo 1° rata: 300 euro × 12) + 108 (numero di rate rimanenti: 120 − 12) × 300 euro (rata standard) = 3.600 + 32.400 = 36.000 euro.
Su questo importo viene applicata la commissione d’ingresso dell’1,5%: moltiplicando 36.000 euro × 1,5% otteniamo 540 euro: l’importo complessivo delle commissioni d’ingresso del PAC.
Il 30% dei 540 euro di commissioni d’ingresso è pari a 162 euro. Questa somma verrà stornata dal primo versamento.
Le commissioni applicate su ciascuna delle 108 rate rimanenti saranno determinate nel modo seguente: (540 euro (commissioni d’ingresso totali) − 162 euro (30% del valore complessivo delle commissioni di ingresso)) / 108 (rate rimanenti) = 378/108 = 3,50 euro.
Al momento del versamento della maxi-rata iniziale il controvalore investito sul fondo XYZ sarà di 3.600 − 162 = 3.438 euro.
Ogni rata successiva avrà invece un costo pari a 300,95 euro (300 euro rata + 0,95 euro di diritti fissi): di questi, soltanto 296,50 euro saranno effettivamente investiti sul fondo XYZ (300 − 3,50 euro di quota parte delle commissioni d’ingresso su ciascuna rata standard).
Verifichiamo l’impatto delle commissioni sulle performance del PAC, lanciando la stessa analisi del capitolo precedente con commissioni d’ingresso dell’1,5% e solite commissioni di transazione.
Questi sono i risultati:
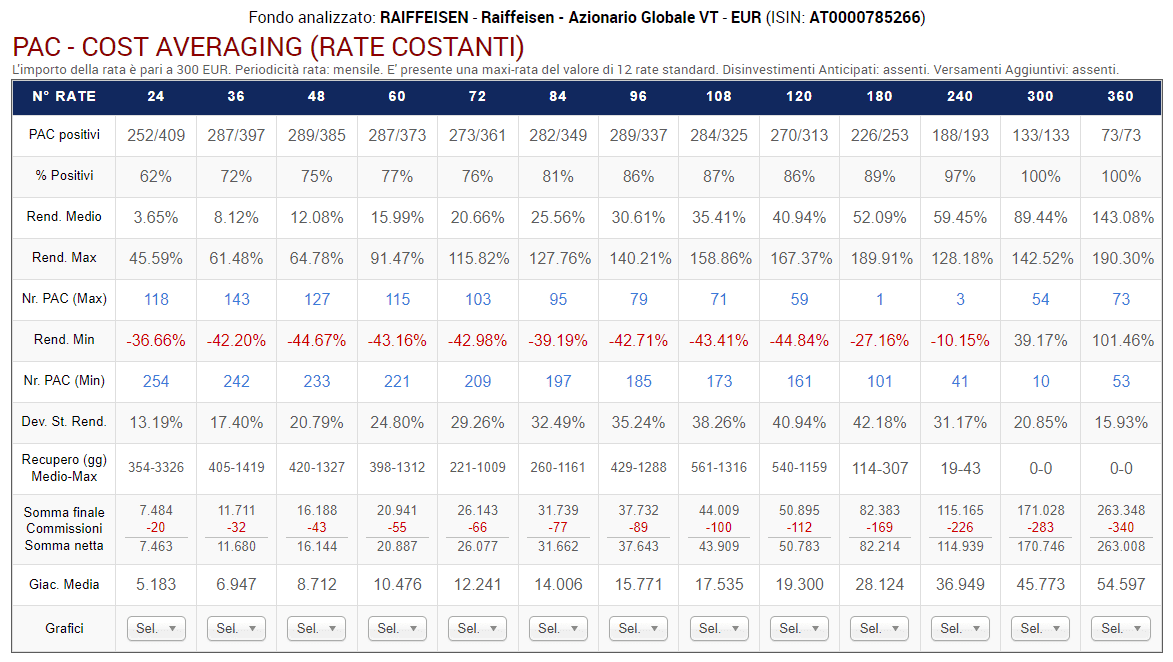
Fig. 81 – Raiffeisen: PAC Cost Averaging. Rata: 300 euro. Maxi-rata pari a 12 rate standard. Commissioni d’ingresso: 1,5% (30% prima rata)
Le performance sono ovviamente peggiorate.
L’1,5% di commissioni d’ingresso non causa una semplice diminuzione dei rendimenti medi di pari entità: il sottostante, avendo seguito un trend crescente, ha amplificato gli effetti del mancato investimento delle somme destinate alle commissioni d’ingresso.
La diminuzione dei rendimenti medi oscilla tra il −1,56% dei PAC di 24 rate (non è troppo corretto parlare di PAC biennali in questo contesto, dato che la maxi-rata ha scorciato i piani a 13 mesi) e il −4,81% di quelli di 360 rate.
Tradotto in euro, significa approssimativamente:
- Un minor rendimento di 113 euro a fronte di commissioni d’ingresso pari a 108 euro, nei piani di 24 rate.
- Un minor rendimento di 5.213 euro a fronte di commissioni d’ingresso pari a 1.620 euro, nei piani di 360 rate.
Si registra inoltre una sensibile diminuzione della “% PAC positivi”: 5% in meno nei piani di accumulo più brevi e 1% in meno in quelli di 240 rate (rimane invariata nelle durate superiori).
I rendimenti massimi e minimi subiscono la stessa sorte di quelli medi. La deviazione standard è adesso leggermente inferiore, ma è una magra consolazione di cui l’investitore avrebbe volentieri fatto a meno.
La giacenza media, infine, è diminuita.
Vediamo l’impatto delle commissioni d’ingresso sul fondo Aberdeen, il cui sottostante ha seguito un trend di decrescita di lungo termine.
La prima tabella è quella dell’analisi dei PAC con maxi-rata, ma senza commissioni d’ingresso:
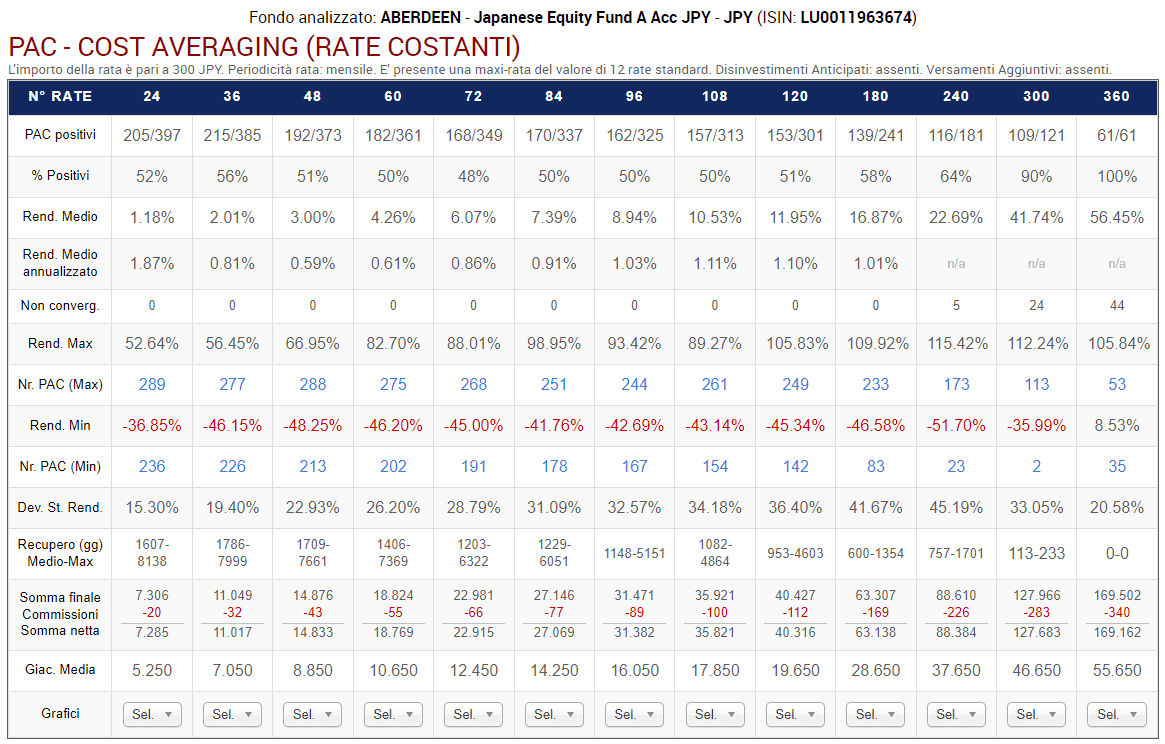
Fig. 82 – Aberdeen: PAC Cost Averaging. Rata: 300 euro. Maxi-rata pari a 12 rate standard
I rendimenti medi sono molto inferiori a quelli del Raiffeisen. In generale, tutte le misure statistiche calcolate sono peggiori.
La stessa analisi sui piani di accumulo gravati da una commissione d’ingresso dell’1,5% ha invece generato i seguenti risultati:
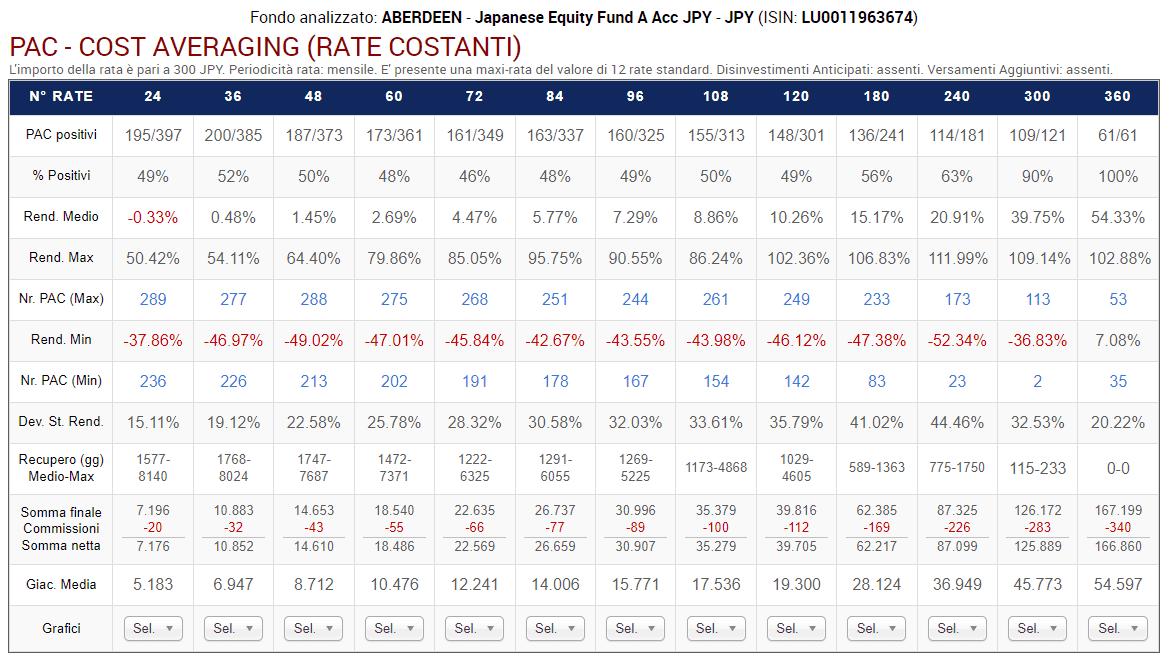
Fig. 83 – Aberdeen: PAC Cost Averaging. Rata: 300 euro. Maxi-rata pari a 12 rate standard. Commissioni d’ingresso: 1,5% (30% prima rata)
I rendimenti dei piani di accumulo di 24 rate, che in precedenza erano stati mediamente positivi (seppure di poco), sono adesso passati in territorio negativo.
In generale, le diminuzioni dei rendimenti medi oscillano tra il −1,51% (24 rate) e il −2,12%. Rispetto al fondo Raiffeisen, la perdita di rendimento dovuta al mancato investimento delle somme destinate alle commissioni d’ingresso è molto più bassa.
Anche la diminuzione della % PAC positivi è inferiore a prima: 3-4% nei piani di accumulo più brevi e l’1% in quelli di 240 rate (rimane di nuovo invariata nelle durate superiori).
I rendimenti massimi e minimi diminuiscono, così come la deviazione standard dei rendimenti e la giacenza media.
Come già accennato, al giorno d’oggi le commissioni d’ingresso nei piani di accumulo non hanno più ragione di esistere: l’avvento dei fondi a gestione passiva e l’alta concorrenza sviluppatasi tra le società d’investimento fanno dell’applicazione delle commissioni d’ingresso una pratica anacronistica.
L’unica eccezione potrebbe essere accettabile (il condizionale è d’obbligo) se il vostro consulente finanziario venisse remunerato con una parte di quelle commissioni (di solito, un consulente finanziario abilitato all’offerta fuori sede o CFAOFS).
Un CFAOFS, di solito, non fattura la sua consulenza. Eppure, lavora (anche) per il cliente. Ipotizzando un piano di accumulo inserito in un contesto più ampio di consulenza relativa alla gestione del portafoglio, il consulente dedica tempo a ogni suo cliente. Inoltre, quando un cliente va a trovarlo in ufficio, la visita può durare anche un’ora o due. Quando il cliente lo chiama sul cellulare, il consulente di solito risponde.
Il lavoro, senza voler entrare nel merito delle effettive competenze finanziarie di ciascun consulente, deve essere pagato. Il CFAOFS guadagna incassando una parte delle commissioni di gestione che gravano su un fondo a gestione attiva e, se presenti, una parte di quelle d’ingresso.
Se nessuna di queste due commissioni venisse pagata dal cliente, il consulente non guadagnerebbe niente (salvo contratti ibridi che avvicinano un CFAOFS a un Consulente Finanziario Autonomo).
Volendo collaborare con un CFAOFS, quindi, potrebbe essere necessario scegliere una di queste varianti (altrimenti il consulente non avrebbe alcun interesse a seguire il cliente):
- Costruire il piano di accumulo utilizzando strumenti finanziari a gestione attiva.
- Costruire il piano di accumulo utilizzando strumenti finanziari a gestione passiva, pagando una commissione d’ingresso (se applicabile).
- Costruire il piano di accumulo utilizzando strumenti finanziari a gestione passiva, senza pagare una commissione d’ingresso, ma retribuendo il consulente con una commissione annuale (caso ibrido accennato in precedenza). In questo caso, è auspicabile che il consulente si occupi dell’intero portafoglio finanziario del cliente, che probabilmente non sarà composto da un singolo piano di accumulo.
L’ultima opzione è applicabile anche agli investitori affiancati da un Consulente Finanziario Autonomo che, ricordiamo, è quello che opera con il minor livello di conflitto d’interessi con il cliente.
Ogni investitore dovrà fare le proprie considerazioni in merito all’opzione da utilizzare e alla tipologia di consulente a cui affidarsi.
Molti fattori entrano in gioco nel processo che conduce alla scelta più appropriata (non è questo il contesto più adatto per approfondire l’argomento).
In ogni caso, si possono trarre alcune considerazioni finali:
- Le commissioni d’ingresso (ma anche quelle di transazione, se irragionevolmente alte) hanno un impatto significativo sulla performance di un investimento.
- Investire in un fondo a gestione attiva pagando anche una commissione d’ingresso è decisamente troppo, senza eccezioni.
- Se non avete bisogno di un consulente finanziario, scegliete uno strumento finanziario a gestione passiva (a maggior ragione se il piano di accumulo è di lungo termine), senza pagare commissioni d’ingresso o di consulenza.
Le commissioni costituiscono una variabile rilevante e la loro minimizzazione è, al giorno d’oggi, una necessità per tutti gli investitori: “I costi sono certi, i rendimenti no” è una massima che negli ultimi tempi è possibile leggere in ogni sito o forum finanziario.
L’avvertenza è senz’altro corretta, ma quando si decide di investire – anche in un piano di accumulo – è di capitale importanza fare attenzione anche ad altre variabili che, se sottovalutate, rischiano di avere un impatto sul risultato finale dell’investimento molto più consistente di quello delle commissioni:
- La tipologia dello strumento finanziario scelto in funzione dell’orizzonte temporale d’investimento: i PAC vengono spesso associati al mercato azionario. È un mercato molto volatile e le sue caratteristiche si coniugano ottimamente con quelle di un piano di accumulo. L'alta volatilità comporta, però, un maggior rischio e, se l’orizzonte temporale d’investimento è di breve/medio termine, la probabilità di ottenere un rendimento negativo potrebbe essere troppo alta.
- La propensione al rischio: si legge spesso (forse troppo) che un piano di accumulo diminuisce il rischio di sbagliare il timing d’ingresso. Ne abbiamo parlato nei capitoli precedenti. Tuttavia, diminuire il rischio non vuol dire eliminarlo: il rischio di un PAC è minore di quello di un investimento in un’unica soluzione, ma è pur sempre presente. Un investitore poco propenso a rischiare potrebbe non sopportare psicologicamente i forti drawdown che caratterizzano i piani di accumulo azionari.
- Strategie di contenimento del rischio o di potenziamento del piano di accumulo: pagare un consulente che fornisce informazioni preziose e dall’alto valore aggiunto (non solo conoscitive ma anche operative, laddove possibile), comporterà dei benefici di lungo termine per l’investitore.
15. La scelta del giorno d’investimento della rata

«Before anything else, preparation is the key to success».
Alexander Graham Bell
Una delle domande che l’investitore in un piano di accumulo potrebbe porsi è quella del giorno del mese d’investimento della rata. Di solito, il giorno utilizzato è il primo, il 15 o l’ultimo del mese.
Nei backtest effettuati sulle serie storiche reali abbiamo sempre scelto come giorno di versamento delle rate il 15 del mese. Qualora fosse stato un sabato, una domenica, un giorno festivo o uno mancante dalla serie storica del fondo per qualsiasi motivo, sarebbe stato sostituito dal primo giorno disponibile successivo a quello mancante.
Il 15 del mese non ha niente di speciale: poteva essere scelto un qualsiasi altro giorno. Quando un investitore utilizza un piano di accumulo automatico, la scelta del giorno potrebbe non essere disponibile, in quanto predefinita dalla banca o dalla società di investimento.
La scelta del giorno d’investimento in un piano di accumulo non è una variabile che può avere un impatto eccessivo sulle performance medie: potrebbe averne, però, su singoli PAC.
Vediamo quale sarebbe stata l’entità delle differenze tra i piani di accumulo iniziati il giorno 1 e quelli iniziati il 15 del mese. Lanceremo due serie di backtest sul fondo Raiffeisen, già molte volte utilizzato nei capitoli precedenti.
I risultati seguenti sono relativi ai backtest con versamento delle rate il giorno 15 del mese (periodicità mensile, senza commissioni d’ingresso, senza maxi-rata):
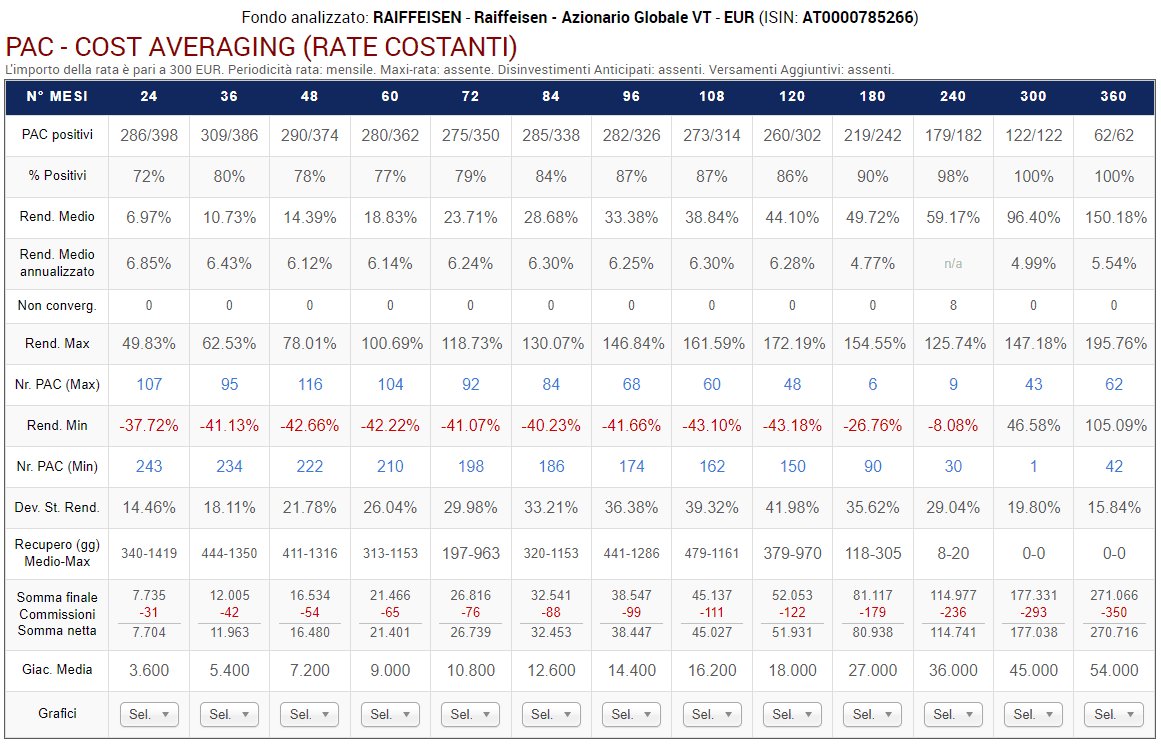
Fig. 84 – Raiffeisen: PAC Cost Averaging. Rata: 300 euro. Investimento: giorno 15 del mese
Sono gli stessi risultati della fig. 11.
Quelli che seguono, invece, sono relativi ai piani di accumulo iniziati il giorno 1 del mese:
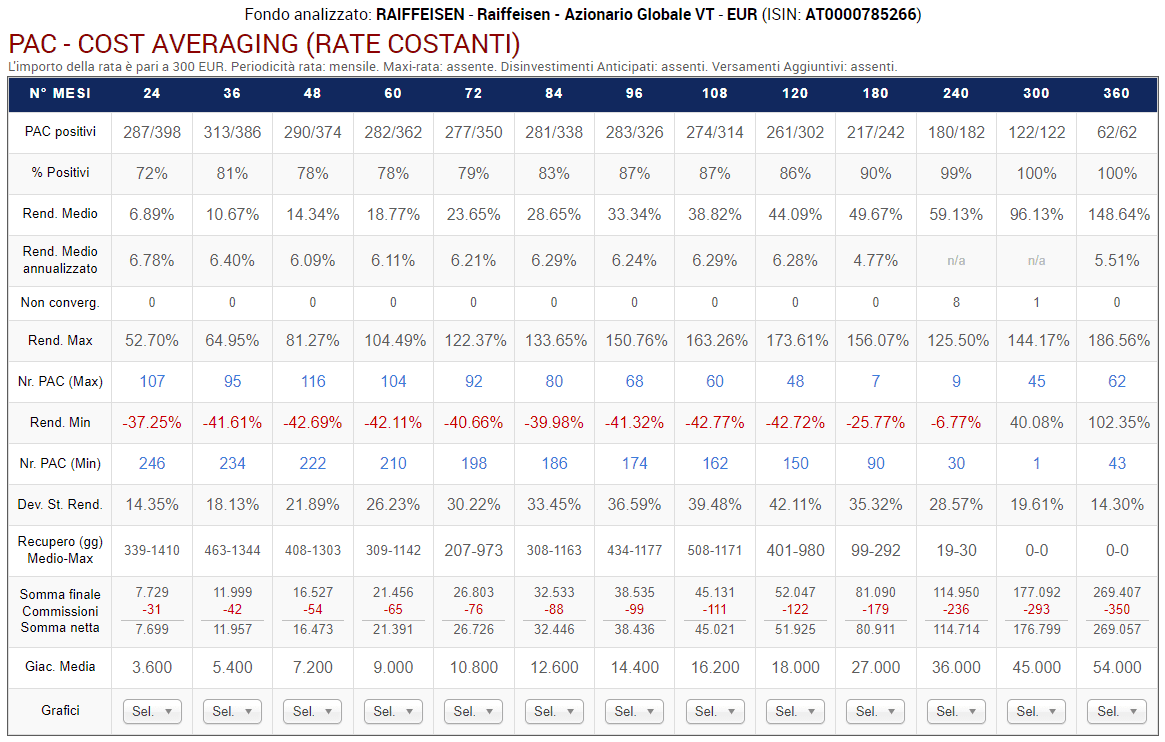
Fig. 85 – Raiffeisen: PAC Cost Averaging. Rata: 300 euro. Investimento: giorno 1 del mese
I rendimenti medi, medi annualizzati e le percentuali di PAC positivi sono molto simili. I rendimenti massimi presentano alcuni punti percentuali di differenza, mentre quelli minimi sono quasi uguali fino alla durata dei 20 anni, per poi distanziarsi nei PAC di più lunga durata.
La deviazione standard dei rendimenti è molto simile in ogni durata.
Non riportiamo le tabelle con i risultati dei backtest sul fondo Aberdeen: possiamo estendere anche a quest’ultimo le considerazioni precedenti.
Le differenze sono dovute al caso. L’unico consiglio utile – laddove sia possibile una scelta – è forse quello di investire il prima possibile, dal momento che:
- Esiste un'aspettativa di crescita di lungo termine dei mercati azionari (e la storia, almeno fino ad oggi, lo dimostra).
- Minimizzando il tempo che intercorre tra la ricezione di un reddito periodico e l’impiego di una parte di esso nel piano di accumulo, si riduce la possibilità di consumare anche la parte inizialmente destinata all’investimento.
- È impossibile prevedere il giorno del mese che favorirà la performance migliore.
L’investimento in un piano di accumulo è l’espressione di una filosofia di pensiero opposta al market timing: l’obiettivo di un piano di accumulo è costruire un capitale nel tempo grazie all’accumulazione delle quote acquistate, sfruttando la crescita del mercato sottostante nel lungo termine.
16. Letteratura sul Cost Averaging

«Literature is analysis after the event».
Doris Lessing
Sui Piani di Accumulo del Capitale Cost Averaging hanno scritto un po’ tutti i principali esperti di economia e di finanza. Nessun autore, però, gli ha mai dedicato un intero libro: al limite qualche capitolo in trattazioni più estese.
Il mondo accademico, invece, li ha analizzati più in profondità, senza tuttavia giungere a un giudizio unanime.
La maggior parte degli articoli scientifici ha espresso pareri negativi sui piani di accumulo Cost Averaging. La critica più diffusa è senz’altro quella dell’inefficienza o della sub-ottimalità, in quanto è stato dimostrato che un investimento in un’unica soluzione (detto anche PIC o, in inglese, Lump-sum investment o LSI) genera, mediamente, un rendimento più elevato di quello dei piani di accumulo (nel capitolo 10 ci siamo occupati delle differenze tra un PIC e un PAC a rate costanti).
Le conclusioni, analizzando essenzialmente i rendimenti e facendo backtest soprattutto sui mercati azionari dell’ultimo secolo (specialmente quelli americani), non potevano essere molto diverse.
Per fortuna, ci sono anche autori che la pensano diversamente.
In questo capitolo, faremo un rapido excursus delle critiche e dei pareri positivi che sono stati indirizzati negli ultimi decenni al Cost Averaging (di solito identificato come Dollar Cost Averaging). Esamineremo alcuni dei principali articoli pubblicati in riviste scientifiche o su siti Internet autorevoli, a partire dal 1979.
I Piani di Accumulo del Capitale, comunque, sono una metodologia di investimento conosciuta e utilizzata già prima della fine degli anni ‘70 del secolo scorso: alcuni degli autori che ne hanno fatto uso e hanno iniziato a renderli popolari sono, tra gli altri, Lucile Tomlinson e Benjamin Graham.
Risale al 1979 uno dei primi contributi critici sul Dollar Cost Averaging, il cui autore è George Constantinides: A note on the suboptimality of Dollar-Cost Averaging as an investment policy. L’articolo inizia con una citazione al best seller di Burton Malkiel, A random walk down Wall Street: Malkiel sostiene che investire periodicamente una cifra costante in azioni può ridurre sostanzialmente (ma non evitare) il rischio di acquistare a un prezzo eccessivo, in quanto si compreranno meno azioni quando i prezzi sono alti e più azioni quando i prezzi sono bassi.
Constantinides non è d’accordo con Malkiel e la sua critica del Dollar Cost Averaging può riassumersi nel modo seguente: dovendo investire una somma fissa con una periodicità costante (seguendo quindi una rigida strategia completamente definita all’inizio dell’investimento, ovvero a nonsequential policy), ci si ritrova nella condizione di non poter sfruttare informazioni che saranno disponibili in futuro; informazioni che permetterebbero di agire in modo più efficiente (il Dollar Cost Averaging sarebbe ad esempio sempre inferiore a un portafoglio che viene ribilanciato regolarmente con le ultime informazioni disponibili: operatività che viene definita da Constantinides come sequential policy).
Constantinides ritiene che il Dollar Cost Averaging sia dominato da una metodologia ottimale di investimento sequenziale (il ribilanciamento periodico di un portafoglio), ma anche da una metodologia ottimale non sequenziale, come ad esempio quella ottenuta da un’ottimizzazione di varie strategie con un’ipotetica funzione di utilità dell’investitore: il Dollar Cost Averaging potrebbe essere la strategia ottimale solo per caso; in realtà, non lo sarà quasi mai.
Constantinides constata infine come, alla luce delle sue conclusioni, sia addirittura ironico che i sostenitori del Dollar Cost Averaging pongano grossa enfasi sulla necessità di seguire in modo rigoroso una strategia non sequenziale, ignorando le eventuali nuove informazioni disponibili nel tempo.
Nel 1993, Knight e Mandell pubblicano l’articolo Nobody Gains from Dollar Cost Averaging – Analytical, Numerical and Empirical Results. Già dal titolo, si capisce come il risultato dell’analisi non ammetta repliche: il Dollar Cost Averaging è una strategia inferiore sia al Buy and Hold senza ribilanciamento che a quello periodicamente ribilanciato (portafogli composti al 50% da asset rischiosi e al 50% da asset non o poco rischiosi).
Il rischio crescente penalizzerebbe il Dollar Cost Averaging: l’investitore si assumerebbe un rischio progressivo con il passare del tempo, mentre con le due strategie alternative proposte il rischio rimarrebbe costante.
Nel 1994, Rozeff afferma che un investimento lump-sum, non soltanto produce un rendimento più alto del Dollar Cost Averaging, ma riesce a farlo con una varianza minore. Il Dollar Cost Averaging, infatti, ha il difetto di lasciare la maggior parte del guadagno in balia dei rendimenti del sottostante nell’ultima parte di vita del piano di accumulo, quando il capitale dell’investitore è quasi totalmente investito.
Nel 2003, tocca a Leggio e Lien criticare duramente il Dollar Cost Averaging. Nel loro articolo intitolato An Empirical Examination of the Effectiveness of Dollar-Cost Averaging Using Downside Risk Performance Measures, gli autori criticano la stessa appartenenza del Dollar Cost Averaging alle strategie di investimento, in quanto subottimale rispetto a un investimento in un’unica soluzione (Lump Sum).
Nel confronto, sarebbero state usate misure di rendimento aggiustate per il rischio (indice di Sharpe, indice di Sortino e Upside Potential Ratio) e il Dollar Cost Averaging risulterebbe inappropriato sia per investimenti in sottostanti volatili o molto volatili come le azioni Large o Small Cap, sia per sottostanti poco volatili come le obbligazioni governative o corporate. Infine, sarebbe inadatto anche per portafogli misti.
In un articolo del 2003, intitolato A Continuous-time Reexamination of Dollar-Cost Averaging, Milevsky e Posner giustificano la popolarità di questa strategia da un punto di vista comportamentale e dimostrano, attraverso diverse pagine di formule matematiche molto complesse, come il Dollar Cost Averaging possa essere assimilato a un’opzione asiatica e riesca a produrre risultati migliori con sottostanti molto volatili.
I due autori affermano che gli investitori sono probabilmente più sofisticati di quello che siamo disposti ad ammettere. In ogni caso, concludono che la strategia Buy and Hold domina quella Dollar Cost Averaging per ogni livello di volatilità.
In tempi più recenti, troviamo la critica di Hayley, sviluppata nell’articolo Dollar Cost Averaging – The Role of Cognitive Error, pubblicato nel 2010. Secondo Hayley, i sostenitori del Dollar Cost Averaging – e in particolare dell’opinione che questa metodologia di investimento ridurrebbe il costo medio delle quote acquistate – si sono creati un’idea di superiorità del Dollar Cost Averaging illusoria, in quanto basata su un confronto distorto con una strategia alternativa (l’acquisto di un numero fisso di quote), impossibile da realizzare se si ipotizza una perfetta parità di somme investite.
In altre parole, i fautori del Dollar Cost Averaging commettono un errore cognitivo specifico e dimostrabile, che è il motivo principale per cui questa metodologia di investimento continua a riscuotere un grande successo nonostante le innumerevoli dimostrazioni sulla sua inefficienza.
Per finire, l’ultima critica che menzioniamo è quella di Kowara e Kaplan, pubblicata in un articolo dell’ottobre 2019 intitolato Dollar-Cost Averaging – Truth and Fiction. L’articolo inizia ricordando come i difensori del Dollar Cost Averaging sostengano 3 vantaggi di questa metodologia:
- La possibilità di comprare più azioni/quote quando i prezzi sono bassi (e viceversa).
- Il minor rischio.
- L’imposizione di una disciplina.
Gli autori affermano subito che il loro articolo non si occupa del terzo punto, in quanto appartenente a un aspetto comportamentale degli investitori. Fatta questa premessa, impongono la netta distinzione tra chi investe in concomitanza del pagamento dello stipendio e gli investitori in un piano Dollar Cost Averaging veri e propri: i primi, secondo gli autori, non starebbero attuando il Dollar Cost Averaging.
L’analisi si indirizza quindi verso un confronto tra investimento lump-sum e Dollar Cost Averaging, effettuato con la suddivisione dei rendimenti del mercato US large-cap tra gennaio 1926 e agosto 2019 in sottoperiodi della lunghezza compresa tra 2 e 120 mesi.
Le conclusioni sono le seguenti:
- In un mercato crescente, come quello US large-cap degli ultimi 100 anni, il Dollar Cost Averaging sovraperforma l’investimento in un’unica soluzione con percentuali molto esigue: meno del 40% nei piani più corti (addirittura di 2 soli mesi) e meno del 10% in quelli più lunghi (120 mesi). La misura scelta per il confronto è il final wealth, corrispondente alla “Somma finale” dei nostri backtest.
- L’investimento in un’unica soluzione è meno rischioso di un corrispondente Piano di Accumulo del Capitale. Per dimostrare questo assunto, la rischiosità del Dollar Cost Averaging viene misurata con l’IRR (Internal Rate of Return, che in italiano si traduce con Tasso Interno di Rendimento o TIR), mentre quella dell’investimento lump-sum viene misurata con il TWR (Time-weighted return), un caso particolare dell’IRR. Le misurazioni vengono effettuate su 120 rendimenti mensili storici estratti casualmente dal campione di cui al punto precedente per 10.000 volte: su ogni campione estratto viene calcolato il rendimento totale con entrambe le metodologie. Le frequenze vengono plottate e i rendimenti calcolati con il metodo IRR mostrano una maggiore variabilità (la deviazione standard dei rendimenti calcolati col TWR è del 6,10% e quella dei rendimenti calcolati con l’IRR è del 6,84%). Il motivo, secondo gli autori, è il seguente: l’IRR riflette due tipi di variabilità: quella del mercato (a cui è sottoposto anche il TWR), e quella dell’ordinamento dei rendimenti, che influenza soltanto l’IRR.
Le conclusioni di Kowara e Kaplan sono perentorie: un investimento in un’unica soluzione non soltanto ha un rendimento atteso maggiore di un piano di accumulo, ma ha anche un rischio inferiore.
Ma c’è di più. Gli autori rincarano la dose affermando che il problema fondamentale del Dollar Cost Averaging è che si tratti di una strategia di market-timing: tenere dei soldi liquidi per investirli in un momento successivo equivale a fare market-timing, perché significa credere che i prezzi del sottostante subiranno un trend discendente per un certo periodo e poi risaliranno. Ora, a meno che gli investitori giungano a questa decisione sulla base di forecast specifici (cosa improbabile), il Dollar Cost Averaging dovrebbe essere evitato.
Scegliere di investire costruendo un Piano di Accumulo del Capitale, laddove sia presente fin dall’inizio la liquidità per poter scegliere un investimento in un’unica soluzione, equivale a fare market-timing. Non sarebbe quindi vero l’esatto contrario, che viene invece pacificamente riconosciuto tra gli investitori e anche in larga parte della comunità scientifica.
La critica accademica è stata molto dura nei confronti dei Piani di Accumulo del Capitale. Non tutti gli articoli sul Dollar Cost Averaging, però, sono ostili verso questa metodologia di investimento.
Meir Statman ha pubblicato A Behavioral Framework for Dollar-Cost Averaging nel 1995. Tra gli articoli analizzati, è quello che condividiamo maggiormente.
Statman non mette in dubbio che il Dollar Cost Averaging sia una strategia subottimale rispetto a un investimento lump-sum ma si chiede anche perché, nonostante la finanza standard continui a ribadire la sua inefficienza, il Dollar Cost Averaging sia una strategia che viene sempre più utilizzata.
Statman inserisce nell’analisi, forse per la prima volta, la componente psicologica: questa strategia va analizzata sotto i riflettori della finanza comportamentale, non di quella classica.
Secondo Statman, ci sono quattro elementi di finanza comportamentale che contraddistinguono il Dollar Cost Averaging: la teoria del prospetto, sviluppata da Kahneman e Tversky, la teoria del regret aversion (che potremmo tradurre come “avversione al rimpianto”), gli errori cognitivi e il self-control (autocontrollo).
Tutti hanno la loro importanza e tutti vengono regolarmente ignorati dalla finanza standard, che continua a chiedersi come sia possibile che il Dollar Cost Averaging continui a essere una metodologia largamente utilizzata, nonostante che sulla base delle proprie teorie (e in particolare dell’assioma di razionalità), non dovrebbe nemmeno esistere.
Il sottotitolo dell’articolo di Statman è “Dollar-cost averaging may not be rational behavior, but it is perfectly normal behavior”. L'accettazione di questa semplice affermazione sembra essere troppo per i sostenitori della finanza standard. Le ultime due frasi dell’articolo sono invece le seguenti: “…Meanwhile, I offer an hypothesis. The practice of dollar-cost averaging will persist”. A distanza di oltre 25 anni, l’ipotesi avanzata da Statman è molto lontana dall’essere smentita.
Brennan, Li e Torous affermano che il Dollar Cost Averaging sia un’euristica quasi completamente ignorata dagli accademici sin da quando la teoria della random walk dei mercati finanziari è stata sviluppata. Il Dollar Cost Averaging è una strategia subottimale, ma che sembra essere utile, nella realtà, agli investitori nei mercati finanziari.
Liu, Chen, Liu giungono invece alla conclusione che il Dollar Cost Averaging sia più efficiente nel lungo termine, in un contesto di ottimalità media-varianza, del lump-sum.
In altre parole, più è lungo l’orizzonte temporale d’investimento, maggiore è la riduzione del rischio e la somma finale generata dal Dollar Cost Averaging rispetto al lump-sum. Di conseguenza, il Dollar Cost Averaging sarebbe più adatto del lump-sum agli investimenti di lungo termine. Gli autori sono consapevoli che questa conclusione sia in disaccordo con numerosi studi precedenti.
Nel 2015, Cho e Kuvvet pubblicano l’articolo Dollar-Cost Averaging: The Trade-Off Between Risk and Return. Le conclusioni sono favorevoli al Dollar Cost Averaging e lo studio che portano avanti fornisce una giustificazione teorica della popolarità di questa strategia sulla base di un’analisi di tipo media-varianza: viene dimostrato un trade-off tra rischio e rendimento. L’investimento in un’unica soluzione ha un rendimento atteso più elevato; il Dollar Cost Averaging ha un rischio minore.
Per questo motivo, i consulenti finanziari dovrebbero suggerire l’una o l’altra strategia in base all’avversione al rischio dei loro clienti (optando ovviamente per il Dollar Cost Averaging con i clienti dalla propensione al rischio più bassa).
L’ultimo articolo del nostro excursus è quello di Smith e Artigue, del 2018: Another Look at Dollar Cost Averaging. Smith e Artigue sostengono che il Dollar Cost Averaging non sia una strategia sciocca come qualche volta viene dipinta. Alcuni dei suoi ben noti vantaggi sono quelli di favorire il risparmio (grazie alla meccanicità degli investimenti periodici) e di ridurre lo stress psicologico associato alle decisioni di investimento. Un vantaggio meno noto sarebbe invece quello della diversificazione temporale, attraente soprattutto su orizzonti temporali d’investimento lunghi e con sottostanti volatili.
Gli autori concludono come il Dollar Cost Averaging non sia sempre una strategia ottimale ma, in alcuni casi, costituisca una sua ragionevole approssimazione.
17. Conclusioni

«Life is the art of drawing sufficient conclusions from insufficient premises».
Samuel Butler
Il Piano di Accumulo del Capitale Cost Averaging è una modalità di investimento molto utilizzata. È facilmente comprensibile e può essere agevolmente automatizzata.
Un piano di accumulo è anche una modalità di risparmio, perché la cifra periodicamente accantonata viene sottratta al consumo. La scelta di costruire un piano di accumulo ha il notevole pregio di imporre una disciplina nel rapporto con i propri soldi.
Un piano di accumulo può essere anche trasformato in uno strumento previdenziale: esistono senz’altro degli strumenti finanziari più adatti a questo scopo, ma è indubbio che un piano di accumulo con un orizzonte temporale pianificato in concomitanza col termine della vita lavorativa possa generare un reddito aggiuntivo, capace di integrare almeno parzialmente la pensione.
La costruzione di un capitale nel tempo è una delle principali funzioni di un piano di accumulo. Molti degli autori che si sono occupati di questa metodologia di investimento (non fanno eccezione alcuni di quelli del capitolo precedente) sono stati però molto attenti a puntualizzare che, quando si parla di Dollar Cost Averaging, si fa riferimento a una metodologia di investimento in cui il capitale è interamente disponibile fin dall’inizio. Il capitale sarà impiegato a intervalli periodici nei mesi o negli anni futuri, ma è già liquido e pronto a essere investito nella sua totalità al tempo zero.
Questa forzatura è dovuta alla necessità di confrontare il Dollar Cost Averaging con altre metodologie di investimento: non lo si potrebbe caratterizzare come inefficiente o subottimale se non esiste un’alternativa da definire, di conseguenza, più efficiente o ottimale. Il confronto tipico, come abbiamo visto, è stato quello con l’investimento in un’unica soluzione (lump sum).
Un piano di accumulo, però, è una strategia appropriata per costruire un capitale nel tempo: la sua funzione, ancor prima di generare un rendimento positivo, è quella di creare un capitale attraverso il risparmio.
In realtà, la maggior parte degli investitori che utilizzano un piano di accumulo non ha la disponibilità dell’intera somma al tempo zero: ha soltanto quella necessaria al versamento di ogni rata (ovvero quando serve). L’importo richiesto sarà in molti casi generato dal reddito da lavoro dell’investitore.
Spesso, un piano di accumulo sarà l’unico modo a disposizione di un investitore per costruirsi il suo capitale. La maggior parte delle volte, il confronto stesso con un investimento in un’unica soluzione perde di significato.
Stranamente, molti accademici non tengono minimamente conto di questa eventualità, o tendono a liquidarla affermando che non è ciò a cui si riferiscono quando parlano di Dollar Cost Averaging.
Anche volendo seguire il modo in cui gli accademici interpretano il Dollar Cost Averaging, non si capisce perché, nei loro backtest, la liquidità disponibile fin da subito non venga impiegata in qualche investimento risk free mentre attende di essere investita.
Proiettiamoci idealmente nel lontano 1979, al tempo in cui Constantinides scriveva la sua critica al Dollar Cost Averaging. Durante tutti gli anni ‘70 l’inflazione media negli Stati Uniti è oscillata tra il 3,27% e l’11,22% (proprio nel 1979). Negli anni ‘80, tra l’1,91% e il 13,58%. Il tasso di rendimento risk free non era minimamente paragonabile a quello attuale: tra il 1970 e il 1990 il risk free rate degli Stati Uniti (3-Month Treasury Bill Rate, analoghi ai BOT trimestrali italiani) non è mai sceso sotto al 3%, arrivando a superare il 15%, come il seguente grafico dimostra:
Fig. 86 – Grafico storico dell’1-year Treasury Rate (gennaio 1962 – aprile 2020)
Constantinides, e molti altri autori insieme a lui, impongono il possesso di tutto il capitale fin dall’inizio dell’investimento, in modo che il confronto tra il Dollar Cost Averaging e un investimento in un’unica soluzione abbia un senso. Nello stesso tempo, non si capisce perché il capitale inutilizzato (talvolta per molti anni) non sia stato contabilizzato al tasso di rendimento risk free, che in quegli anni era molto più alto di quello odierno.
Gli investitori un po’ in là con gli anni ricorderanno come, anche in Italia, non fossero rari i rendimenti dei BOT a due cifre. Gli stessi conti correnti bancari garantivano interessi attivi inimmaginabili al giorno d’oggi.
Non vogliamo mettere in discussione i maggiori rendimenti generati da un investimento in un’unica soluzione rispetto a un piano d’accumulo. Questo risultato è stato verificato anche nelle nostre analisi, sia grazie ai backtest storici che alle simulazioni Monte Carlo parametriche e non parametriche.
Il confronto, però, non è così immediato e necessita delle due forzature appena discusse, che non andrebbero ignorate.
Un’altra critica importante, sostenuta da molti accademici, è quella della rischiosità. Un piano di accumulo sembrerebbe essere meno rischioso di un investimento lump sum, ma in realtà non lo sarebbe: il grosso del capitale risulta investito nella parte finale della vita del piano, quando la volatilità dell’investimento è massima. Quest’ultima affermazione è senz’altro vera: ciò che non è chiaro è il motivo per cui questa più alta volatilità nella parte finale di vita del piano di accumulo sarebbe superiore alla volatilità di un investimento lump sum.
Ipotizziamo che il capitale totale investito in un piano di accumulo sia 100.000 euro. Il piano è costituito da 100 rate mensili di mille euro ciascuna. Ci troviamo al 99° mese: il capitale investito è di 99.000 euro e il suo valore corrente dipenderà dal prezzo del sottostante e dall’andamento del prezzo stesso in tutti i 99 mesi precedenti.
L’investimento lump sum avrebbe visto l’impiego integrale di 100.000 euro fin dall’inizio. Anche dopo 99 mesi, il capitale investito continua a essere pari a 100.000 euro e il suo valore corrente dipenderà, stavolta, dal prezzo corrente del sottostante e soltanto da quello di 99 mesi prima: il prezzo pagato al momento dell’acquisto.
La giacenza media di un investimento lump sum è doppia di quella di un piano di accumulo: come fa a essere meno rischioso di un piano di accumulo?
È una conclusione assurda.
Anche ammesso che così fosse da un punto di vista strettamente matematico (e non sembra affatto esserlo), vogliamo davvero ignorare l’aspetto psicologico e paragonare la rischiosità di un investimento di 100.000 euro (somma investita da un PIC fin dall’inizio) con quella di 1.000 euro? (importo di ogni rata di un PAC, nel nostro precedente esempio).
Se nell’ultima parte della vita di un PAC la rischiosità aumenta, come sostenuto da alcuni autori, perché invece viene ignorata la maggior rischiosità iniziale dei PIC?
Se la logica non basta, possiamo ricorrere ai backtest effettuati, dove i risultati confermano la minor rischiosità dei piani di accumulo rispetto agli investimenti in un’unica soluzione:
- La deviazione standard dei rendimenti finali dei PIC è quasi sempre superiore a quella dei PAC, sia nei backtest di serie storiche reali, sia nelle simulazioni Monte Carlo parametriche e non parametriche.
- La volatilità interna dei rendimenti dei PIC è quasi sempre superiore a quella dei PAC, sia nei backtest di serie storiche reali, sia nelle simulazioni Monte Carlo parametriche e non parametriche.
- I rendimenti minimi sono stati, nella maggior parte dei casi, a sfavore dei PIC.
- Nel capitolo 9, dove abbiamo trattato il PAC peggiore (serie storiche reali), i rendimenti minimi sono stati a sfavore dei PIC nella maggior parte dei casi.
- I periodi medi e massimi di recupero sono quasi sempre stati a sfavore dei PIC.
In base a tutti i backtest effettuati nel nostro studio, e ancor prima in base alla logica e all’esperienza degli investitori, non possiamo che giungere alla conclusione che i PIC siano più rischiosi dei PAC.
L’articolo di Kowara e Kaplan merita un commento a parte. Gli autori si prefiggono di smontare 3 dei principali vantaggi del Cost Averaging: la possibilità di comprare più azioni/quote quando i prezzi sono bassi (e viceversa), il minor rischio e l’imposizione di una disciplina.
Partiamo dall’ultimo: secondo Kowara e Kaplan l’imposizione di una disciplina è un aspetto comportamentale e per questo motivo non viene minimamente trattato.
Perché ignorarlo?
La finanza comportamentale è ormai parte integrante della scienza economica: non a caso, diversi autori che se ne sono occupati a fondo, negli ultimi decenni hanno vinto il premio Nobel per l’Economia.
La finanza comportamentale (o psicologia della finanza) è ormai parte integrante dell’economia e della finanza stessa. Molti autori continuano tuttavia a criticarla o, nel migliore dei casi, a ignorarla, esattamente come i due autori di questo articolo.
Molti sostenitori della finanza classica si domandano come certi comportamenti irrazionali possano anche solo esistere (per alcuni, l’investimento in un piano di accumulo è irrazionale). Probabilmente non trovano le riposte alle loro domande perché si rifiutano di cercarle là dove potrebbero essere ottenute: nella finanza comportamentale.
Kowara e Kaplan si concentrano quindi sui primi 2 vantaggi. I loro backtest, come quelli di molti altri autori, confermano che gli investimenti lump sum generano rendimenti mediamente più elevati del Dollar Cost Averaging (in un mercato tendenzialmente crescente non può essere diversamente).
Più sorprendenti sono le seguenti conclusioni:
- I piani di accumulo sono più rischiosi di un investimento in un’unica soluzione. In base ai 10.000 backtest effettuati dagli autori (simulazioni Monte Carlo non parametriche), i rendimenti degli investimenti lump sum variano meno di quelli dei piani di accumulo.
- Il Dollar Cost Averaging è una metodologia di investimento market timing: il market timing è il problema fondamentale dei piani di accumulo.
Nell’articolo non vengono mostrati i calcoli effettuati, ma sembrano conclusioni molto strane. Molti critici del Dollar Cost Averaging non si sono spinti fino al punto di mettere in dubbio la minor rischiosità dei piani di accumulo.
Il dubbio sulla validità di questi risultati, da parte nostra, rimane. Nelle analisi che abbiamo condotto nei capitoli precedenti, gli esiti dei backtest su serie storiche reali e su milioni di serie storiche simulate col metodo Monte Carlo sono stati diametralmente opposti.
Al di là dei backtest e dei freddi numeri, chi ha effettuato almeno una volta un investimento azionario in un’unica soluzione e in un Piano di Accumulo del Capitale non avrà la minima esitazione nel definire più rischioso il primo (a parità di somma totale investita): lo stress psicologico associato al mettere in gioco tutto il capitale fin dall’inizio è inevitabilmente superiore.
Una volta effettuato l’investimento, in un PIC tutta la somma è fin da subito in balia del mercato. Se arriva una crisi finanziaria, colpisce tutto il capitale. Prima arriva e peggio è, perché non c’è nemmeno il tempo di farlo crescere un po’.
In un piano di accumulo vale la conclusione opposta: prima la crisi arriva e meglio è, dato che fin da subito si possono comprare più quote a parità di somma investita (le rate sono costanti). Inoltre, all’inizio dell’investimento, quando solo poche rate sono state versate, il capitale investito è piccolo e, per quanto non faccia piacere vedere il rendimento del piano di accumulo col segno meno davanti, il controvalore della perdita è ancora minore.
Ironicamente, un investitore che avesse seguito il consiglio di Kowara e Kaplan, ovvero impiegare il proprio capitale in un’unica soluzione piuttosto che in un piano di accumulo, si sarebbe trovato a fronteggiare la recente crisi del COVID-19 con l’intero capitale in gioco, passando dei brutti momenti (l’articolo di Kowara e Kaplan è stato pubblicato a ottobre 2019); chi avesse iniziato a costruire il capitale con un piano di accumulo, si sarebbe trovato a fronteggiarla con 3 o 4 rate versate e con la consapevolezza di acquistare, durante la crisi, a prezzi scontati.
Non c’è dubbio su quale dei due investitori avrebbe attraversato momenti emotivamente più difficili.
Quando la crisi arriva verso la fine dell’investimento, una volta che quasi tutto il capitale è stato investito anche in un piano di accumulo, le cose cambiano. Lo stress psicologico aumenta molto anche per chi ha costruito un PAC, ma crescerà altrettanto, se non di più, per coloro che hanno investito una somma lump sum, dal momento che il controvalore prima dell’arrivo della crisi sarebbe presumibilmente superiore a quello del piano di accumulo.
Una delle prime regole da rispettare quando si investe dovrebbe essere quella di scegliere una modalità di investimento che trasmetta calma e tranquillità, con lo scopo di minimizzare la probabilità di interromperlo o sospenderlo prematuramente, magari in preda al panico generato da una crisi finanziaria inaspettata.
Se il rendimento atteso dell’investimento è inferiore a quello di altre tipologie di investimento più stressanti, poco importa. La pace mentale è molto più importante, almeno per la stragrande maggioranza degli investitori non professionali.
Il mondo accademico, ancora troppo succube della finanza classica e in particolare dell’assioma di razionalità, non è forse ancora pronto a fare i conti la finanza comportamentale, anche se le cose stanno lentamente cambiando.
Se la finanza classica teorizza l’inesistenza dei Piani di Accumulo del Capitale e questi, in realtà, costituiscono una delle modalità di investimento più utilizzate in assoluto, non si dovrebbero incolpare gli investitori di irrazionalità: forse il problema è negli assiomi della teoria che ci si ostina a seguire.
Sulla falsariga del sottotitolo dell’articolo di Meir Statman, sembra evidente che per gli esseri umani sia assolutamente normale comportarsi in modi che la finanza classica definisce irrazionali.
Dopo 25 anni, l’ipotesi avanzata dallo stesso Statman (“The practice of dollar-cost averaging will persist”) non soltanto è attualissima, ma è probabilmente destinata a rimanere tale per molti altri anni ancora.
18. Bibliografia

«Una stanza senza libri è come un corpo senz’anima».
Marco Tullio Cicerone
Brennan M., Li F., Torous W., Dollar Cost Averaging, Review of Finance, Vol. 9, Issue 4, 2005, pp. 509-535.
Cho D., Kuvvet E., Dollar-Cost Averaging: The Trade-Off Between Risk and Return, Journal of Financial Planning, 28 (10), 2005, pp. 52-58.
Constantinides G., A note on the suboptimality of Dollar-Cost Averaging as an investment policy, Journal of financial and quantitative analysis, Vol. XIV, No. 2, June 1979, pp. 443-450.
Graham B., The Intelligent Investor, Harper & Brothers, 1949.
Hayley, S., Dollar Cost Averaging - The Role of Cognitive Error (January 14, 2012). Available at SSRN: https://ssrn.com/abstract=1473046 or http://dx.doi.org/10.2139/ssrn.1473046.
Kahneman D., Tversky A., Prospect Theory: An Analysis of Decision under Risk, Econometrica, Vol. 47, No. 2, Mar. 1979, pp. 263-291.
Knight J., Mandell L., Nobody Gains from Dollar Cost Averaging – Analytical, Numerical and Empirical Results, Financial Services Review, 2(1), 1993, pp. 51-61.
Kowara M., Kaplan P., Dollar-Cost Averaging – Truth and Fiction, Morningstar Manager Research, 17 October 2019.
Leggio K., Lien D., An Empirical Examination of the Effectiveness of Dollar-Cost Averaging Using Downside Risk Performance Measures, Journal of Economics and Finance, Volume 27, Number 2, Summer 2003, pp. 211-223.
Liu Y., Chen H., Liu W., A Comparison of Dollar-Cost Averaging with Lump-Sum Investing for Mutual Funds, Journal of Management & Systems, Vol. 15, No. 4, October 2008, pp. 563-590.
Malkiel B., A random walk down Wall Street – The time-tested strategy for successful investing, Norton & Company (1975).
Milevsky M., Posner S., A Continuous-time Reexamination of Dollar-Cost Averaging, International Journal of Theoretical and Applied Finance, Vol. 6, No. 2, 2003, pp. 173-194.
Rozeff M., Lump-Sum Investing versus Dollar-Averaging, The Journal of Portfolio Management, Winter 1994, pp. 45-50.
Smith G., Artigue H., Another Look at Dollar Cost Averaging, The Journal of Investing, Summer 2018, 27 (2), pp. 66-75.
Statman M., A Behavioral Framework for Dollar-Cost Averaging, The Journal of Portfolio Management, Fall 1995, pp. 70-78.
Tomlinson L., Successful Investing Formulas, Barron’s Publishing Company, 1947.
Il Percorso per principianti continua con l'articolo:


