Value Averaging: investire senza temere una crisi finanziaria
- Information
- PAC
- Prima pubblicazione: 27 Febbraio 2020
«In everything one thing is impossible: rationality».
Friedrich Nietzsche
L'ebook dell'articolo in formato PDF può essere scaricato dagli utenti BASIC (registrazione gratuita): una volta effettuato il log in, basterà selezionare l'opzione "Download" dal menu utente in alto a destra.
Questo articolo fa parte del Percorso intermedio, pensato per chi possiede già le basi e vuole approfondire strategie di investimento e concetti teorici per una comprensione più approfondita della finanza. In fondo alla pagina, troverai il link al prossimo articolo del percorso.
Il Value Averaging (VA) è una strategia di investimento sviluppatasi verso la fine degli anni ’80 del secolo scorso ed è, ancora oggi, al centro di opinioni contrastanti.
Sono stati scritti pochissimi libri sul Value Averaging e, al di là delle solite descrizioni sommarie, in rete non si trovano molte informazioni, neppure in lingua inglese. Molte implicazioni di questa strategia di investimento sono quasi sconosciute.
Questo articolo, suddiviso in 15 capitoli, ha i seguenti obiettivi:
- Approfondirne lo studio con una metodologia di analisi nuova, supportata da numerosi grafici, backtest su serie storiche reali e simulazioni col metodo Monte Carlo.
- Analizzare e valutare le critiche mosse al Value Averaging in passato.
- Confrontarlo con il Cost Averaging (rate costanti).
- Proporre una nuova modalità di utilizzo anche a chi sia già in possesso di un capitale iniziale, alternativo all’investimento in un’unica soluzione.
Si consiglia la lettura dei capitoli nell'ordine proposto. Dall’indice è comunque possibile accedere direttamente a ciascuno di essi.
Il backtest del Value Averaging su singoli fondi è disponibile nella sezione Analisi PAC di Dedalo Invest.
Indice
- Introduzione
- Limiti e critiche al Value Averaging
- Tipologie di Value Averaging
- Vantaggi del Value Averaging
- Value Averaging vs Cost Averaging: simulazioni grafiche di varie tipologie di un PAC
- Value Averaging vs Cost Averaging: simulazione di migliaia di PAC su un unico fondo
- Simulazioni su un fondo dal trend discendente
- Value Averaging vs Cost Averaging: simulazioni non parametriche col metodo Monte Carlo
- Value Averaging vs Cost Averaging: simulazioni parametriche col metodo Monte Carlo
- Quando le cose vanno male: il PAC peggiore (serie storiche reali)
- Value Averaging con l’utilizzo di extra-liquidità: perché no?
- Risposte alle critiche al Value Averaging
- PIC Value Averaging
- Conclusioni
- Bibliografia
1. Introduzione

«There is no subject so old that something new cannot be said about it».
Fëdor Dostoevskij
Il Value Averaging (VA) è una strategia di investimento che viene sempre associata ad un Piano di Accumulo del Capitale (PAC).
Il Value Averaging è molto diverso dal Cost Averaging (o Dollar Cost Averaging): in un piano di accumulo Cost Averaging le rate sono costanti; in uno Value Averaging i versamenti sono variabili e hanno l’obiettivo di riallineare il valore dello strumento finanziario a quello del target prefissato.
Un esempio aiuterà a capire meglio la differenza tra queste due modalità di PAC. Supponiamo che il PAC sia mensile:
- Un Piano di Accumulo Cost Averaging prevede l’acquisto di un numero di quote del sottostante corrispondenti alla rata stabilita (ad esempio, 100 euro). L’importo del versamento è costante, ma il numero di quote sottoscritte varia a ogni acquisto, dato che si modifica in funzione del loro prezzo corrente.
- In un Piano di Accumulo Value Averaging, invece, è il valore corrente delle quote accumulate che, ogni mese, si dovrà incrementare di una quota fissa (ad esempio, 100 euro). Il primo mese non ci saranno differenze con un PAC Cost Averaging, dato che l’importo versato sarà in entrambi i casi pari a 100 euro. A partire dal secondo mese, però, i valori inizieranno a essere diversi.
Immaginiamo di costruire due piani di accumulo mensili, uno Cost Averaging e uno Value Averaging, su uno stesso fondo azionario. Il giorno del primo versamento, il prezzo di una quota del fondo è pari a 10 euro. Acquisteremo perciò 10 quote per ciascun PAC. Ipotizziamo che il mese successivo, nel giorno del secondo versamento, il prezzo della quota del fondo sia salito a 12 euro:
- Nel PAC Cost Averaging, lo scopo è quello di accumulare mensilmente un numero di quote pari a un controvalore di 100 euro: acquisteremo perciò 100/12 = 8,3333 quote del fondo. Dopo il secondo versamento avremo in portafoglio 18,3333 quote, il cui controvalore sarà di 18,3333 x 12 = 220 euro.
- Nel PAC Value Averaging, lo scopo è invece quello di incrementare di 100 euro il valore corrente del fondo, portandolo quindi a 200 euro. Dato che abbiamo già in portafoglio 10 quote, che adesso valgono 10 x 12 = 120 euro, il versamento richiesto sarà questa volta di soli 80 euro e ci permetterà di acquistare 80/12 = 6,6667 quote. Dopo il secondo versamento avremo in portafoglio 16,6667 quote dal valore di 16,6667 x 12 = 200 euro. Se il prezzo della quota fosse sceso a 8 euro, il secondo versamento sarebbe stato pari a 120 euro, dato che le 10 quote già in portafoglio avrebbero avuto un valore di 80 euro.
Mentre nei PAC Cost Averaging le rate sono costanti, nel Value Averaging l’importo di ogni rata varia in funzione dell’andamento del prezzo dello strumento finanziario accumulato.
Come vedremo, una rata potrà non essere versata o addirittura avere un valore negativo: in quest’ultimo caso, dovremo vendere una parte delle quote.
Dobbiamo il Value Averaging al lavoro di Michael E. Edleson, che nel 1993 ha pubblicato la prima edizione di “Value Averaging - The Safe and Easy Strategy for Higher Investment Returns”, il libro che ha introdotto questa metodologia di Piano di Accumulo del Capitale al grande pubblico.
Il Value Averaging ha in un certo senso rivoluzionato l’idea di PAC. Come spesso accade alle idee innovative, i benefici sono stati in parte controbilanciati da alcune complicazioni che questa metodologia comporta e da alcune critiche che le sono state indirizzate, anche in tempi recenti.
Nonostante questo, il Value Averaging rimane una soluzione d’investimento molto utile e questo articolo ha lo scopo di approfondirlo, rivalutarlo e ampliarne l’interesse, fino a renderlo un possibile anello di congiunzione tra un PAC e un investimento in un’unica soluzione (PIC, Piano di Investimento di Capitale).
Come lo stesso Edleson fa notare, col Value Averaging ci si avvicina quanto più possibile alla realizzazione del sogno di ogni investitore: comprare a prezzi bassi e vendere a prezzi alti.
Per la prima volta, però, non si prova a raggiungere questo obiettivo con tecniche di previsione o di stima dei prezzi futuri, ma con un metodo di calcolo della quantità di quote da acquistare o da vendere che si plasma all’andamento dei prezzi: l’investitore sa esattamente cosa fare sia quando i prezzi salgono che quando scendono.
Il libro di Edleson è stato ristampato nel 2006, in un’edizione ampliata nella quale sono state aggiunte molte osservazioni sull’applicazione del Value Averaging nei 15 anni successivi alla prima pubblicazione: i risultati ne confermano la bontà e l’utilità.
Un’ulteriore riprova della validità del Value Averaging è arrivata da Paul S. Marshall che, nell’articolo pubblicato nel 2000 nel Journal of Financial and Strategic Decisions, giunge alle stesse conclusioni di Edleson e ne elogia l’importante lavoro.
Marshall suggerisce di sfruttare gli strumenti finanziari a maggiore volatilità, in un arco di tempo il più lungo possibile, in modo che il Value Averaging abbia l’opportunità di sviluppare al meglio la sua “magia”:
As might be expected from a technique that does outperform, the higher the price variability and the longer the investment time horizon the better. Each gives value averaging the time and the opportunity to work its “magic”.
Paul S. Marshall, A Statistical Comparison of Value Averaging vs. Dollar Cost Averaging and Random Investment Techniques,
Journal of Financial and Strategic Decisions, Vol. 13, No. 1, Spring 2000, p. 98
Il vantaggio del Value Averaging, dunque, sarebbe quello di realizzare una performance migliore di quella del Cost Averaging: in particolare, si riuscirebbe a ottenere, in media, un rendimento complessivo e annualizzato maggiore, senza aumentarne il rischio.
Una soluzione vincente e apparentemente senza controindicazioni.
Vedremo nei capitoli successivi quanto di ciò che Edleson e Marshall sostengono sia corretto, quali siano i limiti di applicazione e come superarli.
Dopo aver approfondito lo studio del Value Averaging da un punto di vista teorico, analizzeremo in dettaglio uno specifico piano di accumulo costruito su dati reali e scopriremo, con l’aiuto di molti grafici, le differenze tra le varie tipologie di Value Averaging.
Successivamente, utilizzeremo i backtest di numerosi piani di accumulo per misurare le performance del Value Averaging su serie storiche reali.
Il passo seguente sarà quello di estendere l’analisi alle simulazioni parametriche e non parametriche con il metodo Monte Carlo.
Il risultato della nostra ricerca sarà quello di sistematizzare l’utilizzo del Value Averaging in varie strategie di investimento:
- PAC Value Averaging senza un fondo di liquidità iniziale.
- PAC Value Averaging con un fondo di liquidità iniziale di lungo termine (10 o più anni) o di breve/medio termine (da 2 a 10 anni).
- PIC Value Averaging, inteso come investimento di un capitale in più versamenti, da completarsi entro 2 anni.
2. Limiti e critiche al Value Averaging

«Critico portando idee nuove, non dando colpe.».
Marco Tullio Cicerone
Perché questa metodologia è per lo più sconosciuta agli investitori, nonostante i suoi tanti vantaggi?
Verrebbe da pensare che ci siano alcuni validi motivi che ne ostacolano la diffusione, e che forse sono stati sottovalutati o ignorati dai suoi divulgatori.
Procediamo a elencare le critiche, gli ipotetici svantaggi e le principali difficoltà della sua applicazione.
Vedremo quindi se queste argomentazioni siano sufficienti o meno a giustificare la poca diffusione del Value Averaging.
1) Mancanza di piattaforme di investimento automatizzato
Le piattaforme d’investimento, al giorno d’oggi quasi universalmente attrezzate per l’esecuzione automatica di Piani di Accumulo a rate costanti, non prevedono simili agevolazioni per il Value Averaging. Chi vuole investire utilizzando il Value Averaging dovrà fare i calcoli ed eseguire le transazioni finanziarie in prima persona (o con l’aiuto del suo consulente finanziario).
Questo implica che, ogni mese o trimestre, l’investitore stesso debba verificare il prezzo di mercato delle quote, calcolarne il valore corrente, quantificare il valore del versamento (che potrebbe anche essere zero o negativo) ed eseguire l’operazione di acquisto o di vendita utilizzando la sua piattaforma di investimento.
I calcoli sono semplici: un foglio Excel è più che sufficiente a determinare e tracciare tutto ciò che serve; non è questo il vero problema. La difficoltà consiste nella disciplina richiesta per fare questa serie di operazioni con rigorosità e puntualità: due qualità molto rare.
Bisogna poi considerare che acquistare e vendere quote di uno o più strumenti finanziari al di fuori di un piano automatico predisposto dalla propria banca potrebbe comportare dei costi maggiori (i piani automatici di investimento Cost Averaging prevedono delle commissioni fisse generalmente inferiori a quelle standard).
2) Importo dei versamenti
Nei piani di accumulo Value Averaging, soprattutto se di lunga durata, può essere richiesto il versamento di somme anche decine di volte superiori alla rata iniziale. La liquidità dovrà essere disponibile al momento opportuno, che non è possibile conoscere a priori.
Questa complicazione può essere mitigata dalla vendita (che genera liquidità) o dal mancato acquisto di quote: le somme incassate o non versate potranno essere accantonate per far fronte a eventuali maxi-rate future.
Per evitare l’esborso di grosse somme di denaro è inoltre possibile stabilire un massimale all’importo dei versamenti.
È indubbio che la presenza di versamenti rilevanti sia uno dei limiti principali del Value Averaging rispetto al classico Cost Averaging, di più facile comprensione e gestione.
3) Importo medio delle rate (giacenza media e liquidità residua)
In un Piano di Accumulo del Capitale Value Averaging l’ammontare complessivamente investito è generalmente inferiore a quello di un piano Cost Averaging di simili caratteristiche. In altri termini, la giacenza media è inferiore.
In un PAC Value Averaging, infatti, capita spesso di ritrovarsi con somme liquide, momentaneamente non investite, generate dalle vendite o dell’accantonamento di quote non versate. Nel Cost Averaging questo fenomeno non avviene mai, dato che ogni mese l’intera somma a disposizione viene investita.
Si tratta di un limite importante perché, ad esempio, a parità di rischio è preferibile ottenere un rendimento del 10% su 1000 euro (100 euro) piuttosto che uno del 12% su 800 euro (96 euro).
Come vedremo, si crea anche una distorsione nel calcolo del rendimento dei PAC: nell’esempio precedente, se ci si limita a valutare il rendimento percentuale, senza prendere in considerazione la somma generata in euro e l’eventuale liquidità residua, si potrebbe giungere all’errata conclusione che la seconda opzione sia migliore della prima (12% di rendimento).
Un modo per superare questo limite sarà quello di incrementare il target in modo crescente, così da diminuire o annullare la liquidità inutilizzata.
4) Volatilità del sottostante
Come sottolineato dagli stessi Edleson e Marshall, il Value Averaging performa meglio con sottostanti molto volatili. È anche noto, però, che un’eccessiva varianza può essere pericolosa, dato che aumenta soprattutto in periodi di crisi finanziarie, durante i quali i prezzi scendono bruscamente.
Se è vero che un’alta volatilità migliora la performance del Value Averaging, si deve fare attenzione a non sviluppare il Value Averaging (ma anche il Cost Averaging) su:
- Strumenti finanziari che replicano mercati troppo volatili: potrebbero avere difficoltà a riprendersi dopo una grave crisi finanziaria.
- Azioni di singole società: si rischia di accumulare valore su una società che potrebbe fallire, causando la perdita dell’intero capitale investito.
5) Distorsioni nella modalità di calcolo del rendimento annualizzato
In un articolo del 2010, Simon Hayley ha avanzato una solida critica alla modalità di misurazione della performance del Value Averaging e, in particolar modo, al tasso interno di rendimento (IRR ovvero Internal rate of return, quello che spesso in finanza viene denominato rendimento annualizzato).
Essenzialmente Hayley sostiene come il Value Averaging sia una strategia di investimento inefficiente e, nello specifico, che il rendimento annualizzato di un piano di accumulo Value Averaging sia quasi sempre superiore a quello di un simile piano Cost Averaging in quanto il procedimento di calcolo è distorto: non considera la quantità di denaro che deve essere messa da parte, fin dall’inizio di un PAC, per far fronte ai maxi-versamenti che saranno richiesti in concomitanza di grosse crisi finanziarie. Se queste somme venissero conteggiate, il valore del rendimento annualizzato sarebbe più basso e meno attraente per l’investitore.
Analizzeremo le molte implicazioni di questa insidiosa critica. In particolar modo, proveremo a trasformarla in un punto di forza del Value Averaging, che da strategia di investimento limitata ad un Piano di Accumulo del Capitale si amplierà fino a diventare una possibile variante dell’investimento in un’unica soluzione.
3. Tipologie di Value Averaging

«Don't be seduced into thinking that that which does not make a profit is without value».
Arthur Miller
Esistono molti tipi di Value Averaging.
La versione pura prevede la vendita di quote quando l’importo della rata è negativo (cioè quando il valore delle quote presenti in portafoglio è superiore al target del versamento successivo), mentre la versione semplificata implica di non comprare e non vendere niente (No-Sell Value Averaging).
Seguendo la terminologia di Edleson, chiameremo d’ora in avanti "No-Sell" quest’ultima modalità di Value Averaging.
Perché esistono due tipi di Value Averaging?
Per diversi motivi:
- Evitare il pagamento di imposte sul capital gain (le vendite avvengono quando i prezzi sono alti, generando perciò capital gain, imponibile fiscalmente).
- Evitare il pagamento di commissioni di negoziazione (le stesse che si pagano quando si acquista).
- Semplificare la gestione.
- Migliorare la performance.
Ciascuna di queste due versioni del Value Averaging prevede inoltre la possibilità di incrementare il target in modo crescente.
L’incremento, soprattutto nei piani di accumulo di lungo termine, ha lo scopo di aumentare la giacenza media e migliorare la performance dell'investimento.
Si dovrà fare attenzione a non impostare percentuali di crescita eccessive, insostenibili nel lungo termine: un 1% non pone alcun problema in un PAC mensile di breve durata ma, in un piano di accumulo lungo, può implicare target irragionevoli.
Per calcolare l’impatto preciso di questi incrementi bisogna usare la formula della capitalizzazione composta, dove al posto del tasso di interesse o di rendimento poniamo la nostra percentuale di incremento:
Incremento al tempo t360 = (1 + 0,01)360 = 35,95
Il valore del target del trecentosessantesimo mese sarà di circa 36 volte quello iniziale! Una enormità, considerando che partendo da soli 100 euro si raggiungeranno i 3.600 euro. D’altra parte, un 1% mensile è molto di più del tasso di inflazione a cui ci siamo abituati negli ultimi anni.
Le cose cambiano drasticamente ipotizzando un incremento dello 0,25%:
Incremento al tempo t360 = (1 + 0,0025)360 = 2,46
Il target al 360° mese sarà adesso di circa 2 volte e mezzo quello iniziale, un valore molto più plausibile.
L’1% di incremento non è però da scartare a priori: in un PAC Value Averaging quinquennale, ad esempio, può essere sostenuto senza grandi problemi.
La formula precedente diventa:
Incremento al tempo t60 = (1 + 0,01)60 = 1,82
Partendo dai soliti 100 euro, dopo 5 anni saremmo intorno a 182, meno del doppio quindi. Un valore accettabile.
Si può concludere ribadendo l'importanza di impostare un incremento periodico del target che sia coerente con il numero delle rate che si verseranno: l’1% potrà andar bene anche in un PAC Value Averaging trentennale se la frequenza delle rate, ad esempio, sarà semestrale invece che mensile (si avrebbero in questo caso 60 semestri in un trentennio: l’incremento del target, al termine dei 30 anni, arriverebbe a essere 1,82 volte quello iniziale, esattamente come nel caso di un PAC Value Averaging mensile quinquennale).
Vedremo infine come un 1% o più sarà utilizzabile anche in piani di accumulo Value Averaging particolari, sviluppati e gestiti con l’ausilio di un fondo di liquidità iniziale.
4. Vantaggi del Value Averaging

«No advantages in this world are pure and unmixed».
David Hume
Secondo Edleson, il grande vantaggio del Value Averaging è il rendimento complessivo generalmente più alto di quello di un Cost Averaging associato a un minor prezzo medio di acquisto di ogni quota.
Come vedremo, questa affermazione non è vera in senso assoluto, dal momento che dipende dall’andamento della serie storica del rendimento dello strumento finanziario sottostante: ciò che abbiamo riscontrato, invece, è come la deviazione standard dei rendimenti del Value Averaging sia quasi sempre minore di quella del Cost Averaging (ceteris paribus).
Il rischio, quindi, è inferiore.
Un altro importante beneficio del Value Averaging è di tipo psicologico: gli investitori temono le crisi finanziarie e sono sempre alla ricerca di stratagemmi per evitarle. La risposta più spesso utilizzata è il market timing: provare a prevedere i movimenti futuri dei mercati per poterli anticipare.
Purtroppo, si tratta di una strategia molto complicata e piena di insidie: quasi sempre, chi decide di intraprendere questa strada finisce per fare peggio del Buy and Hold.
Il Value Averaging è una strategia molto diversa dal market timing, dato che gli acquisti e le vendite:
- Non sono l’espressione di previsioni dell’andamento del mercato e non hanno lo scopo di anticipare i movimenti dei prezzi.
- Vengono effettuati a posteriori, in risposta agli effettivi andamenti dei prezzi del sottostante.
Comprare quando i prezzi sono bassi e vendere (o non acquistare) quando i prezzi sono alti offre una certa tranquillità mentale e limita lo stress generato da una potenziale crisi finanziaria.
Sono vantaggi sufficienti a preferire un Value Averaging in ogni circostanza?
Per rispondere correttamente alla domanda dovranno considerarsi alcuni fattori, per lo più soggettivi:
- Esperienza finanziaria dell’investitore e capacità di gestire un Piano di Accumulo del Capitale Value Averaging in prima persona.
Un investitore inesperto o che si appresta a investire per la prima volta è meglio che opti per un PAC a rate costanti: è automatizzabile e non richiede un’attenzione continua. Anche chi non ha molta familiarità con Excel o software simili è meglio che non si complichi la vita con il Value Averaging.
Come già accennato, il Value Averaging non richiede calcoli complicati; possono essere tracciati anche con un semplice quaderno e l’aiuto della sola calcolatrice: è indiscutibile, però, che il vantaggio offerto da un foglio elettronico sia considerevole. - Livello di comprensione del Value Averaging.
Se non si è ben capito il funzionamento del Value Averaging e le differenze che lo distinguono dal Cost Averaging, è meglio limitarsi a quest’ultimo. In finanza, una delle regole più importanti è quella di capire lo strumento finanziario che si utilizza: in questo caso, è bene che si capisca anche la strategia di investimento utilizzata, onde evitare spiacevoli sorprese (maxi-versamenti inaspettati, lunghi periodi di inattività, necessità di extra-liquidità ecc.). - Propensione al rischio dell’investitore.
Il Value Averaging funziona meglio su strumenti finanziari volatili, che possono quindi subire ingenti diminuzioni di valore al verificarsi delle crisi finanziarie. Il PAC è una modalità di investimento che riduce – ma non elimina – il rischio di subire perdite: neppure il Value Averaging può fare miracoli in questo senso.
Su prodotti meno volatili, come i fondi obbligazionari, le differenze con un Cost Averaging sono minime e non ha senso complicarsi la vita se il mercato sottostante oscilla poco. - Orizzonte temporale d’investimento.
Nei piani di accumulo brevi, le differenze di performance tra PAC Cost Averaging e Value Averaging sono mediamente piccole.
Chi è particolarmente prudente o volenteroso, tuttavia, non sbaglia a scegliere il Value Averaging dato che, come vedremo, nei casi più sfortunati riesce a ottenere perdite inferiori al Cost Averaging. - Disciplina.
Gestire un piano di accumulo Value Averaging richiede una costante disciplina: è bene essere consapevoli in anticipo delle sue difficoltà per evitare di finire con l’interromperlo o trasformarlo in un Cost Averaging dopo pochi versamenti. Nei primi anni di vita, inoltre, è probabile che non si vedano grosse differenze con un Cost Averaging e il rischio di credere che si stia facendo un lavoro inutile è alto.
Per questo motivo, se non si è sicuri di avere il tempo e la voglia per occuparsene, è meglio optare fin dall’inizio per il Cost Averaging.
Il supporto di un consulente finanziario permette di superare alcuni di questi limiti, ma non è garanzia di successo: non è detto che un consulente sia disposto a fornire con puntualità le informazioni richieste.
La propensione al rischio e l’orizzonte temporale d’investimento sono variabili soggettive e il consulente non ha modo e nemmeno dovrebbe provare a influenzarle: per certi investitori, il Value Averaging potrebbe semplicemente non essere la soluzione giusta.
5. Value Averaging vs Cost Averaging: simulazioni grafiche di varie tipologie di un PAC

«What is consciousness? Our brain simulates reality. So, our everyday experiences are a form of dreaming, which is to say, they are mental models, simulations, not the things they appear to be».
Stephen LaBerge
Prima di procedere con l’analisi generalizzata del Value Averaging, è importante capire che cosa lo contraddistingua dal Cost Averaging e quali siano le differenze tra il Value Averaging No-Sell e quello puro. Ci serviremo del supporto di numerosi grafici, che verranno utilizzati in modo sistematico.
Partiamo con la simulazione di un Piano di Accumulo del Capitale Cost Averaging e di varie tipologie di Value Averaging su una serie storica reale, appartenente a un fondo azionario a gestione attiva: Raiffeisen Azionario Globale VT (ISIN: AT0000785266). Il fondo appartiene alla categoria Azionari Internazionali Large Cap Blend.
Il grafico dei NAV del Raiffeisen Azionario Globale VT dal 15 novembre 1986 al 15 novembre 2016 è il seguente:
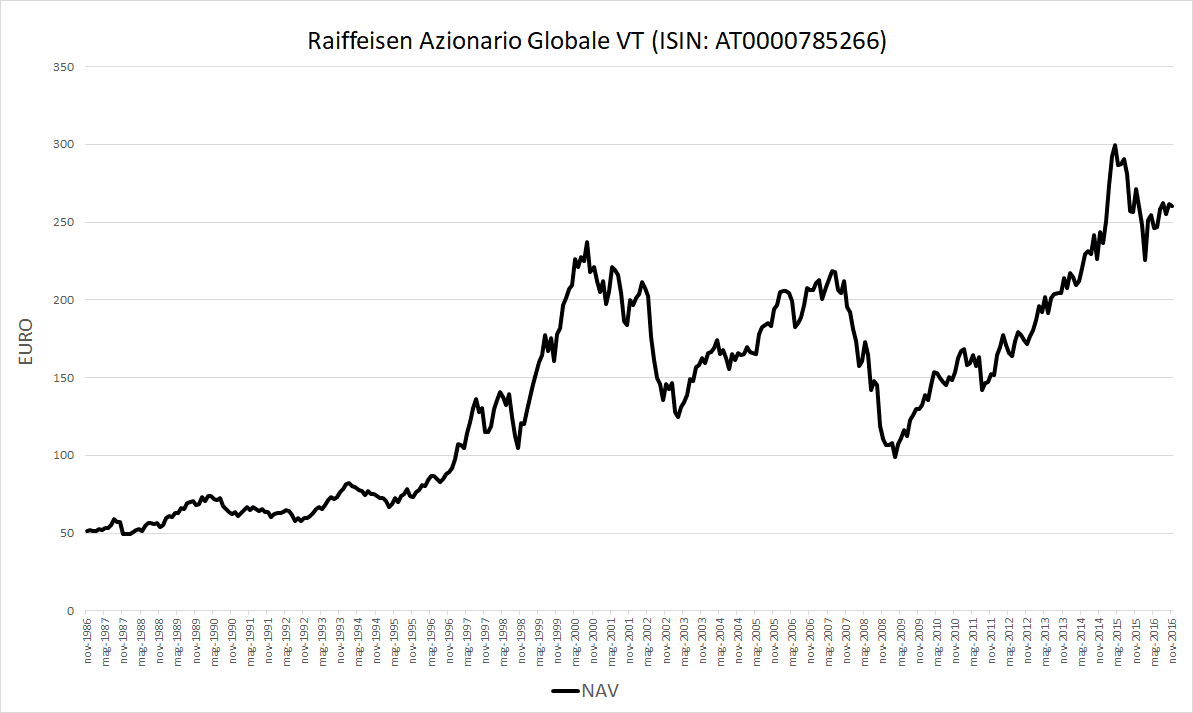
Fig. 1 – Grafico del NAV (Raiffeisen Azionario Globale VT)
Balzano agli occhi le due più importanti crisi dell’ultimo ventennio: la dotcom, esplosa negli anni 2000-2003 e la crisi dei subprime, iniziata verso la fine del 2007 e durata fino ai primi mesi del 2009.
Altri periodi di forte volatilità si sono verificati intorno al 1998 e al 2014-2015. Il decennio compreso tra il 1986 e il 1996 sembrerebbe un periodo abbastanza piatto, con poche oscillazioni.
I grafici di lungo periodo, tuttavia, tendono a schiacciare i trend di crescita e di decrescita nelle fasi iniziali, in corrispondenza dei prezzi più bassi.
Per ovviare a questo problema si può utilizzare un grafico logaritmico:
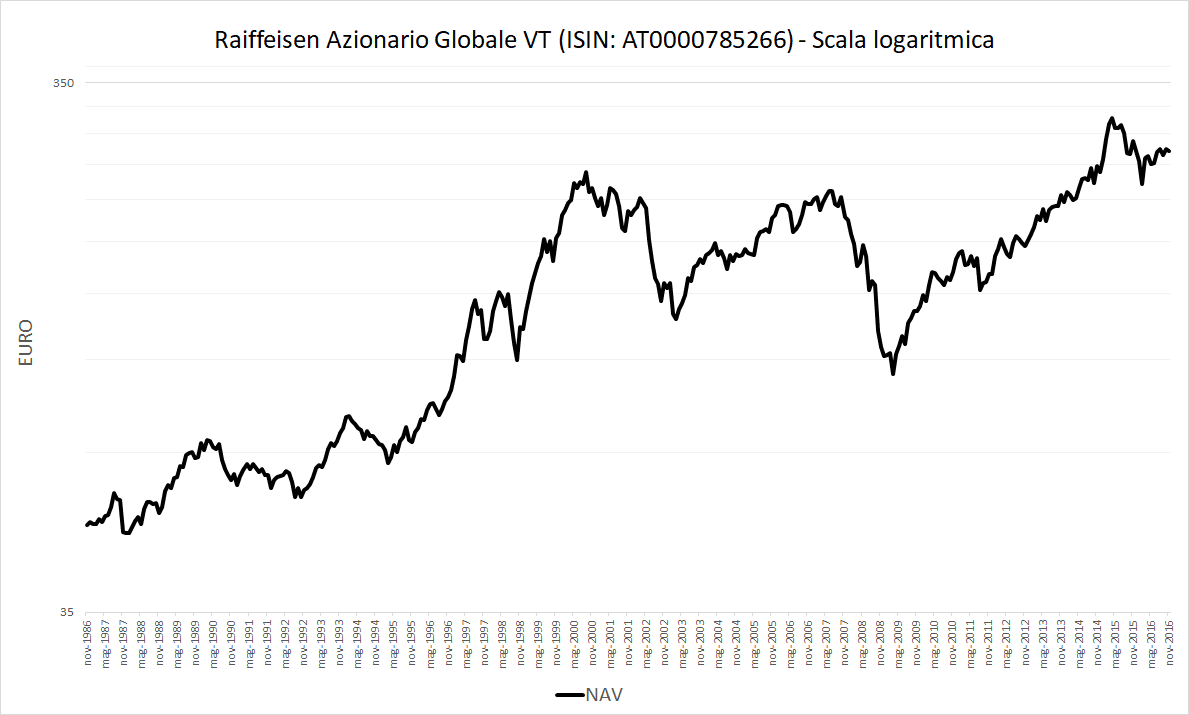
Fig. 2 – Grafico con scala logaritmica del NAV (Raiffeisen Azionario Globale VT)
In realtà, il decennio 1986-1996 non è stato un periodo troppo tranquillo e non ha vissuto lunghe fasi di bassa volatilità.
A cosa può essere utile l’analisi grafica delle varie modalità di PAC Value Averaging?
L’analisi grafica facilita la comprensione delle variabili più importanti di un PAC Value Averaging (target, valore corrente, pagamenti effettuati e così via) e permette di visualizzare l’impatto generato dalle modifiche di alcuni parametri (possibilità o meno di vendite di quote, incrementi del target costanti o crescenti e presenza di un limite massimo ai versamenti).
È un modo per conoscerlo più a fondo: quasi sempre, infatti, il Value Averaging viene presentato in modo teorico e quantitativo, senza essere accompagnato da una simulazione grafica basata su dati reali.
Per rendere possibile questa visualizzazione, abbiamo scelto uno specifico piano di accumulo sul fondo Raiffeisen Azionario Globale VT: il primo disponibile tra i numerosi PAC a 30 anni che sarebbe stato possibile simulare.
Una serie storica di questa lunghezza permette infatti la realizzazione di centinaia di simulazioni rolling di piani di accumulo di diverse durate (nei nostri backtest saranno comprese tra 2 e 30 anni). I risultati di queste simulazioni saranno presentati in seguito.
Il grafico seguente rappresenta l’andamento di un PAC a rate costanti (Cost Averaging) sul fondo Raiffeisen Azionario Globale VT nel periodo in esame:
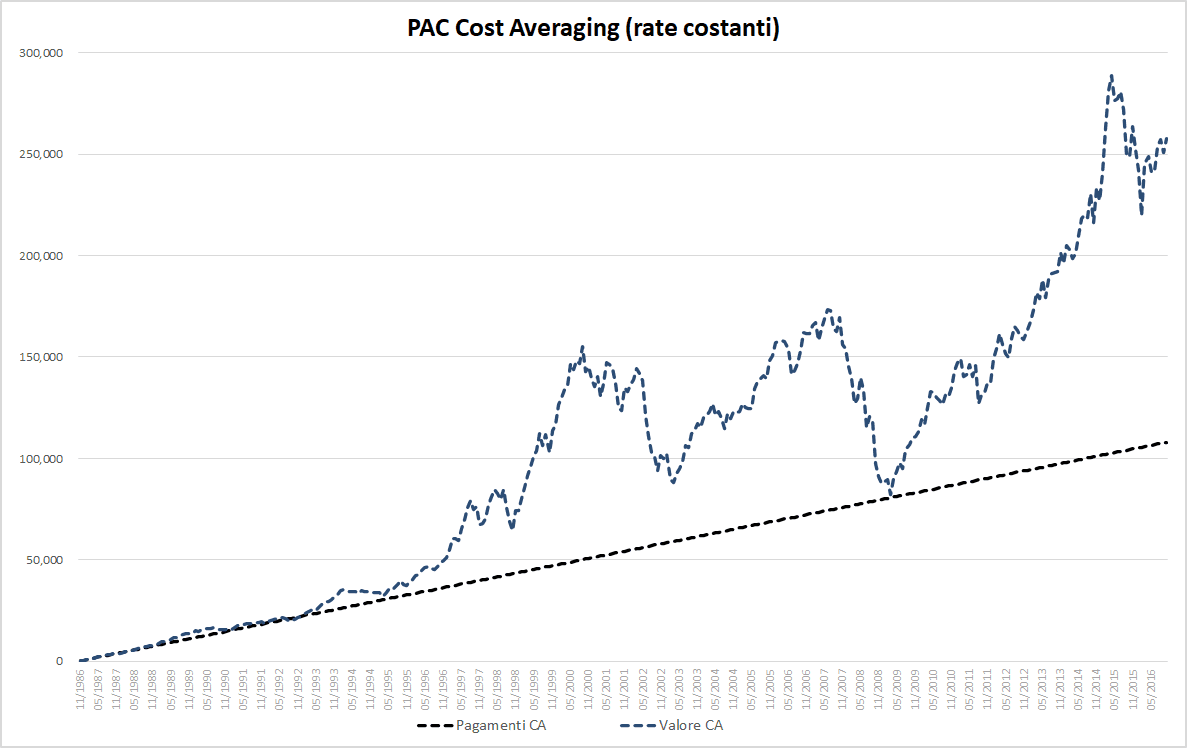
Fig. 3 – PAC Cost Averaging. Rata: 300 euro
Il PAC simulato è costituito da 360 rate mensili dell’importo di 300 euro ciascuna. Per semplicità, non sono stati considerati i costi di transazione (saranno inseriti in seguito).
La linea nera tratteggiata misura il totale dei pagamenti effettuati. La crescita è costante e, alla fine del PAC, saranno stati versati 108.000 euro (360 rate da 300 euro ciascuna).
La linea blu tratteggiata rappresenta il valore corrente (o valore di mercato) delle quote accumulate (il grafico segue approssimativamente l’andamento del NAV del fondo).
Il valore corrente, una volta versata l’ultima rata, corrisponde al valore finale del piano di accumulo, che chiameremo per semplicità montante del PAC. La distinzione tra montante e valore di mercato di un PAC è superflua nel Cost Averaging, ma sarà fondamentale nel Value Averaging, dove la liquidità giocherà un ruolo molto importante, sia durante che alla fine dell’investimento.
Col grafico seguente entriamo nel mondo del Value Averaging.
La tipologia di Value Averaging utilizzata è quella più semplice:
- Senza vendita delle quote in eccesso (VA No-Sell).
- Target costante, pari al valore della rata iniziale di 300 euro.
- Nessun massimale ai versamenti.
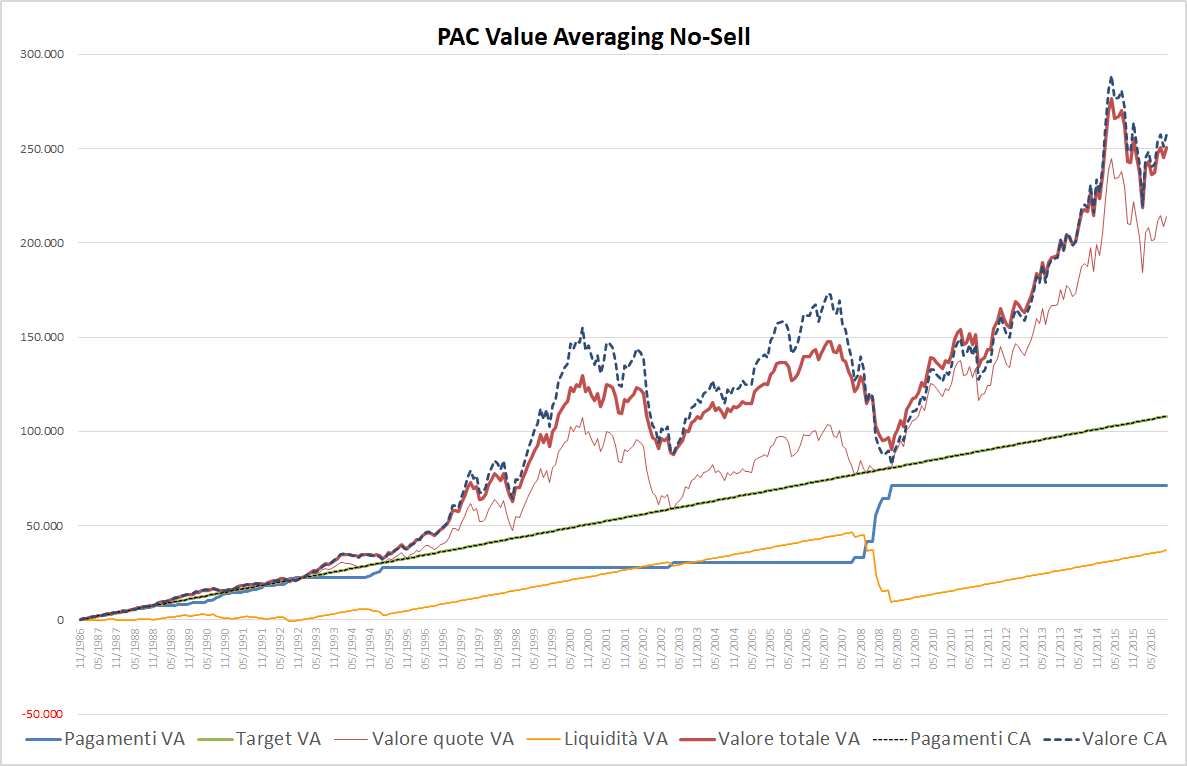
Fig. 4 – PAC Value Averaging No-Sell. Rata: 300 euro. Target costante. Senza massimale
Anche se da qui in avanti ci concentreremo sul Value Averaging, nei grafici saranno sempre presenti anche gli andamenti dei pagamenti e del valore corrente di un piano di accumulo Cost Averaging simile. Queste due quantità saranno misurate dalle linee tratteggiate. Le linee continue, invece, contraddistingueranno il Value Averaging.
Passiamo all’analisi specifica del grafico:
- La linea verde individua il target: è una linea retta che cresce in modo costante (ogni mese si aggiungono 300 euro).
- La linea rossa rappresenta il valore corrente delle quote acquistate durante la vita del piano di accumulo Value Averaging.
- La linea blu mostra il valore cumulato dei pagamenti del Value Averaging effettuati (la somma delle rate versate): non è mai decrescente, perché in un No-Sell non sono previste vendite di quote. Per lunghi periodi segue un andamento orizzontale (quando, appunto, non vengono effettuati pagamenti: il valore corrente è superiore al target).
- La linea arancione quantifica la differenza tra i pagamenti effettuati in un PAC Cost Averaging e quelli di un PAC Value Averaging: è una misura molto importante, dato che corrisponde alla liquidità inutilizzata quando è positiva e all'extra-liquidità utilizzata quando è negativa. La liquidità, sommata al montante del PAC, produce la somma finale generata dall’investimento.
- La linea nera tratteggiata, che in questo grafico è sovrapposta a quella verde, individua il valore cumulato dei pagamenti di un equivalente piano di accumulo Cost Averaging.
- La linea tratteggiata blu, infine, traccia il valore cumulato del piano di accumulo Cost Averaging (stessa lunghezza e rata costante pari a quella iniziale del Value Averaging). Questa linea ci permetterà di seguire, visivamente, la differenza tra l’evoluzione di queste due tipologie di PAC.
La linea più significativa è quella verde: individua l’obiettivo di investimento. In questo grafico, è sovrapposta alla linea dei pagamenti cumulati del Cost Averaging ma, concettualmente, è molto diversa:
- Nel Value Averaging rappresenta il punto ideale di arrivo, il target appunto. Non sappiamo però come lo raggiungeremo, dato che l’importo delle rate è variabile (positive o nulle nel Value Averaging No-Sell, positive o negative – in caso di vendita di quote – nel Value Averaging puro).
- Nel Cost Averaging è il punto di partenza. Conosciamo esattamente la composizione degli apporti di capitale (rate costanti positive), ma non sappiamo quale sarà il punto di arrivo
In questo esempio, l’input del Cost Averaging coincide con l’output del Value Averaging. In seguito, queste due grandezze potranno non coincidere.
Nel Value Averaging il valore di mercato dell’investimento (linea rossa) dovrebbe, al momento di ogni versamento o prelievo, sovrapporsi al target (linea verde). L’obiettivo è infatti quello di mantenere il valore corrente dell’investimento il più possibile allineato al target, almeno nel momento in cui una vendita o un versamento vengono effettuati.
I pagamenti cumulati del Value Averaging (linea blu) si mantengono sempre al di sotto di quelli del Cost Averaging (linea nera tratteggiata): la liquidità, infatti, è sempre positiva (linea gialla).
Il valore corrente dell’investimento è, per gran parte della vita del PAC, al di sopra del target. I motivi sono essenzialmente due:
- Si tratta di un piano di accumulo Value Averaging No-Sell.
- Il trend di lungo periodo del fondo sottostante è positivo, seppur con un’alternanza di periodi di crescita e di decrescita.
Nel Value Averaging puro, saranno le vendite di quote a riportare in equilibrio target e valore corrente nel caso in cui quest’ultimo sia più alto. Nel No-Sell, non essendoci alcuna vendita, sarà il tempo a far sì che il valore corrente si riallinei al target (con il primo che prima o poi scenderà ed il secondo che continuerà a crescere).
Le dinamiche di queste due grandezze cambieranno drasticamente nel Value Averaging puro.
Concentriamoci un attimo sulla linea rossa: abbiamo detto che rappresenta il valore corrente delle quote investite col piano di accumulo Value Averaging ed è sempre decisamente minore del valore corrente del Cost Averaging.
L’investitore in un PAC Value Averaging, però, dispone anche di un certo livello di liquidità che è assente nel Cost Averaging: la ricchezza posseduta, il valore totale del Value Averaging è quindi pari al valore corrente delle quote investite più la liquidità.
Misuriamo graficamente anche questa quantità: noteremo come essa sia molto vicina alla linea tratteggiata blu: in diversi momenti, le due linee sono sovrapposte.
Eccola:

Fig. 4-bis – PAC Value Averaging No-Sell. Rata: 300 euro. Target costante. Senza massimale. Il grafico include il Valore totale VA
La linea rossa più spessa è quella che quantifica il Valore totale del VA. Verrà visualizzata anche in tutti i grafici futuri, rendendo quindi possibile un facile confronto tra questa e il valore del Cost Averaging (line blu tratteggiata).
Approfondiamo i piani di accumulo Value Averaging No-Sell, iniziando con l’incrementare il target in modo crescente.
Partiamo dallo 0,25%:
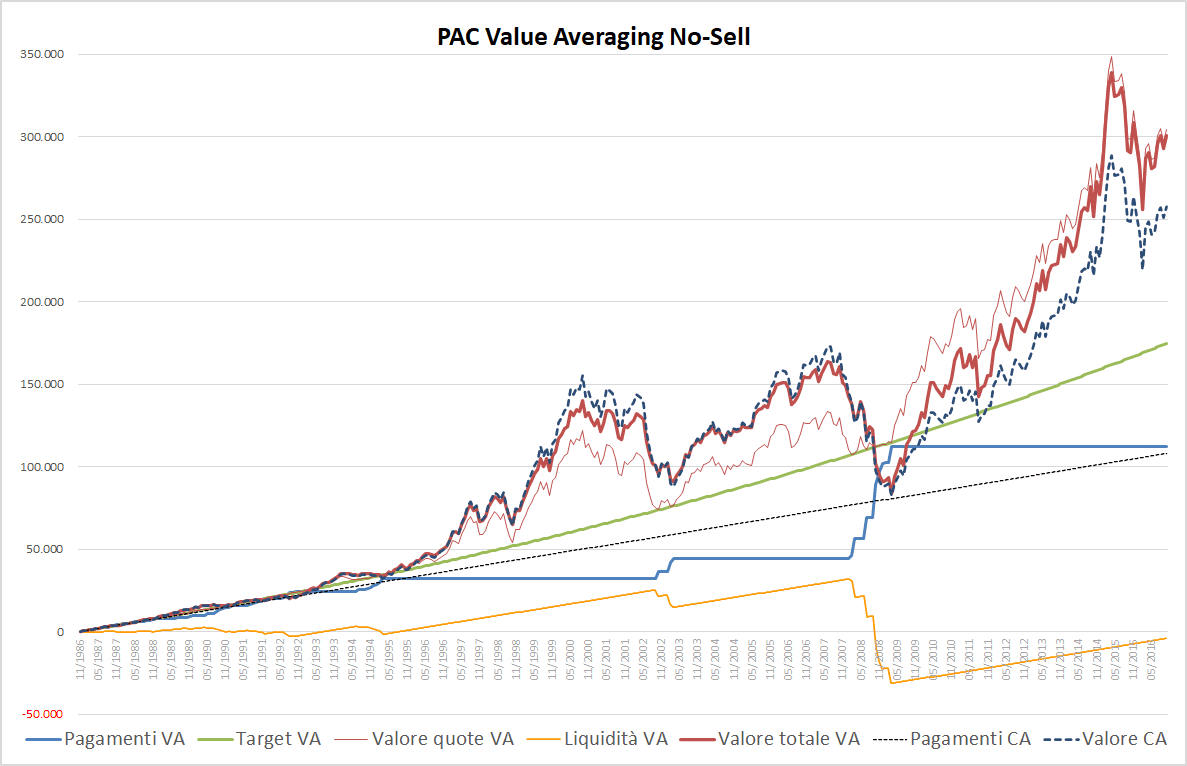
Fig. 5 – PAC Value Averaging No-Sell. Rata iniziale: 300 euro. Target crescente: 0,25%. Senza massimale
Il target si è trasformato in una curva posizionata sopra alla retta dei pagamenti del Cost Averaging.
Facendo aumentare il target del PAC Value Averaging più velocemente, i pagamenti cresceranno di conseguenza. La linea blu, adesso, supera bruscamente quella nera tratteggiata a partire dalla fine del 2007, stabilizzandosi poco dopo. Non è un caso: nel 2007 è iniziata la tremenda crisi finanziaria dei subprime, che ha fatto crollare i mercati azionari in tutto il mondo.
Quando i prezzi scendono e si allontanano dal target sorge la necessità di effettuare dei versamenti più consistenti di quelli abituali, per riportare il valore corrente ai livelli del target.
Il valore totale del Value Averaging (linea rossa più spessa) si posiziona sopra a quella blu tratteggiata del Cost Averaging a partire dal 2008/2009 e, a fine investimento, la differenza è di oltre 47.000 euro mentre i versamenti totali del Value Averaging sono stati di soli 4.000 euro superiori a quelli del Cost Averaging.
Il grafico ci consente però di capire come, in precedenza, vi sia stato un bisogno di extra-liquidità superiore, pari ad una cifra di oltre 31.000 euro (differenza tra linea blu e nera tratteggiata, confermata dal punto di minimo assoluto della linea arancione).
Stiamo entrando nel merito della più insidiosa delle critiche al Value Averaging: la necessità di un fondo di liquidità e la corrispondente distorsione nel calcolo dei rendimenti totali ed annualizzati.
Abbiamo visto come, a un certo punto (intorno al 2008), l’elevato fabbisogno di liquidità avrebbe richiesto l’esistenza di un fondo apposito:
- Da costituirsi all’inizio del piano di accumulo, perché non si sa a priori quando si devono effettuare i maxi-versamenti.
- Di importo consistente, dato che i maxi-versamenti possono arrivare a essere decine di volte superiori alla rata standard.
Tra marzo 2008 e marzo 2009, ovvero dopo oltre 20 anni dall’inizio del PAC, l’investitore di questo piano di accumulo Value Averaging avrebbe dovuto versare 7 rate (non consecutive) di importo ragguardevole: 1.560, 10.395, 13.011, 19.640, 8.338, 4.888 e 9.826 euro, per un totale di circa 68.000 euro. È anche vero che molte volte, nei 20 anni precedenti, non ci sarebbe stato bisogno di versare alcuna rata, rendendo quindi possibile l’accumulazione di una buona parte di questi 68.000 euro proprio con le somme non versate.
E se il bisogno di versare una maxi-rata si fosse presentato molto prima? Come avremmo potuto accumulare questa somma senza un fondo di liquidità apposito?
Non avremmo potuto. Non sarebbe stato possibile accumulare una cifra tale da coprire l’intero importo di 68.000 euro: sarebbe servita una somma maggiore, come ci dimostra la linea blu, collocatasi ben al di sopra di quella nera tratteggiata a partire da ottobre 2008.
Dopo il versamento della rata da 9.826 euro la somma in eccesso avrebbe raggiunto un valore di circa 31.500 euro.
Se questa somma, o una maggiore, fosse stata inserita in un fondo di liquidità fin dall’inizio, il rendimento totale e quello annualizzato, come siamo abituati a calcolarli, non ne avrebbe tenuto conto (e sarebbero quindi stati non veritieri); se, invece, il fondo di liquidità non fosse stato costituito, quei versamenti non si sarebbero potuti effettuare: ecco la distorsione oggetto delle critiche di Hayley.
I “veri” rendimenti sarebbero stati inferiori, a meno di non impiegare la somma accantonata nel fondo di liquidità iniziale in un investimento risk-free non vincolato con un rendimento pari a quello medio del PAC (cosa pressoché impossibile nel lungo termine).
Senza un fondo di liquidità, quei maxi-versamenti non potevano dunque essere effettuati, quanto meno, non per la parte eccedente la liquidità accumulata durante la vita del PAC.
La critica di Hayley è solida e non colpisce solo il Value Averaging: ne è vittima ogni metodologia di investimento che preveda impieghi futuri di somme non quantificabili con precisione fin dall'inizio.
A questo punto, essendo consapevoli di questa limitazione, possiamo scegliere di procedere in uno dei seguenti tre modi:
- Seguendo le orme di Hayley, bollando il Value Averaging come strategia di investimento inefficiente e scartandola in ogni caso: un PIC Buy and Hold o un Piano di Accumulo del Capitale a rate costanti saranno da preferire. Soltanto gli investitori affetti da bias cognitivi sceglierebbero il Value Averaging.
- Sviluppando un piano di accumulo Value Averaging senza un fondo iniziale di liquidità. Se si verificherà la necessità di versare una grossa somma, l'investimento sarà effettuato nei limiti della liquidità accumulata durante la vita del PAC.
- Costituendo un fondo iniziale di liquidità parallelamente allo sviluppo di un piano di accumulo Value Averaging. Fare cioè quello che secondo Hayley è inefficiente ed irrazionale. Approfondiremo questo discorso in due capitoli appositi, dato che forse si tratta di un’alternativa con molte implicazioni positive, anche di tipo psicologico.
Sulla prima opzione non c’è molto da aggiungere: tutto ciò che seguirà si inquadrerà nella seconda e nella terza alternativa.
Partiamo proprio dallo sviluppo di un PAC Value Averaging senza fondo di liquidità iniziale. L’investimento consisterà nelle sole somme allocate mensilmente al piano di accumulo (esattamente come in un Cost Averaging) più gli eventuali fondi accumulati grazie alle rate non versate o alle vendite effettuate durante la vita del piano di accumulo (in caso di VA puro).
Verificheremo se, applicando questa strategia, il Value Averaging sarà ancora preferibile al Cost Averaging.
Torniamo al grafico del PAC Value Averaging. Se viene costruito senza l’utilizzo di un fondo di liquidità iniziale, si trasforma nel modo seguente:
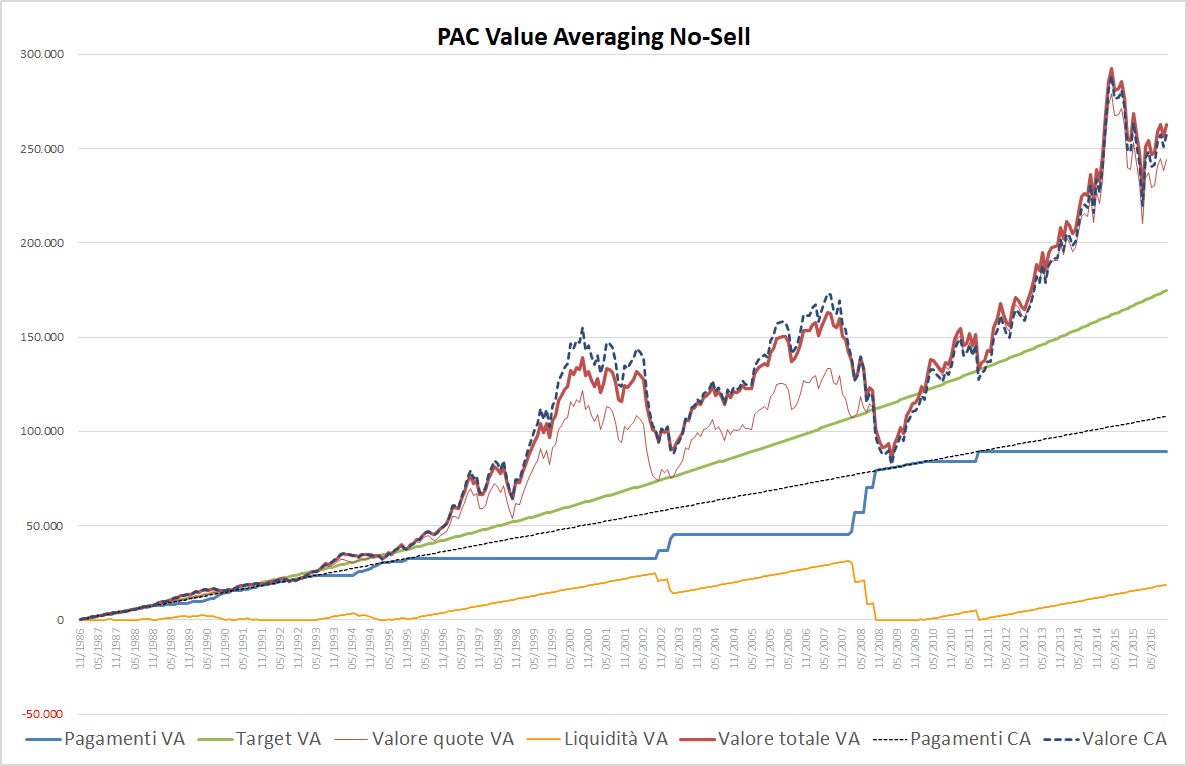
Fig. 6 – PAC Value Averaging No-Sell. Rata iniziale: 300 euro. Target crescente: 0,25%. Senza massimale. Filtro anti-Hayley: presente
La linea blu non supera mai quella nera tratteggiata. In altre parole, non abbiamo mai bisogno di una liquidità superiore a quella che serve per costruire un piano di accumulo Cost Averaging (pari a una rata standard per ogni periodo). Non c’è bisogno di un fondo di liquidità iniziale.
Analizzando la linea arancione, si riscontra come alla fine del piano di accumulo i pagamenti totali del Value Averaging siano comunque inferiori a quelli di un Cost Averaging: a partire da settembre 2011, ultimo momento in cui tutta la liquidità risultava investita, non sono state più versate rate.
La differenza finale è di 18.648 euro e rappresenta la liquidità inutilizzata a fine investimento.
La somma finale generata con un piano di accumulo Value Averaging è pari al montante del PAC più la liquidità inutilizzata. Nel nostro esempio, la somma finale sarebbe stata pari a 244.115 euro (montante del PAC, linea rossa sottile) più i 18.648 euro di liquidità inutilizzata, per un totale di 262.763 euro (linea rossa spessa).
L’analogo PAC Cost Averaging avrebbe invece generato una somma pari a 257.517 euro (linea tratteggiata blu).
La differenza è di 5.246 euro: non è una cifra enorme, ma costituisce un primo risultato a favore del Value Averaging. Se il Value Averaging è riuscito in questo caso a battere – lottando ad armi pari – il Cost Averaging, magari può farlo anche in altre circostanze. Forse non è tutto da buttar via.
Se l’incremento del target fosse stato superiore allo 0,25%, avremmo probabilmente utilizzato l’intera liquidità disponibile (pari a 108.000 euro).
Alziamo la percentuale di incremento del target allo 0,50%:
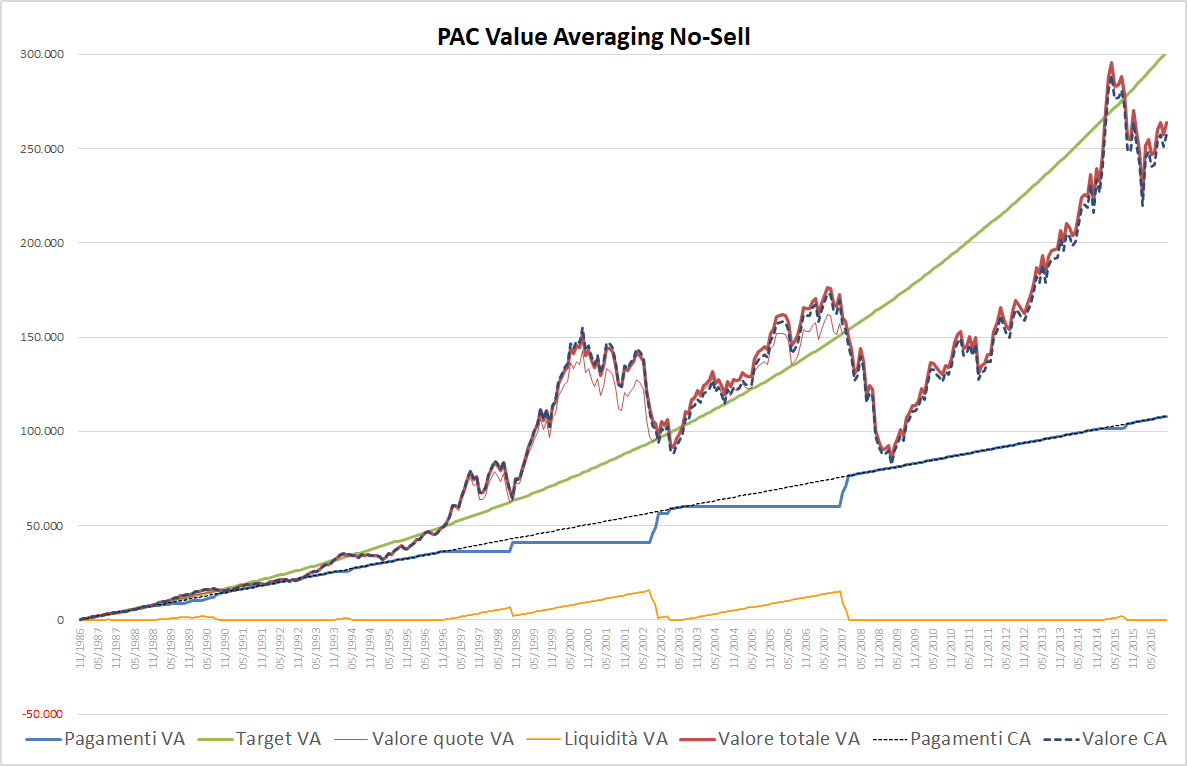
Fig. 7 – PAC Value Averaging No-Sell. Rata iniziale: 300 euro. Target crescente: 0,50%. Senza massimale. Filtro anti-Hayley: presente
I 108.000 euro sono stati interamente utilizzati. La linea arancione, a partire da gennaio 2008, è pressoché orizzontale e pari a 0, valore che mantiene anche a fine piano di accumulo.
Il montante del PAC, che in questo caso corrisponde alla somma finale generata dall’investimento, è adesso pari a 263.992 euro: 1.229 euro più di prima (a fine investimento, la linea rossa sottile e quella spessa sono sovrapposte).
Un’altra variante di PAC Value Averaging è quella che prevede un massimale all’importo dei versamenti, che utilizzeremo insieme al filtro extra-liquidità (d’ora in avanti filtro anti-Hayley). Il ruolo del massimale è quello di trasformare una o poche rate di valore elevato in una serie di versamenti di importo più basso.
Vediamo l’impatto di questa variante di Value Averaging, applicando il filtro anti-Hayley e ipotizzando una rata massima di 1000 euro:
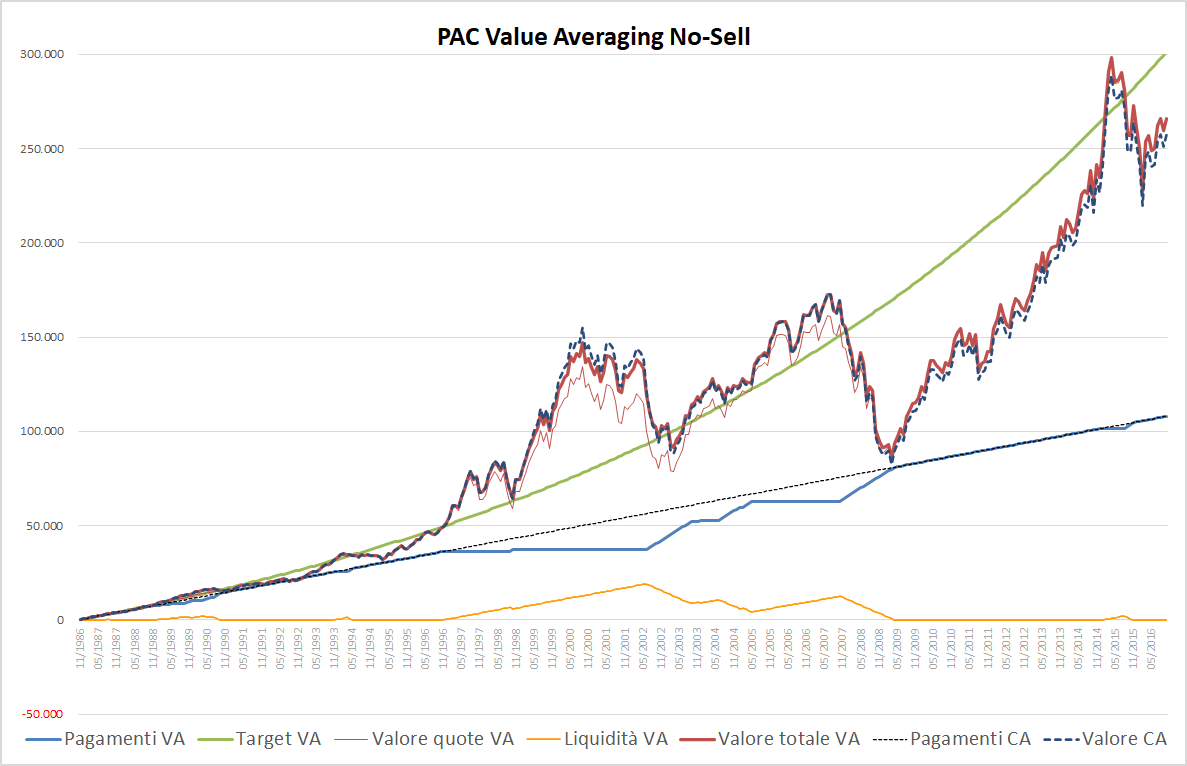
Fig. 8 – PAC Value Averaging No-Sell. Rata iniziale: 300 euro. Target crescente: 0,50%. Versamento massimo: 1000 euro. Filtro anti-Hayley: presente
La linea blu cresce in modo meno repentino: i maxi-versamenti sono sostituiti da serie di versamenti di 1000 euro, che terminano quando le riserve accumulate durante la vita del PAC si esauriscono.
Questo ulteriore vincolo aumenta il valore finale del piano di accumulo. Il montante sale a 266.219 euro e corrisponde alla somma finale, dal momento che la liquidità residua è pari a 0.
Vediamo che cosa succede togliendo il filtro anti-Hayley:
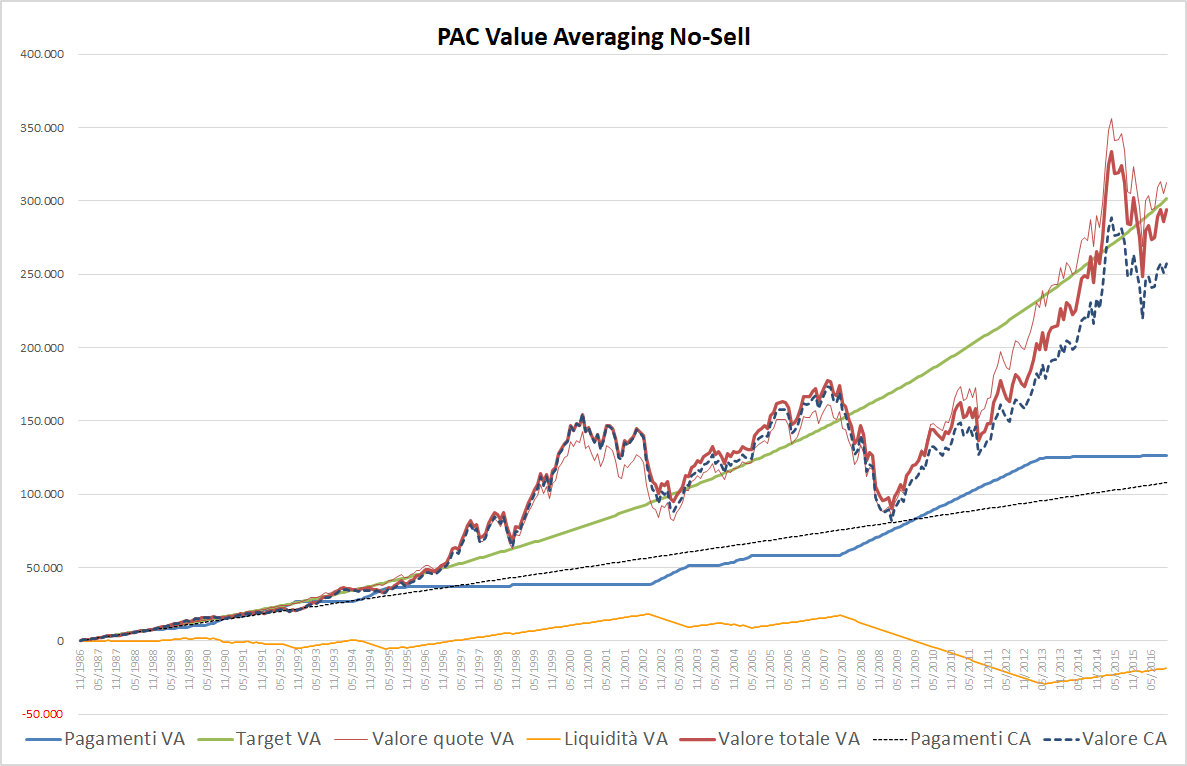
Fig. 9 – PAC Value Averaging No-Sell. Rata iniziale: 300 euro. Target crescente: 0,50%. Versamento massimo: 1000 euro. Filtro anti-Hayley: assente
Il fabbisogno di extra-liquidità si manifesta già a partire dei primi anni di vita del PAC, con un massimo relativo intorno ad aprile 1995. Si ripresenta di prepotenza alla fine del 2009, con un massimo assoluto che viene toccato nel giugno 2013 (29.261 euro).
La somma finale di questo PAC sarebbe stata di ben 294.055 euro (montante del PAC: 312.675 euro e liquidità finale −18.619 euro). Il valore negativo della liquidità è l’ulteriore conferma che per costruire un piano di accumulo del genere non basta il fondo accumulato durante la vita del PAC: servono capitali extra.
Rispetto a prima, negli ultimi anni di vita del PAC la linea rossa sottile si è posizionata sopra a quella spessa: per ottenere la somma totale generata dall’investimento, al valore delle quote investite deve essere sottratta l’extra-liquidità impiegata.
La regola generale è quindi la seguente: la linea rossa spessa è posizionata sopra a quella sottile quando è presente della liquidità inutilizzata (linea arancione positiva); è posizionata sotto, quando si sta utilizzando extra-liquidità (linea arancione negativa).
Per finire, ipotizziamo di abbassare il massimale a 300 euro, lo stesso valore della rata iniziale. Così facendo, il piano di accumulo Value Averaging si trasforma in un Cost Averaging dove la rata viene versata solo quando il valore corrente è sotto al target.
In questo caso il capitale totale impiegato sarà per forza di cose sempre minore o uguale a quello di un PAC Cost Averaging. Di conseguenza, applicare o non applicare il filtro anti-Hayley produce lo stesso risultato.
Graficamente:
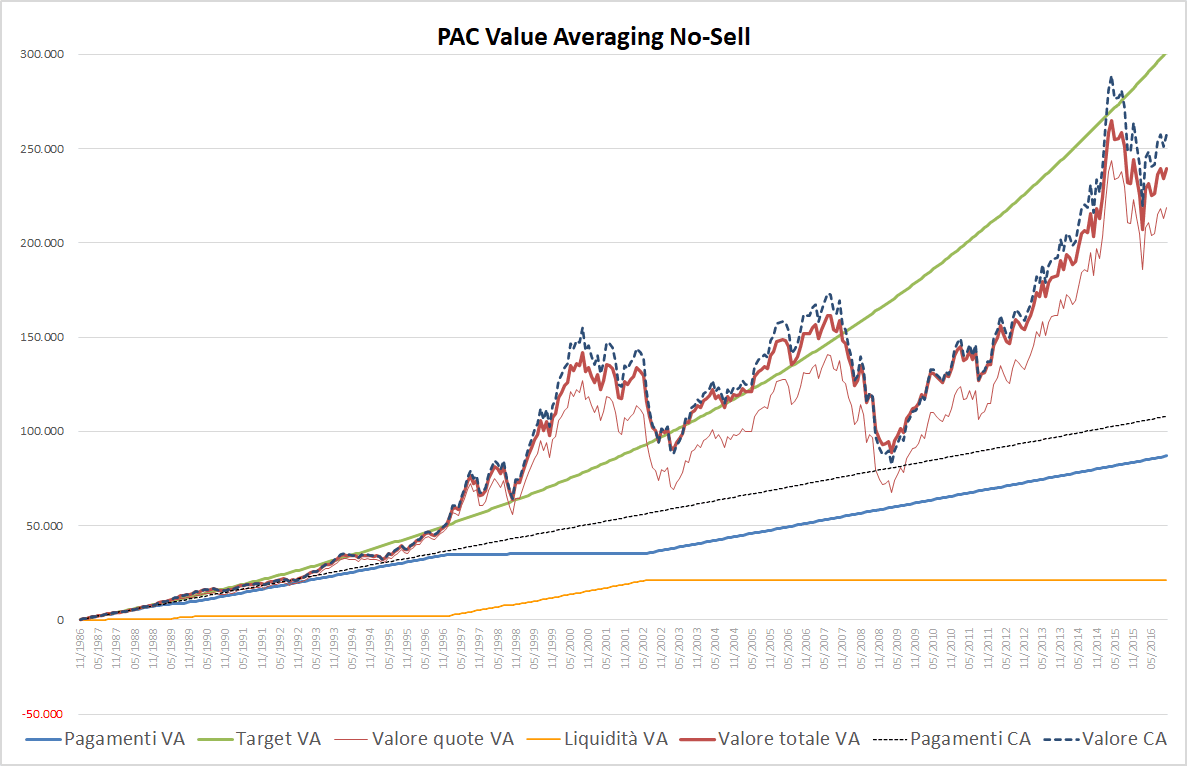
Fig. 10 – PAC Value Averaging No-Sell. Rata iniziale: 300 euro. Target crescente: 0,50%. Versamento massimo: 300 euro
Con l’eccezione del periodo compreso tra il 1997 e il 2002, questo PAC Value Averaging è esattamente uguale ad un Cost Averaging.
Non sembra esserci alcun vantaggio dall’applicazione di questa strategia: si versa di meno ed a fine investimento il valore delle quote in portafoglio è minore (per l’esattezza, la somma finale disponibile sarebbe stata pari a 239.542 euro, originata da un montante del PAC di 218.492 euro ed una liquidità residua di 21.050 euro).
Rispetto ad un Cost Averaging, qualche beneficio si potrebbe avere nel caso in cui il prezzo finale delle quote del fondo fosse minore di quello che in media abbiamo evitato di pagare, non comprando quote, nel periodo di sospensione dei versamenti.
Iniziamo adesso ad analizzare i Piani di Accumulo del Capitale Value Averaging puri, che prevedono la vendita delle quote in eccesso quando il valore corrente è superiore al target.
Partiamo con un incremento target costante di 300 euro, senza nessun ulteriore vincolo:
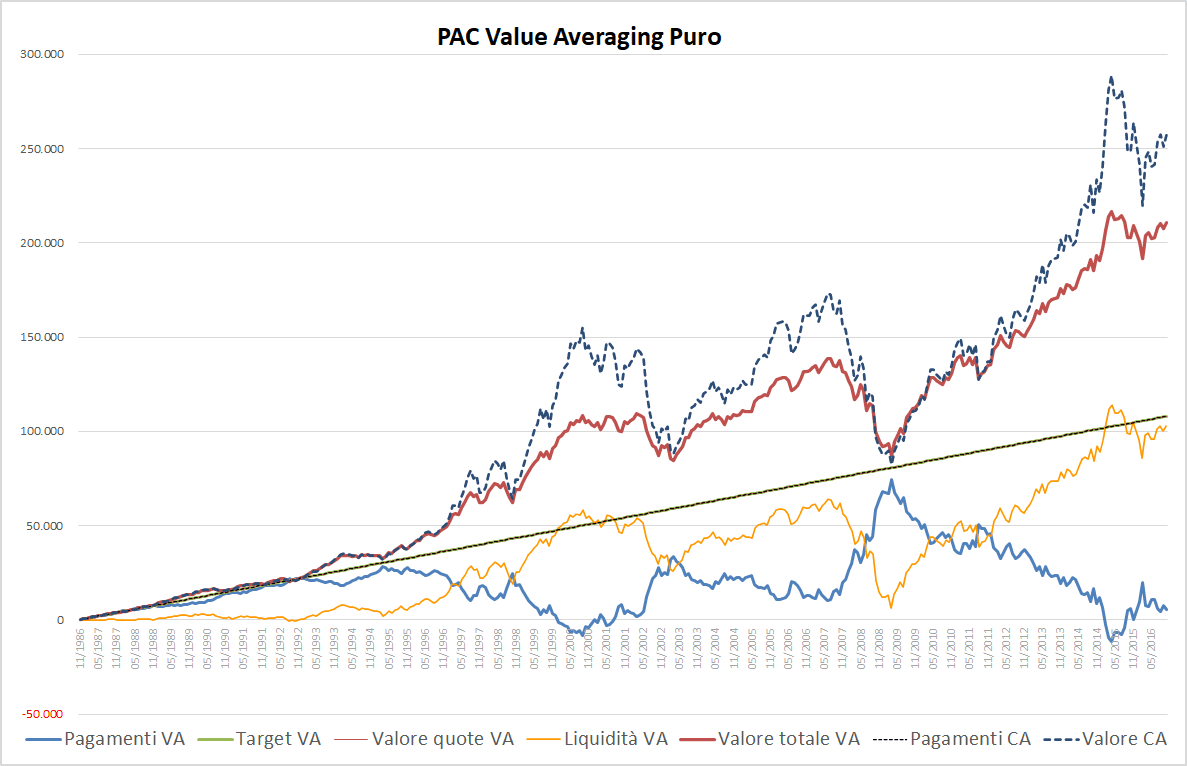
Fig. 11 – PAC Value Averaging puro. Rata iniziale: 300 euro. Incremento target: costante
Il grafico evidenzia la profonda differenza esistente tra un piano di accumulo Value Averaging puro e uno No-Sell.
Se prima il valore di mercato (linea rossa sottile) si posizionava stabilmente sopra al target (linea verde), adesso le due linee combaciano perfettamente. Nello specifico, anche la linea nera tratteggiata che misura i pagamenti del Cost Averaging è sovrapposta alle due precedenti.
Il valore totale del Value Averaging, indicato dalla linea rossa spessa, segue invece un trend simile a quello del Cost Averaging, pur rimanendo sempre ampiamente al di sotto di quest’ultimo (al valore delle quote si aggiunge quello della liquidità inutilizzata, che è molto più consistente nel Value Averaging puro rispetto al No-Sell).
Per mantenere il valore di mercato allineato al target, abbiamo una continua alternanza di acquisti e vendite, che rendono la linea dei pagamenti/vendite molto frastagliata (linea blu). Nell’equivalente Value Averaging No-Sell, essa seguiva un andamento molto più lineare: a essere frastagliato era il valore di mercato (linea rossa).
La linea dei pagamenti di un Value Averaging non supera quasi mai quella dei pagamenti di un Cost Averaging, neppure durante la crisi del 2007-2009 (lo fa solo per piccoli importi nelle fasi iniziali di vita del PAC). Il risultato è significativo: in questo specifico piano di accumulo non sarebbe servito costituire una riserva iniziale di liquidità, necessaria a fronteggiare gli ingenti versamenti di quel biennio o di qualsiasi altro periodo (bastavano poche centinaia di euro da parte, da utilizzare nel 1987/88 e nel 1992).
La riserva di liquidità si sarebbe formata grazie alle vendite di quote ed agli acquisti di importo inferiore all’incremento del target. La critica di Hayley, in questo specifico piano di accumulo Value Averaging, è poco pertinente.
È interessante notare la grande differenza tra la somma finale generata da un piano di accumulo Cost Averaging e da un Value Averaging puro, che evidenzia la profonda diversità tra queste due strategie di investimento:
- In un PAC Cost Averaging, sono stati versati 108.000 euro (360 rate da 300 euro ciascuna) e il montante delle 984,0549 quote acquistate nell’arco dei 30 anni è stato pari a 257.517 euro.
- In un PAC Value Averaging, sono stati versati fino a 74.414,55 euro nel punto di massimo assoluto dei pagamenti VA (raggiunto a marzo 2009) ma, poiché con le continue vendite parte del capitale è stato smobilizzato, a fine investimento abbiamo:
- Liquidità per 102.648 euro (linea arancione).
- Un valore delle 412,7021 quote ancora in portafoglio pari a 108.000 euro (se l’incremento è costante, il target di un Value Averaging puro è uguale al totale dei pagamenti effettuati in un Cost Averaging di pari rata).
- Una somma finale disponibile di 210.648 euro.
Passiamo alla variante con incrementi crescenti del target (0,25%). Il grafico si trasforma nel modo seguente:
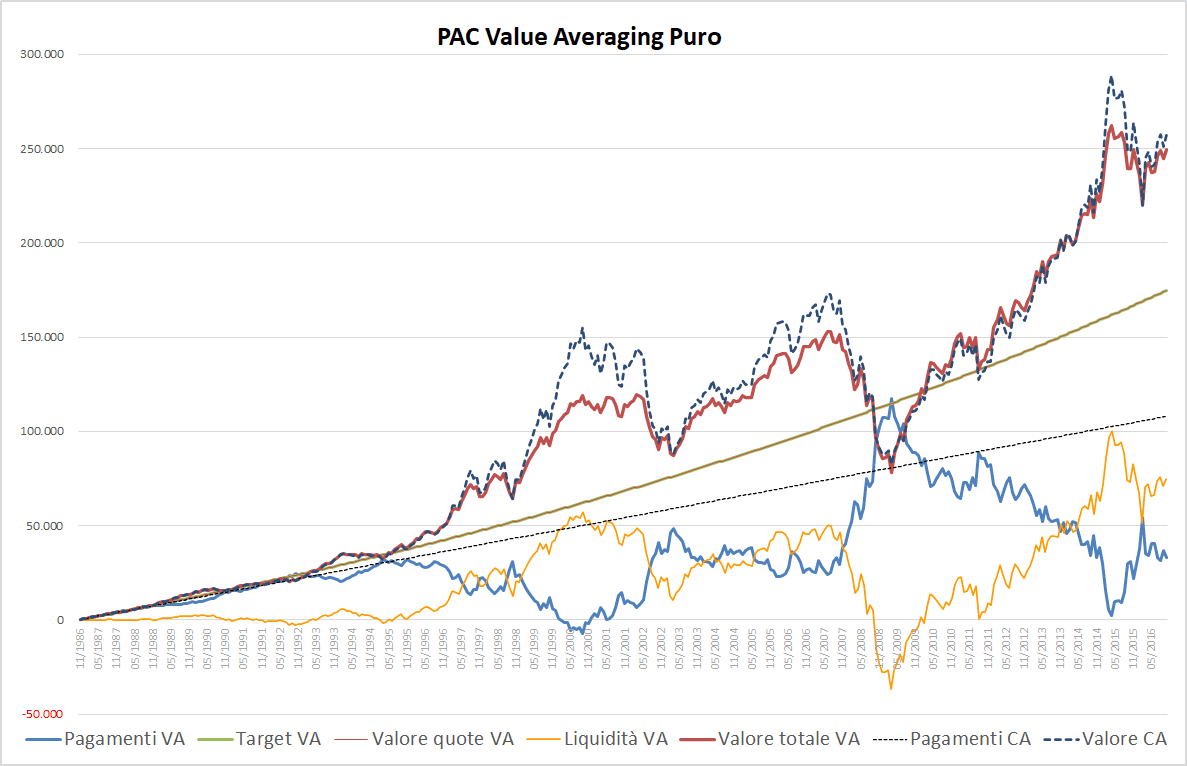
Fig. 12 – PAC Value Averaging puro. Rata iniziale: 300 euro. Incremento target: 0,25%. Filtro anti-Hayley: assente
La linea nera tratteggiata si è separata da quelle del target (verde) e del valore di mercato (rossa sottile), che sono ancora sovrapposte e, adesso, leggermente convesse.
La linea dei pagamenti/vendite di un PAC Value Averaging continua a essere molto frastagliata: supera la linea nera tratteggiata nel biennio 2007-2009 fino ad un valore massimo di 36.659 euro, nel marzo 2009.
In questo caso la critica di Hayley coglie nel segno: questa somma era veramente stata messa da parte all’inizio del PAC, rimanendo inutilizzata per 23 anni prima di essere investita?
E, se anche ci fosse stata la volontà di creare un fondo di liquidità iniziale, quanto avremmo in realtà accantonato in quel fondo?
Avremmo scoperto soltanto 23 anni dopo che il fabbisogno sarebbe arrivato ad essere pari ad oltre 36 mila euro: l’unica possibilità sarebbe stata quella di stimarne il valore nel modo più preciso possibile.
Nonostante questo, a partire dal 2010, quando i mercati sono tornati a crescere, le vendite hanno ripreso il sopravvento e la linea blu si è nuovamente posizionata sotto a quella nera tratteggiata, accumulando un valore di quasi 75 mila euro a fine piano di accumulo (linea arancione).
Il montante finale del PAC, coincidente con il target, sarebbe stato pari a 174.821 euro. Considerando una liquidità di 74.754 euro, la somma finale disponibile sarebbe stata di 249.575 euro.
Vediamo come sarebbero andate le cose se avessimo sviluppato questo PAC senza eccedere con i versamenti rispetto al fondo di liquidità accumulato durante la vita del piano di accumulo, evitando in questo modo la critica di Hayley:
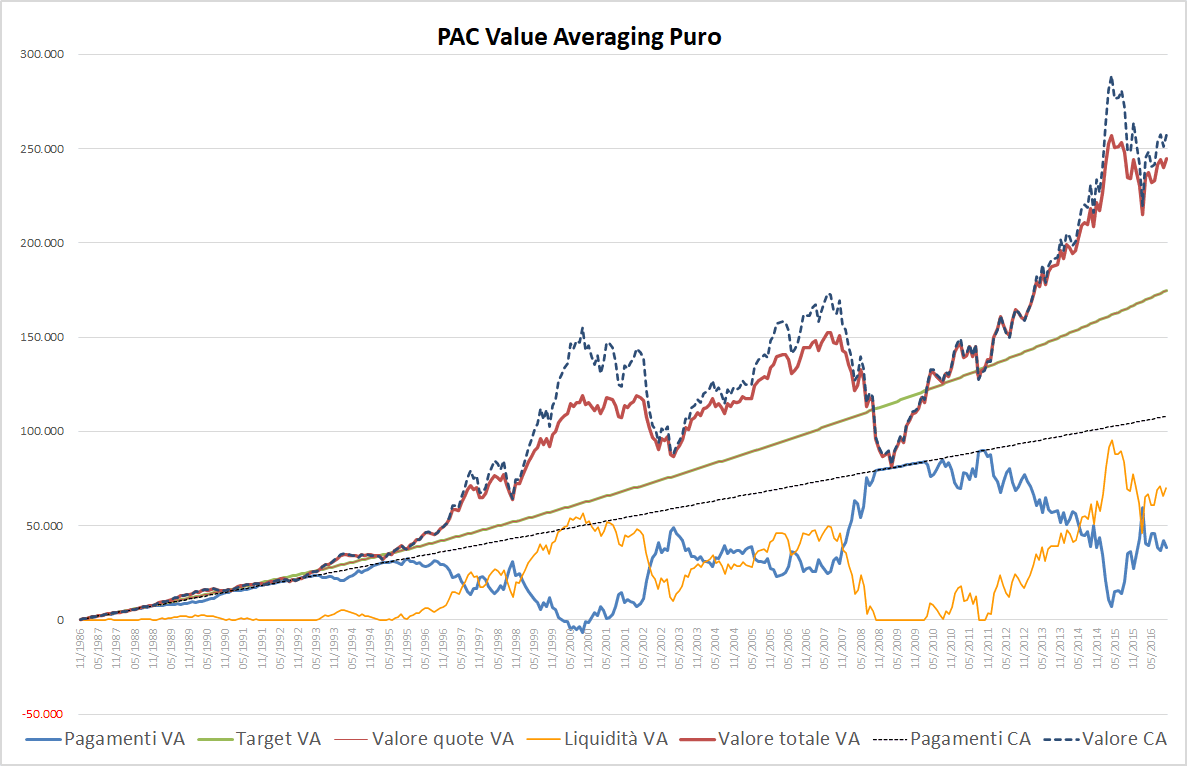
Fig. 13 – PAC Value Averaging puro. Rata iniziale: 300 euro. Incremento target: 0,25%. Filtro anti-Hayley: presente
Le osservazioni principali sono le seguenti:
- La linea nera tratteggiata non viene oltrepassata. È esattamente ciò che volevamo ottenere per evitare la critica di Hayley.
- Durante la crisi 2007-2009, si è versato meno di quello che un piano di accumulo Value Averaging puro senza filtro avrebbe richiesto, portando il valore di mercato delle quote a disallinearsi dal target fino a marzo 2010, quando il gap è stato colmato e le vendite di quote sono tornate a prendere il sopravvento (un altro brevissimo periodo in cui il filtro anti-Hayley è entrato in azione è stato quello compreso tra agosto e ottobre 2011).
- Alla fine dell’investimento, abbiamo raggiunto lo stesso valore corrente (174.821 euro) ottenuto dal piano precedente, che non aveva utilizzato il filtro anti-Hayley: è un risultato importante perché, a differenza del No-Sell, mostra come nel Value Averaging puro il filtro anti-Hayley non causi necessariamente una perdita di efficienza,
Fino a dove ci possiamo spingere, in termini di incremento della rata, senza che il valore corrente finale, in caso di applicazione del filtro, si allontani dal target?
Vediamo i due grafici di un piano Value Averaging con incremento pari allo 0,50%, con o senza filtro anti-Hayley:
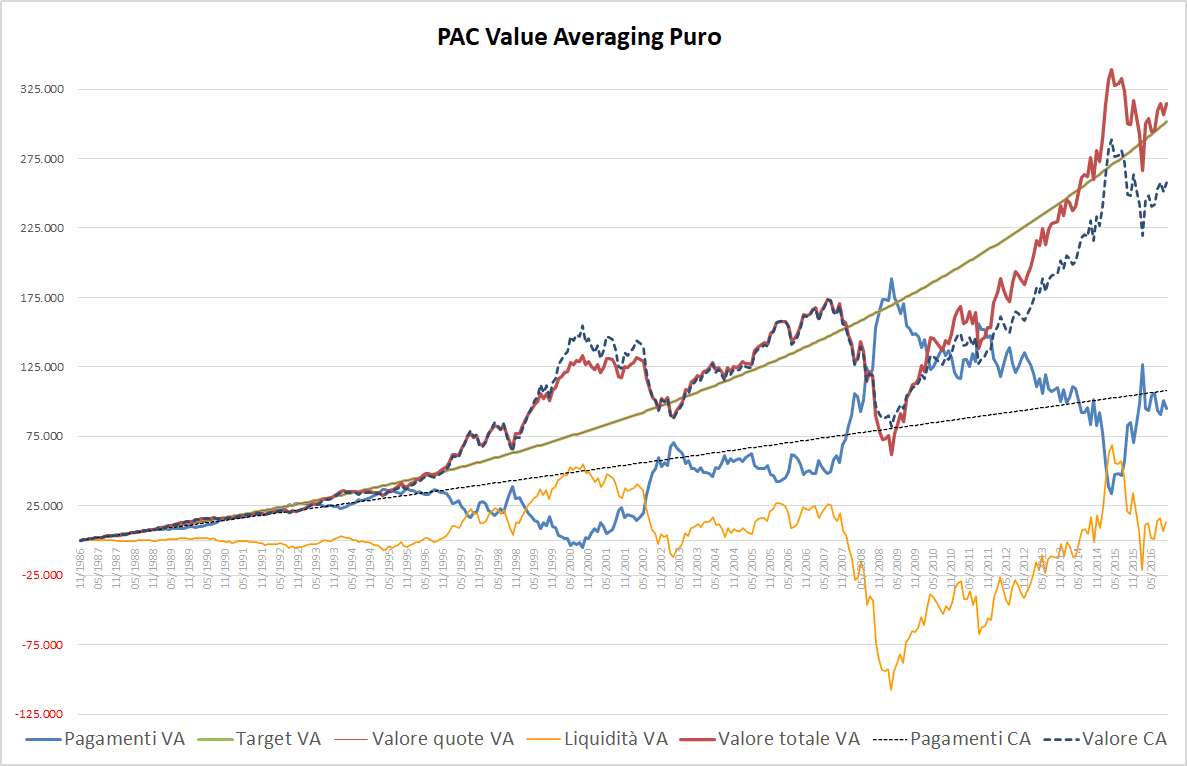
Fig. 14 – PAC Value Averaging puro. Rata iniziale: 300 euro. Incremento target: 0,50%. Filtro anti-Hayley: assente
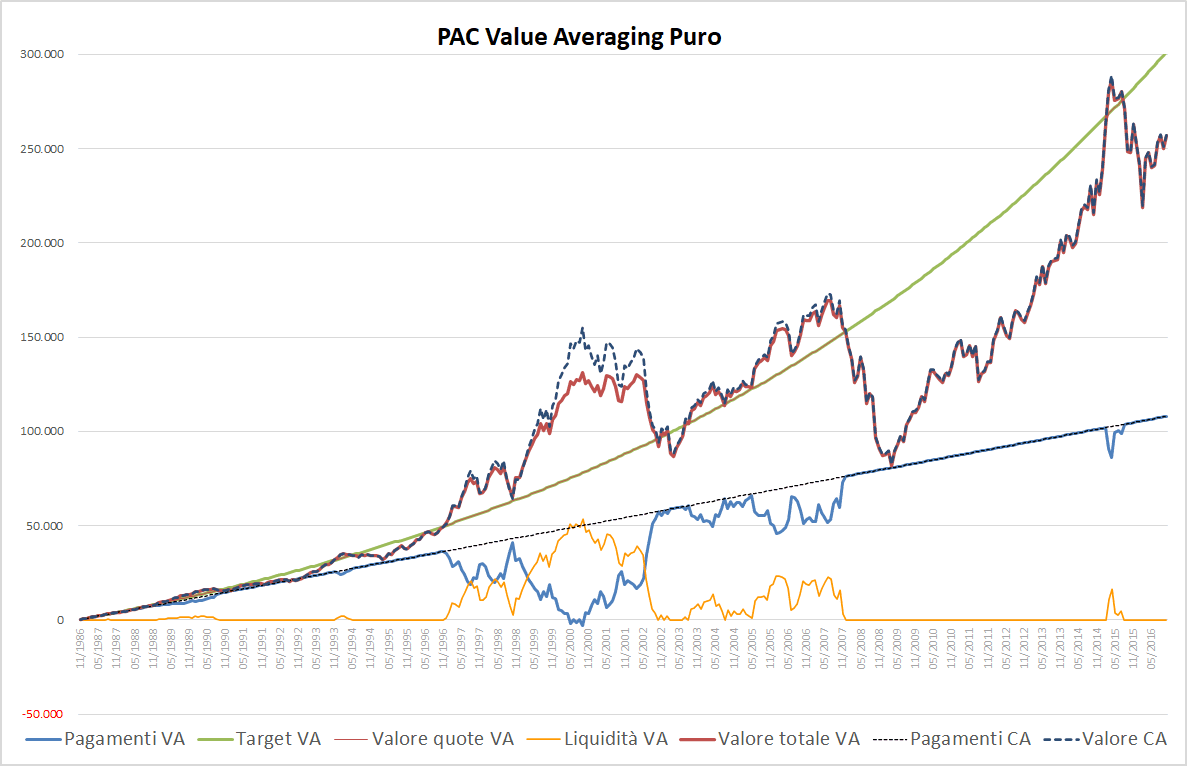
Fig. 15 – PAC Value Averaging puro. Rata iniziale: 300 euro. Incremento target: 0,50%. Filtro anti-Hayley: presente
In questo caso, con la presenza del filtro anti-Hayley non si riesce a generare lo stesso montante. La differenza, seppur consistente, non è enorme.
Nel secondo grafico, si osserva come il valore di mercato, a partire dalla crisi del 2007, si sia allontanato sensibilmente dal target, riuscendo a completare l’inseguimento intorno al 2014. Il riallineamento è durato molto poco e le due curve sono tornate a distanziarsi subito dopo: la differenza finale è stata di circa 44.500 euro.
Con un incremento del target dello 0,50% e la presenza del filtro anti-Hayley, il piano di accumulo Value Averaging ha generato una somma finale di 256.800 euro.
Anche in questo caso, possiamo testare la presenza di altri vincoli, come il massimale ai versamenti di 1000 o di 300 euro.
Diamo un’occhiata ai grafici del PAC Value Averaging con il limite dei 1000 euro, senza e con la presenza del filtro anti-Hayley:
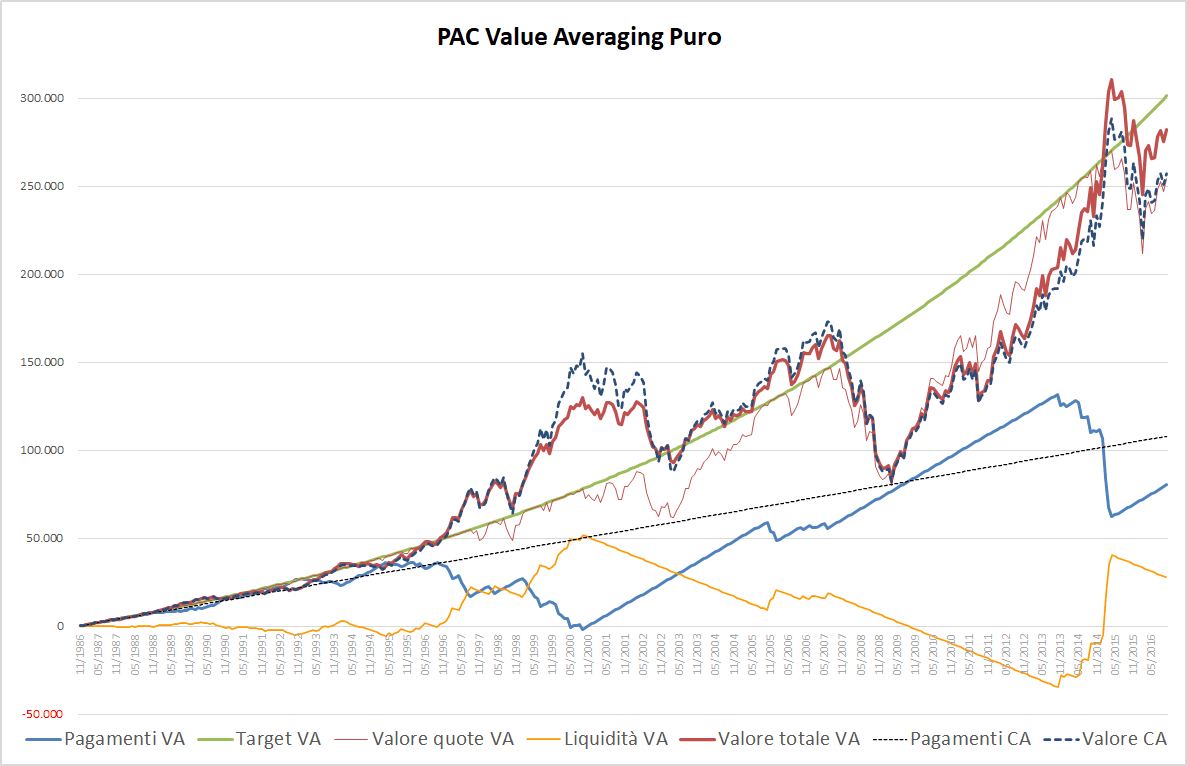
Fig. 16 – PAC Value Averaging puro. Rata iniziale: 300 euro. Incremento target: 0,50%. Versamento Massimo: 1000 euro. Filtro anti-Hayley: assente
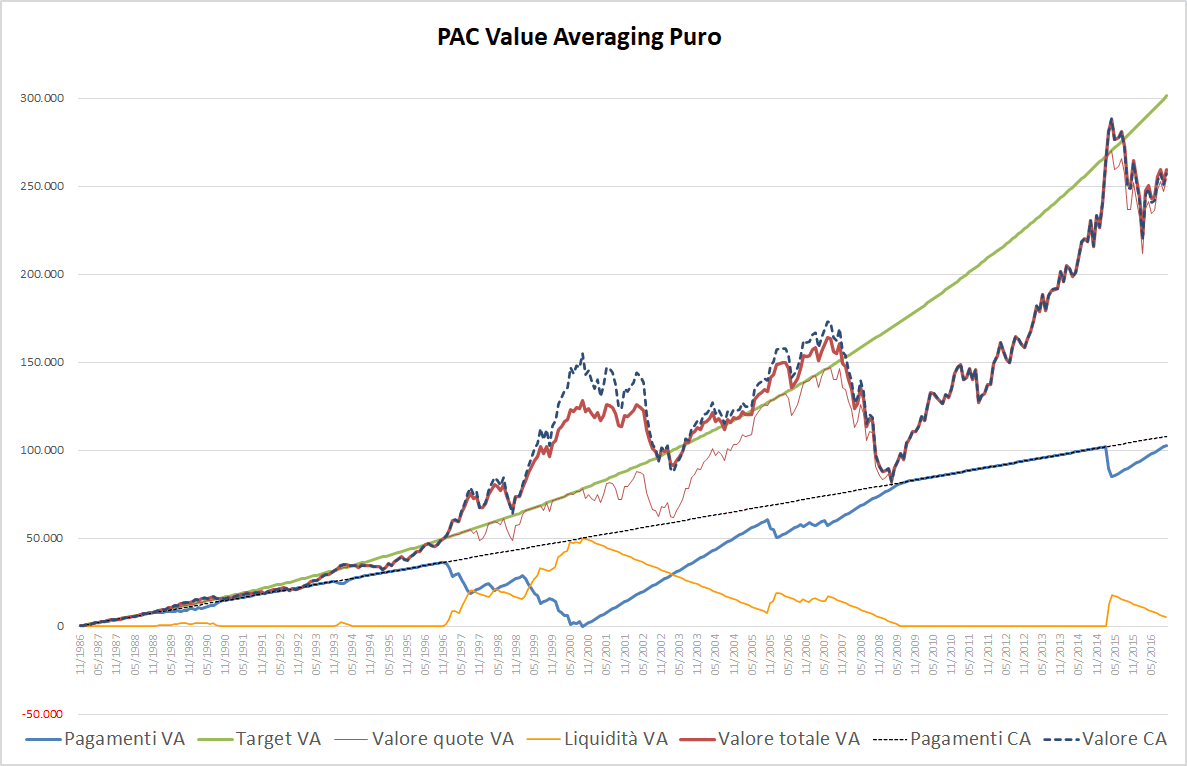
Fig. 17 – PAC Value Averaging puro. Rata iniziale: 300 euro. Incremento target: 0,50%. Versamento Massimo: 1000 euro. Filtro anti-Hayley: presente
Paradossalmente, con un massimale di 1000 euro questo specifico PAC avrebbe generato una somma finale superiore a quello non vincolato: 259.465 contro 256.800 euro.
Per finire, vediamo il grafico che limita i versamenti a 300 euro:
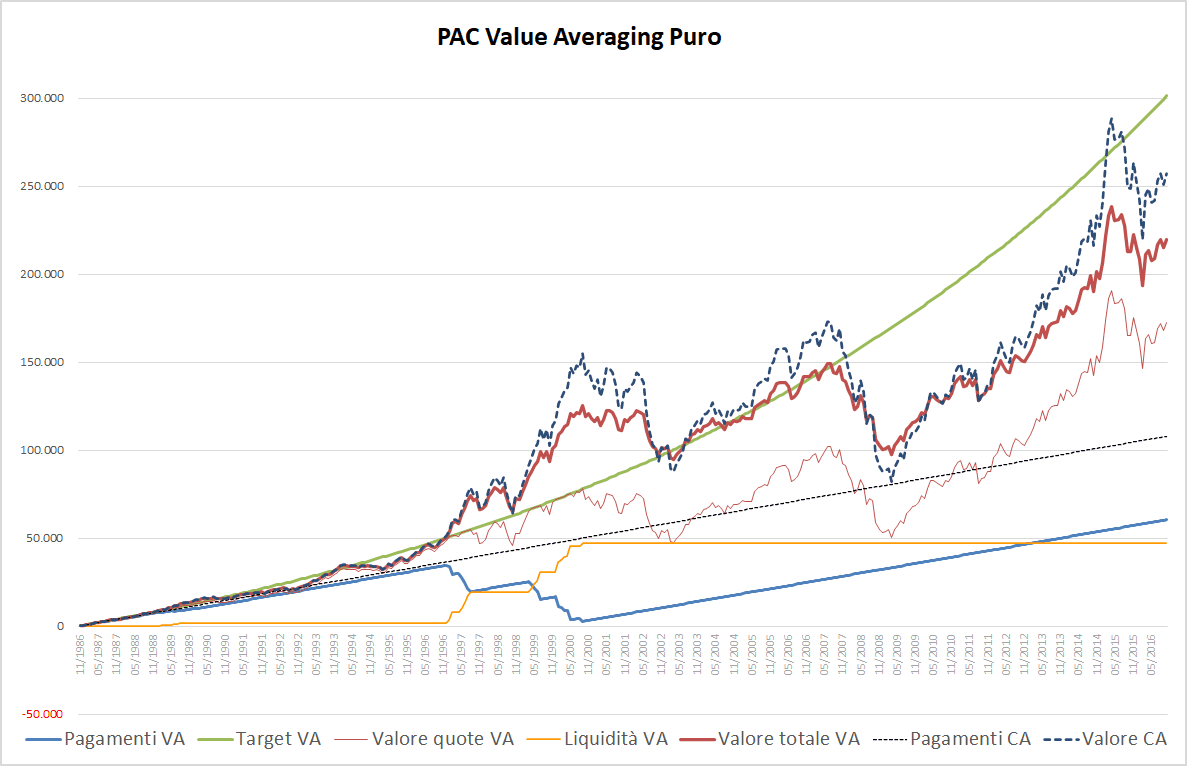
Fig. 18 – PAC Value Averaging puro. Rata iniziale: 300 euro. Incremento target: 0,50%. Versamento Massimo: 300 euro
Non è un’opzione conveniente, dato che non si può mai versare una rata di importo superiore a 300 euro, pur potendo vendere quote.
Il risultato finale è nettamente peggiore, in termini di somma finale disponibile, di quello del Value Averaging No-Sell equivalente. La presenza del filtro anti-Hayley è ininfluente, essendo impossibile versare più di 300 euro al mese.
Riassumiamo tutti i risultati ottenuti nella seguente tabella, che raggruppa le somme finali generate da tutte le tipologie di PAC analizzate finora:
| Singolo PAC mensile a 30 anni con rata/incremento target di 300 euro | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Mod. PAC | Tipol. | Increm. | Filtro Hayley | Rata max | Rend. dist. | Rend. corr. | Mont. PAC | Liquid. | Somma finale |
| CA | n/a | 0,00% | n/a | n/a | 138,44% | 138,44% | 257.517 | 0 | 257.517 |
| CA | n/a | 0,25% | n/a | n/a | 111,98% | 111,98% | 370.589 | 0 | 370.589 |
| CA | n/a | 0,50% | n/a | n/a | 89,82% | 89,82% | 572.038 | 0 | 572.038 |
| VA | No-Sell | 0,00% | NO | NO | 200,56% | 132,21% | 213.987 | 36.804 | 250.791 |
| VA | No-Sell | 0,25% | NO | NO | 171,75% | 171,75% | 304.668 | −4.115 | 300.554 |
| VA | No-Sell | 0,50% | NO | NO | 147,82% | 147,82% | 449.507 | −73.383 | 376.124 |
| VA | No-Sell | 0,00% | SI | NO | 200,16% | 132,13% | 213.987 | 36.710 | 250.697 |
| VA | No-Sell | 0,25% | SI | NO | 173,21% | 143,30% | 244.115 | 18.648 | 262.763 |
| VA | No-Sell | 0,50% | SI | NO | 144,44% | 144,44% | 263.992 | 0 | 263.992 |
| VA | No-Sell | 0,00% | NO | 1.000 | 230,34% | 106,31% | 164.661 | 58.154 | 222.815 |
| VA | No-Sell | 0,25% | NO | 1.000 | 184,85% | 135,64% | 225.732 | 28.754 | 254.487 |
| VA | No-Sell | 0,50% | NO | 1.000 | 146,94% | 146,94% | 312.675 | −18.619 | 294.055 |
| VA | No-Sell | 0,00% | SI | 1.000 | 229,88% | 106,25% | 164.661 | 58.084 | 222.746 |
| VA | No-Sell | 0,25% | SI | 1.000 | 183,07% | 135,17% | 225.732 | 28.254 | 253.987 |
| VA | No-Sell | 0,50% | SI | 1.000 | 146,50% | 146,50% | 266.219 | 0 | 266.219 |
| VA | Puro | 0,00% | NO | NO | 1.917,92% | 95,04% | 108.000 | 102.648 | 210.648 |
| VA | Puro | 0,25% | NO | NO | 425,83% | 131,09% | 174.821 | 74.754 | 249.575 |
| VA | Puro | 0,50% | NO | NO | 217,90% | 191,26% | 301.355 | 13.205 | 314.560 |
| VA | Puro | 0,00% | SI | NO | 1.895,15% | 94,99% | 108.000 | 102.587 | 210.587 |
| VA | Puro | 0,25% | SI | NO | 356,27% | 126,39% | 174.821 | 69.685 | 244.506 |
| VA | Puro | 0,50% | SI | NO | 137,78% | 137,78% | 256.800 | 0 | 256.800 |
| VA | Puro | 0,00% | NO | 1.000 | 1.098,05% | 91,45% | 107.757 | 99.006 | 206.763 |
| VA | Puro | 0,25% | NO | 1.000 | 442,89% | 120,51% | 159.539 | 78.613 | 238.152 |
| VA | Puro | 0,50% | NO | 1.000 | 217,00% | 161,19% | 254.310 | 27.775 | 282.085 |
| VA | Puro | 0,00% | SI | 1.000 | 1.093,83% | 91,42% | 107.757 | 98.974 | 206.731 |
| VA | Puro | 0,25% | SI | 1.000 | 436,31% | 120,18% | 159.539 | 78.252 | 237.791 |
| VA | Puro | 0,50% | SI | 1.000 | 147,28% | 140,25% | 254.310 | 5.156 | 259.465 |
Fig. 19 - Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging di un singolo PAC.
Quale sarebbe stata l’opzione migliore per questo specifico PAC?
Escludendo le simulazioni che hanno utilizzato extra-liquidità (valori in grigio, generati in assenza del filtro anti-Hayley), in ordine di somma finale disponibile troviamo:
- PAC Value Averaging No-Sell con incremento del target dello 0,50% e rata massima di 1000 euro (somma finale di 266.219 euro e rendimento del 146,50%).
- PAC Value Averaging No-Sell con incremento del target dello 0,50% senza rata massima (somma finale di 263.992 euro e rendimento del 144,44%).
- PAC Value Averaging No-Sell con incremento del target dello 0,25% senza rata massima (somma finale di 262.763 euro e rendimento del 143,30%).
Questi risultati ci permettono di trarre alcune conclusioni:
- Il PAC Cost Averaging non si classifica nelle prime 3 posizioni, che sono tutte appannaggio del Value Averaging
- Nella tabella è presente una colonna chiamata “Rendimento distorto”. È il rendimento che si ottiene ignorando la liquidità inutilizzata: se non si confrontano le somme finali disponibili – che includono anche la liquidità residua – questo rendimento trae in inganno. Quando la liquidità è pari a 0, il rendimento distorto coincide con quello corretto: in altre parole, la distorsione viene eliminata. Se la liquidità è alta, invece, la distorsione è altrettanto grande e, nei PAC puri a incremento costante, raggiunge valori irragionevoli (fino a quasi il 2000% quando, in realtà, il rendimento corretto è inferiore al 100%).
Gli investitori sono interessati a massimizzare la somma in euro generata dall’investimento. I rendimenti sono importanti ma ciò che conta di più sono gli euro. Per portare avanti un piano di accumulo Value Averaging, gli investitori non sono obbligati a creare un fondo di liquidità iniziale, ma devono quantomeno accantonare le rate non versate, che dovranno perciò essere conteggiate nel rendimento finale del PAC, anche nel caso in cui non vengano impiegate.
Il rendimento corretto è la misura giusta: include sia la somma investita nel fondo che la liquidità residua.
Avevamo introdotto questa problematica nella terza critica al Value Averaging: nel capitolo successivo vedremo la vera dimensione della distorsione causata e il modo di fronteggiarla.
Abbiamo scoperto diverse cose interessanti sul Value Averaging, ma abbiamo analizzato soltanto un piano di accumulo: il PAC mensile costruito sul fondo Raiffeisen Azionario Globale VT della durata di 30 anni (iniziato il 17/11/1986 e terminato il 17/10/2016).
È lecito chiedersi se le conclusioni a cui siamo arrivati siano soltanto il frutto del caso o possano essere generalizzate.
Per rispondere a questa domanda estenderemo l’analisi a tutti i possibili piano di accumulo simulabili su questo stesso fondo, utilizzando la serie storica che va dal 17/11/1986 al 15/11/2021: non soltanto piani trentennali, ma anche di più corta durata (25, 20, 15, 10, 9, 8, 7, 6, 5, 4, 3 e 2 anni).
In seguito, estenderemo l’analisi anche ad altri fondi.
6. Value Averaging vs Cost Averaging: simulazione di migliaia di PAC su un unico fondo

«If I could explain it to the average person, it wouldn't have been worth the Nobel Prize».
Richard P. Feynman
Passiamo al backtest di un numero molto più elevato di Piani di Accumulo del Capitale Value Averaging e Cost Averaging sul fondo Raiffeisen Azionario Globale VT.
Oltre ai trentennali, saranno simulati i piani di accumulo delle seguenti durate: 2, 3, 4, 5, 6, 7, 8, 9, 10, 15, 20 e 25 anni. L’ammontare della rata sarà ancora pari a 300 euro. Il periodo di analisi è compreso tra novembre 1986 e novembre 2021.
Nei risultati, vengono adesso incluse anche le commissioni di transazione: 9 euro all’inizio del PAC (pagate insieme alla prima rata) e 0,95 euro per ogni acquisto o vendita successiva.
Il giorno del pagamento delle rate (o di eventuali vendite di quote) è il 15 di ogni mese o il primo giorno di borse aperte successivo, nel caso in cui il 15 cada di sabato, domenica o altro giorno festivo.
Simuleremo tutte le varianti di Value Averaging che possono essere analizzate nella sezione Analisi PAC di Dedalo Invest e le confronteremo con i piani di accumulo Cost Averaging di pari rata e durata.
Partiamo dall’analisi dei PAC Cost Averaging:
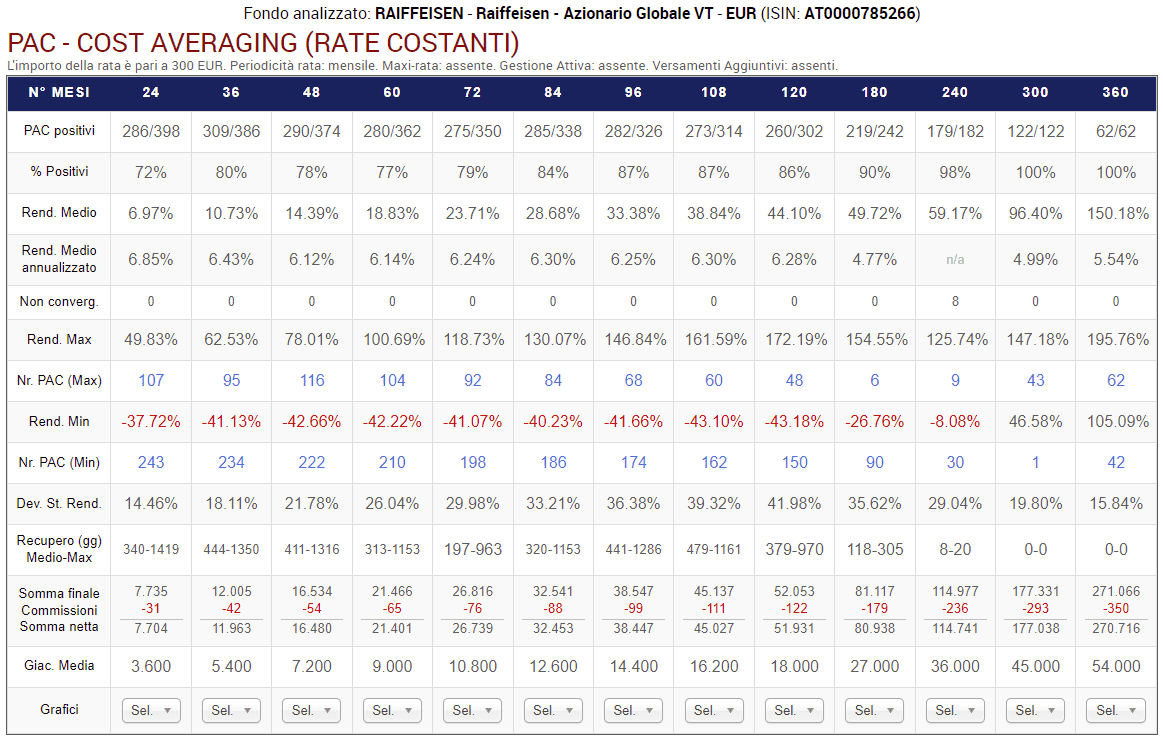
Fig. 20 – PAC Cost Averaging. Rata: 300 euro
Questa tabella costituisce il punto di riferimento di tutte quelle seguenti: con questa tabella saranno confrontati i risultati delle diverse tipologie di Value Averaging.
Il piano di accumulo Cost Averaging trentennale analizzato in precedenza aveva generato 257.517,32 euro con un rendimento del 138,44%. I piani Cost Averaging di durata trentennale sono adesso 62 (ultima colonna sulla destra), con una somma netta finale media di 270.716 euro, circa 13.000 euro in più.
Il piano di accumulo analizzato nel capitolo precedente è il primo di questi 62 ed è, evidentemente, un PAC che ha performato sotto la media.
6.1 Value Averaging No-Sell
Vediamo adesso alcune tipologie di Piano di accumulo Value Averaging No-Sell. Iniziamo l'analisi con le seguenti impostazioni:
- Target costante.
- Assenza di massimale.
- Filtro anti-Hayley disattivato.
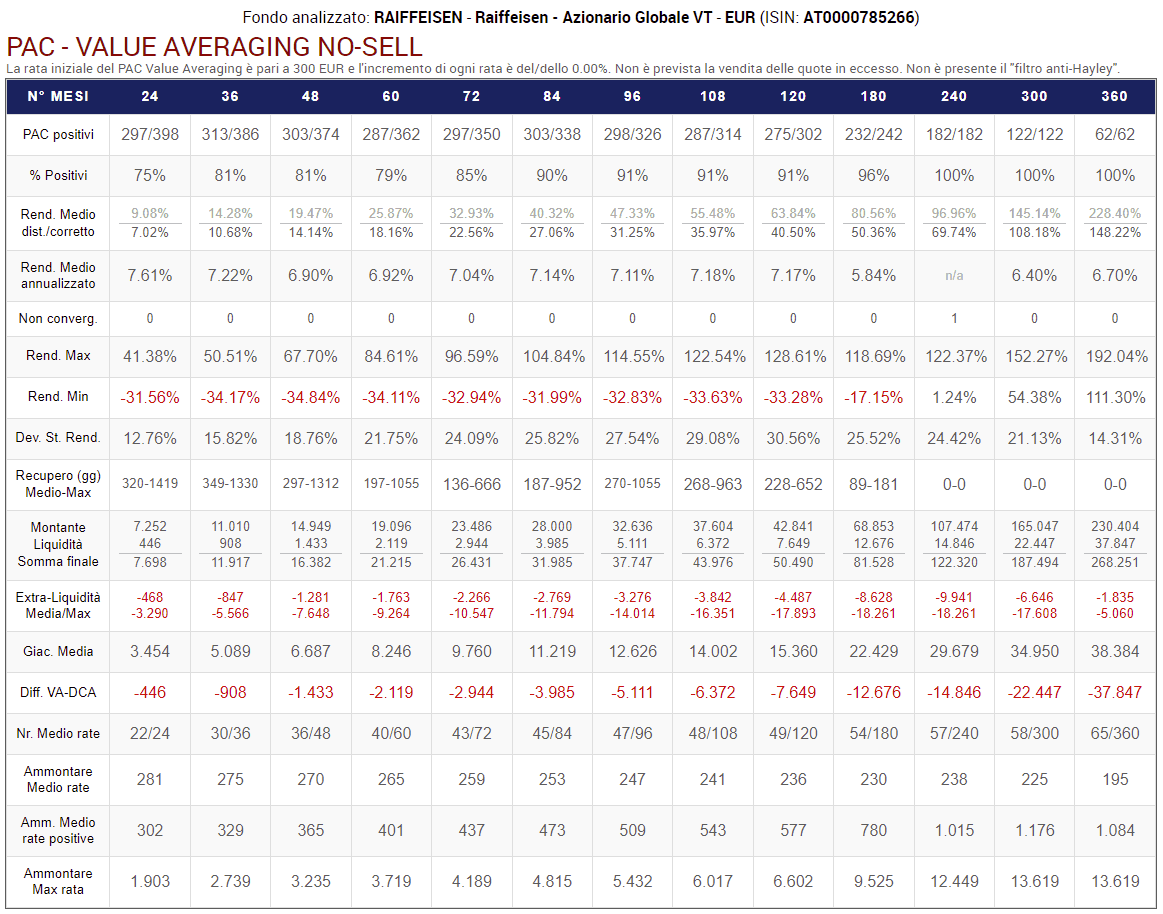
Fig. 21 – PAC Value Averaging No-Sell. Rata iniziale: 300 euro. Target costante. Versamento massimo non previsto. Filtro anti-Hayley: assente
La tabella fornisce molte informazioni, che saranno commentate e confrontate con quelle del Cost Averaging:
- Il numero e la percentuale di piani di accumulo positivi sono superiori (o uguali) in ogni durata. Ad esempio, 3 PAC Cost Averaging su 182 della durata di 20 anni hanno prodotto un rendimento negativo: tutti i PAC Value Averaging, invece, sono risultati positivi.
- Vengono visualizzati due rendimenti medi: il primo, in grigio più chiaro, è il rendimento medio distorto, ovvero quello calcolato senza tenere conto della liquidità residua. Il secondo rendimento medio è corretto: in alcune durate, è inferiore a quello dei PAC Cost Averaging (3, 4, 5, 6, 7, 8, 9, 10 e 30 anni); in altre, è superiore (2, 15, 20 e 25 anni). Il rendimento distorto, invece, sarebbe stato sempre nettamente superiore. Questi risultati aiutano a capire l’entità della distorsione di cui avevamo accennato nella parte finale del capitolo precedente e nella terza critica al Value Averaging.
- I rendimenti annualizzati sono più elevati: 7,61% contro 6,85% nei PAC della durata più breve (2 anni); 6,70% contro 5,54% nei piani di accumulo di durata massima. Vedremo in seguito quanto questa differenza sia causata da due distorsioni: quella originata dalla liquidità residua e quella evidenziata da Hayley, che era alla base della quinta critica al Value Averaging. Per questo motivo, i rendimenti annualizzati sono la misura meno affidabile nella valutazione del Value Averaging.
- I rendimenti massimi e minimi sono, rispettivamente, inferiori e superiori a quelli dei piani di accumulo Cost Averaging di pari durata. Questi valori sono corretti e costituiscono un primo indizio di come i rendimenti del Value Averaging siano meno volatili di quelli del Cost Averaging.
- La miglior riprova della minore volatilità viene fornita dalla deviazione standard dei rendimenti finali, che nei PAC Value Averaging è nettamente inferiore a quella dei Cost Averaging, in quasi tutte le durate. È un risultato importante, perché gli investitori sono spesso disposti a rinunciare ad un po’ di rendimento atteso in cambio di un rischio minore.
- I periodi di recupero medi e massimi del Value Averaging sono sempre inferiori o uguali a quelli del Cost Averaging. Un periodo di recupero più corto è preferibile: nei PAC in perdita (eventualità che nessuna strategia di investimento riuscirà mai a evitare nel 100% dei casi), il numero di giorni che devono trascorrere prima che un investimento in perdita torni in parità è minore.
- Giacenza media: è minore nei piani di accumulo Value Averaging. Giacenza media e liquidità residua sembrano essere grandezze inversamente proporzionali. Una giacenza media bassa si verifica, di solito, in concomitanza di PAC Value Averaging dall’alta liquidità residua. L’assenza di liquidità residua non comporta necessariamente una giacenza media uguale a quella di un PAC Cost Averaging: tuttavia, è probabile che vi si avvicini sensibilmente.
- Montante/Liquidità/Somma finale: Il montante è il valore delle quote che, a fine investimento, risultano ancora investite. La liquidità (residua) è la somma non investita che, a fine PAC, sarà rimasta sul conto corrente o sul conto deposito (è sempre pari a 0 in un PAC Cost Averaging). La somma finale è la cifra totale generata dal piano di accumulo e si ottiene addizionando il montante con la liquidità.
La somma finale generata dai PAC Value Averaging è superiore a quella dei Cost Averaging soltanto per le durate pari a 15, 20 e 25 anni. L’utilizzo di un target crescente dovrebbe permettere di migliorare questo risultato.
La tabella dei risultati dell'analisi dei PAC Value Averaging dispone di alcune misure statistiche che non sono presenti nel Cost Averaging:
- Extra-liquidità Media/Max: quando non si applica il filtro anti-Hayley, è molto probabile che durante la vita dei piani di accumulo debba essere impiegata extra-liquidità. Anche quando a fine investimento rimane molta liquidità inutilizzata, ci potrebbero essere stati dei momenti precedenti in cui un po’ di extra-liquidità sarebbe servita. Le due misure importanti da conoscere sono il valore medio e il valore massimo di extra-liquidità richiesta da tutti i piani di accumulo per ogni durata. Anche in caso di media positiva, è possibile che alcuni PAC non ne abbiano fatto uso. Vedremo in seguito come sfruttare queste informazioni.
- Differenza tra i pagamenti cumulati di un piano di accumulo Value Averaging e di un Cost Averaging: si tratta della liquidità inutilizzata a fine investimento (con segno opposto) e non comprende eventuali fondi di liquidità iniziali.
- Numero medio delle rate versate: nel Value Averaging, i versamenti sono generalmente inferiori al numero dei mesi. Questa differenza cresce con l’aumentare della lunghezza dei piani di accumulo (nei PAC di 24 mesi sono state mediamente versate 22 rate, il 92% del totale; in quelli di 360 mesi, sono state versate 65 rate, soltanto il 18% del totale).
- Ammontare medio delle rate versate (rate nulle incluse): nei piani di accumulo brevi è di poco inferiore alla rata iniziale di 300 euro. In quelli più lunghi, questa differenza cresce: ad esempio, l’ammontare medio delle rate versate nei PAC a 30 anni è di soli 195 euro.
- Ammontare medio delle sole rate positive: è una misura simile a quella appena vista, ma esclude le rate nulle (e le vendite, nel Value Averaging puro). Il valore è ovviamente più alto del precedente. L’importo medio di tutte le rate moltiplicato per il numero di rate previste da un PAC dovrà essere uguale all’importo medio delle sole rate positive moltiplicato per il numero di rate effettivamente versate. Nei piani trentennali, ad esempio, 195 x 360 = 1084 x 65 (la differenza è dovuta alle approssimazioni ai valori interi sia degli importi medi che del numero di rate).
- Ammontare massimo versato: identifica il valore della più alta rata versata. È l’importo più elevato in assoluto tra quelli versati in tutti i piani di accumulo di una certa durata; non si tratta quindi di una media delle rate più alte. La seconda critica al Value Averaging si riferiva proprio all’ammontare molto alto di alcuni versamenti, che adesso possono essere misurati con precisione. Sono valori significativi: dai 300 euro iniziali si arriva fino a 1.903 euro nei piani a 24 rate e addirittura a 13.619 euro in quelli a 360 rate.
Vista l’entità dell'ammontare massimo versato, verrebbe da pensare che il Value Averaging sia per i pochi fortunati che possono disporre in ogni momento di grosse somme liquide. In realtà, anche se i piani di accumulo Value Averaging No-Sell non richiedono mai la vendita di quote, molti dei versamenti previsti non vengono effettuati. Ogni volta che questo accade, è possibile (e consigliabile) accantonare quei 300 euro non investiti, magari in un conto deposito dedicato. Le somme accumulate permetteranno, in molti casi, di fronteggiare il versamento di eventuali maxi-rate future.
Alcune volte, potrebbe accadere che una maxi-rata sia superiore alla liquidità accumulata. La critica di Hayley è generica, ma dovrebbe invece focalizzarsi su queste specifiche somme, che il Value Averaging assume implicitamente che siano sempre disponibili.
Quando questo avviene, il calcolo del rendimento totale ed annualizzato risulterà distorto: sarà superiore al “vero” rendimento, perché avrà ignorato che quelle somme, per essere prontamente utilizzabili al momento giusto, potrebbero essere state per anni ferme su un conto corrente infruttifero o investite al tasso privo di rischio.
Vedremo in seguito quale sarà l’impatto – in termini di minor rendimento – delle misure da adottare per aggirare questo problema.
Passiamo ai risultati dei backtest con incremento del target dello 0,25%:
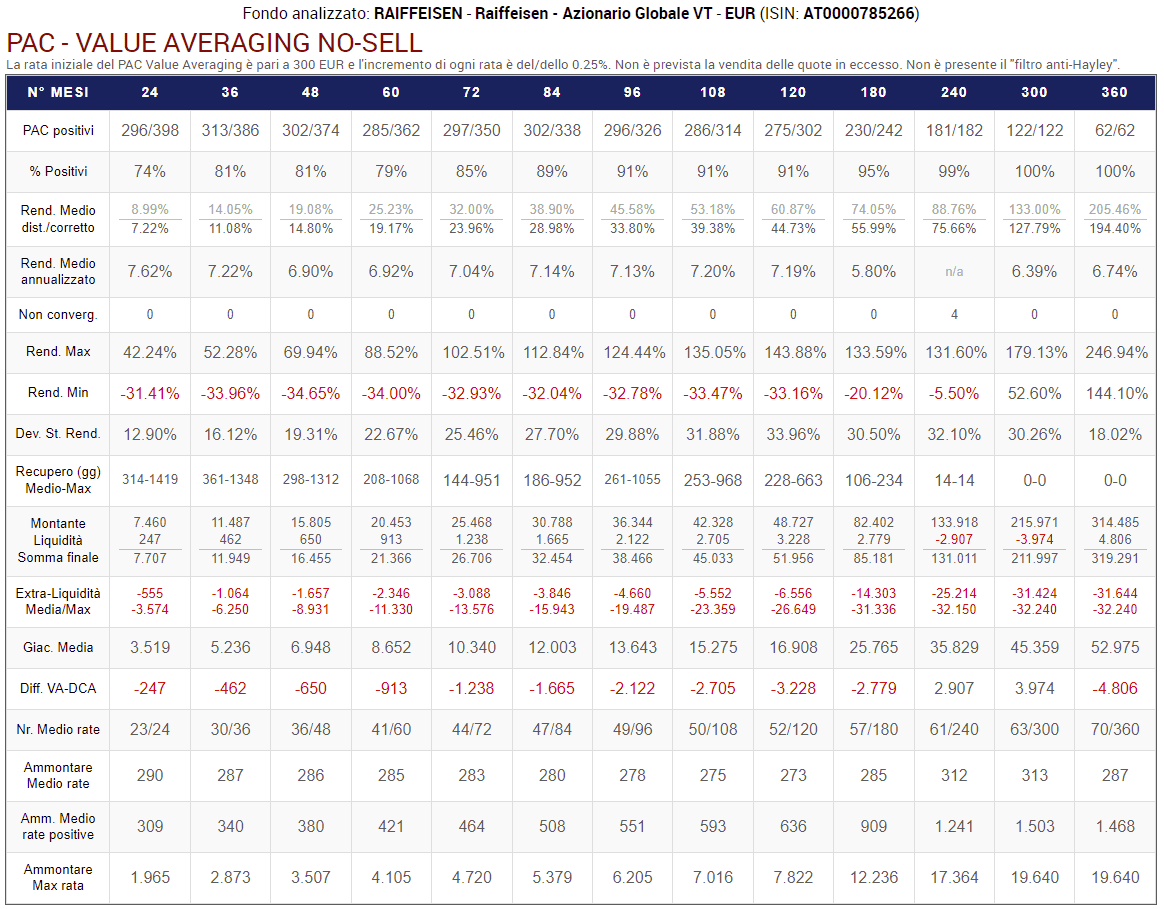
Fig. 22 – PAC Value Averaging No-Sell. Rata iniziale: 300 euro. Incremento target: 0,25%. Versamento massimo non previsto. Filtro anti-Hayley: assente
In un piano di accumulo Value Averaging con incremento del target dello 0,25%, quest'ultimo crescerà di:
- Prima rata: 300 * (1 + 0,0025)rate versate - 1 = 300 * (1 + 0,0025)0 = 300 * 1 = 300 euro.
- Seconda rata: 300 + 300 * (1 + 0,0025)1 = 300 + 300,625 = 600,625 (incremento di 300,625 euro).
- Terza rata: 600,625 + 300 * (1 + 0,0025)2 = 600,625 + 301,50 = 902,125 (incremento di 301,50 euro).
- Quarta rata: 902,125 + 300 * (1 + 0,0025)3 = 902,125 + 302,26 = 1.204,39 (incremento di 302,26 euro).
- …
I risultati sono incoraggianti: il rendimento medio corretto di tutti i piani di accumulo cresce notevolmente mentre quello annualizzato (distorto) rimane sugli stessi livelli.
Il valore medio delle rate si è avvicinato molto ai 300 euro e, data l’assenza del filtro di Hayley, li ha superati in alcuni casi (è compreso tra 273 e 313 euro).
Il numero medio di rate versate è anch’esso cresciuto, pur rimanendo ancora molto inferiore a quello del Cost Averaging. La stessa dinamica viene seguita dall’ammontare massimo delle rate (che sfiora i 20 mila euro nelle durate di 25/30 anni).
A questo punto bisogna prendere le giuste contromisure per neutralizzare le distorsioni segnalate da Hayley. Attiviamo quello che abbiamo battezzato “filtro anti-Hayley”: si tratta di un limite, imposto ai versamenti, affinché non eccedano il fondo di liquidità costituitosi dalle rate non versate o non interamente versate durante la vita del piano di accumulo (e dalle vendite, nel Value Averaging puro).
Non si accantona liquidità all’inizio del PAC.
I rendimenti totali e annualizzati del Value Averaging saranno adesso corretti e potranno essere confrontati con quelli del Cost Averaging.
Ecco i risultati applicando il filtro:
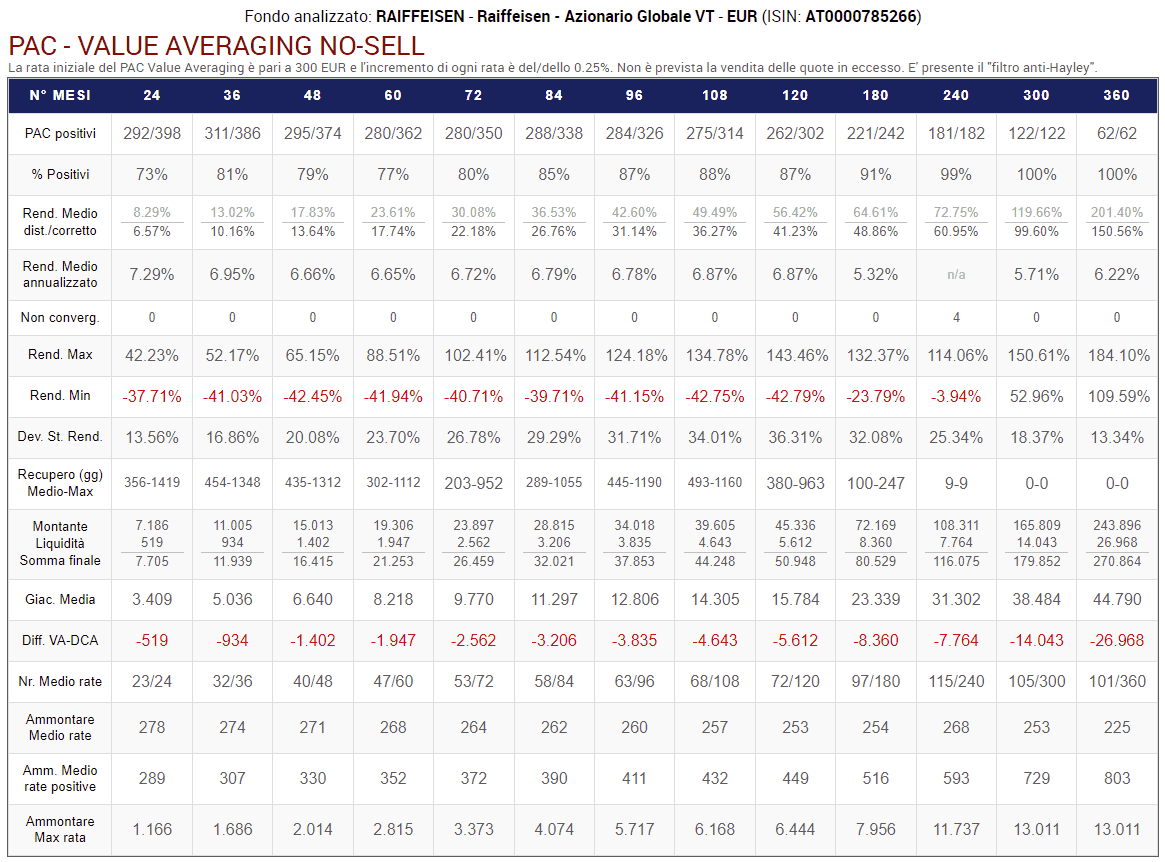
Fig. 23 – PAC Value Averaging No-Sell. Rata iniziale: 300 euro. Incremento target: 0,25%. Versamento massimo non previsto. Filtro anti-Hayley: presente
Le differenze con la tabella precedente sono considerevoli. I rendimenti totali ed annualizzati non distorti, come giustamente previsto da Hayley, sono inferiori. In generale, quasi tutte le misure calcolate sono peggiori.
In questa tabella, l’Extra-Liquidità Media/Max non viene visualizzata, dato che con l’applicazione del filtro di Hayley è sempre pari a 0.
Il confronto con la tabella dei risultati del Cost Averaging, invece, è ancora a favore dei PAC Value Averaging sulle durate più lunghe. Le differenze, però, si sono ridotte.
Rispetto al Cost Averaging rimangono tuttavia delle grosse differenze in termini di giacenza media e ammontare medio delle rate: il Value Averaging ha ancora un margine di miglioramento.
Incrementiamo il target allo 0,50%:
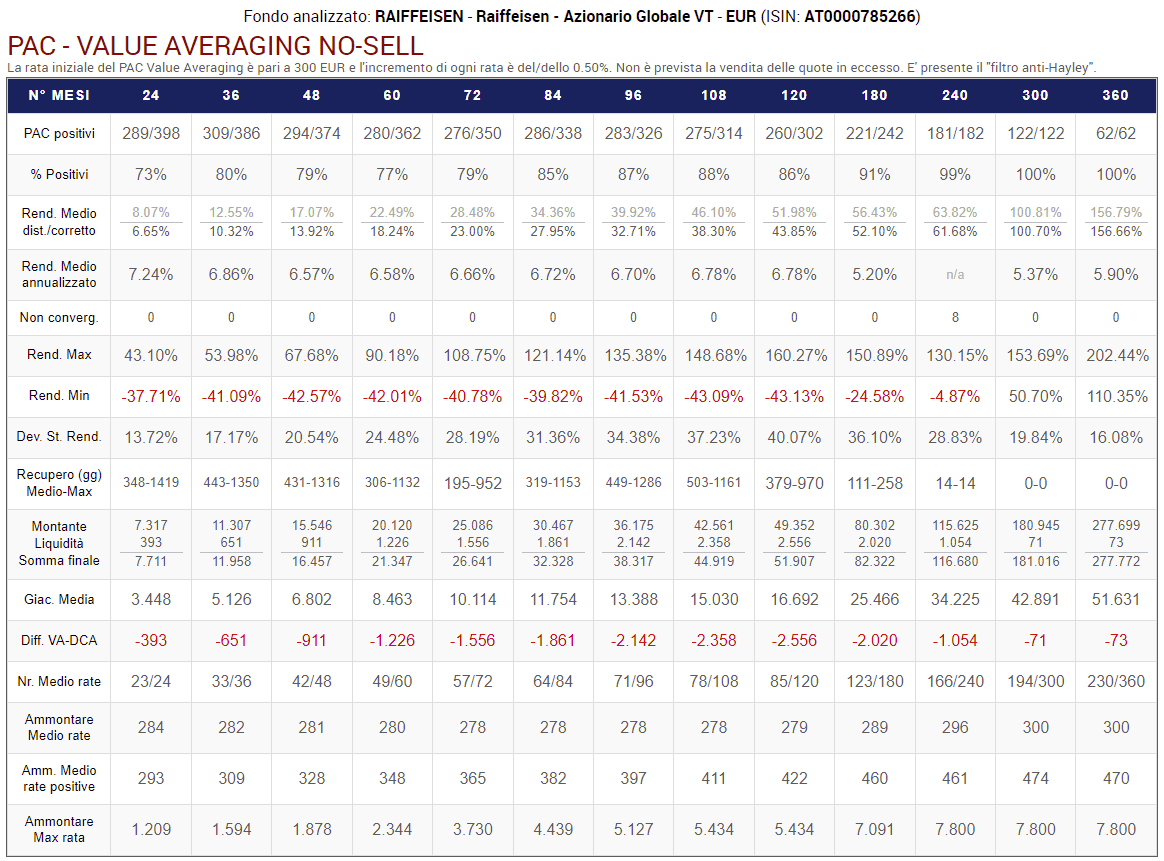
Fig. 24 – PAC Value Averaging No-Sell. Rata iniziale: 300 euro. Incremento target: 0,50%. Versamento massimo non previsto. Filtro anti-Hayley: presente
I cambiamenti principali nei risultati sono i seguenti:
- I rendimenti medi vengono nuovamente ritoccati verso l’alto. A partire dalla durata di 15 anni (180 mesi) superano quelli del Cost Averaging.
- La giacenza media si avvicina molto a quella del Cost Averaging.
- La liquidità residua si mantiene leggermente positiva per la maggior parte delle durate e nei PAC di 25 e 30 anni è di poche decine di euro (71 e 73): abbiamo perciò investito quasi tutti i 90.000 e 108.000 euro che erano stati destinati ai PAC. Siamo riusciti a neutralizzare la terza critica al Value Averaging, almeno per quanto riguarda i piani di accumulo di più lunga durata.
- Il numero medio di rate versate cresce tantissimo, soprattutto nei PAC più lunghi.
- L’ammontare medio delle rate cresce: tocca i 300 euro nei PAC a 25 e 30 anni e si avvicina molto a questa soglia in tutte le altre durate dei PAC.
- L’ammontare medio delle sole rate positive e quello del massimo versamento diminuiscono significativamente. Il filtro anti-Hayley riduce la distanza tra il Value Averaging e il Cost Averaging.
Aggiungiamo adesso un ulteriore vincolo: un limite massimo all’importo di ogni versamento, che non potrà superare i 1000 euro.
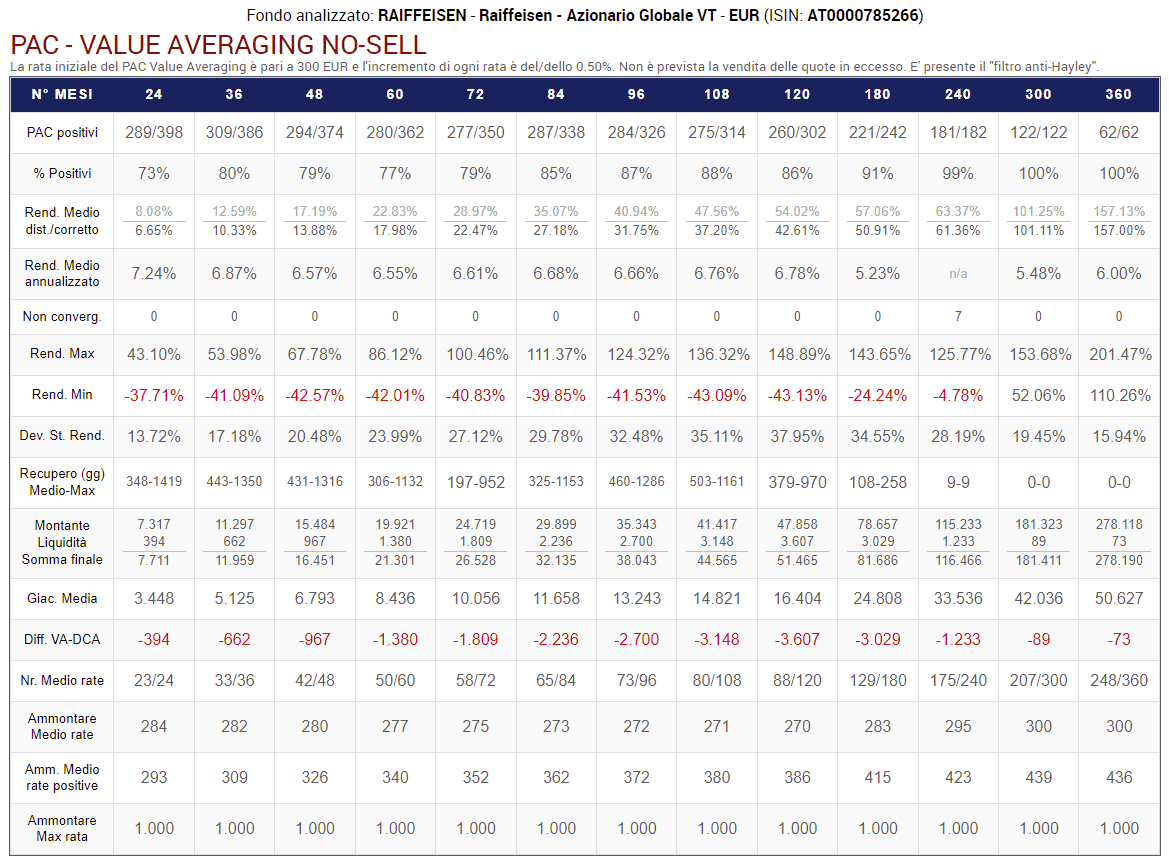
Fig. 25 – PAC Value Averaging No-Sell. Rata iniziale: 300 euro. Incremento target: 0,50%. Versamento massimo: 1000 euro. Filtro anti-Hayley: presente
L’imposizione di un massimale produce l’effetto di spalmare eventuali maxi-rate in più versamenti dell’importo di 1000 euro. I risultati sono molto simili ai precedenti.
In definitiva, le somme finali generate dai piani di accumulo Value Averaging No-Sell sono superiori a quelle dei corrispondenti piani Cost Averaging su durate maggiori o uguali a 15 anni.
Tanto più un PAC è lungo, tanto maggiore sembra essere l’extra-performance del Value Averaging sul Cost Averaging.
Nei piani di accumulo più corti, il Cost Averaging ha generato somme leggermente superiori. Tuttavia, col Value Averaging le percentuali di PAC positivi non sono mai inferiori e la deviazione standard dei rendimenti finali è quasi sempre più bassa.
I PAC Value Averaging sembrano quindi essere meno rischiosi dei Cost Averaging e, sulle durate più lunghe, più redditizi di questi ultimi.
6.2 Value Averaging Puro
Passiamo adesso all’analisi dei PAC Value Averaging puri.
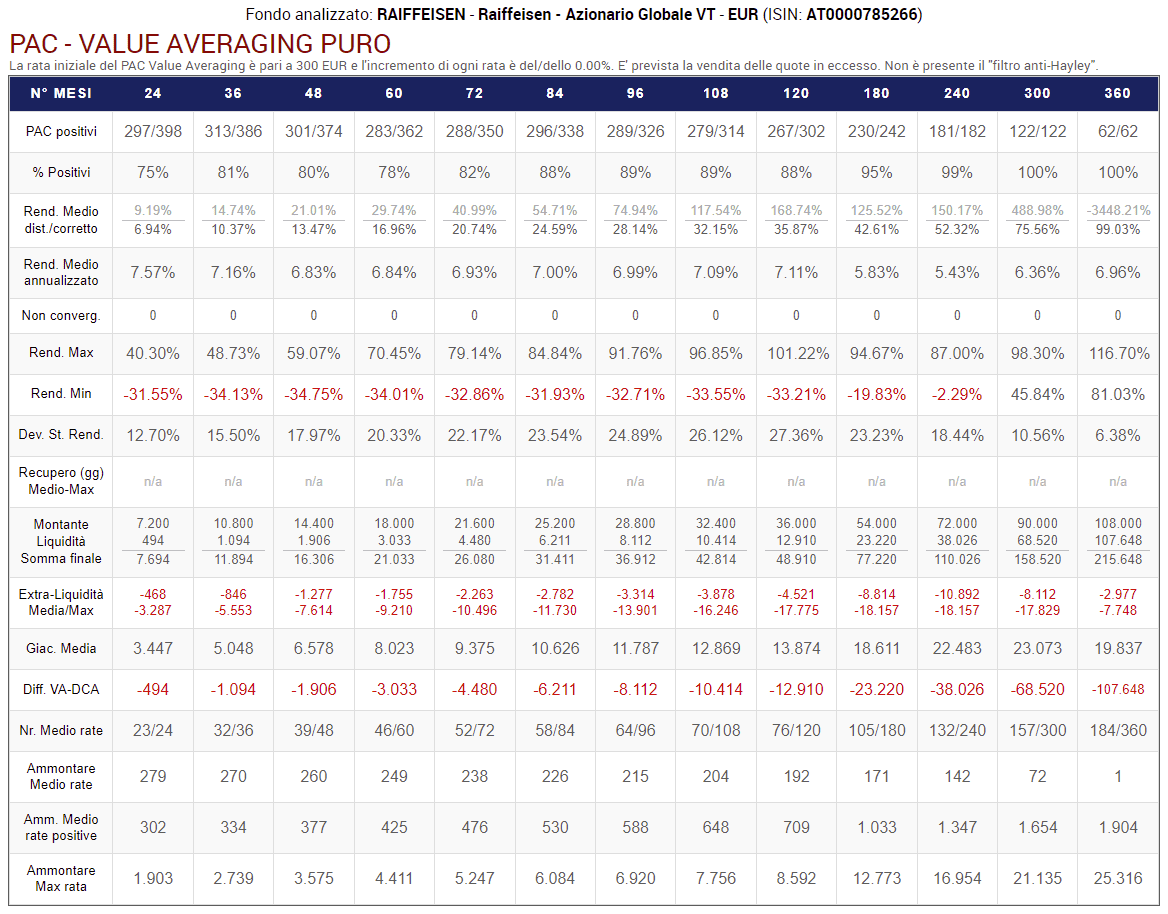
Fig. 26 – PAC Value Averaging puro. Rata iniziale: 300 euro. Target costante. Versamento massimo non previsto. Filtro anti-Hayley: assente
In questa tabella, vengono riportati i risultati dei piani di accumulo Value Averaging puri: sono quelli che prevedono la vendita di quote quando il valore corrente di queste ultime è superiore al target.
Questa prima versione prevede incrementi del target costanti, l’assenza del filtro anti-Hayley e del massimale ai versamenti.
Le percentuali di successo sono alte, anche nei piani di breve durata (75-81% per i PAC di 2 e 3 anni).
I rendimenti medi sono inferiori sia a quelli generati dal Value Averaging No-Sell, sia a quelli del Cost Averaging. L’ammontare massimo delle rate è in linea con il No-Sell.
I rendimenti medi annualizzati si attestano intorno al 7% ma, dal momento che il filtro anti-Hayley non è stato attivato, sono distorti.
Delle differenze importanti sono invece presenti nel numero medio di rate versate e nell’ammontare medio delle rate a partire dalle durate di 4-5 anni: col crescere della lunghezza dei piani di accumulo, l’ammontare medio diminuisce drasticamente (bisogna ricordarsi che adesso abbiamo anche rate di importo negativo, quelle che originano le vendite), mentre l’ammontare medio delle sole rate positive segue il trend inverso: cresce sensibilmente con l’aumentare delle durate dei PAC.
La giacenza media è molto più bassa: in questi piani di accumulo, i disinvestimenti sono frequenti.
La misura più sorprendente è la differenza nella liquidità residua tra il Value Averaging puro ed il Cost Averaging: addirittura superiore ai 100.000 euro nei piani più lunghi. Non è un errore di calcolo e questo risultato non deve meravigliare più di tanto: significa semplicemente che al termine del PAC una buona parte di quote è già stata liquidata.
Dato che nel Value Averaging puro le vendite si effettuano quando i prezzi sono più alti, alla fine dell’investimento dovremmo aver già ottenuto dei buoni rendimenti dalle quote vendute, mentre una cospicua parte di esse sarà ancora investita (anche questa sembra una contraddizione ma non lo è: basta ricordarsi della linea blu e di quelle rosse nei grafici del piano di accumulo analizzato nel capitolo precedente).
Il Value Averaging puro ha un'altra peculiarità: se nel Value Averaging No-Sell dalla durata più lunga (30 anni) il totale dei versamenti era stato pari a 70.460 euro (rata media di 195 euro x 360 rate, o rata positiva media di 1.084 euro x 65 rate), nel Value Averaging puro la cifra totale versata è salita in modo esponenziale: 350.336 euro (rata media di 1.904 euro x 184 rate versate). La differenza è enorme, ma è dovuta all’alternanza dei flussi monetari in entrata e in uscita: gran parte di questa somma è stata generata dai continui investimenti e disinvestimenti di denaro.
In altre parole, nei piani di accumulo Value Averaging No-Sell (così come in quelli Cost Averaging) il denaro investito è sempre denaro “fresco”; nei PAC Value Averaging puri, invece, il denaro già investito può essere reimpiegato.
Questo fenomeno è positivo e costituisce il fulcro della filosofia di investimento del Value Averaging: generare valore senza dover necessariamente apportare denaro fresco ogni volta che si effettua un versamento.
Anche nei piani di breve durata si verifica lo stesso fenomeno, seppure in maniera molto limitata. Nei PAC No-Sell della durata di 2 anni (24 rate), erano state mediamente versate 22 rate da 302 euro ciascuna; nel Value Averaging puro, sono state versate 23 rate da 302 euro ciascuna. In entrambi i casi, la rata più alta è stata di 1.903 euro.
Incrementiamo adesso il target dello 0,25%.
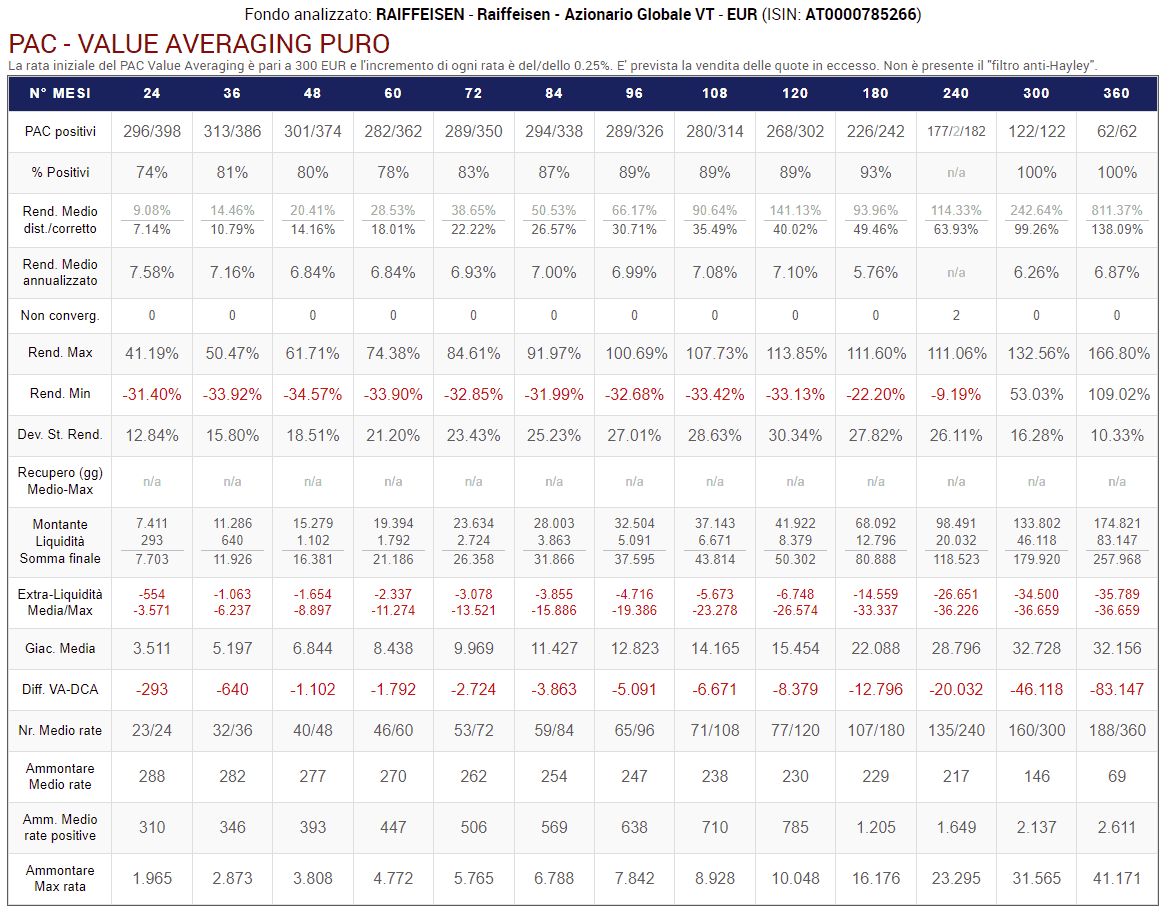
Fig. 27 – PAC Value Averaging puro. Rata iniziale: 300 euro. Incremento target: 0,25%. Versamento massimo non previsto. Filtro anti-Hayley: assente
Rispetto ai PAC precedenti, si sono verificati i seguenti cambiamenti:
- I rendimenti medi sono più alti.
- La giacenza media è cresciuta (quasi raddoppiata nei piani di accumulo più lunghi); la liquidità residua a fine investimento è diminuita mentre l’extra-liquidità media e massima utilizzata durante la vita del PAC è aumentata.
- È leggermente aumentato il numero di rate versate.
- È cresciuto l’ammontare medio delle rate e delle sole rate positive. Nei PAC più lunghi, l’incremento è considerevole (la media totale è passata da 192/171/142/72/1 a 230/229/217/146/69 euro nei PAC a 10, 15, 20, 25 e 30 anni; la media delle rate positive, da 709/1033/1347/1654/1904 a 785/1205/1649/2137/2611 euro).
- L’ammontare massimo delle rate è superiore.
I risultati sono incoraggianti ma distorti, dato che il filtro anti-Hayley non è stato attivato.
Il passo successivo sarà perciò quello di applicarlo, nella speranza che le performance non ne risentano eccessivamente.
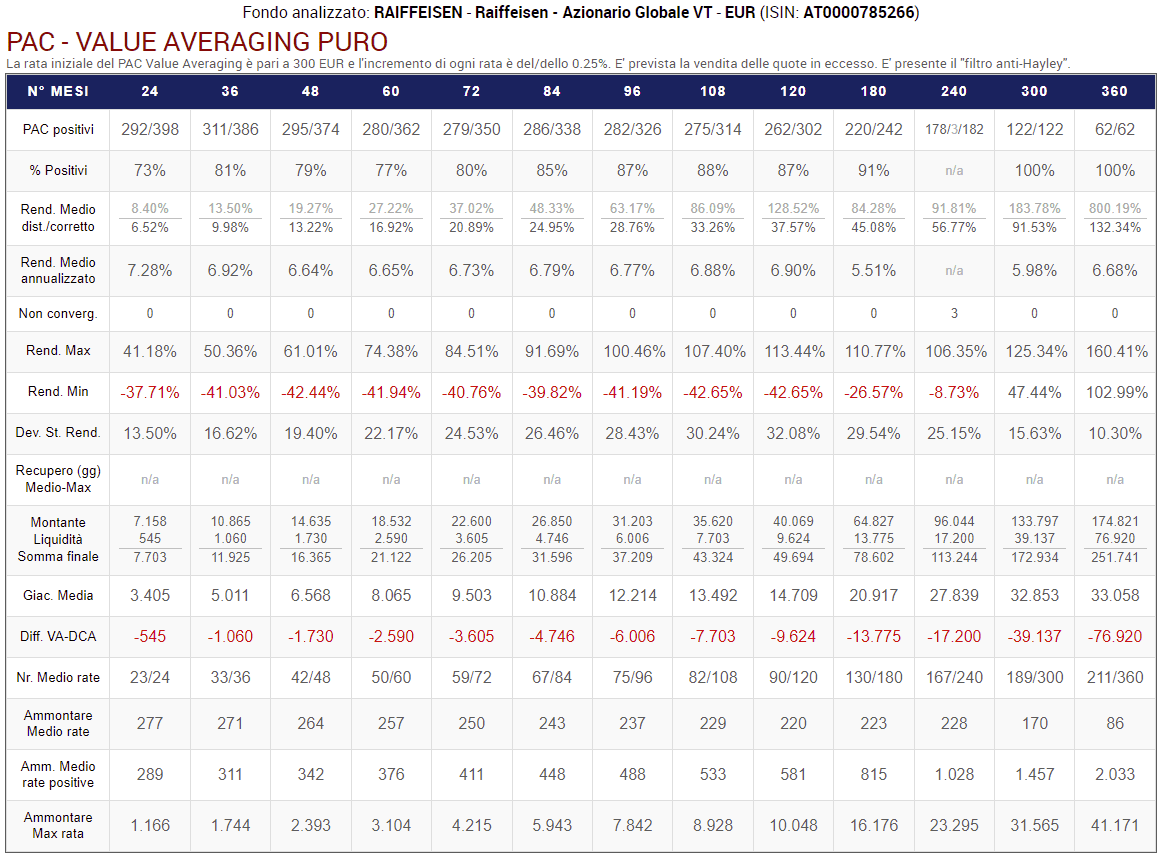
Fig. 28 – PAC Value Averaging puro. Rata iniziale: 300 euro. Incremento target: 0,25%. Versamento massimo non previsto. Filtro anti-Hayley: presente
I risultati sono buoni, nonostante la presenza del filtro faccia diminuire i rendimenti e la somma finale generata dai PAC.
Tra gli aspetti positivi, ci sono il maggior numero medio di rate e valori più contenuti dell’ammontare medio delle rate positive. Le potenzialità del Value Averaging non sembrano essere messe in discussione.
Per rendere più efficiente l’impiego del capitale disponibile, aumentiamo ulteriormente l’incremento percentuale del target, portandolo allo 0,50%.
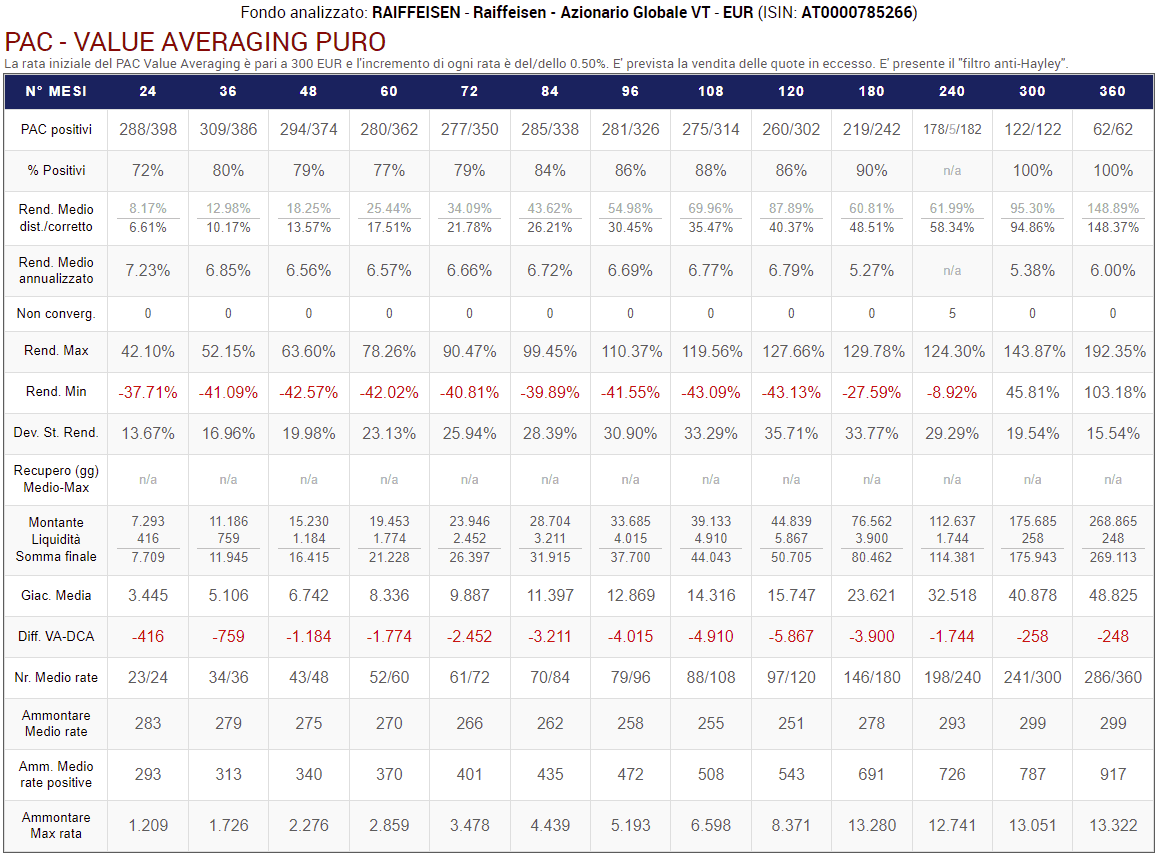
Fig. 29 – PAC Value Averaging puro. Rata iniziale: 300 euro. Incremento target: 0,50%. Versamento massimo non previsto. Filtro anti-Hayley: presente
Analizziamo i risultati:
- I rendimenti medi non distorti migliorano ancora.
- La giacenza media è più elevata e si avvicina a quella dei piani di accumulo a rate costanti.
- La liquidità residua continua ad essere presente, anche se nei piani a 25 e a 30 anni è molto piccola. Considerando che con il filtro anti-Hayley attivato la liquidità residua non può essere negativa, significa che su queste durate abbiamo investito quasi tutti gli euro che erano stati destinati ai piani di accumulo (90.000 e 108.000 euro). Siamo di nuovo riusciti a neutralizzare quasi totalmente la terza critica al Value Averaging, almeno nei piani dalla durata più lunga, dove il rendimento medio distorto è vicinissimo a quello corretto (nelle altre durate, le differenze sono più marcate).
- Il numero medio di rate versate cresce molto, soprattutto nei PAC più lunghi.
- L’ammontare medio delle rate cresce anch’esso: sfiora i 300 euro nei piani di accumulo più lunghi e si avvicina molto a questa soglia anche in quelli brevi.
Queste osservazioni sono abbastanza simili a quelle relative ai Piani di Accumulo del Capitale Value Averaging No-Sell. II risultati sono convincenti: affrontiamo adesso l’ultimo backtest, aggiungendo il limite massimo per versamento di 1000 euro.
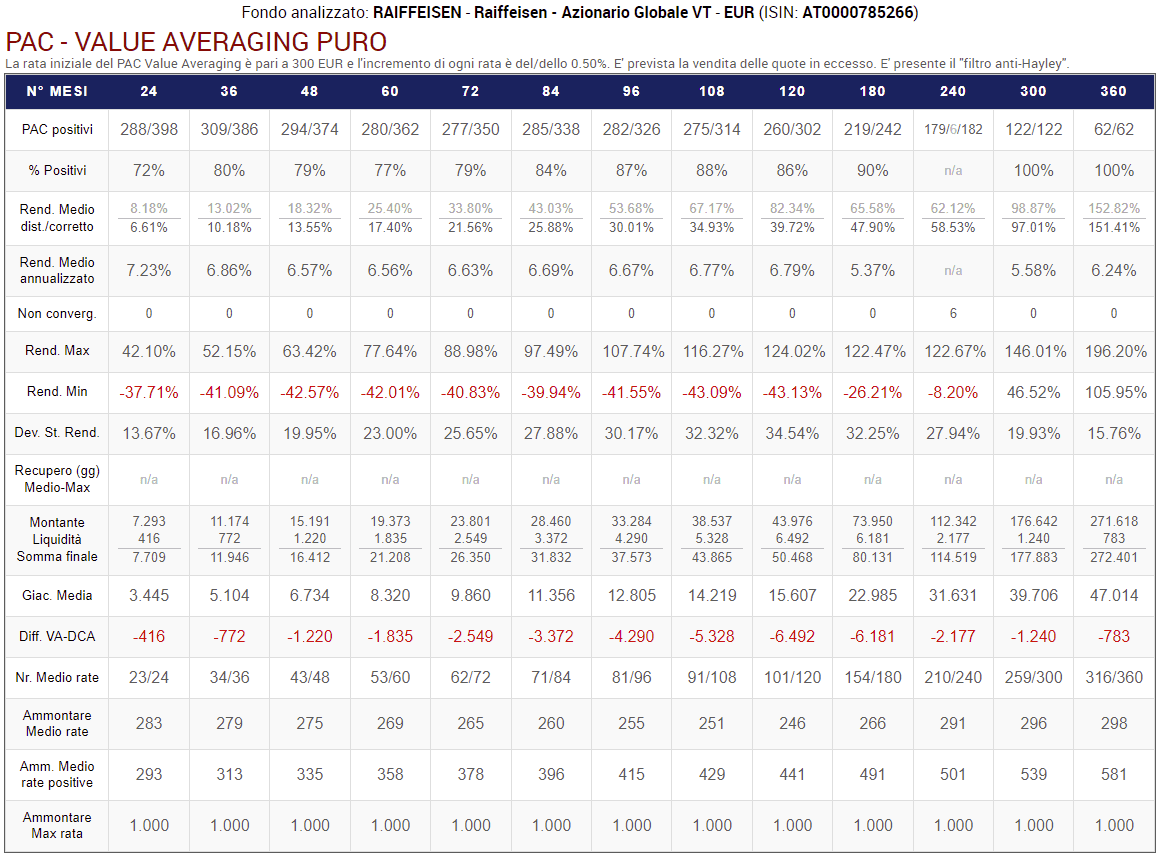
Fig. 30 – PAC Value Averaging puro. Rata iniziale: 300 euro. Incremento target: 0,50%. Versamento massimo: 1000 euro. Filtro anti-Hayley: presente
I rendimenti migliorano soltanto nei piani di accumulo di lunghezza uguale o superiore a 20 anni. Di conseguenza, anche le somme finali sono più elevate (nei trentennali si raggiungono i 272.401 euro contro i 269.113 di quelli senza massimale). Nei PAC più corti le differenze sono minime e rimangono a vantaggio dei piani senza massimale.
La giacenza media, l’ammontare medio delle rate e delle sole rate positive diminuiscono. La liquidità residua, invece, aumenta.
Come per il singolo piano di accumulo analizzato nel precedente capitolo, riassumiamo tutti i risultati dei backtest effettuati sui piani di accumulo trentennali in un’unica tabella:
| Tutti i PAC mensili a 30 anni su singolo fondo con rata/incremento target di 300 euro | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mod. PAC | Tipol. | Increm. | Filtro Hayley | Rata max | Rend. dist. | Rend. corr. | Dev. St. | Rend./ Rischio | Mont. PAC | Liquid. | Somma finale |
| CA | n/a | 0,00% | n/a | n/a | 150,18% | 150,18% | 15,84% | 9,48 | 270.716 | 0 | 270.716 |
| CA | n/a | 0,25% | n/a | n/a | n/a | n/a | n/a | n/a | n/a | n/a | n/a |
| CA | n/a | 0,50% | n/a | n/a | n/a | n/a | n/a | n/a | n/a | n/a | n/a |
| VA | No-Sell | 0,00% | NO | NO | 228,40% | 148,22% | 14,31% | 10,36 | 230.404 | 37.847 | 268.251 |
| VA | No-Sell | 0,25% | NO | NO | 205,46% | 194,40% | 18,02% | 10,79 | 314.485 | 4.806 | 319.291 |
| VA | No-Sell | 0,50% | NO | NO | 185,58% | 185,58% | 25,98% | 7,14 | 441.867 | −47.585 | 394.282 |
| VA | No-Sell | 0,00% | SI | NO | 227,63% | 145,31% | 11,76% | 12,36 | 226.247 | 38.869 | 265.116 |
| VA | No-Sell | 0,25% | SI | NO | 201,40% | 150,56% | 13,34% | 11,29 | 243.896 | 26.968 | 270.864 |
| VA | No-Sell | 0,50% | SI | NO | 156,79% | 156,66% | 16,08% | 9,74 | 277.699 | 73 | 277.772 |
| VA | No-Sell | 0,00% | NO | 1000 | 244,81% | 117,59% | 11,24% | 10,46 | 179.030 | 56.166 | 235.196 |
| VA | No-Sell | 0,25% | NO | 1000 | 208,71% | 149,41% | 14,18% | 10,54 | 239.045 | 30.607 | 269.652 |
| VA | No-Sell | 0,50% | NO | 1000 | 171,82% | 171,82% | 20,69% | 8,30 | 328.311 | −12.783 | 315.528 |
| VA | No-Sell | 0,00% | SI | 1000 | 244,22% | 117,50% | 11,26% | 10,44 | 179.030 | 56.079 | 235.109 |
| VA | No-Sell | 0,25% | SI | 1000 | 207,38% | 148,81% | 13,82% | 10,77 | 238.649 | 30.372 | 269.021 |
| VA | No-Sell | 0,50% | SI | 1000 | 157,13% | 157,00% | 15,94% | 9,85 | 278.118 | 73 | 278.191 |
| VA | Puro | 0,00% | NO | NO | −3.448,21% | 99,03% | 6,38% | 15,52 | 108.000 | 107.648 | 215.648 |
| VA | Puro | 0,25% | NO | NO | 811,37% | 138,09% | 10,33% | 13,37 | 174.821 | 83.147 | 257.968 |
| VA | Puro | 0,50% | NO | NO | 300,68% | 202,40% | 20,56% | 9,84 | 301.355 | 27.490 | 328.845 |
| VA | Puro | 0,00% | SI | NO | 17.516,15% | 98,75% | 6,33% | 15,60 | 108.000 | 107.350 | 215.350 |
| VA | Puro | 0,25% | SI | NO | 800,19% | 132,34% | 10,30% | 12,85 | 174.821 | 76.920 | 251.741 |
| VA | Puro | 0,50% | SI | NO | 148,89% | 148,37% | 15,54% | 9,55 | 268.865 | 248 | 269.113 |
| VA | Puro | 0,00% | NO | 1000 | 2.811,90% | 95,24% | 6,04% | 15,77 | 105.671 | 105.869 | 211.540 |
| VA | Puro | 0,25% | NO | 1000 | 487,31% | 127,43% | 9,72% | 13,11 | 169.283 | 77.139 | 246.422 |
| VA | Puro | 0,50% | NO | 1000 | 206,65% | 174,33% | 16,76% | 10,40 | 281.999 | 15.293 | 297.292 |
| VA | Puro | 0,00% | SI | 1000 | 676,29% | 95,17% | 6,06% | 15,70 | 105.671 | 105.799 | 211.470 |
| VA | Puro | 0,25% | SI | 1000 | 481,98% | 127,19% | 9,74% | 13,06 | 169.283 | 76.872 | 246.155 |
| VA | Puro | 0,50% | SI | 1000 | 152,82% | 151,41% | 15,76% | 9,61 | 271.618 | 783 | 272.401 |
Fig. 31 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging di tutti i PAC trentennali su un singolo fondo
I risultati sono migliori di quelli della figura 19. È la conferma che il singolo PAC analizzato in precedenza aveva ottenuto delle performance inferiori alla media (si trattava del primo dei 62 piani di accumulo che hanno generato i risultati di questa tabella).
Ovviamente, le differenze non sono enormi, dato che nonostante i 62 PAC siano stati backtestati in modalità rolling, buona parte della serie storica utilizzata è comune a tutte le 62 simulazioni.
Quale sarebbe stata l’opzione migliore per questi 62 PAC trentennali?
Escludendo le simulazioni effettuate senza la presenza del filtro anti-Hayley (valori in grigio), in ordine di somma finale troviamo:
- PAC Value Averaging No-Sell con incremento del target dello 0,50% e rata massima di 1.000 euro (somma finale di 278.191 euro e rendimento del 157,00%).
- PAC Value Averaging No-Sell con incremento del target dello 0,50% senza rata massima (somma finale di 277.772 euro e rendimento del 156,66%).
- PAC Value Averaging Puro con incremento del target dello 0,50% e rata massima di 1.000 euro (somma finale di 272.401 euro e rendimento del 151,41%).
È lo stesso ordine ottenuto analizzando un solo piano di accumulo, con l'eccezione della terza posizione che è adesso occupata dal PAC Value Averaging Puro con target 0,50% e rata massima di 1.000 euro.
Ancora una volta, il Cost Averaging non si classifica nelle prime 3 posizioni.
Il rendimento è fondamentale, ma non è l’unica misura da analizzare in materia di investimenti: l’altra, anch'essa essenziale, è la volatilità. La volatilità è un importante indicatore di rischio.
L’ordine in base alla volatilità dei PAC Value Averaging che abbiamo analizzato è il seguente:
- Value Averaging Puro con incremento del target costante e rata massima di 1.000 euro (6,06%).
- Value Averaging Puro con incremento del target costante senza rata massima (6,33%).
- Value Averaging Puro con incremento del target dello 0,25% e rata massima di 1.000 euro (9,74%).
I PAC meno volatili sono, in generale, quelli che avevano generato i rendimenti più bassi. L’economia e la finanza sono costellate da trade-off: quello tra rischio e rendimento è forse il più importante. Anche in questo caso, viene confermata la regola che se si vuole conseguire un alto rendimento, dobbiamo accollarci un rischio altrettanto alto.
I piani di accumulo Cost Averaging trentennali hanno registrato una volatilità del 15,84%: leggermente più bassa di quella dei piani posizionatisi nelle prime due posizioni, ma superiore a quella dei PAC in terza posizione. Un altro indizio che può essere interpretato in favore di una maggior efficienza del Value Averaging sul Cost Averaging.
Accanto alla volatilità, troviamo il rapporto tra rendimento e rischio. Questa misura è tanto migliore quanto più alto è il suo valore, dal momento che al numeratore si trova il rendimento (che vogliamo massimizzare), e al denominatore il rischio (che vogliamo minimizzare).
Il rapporto tra rendimento e rischio può aiutare a confrontare i PAC sulla base di queste due quantità. Si tratta di un indicatore ausiliario e non si dovrebbero effettuare scelte di investimento a partire dal solo rapporto rendimento/rischio: un valore elevato può essere causato sia da un alto rendimento che da una bassa volatilità. La preferenza dell’una o dell’altra è una scelta personale, che non può e non deve mai essere generalizzata.
62 piani di accumulo costituiscono un campione ancora troppo piccolo: abbiamo perciò deciso di riassumere in un’altra tabella i risultati dei 302 piani di accumulo della durata di 10 anni.
Essendo molti di più, la maggior parte di questi PAC non condivide alcun valore della serie storica dello strumento finanziario sottostante: in altre parole, sono dei PAC che si sono sviluppati in contesti di mercato molto diversi.
Vediamo i risultati:
| Tutti i PAC mensili a 10 anni su singolo fondo con rata/incremento target di 300 euro | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mod. PAC | Tipol. | Increm. | Filtro Hayley | Rata max | Rend. dist. | Rend. corr. | Dev. St. | Rend./ Rischio | Mont. PAC | Liquid. | Somma finale |
| CA | n/a | 0,00% | n/a | n/a | 44,10% | 44,10% | 41,98% | 1,05 | 51.931 | 0 | 51.931 |
| CA | n/a | 0,25% | n/a | n/a | n/a | n/a | n/a | n/a | n/a | n/a | n/a |
| CA | n/a | 0,50% | n/a | n/a | n/a | n/a | n/a | n/a | n/a | n/a | n/a |
| VA | No-Sell | 0,00% | NO | NO | 63,84% | 40,50% | 30,56% | 1,33 | 42.841 | 7.649 | 50.490 |
| VA | No-Sell | 0,25% | NO | NO | 60,87% | 44,73% | 33,96% | 1,32 | 48.727 | 3.228 | 51.955 |
| VA | No-Sell | 0,50% | NO | NO | 57,81% | 48,91% | 38,24% | 1,28 | 56.000 | −2.316 | 53.684 |
| VA | No-Sell | 0,00% | SI | NO | 60,70% | 38,03% | 32,82% | 1,16 | 40.755 | 9.027 | 49.782 |
| VA | No-Sell | 0,25% | SI | NO | 56,42% | 41,23% | 36,31% | 1,14 | 45.336 | 5.612 | 50.948 |
| VA | No-Sell | 0,50% | SI | NO | 51,98% | 43,85% | 40,07% | 1,09 | 49.352 | 2.556 | 51.908 |
| VA | No-Sell | 0,00% | NO | 1.000 | 64,55% | 39,11% | 30,40% | 1,29 | 40.713 | 9.366 | 50.079 |
| VA | No-Sell | 0,25% | NO | 1.000 | 61,97% | 42,84% | 33,32% | 1,29 | 45.710 | 5.680 | 51.390 |
| VA | No-Sell | 0,50% | NO | 1.000 | 59,11% | 46,83% | 36,86% | 1,27 | 51.876 | 1.072 | 52.948 |
| VA | No-Sell | 0,00% | SI | 1.000 | 62,12% | 37,31% | 31,99% | 1,17 | 39.640 | 9.885 | 49.525 |
| VA | No-Sell | 0,25% | SI | 1.000 | 58,34% | 40,13% | 35,03% | 1,15 | 43.788 | 6.766 | 50.554 |
| VA | No-Sell | 0,50% | SI | 1.000 | 54,02% | 42,61% | 37,95% | 1,12 | 47.858 | 3.607 | 51.465 |
| VA | Puro | 0,00% | NO | NO | 168,74% | 35,87% | 27,36% | 1,31 | 36.000 | 12.910 | 48.910 |
| VA | Puro | 0,25% | NO | NO | 141,13% | 40,02% | 30,34% | 1,32 | 41.922 | 8.379 | 50.301 |
| VA | Puro | 0,50% | NO | NO | 98,93% | 44,47% | 34,16% | 1,30 | 49.164 | 2.758 | 51.922 |
| VA | Puro | 0,00% | SI | NO | 132,59% | 34,48% | 28,86% | 1,19 | 35.209 | 13.370 | 48.579 |
| VA | Puro | 0,25% | SI | NO | 128,52% | 37,57% | 32,08% | 1,17 | 40.069 | 9.624 | 49.693 |
| VA | Puro | 0,50% | SI | NO | 87,89% | 40,37% | 35,71% | 1,13 | 44.839 | 5.867 | 50.706 |
| VA | Puro | 0,00% | NO | 1.000 | 278,60% | 35,44% | 26,76% | 1,32 | 35.012 | 13.836 | 48.848 |
| VA | Puro | 0,25% | NO | 1.000 | 115,68% | 39,33% | 29,52% | 1,33 | 40.437 | 9.757 | 50.194 |
| VA | Puro | 0,50% | NO | 1.000 | 78,93% | 54,95% | 31,95% | 1,72 | 46.932 | 4.790 | 51.722 |
| VA | Puro | 0,00% | SI | 1.000 | 239,70% | 34,16% | 28,07% | 1,22 | 34.569 | 13.892 | 48.461 |
| VA | Puro | 0,25% | SI | 1.000 | 108,88% | 37,01% | 31,22% | 1,19 | 39.211 | 10.281 | 49.492 |
| VA | Puro | 0,50% | SI | 1.000 | 82,34% | 39,72% | 34,54% | 1,15 | 43.976 | 6.492 | 50.468 |
Fig. 32 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging di tutti i PAC decennali su un singolo fondo
Quale sarebbe stata l’opzione migliore per questi 302 PAC decennali?
Come sempre, escludiamo le simulazioni effettuate senza la presenza del filtro anti-Hayley (valori in grigio). In ordine di somma finale disponibile troviamo:
- PAC Cost Averaging (somma finale di 51.931 euro e rendimento del 44,10%).
- PAC Value Averaging No-Sell con incremento del target dello 0,50% senza rata massima (somma finale di 51.908 euro e rendimento del 43,85%).
- PAC Value Averaging No-Sell con incremento del target dello 0,50% e rata massima di 1.000 euro (somma finale di 51.465 euro e rendimento del 42,61%).
La volatilità del Value Averaging è inferiore a quella del Cost Averaging e tutti i rapporti rendimento/rischio sono a favore del Value Averaging.
Per quanto siano molto vicini, i piani Value Averaging con un incremento del target dello 0,50% non riescono ancora a eguagliare i rendimenti del Cost Averaging.
Troppa liquidità rimane inutilizzata; il tasso di crescita del target potrebbe essere troppo basso per una durata di 10 anni (120 mesi):
→ Incremento al tempo t120 = (1 + 0,005)120 = 1,82
Alla fine dei 10 anni, il target è di sole 1,82 volte più grande di quello iniziale.
Se l’orizzonte temporale è di 10 anni, l’incremento del target dovrà essere superiore. Vediamo a quali moltiplicatori corrispondono le percentuali dello 0,75%, dell’1% e dell’1,5%:
→ Incremento al tempo t120 = (1 + 0,0075)120 = 2,45
→ Incremento al tempo t120 = (1 + 0,01)120 = 3,30
→ Incremento al tempo t120 = (1 + 0,015)120 = 5,97
Verifichiamo se questi moltiplicatori sono sufficienti a sfruttare tutta la liquidità disponibile.
Abbiamo nuovamente backtestato i PAC Value Averaging No-Sell e puri a 10 anni (soltanto con il filtro anti-Hayley attivato). I risultati sono i seguenti:
| Tutti i PAC mensili a 10 anni su singolo fondo con rata/incremento target di 300 euro | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mod. PAC | Tipol. | Increm. | Filtro Hayley | Rata max | Rend. dist. | Rend. corr. | Dev. St. | Rend./ Rischio | Mont. PAC | Liquid. | Somma finale |
| CA | n/a | 0,00% | n/a | n/a | 44,10% | 44,10% | 41,98% | 1,05 | 51.931 | 0 | 51.931 |
| CA | n/a | 0,25% | n/a | n/a | 0,00% | 0,00% | 0,00% | 0,00 | 0 | 0 | 0 |
| CA | n/a | 0,50% | n/a | n/a | 0,00% | 0,00% | 0,00% | 0,00 | 0 | 0 | 0 |
| VA | No-Sell | 0,75% | SI | NO | 48,75% | 44,39% | 41,51% | 1,07 | 51.037 | 1.081 | 52.118 |
| VA | No-Sell | 1,00% | SI | NO | 46,65% | 44,36% | 41,92% | 1,06 | 51.594 | 513 | 52.107 |
| VA | No-Sell | 1,50% | SI | NO | 44,20% | 44,20% | 41,99% | 1,05 | 52.082 | 0 | 52.082 |
| VA | No-Sell | 0,75% | SI | 1000 | 49,60% | 44,23% | 40,61% | 1,09 | 50.599 | 1.464 | 52.063 |
| VA | No-Sell | 1,00% | SI | 1000 | 47,21% | 44,42% | 42,00% | 1,06 | 51.480 | 664 | 52.144 |
| VA | No-Sell | 1,50% | SI | 1000 | 44,12% | 44,12% | 42,02% | 1,05 | 52.053 | 0 | 52.053 |
| VA | Puro | 0,75% | SI | NO | 65,74% | 42,15% | 38,71% | 1,09 | 48.423 | 2.923 | 51.346 |
| VA | Puro | 1,00% | SI | NO | 53,41% | 43,32% | 41,00% | 1,06 | 50.401 | 1.367 | 51.768 |
| VA | Puro | 1,50% | SI | NO | 44,11% | 44,11% | 42,09% | 1,05 | 52.056 | 0 | 52.056 |
| VA | Puro | 0,75% | SI | 1000 | 65,53% | 41,71% | 37,71% | 1,11 | 47.758 | 3.429 | 51.187 |
| VA | Puro | 1,00% | SI | 1000 | 55,25% | 42,92% | 40,48% | 1,06 | 49.821 | 1.804 | 51.625 |
| VA | Puro | 1,50% | SI | 1000 | 44,06% | 44,06% | 42,11% | 1,05 | 52.039 | 0 | 52.039 |
Fig. 33 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging di tutti i PAC decennali su un singolo fondo con incrementi dello 0,75%, 1% e 1,50%
Stiliamo la solita classifica relativa alle 3 tipologie più performanti:
- PAC Value Averaging No-Sell con incremento del target dell’1% e rata massima di 1.000 euro (somma finale di 52.144 euro e rendimento del 44,42%).
- PAC Value Averaging No-Sell con incremento del target dello 0,75% senza rata massima (somma finale di 52.118 euro e rendimento del 44,39%).
- PAC Value Averaging No-Sell con incremento del target dell’1% senza rata massima (somma finale di 52.107 euro e rendimento del 44,36%).
Di nuovo, il Cost Averaging esce dalla classifica quando nel Value Averaging si riesce a minimizzare o azzerare la liquidità residua.
Il Value Averaging puro, a parità di caratteristiche, non riesce a tenere il passo del No-Sell.
La volatilità di tutti questi PAC è molto simile. I migliori tre, comunque, hanno una deviazione standard dei rendimenti finali appena superiore (42,00%) o inferiore (41,51% e 41,92%) a quella dei PAC Cost Averaging (41,98%).
Concludendo, le differenze tra Cost Averaging e Value Averaging nelle durate fino a 10-15 anni sono limitate. Esistono – anche applicando il filtro anti-Hayley – e sembrano favorire il Value Averaging soltanto se si riesce a svilupparlo in modo da minimizzarne la liquidità residua.
7. Simulazioni su un fondo dal trend discendente

«The depth of darkness to which you can descend and still live is an exact measure of the height to which you can aspire to reach».
Plinio il Vecchio
Il fondo Raiffeisen, utilizzato finora per le simulazioni delle varie metodologie di Value Averaging, ha seguito un trend di crescita nel periodo considerato: basti pensare che quotava intorno a 51 euro a fine 1986 ed è arrivato a superare i 430 euro nel novembre 2021.
Vediamo come si sarebbero comportati i piani di accumulo Value Averaging, sempre in rapporto al Cost Averaging, in un fondo con una serie storica altrettanto lunga, ma che non è cresciuto come il precedente: Aberdeen Japanese Equity Fund A Acc JPY (ISIN: LU0011963674), appartenente alla categoria “Azionari Giappone”.
I mercati giapponesi, dopo i massimi toccati sul finire degli anni ’80 del secolo scorso, hanno subito due decenni di crisi, tornando a crescere soltanto a partire dal 2010/2012, ma senza riuscire a recuperare il terreno perso.
Il fondo Aberdeen Japanese Equity Fund A Acc, ad esempio, nella sua versione in JPY, ha toccato un valore massimo intorno ai 720 JPY nel dicembre 1989, per poi iniziare un’inesorabile discesa che lo ha portato a quotare circa 162 JPY nel marzo del 2009, con una perdita del 77,50% in poco meno di 20 anni (nel settembre 2021 era tornato a quotare vicino ai 700 JPY).
Il grafico del NAV del fondo è il seguente:
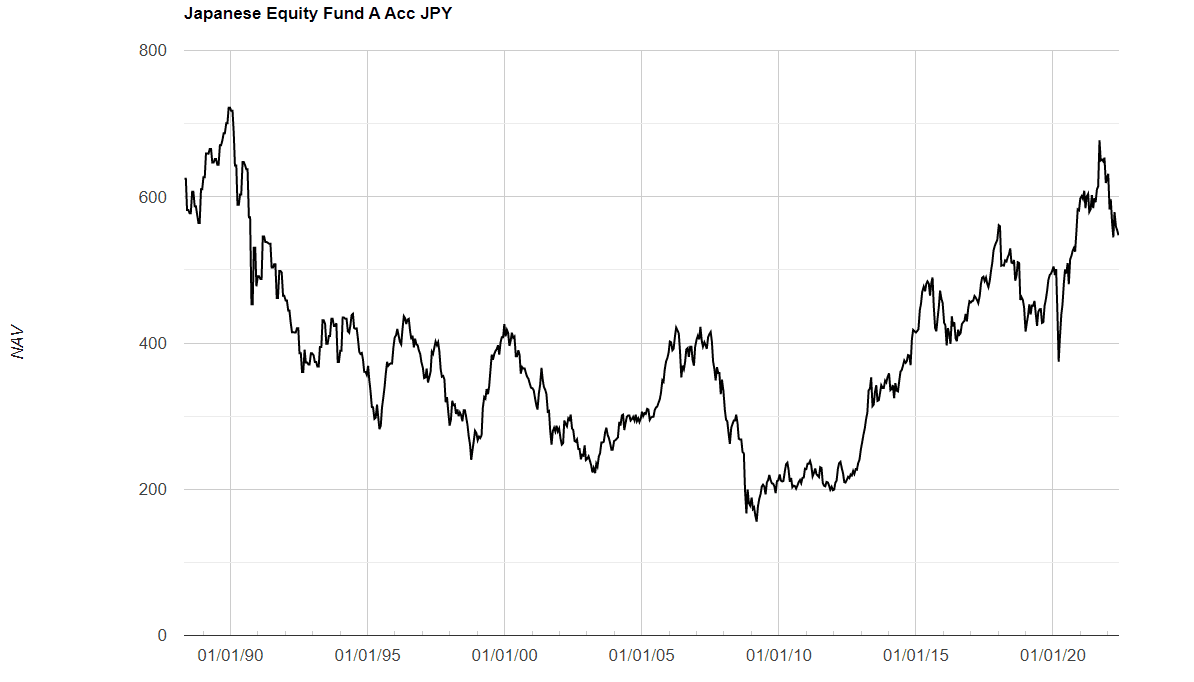
Fig. 34 – Grafico del NAV del fondo Aberdeen Japanese Equity Fund A Acc JPY
Quando si dice che i mercati azionari sono rischiosi – e si leggono tutti quei disclaimer relativi ai rendimenti passati che non sono indicativi di quelli futuri – si fa anche riferimento al verificarsi di eventi simili a questo: nel 1989, nessuno si sarebbe aspettato che i mercati giapponesi – tra i migliori al mondo negli anni ’80 – avrebbero potuto subire un tracollo del genere. Eppure, è successo e potrebbe accadere di nuovo.
Vediamo i risultati dei backtest dei piani di accumulo Cost Averaging e Value Averaging su questo fondo.
Dato che, a differenza del Raiffeisen, l'Aberdeen Japanese Equity Fund A Acc JPY è ancora in vita nel momento in cui stiamo scrivendo[1], i backtest che effettueremo utilizzeranno tutta la serie storica disponibile.
Iniziamo dal Cost Averaging:
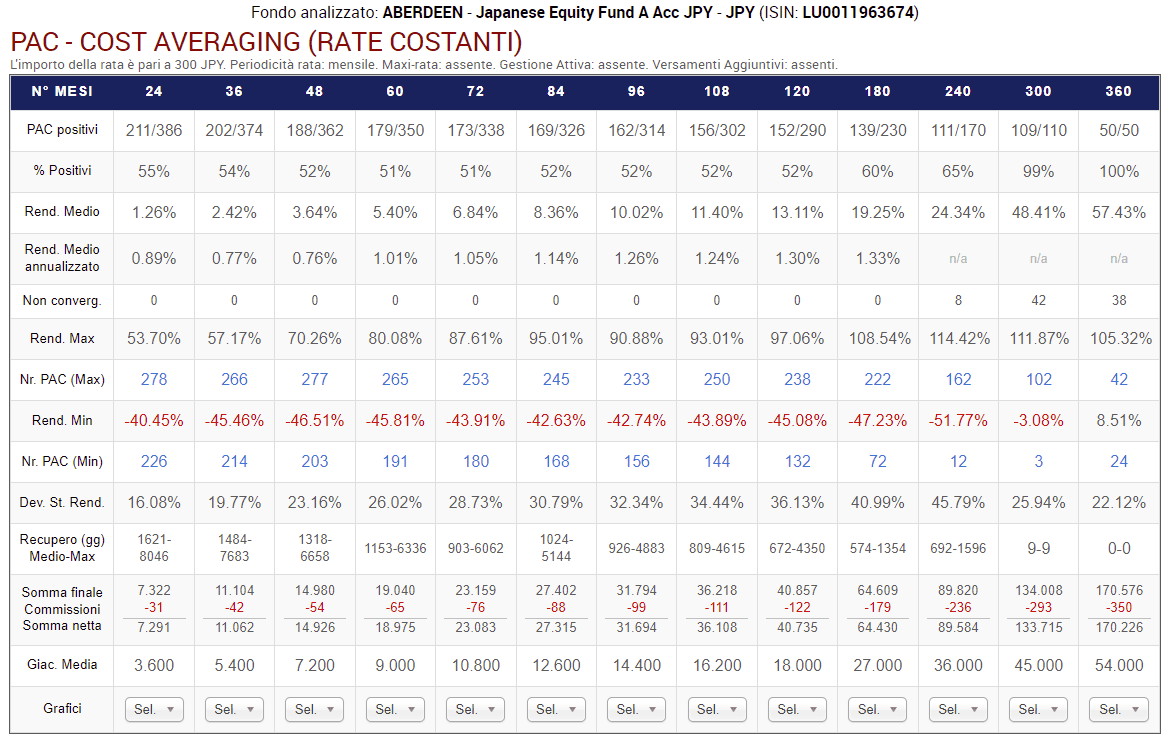
Fig. 35 – PAC Cost Averaging. Rata: 300 euro
Incredibilmente, i rendimenti medi e medi annualizzati sono positivi anche nelle durate più corte.
I rendimenti minimi, come era da aspettarsi, hanno generato perdite molto pesanti anche su durate che, normalmente, non conoscono segni negativi (il peggior PAC Cost Averaging di 20 anni ha generato il −51,77% e quello di 25 anni il −3,08%; l’unica durata che non ha prodotto risultati negativi è quella trentennale).
Questi sono invece i risultati del Value Averaging No-Sell con incremento del target dello 0,50%, filtro anti-Hayley attivato e versamento massimo di 1.000 euro:
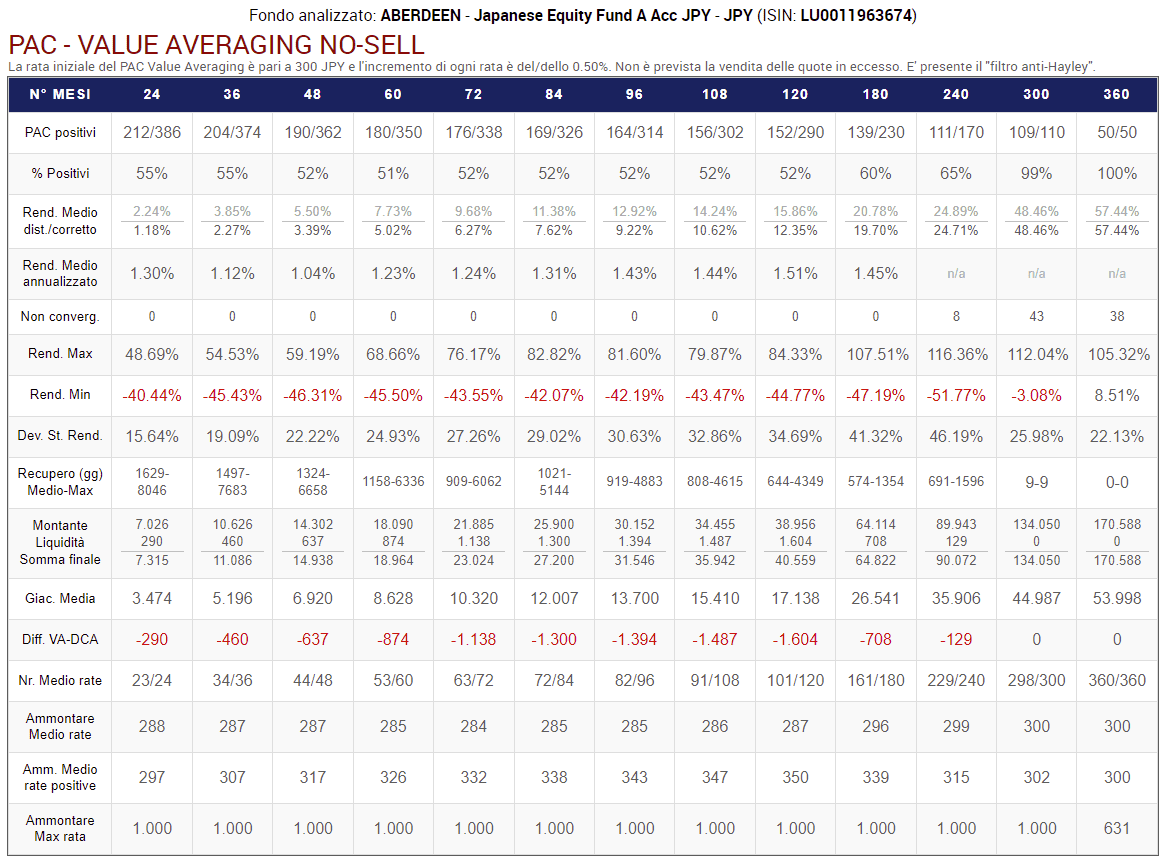
Fig. 36 – PAC Value Averaging No-Sell. Rata iniziale: 300 euro. Incremento target: 0,50%. Versamento massimo: 1000 euro. Filtro anti-Hayley: presente
Le performance sono molto simili a quelle del Cost Averaging:
- I rendimenti medi corretti e le somme finali del Value Averaging sono superiori a partire dai 15 anni di durata.
- Senza il massimale di 1.000 euro, avremmo ottenuto dei risultati molto simili. Addirittura, nei PAC di 30 anni il massimale non è stato raggiunto, come si può vedere dall’ammontare della rata max, pari a 631 euro.
Vediamo i risultati del Value Averaging puro:
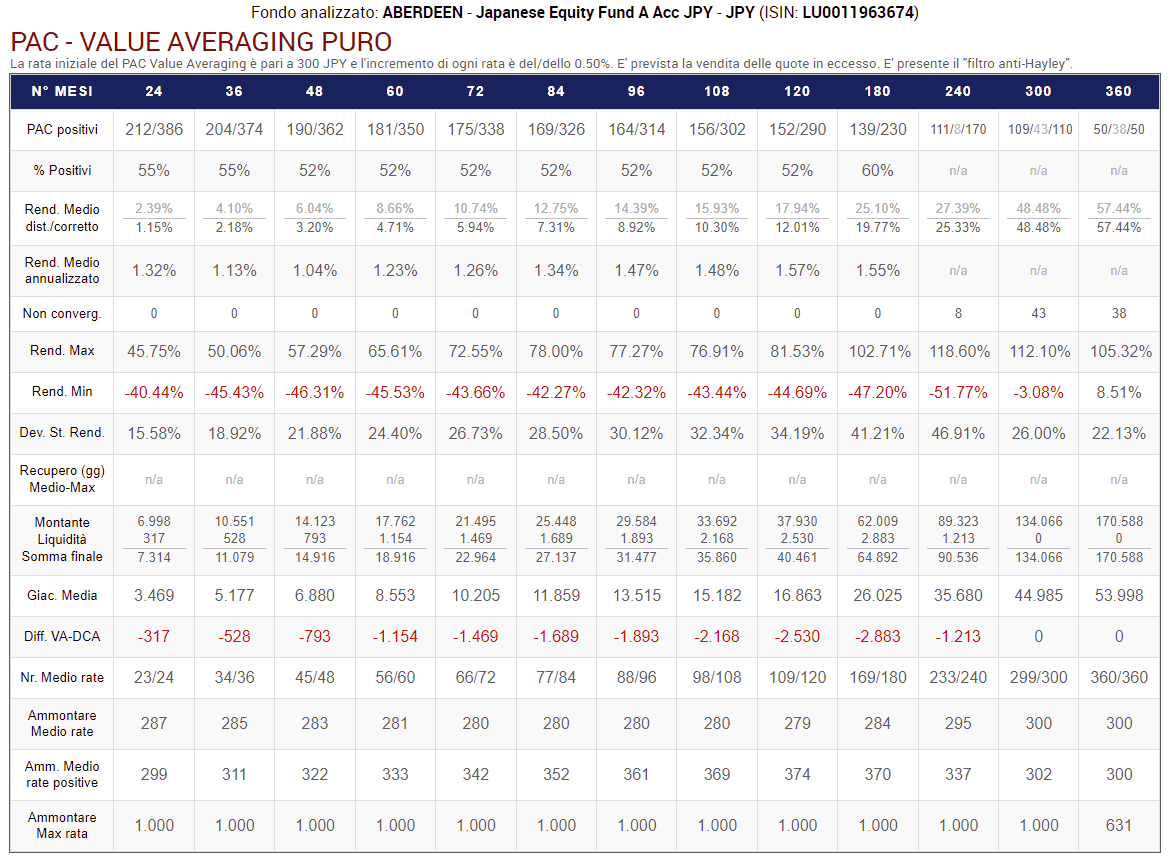
Fig. 37 – PAC Value Averaging puro. Rata iniziale: 300 euro. Incremento target: 0,50%. Versamento massimo: 1000 euro. Filtro anti-Hayley: presente
Le differenze con il No-Sell sono minime. Le considerazioni fatte in precedenza possono estendersi al Value Averaging puro.
Perché questa anomalia? Perché i piani di accumulo Value Averaging No-Sell e puri generano risultati così simili?
In un mercato che per tantissimi anni ha seguito un trend discendente, è una cosa normale: più che vendere quote o evitare un acquisto, si è quasi sempre dovuto versare l’intera rata. Anzi, per rimanere in linea con il target, spesso e volentieri avremmo dovuto versare un importo maggiore della rata prevista, cosa che non è stata possibile a causa del filtro anti-Hayley.
Tuttavia, un investitore potrebbe essere disposto a utilizzare extra-liquidità. Le critiche di Hayley sono corrette; ciò non toglie che chi ha molta liquidità e non ha il coraggio di effettuare un ingresso lump sum, possa scegliere questa alternativa. Poco importa se il rendimento annualizzato così calcolato risulterà distorto: ciò che conta è avere una strategia di investimento che incentivi l’azione e in cui si si riponga fiducia.
Quali sarebbero i rendimenti del Value Averaging senza il filtro anti-Hayley?
Vediamoli, cominciando dal No-Sell:
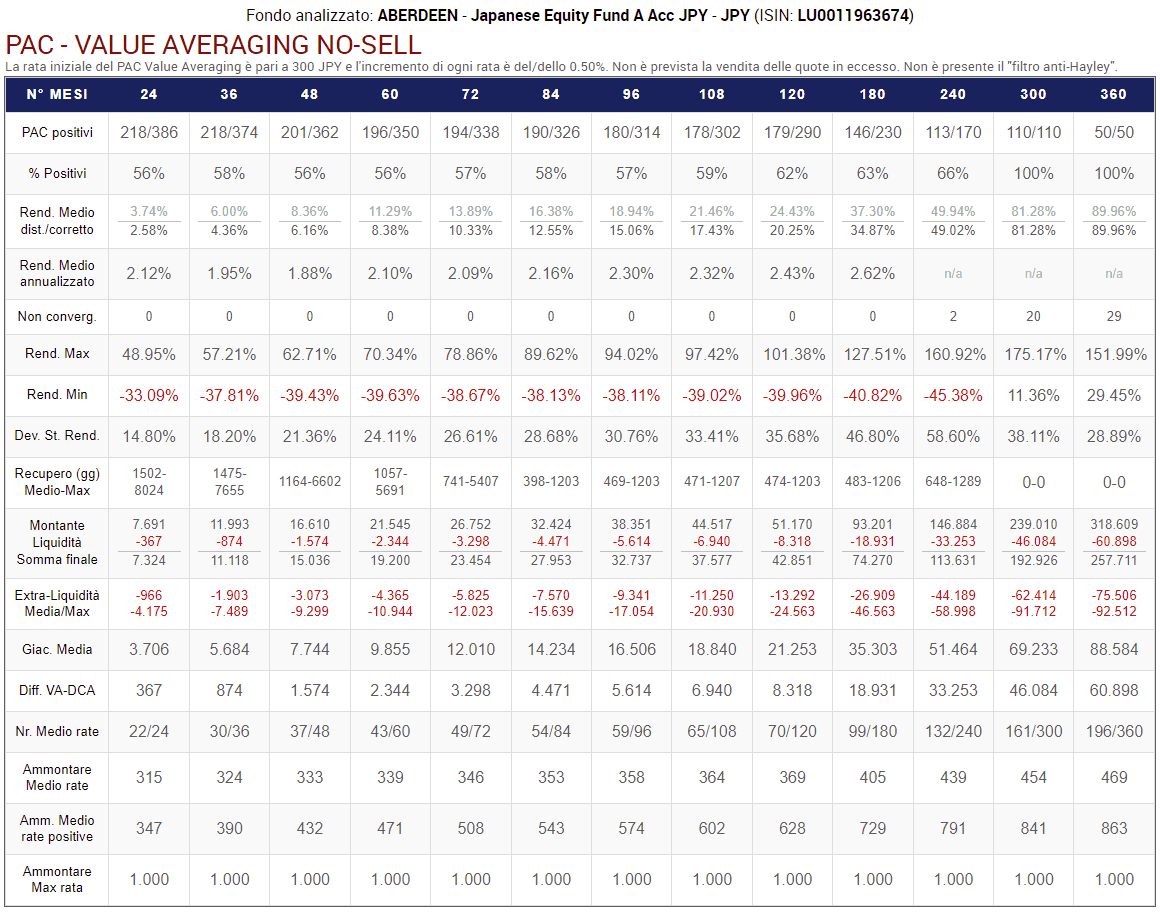
Fig. 38 – PAC Value Averaging No-Sell. Rata iniziale: 300 euro. Incremento target: 0,50%. Versamento massimo: 1000 euro. Filtro anti-Hayley: assente
I risultati sono migliori.
La somma finale generata dai piani di accumulo trentennali passa da 170.588 a 257.711 euro, ovvero 87.123 euro in più.
In realtà, i PAC hanno mediamente prodotto un montante di 318.609 euro: per ottenerlo, però, sono stati utilizzati 60.898 euro di extra-liquidità rispetto al Cost Averaging (360 rate x 300 euro ciascuna = 108.000 euro).
Il miglioramento è enorme e anche il rendimento medio lo conferma: dal 57,44% si passa all'89,96%. Anche i piani di accumulo di tutte le altre durate hanno incrementato la loro performance.
Ecco i risultati dei PAC Value Averaging puri:
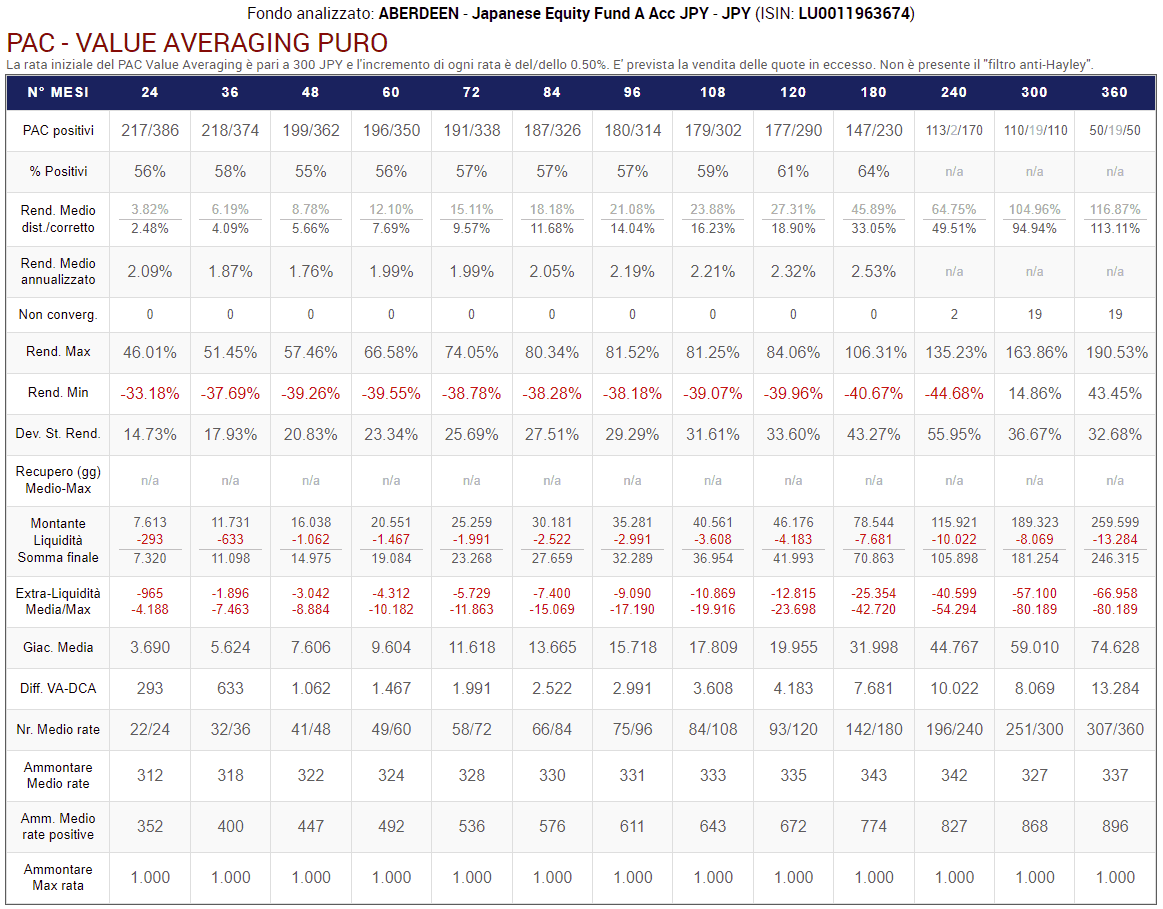
Fig. 39 – PAC Value Averaging puro. Rata iniziale: 300 euro. Incremento target: 0,50%. Versamento massimo: 1000 euro. Filtro anti-Hayley: assente
Le somme finali sono un po’ inferiori rispetto a quelle di un Value Averaging No-Sell, ma il rendimento è aumentato.
Nel PAC trentennale, la somma finale è di 246.315 euro contro i 257.711 euro precedenti. Tuttavia, sono stati richiesti soltanto 13.284 euro di liquidità rispetto ai 60.898 dei PAC No-Sell: è il vantaggio di comprare e vendere in continuazione e far circolare lo stesso capitale. La conseguenza è un ulteriore incremento del rendimento medio, che da 89,96% raggiunge il 113,11%.
Abbiamo visto che l’applicazione di un massimale ai versamenti in presenza del filtro anti-Hayley non ha fatto alcuna differenza.
Che cosa sarebbe accaduto, invece, se non avessimo avuto un limite massimo di 1.000 euro in assenza del filtro anti-Hayley?
Ecco i risultati di un PAC Value Averaging No-Sell:
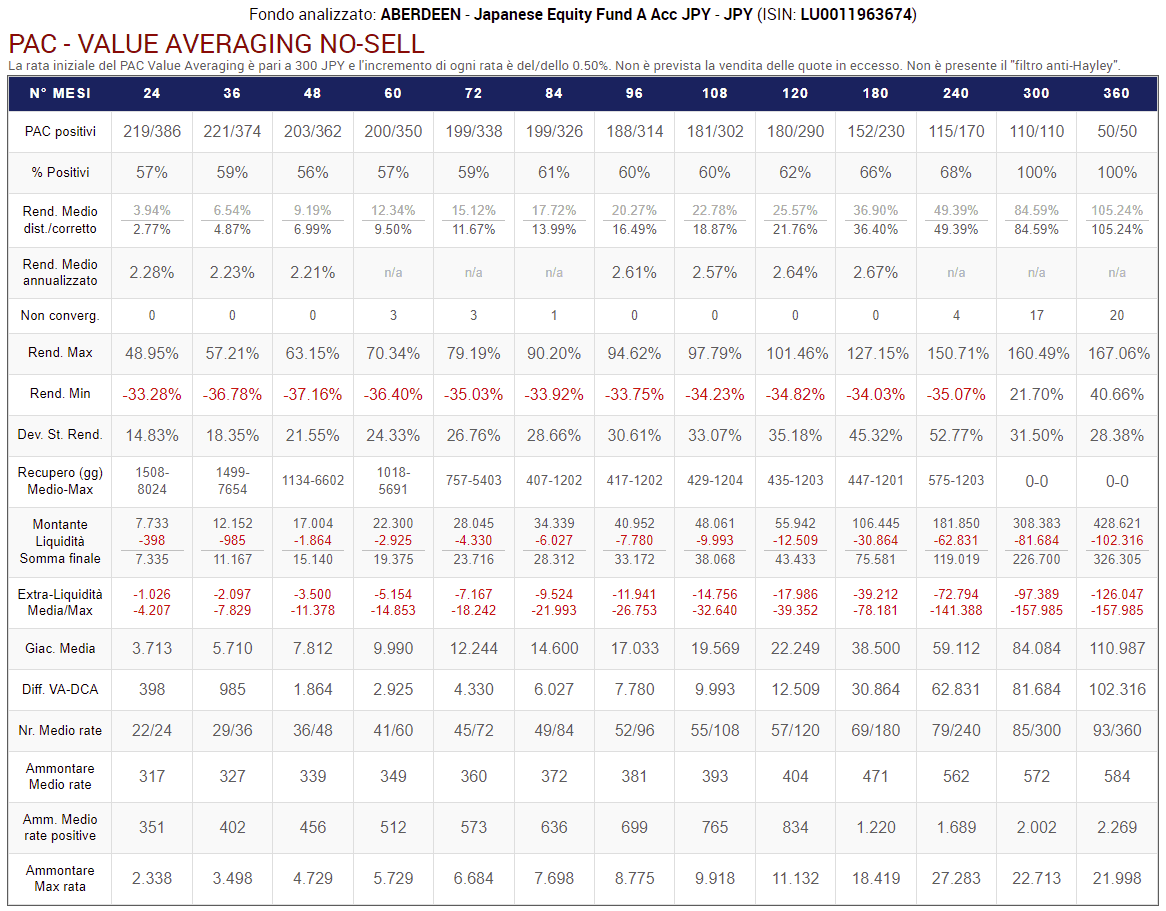
Fig. 40 – PAC Value Averaging No-Sell. Rata iniziale: 300 euro. Incremento target: 0,50%. Versamento massimo non previsto. Filtro anti-Hayley assente
Nei PAC trentennali è stata utilizzata extra-liquidità per 102.316 euro e il montante è stato di 428.621 euro. La somma finale generata è stata in media di 326.305 euro, con un rendimento medio del 105,24%.
L’ammontare medio delle rate è cresciuto sensibilmente mentre il numero dei versamenti è diminuito: il più alto è stato, però, di ben 27.283 euro.
L’extra-liquidità Media/Max ci dice che durante la vita del PAC è stata richiesta, mediamente, una extra-liquidità ancora maggiore. Approfondiremo questo discorso in seguito.
Diamo infine un’occhiata al Value Averaging puro:
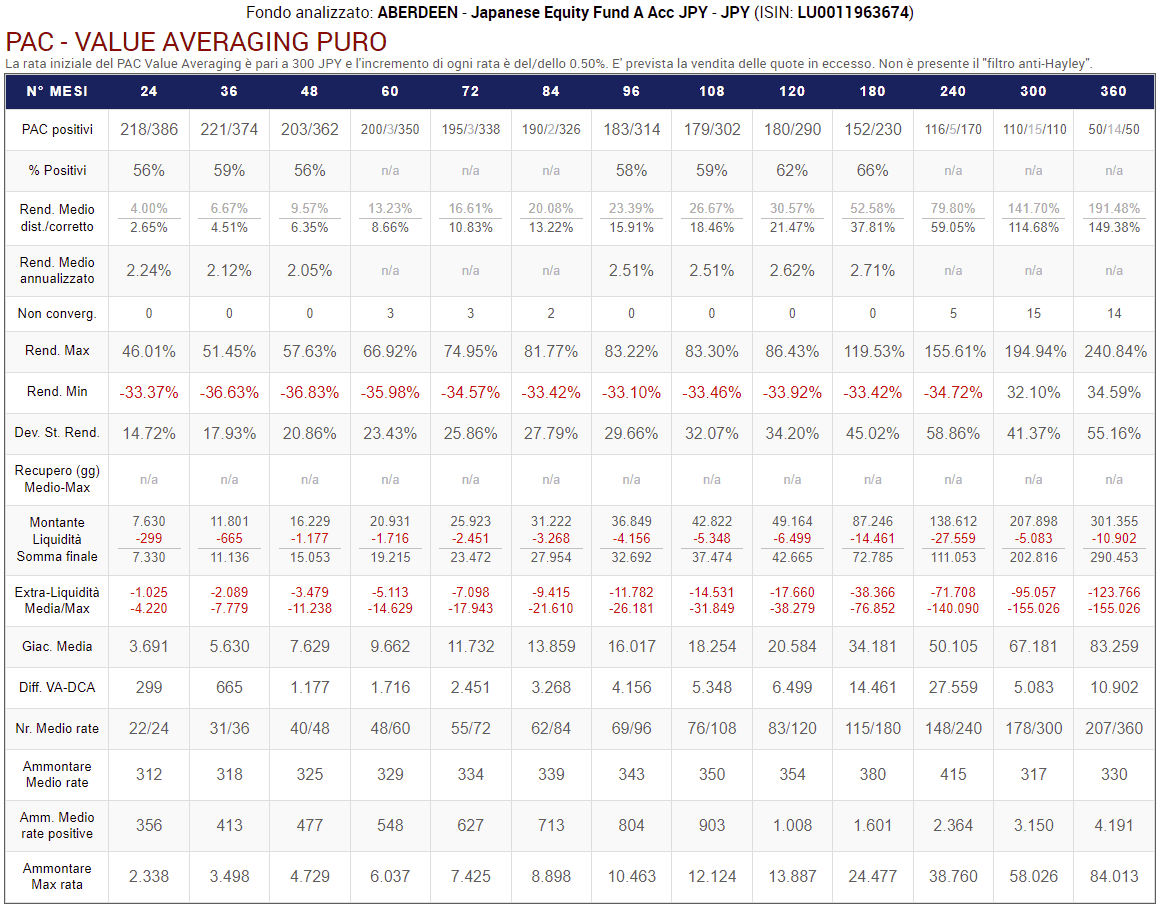
Fig. 41 – PAC Value Averaging puri. Rata iniziale: 300 euro. Incremento target: 0,50%. Versamento massimo non previsto. Filtro anti-Hayley: assente
Nei piani trentennali, sono stati generati 290.453 euro con un impiego di 10.902 euro di extra-liquidità. Il montante dei PAC è stato, in media, di 301.355 euro. Il rendimento medio è salito ulteriormente, raggiungendo il 149,38%.
Molto alti sono stati gli importi medi delle rate positive (4.191 euro) e ancora più alta la massima rata versata, che ha raggiunto ben 84.013 euro.
Ciò che scopriamo analizzando questo fondo è che, in presenza di lunghi trend discendenti, il Value Averaging è una scelta prudente e l’eventuale disponibilità di extra-liquidità aggiunge valore alla strategia.
8. Value Averaging vs Cost Averaging: simulazioni non parametriche col metodo Monte Carlo

«We don't see very far in the future, we are very focused on one idea at a time, one problem at a time, and all these are incompatible with rationality as economic theory assumes it».
Daniel Kahneman
La serie storica dei rendimenti analizzata finora (fondo Raiffeisen) è molto correlata con l’andamento dei mercati azionari globali. Backtestando dei piani di accumulo dalle stesse caratteristiche su altri fondi azionari, o direttamente sull’indice azionario globale, avremmo ottenuto risultati simili.
Se è vero che la storia si ripete, non lo fa tuttavia in maniera identica: non possiamo aspettarci che il futuro si ripresenti in modo analogo.
La storia ci offre una specifica traiettoria, ovvero una particolare sequenza di variabili casuali generatasi a partire da un processo stocastico (le nostre variabili casuali sono i rendimenti). Una serie storica è una possibile traiettoria temporale di un processo stocastico: una delle tante ipotetiche traiettorie che avrebbero potuto realizzarsi.
In altre parole, un campione estratto da un universo sconosciuto.
Quando si analizza una serie storica economica, è essenziale chiedersi che cosa sarebbe potuto succedere se in passato si fossero verificate traiettorie diverse, che è un po’ la stessa cosa che domandarsi cosa potrebbe accadere in futuro.
È senz’altro possibile eseguire altre simulazioni con il servizio di Analisi PAC di Dedalo Invest; tuttavia, pubblicare e commentare una decina di tabelle per ogni altro singolo fondo diventerebbe un lavoro interminabile.
È più semplice, invece, utilizzare un procedimento che è stato pensato proprio con questa finalità: il metodo Monte Carlo.
Utilizzeremo R, un ambiente che è nello stesso tempo un software statistico ed un linguaggio di programmazione. Grazie ad R potremo simulare un’ampia gamma di possibili scenari e analizzare il comportamento delle nostre strategie di investimento al verificarsi di ognuno di essi.
In massima sintesi, il metodo Monte Carlo si basa sulla generazione di serie di numeri che seguono la distribuzione di probabilità desiderata (che, ovviamente, si dovrà avvicinare il più possibile a quella del fenomeno da studiare): queste simulazioni sono dette parametriche.
La generazione di scenari ipotetici può avvenire anche per mezzo di simulazioni non parametriche, ovvero che non necessitano di modelli statistici basati su distribuzioni di probabilità: ci concentreremo inizialmente su queste.
Svilupperemo delle serie storiche alternative a quelle già analizzate, permutando l’ordine in cui i rendimenti si sono presentati.
La nostra serie storica iniziale è composta da 360 rendimenti mensili: quelli del primo PAC simulato sul fondo Raiffeisen Azionario Globale VT. Questi 360 valori saranno rimescolati in modo casuale per 100.000 volte, generando traiettorie anche molto diverse da quella iniziale.
A partire da ognuna di queste 100.000 serie storiche dei rendimenti, sarà ricostruita la rispettiva serie dei prezzi, sulla quale saranno simulate le tipologie di Piani di Accumulo del Capitale che conosciamo.
Iniziamo dai PAC con le seguenti caratteristiche: rata iniziale di 300 euro, target costante, assenza di massimale e filtro anti-Hayley attivato.
I risultati medi ottenuti sono riportati nella seguente tabella:
| Incremento 0% - No massimale - 100.000 simulazioni | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. totale | Stand. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. |
| PAC | 360 | CA | 166,67% | 69,40% | 288.002 | 0 | 288.002 | 300 | 736,16% | 1,52% | 100,000% | 156,45% | 0,977 | 1,725 |
| PAC | 300 | CA | 128,96% | 72,34% | 206.068 | 0 | 206.068 | 300 | 647,86% | −34,50% | 99,629% | 117,52% | 1,069 | 2,041 |
| PAC | 240 | CA | 94,72% | 64,54% | 140.197 | 0 | 140.197 | 300 | 934,62% | −50,12% | 97,603% | 84,21% | 1,143 | 2,577 |
| PAC | 180 | CA | 65,44% | 52,46% | 89.340 | 0 | 89.340 | 300 | 580,98% | −59,62% | 93,440% | 56,99% | 1,079 | 2,204 |
| PAC | 120 | CA | 39,59% | 38,26% | 50.253 | 0 | 50.253 | 300 | 331,23% | −58,58% | 86,816% | 34,26% | 0,899 | 1,464 |
| PAC | 60 | CA | 18,04% | 23,64% | 21.247 | 0 | 21.247 | 300 | 159,07% | −50,29% | 76,971% | 15,72% | 0,617 | 0,679 |
| PAC | 36 | CA | 10,32% | 17,01% | 11.915 | 0 | 11.915 | 300 | 112,31% | −47,96% | 71,469% | 9,19% | 0,420 | 0,342 |
| PAC | 24 | CA | 6,63% | 13,36% | 7.677 | 0 | 7.677 | 300 | 79,20% | −39,98% | 67,801% | 6,07% | 0,279 | 0,142 |
| PAC | 360 | VA No-Sell | 130,00% | 53,84% | 193.754 | 54.646 | 248.400 | 19.827 | 594,04% | −3,29% | 99,998% | 120,82% | 1,110 | 2,121 |
| PAC | 300 | VA No-Sell | 102,24% | 50,62% | 142.157 | 39.860 | 182.017 | 16.564 | 551,65% | −34,79% | 99,761% | 94,17% | 1,097 | 2,387 |
| PAC | 240 | VA No-Sell | 76,83% | 44,27% | 100.281 | 27.037 | 127.319 | 13.300 | 655,01% | −48,72% | 98,345% | 71,30% | 0,934 | 2,190 |
| PAC | 180 | VA No-Sell | 54,51% | 36,83% | 66.876 | 16.561 | 83.437 | 10.036 | 370,71% | −59,74% | 94,879% | 51,41% | 0,667 | 1,318 |
| PAC | 120 | VA No-Sell | 34,18% | 28,69% | 39.969 | 8.334 | 48.304 | 6.773 | 230,41% | −58,26% | 88,717% | 33,00% | 0,357 | 0,449 |
| PAC | 60 | VA No-Sell | 16,32% | 19,69% | 18.274 | 2.663 | 20.937 | 3.509 | 112,52% | −50,17% | 78,944% | 16,16% | 0,132 | −0,059 |
| PAC | 36 | VA No-Sell | 9,60% | 15,02% | 10.680 | 1.157 | 11.836 | 2.204 | 75,06% | −47,82% | 73,187% | 9,71% | 0,039 | −0,149 |
| PAC | 24 | VA No-Sell | 6,26% | 12,21% | 7.058 | 593 | 7.651 | 1.551 | 58,18% | −39,98% | 69,257% | 6,44% | −0,012 | −0,162 |
| PAC | 360 | VA Puro | 99,79% | 24,76% | 108.000 | 107.775 | 215.775 | 19.827 | 202,38% | −4,46% | 99,999% | 99,97% | −0,032 | −0,024 |
| PAC | 300 | VA Puro | 83,00% | 28,02% | 89.987 | 74.714 | 164.702 | 16.564 | 191,57% | −35,53% | 99,832% | 82,94% | −0,014 | −0,007 |
| PAC | 240 | VA Puro | 65,94% | 29,18% | 71.902 | 47.572 | 119.473 | 13.300 | 213,87% | −47,69% | 98,689% | 66,05% | −0,034 | 0,010 |
| PAC | 180 | VA Puro | 49,26% | 28,40% | 53.729 | 26.873 | 80.602 | 10.036 | 172,23% | −59,87% | 95,547% | 49,50% | −0,035 | −0,068 |
| PAC | 120 | VA Puro | 32,39% | 25,28% | 35.549 | 12.111 | 47.660 | 6.773 | 133,66% | −58,15% | 89,377% | 32,65% | −0,025 | −0,158 |
| PAC | 60 | VA Puro | 16,06% | 19,04% | 17.610 | 3.280 | 20.890 | 3.509 | 89,45% | −50,16% | 79,278% | 16,28% | 0,014 | −0,216 |
| PAC | 36 | VA Puro | 9,55% | 14,87% | 10.541 | 1.290 | 11.831 | 2.204 | 71,28% | −47,82% | 73,327% | 9,76% | −0,001 | −0,197 |
| PAC | 24 | VA Puro | 6,26% | 12,18% | 7.026 | 624 | 7.650 | 1.551 | 56,73% | −39,98% | 69,300% | 6,46% | −0,025 | −0,180 |
Fig. 42 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging di tutti i PAC di varie durate su serie storiche simulate con tecniche non parametriche (target costante, senza massimale, Filtro anti-Hayley: presente)
Il Cost Averaging ottiene i rendimenti migliori (generando quindi una somma finale superiore).
Il rendimento effettivo del solo capitale impiegato è più basso di quello del Value Averaging No-Sell e soprattutto del Value Averaging puro: come abbiamo già visto, però, utilizzare quelle percentuali di rendimento non sarebbe corretto, perché si ignorerebbe la liquidità inutilizzata.
Il problema principale del Value Averaging, soprattutto puro, è infatti quello di non investire tutta la liquidità disponibile, indipendentemente dalla lunghezza dei piani di accumulo.
I rendimenti del Value Averaging (soprattutto quello puro) sono molto meno volatili di quelli del Cost Averaging, come dimostrato dalla loro minore deviazione standard. Questo risultato riesce a compensare, almeno in parte, il rendimento medio inferiore.
Come spesso avviene in finanza, siamo in presenza di un trade-off rendimento/volatilità: non si riesce ad aumentare l’uno lasciando invariato (o diminuendo) l’altro.
L’investitore prudente sarà probabilmente più attratto dalla strategia meno volatile; l'investitore più propenso a rischiare, da quella più redditizia. Non esiste la strategia migliore in assoluto: ognuno dovrà scegliere quella più coerente con la propria propensione al rischio.
Nelle simulazioni Monte Carlo dei 100.000 piani di accumulo, abbiamo calcolato anche altre misure statistiche:
- Rata max: ci dà un’idea dell'importo della rata che potremmo arrivare a pagare. Attenzione, è un limite massimo nel vero senso della parola: rappresenta il valore più alto che è stato versato tra tutti i 100.000 PAC simulati. La presenza del filtro anti-Hayley, comunque, non ci obbliga alla costituzione di un fondo di liquidità iniziale: quello che si costruisce con le rate non versate o con la vendita di quote è sufficiente a coprire questi ingenti versamenti. Nel Cost Averaging la rata max è ovviamente quella iniziale: si versano sempre 300 euro. Nel Value Averaging, invece, i versamenti più alti arrivano a sfiorare i 20.000 euro nelle durate più lunghe.
- Rendimento max e min: sono utili a capire le enormi differenze ottenibili nei risultati. In fin dei conti, è il caso – ovvero un eventuale grosso colpo di fortuna o sfortuna – a decretare se un certo PAC genererà una performance fantastica o una da dimenticare.
- % Positivi: la percentuale di piani di accumulo che hanno ottenuto un rendimento finale positivo.
- Mediana: è il valore assunto dalle unità statistiche che si trovano nel mezzo della distribuzione. Rispetto alla media, la mediana non è influenzata dalla presenza di outliers, cioè di dati anomali (nel nostro caso, gli outliers sono rendimenti eccezionalmente alti o bassi). Tutte le mediane sono inferiori ai valori medi nel Cost Averaging, mentre nel Value Averaging accade spesso il fenomeno contrario, (soprattutto nel Value Averaging puro).
- Skewness: è una misura dell’asimmetria della distribuzione di probabilità della variabile casuale rispetto alla sua media. Quando è positiva, significa che la distribuzione ha una coda destra più lunga (e viceversa). La skewness della distribuzione normale è pari a zero, essendo perfettamente simmetrica.
Tutti i rendimenti del Cost Averaging e del Value Averaging No-sell (con l’eccezione dei piani più corti), hanno una skewness positiva: la skewness del Value Averaging puro, invece, è lievemente negativa, con la sola eccezione delle durate quinquennali. È una conferma della minor variabilità nei rendimenti. Un’ulteriore riprova di questo risultato ci viene offerta dal rendimento max, che è nettamente inferiore di quello del Cost Averaging e del Value Averaging No-Sell (bisogna ammettere che una minor variabilità dovuta a una limitazione dei soli outliers positivi non sia poi un gran risultato).
La cosa non deve sorprendere, dato che il Value Averaging puro ha come obiettivo quello di mantenere allineati valore corrente e target nel modo più preciso possibile: acquistando, ma anche vendendo quote. Il Value Averaging No-sell ha lo stesso obiettivo, ma meno strumenti per raggiungerlo (si possono solo acquistare quote). Il Cost Averaging, invece, non ha un target.
Si può verificare come il montante dei piani di accumulo Value Averaging puri trentennali sia esattamente uguale alla liquidità totale impiegata nel Cost Averaging (108.000 euro, ovvero 360 rate da 300 euro); avevamo osservato questo fenomeno anche nell’analisi di un singolo PAC Raiffeisen.
Gli istogrammi seguenti ci mostrano la distribuzione delle frequenze dei rendimenti dei 100.000 piani di accumulo Cost Averaging (trentennali). Il supporto grafico aiuta a capire meglio la skewness:
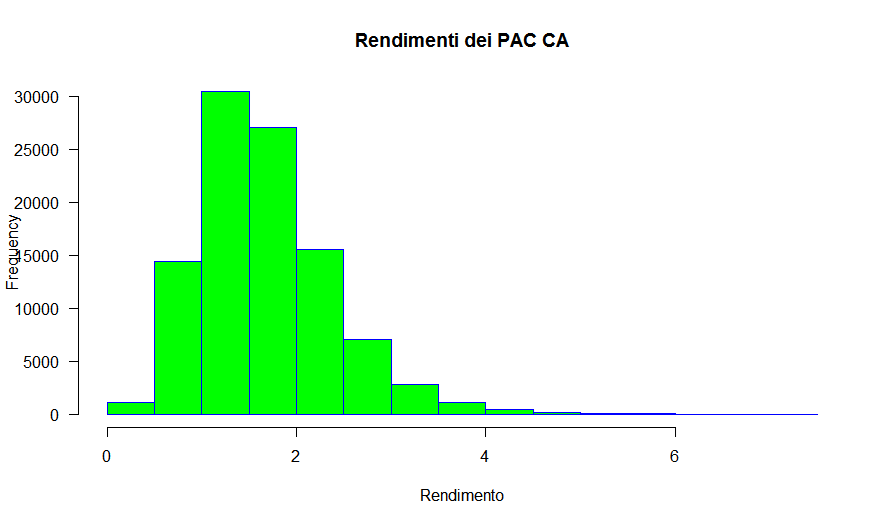
Fig. 43 – Istogramma delle frequenze dei rendimenti dei 100.000 PAC Cost Averaging trentennali simulati con tecniche non parametriche (target costante, senza massimale, Filtro anti-Hayley: presente)
La coda lunga sulla destra è ben visibile. Sulla sinistra la coda è molto più breve, anche perché non si sono verificati rendimenti negativi (il rendimento minimo è stato del +1,52%).
Vediamo la distribuzione delle frequenze dei 100.000 piani di accumulo Value Averaging No-Sell:
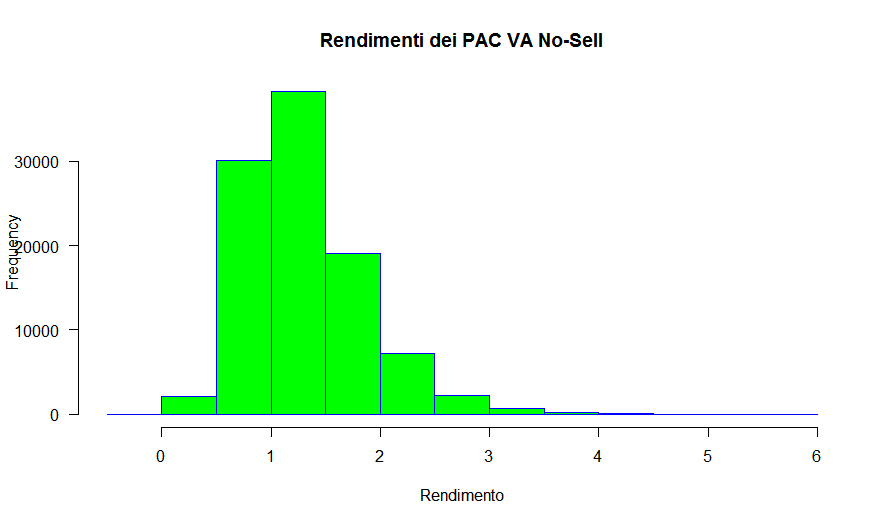
Fig. 44 – Istogramma delle frequenze dei rendimenti dei 100.000 PAC Value Averaging No-sell trentennali simulati con tecniche non parametriche (target costante, senza massimale, Filtro anti-Hayley: presente)
La coda destra è ancora presente e distinguibile. La skewness precedente era pari a 0,977; quella attuale è 1,110: abbastanza simile. La skewness del Value Averaging puro, invece, è di −0,032 e questa ampia differenza si nota benissimo negli istogrammi seguenti:
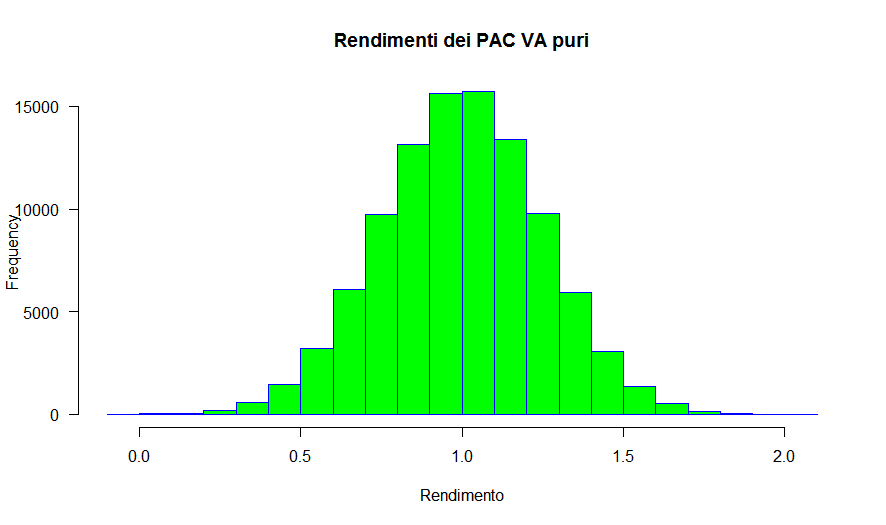
Fig. 45 – Istogramma delle frequenze dei rendimenti dei 100.000 PAC Value Averaging puri trentennali simulati con tecniche non parametriche (target costante, senza massimale, Filtro anti-Hayley: presente)
C’è molta più simmetria rispetto a prima. La forma della distribuzione delle frequenze ricorda molto di più quella di una normale. Una minor dispersione nei rendimenti, che sono molto concentrati intorno al valore medio (99,79%), può essere intrepretata come minor rischio e può essere vista come una soluzione preferibile da parte di investitori prudenti.
- Kurtosis (curtosi): è una misura dello spessore delle code di una distribuzione di probabilità. Il coefficiente di curtosi di una distribuzione normale è pari a 3 e di solito – come faremo anche noi – si tende a misurare l’eccesso di curtosi rispetto a questo valore; se il coefficiente è negativo, significa che il suo valore è minore di 3. Un coefficiente pari a zero descrive una distribuzione mesocurtica (come la normale); un coefficiente positivo descrive una distribuzione leptocurtica (code più spesse della normale); un coefficiente negativo descrive invece una distribuzione platicurtica (code meno spesse della normale).
La kurtosis dei PAC trentennali è positiva nel Cost Averaging e nel Value Averaging No-Sell (1,725 e 2,121) e negativa nel Value Averaging puro (−0,024): evidentemente le lunghe code destre nelle prime due tipologie di PAC, nonché la maggior densità delle frequenze intorno alla media nell’ultima, sono alla radice di queste differenze.
Vediamo che cosa succede incrementando il target dello 0,50%:
| Incremento 0,50% - No massimale - 100.000 simulazioni | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. totale | Stand. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. |
| PAC | 360 | CA | 166,37% | 68,98% | 287.679 | 0 | 287.679 | 300 | 751,64% | 3,18% | 100,000% | 156,37% | 0,954 | 1,627 |
| PAC | 300 | CA | 128,75% | 71,87% | 205.872 | 0 | 205.872 | 300 | 789,55% | −32,79% | 99,632% | 117,64% | 1,065 | 2,096 |
| PAC | 240 | CA | 95,18% | 64,60% | 140.532 | 0 | 140.532 | 300 | 690,22% | −50,52% | 97,606% | 84,69% | 1,116 | 2,287 |
| PAC | 180 | CA | 64,95% | 52,18% | 89.071 | 0 | 89.071 | 300 | 452,27% | −53,00% | 93,298% | 56,66% | 1,046 | 1,888 |
| PAC | 120 | CA | 39,71% | 38,22% | 50.296 | 0 | 50.296 | 300 | 352,92% | −56,34% | 86,973% | 34,40% | 0,906 | 1,526 |
| PAC | 60 | CA | 17,98% | 23,54% | 21.237 | 0 | 21.237 | 300 | 189,81% | −51,66% | 76,978% | 15,69% | 0,613 | 0,690 |
| PAC | 36 | CA | 10,32% | 17,07% | 11.914 | 0 | 11.914 | 300 | 107,62% | −45,73% | 71,519% | 9,10% | 0,406 | 0,265 |
| PAC | 24 | CA | 6,73% | 13,36% | 7.684 | 0 | 7.684 | 300 | 70,97% | −39,62% | 68,098% | 6,15% | 0,279 | 0,129 |
| PAC | 360 | VA No-Sell | 164,86% | 68,43% | 282.187 | 3.859 | 286.046 | 53.812 | 731,54% | −12,48% | 99,984% | 156,63% | 0,770 | 1,130 |
| PAC | 300 | VA No-Sell | 126,08% | 67,80% | 198.484 | 4.990 | 203.474 | 38.785 | 721,61% | −34,19% | 99,574% | 117,33% | 0,854 | 1,330 |
| PAC | 240 | VA No-Sell | 92,10% | 58,77% | 133.345 | 4.965 | 138.310 | 25.941 | 579,27% | −50,60% | 97,591% | 84,75% | 0,820 | 1,234 |
| PAC | 180 | VA No-Sell | 62,20% | 46,47% | 83.532 | 4.056 | 87.588 | 16.418 | 358,34% | −52,78% | 93,390% | 57,03% | 0,677 | 0,674 |
| PAC | 120 | VA No-Sell | 37,81% | 33,87% | 46.867 | 2.745 | 49.612 | 9.359 | 245,27% | −56,21% | 87,271% | 35,01% | 0,488 | 0,254 |
| PAC | 60 | VA No-Sell | 17,13% | 21,31% | 19.862 | 1.222 | 21.084 | 4.125 | 135,42% | −51,65% | 77,573% | 16,26% | 0,245 | −0,140 |
| PAC | 36 | VA No-Sell | 9,89% | 15,81% | 11.237 | 631 | 11.868 | 2.432 | 77,20% | −45,71% | 72,243% | 9,55% | 0,116 | −0,219 |
| PAC | 24 | VA No-Sell | 6,49% | 12,57% | 7.305 | 362 | 7.667 | 1.659 | 58,96% | −39,28% | 68,839% | 6,47% | 0,045 | −0,201 |
| PAC | 360 | VA Puro | 162,43% | 62,76% | 263.488 | 19.936 | 283.424 | 56.111 | 452,68% | −14,80% | 99,973% | 158,53% | 0,269 | −0,298 |
| PAC | 300 | VA Puro | 122,26% | 59,12% | 181.729 | 18.304 | 200.033 | 38.785 | 385,41% | −33,98% | 99,552% | 118,32% | 0,292 | −0,373 |
| PAC | 240 | VA Puro | 88,76% | 51,14% | 122.030 | 13.875 | 135.905 | 25.941 | 307,38% | −50,52% | 97,609% | 85,72% | 0,274 | −0,389 |
| PAC | 180 | VA Puro | 60,17% | 41,71% | 77.584 | 8.907 | 86.491 | 16.418 | 225,32% | −52,81% | 93,493% | 57,90% | 0,260 | −0,417 |
| PAC | 120 | VA Puro | 36,94% | 31,69% | 44.558 | 4.741 | 49.299 | 9.359 | 182,52% | −56,19% | 87,454% | 35,55% | 0,223 | −0,365 |
| PAC | 60 | VA Puro | 16,98% | 20,87% | 19.465 | 1.592 | 21.057 | 4.125 | 110,90% | −51,65% | 77,682% | 16,42% | 0,155 | −0,308 |
| PAC | 36 | VA Puro | 9,86% | 15,70% | 11.146 | 719 | 11.865 | 2.432 | 73,60% | −45,71% | 72,291% | 9,60% | 0,085 | −0,268 |
| PAC | 24 | VA Puro | 6,48% | 12,55% | 7.283 | 384 | 7.667 | 1.659 | 55,47% | −39,28% | 68,862% | 6,48% | 0,035 | −0,218 |
Fig. 46 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging di tutti i PAC di varie durate su serie storiche simulate con tecniche non parametriche (incremento target 0,50%, senza massimale, Filtro anti-Hayley: presente)
Sono state simulate 100.000 nuove serie storiche, sempre permutando i 360 rendimenti iniziali. Le serie storiche dei prezzi non sono perciò uguali alle precedenti. Il campione è comunque sufficientemente grande da rendere il confronto tra i valori medi significativo.
Il Cost Averaging conferma i rendimenti migliori e la somma finale più alta. I rendimenti del Value Averaging (soprattutto quello puro) sono ancora una volta meno volatili di quelli del Cost Averaging. Vediamo brevemente i valori delle altre misure:
- Rata max: è cresciuta notevolmente, arrivando a superare i 50.000 euro nel Value Averaging.
- Rendimento max e min: il rendimento massimo è cresciuto in entrambe le tipologie di Value Averaging.
- % Positivi: è rimasta pressoché invariata.
- Mediana: è sensibilmente aumentata nel Value Averaging.
- Skewness: è positiva per tutte le durate di tutte le tipologie di piani di accumulo. Graficamente (piani trentennali):
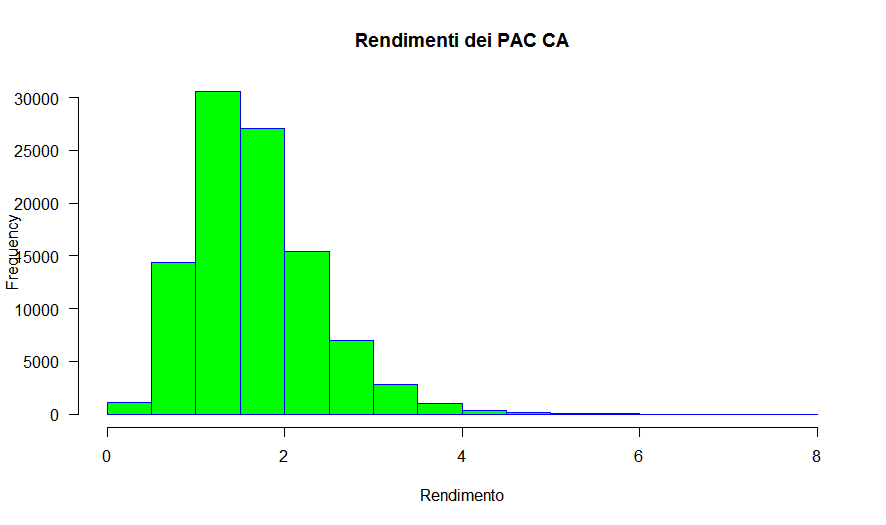
Fig. 47 – Istogramma delle frequenze dei rendimenti dei 100.000 PAC Cost Averaging trentennali simulati con tecniche non parametriche (incremento target 0,50%, senza massimale, Filtro anti-Hayley: presente)
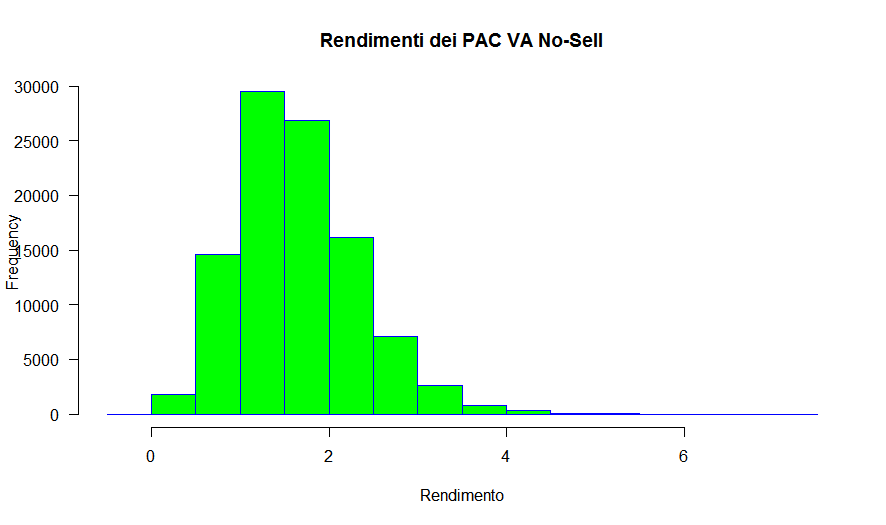
Fig. 48 – Istogramma delle frequenze dei rendimenti dei 100.000 PAC Value Averaging No-sell trentennali simulati con tecniche non parametriche (incremento target 0,50%, senza massimale, Filtro anti-Hayley: presente)
La skewness del Cost Averaging è pari a 0,954; quella del Value Averaging No-Sell è 0,770: non troppo diversa, quindi. La skewness del Value Averaging puro, invece, è di 0,269 e questa differenza, seppure meno marcata di prima, si vede ancora bene negli istogrammi seguenti: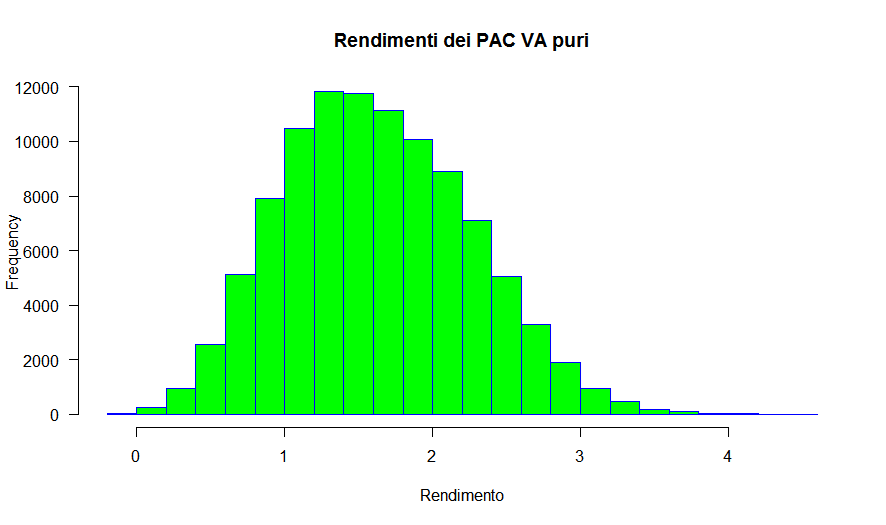
Fig. 49 – Istogramma delle frequenze dei rendimenti dei 100.000 PAC Value Averaging puri trentennali simulati con tecniche non parametriche (incremento target 0,50%, senza massimale, Filtro anti-Hayley: presente)
- Kurtosis (curtosi): i valori sono di nuovo positivi nel Cost Averaging e nel Value Averaging No-Sell (1,627 e 1,130) e negativi nel Value Averaging puro (−0,298).
Anche incrementando il target dello 0,50%, il Value Averaging non è stato mediamente in grado di utilizzare tutta la liquidità disponibile. Vediamo cosa succede portando questa percentuale allo 0,75%:
| Incremento 0,75% - No massimale - 100.000 simulazioni | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. totale | Stand. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. |
| PAC | 360 | CA | 167,09% | 69,81% | 288.462 | 0 | 288.462 | 300 | 781,21% | −8,03% | 99,999% | 156,48% | 1,024 | 2,015 |
| PAC | 300 | CA | 129,07% | 72,31% | 206.166 | 0 | 206.166 | 300 | 725,63% | −41,80% | 99,611% | 117,58% | 1,081 | 2,080 |
| PAC | 240 | CA | 94,81% | 64,35% | 140.260 | 0 | 140.260 | 300 | 658,07% | −50,18% | 97,587% | 84,43% | 1,091 | 2,093 |
| PAC | 180 | CA | 64,88% | 52,15% | 89.035 | 0 | 89.035 | 300 | 545,34% | −52,83% | 93,412% | 56,49% | 1,064 | 2,021 |
| PAC | 120 | CA | 39,51% | 38,21% | 50.224 | 0 | 50.224 | 300 | 353,48% | −58,73% | 86,723% | 34,19% | 0,897 | 1,451 |
| PAC | 60 | CA | 18,11% | 23,57% | 21.259 | 0 | 21.259 | 300 | 183,63% | −49,82% | 77,151% | 15,85% | 0,608 | 0,693 |
| PAC | 36 | CA | 10,40% | 17,16% | 11.923 | 0 | 11.923 | 300 | 107,12% | −45,59% | 71,496% | 9,29% | 0,418 | 0,328 |
| PAC | 24 | CA | 6,63% | 13,34% | 7.678 | 0 | 7.678 | 300 | 82,41% | −38,97% | 67,919% | 6,04% | 0,276 | 0,159 |
| PAC | 360 | VA No-Sell | 166,80% | 70,46% | 288.120 | 25 | 288.146 | 48.600 | 775,92% | −25,09% | 99,991% | 156,70% | 0,974 | 1,886 |
| PAC | 300 | VA No-Sell | 128,56% | 72,02% | 205.421 | 279 | 205.700 | 46.468 | 668,38% | −42,09% | 99,566% | 117,26% | 1,027 | 1,782 |
| PAC | 240 | VA No-Sell | 93,99% | 62,90% | 138.945 | 726 | 139.671 | 31.505 | 602,04% | −50,07% | 97,542% | 84,14% | 0,968 | 1,456 |
| PAC | 180 | VA No-Sell | 63,89% | 49,88% | 87.421 | 1.079 | 88.501 | 20.110 | 483,50% | −54,08% | 93,391% | 56,42% | 0,855 | 1,098 |
| PAC | 120 | VA No-Sell | 38,57% | 35,84% | 48.762 | 1.122 | 49.884 | 11.123 | 275,27% | −58,66% | 86,813% | 34,27% | 0,610 | 0,388 |
| PAC | 60 | VA No-Sell | 17,56% | 22,04% | 20.437 | 723 | 21.160 | 4.484 | 128,55% | −49,82% | 77,453% | 16,17% | 0,319 | −0,077 |
| PAC | 36 | VA No-Sell | 10,08% | 16,19% | 11.452 | 436 | 11.888 | 2.557 | 86,16% | −45,59% | 71,902% | 9,57% | 0,169 | −0,192 |
| PAC | 24 | VA No-Sell | 6,45% | 12,72% | 7.400 | 264 | 7.665 | 1.716 | 63,69% | −38,95% | 68,447% | 6,25% | 0,073 | −0,177 |
| PAC | 360 | VA Puro | 166,92% | 70,83% | 287.989 | 288 | 288.277 | 102.349 | 673,91% | −34,16% | 99,982% | 157,19% | 0,915 | 1,520 |
| PAC | 300 | VA Puro | 128,19% | 70,77% | 203.721 | 1.649 | 205.370 | 63.275 | 494,61% | −42,01% | 99,544% | 117,30% | 0,873 | 0,929 |
| PAC | 240 | VA Puro | 93,21% | 60,47% | 136.357 | 2.758 | 139.115 | 37.793 | 381,39% | −50,05% | 97,535% | 84,23% | 0,729 | 0,360 |
| PAC | 180 | VA Puro | 63,12% | 47,52% | 85.196 | 2.886 | 88.082 | 21.518 | 293,07% | −54,27% | 93,424% | 56,55% | 0,593 | 0,046 |
| PAC | 120 | VA Puro | 38,12% | 34,51% | 47.588 | 2.135 | 49.723 | 11.123 | 194,61% | −58,66% | 86,863% | 34,49% | 0,423 | −0,194 |
| PAC | 60 | VA Puro | 17,45% | 21,70% | 20.166 | 976 | 21.141 | 4.484 | 116,98% | −49,82% | 77,514% | 16,25% | 0,242 | −0,257 |
| PAC | 36 | VA Puro | 10,05% | 16,11% | 11.383 | 502 | 11.886 | 2.557 | 77,36% | −45,59% | 71,935% | 9,60% | 0,141 | −0,250 |
| PAC | 24 | VA Puro | 6,45% | 12,70% | 7.383 | 281 | 7.664 | 1.716 | 61,87% | −38,95% | 68,471% | 6,26% | 0,064 | −0,196 |
Fig. 50 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging di tutti i PAC di varie durate su serie storiche simulate con tecniche non parametriche (incremento target 0,75%, senza massimale, Filtro anti-Hayley: presente)
Le differenze di rendimento e delle somme finali sono minime, ma ancora a favore del Cost Averaging. Il Value Averaging si conferma una strategia di investimento meno volatile soltanto per le durate fino a 20 anni.
Diamo infine un’occhiata alle altre misure:
- Rata max: elevatissima nel Value Averaging puro di lunga durata, ma pur sempre affrontabile con la liquidità accumulata durante la vita del PAC.
- Rendimento max e min: la forbice tra il Cost Averaging ed il Value Averaging si è ridotta ulteriormente. Questa serie di simulazioni ha generato almeno un risultato negativo anche per il Cost Averaging (nelle simulazioni precedenti non era successo).
- % Positivi e Mediana: praticamente immutati.
- Skewness: è aumentata leggermente nel Cost Averaging, un po’ di più nel Value Averaging No-Sell e molto in quello puro, che è ormai simile agli altri da questo punto di vista. In generale, più si aumenta la percentuale di incremento del target, più il Value Averaging tende ad avvicinarsi al Cost Averaging. Oltre una certa soglia non ci sarà più alcuna differenza: il target crescerà troppo velocemente e i versamenti non riusciranno a stargli dietro, nonostante ognuno di essi sia dell’importo massimo (300 euro, esattamente come nel Cost Averaging). In tal caso, il Value Averaging e il Cost Averaging coincideranno.
Gli istogrammi seguenti confermano le nostre conclusioni:
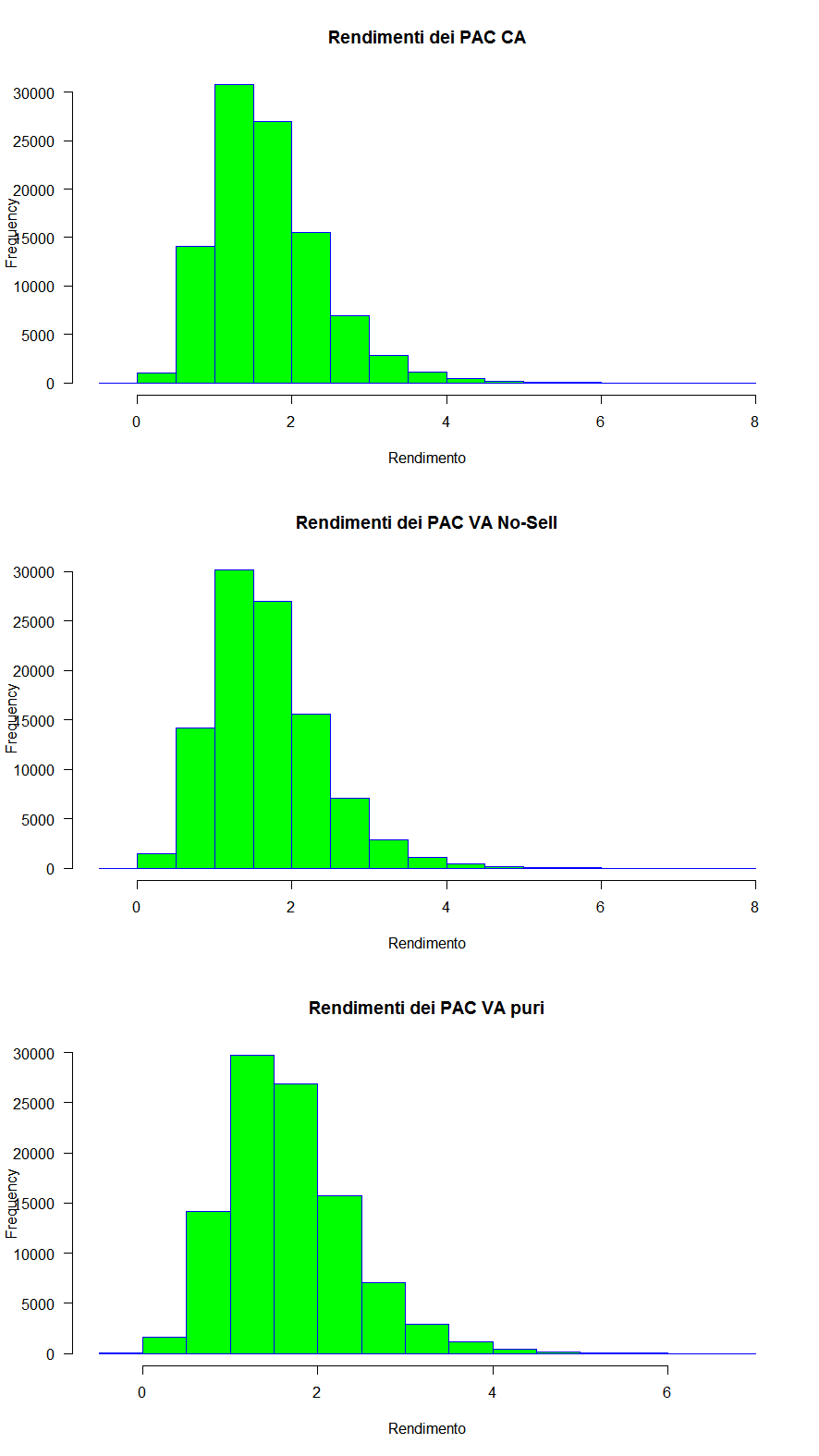
Fig. 51 – Istogramma delle frequenze dei rendimenti dei 100.000 PAC Cost Averaging, Value Averaging No-sell e Value Averaging puri trentennali simulati con tecniche non parametriche (incremento target 0,75%, senza massimale, Filtro anti-Hayley: presente)
Anche visivamente, le differenze tra le distribuzioni dei rendimenti di queste tipologie di PAC sono impercettibili.
Abbiamo effettuato il backtest degli stessi piani di accumulo con il massimale dei versamenti fissato a 1.000 euro. Non riportiamo tutti i risultati per motivi di spazio, anche perché sono molto simili a quelli appena visti.
È più interessante realizzare le stesse simulazioni non parametriche su una diversa serie storica: utilizziamo quella del fondo Aberdeen Japanese Equity Fund A Acc, che aveva ottenuto delle performance molto peggiori del fondo Raiffeisen Azionario Globale VT.
Il motivo di questa duplice analisi è semplice: dopo aver verificato come si comporta il Value Averaging con mercati in rialzo, è bene esaminare che cosa accade in periodi di crisi o con trend di decrescita di lungo termine.
Partiamo come al solito dai piani di accumulo con rata iniziale di 300 euro, target costante, assenza di massimale e filtro anti-Hayley attivato. I risultati ottenuti sono i seguenti:
| Incremento 0% - No massimale - 100.000 simulazioni | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. totale | Stand. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. |
| PAC | 360 | CA | 1,69% | 34,16% | 109.821 | 0 | 109.821 | 300 | 321,56% | −72,78% | 44,499% | −4,40% | 1,239 | 2,853 |
| PAC | 300 | CA | 4,09% | 38,66% | 93.683 | 0 | 93.683 | 300 | 367,50% | −75,15% | 46,521% | −3,09% | 1,301 | 3,110 |
| PAC | 240 | CA | 5,87% | 40,79% | 76.225 | 0 | 76.225 | 300 | 481,48% | −77,74% | 48,056% | −1,76% | 1,384 | 3,629 |
| PAC | 180 | CA | 5,93% | 39,24% | 57.203 | 0 | 57.203 | 300 | 425,90% | −74,33% | 48,566% | −1,27% | 1,363 | 3,589 |
| PAC | 120 | CA | 4,96% | 34,53% | 37.786 | 0 | 37.786 | 300 | 372,37% | −71,02% | 48,862% | −0,87% | 1,203 | 2,814 |
| PAC | 60 | CA | 3,12% | 25,27% | 18.561 | 0 | 18.561 | 300 | 212,09% | −64,55% | 49,561% | −0,25% | 0,882 | 1,472 |
| PAC | 36 | CA | 1,89% | 19,51% | 11.004 | 0 | 11.004 | 300 | 128,32% | −54,09% | 49,796% | −0,10% | 0,658 | 0,776 |
| PAC | 24 | CA | 1,26% | 15,72% | 7.291 | 0 | 7.291 | 300 | 127,57% | −51,78% | 50,018% | 0,01% | 0,523 | 0,635 |
| PAC | 360 | VA No-Sell | 5,96% | 32,69% | 109.063 | 5.375 | 114.438 | 22.597 | 301,14% | −72,21% | 51,640% | 1,31% | 0,973 | 1,861 |
| PAC | 300 | VA No-Sell | 7,41% | 36,98% | 90.701 | 5.966 | 96.667 | 18.922 | 331,68% | −74,32% | 52,382% | 2,16% | 0,952 | 1,690 |
| PAC | 240 | VA No-Sell | 8,04% | 38,17% | 72.183 | 5.608 | 77.791 | 15.185 | 330,19% | −77,24% | 52,806% | 2,69% | 0,950 | 1,682 |
| PAC | 180 | VA No-Sell | 7,11% | 36,04% | 53.303 | 4.538 | 57.841 | 11.448 | 333,50% | −74,32% | 52,545% | 2,37% | 0,865 | 1,386 |
| PAC | 120 | VA No-Sell | 5,38% | 31,43% | 34.875 | 3.063 | 37.938 | 7.712 | 243,02% | −70,60% | 52,240% | 1,85% | 0,701 | 0,775 |
| PAC | 60 | VA No-Sell | 3,14% | 23,18% | 17.175 | 1.390 | 18.565 | 3.975 | 137,49% | −64,49% | 52,196% | 1,28% | 0,458 | 0,162 |
| PAC | 36 | VA No-Sell | 1,86% | 18,17% | 10.274 | 728 | 11.001 | 2.480 | 92,36% | −54,08% | 51,808% | 0,90% | 0,322 | −0,056 |
| PAC | 24 | VA No-Sell | 1,24% | 14,82% | 6.869 | 421 | 7.290 | 1.732 | 79,79% | −51,66% | 51,721% | 0,69% | 0,239 | −0,043 |
| PAC | 360 | VA Puro | 12,28% | 30,23% | 100.565 | 20.700 | 121.264 | 22.659 | 149,93% | −69,85% | 63,095% | 11,03% | 0,300 | −0,230 |
| PAC | 300 | VA Puro | 11,07% | 34,09% | 81.993 | 17.970 | 99.963 | 18.922 | 162,81% | −73,14% | 59,305% | 9,28% | 0,328 | −0,356 |
| PAC | 240 | VA Puro | 9,88% | 34,96% | 65.011 | 14.104 | 79.115 | 15.185 | 177,18% | −76,95% | 57,560% | 7,83% | 0,361 | −0,332 |
| PAC | 180 | VA Puro | 7,87% | 33,32% | 48.663 | 9.588 | 58.251 | 11.448 | 153,38% | −74,32% | 55,614% | 5,67% | 0,377 | −0,303 |
| PAC | 120 | VA Puro | 5,55% | 29,65% | 32.606 | 5.390 | 37.997 | 7.712 | 149,84% | −70,54% | 54,153% | 3,52% | 0,364 | −0,282 |
| PAC | 60 | VA Puro | 3,14% | 22,60% | 16.625 | 1.939 | 18.565 | 3.975 | 106,74% | −64,49% | 52,923% | 1,77% | 0,314 | −0,214 |
| PAC | 36 | VA Puro | 1,86% | 17,98% | 10.113 | 888 | 11.001 | 2.480 | 82,57% | −54,08% | 52,110% | 1,05% | 0,258 | −0,207 |
| PAC | 24 | VA Puro | 1,24% | 14,75% | 6.816 | 473 | 7.289 | 1.732 | 76,99% | −51,66% | 51,821% | 0,74% | 0,207 | −0,126 |
Fig. 52 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging di tutti i PAC di varie durate su serie storiche simulate con tecniche non parametriche (target costante, senza massimale, Filtro anti-Hayley: presente)
La situazione è completamente diversa. Il Cost Averaging ottiene i rendimenti peggiori (generando quindi una somma finale inferiore).
I rendimenti più alti, almeno per le durate uguali o superiori a 5 anni, sono quelli del Value Averaging puro. Questa tipologia di PAC è anche quella meno volatile, come la deviazione standard ci dimostra.
Si verifica una situazione più unica che rara: il venir meno del trade-off rischio/rendimento. Non è finita qui: anche la percentuale di PAC positivi è decisamente superiore a quella del Value Averaging No-sell e, soprattutto, a quella del Cost Averaging. Lo stesso ordinamento si conferma anche nei confronti della mediana.
I rendimenti max sono ancora appannaggio del Cost Averaging, che su tutte le durate genera però anche i rendimenti peggiori.
La skewness è positiva per tutte le tipologie di PAC, mentre la kurtosis cresce nel Cost Averaging e diminuisce sia nel Value Averaging No-Sell che in quello puro (tutti con kurtosis negativa).
Vediamo le distribuzioni delle frequenze dei rendimenti dei 100.000 piani di accumulo trentennali Cost Averaging, Value Averaging No-sell e puri:
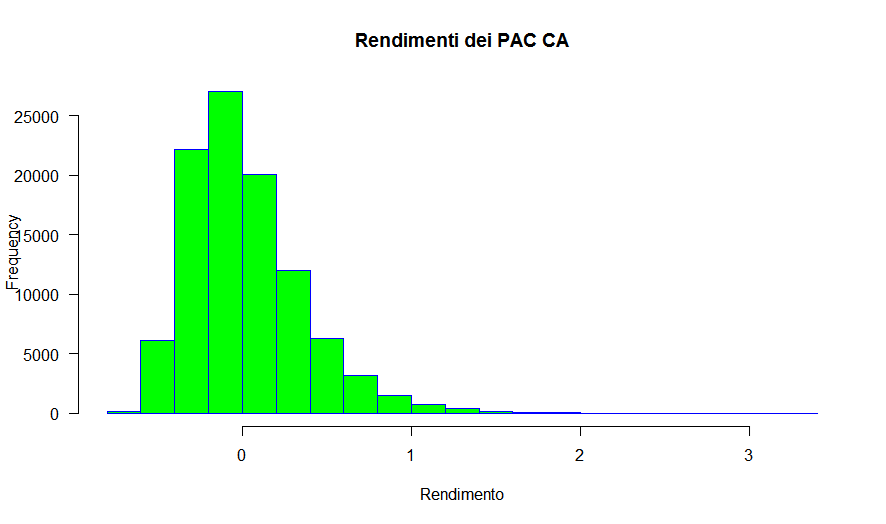
Fig. 53 – Istogramma delle frequenze dei rendimenti dei 100.000 PAC Cost Averaging trentennali simulati con tecniche non parametriche (target costante, senza massimale, Filtro anti-Hayley: presente)
Si nota una lunga coda destra. La media e la mediana si posizionano intorno a zero. Oltre la metà dei rendimenti sono negativi.
Queste sono invece le frequenze del Value Averaging No-sell:
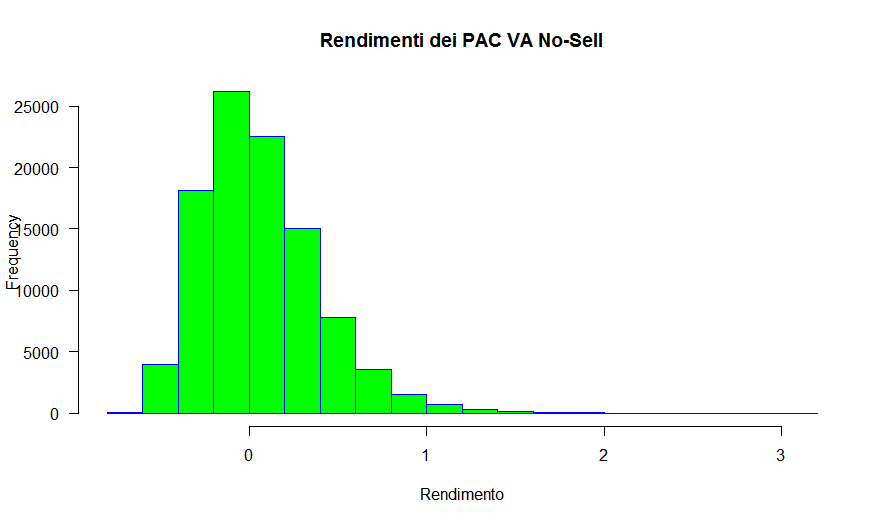
Fig. 54 – Istogramma delle frequenze dei rendimenti dei 100.000 PAC Value Averaging No-sell trentennali simulati con tecniche non parametriche (target costante, senza massimale, Filtro anti-Hayley: presente)
Il grafico è molto simile al precedente.
Quello del Value Averaging puro è il seguente:
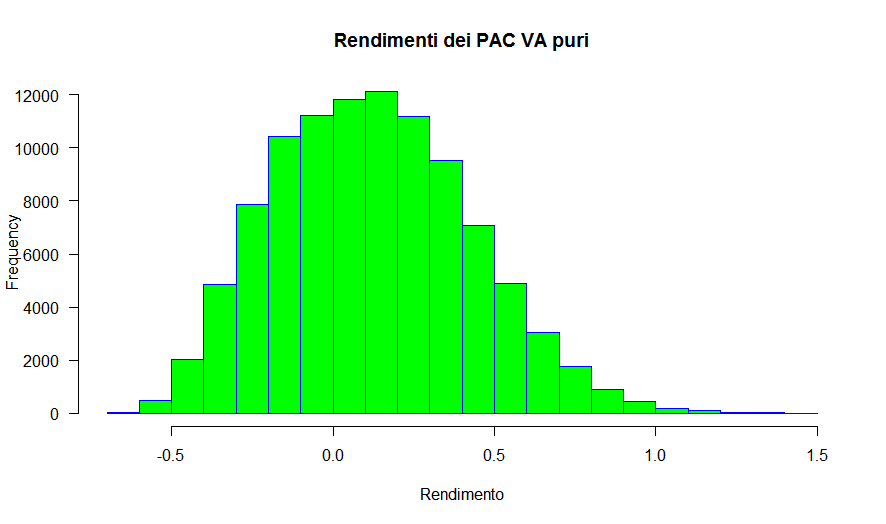
Fig. 55 – Istogramma delle frequenze dei rendimenti dei 100.000 PAC Value Averaging puri trentennali simulati con tecniche non parametriche (target costante, senza massimale, Filtro anti-Hayley: presente)
La coda lunga destra è ancora presente ma la forma della distribuzione è un po’ più simile a quella della normale.
La media e la mediana sono ben posizionate in terreno positivo e la percentuale dei piani di accumulo positivi è decisamente superiore a quella delle altre tipologie di PAC.
I benefici del Value Averaging, soprattutto quello puro, sono evidenti. In queste condizioni di mercato, il Value Averaging riesce davvero a sviluppare la sua magia: rendimenti più alti con minor volatilità.
Vediamo cosa succede con un aumento del target dello 0,50%:
| Incremento 0% - No massimale - 100.000 simulazioni | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. totale | Stand. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. |
| PAC | 360 | CA | 1,69% | 34,26% | 109.827 | 0 | 109.827 | 300 | 363,15% | −70,08% | 44,482% | −4,41% | 1,261 | 2,988 |
| PAC | 300 | CA | 4,08% | 38,56% | 93.671 | 0 | 93.671 | 300 | 429,36% | −75,50% | 46,551% | −2,97% | 1,309 | 3,229 |
| PAC | 240 | CA | 5,63% | 40,56% | 76.053 | 0 | 76.053 | 300 | 463,95% | −74,39% | 47,685% | −2,05% | 1,353 | 3,530 |
| PAC | 180 | CA | 5,97% | 39,32% | 57.226 | 0 | 57.226 | 300 | 500,77% | −73,06% | 48,443% | −1,38% | 1,342 | 3,419 |
| PAC | 120 | CA | 4,97% | 34,51% | 37.790 | 0 | 37.790 | 300 | 337,42% | −71,12% | 48,868% | −0,86% | 1,185 | 2,605 |
| PAC | 60 | CA | 3,08% | 25,15% | 18.554 | 0 | 18.554 | 300 | 188,55% | −62,50% | 49,730% | −0,17% | 0,859 | 1,340 |
| PAC | 36 | CA | 2,00% | 19,55% | 11.016 | 0 | 11.016 | 300 | 167,52% | −53,29% | 49,942% | −0,03% | 0,654 | 0,808 |
| PAC | 24 | CA | 1,26% | 15,76% | 7.291 | 0 | 7.291 | 300 | 98,43% | −48,47% | 49,772% | −0,09% | 0,538 | 0,600 |
| PAC | 360 | VA No-Sell | 1,96% | 34,21% | 110.117 | 3 | 110.121 | 31.172 | 362,32% | −70,91% | 44,831% | −4,12% | 1,262 | 3,002 |
| PAC | 300 | VA No-Sell | 4,46% | 38,66% | 93.971 | 45 | 94.016 | 29.645 | 412,66% | −75,56% | 47,013% | −2,61% | 1,297 | 3,089 |
| PAC | 240 | VA No-Sell | 6,09% | 40,63% | 76.184 | 203 | 76.387 | 23.751 | 434,84% | −74,25% | 48,193% | −1,63% | 1,292 | 2,986 |
| PAC | 180 | VA No-Sell | 6,39% | 38,97% | 56.970 | 478 | 57.449 | 18.231 | 429,94% | −73,04% | 49,033% | −0,90% | 1,191 | 2,365 |
| PAC | 120 | VA No-Sell | 5,21% | 33,62% | 37.185 | 690 | 37.875 | 10.637 | 255,12% | −71,11% | 49,585% | −0,34% | 0,945 | 1,283 |
| PAC | 60 | VA No-Sell | 3,12% | 24,12% | 17.982 | 580 | 18.562 | 4.664 | 145,99% | −62,43% | 50,649% | 0,39% | 0,590 | 0,319 |
| PAC | 36 | VA No-Sell | 1,99% | 18,73% | 10.621 | 395 | 11.015 | 2.733 | 120,80% | −53,29% | 50,940% | 0,45% | 0,407 | 0,049 |
| PAC | 24 | VA No-Sell | 1,25% | 15,15% | 7.031 | 259 | 7.290 | 1.851 | 79,87% | −48,46% | 50,757% | 0,30% | 0,317 | 0,000 |
| PAC | 360 | VA Puro | 2,47% | 34,25% | 110.628 | 35 | 110.663 | 59.547 | 321,65% | −71,19% | 45,431% | −3,61% | 1,272 | 3,022 |
| PAC | 300 | VA Puro | 5,15% | 39,03% | 94.342 | 292 | 94.634 | 44.217 | 303,97% | −75,48% | 47,647% | −2,10% | 1,264 | 2,614 |
| PAC | 240 | VA Puro | 6,78% | 40,75% | 75.988 | 895 | 76.883 | 29.560 | 290,57% | −74,17% | 48,816% | −1,12% | 1,151 | 1,796 |
| PAC | 180 | VA Puro | 6,83% | 38,52% | 56.218 | 1.470 | 57.688 | 18.693 | 269,17% | −73,04% | 49,600% | −0,37% | 0,981 | 1,027 |
| PAC | 120 | VA Puro | 5,37% | 32,95% | 36.443 | 1.490 | 37.933 | 10.637 | 183,69% | −71,11% | 50,002% | 0,00% | 0,753 | 0,370 |
| PAC | 60 | VA Puro | 3,13% | 23,78% | 17.695 | 868 | 18.564 | 4.664 | 108,55% | −62,43% | 50,926% | 0,57% | 0,487 | −0,038 |
| PAC | 36 | VA Puro | 1,99% | 18,60% | 10.518 | 497 | 11.015 | 2.733 | 104,43% | −53,29% | 51,081% | 0,52% | 0,354 | −0,110 |
| PAC | 24 | VA Puro | 1,25% | 15,10% | 6.994 | 295 | 7.290 | 1.851 | 71,24% | −48,46% | 50,837% | 0,33% | 0,291 | −0,079 |
Fig. 56 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging di tutti i PAC di varie durate su serie storiche simulate con tecniche non parametriche (incremento target 0,50%, senza massimale, Filtro anti-Hayley: presente)
La magia sembra essere svanita. Il Value Averaging mantiene un piccolo vantaggio sul Cost Averaging, ma le differenze si sono quasi azzerate. Il target costante è la scelta ottimale in caso di mercati con trend negativi.
È inutile mostrare i grafici delle distribuzioni delle frequenze perché sono tutte e tre molto simili a quella del Cost Averaging vista in precedenza.
Alzare ulteriormente l’incremento del target non avrebbe migliorato le cose. Fissando un massimale ai versamenti di 1.000 euro, invece, avrebbe migliorato ulteriormente i risultati in caso di target costante, come dimostra la seguente tabella:
| Incremento 0% - Massimale 1000 euro - 100.000 simulazioni | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. totale | Stand. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. |
| PAC | 360 | CA | 1,98% | 34,31% | 110.137 | 0 | 110.137 | 300 | 378,79% | −70,40% | 44,703% | −4,21% | 1,247 | 2,857 |
| PAC | 300 | CA | 4,01% | 38,58% | 93.612 | 0 | 93.612 | 300 | 443,34% | −75,31% | 46,510% | −3,05% | 1,335 | 3,444 |
| PAC | 240 | CA | 5,53% | 40,55% | 75.985 | 0 | 75.985 | 300 | 376,48% | −77,97% | 47,737% | −2,01% | 1,369 | 3,457 |
| PAC | 180 | CA | 5,97% | 39,30% | 57.222 | 0 | 57.222 | 300 | 407,85% | −75,14% | 48,537% | −1,28% | 1,360 | 3,520 |
| PAC | 120 | CA | 5,04% | 34,56% | 37.815 | 0 | 37.815 | 300 | 331,03% | −71,06% | 49,103% | −0,72% | 1,196 | 2,699 |
| PAC | 60 | CA | 3,03% | 25,18% | 18.545 | 0 | 18.545 | 300 | 190,15% | −61,98% | 49,714% | −0,18% | 0,878 | 1,475 |
| PAC | 36 | CA | 1,97% | 19,51% | 11.012 | 0 | 11.012 | 300 | 129,28% | −53,70% | 49,953% | −0,02% | 0,661 | 0,781 |
| PAC | 24 | CA | 1,35% | 15,71% | 7.297 | 0 | 7.297 | 300 | 103,93% | −47,44% | 50,240% | 0,08% | 0,521 | 0,543 |
| PAC | 360 | VA No-Sell | 7,14% | 31,94% | 107.660 | 8.055 | 115.715 | 1.000 | 333,40% | −66,48% | 53,693% | 2,77% | 0,995 | 2,019 |
| PAC | 300 | VA No-Sell | 7,82% | 36,19% | 89.129 | 7.905 | 97.034 | 1.000 | 341,72% | −74,94% | 53,506% | 3,03% | 0,972 | 1,975 |
| PAC | 240 | VA No-Sell | 7,91% | 37,38% | 70.815 | 6.879 | 77.694 | 1.000 | 303,54% | −77,93% | 53,332% | 3,08% | 0,918 | 1,602 |
| PAC | 180 | VA No-Sell | 7,22% | 35,68% | 52.596 | 5.303 | 57.900 | 1.000 | 351,97% | −75,11% | 53,133% | 2,87% | 0,865 | 1,502 |
| PAC | 120 | VA No-Sell | 5,48% | 31,23% | 34.579 | 3.394 | 37.974 | 1.000 | 256,14% | −70,93% | 52,697% | 2,23% | 0,693 | 0,800 |
| PAC | 60 | VA No-Sell | 3,06% | 23,04% | 17.105 | 1.445 | 18.550 | 1.000 | 139,37% | −61,93% | 52,363% | 1,43% | 0,446 | 0,152 |
| PAC | 36 | VA No-Sell | 1,94% | 18,16% | 10.268 | 742 | 11.010 | 1.000 | 99,17% | −53,70% | 52,059% | 0,98% | 0,327 | −0,033 |
| PAC | 24 | VA No-Sell | 1,33% | 14,81% | 6.870 | 425 | 7.296 | 1.000 | 75,73% | −47,32% | 51,843% | 0,76% | 0,242 | −0,072 |
| PAC | 360 | VA Puro | 13,50% | 27,76% | 93.072 | 29.505 | 122.577 | 1.000 | 156,28% | −64,64% | 66,931% | 12,39% | 0,286 | −0,057 |
| PAC | 300 | VA Puro | 11,46% | 32,10% | 77.250 | 23.067 | 100.317 | 1.000 | 170,06% | −73,50% | 61,658% | 10,16% | 0,295 | −0,226 |
| PAC | 240 | VA Puro | 9,73% | 33,52% | 62.079 | 16.928 | 79.007 | 1.000 | 151,87% | −77,90% | 58,795% | 8,11% | 0,322 | −0,273 |
| PAC | 180 | VA Puro | 7,92% | 32,51% | 47.153 | 11.126 | 58.279 | 1.000 | 157,94% | −75,10% | 56,669% | 6,10% | 0,351 | −0,258 |
| PAC | 120 | VA Puro | 5,63% | 29,30% | 32.041 | 5.986 | 38.027 | 1.000 | 141,08% | −70,89% | 54,835% | 3,92% | 0,347 | −0,256 |
| PAC | 60 | VA Puro | 3,06% | 22,46% | 16.536 | 2.015 | 18.551 | 1.000 | 101,86% | −61,92% | 53,118% | 1,91% | 0,304 | −0,214 |
| PAC | 36 | VA Puro | 1,94% | 17,96% | 10.103 | 906 | 11.009 | 1.000 | 81,96% | −53,70% | 52,373% | 1,13% | 0,259 | −0,201 |
| PAC | 24 | VA Puro | 1,33% | 14,75% | 6.817 | 479 | 7.295 | 1.000 | 64,23% | −47,32% | 51,980% | 0,81% | 0,212 | −0,147 |
Fig. 57 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging di tutti i PAC di varie durate su serie storiche simulate con tecniche non parametriche (target costante, massimale 1000 euro, Filtro anti-Hayley: presente)
Rispetto a prima, queste 100.000 simulazioni migliorano i rendimenti di tutte le tipologie di PAC ma, mentre per il Cost Averaging gli incrementi del rendimento medio e della mediana sono minimi, quelli del Value Averaging sono significativi: aumentano tutti i rendimenti, la mediana e la % di PAC positivi. Nello stesso tempo, diminuisce ulteriormente la volatilità. Davvero un ottimo risultato.
Questi sono i grafici delle distribuzioni delle frequenze:
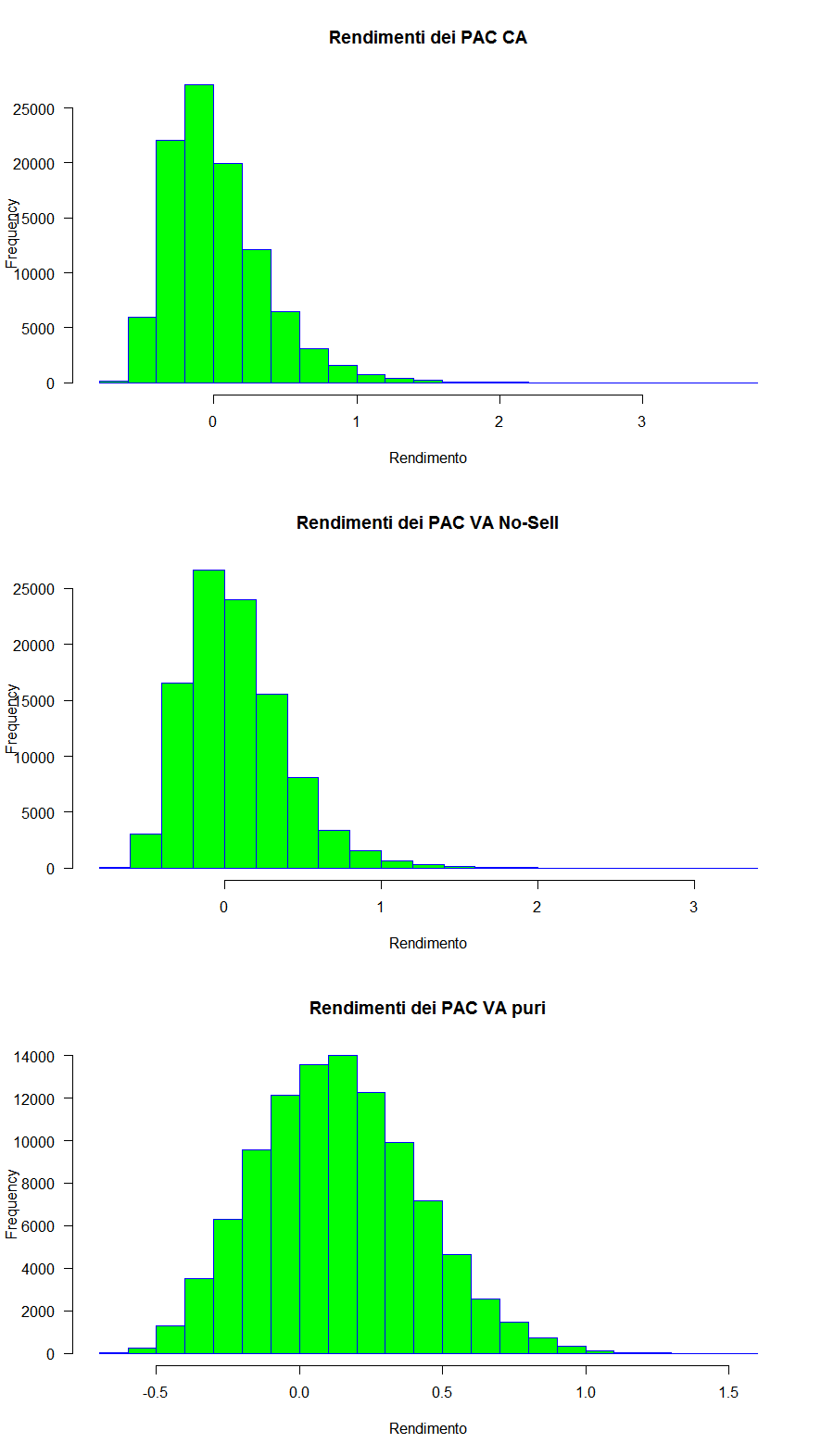
Fig. 58 – Istogramma delle frequenze dei rendimenti dei 100.000 PAC Cost Averaging, Value Averaging No-sell e Value Averaging puri trentennali simulati con tecniche non parametriche (target costante, massimale 1000 euro, Filtro anti-Hayley: presente)
Affrontare un trend discendente con un PAC Value Averaging puro, a target costante e versamenti massimi di 1000 euro sarebbe stata la scelta migliore.
Naturalmente, nel momento in cui si inizia un piano di accumulo non c’è modo di sapere il trend che seguirà il mercato, ma un investitore molto prudente potrebbe preventivamente scegliere questa soluzione di investimento. Se il trend sarà positivo, questa scelta non sarà ottimale, ma i rendimenti del Value Averaging puro non sono da disprezzare e la volatilità è minore di quella delle altre tipologie di PAC.
In caso di incremento del target dello 0,50%, le differenze tra le tre tipologie di piani di accumulo si assottigliano sensibilmente: le performance si avvicinano a quelle del Cost Averaging e il Value Averaging perde gran parte dei suoi benefici.
In definitiva, le simulazioni non parametriche effettuate col metodo Monte Carlo confermano che, laddove non si predisponga una riserva di liquidità iniziale, il Value Averaging diminuisce il rischio associato con l’investimento anche se, in media:
- Genera dei rendimenti leggermente inferiori con i mercati in crescita (questo risultato non si era verificato nei backtest delle serie storiche reali, effettuati nei capitoli precedenti).
- Il Value Averaging con target costante dimostra di essere la strategia migliore, riuscendo a produrre rendimenti più elevati a fronte di una volatilità inferiore, nei mercati con un andamento negativo.
Nel prossimo capitolo, utilizzeremo il metodo Monte Carlo per la misurazione dei risultati di simulazioni parametriche.
9. Value Averaging vs Cost Averaging: simulazioni parametriche col metodo Monte Carlo

«Try not to become a man of success, but rather try to become a man of value».
Albert Einstein
Continuiamo la nostra analisi effettuando altre simulazioni Monte Carlo, utilizzando stavolta metodologie parametriche.
Nei nostri test simuleremo 100.000 serie storiche di rendimenti mensili che seguono la distribuzione normale con:
- Media pari a 0,5% e deviazione standard del 5% (simulazione di rendimenti azionari).
- Media pari a 0 e deviazione standard del 5% (simulazione di rendimenti azionari in un mercato laterale).
- Media pari a −0,50% e deviazione standard del 5% (simulazione di rendimenti azionari in un mercato in decrescita).
- Media pari a 0,25% e deviazione standard del 2,5% (simulazione di rendimenti obbligazionari).
Questi valori sono mensili e, seppur arbitrari, non dovrebbero essere troppo lontani dalla realtà.
A partire da queste serie di rendimenti “sintetici”, abbiamo ricostruito quelle dei prezzi (partendo da 100). Sulle serie dei prezzi sono stati quindi simulati i piani di accumulo Value Averaging e Cost Averaging.
Il fatto che sia stata scelta la distribuzione normale che, come è noto, è solo un’approssimazione della reale (ma sconosciuta) distribuzione dei rendimenti azionari, non deve preoccupare più di tanto: non stiamo ottimizzando un modello econometrico che abbia l’obiettivo di stimare i prezzi futuri nel modo più preciso possibile.
Quello che vogliamo fare, invece, è confrontare due modalità di investimento, il Cost Averaging e il Value Averaging, per verificare quale delle due permetta di ottenere le performance migliori.
Lo stesso Edleson ha utilizzato questo tipo di simulazioni, affermando che l’utilizzo dei soli dati storici, per quanto rassicurante, potrebbe essere pericoloso: se lo scenario futuro fosse anche soltanto leggermente diverso da quello passato, i risultati potrebbero essere radicalmente diversi.
Anche stavolta, le nostre simulazioni sono state realizzate in R.
Questa è la prima tabella di risultati:
| Incremento 0% - No massimale - Media 0,50% - Deviazione Standard 5% - 100.000 simulazioni | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. totale | Stand. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. |
| PAC | 360 | CA | 178,45% | 212,59% | 300.721 | 0 | 300.721 | 300 | 3.897,78% | −78,92% | 90,633% | 119,74% | 3,102 | 18,915 |
| PAC | 300 | CA | 131,37% | 153,78% | 208.234 | 0 | 208.234 | 300 | 3.019,17% | −75,71% | 88,682% | 91,43% | 2,788 | 16,225 |
| PAC | 240 | CA | 92,34% | 107,03% | 138.483 | 0 | 138.483 | 300 | 1.696,40% | −77,61% | 85,746% | 66,79% | 2,147 | 8,862 |
| PAC | 180 | CA | 61,69% | 73,37% | 87.314 | 0 | 87.314 | 300 | 1.141,40% | −67,48% | 82,484% | 46,13% | 1,746 | 6,195 |
| PAC | 120 | CA | 36,92% | 48,05% | 49.290 | 0 | 49.290 | 300 | 575,63% | −68,01% | 77,933% | 28,40% | 1,315 | 3,292 |
| PAC | 60 | CA | 16,27% | 27,05% | 20.929 | 0 | 20.929 | 300 | 219,22% | −54,34% | 70,547% | 12,72% | 0,871 | 1,421 |
| PAC | 36 | CA | 9,18% | 18,99% | 11.791 | 0 | 11.791 | 300 | 113,19% | −49,43% | 66,112% | 7,37% | 0,585 | 0,555 |
| PAC | 24 | CA | 5,98% | 14,77% | 7.630 | 0 | 7.630 | 300 | 92,27% | −40,93% | 63,393% | 4,84% | 0,463 | 0,385 |
| PAC | 360 | VA No-Sell | 129,50% | 131,47% | 204.475 | 43.382 | 247.857 | 21.305 | 2.277,41% | −78,64% | 92,202% | 99,89% | 2,649 | 14,865 |
| PAC | 300 | VA No-Sell | 98,22% | 96,98% | 145.872 | 32.529 | 178.400 | 17.054 | 1.903,18% | −75,69% | 90,404% | 79,62% | 2,164 | 11,061 |
| PAC | 240 | VA No-Sell | 71,62% | 70,70% | 100.889 | 22.677 | 123.566 | 15.590 | 835,11% | −77,48% | 87,606% | 61,10% | 1,513 | 5,266 |
| PAC | 180 | VA No-Sell | 49,85% | 51,28% | 66.574 | 14.346 | 80.919 | 10.371 | 647,97% | −67,38% | 84,519% | 44,37% | 1,050 | 2,967 |
| PAC | 120 | VA No-Sell | 31,24% | 36,22% | 39.756 | 7.490 | 47.246 | 7.547 | 293,68% | −67,87% | 80,049% | 28,79% | 0,621 | 0,956 |
| PAC | 60 | VA No-Sell | 14,60% | 22,68% | 18.178 | 2.449 | 20.628 | 3.811 | 138,42% | −54,26% | 72,542% | 13,67% | 0,330 | 0,108 |
| PAC | 36 | VA No-Sell | 8,49% | 16,88% | 10.629 | 1.088 | 11.717 | 2.437 | 82,53% | −49,25% | 67,864% | 8,09% | 0,193 | −0,142 |
| PAC | 24 | VA No-Sell | 5,62% | 13,53% | 7.031 | 574 | 7.605 | 1.698 | 70,12% | −40,90% | 64,875% | 5,35% | 0,146 | −0,155 |
| PAC | 360 | VA Puro | 87,60% | 55,76% | 106.497 | 96.116 | 202.613 | 25.134 | 319,87% | −78,31% | 93,566% | 88,00% | 0,005 | −0,159 |
| PAC | 300 | VA Puro | 73,04% | 50,66% | 88.520 | 67.214 | 155.734 | 21.661 | 296,90% | −75,69% | 91,750% | 73,50% | 0,035 | −0,186 |
| PAC | 240 | VA Puro | 58,04% | 45,25% | 70.484 | 43.308 | 113.792 | 15.873 | 239,50% | −77,39% | 88,994% | 58,50% | 0,045 | −0,235 |
| PAC | 180 | VA Puro | 43,54% | 38,80% | 52.646 | 24.867 | 77.514 | 12.664 | 217,58% | −67,36% | 85,763% | 43,70% | 0,077 | −0,254 |
| PAC | 120 | VA Puro | 29,03% | 31,42% | 34.929 | 11.523 | 46.452 | 7.931 | 173,19% | −67,86% | 81,017% | 29,03% | 0,114 | −0,254 |
| PAC | 60 | VA Puro | 14,27% | 21,77% | 17.404 | 3.166 | 20.569 | 4.173 | 108,69% | −54,26% | 72,955% | 13,94% | 0,167 | −0,223 |
| PAC | 36 | VA Puro | 8,42% | 16,65% | 10.447 | 1.263 | 11.710 | 2.437 | 72,18% | −49,25% | 68,042% | 8,19% | 0,133 | −0,244 |
| PAC | 24 | VA Puro | 5,61% | 13,47% | 6.981 | 623 | 7.604 | 1.694 | 64,98% | −40,90% | 64,934% | 5,39% | 0,123 | −0,198 |
Fig. 59 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging (target costante, senza massimale, Filtro anti-Hayley: presente) di tutti i PAC di varie durate su serie storiche simulate con tecniche parametriche: distribuzione normale con media mensile dello 0,50% e deviazione standard del 5%
Sono stati analizzati 300.000 piani di accumulo, simulati sulle 100.000 serie storiche dei prezzi costruiti a partire dai rendimenti generati col metodo Monte Carlo (un piano di accumulo Cost Averaging, uno Value Averaging No-Sell e uno Value Averaging puro su ogni serie di prezzi): i parametri utilizzati sono stati 0,50% (media) e 5% (deviazione standard).
Nella tabella, sono riportati i risultati medi dei 100.000 piani di accumulo simulati per ogni tipologia.
Per rendere questa analisi conforme alle precedenti, le caratteristiche dei PAC Value Averaging simulati (No-Sell e puri) sono state le seguenti: rata mensile di 300 euro (stesso importo per il Cost Averaging), assenza di massimale, assenza di commissioni, incremento target costante, presenza del filtro anti-Hayley.
I risultati ottenuti sono interessanti. Come sempre, commentiamo quelli dalla durata più lunga, che amplificano le differenze tra le varie strategie:
- Rendimento totale: come nelle simulazioni non parametriche, il Cost Averaging ottiene il valore più alto e genera una somma finale superiore (abbiamo visualizzato i rendimenti corretti e non quelli distorti, ovvero quei rendimenti che non prendono in considerazione la liquidità inutilizzata).
Anche stavolta, i rendimenti del Value Averaging – soprattutto quello puro – sono molto meno volatili di quelli del Cost Averaging. Siamo in presenza del trade-off tra rendimento e volatilità. - Rata max: come ci aspettavamo, nel Cost Averaging la rata max è quella iniziale (300 euro), mentre nel Value Averaging i versamenti più alti arrivano a oltre 20.000 euro nelle durate più lunghe. È bene ribadire che questi valori sono dei massimi assoluti (rappresentano il più alto versamento tra le 360 rate * 100.000 PAC simulati).
- Rendimento max e min: sono più estremi di quelli ottenuti nelle simulazioni non parametriche. Non deve sorprendere: 100.000 serie storiche sono davvero tante e in un numero di simulazioni così elevato è normale avere delle serie storiche molto improbabili, in un senso e nell’altro.
- % Positivi: più alta nel Value Averaging puro, seguito dal Value Averaging No-Sell e dal Cost Averaging.
- Mediana: soltanto nel Value Averaging puro, la mediana è appena superiore alla media. Nelle altre tipologie, avviene il fenomeno contrario (le medie sono molto più alte delle mediane).
- Skewness: tutti i rendimenti del Cost Averaging e del Value Averaging No-sell hanno una skewness decisamente positiva. La skewness del Value Averaging puro, pur essendo positiva, è vicinissima a zero. È una conferma della minor variabilità nei rendimenti di questi ultimi (una skewness positiva implica la presenza di una coda destra; una skewness nulla, la simmetria della distribuzione). Non bisogna dimenticarsi che l’obiettivo del Value Averaging è quello di seguire – e possibilmente raggiungere – il target nel modo più preciso possibile: acquistando e – nel Value Averaging puro – vendendo quote.
Gli istogrammi seguenti ci mostrano la distribuzione delle frequenze dei rendimenti dei 100.000 PAC trentennali Cost Averaging, Value Averaging No-Sell e Value Averaging puri:
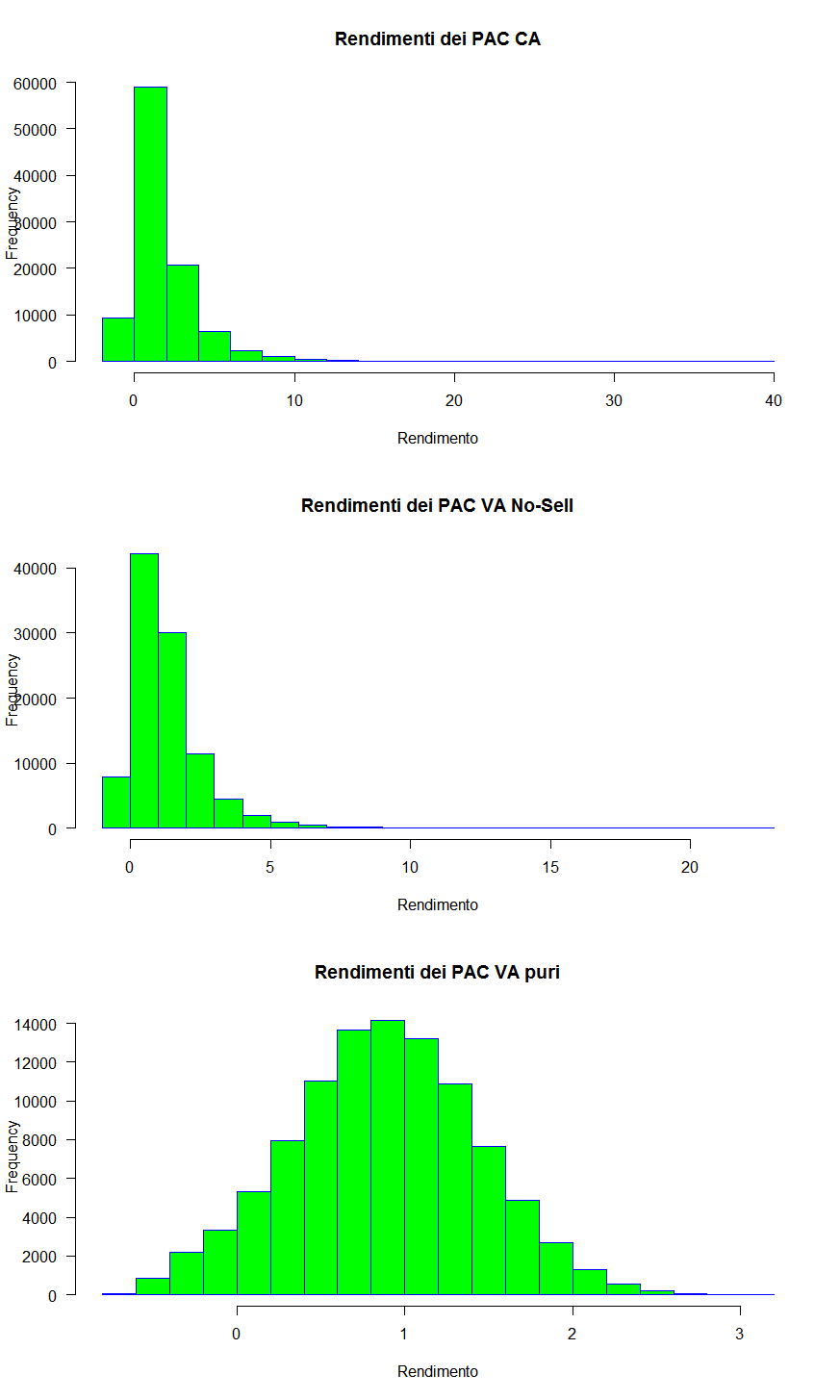
Fig. 60 – Istogramma delle frequenze dei rendimenti dei 100.000 PAC Cost Averaging, Value Averaging No-sell e Value Averaging puri trentennali simulati con tecniche parametriche: media 0,5%, deviazione standard 5% (target costante, senza massimale, Filtro anti-Hayley: presente)
La somiglianza della distribuzione dei rendimenti del Value Averaging puro a una normale è evidente, così come la presenza di code destre nelle altre due tipologie.
- Kurtosis (curtosi): fortemente leptocurtica nel Cost Averaging e nel Value Averaging No-Sell (code più spesse della normale) e platicurtica nel Value Averaging puro (maggior densità delle frequenze intorno alla media).
Vediamo che cosa succede simulando serie storiche con media pari a 0 (lasciando tutti gli altri parametri invariati):
| Incremento 0% - No massimale - Media 0%, Deviazione Standard 5% - 100.000 simulazioni | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. totale | Stand. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. |
| PAC | 360 | CA | −0,34% | 60,90% | 107.635 | 0 | 107.635 | 300 | 1.265,04% | −84,33% | 37,029% | −15,79% | 2,746 | 16,951 |
| PAC | 300 | CA | 0,02% | 54,87% | 90.014 | 0 | 90.014 | 300 | 1.000,67% | −83,59% | 38,450% | −13,39% | 2,409 | 12,546 |
| PAC | 240 | CA | 0,21% | 47,80% | 72.150 | 0 | 72.150 | 300 | 624,26% | −82,61% | 40,009% | −10,40% | 1,885 | 6,990 |
| PAC | 180 | CA | 0,06% | 40,68% | 54.032 | 0 | 54.032 | 300 | 520,06% | −78,58% | 41,077% | −8,22% | 1,571 | 4,685 |
| PAC | 120 | CA | 0,11% | 32,78% | 36.041 | 0 | 36.041 | 300 | 287,31% | −69,80% | 42,753% | −5,53% | 1,242 | 2,834 |
| PAC | 60 | CA | 0,01% | 22,49% | 18.001 | 0 | 18.001 | 300 | 162,05% | −60,75% | 44,858% | −2,79% | 0,828 | 1,278 |
| PAC | 36 | CA | 0,03% | 17,16% | 10.803 | 0 | 10.803 | 300 | 118,59% | −54,40% | 46,263% | −1,56% | 0,585 | 0,627 |
| PAC | 24 | CA | −0,05% | 13,78% | 7.196 | 0 | 7.196 | 300 | 89,86% | −46,47% | 46,605% | −1,12% | 0,480 | 0,457 |
| PAC | 360 | VA No-Sell | −0,25% | 53,69% | 99.583 | 8.150 | 107.733 | 21.293 | 779,54% | −84,33% | 39,954% | −13,15% | 1,730 | 6,141 |
| PAC | 300 | VA No-Sell | 0,02% | 48,54% | 83.073 | 6.944 | 90.018 | 18.644 | 576,61% | −83,55% | 41,227% | −10,74% | 1,518 | 4,827 |
| PAC | 240 | VA No-Sell | 0,24% | 42,78% | 66.619 | 5.551 | 72.171 | 14.608 | 440,65% | −82,57% | 42,879% | −7,95% | 1,176 | 2,494 |
| PAC | 180 | VA No-Sell | 0,07% | 36,74% | 49.979 | 4.060 | 54.040 | 11.969 | 421,42% | −78,53% | 43,764% | −6,02% | 0,962 | 1,553 |
| PAC | 120 | VA No-Sell | 0,08% | 29,88% | 33.419 | 2.611 | 36.030 | 7.263 | 226,82% | −69,69% | 45,290% | −3,78% | 0,724 | 0,704 |
| PAC | 60 | VA No-Sell | 0,01% | 20,94% | 16.859 | 1.142 | 18.001 | 3.541 | 113,09% | −60,74% | 46,936% | −1,71% | 0,444 | 0,073 |
| PAC | 36 | VA No-Sell | 0,03% | 16,20% | 10.198 | 605 | 10.803 | 2.288 | 87,06% | −54,39% | 48,090% | −0,82% | 0,288 | −0,126 |
| PAC | 24 | VA No-Sell | −0,05% | 13,14% | 6.847 | 349 | 7.196 | 1.518 | 63,54% | −46,46% | 48,190% | −0,61% | 0,233 | −0,104 |
| PAC | 360 | VA Puro | −0,18% | 46,58% | 87.164 | 20.639 | 107.803 | 29.776 | 242,63% | −84,33% | 43,541% | −9,45% | 0,716 | 0,003 |
| PAC | 300 | VA Puro | 0,05% | 43,07% | 74.048 | 15.995 | 90.043 | 20.384 | 212,28% | −83,53% | 44,203% | −7,67% | 0,664 | −0,051 |
| PAC | 240 | VA Puro | 0,27% | 39,04% | 60.536 | 11.658 | 72.193 | 17.045 | 183,57% | −82,55% | 45,325% | −5,60% | 0,588 | −0,145 |
| PAC | 180 | VA Puro | 0,08% | 34,34% | 46.410 | 7.633 | 54.044 | 12.494 | 166,28% | −78,53% | 45,681% | −4,36% | 0,539 | −0,164 |
| PAC | 120 | VA Puro | 0,08% | 28,63% | 31.801 | 4.226 | 36.027 | 8.514 | 128,00% | −69,66% | 46,481% | −2,90% | 0,467 | −0,170 |
| PAC | 60 | VA Puro | 0,00% | 20,60% | 16.492 | 1.509 | 18.001 | 4.115 | 92,65% | −60,74% | 47,467% | −1,46% | 0,345 | −0,195 |
| PAC | 36 | VA Puro | 0,03% | 16,10% | 10.096 | 707 | 10.803 | 2.312 | 76,87% | −54,39% | 48,267% | −0,74% | 0,249 | −0,218 |
| PAC | 24 | VA Puro | −0,05% | 13,11% | 6.817 | 379 | 7.196 | 1.552 | 61,05% | −46,46% | 48,247% | −0,58% | 0,217 | −0,145 |
Fig. 61 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging (target costante, senza massimale, Filtro anti-Hayley: presente) di tutti i PAC di varie durate su serie storiche simulate con tecniche parametriche: distribuzione normale con media mensile dello 0% e deviazione standard del 5%
Di nuovo, sono stati analizzati 300.000 PAC costruiti sulle 100.000 serie storiche dei prezzi generati a partire dai rendimenti simulati col metodo Monte Carlo (media 0% e deviazione standard 5%).
Questi sono i risultati dei piani di accumulo trentennali:
- Rendimento totale: come ci si poteva aspettare, in tutte le durate i rendimenti sono stati intorno allo 0%. Nei trentennali, però, il rendimento è stato leggermente negativo e il valore migliore è stato ottenuto dal Value Averaging puro, seguito dal No-Sell e dal Cost Averaging (con differenze minime). La liquidità non utilizzata è stata molto più bassa di prima. Il Value Averaging puro continua a essere il meno volatile, seguito dal No-Sell e dal Cost Averaging.
- Rata max: nessun grosso cambiamento, con il Value Averaging puro che anche stavolta ha generato la rata più alta, che sfiora i 30.000 euro.
- Rendimento max e min: molto inferiori di prima, ma pur sempre significativamente alti e, soprattutto, bassi.
- % Positivi: si conferma più alta nel Value Averaging puro, seguito dal No-Sell e dal Cost Averaging. Il Value Averaging puro dimostra ancora una volta di essere la strategia meno rischiosa, seguita dal Value Averaging No-Sell e dal Cost Averaging.
- Mediana: tutte le mediane sono inferiori ai rendimenti medi.
- Skewness: tutti i valori tendono ad avvicinarsi tra di loro. La skewness del Cost Averaging e del Value Averaging No-sell diminuisce; quella del Value Averaging puro cresce notevolmente, pur rimanendo ben al di sotto delle precedenti. Le distribuzioni delle frequenze sono le seguenti:
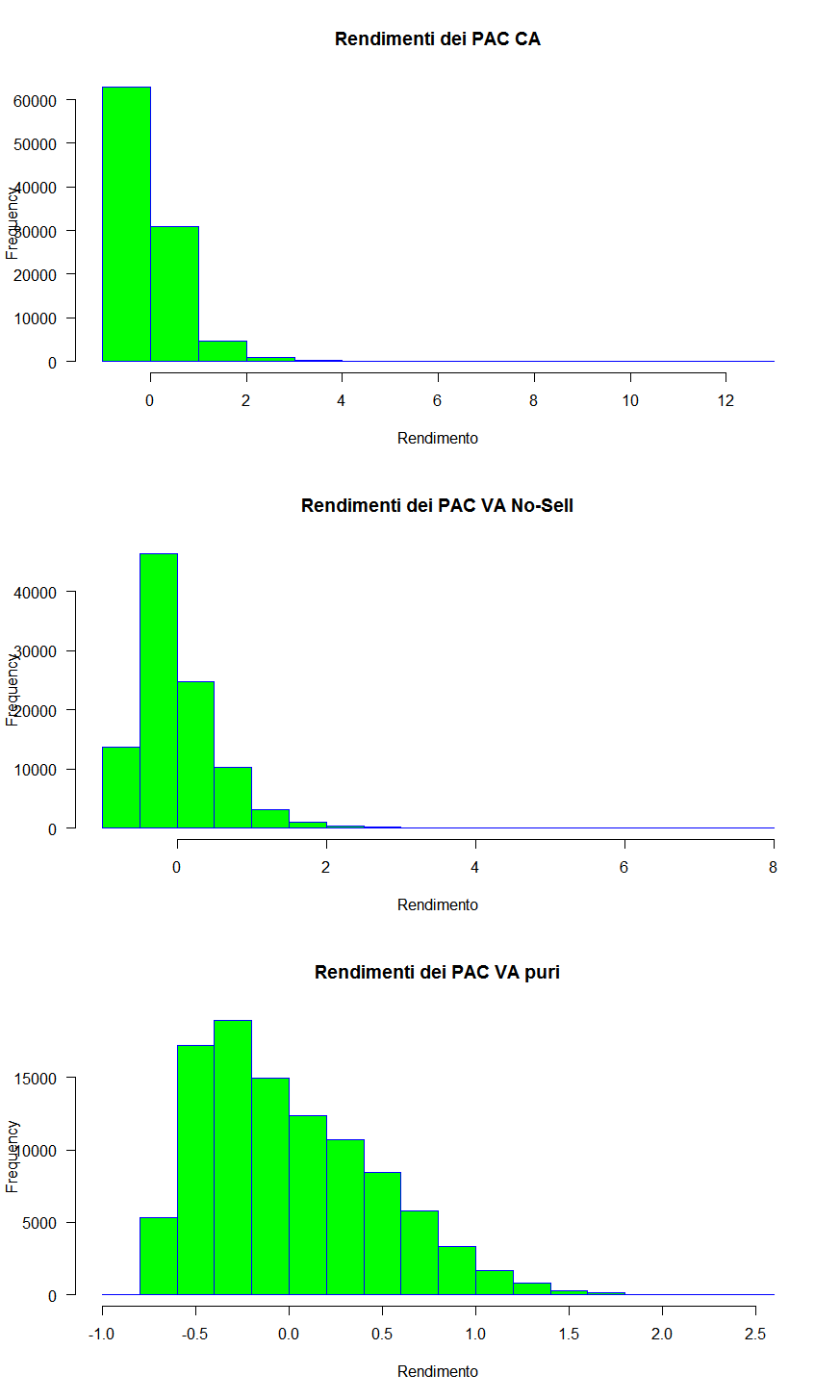
Fig. 62 – Istogramma delle frequenze dei rendimenti dei 100.000 PAC Cost Averaging, Value Averaging No-sell e Value Averaging puri trentennali simulati con tecniche parametriche: media 0%, deviazione standard 5% (target costante, senza massimale, Filtro anti-Hayley: presente)
Anche la distribuzione dei rendimenti dei piani Value Averaging puri inizia a differenziarsi da quella di una normale, sviluppando un’evidente lunga coda destra.
- Kurtosis (curtosi): come nel caso della skewness, diminuisce la curtosi del Cost Averaging e del Value Averaging No-Sell. Cresce, seppur di poco, quella del Value Averaging puro.
Passiamo adesso a serie storiche di prezzi con media negativa: −0,5% (gli altri parametri sono invariati):
| Incremento 0% - No massimale - Media −0,50%, Deviazione Standard 5% - 100.000 simulazioni | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. totale | Stand. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. |
| PAC | 360 | CA | −53,57% | 21,90% | 50.147 | 0 | 50.147 | 300 | 262,99% | −89,73% | 2,801% | −58,57% | 2,104 | 8,852 |
| PAC | 300 | CA | −48,00% | 23,03% | 46.799 | 0 | 46.799 | 300 | 306,78% | −88,05% | 3,963% | −53,08% | 1,953 | 7,719 |
| PAC | 240 | CA | −41,66% | 23,83% | 42.007 | 0 | 42.007 | 300 | 275,00% | −85,60% | 5,799% | −46,65% | 1,702 | 5,727 |
| PAC | 180 | CA | −33,98% | 23,90% | 35.651 | 0 | 35.651 | 300 | 250,76% | −82,37% | 8,532% | −38,52% | 1,467 | 4,352 |
| PAC | 120 | CA | −24,62% | 22,76% | 27.135 | 0 | 27.135 | 300 | 152,31% | −75,25% | 13,131% | −28,39% | 1,147 | 2,397 |
| PAC | 60 | CA | −13,57% | 18,71% | 15.557 | 0 | 15.557 | 300 | 188,92% | −66,49% | 20,923% | −15,80% | 0,824 | 1,453 |
| PAC | 36 | CA | −8,26% | 15,42% | 9.908 | 0 | 9.908 | 300 | 99,46% | −54,26% | 27,144% | −9,72% | 0,578 | 0,574 |
| PAC | 24 | CA | −5,53% | 12,89% | 6.802 | 0 | 6.802 | 300 | 68,68% | −48,93% | 31,040% | −6,48% | 0,467 | 0,422 |
| PAC | 360 | VA No-Sell | −53,26% | 22,20% | 50.197 | 282 | 50.480 | 18.937 | 204,77% | −89,70% | 3,106% | −58,43% | 1,984 | 6,974 |
| PAC | 300 | VA No-Sell | −47,63% | 23,29% | 46.779 | 354 | 47.134 | 16.069 | 282,76% | −88,04% | 4,353% | −52,88% | 1,804 | 5,849 |
| PAC | 240 | VA No-Sell | −41,22% | 24,09% | 41.890 | 431 | 42.321 | 13.034 | 234,62% | −85,60% | 6,327% | −46,39% | 1,553 | 4,079 |
| PAC | 180 | VA No-Sell | −33,50% | 24,03% | 35.418 | 492 | 35.910 | 10.188 | 219,57% | −82,32% | 9,292% | −38,19% | 1,281 | 2,716 |
| PAC | 120 | VA No-Sell | −24,15% | 22,71% | 26.784 | 522 | 27.305 | 6.921 | 138,91% | −75,13% | 14,224% | −27,98% | 0,958 | 1,252 |
| PAC | 60 | VA No-Sell | −13,24% | 18,45% | 15.221 | 396 | 15.617 | 3.837 | 115,99% | −66,33% | 22,312% | −15,37% | 0,611 | 0,424 |
| PAC | 36 | VA No-Sell | −8,05% | 15,15% | 9.648 | 283 | 9.931 | 2.102 | 74,35% | −54,23% | 28,514% | −9,34% | 0,403 | 0,001 |
| PAC | 24 | VA No-Sell | −5,39% | 12,63% | 6.618 | 194 | 6.812 | 1.527 | 53,14% | −48,92% | 32,256% | −6,16% | 0,303 | −0,040 |
| PAC | 360 | VA Puro | −52,84% | 22,69% | 50.025 | 910 | 50.935 | 22.015 | 136,31% | −89,67% | 3,613% | −58,28% | 1,851 | 5,141 |
| PAC | 300 | VA Puro | −47,20% | 23,64% | 46.515 | 1.001 | 47.516 | 18.602 | 150,61% | −88,04% | 4,946% | −52,72% | 1,635 | 3,878 |
| PAC | 240 | VA Puro | −40,82% | 24,33% | 41.536 | 1.073 | 42.609 | 15.704 | 135,29% | −85,60% | 6,994% | −46,22% | 1,400 | 2,617 |
| PAC | 180 | VA Puro | −33,16% | 24,14% | 35.047 | 1.046 | 36.093 | 10.455 | 128,66% | −82,30% | 9,943% | −37,99% | 1,147 | 1,624 |
| PAC | 120 | VA Puro | −23,93% | 22,70% | 26.476 | 909 | 27.385 | 7.048 | 94,85% | −75,09% | 14,863% | −27,83% | 0,867 | 0,748 |
| PAC | 60 | VA Puro | −13,17% | 18,40% | 15.093 | 537 | 15.630 | 3.837 | 98,39% | −66,33% | 22,653% | −15,29% | 0,559 | 0,199 |
| PAC | 36 | VA Puro | −8,02% | 15,12% | 9.599 | 334 | 9.933 | 2.432 | 67,24% | −54,23% | 28,699% | −9,31% | 0,381 | −0,071 |
| PAC | 24 | VA Puro | −5,39% | 12,62% | 6.601 | 211 | 6.812 | 1.527 | 51,66% | −48,92% | 32,315% | −6,14% | 0,293 | −0,071 |
Fig. 63 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging (target costante, senza massimale, Filtro anti-Hayley: presente) di tutti i PAC di varie durate su serie storiche simulate con tecniche parametriche: distribuzione normale con media mensile del -0,50% e deviazione standard del 5%
Il rosso ovviamente predomina. I commenti ai risultati dei piani trentennali sono i seguenti:
- Rendimento totale: mediamente inferiore al −50%. Fa leggermente meglio il Value Averaging puro, seguito dal No-Sell e dal Cost Averaging. La deviazione standard, però, segue l’ordine inverso, confermando il trade-off rischio/rendimento. La liquidità non utilizzata è molto bassa (poche centinaia di euro).
- Rata max: non si registrano grossi cambiamenti. Il Value Averaging puro continua a essere quello con la più alta rata massima, di nuovo sopra ai 20.000 euro.
- Rendimento max e min: continua la discesa di questi valori, con i rendimenti massimi notevolmente ridimensionati e quelli minimi che arrivano a sfiorare il −90%.
- % Positivi: le percentuali sono bassissime e vanno dal 2,8% del Cost Averaging al 3,6% del Value Averaging puro. Sempre seguendo lo stesso ordine, queste percentuali aumentano col diminuire della lunghezza dei PAC. È normale che si verifichino pochissimi piani di accumulo positivi nel lungo termine, dal momento che il valore medio dei rendimenti mensili è del −0,50%.
- Mediana: come nel caso precedente, tutte le mediane sono inferiori ai rendimenti medi.
- Skewness: i valori sono molto vicino a 2 per tutti i piani di accumulo trentennali. Le distribuzioni di frequenze sono le seguenti:
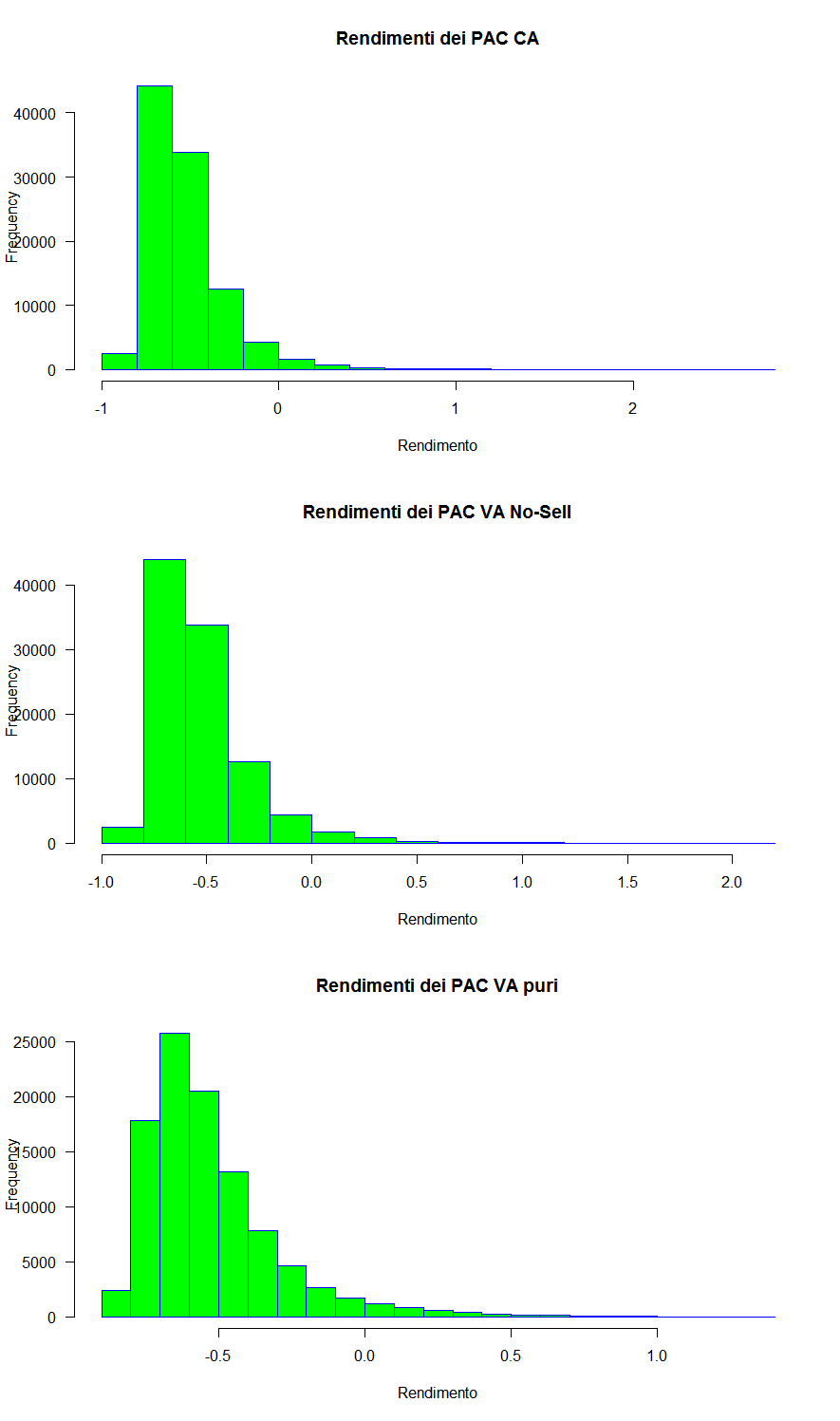
Fig. 64 – Istogrammi delle frequenze dei rendimenti dei 100.000 PAC Cost Averaging, Value Averaging No-sell e Value Averaging puri trentennali simulati con tecniche parametriche: media -0,50%, deviazione standard 5% (target costante, senza massimale, Filtro anti-Hayley: presente)
- Kurtosis (curtosi): continua a diminuire quella del Cost Averaging e del No-Sell e a crescere quella del Value Averaging puro.
Passiamo adesso alle simulazioni con crescita del target pari allo 0,50%. Utilizziamo 100.000 nuove serie storiche. Nella tabella che segue, i parametri della distribuzione normale dei rendimenti sono ancora 0,50% e 5%. I valori del Cost Averaging dovrebbero essere molto simili a quelli precedenti, dato che non sono influenzati dal maggior incremento del target.
Ecco i risultati:
| Incremento 0,5% - No massimale - Media 0,50%, Deviazione Standard 5% - 100.000 simulazioni | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. totale | Stand. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. |
| PAC | 360 | CA | 179,43% | 212,96% | 301.789 | 0 | 301.789 | 300 | 5.267,51% | −78,70% | 90,774% | 120,66% | 3,237 | 23,500 |
| PAC | 300 | CA | 130,51% | 150,82% | 207.461 | 0 | 207.461 | 300 | 2.888,17% | −75,03% | 88,654% | 91,40% | 2,608 | 13,846 |
| PAC | 240 | CA | 93,08% | 108,05% | 139.018 | 0 | 139.018 | 300 | 1.710,06% | −77,87% | 85,832% | 67,10% | 2,176 | 9,248 |
| PAC | 180 | CA | 61,49% | 73,18% | 87.204 | 0 | 87.204 | 300 | 948,56% | −72,81% | 82,472% | 45,86% | 1,718 | 5,656 |
| PAC | 120 | CA | 36,83% | 47,72% | 49.260 | 0 | 49.260 | 300 | 599,07% | −63,88% | 77,840% | 28,48% | 1,300 | 3,316 |
| PAC | 60 | CA | 16,29% | 27,09% | 20.933 | 0 | 20.933 | 300 | 203,06% | −52,96% | 70,387% | 12,84% | 0,848 | 1,340 |
| PAC | 36 | CA | 9,20% | 19,01% | 11.794 | 0 | 11.794 | 300 | 126,90% | −50,26% | 66,096% | 7,39% | 0,612 | 0,696 |
| PAC | 24 | CA | 5,92% | 14,80% | 7.627 | 0 | 7.627 | 300 | 90,73% | −38,44% | 63,204% | 4,82% | 0,482 | 0,430 |
| PAC | 360 | VA No-Sell | 165,10% | 176,42% | 277.092 | 9.211 | 286.303 | 53.391 | 2.994,03% | −78,70% | 90,791% | 119,84% | 2,430 | 12,800 |
| PAC | 300 | VA No-Sell | 120,40% | 125,87% | 190.765 | 7.598 | 198.363 | 32.674 | 1.994,37% | −75,02% | 88,708% | 91,16% | 1,903 | 7,270 |
| PAC | 240 | VA No-Sell | 85,90% | 90,57% | 127.766 | 6.079 | 133.845 | 26.407 | 1.409,48% | −77,85% | 85,928% | 67,27% | 1,531 | 4,851 |
| PAC | 180 | VA No-Sell | 57,05% | 62,48% | 80.419 | 4.388 | 84.807 | 16.397 | 683,17% | −72,78% | 82,671% | 46,41% | 1,140 | 2,536 |
| PAC | 120 | VA No-Sell | 34,34% | 41,50% | 45.581 | 2.782 | 48.363 | 9.891 | 392,39% | −63,87% | 78,157% | 29,14% | 0,759 | 0,970 |
| PAC | 60 | VA No-Sell | 15,37% | 24,47% | 19.574 | 1.193 | 20.767 | 3.931 | 163,01% | −52,86% | 71,043% | 13,47% | 0,439 | 0,130 |
| PAC | 36 | VA No-Sell | 8,77% | 17,60% | 11.133 | 615 | 11.747 | 2.430 | 98,07% | −50,25% | 66,900% | 7,87% | 0,290 | −0,083 |
| PAC | 24 | VA No-Sell | 5,68% | 13,91% | 7.251 | 358 | 7.609 | 1.635 | 73,36% | −38,36% | 64,002% | 5,17% | 0,219 | −0,135 |
| PAC | 360 | VA Puro | 142,48% | 119,33% | 223.888 | 37.988 | 261.875 | 71.183 | 694,49% | −78,70% | 90,876% | 120,37% | 0,616 | −0,289 |
| PAC | 300 | VA Puro | 107,06% | 92,85% | 160.449 | 25.904 | 186.353 | 46.151 | 517,84% | −75,01% | 88,805% | 92,11% | 0,563 | −0,304 |
| PAC | 240 | VA Puro | 78,29% | 71,87% | 111.284 | 17.084 | 128.368 | 29.531 | 411,81% | −77,83% | 86,063% | 68,34% | 0,508 | −0,325 |
| PAC | 180 | VA Puro | 53,50% | 53,59% | 72.858 | 10.031 | 82.889 | 18.779 | 298,18% | −72,77% | 82,864% | 47,34% | 0,457 | −0,296 |
| PAC | 120 | VA Puro | 33,06% | 38,13% | 42.839 | 5.061 | 47.900 | 9.891 | 211,96% | −63,87% | 78,373% | 29,80% | 0,379 | −0,301 |
| PAC | 60 | VA Puro | 15,15% | 23,79% | 19.080 | 1.647 | 20.727 | 4.559 | 117,85% | −52,86% | 71,186% | 13,70% | 0,303 | −0,226 |
| PAC | 36 | VA Puro | 8,72% | 17,42% | 11.008 | 734 | 11.742 | 2.485 | 82,94% | −50,25% | 66,992% | 7,94% | 0,238 | −0,202 |
| PAC | 24 | VA Puro | 5,67% | 13,87% | 7.215 | 393 | 7.608 | 1.760 | 66,90% | −38,36% | 64,025% | 5,19% | 0,199 | −0,178 |
Fig. 65 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging (incremento target 0,50%, senza massimale, Filtro anti-Hayley: presente) di tutti i PAC di varie durate su serie storiche simulate con tecniche parametriche: distribuzione normale con media mensile dello 0,50% e deviazione standard del 5%
- Rendimento totale: il Cost Averaging ottiene ancora il valore più alto, generando una somma finale superiore. Il Value Averaging migliora sensibilmente le proprie performance e continua a essere meno volatile del Cost Averaging.
- Rata max: cresce notevolmente, sia nel Value Averaging No-Sell, dove supera i 50.000 euro, che in quello puro, dove abbatte il muro dei 70.000 euro.
- Rendimento max e min: queste 100.000 serie storiche originano dei rendimenti massimi superiori per tutte le tipologie di PAC (Cost Averaging compreso). Nello stesso tempo, migliorano lievemente i rendimenti minimi.
- % Positivi: il Value Averaging ha una percentuale di esiti positivi poco più alta del Cost Averaging. Le distanze si sono molto assottigliate.
- Mediana: i valori sono molto simili in tutte e tre le tipologie di PAC (inferiori ai rispettivi valori medi).
- Skewness: è aumentata nel Value Averaging puro ed è rimasta pressoché invariata nelle altre due tipologie di PAC. Gli istogrammi delle distribuzioni delle frequenze dei rendimenti dei 100.000 PAC trentennali Cost Averaging, Value Averaging No-Sell e Value Averaging puri, sono i seguenti:
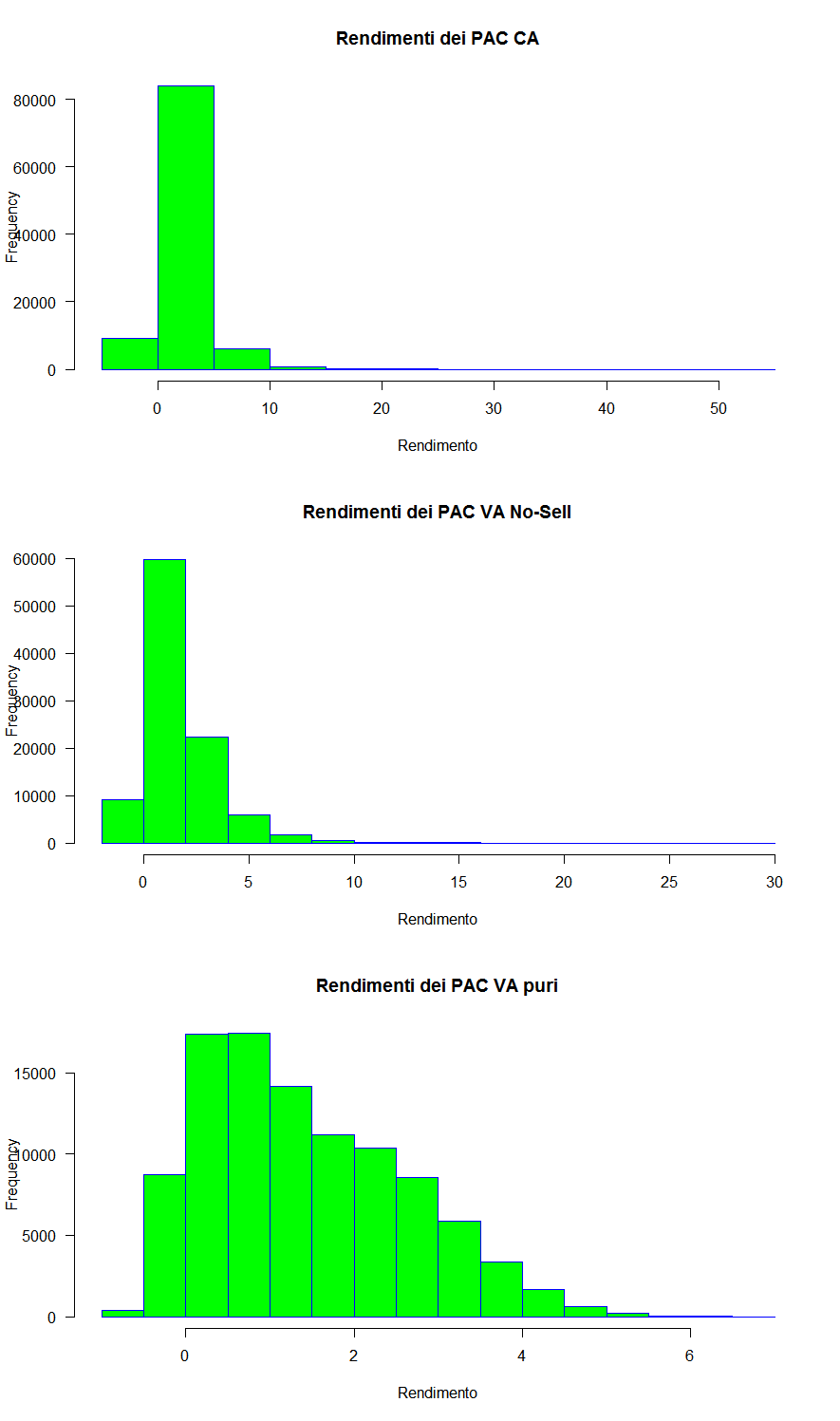
Fig. 66 – Istogrammi delle frequenze dei rendimenti dei 100.000 PAC Cost Averaging, Value Averaging No-sell e Value Averaging puri trentennali simulati con tecniche parametriche: media 0,50%, deviazione standard 5% (incremento target 0,50%, senza massimale, Filtro anti-Hayley: presente)
- Kurtosis (curtosi): con l’incremento del target, i valori della curtosi diminuiscono nel Value Averaging, nonostante che il Cost Averaging subisca l’effetto contrario. In quest’ultimo caso, esso è dovuto esclusivamente all’utilizzo di 100.000 nuove simulazioni.
Abbiamo inoltre effettuato 100.000 nuove simulazioni con media dello 0% e del -0,50%, sempre impostando l’incremento del target allo 0,50%. Non si riportano le rispettive tabelle e distribuzioni delle frequenze, perché le differenze principali si riscontrano essenzialmente in una minore liquidità residua e in valori più elevati dei rendimenti max del Value Averaging.
100.000 simulazioni sono state realizzate anche utilizzando i seguenti parametri: media 0,25% e deviazione standard del 2,5%, sia con target costante che con un suo incremento dello 0,50%. Come avevamo anticipato, questi valori erano stati scelti con lo scopo di simulare dei rendimenti obbligazionari.
Per motivi di spazio, non riportiamo le tabelle e i grafici delle distribuzioni delle frequenze, dato che i risultati ripropongono le stesse dinamiche esaminate in precedenza, anche se su scala minore.
Un’ulteriore variante di PAC Value Averaging, analizzata anche nelle sezioni precedenti, consiste nel fissare un massimale all’importo dei versamenti: 1.000 euro. Tutte le simulazioni parametriche descritte finora sono state ripetute aggiungendo questo vincolo.
Di nuovo, non riportiamo le tabelle e i grafici delle distribuzioni delle frequenze perché i risultati sono molto simili a quelli senza massimale: i rendimenti medi e le deviazioni standard sono generalmente appena inferiori a quelli ottenuti in assenza di questo vincolo.
Abbiamo effettuato anche un set di simulazioni parametriche utilizzando la distribuzione t di Student. La t di Student viene spesso considerata la distribuzione più appropriata a modellare i rendimenti dei mercati azionari: le sue code sono infatti più spesse di quelle di una normale.
La t di Student è contraddistinta da un solo parametro: il numero di gradi di libertà. Nelle simulazioni col metodo Monte Carlo che abbiamo effettuato, sono stati usati 13 gradi libertà.
Questo valore è in linea con quello suggerito da James Picerno, che lo ha ottenuto modellando lo S&P 500 con una t di Student nel periodo 1996-2006.
Anche in questo caso, non riportiamo la tabella con i risultati di queste simulazioni, in quanto non forniscono nessun nuovo elemento rispetto a quanto finora discusso.
Terminiamo questo capitolo con alcuni grafici che visualizzano i valori medi dei rendimenti, della volatilità e della percentuale di PAC positivi di tutte le simulazioni effettuate con un incremento del target dello 0,50%:
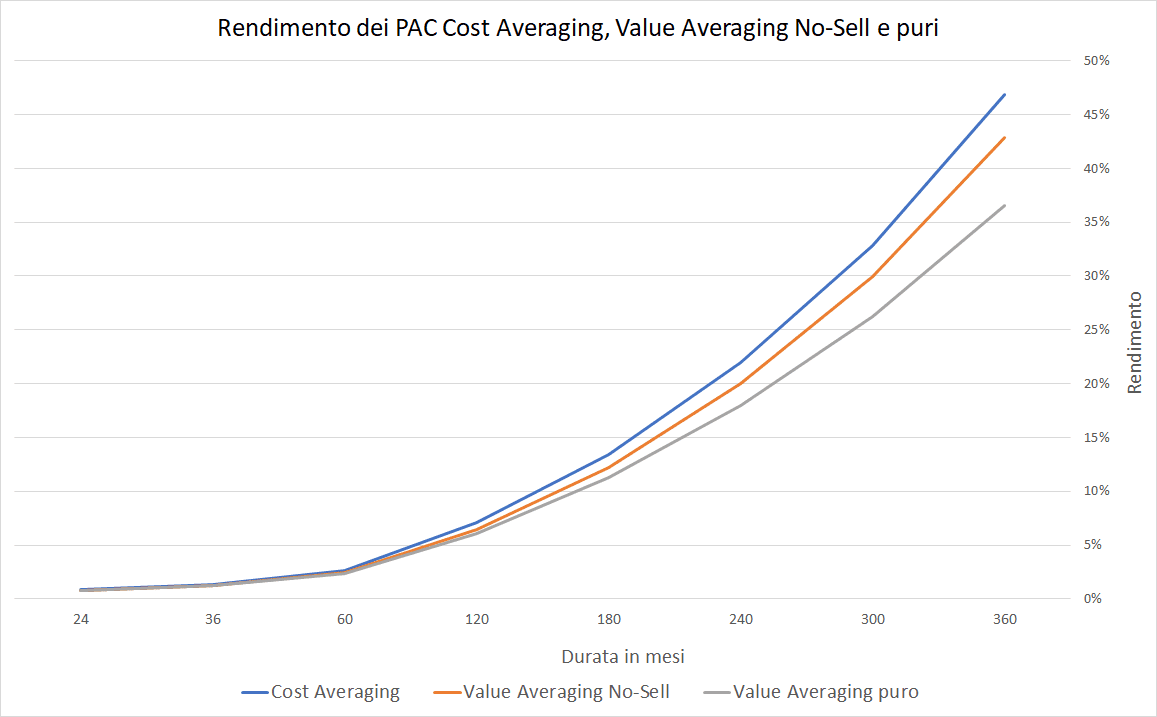
Fig. 67 – Grafico dei rendimenti delle varie tipologie di PAC Cost Averaging e Value Averaging (media di tutti i backtest parametrici con incremento target 0,50%, Filtro anti-Hayley: assente)
Il Cost Averaging genera i rendimenti più elevati, seguito dal Value Averaging No-Sell e puro. Le differenze iniziano a prendere forma a partire dalle durate di 5-10 anni.
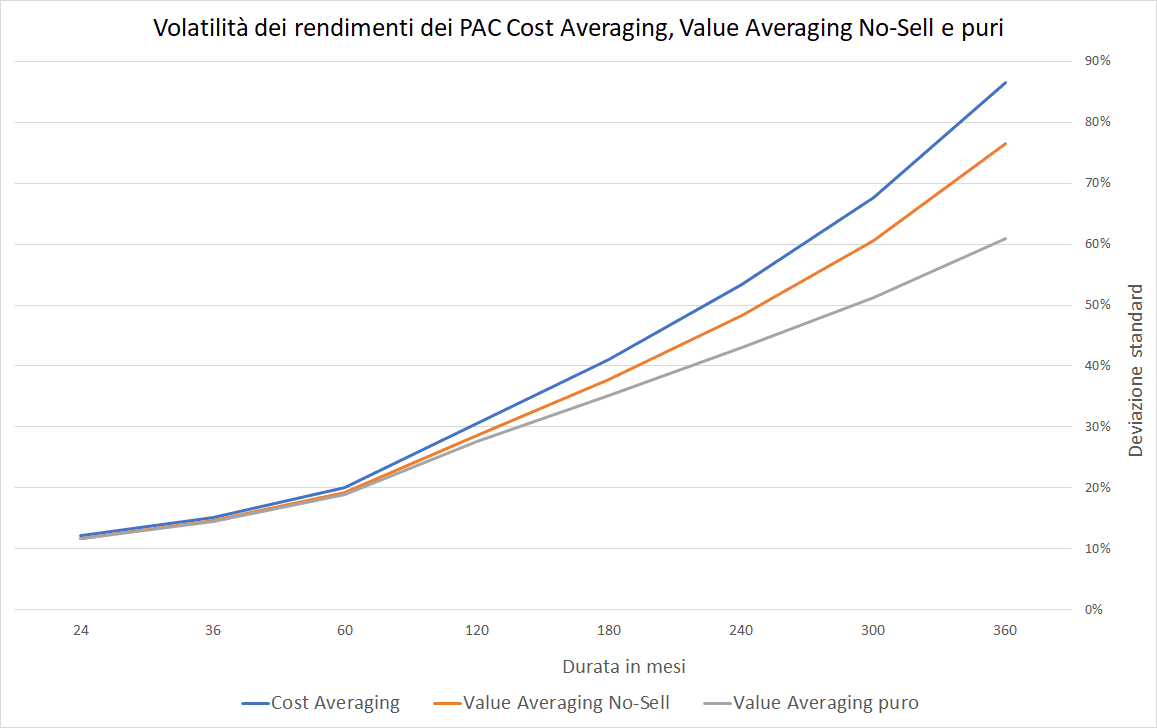
Fig. 68 – Grafico della volatilità delle varie tipologie di PAC Cost Averaging e Value Averaging (media di tutti i backtest parametrici con incremento target 0,50%, Filtro anti-Hayley: assente)
I rendimenti del Cost Averaging sono anche i più volatili: nei PAC più lunghi, 10% in più di volatilità del Value Averaging No-Sell e 25% in più di quello puro.
Anche in questo caso, le differenze iniziano a percepirsi nei piani di accumulo delle durate superiori ai 5-10 anni. È il solito trade-off che esiste tra rendimento e rischio: quasi impossibile aumentare il rendimento senza pagarne il relativo costo in termini di rischio.
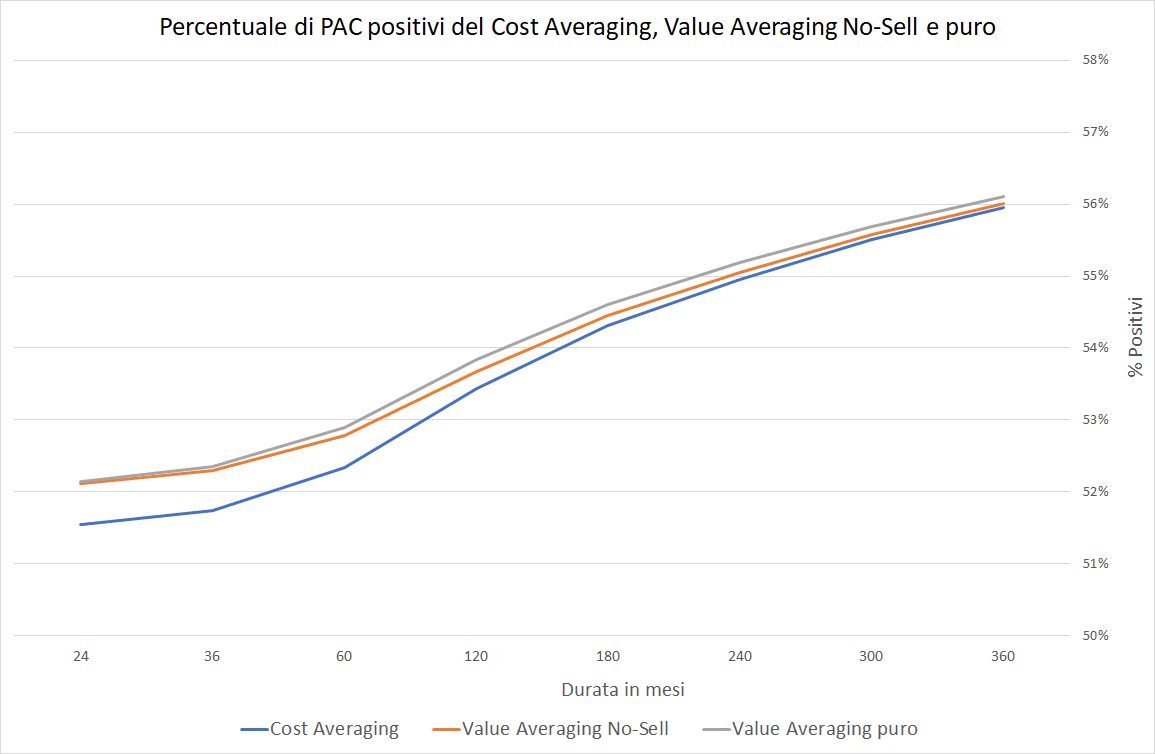
Fig. 69 – Grafico della percentuale di PAC positivi Cost Averaging e Value Averaging (media di tutti i backtest parametrici con incremento target 0,50%, Filtro anti-Hayley: assente)
Il minor rischio del Value Averaging è confermato da una più alta percentuale di PAC positivi.
Le differenze sono comunque esigue e, in questo caso, sono maggiori nei piani di accumulo di durata più breve. Dai 10-15 in su si assottigliano, fin quasi a scomparire nei PAC trentennali.
10. Quando le cose vanno male: il PAC peggiore (serie storiche reali)

«Bad times have a scientific value. These are occasions a good learner would not miss».
Ralph Waldo Emerson
In materia di investimenti finanziari, capita spesso di leggere che un PAC elimina il rischio di sbagliare il timing di ingresso. In realtà non è così: il rischio è minore di quello di un PIC, ma è pur sempre presente.
Escludendo alcune simulazioni volutamente sfavorevoli, come i backtest parametrici a media negativa, le analisi effettuate finora hanno sempre prodotto esiti mediamente positivi.
Entrando nel merito dei singoli PAC, invece, non è stato sempre così: le differenze tra le performance dei piani di accumulo migliori e peggiori per ogni durata, sia Cost Averaging che Value Averaging, sono state talvolta molto elevate.
Per completezza di informazione – e anche un po’ per curiosità – andiamo a verificare la differenza tra le prestazioni del Cost Averaging e del Value Averaging di quei PAC che si sarebbero conclusi nel momento peggiore dei mercati azionari degli ultimi 80 anni: marzo 2009, il mese in cui molti di essi – in conseguenza della violenta crisi dei subprime – hanno toccato il loro minimo assoluto.
Chi avesse investito con l’intenzione di vendere proprio in quel periodo, sarebbe quasi sicuramente andato incontro a una notevole perdita.
Questo test è facilmente riproducibile con il servizio di Analisi PAC di Dedalo Invest, scegliendo un fondo azionario dalla serie storica molto lunga con i seguenti parametri:
- Data di fine analisi: 1° aprile 2009, in modo che l’effettivo termine del PAC sia avvenuto nel giorno scelto del mese di marzo 2009 (il giorno può essere selezionato nel campo “Giorno PAC” del form di Analisi PAC).
- Data di inizio analisi: 1° aprile di X anni prima.
In questo modo, l’analisi dei PAC della lunghezza specificata inizierà ad aprile dell’anno 2009 meno X e terminerà a marzo 2009.
Nella colonna dei risultati delle analisi per durata dei PAC di Dedalo Invest, dovrà risultare un solo piano di accumulo backtestato e i risultati saranno relativi a quel singolo PAC (e molto probabilmente saranno pessimi…).
In conformità alle analisi precedenti, abbiamo seguito questa procedura con il solito fondo Raiffeisen. I parametri scelti, sia per il Value Averaging puro che per il No-Sell, sono stati i seguenti: filtro anti Hayley attivato, rata iniziale di 300 euro, target costante e incremento del target dello 0,50%, assenza di massimale, commissioni di 9 euro a inizio PAC e di 0,95 euro al versamento di ogni rata.
Le durate dei piani di accumulo backtestati vanno da 24 a 240 mesi (da 2 a 20 anni), dato che la lunghezza della serie storica del fondo non permette di andare oltre.
Per completezza, abbiamo anche riportato i risultati dell’analisi di un PIC di pari durata.
Ecco la tabella:
| Performance PAC/PIC peggiore | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Rate | Tipologia | TARGET COSTANTE | INCREMENTO TARGET 0,50% | ||||||
| Rendimento | Montante PAC | Liquidità inut. | Somma finale | Rendimento | Montante PAC | Liquidità inut. | Somma finale | ||
| 240 | PAC CA | −8,08% | 66.398 | 0 | 66.398 | −8,08% | 66.398 | 0 | 66.398 |
| 240 | PAC VA No-Sell | 1,07% | 72.000 | 845 | 72.845 | −4,87% | 68.606 | 0 | 68.606 |
| 240 | PAC VA Puro | −2,50% | 70.433 | 0 | 70.433 | −8,92% | 65.789 | 0 | 65.789 |
| 240 | PIC | 57,35% | n/a | n/a | n/a | 57,35% | n/a | n/a | n/a |
| 180 | PAC CA | −26,76% | 39.682 | 0 | 39.682 | −26,76% | 39.682 | 0 | 39.682 |
| 180 | PAC VA No-Sell | −19,28% | 43.637 | 0 | 43.637 | −24,58% | 40.797 | 0 | 40.797 |
| 180 | PAC VA Puro | −22,66% | 41.900 | 0 | 41.900 | −27,59% | 39.232 | 0 | 39.232 |
| 180 | PIC | 24,38% | n/a | n/a | n/a | 24,38% | n/a | n/a | n/a |
| 120 | PAC CA | −43,18% | 20.523 | 0 | 20.523 | −43,18% | 20.523 | 0 | 20.523 |
| 120 | PAC VA No-Sell | −42,16% | 20.879 | 0 | 20.879 | −43,13% | 20.543 | 0 | 20.543 |
| 120 | PAC VA Puro | −42,13% | 20.903 | 0 | 20.903 | −43,13% | 20.544 | 0 | 20.544 |
| 120 | PIC | −35,34% | n/a | n/a | n/a | −35,34% | n/a | n/a | n/a |
| 108 | PAC CA | −43,10% | 18.497 | 0 | 18.497 | −43,10% | 18.497 | 0 | 18.497 |
| 108 | PAC VA No-Sell | −42,34% | 18.732 | 0 | 18.732 | −43,09% | 18.500 | 0 | 18.500 |
| 108 | PAC VA Puro | −42,34% | 18.747 | 0 | 18.747 | −43,09% | 18.500 | 0 | 18.500 |
| 108 | PIC | −52,93% | n/a | n/a | n/a | −52,93% | n/a | n/a | n/a |
| 96 | PAC CA | −41,66% | 16.860 | 0 | 16.860 | −41,66% | 16.860 | 0 | 16.860 |
| 96 | PAC VA No-Sell | −40,77% | 17.103 | 0 | 17.103 | −41,53% | 16.893 | 0 | 16.893 |
| 96 | PAC VA Puro | −40,85% | 17.093 | 0 | 17.093 | −41,55% | 16.892 | 0 | 16.892 |
| 96 | PIC | −52,02% | n/a | n/a | n/a | −52,02% | n/a | n/a | n/a |
| 84 | PAC CA | −40,23% | 15.114 | 0 | 15.114 | −40,23% | 15.114 | 0 | 15.114 |
| 84 | PAC VA No-Sell | −39,37% | 15.317 | 0 | 15.317 | −39,82% | 15.209 | 0 | 15.209 |
| 84 | PAC VA Puro | −39,47% | 15.307 | 0 | 15.307 | −39,89% | 15.201 | 0 | 15.201 |
| 84 | PIC | −52,46% | n/a | n/a | n/a | −52,46% | n/a | n/a | n/a |
| 72 | PAC CA | −41,07% | 12.773 | 0 | 12.773 | −41,07% | 12.773 | 0 | 12.773 |
| 72 | PAC VA No-Sell | −40,48% | 12.894 | 0 | 12.894 | −40,78% | 12.830 | 0 | 12.830 |
| 72 | PAC VA Puro | −40,54% | 12.889 | 0 | 12.889 | −40,81% | 12.830 | 0 | 12.830 |
| 72 | PIC | −24,53% | n/a | n/a | n/a | −24,53% | n/a | n/a | n/a |
| 60 | PAC CA | −42,22% | 10.438 | 0 | 10.438 | −42,22% | 10.438 | 0 | 10.438 |
| 60 | PAC VA No-Sell | −41,79% | 10.511 | 0 | 10.511 | −42,01% | 10.473 | 0 | 10.473 |
| 60 | PAC VA Puro | −41,79% | 10.515 | 0 | 10.515 | −42,02% | 10.475 | 0 | 10.475 |
| 60 | PIC | −43,34% | n/a | n/a | n/a | −43,34% | n/a | n/a | n/a |
| 48 | PAC CA | −42,66% | 8.287 | 0 | 8.287 | −42,66% | 8.287 | 0 | 8.287 |
| 48 | PAC VA No-Sell | −42,38% | 8.327 | 0 | 8.327 | −42,57% | 8.301 | 0 | 8.301 |
| 48 | PAC VA Puro | −42,37% | 8.329 | 0 | 8.329 | −42,57% | 8.301 | 0 | 8.301 |
| 48 | PIC | −40,53% | n/a | n/a | n/a | −40,53% | n/a | n/a | n/a |
| 36 | PAC CA | −41,13% | 6.383 | 0 | 6.383 | −41,13% | 6.383 | 0 | 6.383 |
| 36 | PAC VA No-Sell | −40,97% | 6.400 | 0 | 6.400 | −41,09% | 6.388 | 0 | 6.388 |
| 36 | PAC VA Puro | −40,97% | 6.400 | 0 | 6.400 | −41,09% | 6.388 | 0 | 6.388 |
| 36 | PIC | −51,78% | n/a | n/a | n/a | −51,78% | n/a | n/a | n/a |
| 24 | PAC CA | −36,34% | 4.603 | 0 | 4.603 | −36,34% | 4.603 | 0 | 4.603 |
| 24 | PAC VA No-Sell | −36,32% | 4.604 | 0 | 4.604 | −36,33% | 4.604 | 0 | 4.604 |
| 24 | PAC VA Puro | −36,32% | 4.604 | 0 | 4.604 | −36,33% | 4.604 | 0 | 4.604 |
| 24 | PIC | −52,58% | n/a | n/a | n/a | −52,58% | n/a | n/a | n/a |
Fig. 70 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging (target costante e con incremento dello 0,50%, senza massimale, Filtro anti-Hayley: presente) di tutti i PAC di varie durate sul PAC peggiore (disinvestimento marzo 2009) del fondo Raiffeisen
Le performance di questi PAC sono state disastrose.
In generale, il Value Averaging ha ottenuto dei rendimenti migliori del Cost Averaging, soprattutto quando è stato utilizzato il target costante e sulle durate superiori ai 10 anni.
È interessante notare come i PIC, che sono considerati più rischiosi dei PAC, hanno performato peggio di questi ultimi in tutte le durate inferiori a 10 anni (con l’eccezione di quelli a 4 e a 6 anni). Nelle durate dai 10 anni in su, hanno invece ottenuto dei rendimenti nettamente superiori.
A tale riguardo, si possono fare due osservazioni:
- Quando si consiglia di investire a lungo termine nel mercato azionario per diminuire la probabilità di perdite, è perché anche nei casi più sfortunati, se la variabile tempo è a nostro favore, si può riuscire a portare a casa un rendimento positivo o contenere eventuali perdite.
- Nel breve termine, il PIC espone a rischi maggiori del PAC.
Limitandoci al confronto tra le varie tipologie analizzate, può essere utile visualizzare graficamente i rendimenti dei “PAC peggiori” per durata e dei corrispondenti PIC:
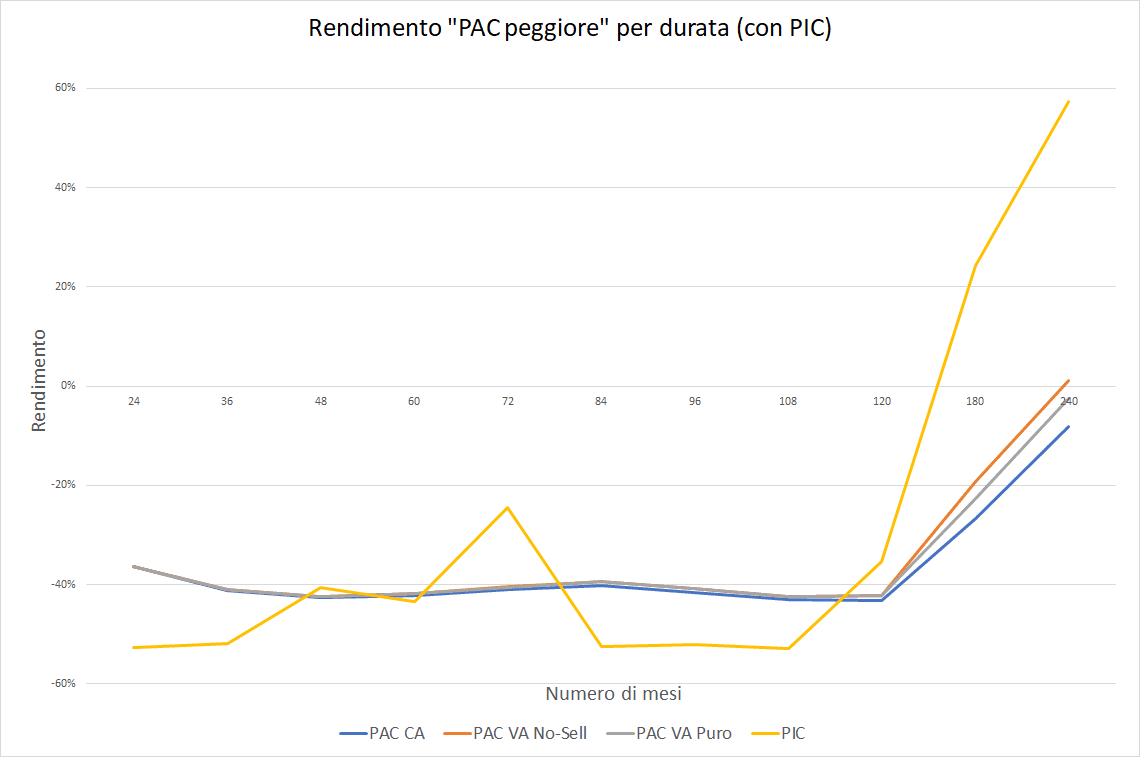
Fig. 71 – Grafico dei rendimenti delle varie tipologie di PAC Cost Averaging e Value Averaging (target costante, senza massimale, Filtro anti-Hayley: presente) per durata dei “PAC peggiori” (disinvestimento marzo 2009) sul fondo Raiffeisen
Le differenze sono minime nei PAC di breve durata e un po’ più evidenti in quelli superiori ai 10 anni. Il Value Averaging No-Sell ottiene i risultati migliori.
Il grafico dei PIC ha un andamento molto diverso: le oscillazioni sono molto più marcate, indice di una maggiore volatilità.
Questa analisi è basata sull’analisi di una singola serie storica: al di là della maggior rischiosità dei PIC, unanimemente riconosciuta, non è corretto tirare conclusioni generiche, che altre simulazioni potrebbero falsificare.
Come si sarebbero dovuti comportare gli sfortunatissimi investitori nei PAC appena esaminati, a marzo 2009?
Quelli che avevano bisogno della somma accumulata in concomitanza della fine del piano di accumulo, non avrebbero potuto far altro che liquidare l’investimento in pesante perdita.
Per gli altri, la soluzione migliore sarebbe stata quella di non disinvestire: una volta terminato, il PAC si sarebbe trasformato in un PIC e le quote accumulate sarebbero state mantenute in portafoglio almeno fin quando il rendimento fosse tornato positivo (o il bisogno di liquidità avesse obbligato a smobilizzare l’investimento prima).
Quanto tempo sarebbe stato necessario?
Nelle tabelle di output dell’analisi dei PAC (e dei PIC) di Dedalo Invest viene visualizzato il tempo di recupero medio e massimo dei piani di accumulo terminati in perdita. Non è detto che il periodo di recupero più lungo per ogni durata sia necessariamente associato al PAC con il rendimento peggiore, ma è sufficiente a darci un’idea approssimativa di quanti giorni borsistici sarebbero occorsi nel caso peggiore: un valore indirettamente proporzionale alla durata dei piani di accumulo.
Più in generale, a parità di durata, il periodo di recupero del Value Averaging è sempre minore o uguale a quello del Cost Averaging.
Quello dei PIC, invece, è generalmente molto più lungo.
Il periodo di recupero è un importante indicatore di rischio, spesso sottovalutato o ignorato (e, in molte occasioni, si tratta di un’informazione molto difficile da reperire).
Perché, in questo specifico piano di accumulo, il rendimento del Value Averaging è appena superiore a quello del Cost Averaging? La sua minor rischiosità non dovrebbe essere sfruttata proprio in queste occasioni?
Il motivo è che la crisi è esplosa nella parte finale di questi PAC. In ogni durata, gli ultimi 5-6 mesi sono stati catastrofici e non c’è più stato tempo per recuperare. In questa fase, col Value Averaging i versamenti saranno senz’altro stati superiori ma, mese dopo mese fino a marzo 2009, il mercato continuava a scendere, causando una perdita di valore anche sulle ultime quote acquistate.
Quando si verifica una situazione del genere non ci sono vie d’uscita per la parte azionaria del portafoglio: il suo valore scenderà drasticamente.
Anche disponendo di extra-liquidità, non avremmo potuto far meglio: va bene versare di più quando il valore corrente scende, ma se la discesa continua fino all’ultimo versamento, avremo paradossalmente perso più soldi.
I frutti dell’utilizzo di extra-liquidità si vedranno soltanto qualche mese dopo, con la ripresa dei mercati. Sei mesi o un anno più tardi, ad esempio, l’extra-liquidità versata nei momenti di massima tensione aumenterà il suo valore, facendo crescere il Montante del PAC.
In un caso del genere, vediamo come l’inefficienza dei rendimenti totali e annualizzati lasci il tempo che trova: chi avesse avuto liquidità in eccesso da investire in quei momenti non sarebbe stato interessato a sapere che, ad esempio a ottobre 2009, il suo investimento ventennale stesse rendendo l’11,40% contro l’ipotetico 14,96% del Cost Averaging. Avrebbe semmai preferito constatare che il valore corrente del suo PAC, al netto dell’extra-liquidità versata, sarebbe stato di 89.380 euro, contro gli 83.046 del Cost Averaging.
Il Cost Averaging, seguendo i canoni di giudizio tipici dell’economia e della finanza classica, sarebbe stato l’investimento più efficiente in questo specifico caso.
Il Value Averaging, seguendo i canoni di giudizio reali dell’investitore medio con extra-liquidità a disposizione, sarebbe stato probabilmente l’investimento preferibile.
Si potrebbe obiettare che l’investitore medio non avrebbe trovato il coraggio di investire massicciamente nei momenti di massima criticità, quando ascoltando qualsiasi notiziario si poteva ogni giorno constatare quante nuove aziende erano fallite, quanti risparmiatori rischiavano di perdere tutto il loro denaro e quanti miliardi di dollari avevano appena bruciato le borse.
Fermo restando che il Value Averaging con un fondo di liquidità iniziale non è una strategia di investimento adatta a tutti, la critica è corretta ed è valida soprattutto quando non c’è una strategia di base: vedremo nel paragrafo/capitolo successivo come impostare nel migliore dei modi un investimento di questo tipo.
11. Value Averaging con l’utilizzo di extra-liquidità: perché no?

«Of all the ways of defining man, the worst is the one which makes him out to be a rational animal».
Anatole France
La critica di Hayley è stata interpretata da alcuni autori come la fine del Value Averaging.
La magia descritta da Edleson e Marshall è svanita nel momento in cui Hayley ha rilevato come le analisi condotte fino a quel momento fossero incomplete, superficiali e distorte.
Uno dei problemi della finanza classica è che spesso si scontra con una realtà molto più complessa delle pur complicate formule matematiche che la descrivono.
La finanza personale, nel suo piccolo, deve fare i conti con la psicologia degli investitori e l’estrema difficoltà a trasferire concetti come razionalità, efficienza e ottimizzazione al comportamento umano.
Il pionieristico lavoro di Daniel Kahneman e Amos Tversky sulla finanza comportamentale, continuato da altri importanti economisti come Richard Thaler e Robert Shiller, ha messo in luce le problematiche ed i numerosi bias che affliggono gli investitori: la razionalità, l’ingrediente fondamentale della scienza economica e di molti modelli economici ed econometrici, è una risorsa molto limitata negli esseri umani quando sono alle prese con i mercati finanziari.
Uno dei principali problemi degli investitori è il timore di prendere posizione su mercati volatili come quelli azionari: sono spaventati dalla possibilità che il valore del loro portafoglio possa scendere nel breve termine, pur avendo magari un orizzonte temporale di lungo termine.
A volte, non se la sentono nemmeno di mettere in gioco il loro capitale. La soggettiva propensione al rischio, quando non è elevata (circostanza rara, che si verifica soprattutto negli investitori più esperti), costringe spesso gli investitori a rimanere in stand-by, in attesa di tempi più favorevoli per agire.
Se le quotazioni azionare viaggiano intorno ai valori massimi, subentra poi un altro fattore che contribuisce a paralizzarli: la paura di un’imminente crisi finanziaria che faccia crollare il mercato. Investendo subito, si esporrebbero troppo a questo rischio e prima di agire preferiscono attendere uno storno dei prezzi.
In realtà, questo tipo di conversazione è sempre presente nella mente degli investitori con una bassa propensione al rischio: sia quando i mercati crescono che durante o dopo una recessione.
Ad inizio 2009, al culmine della crisi finanziaria, in pochi erano disposti a investire nei mercati azionari: la paura originata dal crollo era al suo apice e solo una minima percentuale di investitori ebbe il sangue freddo di fare ciò che, in altri momenti, sembra la cosa più facile del mondo: acquistare quando i prezzi sono bassi.
Purtroppo, l’attesa costa. Nell’aspettare la crisi, si finisce con l’essere spettatori dei mercati, che nel frattempo iniziano o continuano la loro crescita.
Nel 2014, molti investitori si aspettavano un crollo delle quotazioni azionarie e sono rimasti alla finestra in attesa di acquistare a prezzi più bassi: il tracollo, almeno fino a inizio 2020, non c’è ancora stato (salvo breve parentesi come quella di fine 2018) e molti di loro hanno perso oltre 5 anni di uno dei mercati toro più notevoli degli ultimi decenni.
Le statistiche e le analisi delle serie storiche ci dicono che un investimento lump sum (un PIC puro) è la più efficiente modalità di impiego del capitale: un orizzonte temporale di lungo termine, sempre consigliabile quando si investe in mercati volatili come quello azionario, aiuta a recuperare le eventuali perdite o a incrementare i guadagni. Ovviamente, la prima condizione per investire in un PIC è disporre del denaro fin dall’inizio.
Eppure, i bias comportamentali fanno sì che molti investitori non trovino il coraggio di agire: se lo fanno, diversificano tra azionario e obbligazionario (come è giusto che sia), sovrappesando eccessivamente quest’ultimo proprio per far fronte all’eventualità peggiore. In alternativa, scelgono di impiegare il loro capitale attraverso un Piano di Accumulo del Capitale Cost Averaging.
Per ovviare a questo problema, si potrebbe pensare di investire in un PAC Value Averaging con la possibilità di sfruttare una riserva iniziale di extra-liquidità. Si potrebbe fare, cioè, proprio ciò che Hayley ha raccomandato di evitare, in quanto inefficiente: un piano di accumulo Value Averaging che, in certi momenti, comporti l’investimento di una cospicua somma di denaro (non necessariamente l’intera riserva di liquidità).
Agendo in questo modo l’investitore:
- Eviterebbe di attendere inutilmente il momento “opportuno” per prendere posizione sul mercato. Il momento opportuno è un ipotetico scenario favorevole esistente nella mente dell’investitore. Di solito, non arriva mai.
- Eviterebbe il rischio di investire l’intero capitale subito prima di una crisi finanziaria, come avviene con un PIC: il Value Averaging è una forma particolare di PAC che, se la crisi arrivasse presto, sfrutterebbe i prezzi più bassi per acquistare un numero maggiore di quote. Se la crisi arrivasse a PAC avanzato, il Value Averaging si gioverebbe della riserva di extra-liquidità.
- Eviterebbe di doversi affidare a strategie basate su previsioni future: su modelli econometrici che non capisce o che, peggio ancora, non ha modo di sapere se siano overfittati, distorti (Look-Back Bias) o sbagliati (Look-Ahead Bias). Il Value Averaging non prevede niente: semplicemente, asseconda l’andamento del mercato.
- Eviterebbe il market timing.
- Eviterebbe di dover sottoscrivere costosi portafogli composti da molti strumenti finanziari che hanno lo scopo di limitare il rischio. Sarebbe certamente possibile costruire dei piani di accumulo Value Averaging su più prodotti finanziari e di portarli avanti parallelamente (diversificazione “spaziale”); tuttavia, lo strumento principale per la mitigazione del rischio è in questo caso la diversificazione “temporale”
- Risolverebbe il problema di trovare la giusta combinazione tra liquidità e strumenti finanziari:
- La percentuale di liquidità sarebbe molto elevata all’inizio dell’investimento e per lunghi periodi durante la vita del piano di accumulo; il suo impiego in momenti ben definiti, quando i prezzi sono relativamente bassi, compenserebbe il costo-opportunità di questa scelta.
- Con il passare del tempo, il peso della liquidità diminuirebbe, mentre quello dello strumento finanziario su cui si sta costruendo il PAC diventerebbe sempre più grande.
- Nulla vieta, ovviamente, di investire la liquidità in attesa di essere utilizzata al tasso risk-free, in crescita negli ultimi tempi dopo essere stato uguale o molto vicino a zero per molto tempo (possibilmente in un conto deposito non vincolato o in un prodotto facilmente svincolabile).
Se tutto questo fosse vero, la minore efficienza di questa metodologia rispetto a un investimento in un’unica soluzione sarebbe un prezzo che l’investitore potrebbe accettare di pagare volentieri.
Ipotizzando un piano di accumulo Value Averaging No-Sell o puro con rata iniziale e incremento del target di 300 euro al mese, a quanto dovrebbe ammontare la riserva di liquidità iniziale? È possibile trovare una formula che leghi l’importo della riserva di liquidità alla rata e alla durata del Value Averaging?
Prima di rispondere a queste domande torniamo a familiarizzare con i backtest del fondo Raiffeisen Azionario Globale VT.
Nel sesto capitolo avevamo simulato il Value Averaging senza filtro anti-Hayley soltanto con target costante o crescente dello 0,25%. Con questi parametri, la liquidità aggiuntiva richiesta non era molto elevata.
Possiamo fare un passo in avanti e andare a verificare quanta extra-liquidità sarebbe servita ipotizzando incrementi del target più ampi, ad esempio dello 0,50%.
Partiamo dal Value Averaging No-Sell:
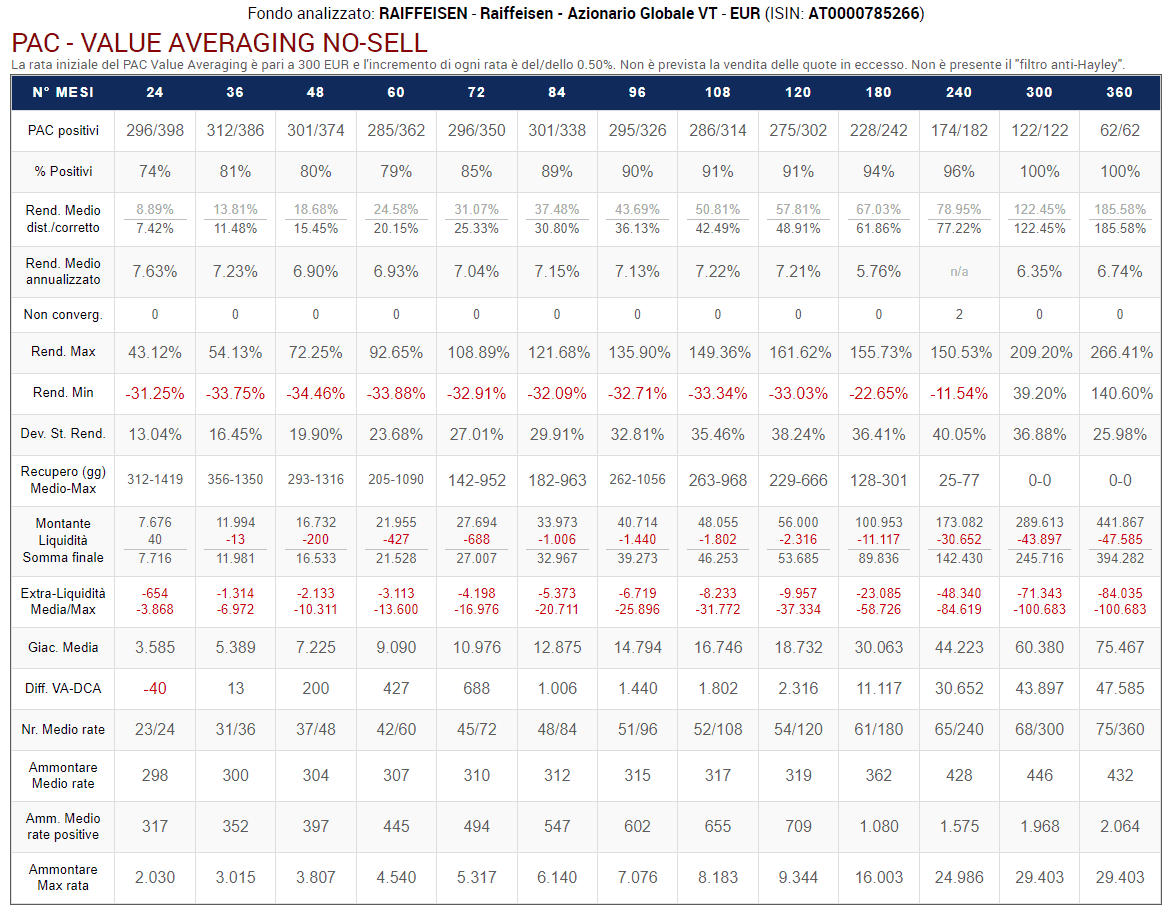
Fig. 72 – PAC Value Averaging No-Sell. Rata iniziale: 300 euro. Incremento target: 0,50%. Versamento massimo non previsto. Filtro anti-Hayley: assente
L’extra-liquidità utilizzata, alla fine del Value Averaging No-Sell trentennale, sarebbe stata mediamente pari a 47.585 euro. Non è una cifra elevata, ma si tratta della extra-liquidità impiegata nel momento finale dell’investimento.
Cos’è successo prima?
10, 20, 30 anni sono lunghi: potrebbe essere stato possibile che, nel corso di questi anni, fosse richiesta una liquidità maggiore?
La risposta è positiva e la riga Extra-Liquidità Media/Max misura esattamente questo.
Nei piani di accumulo trentennali, il fondo di liquidità richiesto sarebbe stato mediamente pari a 84.035 euro. Di tutti i 62 PAC analizzati, il massimo utilizzo è stato di 100.683 euro: più del doppio dell’extra-liquidità media di fine investimento.
Per capire meglio questa differenza ci possiamo servire di un grafico simile a quelli presentati nel quinto capitolo. Possiamo vedere come, durante i 30 anni di vita di uno specifico piano di accumulo (il primo dei 62 della tabella), le cifre versate in un PAC Value Averaging No-Sell siano state, in determinati momenti, maggiori di quelle di un Cost Averaging: l’andamento dei pagamenti del Value Averaging No-Sell e quello di un Cost Averaging sono ben visibili nel grafico sottostante.
In particolare, la linea arancione misura esattamente la differenza tra questi due valori:
- Quando è positiva, rappresenta la liquidità inutilizzata.
- Quando è negativa, quantifica l’extra-liquidità richiesta durante la vita del piano di accumulo.
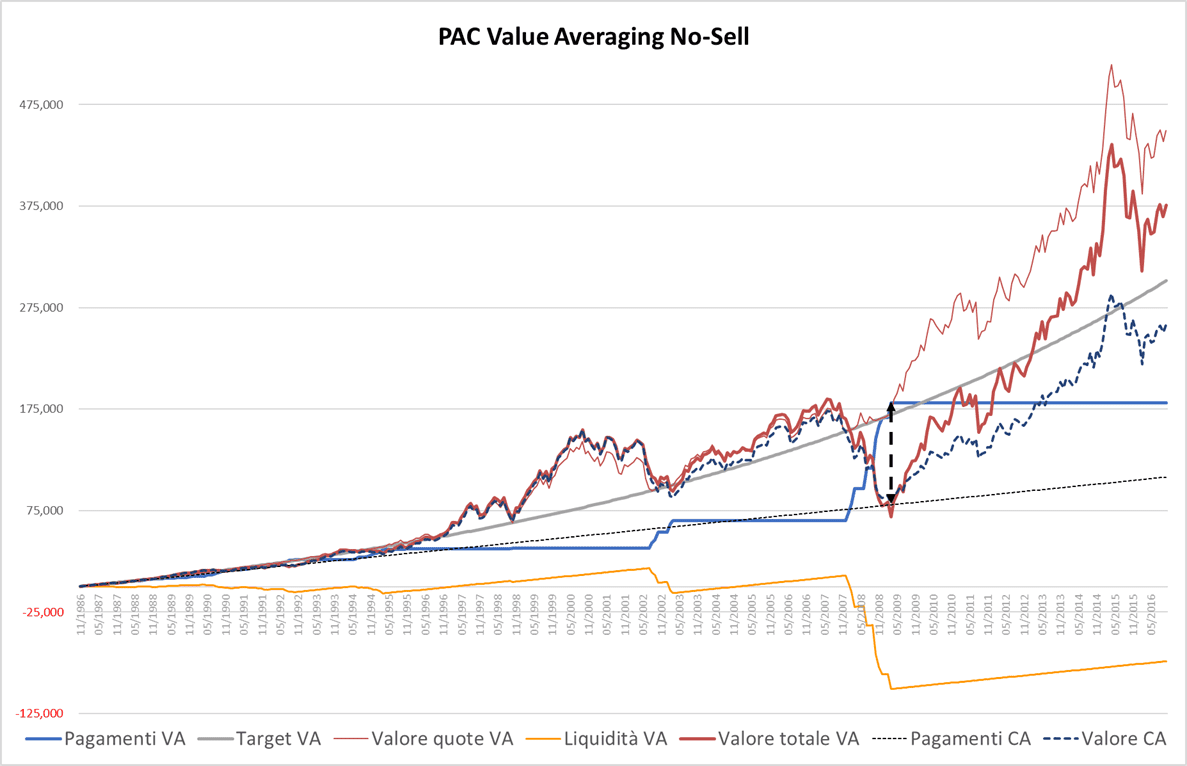
Fig. 73 – PAC Value Averaging No-Sell. Rata iniziale: 300 euro. Target crescente: 0,50%. Versamento massimo non previsto. Filtro anti-Hayley: assente
La linea verticale tratteggiata individua il momento in cui la massima extra-liquidità è stata richiesta: a marzo 2009, nel momento culminante della crisi azionaria, sono stati toccati i 100.683 euro di extra-liquidità versata: il valore massimo di questo PAC che, per inciso, è stato anche il livello massimo di tutti i 62 piani di accumulo analizzati poco prima. In quello specifico punto, la linea arancione ha raggiunto il livello più basso, proprio pari a −100.683 euro.
La tabella precedente ci informa che la stessa somma è stata raggiunta anche dal Value Averaging No-Sell della durata di 25 anni, mentre 84.619 è stato il valore della extra-liquidità massima dei piani di accumulo ventennali. Spostandoci ulteriormente sulla sinistra, l’extra-liquidità massima è scesa a 58.726 per i PAC di 15 anni e a 37.334 per quelli decennali.
Le durate più brevi hanno utilizzato una liquidità minore, fino ad arrivare ai piani di accumulo biennali che hanno consumato fino a 3.868 euro di extra-liquidità.
Vediamo come si è comportato, ceteris paribus, il Value Averaging puro:
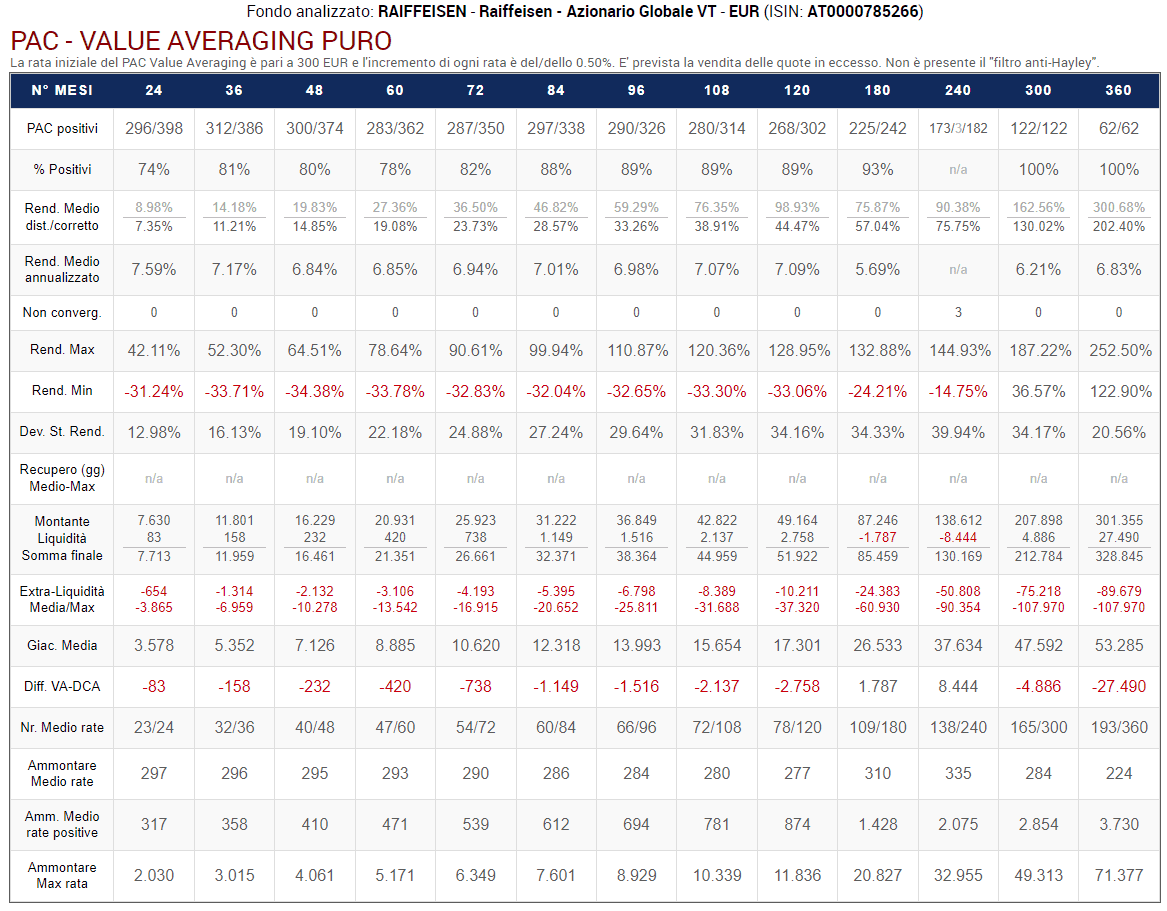
Fig. 74 – PAC Value Averaging puri. Rata iniziale: 300 euro. Incremento target: 0,50%. Versamento massimo non previsto. Filtro anti-Hayley: assente
Al termine dei piani di accumulo rimane della liquidità inutilizzata (a eccezione di quelli di 15 e 20 anni). Sembrerebbe, quindi, che poca o nessuna extra-liquidità sarebbe stata richiesta.
La riga sottostante ci presenta invece una realtà molto diversa: in media, avremmo dovuto utilizzare 89.679 euro di extra-liquidità, con un massimo pari a 107.970 euro.
Anche in questo caso, visualizziamo il grafico del primo dei 62 PAC Value Averaging puri che abbiamo simulato:
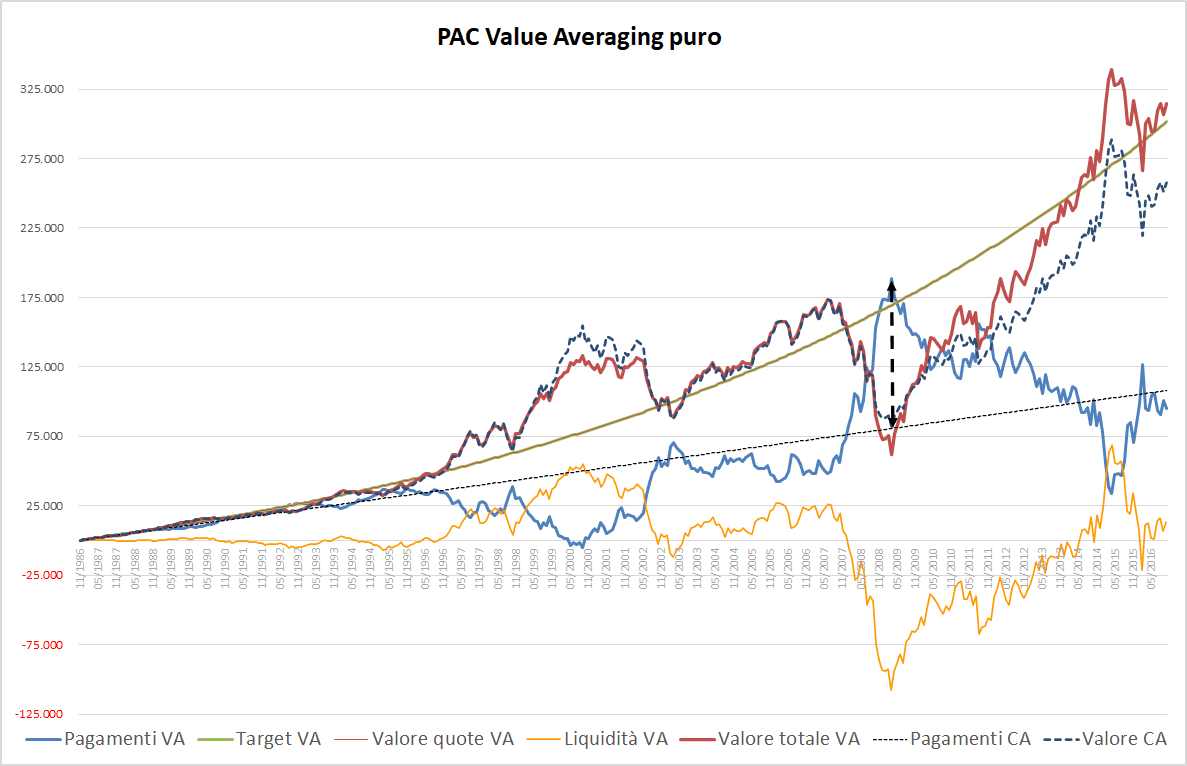
Fig. 75 – PAC Value Averaging puro. Rata iniziale: 300 euro. Target crescente: 0,50%. Versamento massimo non previsto. Filtro anti-Hayley: assente
Il fabbisogno massimo di extra-liquidità è stato nuovamente contrassegnato da una riga verticale tratteggiata.
La liquidità è misurata dalla linea arancione e, ancora una volta nel marzo 2009, ha toccato il suo livello minimo pari a −107.970 euro, per poi tornare a valori positivi negli anni seguenti (il Value Averaging puro prevede vendite di quote, che fanno diminuire l’extra-liquidità richiesta).
Oltre 100 mila euro potrebbero sembrare un’enormità. In realtà, 100 mila euro associati a un piano di accumulo mensile dalla rata iniziale di 300 euro sviluppato su 30 anni non sono poi una cosa eccezionale. Per arginare questa somma, potremmo provare a utilizzare il massimale di 1000 euro, impiegato spesso anche in precedenza.
Vediamo come cambiano le cose aggiungendo questo vincolo nei PAC Value Averaging No-Sell:
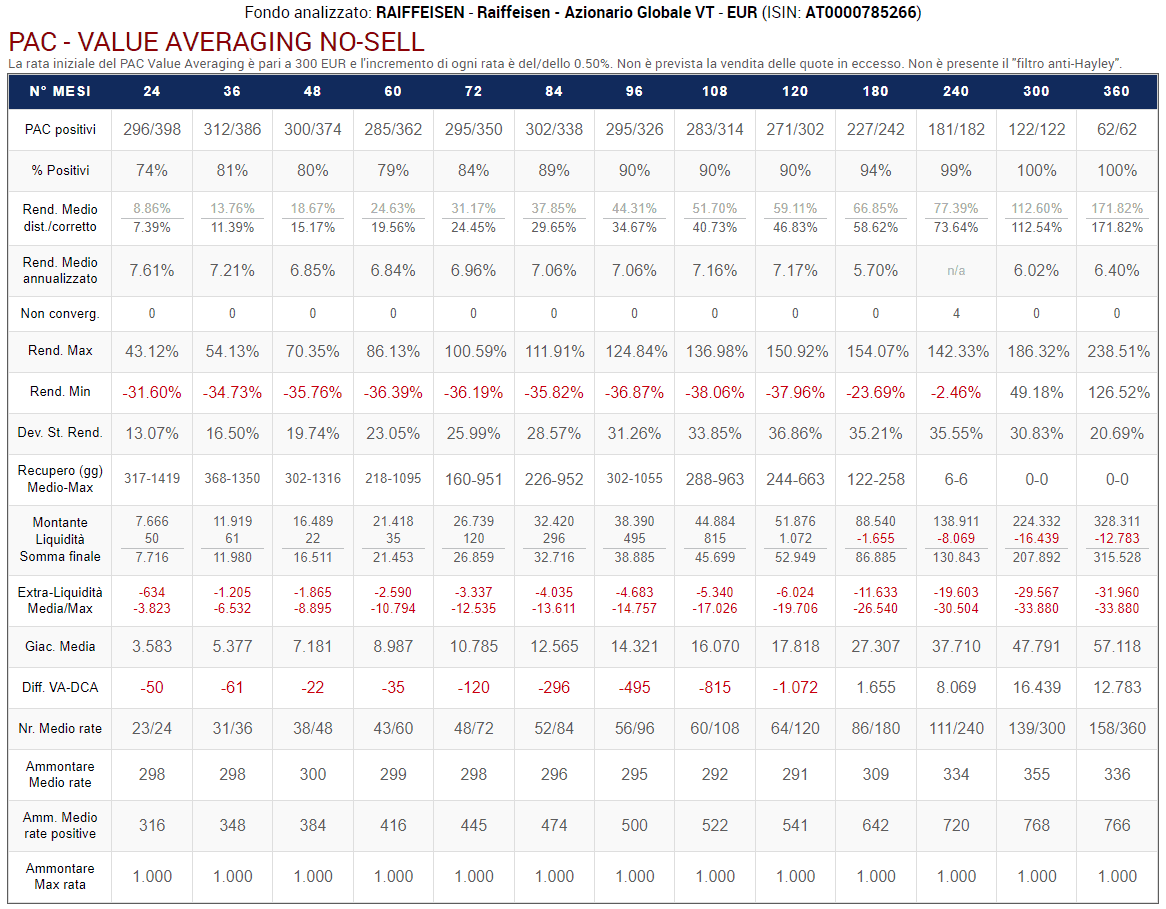
Fig. 76 – PAC Value Averaging No-Sell. Rata iniziale: 300 euro. Incremento target: 0,50%. Versamento massimo: 1000 euro. Filtro anti-Hayley: assente
Il massimale attua un’ottima azione di contenimento: nella durata più lunga, l’extra-liquidità viene drasticamente ridotta da 90/100 mila (media/max) a 32/33 mila euro. Purtroppo, anche il rendimento si riduce: da 185,58% a 171,82%. Nelle altre durate si verificano le stesse diminuzioni, anche se in misura via via minore.
È un risultato importante: con fondi di liquidità relativamente contenuti, si possono costruire dei piani di accumulo Value Averaging performanti. Il Cost Averaging produceva un rendimento inferiore (150,18% sui trentennali) su cifre totali investite più piccole: col Cost Averaging si investono esattamente 108.000 euro; col Value Averaging No-Sell appena esaminato 120.783 euro, pari a 108.000 più la liquidità che risulta ancora impiegata a fine PAC (12.783 euro)
Sembrerebbe impossibile ottenere una riduzione di liquidità di questa portata con un semplice massimale ai versamenti: per convincercene, diamo un’occhiata ai grafici sovrapposti dell’evoluzione dei pagamenti nel Value Averaging e nel Cost Averaging:
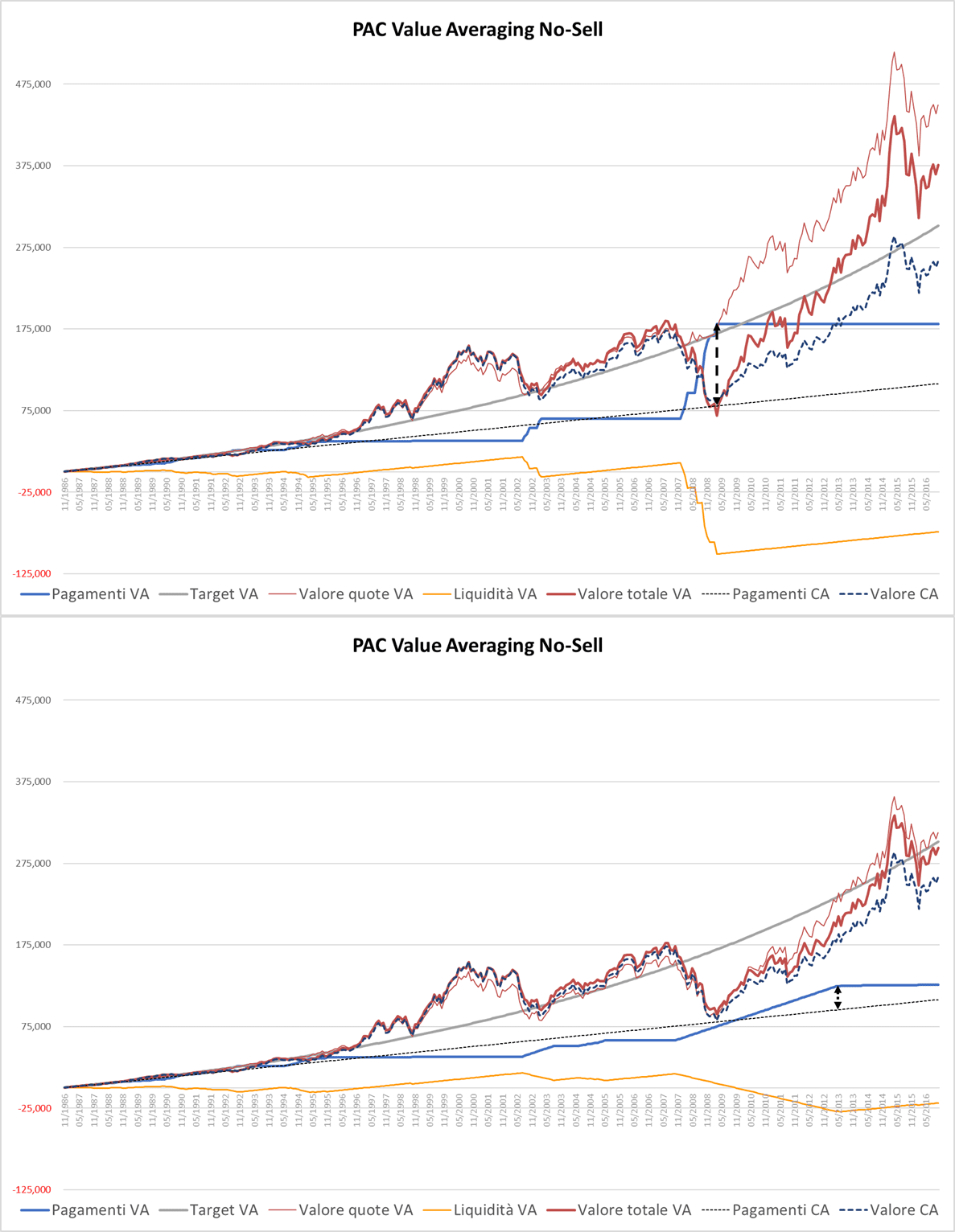
Fig. 77 – PAC Value Averaging No-Sell. Rata iniziale: 300 euro. Target crescente: 0,50%. Massima extra-liquidità richiesta senza massimale versamento (sopra) e con massimale di 1000 euro (sotto)
La linea verticale tratteggiata misura l’extra-liquidità massima. Il primo grafico l’avevamo già commentato in precedenza.
Nel secondo, la linea dei pagamenti del Value Averaging cresce in maniera meno brusca e si mantiene in prossimità dalla linea dei pagamenti del Cost Averaging. Inoltre, si è spostata in avanti di oltre 4 anni (giugno 2013).
Il massimale di 1.000 euro, seppur abbassando il rendimento del PAC, produce due importanti benefici:
- Ridimensiona il fabbisogno di extra-liquidità.
- Evita il versamento di maxi-rate durante le fasi più acute di una crisi finanziaria. Offre un supporto di tipo psicologico, perché non è sempre facile trovare il coraggio di effettuare investimenti consistenti in momenti di forti turbolenze dei mercati.
Non riportiamo la tabella del Value Averaging puro, dato che il massimale di 1000 euro produce lo stesso risultato: l’extra-liquidità media/max passa da 90/108 mila a 33/35 mila euro. Il rendimento scende dal 202,40% al 174,33%; una diminuzione maggiore di quella del Value Averaging No-Sell.
Nel Value Averaging puro l’utilizzo del massimale comporta un ulteriore vantaggio: diminuisce il numero di vendite di quote. Senza massimale avevamo 193 acquisti e 167 vendite; con il massimale, gli acquisti salgono a 287 e le vendite si riducono a 73. Dato che vendere quote implica il pagamento di imposte sul capital gain, questa drastica diminuzione non può che avere un impatto benefico.
Oltre al massimale, quali sono i fattori che influenzano l’ammontare di extra-liquidità richiesta?
- La lunghezza del PAC: è forse il fattore più significativo. Tanto più un piano di accumulo Value Averaging è lungo, tanto maggiore è l'extra-liquidità.
- La rata iniziale/incremento del target: più è grande, maggiore è la liquidità richiesta. Esiste una proporzionalità diretta tra queste due grandezze: se la rata raddoppia, la stessa cosa accade all’extra-liquidità.
- La percentuale di incremento del target: più è alta, maggiore sarà il fondo di liquidità iniziale necessario a far fronte al fabbisogno durante l’investimento.
Approfondiremo questi elementi in seguito.
Vediamo che cosa accade portando la percentuale di incremento del target all’1%. Questi sono i risultati del Value Averaging No-Sell:
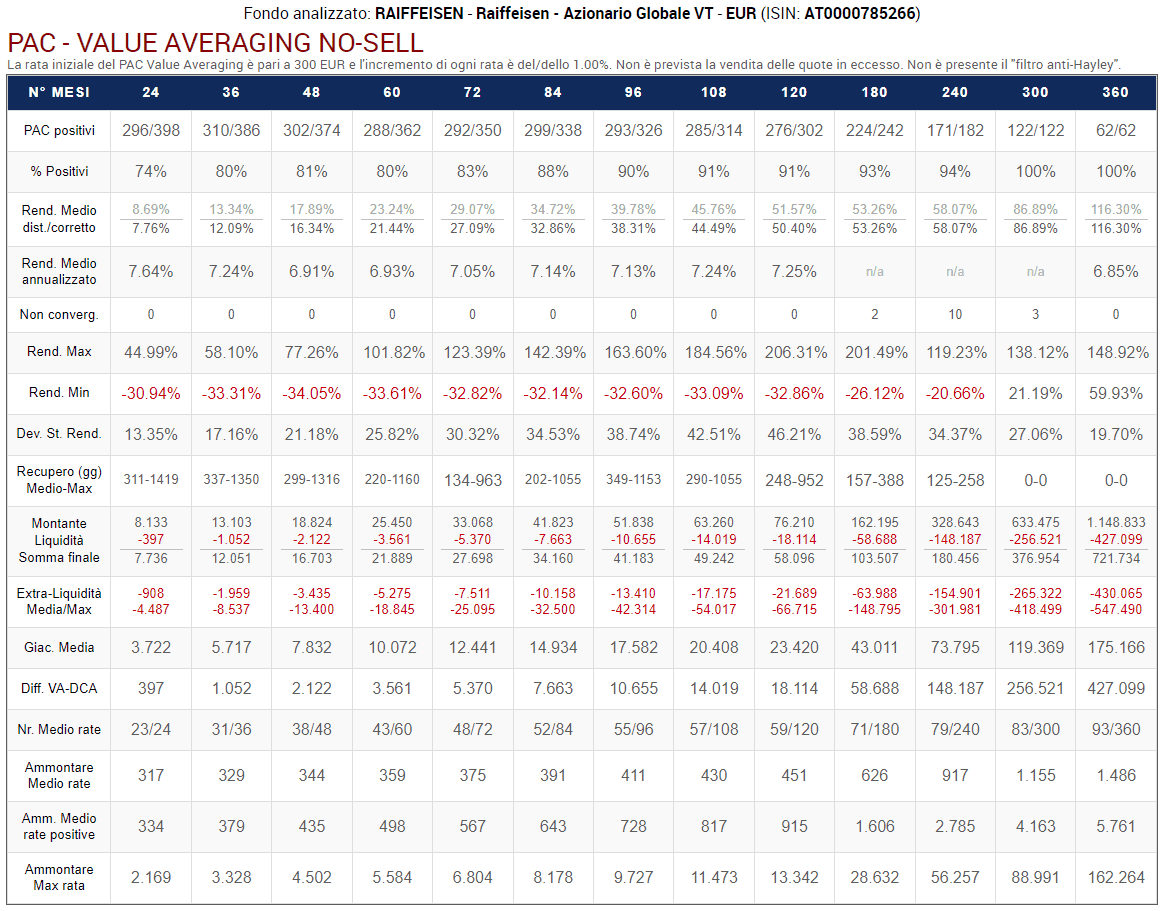
Fig. 78 – PAC Value Averaging No-Sell. Rata iniziale: 300 euro. Incremento target: 1%. Versamento massimo non previsto. Filtro anti-Hayley: assente
I valori crescono in modo più che proporzionale: raddoppiando l’incremento percentuale del target, l’extra-liquidità media/max è più che quintuplicata nei piani trentennali (430/547 mila euro). I PAC più corti, invece, hanno subito aumenti inferiori (16%/39% quelli di 24 mesi).
Non riportiamo la tabella del Value Averaging puro con incremento del target dell’1% perché le dinamiche sono molto simili (l’extra-liquidità è leggermente superiore).
Senza un massimale, le cifre richieste con l’1% di incremento sono probabilmente proibitive, almeno nei piani di accumulo di più lunga durata: è difficile che un investitore decida di dedicare simili somme a un PAC Value Averaging. Dato che anche il rendimento complessivo è sceso al 116,30% (molto al di sotto di quello del Cost Averaging), questa soluzione non sembra essere tra le più invitanti.
Applicando il massimale, l’extra-liquidità scende – nel Value Averaging No-Sell – a 137/159 mila euro: purtroppo, anche il rendimento si riduce al 116,28%.
A questo punto, non rimane che approfondire l’indagine con le simulazioni Monte Carlo. Effettueremo direttamente le simulazioni parametriche, in quanto permettono un più ampio spettro di analisi.
Questi sono i risultati con incremento del target pari allo 0,50%:
| Incremento 0,5% - No Massimale - Media 0,50%, Deviazione standard 5% - 100.000 simulazioni | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. tot. | Stand. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. | Ex.Liq. Med. | Ex.liq. Max |
| PAC | 360 | CA | 180,31% | 215,68% | 302.738 | 0 | 302.738 | 300 | 4.743,06% | −73,30% | 90,775% | 120,83% | 3,283 | 22,574 | 0 | 0 |
| PAC | 300 | CA | 130,96% | 151,32% | 207.865 | 0 | 207.865 | 300 | 3.346,89% | −72,69% | 88,549% | 91,29% | 2,625 | 14,723 | 0 | 0 |
| PAC | 240 | CA | 92,58% | 107,76% | 138.656 | 0 | 138.656 | 300 | 1.764,53% | −70,40% | 85,789% | 66,77% | 2,194 | 9,493 | 0 | 0 |
| PAC | 180 | CA | 61,34% | 73,47% | 87.124 | 0 | 87.124 | 300 | 911,54% | −65,81% | 82,293% | 45,62% | 1,743 | 5,882 | 0 | 0 |
| PAC | 120 | CA | 36,50% | 47,77% | 49.141 | 0 | 49.141 | 300 | 518,69% | −64,28% | 77,679% | 27,90% | 1,295 | 3,112 | 0 | 0 |
| PAC | 60 | CA | 16,35% | 27,12% | 20.942 | 0 | 20.942 | 300 | 292,53% | −52,17% | 70,584% | 13,00% | 0,842 | 1,386 | 0 | 0 |
| PAC | 36 | CA | 9,26% | 19,12% | 11.800 | 0 | 11.800 | 300 | 134,42% | −48,06% | 66,056% | 7,38% | 0,615 | 0,655 | 0 | 0 |
| PAC | 24 | CA | 5,94% | 14,75% | 7.627 | 0 | 7.627 | 300 | 95,04% | −43,78% | 63,298% | 4,81% | 0,474 | 0,391 | 0 | 0 |
| PAC | 360 | VA No-Sell | 194,39% | 210,53% | 439.117 | −76.191 | 362.926 | 62.092 | 4.445,74% | −53,70% | 92,551% | 131,92% | 2,427 | 12,770 | 98.786 | 557.089 |
| PAC | 300 | VA No-Sell | 141,25% | 144,99% | 284.545 | −47.369 | 237.175 | 42.159 | 1.930,26% | −57,53% | 90,920% | 102,63% | 1,912 | 7,043 | 65.422 | 399.493 |
| PAC | 240 | VA No-Sell | 99,49% | 99,76% | 177.782 | −26.839 | 150.944 | 31.070 | 1.661,39% | −51,51% | 88,695% | 76,45% | 1,575 | 5,044 | 40.528 | 233.567 |
| PAC | 180 | VA No-Sell | 65,91% | 66,17% | 104.747 | −13.319 | 91.428 | 18.815 | 632,32% | −49,85% | 85,776% | 53,77% | 1,157 | 2,323 | 22.880 | 122.951 |
| PAC | 120 | VA No-Sell | 39,23% | 42,23% | 55.155 | −5.018 | 50.137 | 11.632 | 347,27% | −51,11% | 81,673% | 33,44% | 0,808 | 0,880 | 10.714 | 65.707 |
| PAC | 60 | VA No-Sell | 17,64% | 23,96% | 21.936 | −920 | 21.016 | 4.747 | 165,13% | −43,42% | 74,176% | 15,78% | 0,483 | 0,100 | 3.187 | 18.996 |
| PAC | 36 | VA No-Sell | 10,06% | 17,13% | 12.042 | −233 | 11.809 | 2.738 | 96,43% | −39,10% | 69,293% | 9,03% | 0,358 | −0,126 | 1.347 | 8.579 |
| PAC | 24 | VA No-Sell | 6,50% | 13,42% | 7.695 | −66 | 7.629 | 1.930 | 72,12% | −37,02% | 66,134% | 5,88% | 0,285 | −0,169 | 684 | 4.915 |
| PAC | 360 | VA Puro | 168,74% | 124,67% | 301.355 | 792 | 302.146 | 71.472 | 667,32% | −52,70% | 93,318% | 179,74% | 0,299 | −0,739 | 97.514 | 541.261 |
| PAC | 300 | VA Puro | 125,59% | 95,17% | 207.898 | 49 | 207.947 | 47.634 | 525,92% | −56,52% | 91,696% | 131,02% | 0,316 | −0,659 | 64.036 | 388.099 |
| PAC | 240 | VA Puro | 90,42% | 71,97% | 138.612 | −97 | 138.515 | 33.189 | 436,63% | −51,56% | 89,564% | 92,38% | 0,346 | −0,550 | 39.467 | 229.668 |
| PAC | 180 | VA Puro | 61,46% | 52,87% | 87.246 | −96 | 87.150 | 20.654 | 284,55% | −49,16% | 86,643% | 61,57% | 0,352 | −0,465 | 22.265 | 119.831 |
| PAC | 120 | VA Puro | 37,49% | 37,13% | 49.164 | −12 | 49.152 | 12.281 | 198,48% | −50,86% | 82,335% | 36,42% | 0,361 | −0,363 | 10.476 | 65.060 |
| PAC | 60 | VA Puro | 17,31% | 22,97% | 20.931 | 8 | 20.939 | 4.753 | 137,48% | −43,28% | 74,527% | 16,41% | 0,329 | −0,263 | 3.153 | 18.903 |
| PAC | 36 | VA Puro | 9,98% | 16,88% | 11.801 | −2 | 11.799 | 2.895 | 88,08% | −39,09% | 69,438% | 9,21% | 0,301 | −0,238 | 1.341 | 8.574 |
| PAC | 24 | VA Puro | 6,48% | 13,36% | 7.630 | −2 | 7.628 | 1.930 | 69,11% | −37,02% | 66,219% | 5,94% | 0,264 | −0,211 | 683 | 4.915 |
Fig. 79 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging (incremento target 0,50%, senza massimale, filtro anti-Hayley assente) di tutti i PAC di varie durate su serie storiche simulate con tecniche parametriche: distribuzione normale con media mensile dello 0,50% e deviazione standard del 5%
Come sempre, la rata mensile iniziale è di 300 euro. Non è previsto alcun massimale, non ci sono commissioni, l’incremento del target è dello 0,50% e il filtro anti-Hayley è assente.
Laddove non specificato diversamente, commentiamo i risultati dei piani di accumulo trentennali:
- Rendimento totale: il Value Averaging No-Sell si colloca nettamente al primo posto, in ogni durata. Anche la somma finale generata è la più alta. La cosa interessante è che la deviazione standard è più bassa di quella del Cost Averaging: di nuovo, il trade-off rendimento/rischio sembra venir meno in questa tipologia di PAC. Il Value Averaging puro rende meno degli altri, ma la sua volatilità è decisamente minore.
- Rata max: poco sopra ai 60.000 euro nel Value Averaging No-sell e ai 70.000 nel Value Averaging puro. Sono i valori di massimo assoluto, quasi triplicati rispetto alle stesse simulazioni con il filtro anti-Hayley attivato.
- Rendimento max e min: i valori massimi sono raddoppiati sia nel Value Averaging No-sell che in quello puro. La cosa davvero interessante è che quelli minimi sono aumentati, passando dal –78% al –53%. Un miglioramento eccezionale. Per completezza, è giusto osservare che questa serie di 100.000 simulazioni ha generato un incremento del 20% circa nel rendimento massimo anche nel Cost Averaging. Il rendimento minimo di quest’ultimo, invece, è migliorato di poco più del 5%, dal –78,92% al –73,30%.
- % Positivi: nessuna variazione di rilievo rispetto alle simulazioni col filtro anti-Hayley attivato.
- Mediana: in linea con i rendimenti, anche la mediana del Value Averaging è adesso molto più alta. In particolare, quella del Value Averaging puro è superiore al rendimento medio di oltre il 10%. Più o meno invariata quella del Cost Averaging.
- Skewness: invariata e positiva nel Cost Averaging e nel Value Averaging No-sell; un po’ cresciuta nel Value Averaging puro, che si conferma quello con la minor variabilità nei rendimenti. Al solito, vediamo i 3 istogrammi delle distribuzioni delle frequenze dei rendimenti dei 100.000 PAC trentennali Cost Averaging, Value Averaging No-Sell e Value Averaging puri:
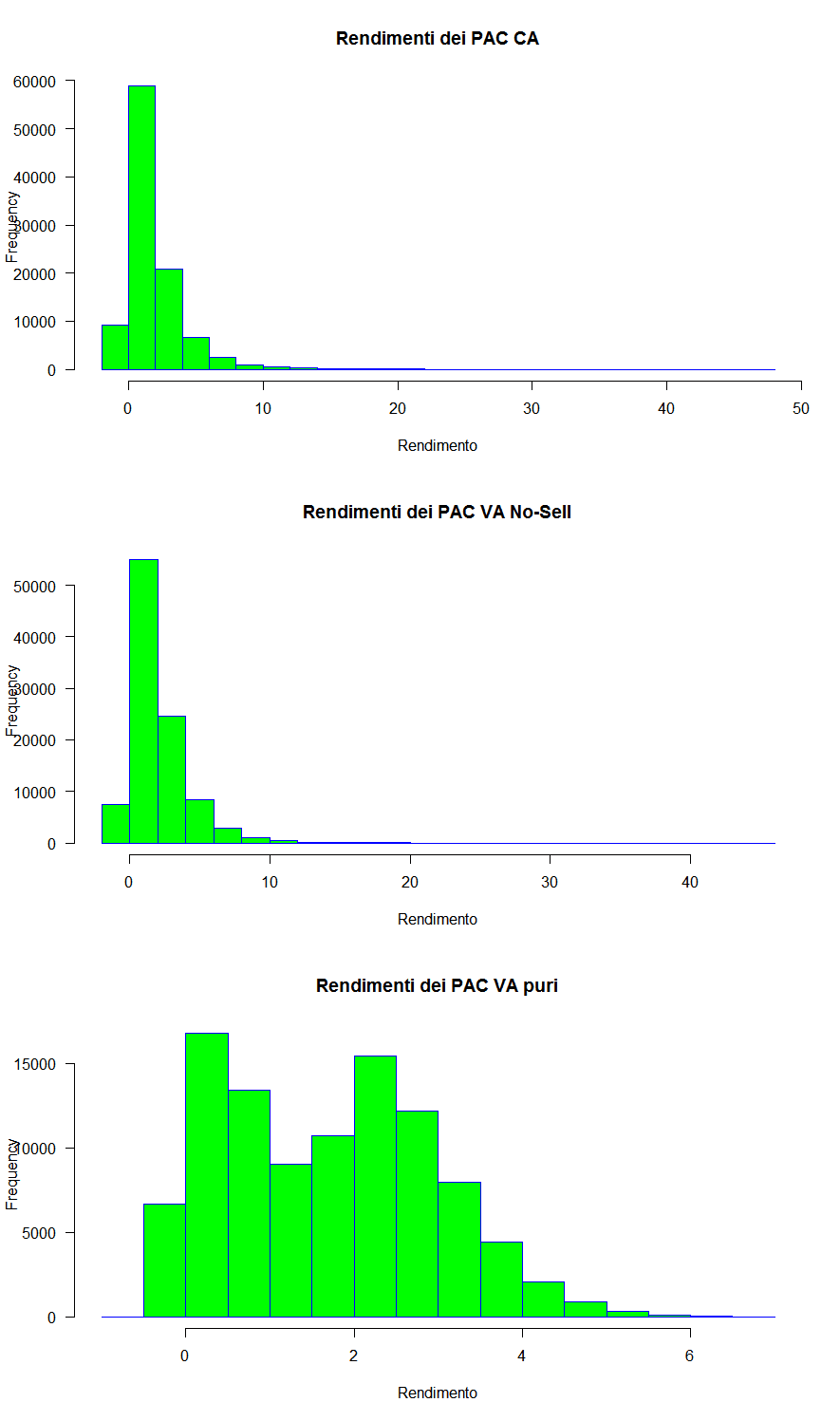
Fig. 80 – Istogrammi delle frequenze dei rendimenti dei 100.000 PAC Cost Averaging, Value Averaging No-sell e Value Averaging puri trentennali simulati con tecniche parametriche: media 0,50%, deviazione standard 5% (incremento target 0,50%, senza massimale, filtro anti-Hayley assente)
- Kurtosis (curtosi): cresciuta nel Cost Averaging, diminuita nel Value Averaging No-Sell e ancora negativa nel Value Averaging puro.
La tabella contiene due colonne che prima non erano presenti: servono a misurare l’extra-liquidità media e massima dei 100.000 PAC simulati.
In entrambe le tipologie di Value Averaging trentennale, l’extra-liquidità mediamente richiesta è di circa 98.000 euro e quella massima di 550.000 euro: il primo valore è in linea con quello ottenuto nei backtest del nostro fondo; il secondo, è di oltre 5 volte superiore.
Non ci dobbiamo sorprendere: le 100.000 simulazioni includono anche serie storiche estreme, molto improbabili nella realtà. Basta un solo outlier, ovvero una serie storica molto lontana dai valori medi, per generare un’extra-liquidità parimenti lontana dal valore medio (si tratta del valore massimo in assoluto, non una media dei valori massimi dei 100.000 PAC simulati).
Portando la percentuale di incremento del target all’1%, l’extra-liquidità prende letteralmente il volo: 599.716 euro la media, 2.253.758 euro la massima nel Value Averaging No-Sell, con valori molto simili nel Value Averaging puro.
L’1% senza massimale può andare bene soltanto per piani di accumulo Value Averaging di durate fino a 15-20 anni, come vedremo in seguito.
Vediamo i cambiamenti prodotti dall’introduzione del massimale di 1000 euro. Ripartiamo testando l’incremento del target dello 0,50%:
| Incremento 0,5% - Massimale 1.000 euro - Media 0,50%, Deviazione standard 5% - 100.000 simulazioni | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. tot. | Stand. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. | Ex.Liq. Med. | Ex.liq. Max |
| PAC | 360 | CA | 179,14% | 211,95% | 301.466 | 0 | 301.466 | 300 | 4.333,21% | −75,89% | 90,678% | 120,76% | 3,035 | 18,053 | n/a | n/a |
| PAC | 300 | CA | 130,10% | 150,69% | 207.087 | 0 | 207.087 | 300 | 3.309,23% | −72,48% | 88,444% | 91,13% | 2,686 | 15,951 | n/a | n/a |
| PAC | 240 | CA | 92,48% | 107,22% | 138.583 | 0 | 138.583 | 300 | 2.054,56% | −77,38% | 86,047% | 66,51% | 2,240 | 10,609 | n/a | n/a |
| PAC | 180 | CA | 61,70% | 73,57% | 87.321 | 0 | 87.321 | 300 | 1.257,37% | −73,89% | 82,370% | 45,91% | 1,750 | 6,323 | n/a | n/a |
| PAC | 120 | CA | 36,54% | 47,82% | 49.155 | 0 | 49.155 | 300 | 436,40% | −65,34% | 77,536% | 27,92% | 1,258 | 2,799 | n/a | n/a |
| PAC | 60 | CA | 16,39% | 27,01% | 20.950 | 0 | 20.950 | 300 | 212,93% | −52,23% | 70,585% | 12,98% | 0,827 | 1,232 | n/a | n/a |
| PAC | 36 | CA | 9,19% | 19,12% | 11.792 | 0 | 11.792 | 300 | 163,03% | −51,24% | 66,101% | 7,35% | 0,630 | 0,791 | n/a | n/a |
| PAC | 24 | CA | 6,01% | 14,78% | 7.633 | 0 | 7.633 | 300 | 89,02% | −41,30% | 63,514% | 4,88% | 0,481 | 0,436 | n/a | n/a |
| PAC | 360 | VA No-Sell | 185,20% | 195,29% | 356.423 | −27.792 | 328.631 | 1.000 | 3.372,02% | −69,97% | 91,703% | 134,65% | 2,294 | 10,675 | 48.167 | 198.114 |
| PAC | 300 | VA No-Sell | 135,08% | 137,24% | 241.105 | −19.498 | 221.608 | 1.000 | 2.726,17% | −68,73% | 90,052% | 103,48% | 1,971 | 8,995 | 36.080 | 153.585 |
| PAC | 240 | VA No-Sell | 95,96% | 95,57% | 157.349 | −12.215 | 145.134 | 1.000 | 1.422,72% | −70,26% | 88,287% | 76,89% | 1,559 | 5,205 | 25.171 | 117.954 |
| PAC | 180 | VA No-Sell | 64,48% | 64,83% | 96.644 | −6.810 | 89.834 | 1.000 | 906,43% | −68,09% | 85,326% | 54,01% | 1,118 | 2,468 | 16.055 | 84.422 |
| PAC | 120 | VA No-Sell | 38,50% | 41,94% | 52.729 | −2.944 | 49.786 | 1.000 | 353,88% | −60,42% | 81,162% | 33,39% | 0,772 | 0,849 | 8.510 | 44.198 |
| PAC | 60 | VA No-Sell | 17,54% | 23,87% | 21.651 | −642 | 21.010 | 1.000 | 163,06% | −45,06% | 74,199% | 15,71% | 0,466 | 0,070 | 2.900 | 17.714 |
| PAC | 36 | VA No-Sell | 9,98% | 17,16% | 12.003 | −203 | 11.801 | 1.000 | 109,20% | −42,30% | 69,240% | 8,99% | 0,360 | −0,072 | 1.312 | 9.126 |
| PAC | 24 | VA No-Sell | 6,57% | 13,45% | 7.692 | −58 | 7.634 | 1.000 | 69,26% | −35,24% | 66,212% | 5,95% | 0,286 | −0,147 | 679 | 4.291 |
| PAC | 360 | VA Puro | 150,41% | 112,26% | 240.053 | 35.034 | 275.087 | 1.000 | 671,34% | −69,25% | 92,480% | 145,27% | 0,413 | −0,396 | 39.587 | 197.735 |
| PAC | 300 | VA Puro | 114,68% | 88,10% | 174.088 | 21.066 | 195.154 | 1.000 | 602,49% | −68,66% | 90,952% | 111,54% | 0,379 | −0,407 | 30.442 | 152.767 |
| PAC | 240 | VA Puro | 84,70% | 68,09% | 121.678 | 11.811 | 133.489 | 1.000 | 394,10% | −69,70% | 89,154% | 82,43% | 0,365 | −0,376 | 21.857 | 116.930 |
| PAC | 180 | VA Puro | 58,99% | 51,51% | 80.000 | 5.665 | 85.664 | 1.000 | 307,32% | −67,94% | 86,162% | 57,37% | 0,343 | −0,371 | 14.437 | 84.203 |
| PAC | 120 | VA Puro | 36,50% | 36,84% | 46.902 | 1.908 | 48.810 | 1.000 | 202,11% | −60,32% | 81,836% | 35,15% | 0,341 | −0,323 | 7.967 | 43.872 |
| PAC | 60 | VA Puro | 17,19% | 22,90% | 20.660 | 273 | 20.933 | 1.000 | 120,98% | −45,05% | 74,550% | 16,24% | 0,320 | −0,257 | 2.836 | 17.711 |
| PAC | 36 | VA Puro | 9,90% | 16,90% | 11.763 | 28 | 11.791 | 1.000 | 99,49% | −42,27% | 69,448% | 9,17% | 0,302 | −0,198 | 1.303 | 9.117 |
| PAC | 24 | VA Puro | 6,55% | 13,38% | 7.626 | 7 | 7.633 | 1.000 | 65,71% | −35,24% | 66,306% | 6,00% | 0,263 | −0,194 | 677 | 4.291 |
Fig. 81 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging (incremento target 0,50%, massimale 1000 euro, filtro anti-Hayley assente) di tutti i PAC di varie durate su serie storiche simulate con tecniche parametriche: distribuzione normale con media mensile dello 0,50% e deviazione standard del 5%
L’extra-liquidità scende notevolmente, attestandosi su 48/198 mila euro contro i 98/550 mila precedenti: sono valori ragionevoli.
Il massimale produce un’ulteriore benefica conseguenza: la diminuzione della volatilità dei rendimenti. Come avevamo visto in precedenza, il massimale ha anche dei risvolti negativi, come la diminuzione del rendimento (consistente nel Value Averaging puro) e un leggero peggioramento della percentuale di PAC positivi.
I vantaggi del Value Averaging sono confermati dalle simulazioni parametriche con media nulla, i cui risultati sono i seguenti:
| Incremento 0,5% - Massimale 1.000 euro - Media 0%, Deviazione standard 5% - 100.000 simulazioni | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. tot. | Stand. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. | Ex.Liq. Med. | Ex.liq. Max |
| PAC | 360 | CA | 0,00% | 61,21% | 108.000 | 0 | 108.000 | 300 | 1.068,60% | −84,94% | 37,284% | −15,65% | 2,613 | 13,495 | n/a | n/a |
| PAC | 300 | CA | 0,01% | 55,32% | 90.006 | 0 | 90.006 | 300 | 843,30% | −84,58% | 38,146% | −13,62% | 2,371 | 11,307 | n/a | n/a |
| PAC | 240 | CA | 0,22% | 48,06% | 72.160 | 0 | 72.160 | 300 | 600,27% | −80,72% | 39,824% | −10,64% | 1,933 | 7,411 | n/a | n/a |
| PAC | 180 | CA | 0,34% | 41,13% | 54.186 | 0 | 54.186 | 300 | 495,89% | −80,93% | 41,390% | −8,04% | 1,654 | 5,578 | n/a | n/a |
| PAC | 120 | CA | −0,06% | 32,56% | 35.979 | 0 | 35.979 | 300 | 306,48% | −67,88% | 42,697% | −5,64% | 1,233 | 2,850 | n/a | n/a |
| PAC | 60 | CA | 0,16% | 22,50% | 18.028 | 0 | 18.028 | 300 | 164,38% | −54,87% | 45,207% | −2,56% | 0,810 | 1,228 | n/a | n/a |
| PAC | 36 | CA | 0,02% | 17,11% | 10.802 | 0 | 10.802 | 300 | 102,98% | −49,13% | 46,125% | −1,65% | 0,607 | 0,634 | n/a | n/a |
| PAC | 24 | CA | 0,01% | 13,78% | 7.201 | 0 | 7.201 | 300 | 81,90% | −41,27% | 47,037% | −1,04% | 0,463 | 0,394 | n/a | n/a |
| PAC | 360 | VA No-Sell | 10,12% | 68,84% | 220.052 | −112.065 | 107.987 | 1.000 | 1.018,73% | −81,96% | 42,891% | −8,34% | 2,764 | 13,132 | 114.815 | 214.067 |
| PAC | 300 | VA No-Sell | 9,85% | 60,91% | 170.361 | −80.392 | 89.969 | 1.000 | 977,09% | −80,87% | 44,168% | −6,25% | 2,413 | 10,343 | 83.515 | 174.718 |
| PAC | 240 | VA No-Sell | 9,19% | 51,22% | 124.799 | −52.465 | 72.334 | 1.000 | 651,81% | −76,48% | 46,210% | −3,68% | 1,874 | 5,796 | 55.779 | 132.934 |
| PAC | 180 | VA No-Sell | 7,83% | 42,08% | 84.132 | −29.876 | 54.256 | 1.000 | 431,66% | −76,62% | 47,705% | −2,05% | 1,526 | 3,819 | 33.027 | 91.232 |
| PAC | 120 | VA No-Sell | 5,36% | 31,87% | 49.396 | −13.411 | 35.984 | 1.000 | 236,38% | −61,33% | 48,410% | −1,12% | 1,099 | 1,658 | 15.927 | 50.892 |
| PAC | 60 | VA No-Sell | 2,95% | 21,09% | 21.290 | −3.256 | 18.033 | 1.000 | 120,93% | −46,88% | 49,866% | −0,06% | 0,673 | 0,364 | 4.634 | 20.242 |
| PAC | 36 | VA No-Sell | 1,67% | 15,89% | 11.938 | −1.134 | 10.804 | 1.000 | 83,19% | −43,61% | 49,751% | −0,11% | 0,500 | 0,038 | 1.907 | 8.299 |
| PAC | 24 | VA No-Sell | 1,07% | 12,82% | 7.677 | −475 | 7.201 | 1.000 | 61,45% | −35,17% | 49,950% | −0,01% | 0,380 | −0,082 | 936 | 4.569 |
| PAC | 360 | VA Puro | 14,03% | 67,34% | 194.171 | −86.103 | 108.068 | 1.000 | 473,56% | −81,58% | 45,042% | −5,90% | 1,730 | 3,332 | 101.541 | 213.628 |
| PAC | 300 | VA Puro | 12,45% | 58,17% | 150.751 | −60.812 | 89.939 | 1.000 | 386,07% | −80,69% | 46,145% | −4,22% | 1,481 | 2,304 | 74.369 | 173.837 |
| PAC | 240 | VA Puro | 10,76% | 48,72% | 111.414 | −39.113 | 72.301 | 1.000 | 317,37% | −76,38% | 47,981% | −2,02% | 1,216 | 1,392 | 50.268 | 130.917 |
| PAC | 180 | VA Puro | 8,52% | 39,83% | 76.358 | −22.123 | 54.235 | 1.000 | 239,49% | −76,39% | 48,988% | −0,93% | 1,012 | 0,854 | 30.342 | 91.220 |
| PAC | 120 | VA Puro | 5,55% | 30,57% | 46.010 | −10.023 | 35.987 | 1.000 | 165,34% | −61,09% | 49,399% | −0,45% | 0,808 | 0,391 | 15.052 | 50.783 |
| PAC | 60 | VA Puro | 2,94% | 20,68% | 20.586 | −2.553 | 18.033 | 1.000 | 100,05% | −46,84% | 50,236% | 0,13% | 0,566 | 0,026 | 4.542 | 20.240 |
| PAC | 36 | VA Puro | 1,66% | 15,77% | 11.754 | −950 | 10.804 | 1.000 | 75,64% | −43,61% | 49,926% | −0,03% | 0,457 | −0,072 | 1.895 | 8.299 |
| PAC | 24 | VA Puro | 1,07% | 12,78% | 7.624 | −423 | 7.201 | 1.000 | 59,15% | −35,17% | 50,053% | 0,02% | 0,363 | −0,125 | 934 | 4.569 |
Fig. 82 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging (incremento target 0,50%, massimale 1000 euro, filtro anti-Hayley assente) di tutti i PAC di varie durate su serie storiche simulate con tecniche parametriche: distribuzione normale con media mensile dello 0% e deviazione standard del 5%
Le somme finali del Value Averaging e del Cost Averaging sono molto simili.
La deviazione standard del Value Averaging è minore su durate inferiori o uguali a 10-15 anni. La minore rischiosità del Value Averaging è però evidenziata da:
- Rendimenti minimi intorno al −82%, contro il −85% del Cost Averaging.
- Percentuale di PAC positivi del 43-45%, contro il 37% del Cost Averaging.
Verifichiamo le performance in caso di incremento del target dell’1%:
| Incremento 1% - Massimale 1.000 euro - Media 0,50%, Deviazione standard 5% - 100.000 simulazioni | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. tot. | Stand. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. | Ex.Liq. Med. | Ex.liq. Max |
| PAC | 360 | CA | 179,45% | 214,63% | 301.802 | 0 | 301.802 | 300 | 6.238,93% | −75,60% | 90,740% | 120,20% | 3,408 | 27,647 | n/a | n/a |
| PAC | 300 | CA | 131,47% | 152,73% | 208.327 | 0 | 208.327 | 300 | 3.217,67% | −73,72% | 88,691% | 91,76% | 2,737 | 15,939 | n/a | n/a |
| PAC | 240 | CA | 92,74% | 107,27% | 138.771 | 0 | 138.771 | 300 | 1.537,50% | −72,54% | 86,087% | 67,11% | 2,172 | 8,888 | n/a | n/a |
| PAC | 180 | CA | 61,34% | 73,25% | 87.123 | 0 | 87.123 | 300 | 1.164,78% | −67,12% | 82,257% | 45,87% | 1,761 | 6,521 | n/a | n/a |
| PAC | 120 | CA | 36,35% | 47,82% | 49.085 | 0 | 49.085 | 300 | 535,39% | −67,36% | 77,556% | 27,73% | 1,293 | 3,075 | n/a | n/a |
| PAC | 60 | CA | 16,19% | 26,90% | 20.915 | 0 | 20.915 | 300 | 214,19% | −58,44% | 70,336% | 12,75% | 0,820 | 1,236 | n/a | n/a |
| PAC | 36 | CA | 9,31% | 19,07% | 11.805 | 0 | 11.805 | 300 | 157,72% | −46,80% | 66,442% | 7,42% | 0,606 | 0,693 | n/a | n/a |
| PAC | 24 | CA | 5,97% | 14,75% | 7.630 | 0 | 7.630 | 300 | 91,54% | −41,46% | 63,447% | 4,85% | 0,459 | 0,359 | n/a | n/a |
| PAC | 360 | VA No-Sell | 172,19% | 244,45% | 575.502 | −132.981 | 442.521 | 1.000 | 5.813,75% | −72,67% | 90,233% | 102,29% | 4,016 | 28,669 | 135.177 | 220.568 |
| PAC | 300 | VA No-Sell | 130,41% | 171,53% | 379.204 | −96.483 | 282.721 | 1.000 | 2.859,41% | −71,36% | 88,459% | 80,07% | 2,968 | 14,439 | 99.123 | 178.819 |
| PAC | 240 | VA No-Sell | 95,89% | 119,04% | 237.357 | −63.678 | 173.679 | 1.000 | 1.611,15% | −68,54% | 86,416% | 61,10% | 2,232 | 7,632 | 66.756 | 141.697 |
| PAC | 180 | VA No-Sell | 66,07% | 78,79% | 136.470 | −36.135 | 100.335 | 1.000 | 819,69% | −61,74% | 83,578% | 44,98% | 1,635 | 3,995 | 39.226 | 95.662 |
| PAC | 120 | VA No-Sell | 40,58% | 48,79% | 68.213 | −15.694 | 52.520 | 1.000 | 428,89% | −61,47% | 80,122% | 29,67% | 1,108 | 1,495 | 18.317 | 59.779 |
| PAC | 60 | VA No-Sell | 18,53% | 25,77% | 24.909 | −3.631 | 21.278 | 1.000 | 178,96% | −53,31% | 73,629% | 14,77% | 0,624 | 0,197 | 5.067 | 21.585 |
| PAC | 36 | VA No-Sell | 10,68% | 17,90% | 13.083 | −1.209 | 11.874 | 1.000 | 112,03% | −40,65% | 69,406% | 8,79% | 0,441 | −0,064 | 2.013 | 9.131 |
| PAC | 24 | VA No-Sell | 6,86% | 13,80% | 8.146 | −498 | 7.648 | 1.000 | 71,34% | −34,93% | 66,085% | 5,81% | 0,334 | −0,170 | 973 | 5.149 |
| PAC | 360 | VA Puro | 184,08% | 228,36% | 493.810 | −93.488 | 400.322 | 1.000 | 1.640,32% | −72,37% | 90,519% | 106,00% | 2,049 | 4,418 | 119.157 | 220.559 |
| PAC | 300 | VA Puro | 138,54% | 160,81% | 327.797 | −67.340 | 260.457 | 1.000 | 1.103,43% | −71,31% | 88,825% | 84,05% | 1,624 | 2,421 | 87.663 | 178.677 |
| PAC | 240 | VA Puro | 100,52% | 110,85% | 207.276 | −44.011 | 163.265 | 1.000 | 671,88% | −68,51% | 86,894% | 64,84% | 1,257 | 1,084 | 59.654 | 140.523 |
| PAC | 180 | VA Puro | 68,12% | 73,42% | 121.621 | −25.091 | 96.530 | 1.000 | 447,89% | −61,54% | 84,077% | 48,21% | 0,946 | 0,324 | 35.744 | 95.171 |
| PAC | 120 | VA Puro | 41,04% | 45,91% | 62.729 | −11.121 | 51.607 | 1.000 | 275,04% | −61,40% | 80,646% | 31,47% | 0,700 | −0,064 | 17.222 | 59.755 |
| PAC | 60 | VA Puro | 18,54% | 25,06% | 23.969 | −2.762 | 21.207 | 1.000 | 134,23% | −53,05% | 73,941% | 15,27% | 0,474 | −0,214 | 4.960 | 21.585 |
| PAC | 36 | VA Puro | 10,67% | 17,69% | 12.856 | −991 | 11.865 | 1.000 | 103,01% | −40,62% | 69,563% | 8,94% | 0,381 | −0,205 | 2.000 | 9.103 |
| PAC | 24 | VA Puro | 6,86% | 13,75% | 8.085 | −438 | 7.647 | 1.000 | 67,80% | −34,93% | 66,159% | 5,87% | 0,312 | −0,215 | 972 | 5.149 |
Fig. 83 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging (incremento target 1%, massimale 1000 euro, filtro anti-Hayley assente) di tutti i PAC di varie durate su serie storiche simulate con tecniche parametriche: distribuzione normale con media mensile dello 0,50% e deviazione standard del 5%
Il massimale limita ottimamente l'extra-liquidità. Nei piani di accumulo più lunghi siamo intorno ai 135/220 mila euro (media/max) nel Value Averaging No-Sell e ai 120/220 mila in quello puro.
I rendimenti medi del No-Sell diminuiscono (dal 185% al 172%) mentre quelli del Value Averaging puro tornano a crescere (dal 150% al 184%). La deviazione standard aumenta in entrambi i casi.
Altri dati interessanti sono il rendimento minimo, giunto al −72% (contro il −75% del Cost Averaging), e la percentuale di positivi, che si attesta intorno al 90% per tutte le tipologie di PAC.
Concludendo, a chi desidera investire in un piano di accumulo di lunga durata non si consiglia un incremento dell’1%. La soluzione migliore sembra essere lo 0,50% con un massimale di 1.000 euro, da utilizzarsi su piani di accumulo di durata maggiore o uguale a 15 anni.
Anche un incremento dello 0,75% potrebbe essere utilizzato da chi avesse una buona disponibilità liquida. Per motivi di spazio non riportiamo le tabelle delle simulazioni col metodo Monte Carlo.
Ovviamente, i risultati si posizionano a un livello intermedio dei precedenti. Si raccomanda anche in questo caso di utilizzare un massimale di 1.000 euro.
Un investitore potrebbe avere un orizzonte temporale più breve. Seppure restio all’idea di un PIC, l'opzione di costruire un PAC di 15, 20 o più anni potrebbe non essere gradita. Avendo il capitale già disponibile, lasciarlo inoperoso per molti anni è un’opzione poco allettante.
La soluzione sarebbe quindi un piano di accumulo Value Averaging di breve durata – compreso tra i 2 e i 10 anni – con fondo di liquidità iniziale. Si dovrebbe allora seguire una delle seguenti due strade:
- Aumentare l’importo della rata iniziale, continuando a utilizzare una percentuale di incremento del target non superiore all’1%.
- Aumentare la percentuale di incremento del target, lasciando invariata la rata iniziale.
11.1 Aumento dell’importo della rata iniziale/incremento target
In caso di aumento della rata iniziale, i calcoli in merito alla liquidità richiesta sono facili: la seconda varia in modo direttamente proporzionale alla prima.
Ad esempio, se per un Value Averaging quinquennale di 300 euro iniziali l’extra-liquidità mediamente richiesta fosse di 5.000 euro, con picco massimo di 20.000 euro, disponendo di 100.000 euro di liquidità ci si potrebbe spingere fino 5 volte l’importo della rata iniziale.
Prendiamo i dati dei nostri backtest sul fondo Raiffeisen.
Nella tabella seguente viene riportata l’extra-liquidità richiesta per i PAC Value Averaging No-Sell con rata di 300 e 1.500 euro (nel secondo piano di accumulo la rata iniziale è, appunto, 5 volte più grande di quella del primo):
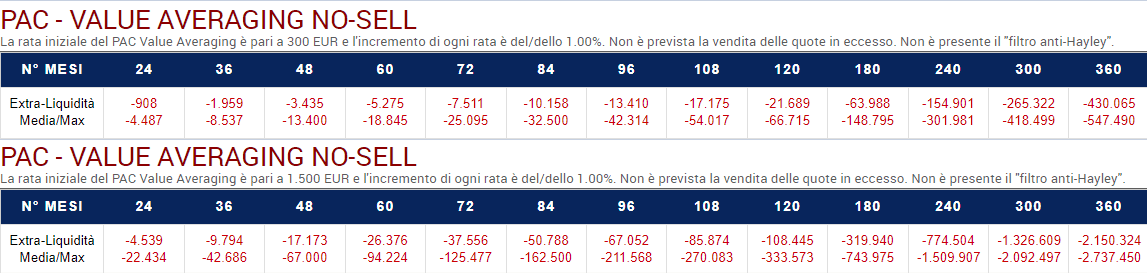
Fig. 84 – Tabella extra-liquidita Value Averaging No-Sell Raiffeisen (incremento target 1%, senza massimale, filtro anti-Hayley: assente)
Salvo piccole approssimazioni, i valori dell’extra-liquidità nel secondo backtest sono esattamente il quintuplo di quelli del primo.
Aumentando la rata, si dovrà verificare, in primo luogo, se il piano di accumulo sia ancora sostenibile:
- Se i 300 euro mensili iniziali diventano 1.500, o si dispone di questo flusso monetario mensilmente, oppure si dovranno prendere i 1.200 euro in eccesso dai 100.000 del fondo iniziale di liquidità.
- Se si sottraggono 1.200 euro al mese dalla liquidità iniziale ci si priva, ogni anno, di 12 x 1.200 = 14.400 euro. In 5 anni, la somma ammonta a 72.000 euro (14.400 x 5). L’extra-liquidità residua scenderebbe quindi a soli 28.000 euro e riuscirebbe a far fronte – basandosi sui valori massimi della seconda tabella soprastante (rata 1.500 euro) – soltanto ai piani di accumulo di 24 rate (dove l’extra-liquidità massima è stata di 22.434 euro).
Sappiamo che il Value Averaging non prevede rate del medesimo importo, ma possiamo considerare il calcolo precedente come un’approssimazione che terrà conto dei seguenti fattori: rate che non verranno versate (VA No-Sell), vendite di quote (VA puro) e versamenti sempre più ingenti, avendo fissato un incremento dell’1% del target.
Saremmo quindi di nuovo di fronte a un bivio:
- Scorciare il piano di accumulo.
- Lasciare invariata la durata del piano di accumulo, sapendo che molto probabilmente ci si troverà senza riserve prima della fine dell’investimento, dato che i backtest ci dicono che i PAC quinquennali con rata iniziale di 1.500 euro necessitano, in media, di una extra-liquidità di 26.376 euro.
Se si opta per la seconda ipotesi, non c’è altro da fare. Si investe, si spera che l’extra-liquidità sia sufficiente o che, magari, si possa contare su altre fonti di liquidità durante la vita del piano di accumulo.
In caso contrario, il PAC avrà vita più breve del previsto: non è necessariamente una conseguenza negativa, dato che l’obiettivo di investire tutta la liquidità disponibile sarebbe stato raggiunto.
Se si opta per la prima ipotesi, invece, si devono rifare i calcoli: un PAC biennale con rata iniziale di 1.500 euro non priva più di 72.000 euro (60 rate di 1.200 euro ciascuna), ma di soli 28.800 euro (24 rate di 1.200 euro). La liquidità residua diventa quindi 100.000 − 28.800 = 71.200 euro che, in base alle tabelle precedenti, permette di far fronte alla massima extra-liquidità richiesta dai piani di accumulo di 48 rate (4 anni).
Se le rate sono 48, tuttavia, dovrebbero essere utilizzati 48 x 1.200 = 57.600 euro del capitale disponibile, abbassando il valore del fondo di liquidità iniziale a 42.400 euro. Con questa somma, il PAC adatto diventerebbe allora quello da 36 rate, che utilizzerebbe 36 x 1.200 = 43.200 euro, portando la liquidità iniziale a 56.800 euro.
Questo processo di aggiustamento si deve ripetere fin quando le cifre convergono verso un’unica durata o verso due durate che rimandano una all’altra. Nel nostro esempio, il processo converge verso i piani di accumulo di 36 e 48 rate: sceglieremo i primi se preferiremo non terminare la liquidità nel tempo previsto; i secondi, se quest’ultima ipotesi non è un problema.
I PAC a 48 rate forse sono la scelta più sensata, visto che nel processo di aggiustamento abbiamo utilizzato i valori di extra-liquidità massima e ci sono delle buone probabilità che non tutta l’extra-liquidità venga utilizzata prima del termine previsto dall’investimento. La scelta è comunque soggettiva.
Il nostro obiettivo è la creazione di una tabella dove, in funzione della somma disponibile e dell’orizzonte temporale dell’investitore, venga suggerito l’importo della rata iniziale del piano di accumulo che permetta il completo utilizzo della liquidità iniziale.
Abbiamo effettuato 1.000.000 di simulazioni Monte Carlo sui PAC dalle durate comprese tra 2 e 10 anni, senza massimale e con incremento del target dell’1% (rata iniziale di 300 euro), sia con media positiva (0,5% su base mensile) che nulla (per un totale, quindi, di 2 milioni di simulazioni).
I risultati sono stati i seguenti:
| Incremento 1% - No massimale - Media 0,50%, Deviazione standard 5% - 1.000.000 simulazioni | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Rend. tot. | Stand. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. | Ex.liq. Med. | Ex.liq. Max |
| PAC | 120 | 36,57% | 47,84% | 49.167 | 0 | 49.167 | 300 | 648,83% | −69,39% | 77,675% | 27,98% | 1,297 | 3,181 | n/a | n/a |
| PAC | 108 | 32,18% | 43,38% | 42.825 | 0 | 42.825 | 300 | 534,63% | −64,95% | 76,505% | 24,78% | 1,204 | 2,725 | n/a | n/a |
| PAC | 96 | 28,00% | 39,10% | 36.863 | 0 | 36.863 | 300 | 464,33% | −63,99% | 75,234% | 21,70% | 1,117 | 2,377 | n/a | n/a |
| PAC | 84 | 23,83% | 34,93% | 31.204 | 0 | 31.204 | 300 | 358,31% | −61,27% | 73,740% | 18,55% | 1,029 | 1,989 | n/a | n/a |
| PAC | 72 | 20,01% | 30,97% | 25.923 | 0 | 25.923 | 300 | 291,86% | −59,35% | 72,254% | 15,68% | 0,933 | 1,633 | n/a | n/a |
| PAC | 60 | 16,29% | 27,02% | 20.933 | 0 | 20.933 | 300 | 278,45% | −56,82% | 70,511% | 12,87% | 0,831 | 1,290 | n/a | n/a |
| PAC | 48 | 12,66% | 23,07% | 16.223 | 0 | 16.223 | 300 | 199,76% | −55,12% | 68,505% | 10,05% | 0,726 | 0,983 | n/a | n/a |
| PAC | 36 | 9,27% | 19,09% | 11.801 | 0 | 11.801 | 300 | 137,99% | −51,27% | 66,143% | 7,38% | 0,609 | 0,658 | n/a | n/a |
| PAC | 24 | 5,95% | 14,76% | 7.629 | 0 | 7.629 | 300 | 103,12% | −45,02% | 63,330% | 4,82% | 0,475 | 0,402 | n/a | n/a |
| PAC | 120 | 41,37% | 49,05% | 75.067 | −21.580 | 53.487 | 17.134 | 564,51% | −51,89% | 80,860% | 29,64% | 1,205 | 1,798 | 24.812 | 107.446 |
| PAC | 108 | 36,59% | 43,86% | 62.416 | −16.627 | 45.789 | 16.161 | 462,16% | −49,26% | 79,822% | 26,73% | 1,093 | 1,402 | 19.524 | 82.726 |
| PAC | 96 | 31,99% | 38,95% | 51.306 | −12.474 | 38.832 | 11.456 | 387,00% | −49,92% | 78,650% | 23,85% | 0,979 | 1,042 | 15.040 | 67.072 |
| PAC | 84 | 27,36% | 34,35% | 41.540 | −9.091 | 32.448 | 9.910 | 301,48% | −47,25% | 77,200% | 20,73% | 0,878 | 0,746 | 11.313 | 49.120 |
| PAC | 72 | 23,02% | 29,99% | 32.965 | −6.312 | 26.652 | 8.886 | 234,08% | −46,73% | 75,705% | 17,77% | 0,764 | 0,452 | 8.184 | 37.368 |
| PAC | 60 | 18,77% | 25,83% | 25.456 | −4.130 | 21.326 | 5.935 | 197,08% | −45,27% | 73,916% | 14,85% | 0,658 | 0,234 | 5.651 | 26.768 |
| PAC | 48 | 14,60% | 21,81% | 18.884 | −2.476 | 16.408 | 4.491 | 180,13% | −44,03% | 71,804% | 11,76% | 0,557 | 0,071 | 3.641 | 18.418 |
| PAC | 36 | 10,67% | 17,89% | 13.150 | −1.279 | 11.870 | 3.211 | 112,23% | −41,75% | 69,224% | 8,76% | 0,454 | −0,071 | 2.094 | 11.384 |
| PAC | 24 | 6,84% | 13,80% | 8.153 | −507 | 7.646 | 2.143 | 81,66% | −36,81% | 65,967% | 5,77% | 0,349 | −0,145 | 982 | 5.607 |
| PAC | 120 | 42,43% | 46,75% | 69.012 | −16.499 | 52.513 | 17.134 | 307,55% | −51,70% | 81,395% | 31,41% | 0,768 | −0,053 | 24.617 | 106.874 |
| PAC | 108 | 37,30% | 41,86% | 57.868 | −12.735 | 45.133 | 16.161 | 243,09% | −49,19% | 80,320% | 28,23% | 0,713 | −0,101 | 19.363 | 82.181 |
| PAC | 96 | 32,44% | 37,29% | 47.978 | −9.572 | 38.407 | 11.671 | 229,88% | −49,84% | 79,114% | 25,06% | 0,657 | −0,145 | 14.914 | 66.842 |
| PAC | 84 | 27,61% | 33,01% | 39.202 | −7.013 | 32.189 | 10.153 | 203,73% | −47,11% | 77,624% | 21,67% | 0,612 | −0,165 | 11.221 | 48.916 |
| PAC | 72 | 23,14% | 28,99% | 31.413 | −4.905 | 26.508 | 8.886 | 165,60% | −46,64% | 76,084% | 18,48% | 0,557 | −0,191 | 8.122 | 37.268 |
| PAC | 60 | 18,82% | 25,14% | 24.501 | −3.247 | 21.254 | 6.122 | 158,33% | −45,09% | 74,227% | 15,34% | 0,503 | −0,205 | 5.614 | 26.619 |
| PAC | 48 | 14,61% | 21,38% | 18.367 | −1.989 | 16.378 | 4.603 | 131,50% | −44,02% | 72,037% | 12,06% | 0,452 | −0,203 | 3.622 | 18.410 |
| PAC | 36 | 10,66% | 17,69% | 12.923 | −1.062 | 11.861 | 3.211 | 99,81% | −41,74% | 69,373% | 8,91% | 0,395 | −0,210 | 2.088 | 11.382 |
| PAC | 24 | 6,84% | 13,74% | 8.092 | −447 | 7.645 | 2.167 | 75,75% | −36,81% | 66,034% | 5,82% | 0,326 | −0,195 | 980 | 5.607 |
Fig. 85 - Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging (incremento target 1%, senza massimale, filtro anti-Hayley assente) di tutti i PAC di varie durate (2-10 anni) su serie storiche simulate con tecniche parametriche: distribuzione normale con media mensile dello 0,50% e deviazione standard del 5%
| Incremento 1% - No massimale - Media 0%, Deviazione standard 5% - 1.000.000 simulazioni | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Rend. tot. | Stand. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. | Ex.liq. Med. | Ex.liq. Max |
| PAC | 120 | −0,01% | 32,61% | 35.998 | 0 | 35.998 | 300 | 334,81% | −75,11% | 42,596% | −5,65% | 1,221 | 2,755 | n/a | n/a |
| PAC | 108 | 0,02% | 30,78% | 32.405 | 0 | 32.405 | 300 | 339,08% | −71,28% | 43,017% | −5,04% | 1,155 | 2,524 | n/a | n/a |
| PAC | 96 | −0,01% | 28,91% | 28.797 | 0 | 28.797 | 300 | 298,53% | −69,85% | 43,388% | −4,54% | 1,077 | 2,188 | n/a | n/a |
| PAC | 84 | 0,00% | 26,91% | 25.199 | 0 | 25.199 | 300 | 357,94% | −67,05% | 43,874% | −3,97% | 0,994 | 1,867 | n/a | n/a |
| PAC | 72 | 0,02% | 24,80% | 21.604 | 0 | 21.604 | 300 | 223,58% | −67,67% | 44,293% | −3,40% | 0,907 | 1,526 | n/a | n/a |
| PAC | 60 | 0,00% | 22,48% | 18.000 | 0 | 18.000 | 300 | 183,01% | −62,91% | 44,853% | −2,79% | 0,805 | 1,172 | n/a | n/a |
| PAC | 48 | −0,03% | 19,98% | 14.396 | 0 | 14.396 | 300 | 155,17% | −61,31% | 45,344% | −2,26% | 0,714 | 0,945 | n/a | n/a |
| PAC | 36 | −0,01% | 17,13% | 10.799 | 0 | 10.799 | 300 | 126,55% | −59,52% | 46,111% | −1,63% | 0,601 | 0,672 | n/a | n/a |
| PAC | 24 | 0,01% | 13,79% | 7.200 | 0 | 7.200 | 300 | 96,56% | −47,01% | 47,002% | −1,04% | 0,468 | 0,387 | n/a | n/a |
| PAC | 120 | 6,81% | 32,62% | 72.835 | −36.839 | 35.996 | 17.178 | 397,10% | −57,91% | 49,232% | −0,51% | 1,616 | 4,061 | 38.554 | 127.979 |
| PAC | 108 | 6,25% | 30,66% | 60.816 | −28.402 | 32.414 | 15.297 | 344,35% | −55,44% | 49,382% | −0,39% | 1,485 | 3,365 | 29.993 | 98.804 |
| PAC | 96 | 5,61% | 28,62% | 50.184 | −21.388 | 28.795 | 11.996 | 260,33% | −54,47% | 49,364% | −0,38% | 1,338 | 2,599 | 22.841 | 76.585 |
| PAC | 84 | 4,96% | 26,46% | 40.787 | −15.592 | 25.195 | 10.334 | 274,10% | −52,32% | 49,463% | −0,31% | 1,202 | 2,000 | 16.894 | 57.012 |
| PAC | 72 | 4,31% | 24,21% | 32.502 | −10.897 | 21.605 | 7.982 | 230,45% | −53,07% | 49,544% | −0,25% | 1,060 | 1,442 | 12.040 | 45.329 |
| PAC | 60 | 3,58% | 21,76% | 25.188 | −7.189 | 18.000 | 6.292 | 160,70% | −50,77% | 49,656% | −0,17% | 0,910 | 0,940 | 8.155 | 31.773 |
| PAC | 48 | 2,81% | 19,16% | 18.750 | −4.355 | 14.395 | 4.853 | 130,91% | −48,36% | 49,680% | −0,15% | 0,767 | 0,566 | 5.130 | 21.170 |
| PAC | 36 | 2,06% | 16,29% | 13.096 | −2.297 | 10.799 | 3.628 | 110,07% | −46,80% | 49,877% | −0,05% | 0,616 | 0,253 | 2.866 | 13.491 |
| PAC | 24 | 1,31% | 13,04% | 8.140 | −939 | 7.200 | 2.289 | 74,76% | −38,11% | 49,994% | −0,00% | 0,459 | 0,004 | 1.292 | 5.875 |
| PAC | 120 | 7,98% | 33,56% | 69.012 | −33.014 | 35.997 | 18.963 | 239,46% | −57,69% | 49,958% | −0,03% | 1,431 | 2,417 | 38.115 | 127.095 |
| PAC | 108 | 7,17% | 31,23% | 57.868 | −25.453 | 32.414 | 15.297 | 224,94% | −55,31% | 50,026% | 0,02% | 1,302 | 1,924 | 29.670 | 98.044 |
| PAC | 96 | 6,31% | 28,91% | 47.978 | −19.182 | 28.796 | 11.996 | 192,27% | −54,42% | 49,949% | −0,03% | 1,174 | 1,474 | 22.614 | 76.471 |
| PAC | 84 | 5,46% | 26,56% | 39.202 | −14.006 | 25.196 | 10.593 | 186,03% | −52,17% | 49,971% | −0,02% | 1,054 | 1,105 | 16.742 | 56.759 |
| PAC | 72 | 4,65% | 24,18% | 31.413 | −9.808 | 21.605 | 8.179 | 154,67% | −53,02% | 49,961% | −0,02% | 0,934 | 0,772 | 11.946 | 45.264 |
| PAC | 60 | 3,78% | 21,67% | 24.501 | −6.501 | 17.999 | 6.292 | 127,51% | −50,77% | 49,996% | 0,00% | 0,811 | 0,490 | 8.102 | 31.770 |
| PAC | 48 | 2,91% | 19,06% | 18.367 | −3.972 | 14.395 | 4.853 | 108,71% | −48,29% | 49,931% | −0,03% | 0,695 | 0,280 | 5.106 | 21.116 |
| PAC | 36 | 2,10% | 16,22% | 12.923 | −2.124 | 10.799 | 3.628 | 92,75% | −46,80% | 50,037% | 0,02% | 0,573 | 0,104 | 2.858 | 13.491 |
| PAC | 24 | 1,32% | 13,02% | 8.092 | −892 | 7.201 | 2.289 | 71,23% | −38,11% | 50,064% | 0,02% | 0,442 | −0,046 | 1.291 | 5.875 |
Fig. 86 - Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging (incremento target 1%, senza massimale, filtro anti-Hayley assente) di tutti i PAC di varie durate (2-10 anni) su serie storiche simulate con tecniche parametriche: distribuzione normale con media mensile dello 0% e deviazione standard del 5%
La performance del Value Averaging è molto positiva, sia nelle simulazioni con media dello 0,50%, che in quelle con lo 0%: rendimenti medi e mediana superiori al Cost Averaging su ogni durata (simulazioni con media 0,50%); deviazione standard minore (salvo pochissime eccezioni); rendimenti minimi superiori e percentuale di risultati positivi migliore.
Questa soluzione d’investimento sembra perciò ottima da ogni punto di vista.
In queste serie di simulazioni Monte Carlo ci sono due novità: 9 durate dei PAC (prima erano 8) e il numero di simulazioni, che è di un milione invece delle solite 100.000.
Dato che utilizzeremo i valori dell’extra-liquidità media e massima stimata (ultime due colonne sulla destra) per definire una tabella che suggerisca l’importo della rata iniziale in funzione della liquidità disponibile e della durata desiderata, avremo che:
- Il maggior numero di simulazioni ci permetterà di ottenere una stima più robusta.
- Il maggior numero di durate dei PAC ci permetterà di ottenere una stima più puntuale.
La tabella che presenteremo a breve servirà a evitare di eseguire manualmente il processo di aggiustamento visto in precedenza.
In ogni riga della tabella, troveremo gli importi potenziali della rata iniziale; nelle colonne, invece, troveremo il capitale iniziale disponibile (partendo da 100 mila euro, con un incremento di 50 mila fino a 300 mila e poi di 100 mila euro fino ad un milione di euro).
La tabella restituisce, per ognuna delle combinazioni precedenti, due possibili durate del PAC Value Averaging: la prima è calcolata in base all’extra-liquidità media; la seconda, in base al valore massimo delle simulazioni Monte Carlo.
Una nota sui valori massimi: utilizzare i valori massimi delle precedenti tabelle (ad esempio 127.979 per i piani decennali), significherebbe aspettarsi che il futuro ci riservi una serie storica dei rendimenti come quella, estrema, che ha generato quei valori. La probabilità che si verifichi una cosa del genere è pressoché nulla. Adopereremo quindi come valori massimi quelli calcolati sommando ai valori medi il 90% della distanza esistente tra il valore di liquidità massimo e quello medio.
L’investitore conosce la liquidità iniziale di cui dispone. Scorrendo dall’alto verso il basso la colonna relativa all’importo corrispondente, verificherà quale sia la rata iniziale del Value Averaging che rimanda all’orizzonte temporale di investimento desiderato (compreso tra 2 a 10 anni):
| Importo della rata in base all'extra-liquidità e alla durata desiderata | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rata mensile | 100.000 | 150.000 | 200.000 | 250.000 | 300.000 | 400.000 | 500.000 | 600.000 | 700.000 | 800.000 | 900.000 | 1.000.000 | ||||||||||||
| Med. | Max | Med. | Max | Med. | Max | Med. | Max | Med. | Max | Med. | Max | Med. | Max | Med. | Max | Med. | Max | Med. | Max | Med. | Max | Med. | Max | |
| 300 | 120 | 108 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 |
| 500 | 120 | 84 | 120 | 96 | 120 | 108-120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 |
| 750 | 108 | 60 | 120 | 72 | 120 | 84-96 | 120 | 96-108 | 120 | 108-120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 |
| 1.000 | 84 | 48-60 | 108 | 60 | 120 | 72 | 120 | 84 | 120 | 96 | 120 | 108 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 |
| 1.250 | 72 | 36 | 96 | 48-60 | 108 | 60 | 120 | 72 | 120 | 84 | 120 | 96 | 120 | 108 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 |
| 1.500 | 60 | 36 | 72-84 | 48 | 96 | 48-60 | 108-120 | 60-72 | 120 | 72 | 120 | 84 | 120 | 96 | 120 | 108 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 |
| 2.000 | 36-48 | 24 | 60 | 36 | 72-84 | 48 | 84-96 | 48-60 | 96-108 | 60 | 120 | 72 | 120 | 84 | 120 | 96 | 120 | 96 | 120 | 108 | 120 | 108-120 | 120 | 120 |
| 2.500 | 36 | 24 | 48 | 24-36 | 60-72 | 36 | 72-84 | 36-48 | 84-96 | 48 | 108 | 60 | 120 | 72 | 120 | 84 | 120 | 84-96 | 120 | 96 | 120 | 96-108 | 120 | 108 |
| 3.000 | 24 | n/a | 36-48 | 24 | 48-60 | 24-36 | 60-72 | 36 | 72 | 36-48 | 96 | 48-60 | 108 | 60 | 120 | 72 | 120 | 72-84 | 120 | 84 | 120 | 84-96 | 120 | 96 |
| 3.500 | 24 | n/a | 36 | 24 | 48 | 24-36 | 60 | 36 | 60-72 | 36-48 | 84 | 48 | 96 | 48-60 | 108 | 60-72 | 120 | 72 | 120 | 72-84 | 120 | 84 | 120 | 84-96 |
| 4.000 | 24 | n/a | 24-36 | 24 | 36-48 | 24 | 48 | 24-36 | 60 | 36 | 72 | 36-48 | 84-96 | 48 | 96-108 | 60 | 108 | 60-72 | 120 | 72 | 120 | 72-84 | 120 | 84 |
| 4.500 | n/a | n/a | 24 | n/a | 36 | 24 | 48 | 24-36 | 48-60 | 24-36 | 60-72 | 36 | 72-84 | 48 | 84-96 | 48-60 | 96-108 | 60 | 108 | 60-72 | 120 | 72 | 120 | 72 |
| 5.000 | n/a | n/a | 24 | n/a | 36 | 24 | 36 | 24 | 48 | 24-36 | 60 | 36 | 72 | 36-48 | 84 | 48 | 96 | 48-60 | 108 | 60 | 108 | 60-72 | 120 | 72 |
Fig. 87 – Importo della rata in base all'extra-liquidità e alla durata desiderata
Immaginiamo di avere 200.000 euro di liquidità e di volerli impiegare in 6 anni (72 rate). Scorrendo dall’alto verso il basso la colonna corrispondente a 200.000, 72 rate si trovano in corrispondenza degli importi di 2000-2500 euro (extra-liquidità media) e di 1000 euro (extra-liquidità massima). Questo significa che, se si preferisce seguire i valori medi di extra-liquidità (come calcolati nel milione di simulazioni Monte Carlo e riparametrati ai vari importi delle rate), con 200.000 euro iniziali dovremmo essere in grado di investire il nostro capitale con un Value Averaging sviluppato su 72 mensilità da 2000 o 2500 euro di rata iniziale, con incremento del target dell’1%. 2500 euro saranno preferibili se non siamo contrari all’eventualità di terminare la liquidità prima che i 6 anni siano trascorsi (e viceversa).
Se, invece, si preferisse fare affidamento sui valori massimi di extra-liquidità, con i soliti 200.000 euro dovremmo poter costruire un Value Averaging di 72 rate da 1000 euro iniziali, sempre con un incremento del target dell’1%.
Ovviamente, si agisce con maggior aggressività scegliendo di basarsi sui valori medi (rata iniziale di 2000 o 2500 euro): in tal caso, la probabilità di un esaurimento del fondo prima dei 72 mesi previsti è intorno al 50%.
Vale la pena ribadire che un esaurimento precoce del fondo di liquidità non è necessariamente un evento negativo: la diversificazione temporale sarà minore, ma le performance prodotte potrebbero anche essere migliori.
È possibile che una certa durata non sia inclusa nella tabella. Ad esempio, avendo 700.000 euro di liquidità e volendo investire in 108 mesi (9 anni) sulla base dei valori massimi dell’extra-liquidità, troveremo 96 in corrispondenza delle rate da 2000 euro e 120 in corrispondenza di quelle da 1500 euro. In tal caso, la rata iniziale più appropriata per un investimento di 108 mesi dovrebbe approssimativamente essere 1750 euro, ovvero il valor medio tra 1500 (120 mesi) e 2000 euro (96 mesi).
Come riprova, vediamo se lanciando delle simulazioni Monte Carlo non parametriche, basate sulla serie storica del nostro fondo Raiffeisen, i valori di extra-liquidità media e massima che si ottengono siano coerenti con quelli utilizzati in precedenza.
I risultati delle 100.000 simulazioni non parametriche sono i seguenti:
| Incremento 1% - No massimale - Fondo Raiffeisen (simulazioni non parametriche) - 100.000 simulazioni | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Rend. tot. | Stand. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. | Ex.liq. Med. | Ex.liq. Max |
| PAC | 120 | 39,83% | 38,45% | 50.339 | 0 | 50.339 | 300 | 319,50% | −51,39% | 86,853% | 34,45% | 0,894 | 1,428 | n/a | n/a |
| PAC | 108 | 35,18% | 35,49% | 43.797 | 0 | 43.797 | 300 | 284,13% | −54,27% | 85,240% | 30,51% | 0,868 | 1,336 | n/a | n/a |
| PAC | 96 | 30,58% | 32,60% | 37.606 | 0 | 37.606 | 300 | 306,12% | −52,50% | 83,232% | 26,54% | 0,804 | 1,138 | n/a | n/a |
| PAC | 84 | 26,24% | 29,62% | 31.811 | 0 | 31.811 | 300 | 249,62% | −53,64% | 81,533% | 22,67% | 0,775 | 1,137 | n/a | n/a |
| PAC | 72 | 22,12% | 26,81% | 26.378 | 0 | 26.378 | 300 | 223,91% | −53,75% | 79,081% | 19,23% | 0,698 | 0,873 | n/a | n/a |
| PAC | 60 | 18,09% | 23,63% | 21.256 | 0 | 21.256 | 300 | 180,61% | −50,13% | 77,018% | 15,75% | 0,626 | 0,718 | n/a | n/a |
| PAC | 48 | 14,00% | 20,36% | 16.417 | 0 | 16.417 | 300 | 134,92% | −49,44% | 74,222% | 12,26% | 0,531 | 0,507 | n/a | n/a |
| PAC | 36 | 10,25% | 17,05% | 11.907 | 0 | 11.907 | 300 | 113,72% | −44,15% | 71,352% | 9,08% | 0,416 | 0,287 | n/a | n/a |
| PAC | 24 | 6,70% | 13,39% | 7.682 | 0 | 7.682 | 300 | 75,78% | −42,21% | 67,877% | 6,10% | 0,279 | 0,128 | n/a | n/a |
| PAC | 120 | 43,62% | 41,12% | 73.975 | −18.681 | 55.294 | 13.315 | 339,00% | −39,14% | 88,698% | 35,23% | 0,949 | 0,876 | 21.807 | 79.837 |
| PAC | 108 | 38,73% | 37,15% | 61.615 | −14.396 | 47.219 | 11.204 | 266,71% | −41,30% | 87,358% | 31,64% | 0,868 | 0,638 | 17.181 | 66.184 |
| PAC | 96 | 33,86% | 33,37% | 50.654 | −10.806 | 39.849 | 9.331 | 249,88% | −40,13% | 85,678% | 28,06% | 0,761 | 0,364 | 13.288 | 51.342 |
| PAC | 84 | 29,18% | 29,72% | 41.070 | −7.837 | 33.234 | 7.669 | 207,18% | −41,34% | 84,209% | 24,45% | 0,688 | 0,263 | 9.986 | 43.787 |
| PAC | 72 | 24,63% | 26,29% | 32.638 | −5.433 | 27.206 | 6.193 | 171,25% | −41,96% | 81,862% | 21,01% | 0,580 | 0,025 | 7.248 | 32.520 |
| PAC | 60 | 20,16% | 22,79% | 25.225 | −3.521 | 21.704 | 4.884 | 154,01% | −39,58% | 79,968% | 17,38% | 0,496 | −0,072 | 4.996 | 22.553 |
| PAC | 48 | 15,63% | 19,33% | 18.742 | −2.115 | 16.627 | 3.722 | 111,94% | −39,19% | 77,256% | 13,72% | 0,397 | −0,191 | 3.231 | 15.804 |
| PAC | 36 | 11,44% | 16,01% | 13.077 | −1.089 | 11.988 | 2.691 | 90,92% | −36,13% | 74,123% | 10,25% | 0,298 | −0,253 | 1.869 | 9.433 |
| PAC | 24 | 7,44% | 12,50% | 8.128 | −425 | 7.703 | 1.776 | 64,09% | −34,19% | 70,382% | 6,90% | 0,188 | −0,273 | 874 | 5.096 |
| PAC | 120 | 45,03% | 40,29% | 69.012 | −14.513 | 54.499 | 13.315 | 229,28% | −38,62% | 89,060% | 36,95% | 0,638 | −0,256 | 21.705 | 79.787 |
| PAC | 108 | 39,73% | 36,25% | 57.868 | −11.180 | 46.687 | 11.204 | 197,87% | −41,08% | 87,681% | 33,10% | 0,588 | −0,301 | 17.087 | 65.815 |
| PAC | 96 | 34,46% | 32,50% | 47.978 | −8.469 | 39.510 | 9.331 | 190,87% | −39,92% | 86,039% | 29,17% | 0,530 | −0,337 | 13.210 | 51.051 |
| PAC | 84 | 29,52% | 28,92% | 39.202 | −6.176 | 33.026 | 7.669 | 161,50% | −41,66% | 84,514% | 25,27% | 0,488 | −0,310 | 9.928 | 43.627 |
| PAC | 72 | 24,81% | 25,69% | 31.413 | −4.321 | 27.092 | 6.193 | 138,78% | −41,88% | 82,113% | 21,62% | 0,428 | −0,359 | 7.207 | 32.448 |
| PAC | 60 | 20,24% | 22,35% | 24.501 | −2.851 | 21.649 | 4.884 | 125,34% | −39,52% | 80,192% | 17,78% | 0,383 | −0,333 | 4.971 | 22.509 |
| PAC | 48 | 15,65% | 19,07% | 18.367 | −1.760 | 16.606 | 3.722 | 101,86% | −39,12% | 77,385% | 13,96% | 0,327 | −0,330 | 3.218 | 15.767 |
| PAC | 36 | 11,44% | 15,89% | 12.923 | −941 | 11.982 | 2.691 | 84,73% | −36,13% | 74,211% | 10,36% | 0,260 | −0,321 | 1.865 | 9.433 |
| PAC | 24 | 7,44% | 12,47% | 8.092 | −390 | 7.702 | 1.776 | 61,80% | −34,19% | 70,410% | 6,93% | 0,176 | −0,294 | 874 | 5.096 |
Fig. 88 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging di tutti i PAC di durate brevi su serie storiche simulate con tecniche non parametriche (dati fondo Raiffeisen, incremento target 1%, senza massimale, filtro anti-Hayley assente)
L’extra-liquidità richiesta è compresa, sia nei valori medi che massimi, in quelli ottenuti dalle simulazioni parametriche.
Vediamo invece che cosa ci dicono le simulazioni non parametriche utilizzando la serie storica del fondo Aberdeen, caratterizzato da un trend decrescente.
I risultati sono i seguenti:
| Incremento 1% - No massimale - Fondo Aberdeen (simulazioni non parametriche) - 100.000 simulazioni | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Rend. tot. | Stand. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. | Ex.liq. Med. | Ex.liq. Max |
| PAC | 120 | 5,03% | 34,43% | 37.810 | 0 | 37.810 | 300 | 400,15% | −69,27% | 48,972% | −0,76% | 1,186 | 2,687 | n/a | n/a |
| PAC | 108 | 4,76% | 33,13% | 33.944 | 0 | 33.944 | 300 | 305,44% | −69,72% | 49,156% | −0,67% | 1,142 | 2,421 | n/a | n/a |
| PAC | 96 | 4,39% | 31,43% | 30.064 | 0 | 30.064 | 300 | 323,93% | −65,05% | 49,306% | −0,54% | 1,080 | 2,191 | n/a | n/a |
| PAC | 84 | 4,00% | 29,65% | 26.208 | 0 | 26.208 | 300 | 247,22% | −64,18% | 49,296% | −0,48% | 1,044 | 1,993 | n/a | n/a |
| PAC | 72 | 3,45% | 27,55% | 22.346 | 0 | 22.346 | 300 | 248,95% | −63,70% | 49,261% | −0,46% | 0,938 | 1,599 | n/a | n/a |
| PAC | 60 | 3,10% | 25,36% | 18.558 | 0 | 18.558 | 300 | 223,46% | −61,00% | 49,464% | −0,31% | 0,892 | 1,514 | n/a | n/a |
| PAC | 48 | 2,64% | 22,74% | 14.780 | 0 | 14.780 | 300 | 183,22% | −55,83% | 49,967% | −0,01% | 0,780 | 1,150 | n/a | n/a |
| PAC | 36 | 1,88% | 19,45% | 11.003 | 0 | 11.003 | 300 | 144,15% | −53,90% | 49,833% | −0,08% | 0,676 | 0,894 | n/a | n/a |
| PAC | 24 | 1,23% | 15,81% | 7.289 | 0 | 7.289 | 300 | 100,34% | −47,65% | 49,777% | −0,09% | 0,544 | 0,614 | n/a | n/a |
| PAC | 120 | 13,22% | 36,12% | 74.395 | −34.381 | 40.013 | 15.104 | 396,90% | −52,00% | 57,086% | 4,99% | 1,570 | 3,871 | 36.575 | 107.767 |
| PAC | 108 | 12,28% | 34,41% | 62.042 | −26.548 | 35.494 | 12.703 | 309,91% | −52,88% | 56,718% | 4,61% | 1,455 | 3,139 | 28.571 | 90.409 |
| PAC | 96 | 11,20% | 32,24% | 51.116 | −19.980 | 31.136 | 10.572 | 258,73% | −49,60% | 56,448% | 4,29% | 1,315 | 2,429 | 21.823 | 68.547 |
| PAC | 84 | 9,98% | 29,95% | 41.450 | −14.551 | 26.900 | 8.681 | 232,51% | −48,97% | 55,910% | 3,77% | 1,213 | 1,991 | 16.195 | 53.189 |
| PAC | 72 | 8,63% | 27,41% | 32.957 | −10.196 | 22.761 | 7.003 | 204,43% | −49,30% | 55,385% | 3,28% | 1,055 | 1,405 | 11.630 | 40.363 |
| PAC | 60 | 7,38% | 24,79% | 25.482 | −6.692 | 18.790 | 5.514 | 181,05% | −47,38% | 55,147% | 2,85% | 0,932 | 1,003 | 7.907 | 28.564 |
| PAC | 48 | 6,01% | 21,88% | 18.926 | −4.032 | 14.894 | 4.193 | 152,24% | −44,76% | 54,875% | 2,54% | 0,781 | 0,593 | 5.002 | 18.848 |
| PAC | 36 | 4,33% | 18,44% | 13.189 | −2.138 | 11.051 | 3.020 | 112,97% | −43,32% | 54,017% | 1,85% | 0,641 | 0,297 | 2.838 | 12.000 |
| PAC | 24 | 2,78% | 14,85% | 8.176 | −875 | 7.301 | 1.979 | 81,37% | −38,19% | 53,166% | 1,18% | 0,501 | 0,107 | 1.301 | 5.891 |
| PAC | 120 | 15,28% | 37,41% | 69.012 | −29.091 | 39.921 | 15.104 | 253,02% | −51,88% | 58,287% | 6,00% | 1,279 | 1,627 | 35.958 | 107.429 |
| PAC | 108 | 13,86% | 35,03% | 57.868 | −22.447 | 35.421 | 12.703 | 221,53% | −52,47% | 57,772% | 5,52% | 1,172 | 1,271 | 28.116 | 89.351 |
| PAC | 96 | 12,37% | 32,44% | 47.978 | −16.894 | 31.084 | 10.572 | 194,10% | −49,40% | 57,464% | 5,06% | 1,061 | 0,948 | 21.500 | 68.266 |
| PAC | 84 | 10,80% | 29,81% | 39.202 | −12.331 | 26.871 | 8.681 | 168,18% | −48,81% | 56,761% | 4,41% | 0,974 | 0,735 | 15.976 | 52.674 |
| PAC | 72 | 9,16% | 27,14% | 31.413 | −8.671 | 22.742 | 7.003 | 155,50% | −49,09% | 56,124% | 3,76% | 0,857 | 0,470 | 11.493 | 40.104 |
| PAC | 60 | 7,67% | 24,45% | 24.501 | −5.722 | 18.779 | 5.514 | 140,36% | −47,35% | 55,710% | 3,21% | 0,767 | 0,300 | 7.829 | 28.536 |
| PAC | 48 | 6,15% | 21,59% | 18.367 | −3.478 | 14.889 | 4.193 | 119,96% | −44,61% | 55,231% | 2,80% | 0,663 | 0,155 | 4.965 | 18.756 |
| PAC | 36 | 4,39% | 18,26% | 12.923 | −1.874 | 11.049 | 3.020 | 99,08% | −43,32% | 54,300% | 1,99% | 0,568 | 0,064 | 2.825 | 12.000 |
| PAC | 24 | 2,79% | 14,77% | 8.092 | −791 | 7.301 | 1.979 | 74,12% | −38,19% | 53,304% | 1,22% | 0,466 | 0,001 | 1.298 | 5.891 |
Fig. 89 – Tabella riassuntiva dei risultati delle varie tipologie di Cost Averaging e Value Averaging di tutti i PAC di durate brevi su serie storiche simulate con tecniche non parametriche (dati fondo Aberdeen, incremento target 1%, senza massimale, filtro anti-Hayley assente)
Le precedenti conclusioni sull’extra-liquidità possono essere estese anche a queste simulazioni.
È interessante notare come le simulazioni non parametriche generino risultati migliori di quelle parametriche: rendimenti più alti, deviazione standard più bassa, rendimenti minimi migliori, percentuale dei PAC positivi superiori, skewness e kurtosis inferiori.
La cosa è confortante per due motivi:
- La probabilità che possa verificarsi, in futuro, una serie storica dei rendimenti che non è stata in qualche modo contemplata nelle nostre simulazioni è bassa.
- Il Value Averaging, potenziato dalle iniezioni di extra-liquidità, permette di ottenere delle performance migliori di quelle del Cost Averaging.
A questo punto abbiamo tutte le informazioni che ci servono per investire sfruttando la diversificazione temporale.
Nulla vieta di diversificare anche "spazialmente", investendo in 2 o più prodotti di pari rischiosità. Naturalmente, anche l’importo della rata iniziale dovrà essere diviso per il numero di prodotti utilizzati, in modo che il fondo di liquidità sia sufficiente a coprire i versamenti che saranno complessivamente richiesti.
Investendo in un portafoglio composto da più strumenti finanziari si hanno due inconvenienti: maggiori costi di transazione e una più complicata gestione del Value Averaging, che potrà essere effettuata indipendentemente su ogni singolo fondo o, meglio ancora, sul portafoglio complessivo.
Per alcuni, o in caso di capitali particolarmente elevati, il beneficio psicologico di questa ulteriore diversificazione potrebbe compensare ampiamente gli svantaggi.
Nel caso di un investimento Value Averaging in un portafoglio di fondi, si dovrà fare attenzione alla tipologia dei prodotti scelti: nel caso in cui alcuni di questi siano meno rischiosi (come ad esempio un fondo obbligazionario), l’extra-liquidità risulterà probabilmente eccessiva. Sarà dunque consigliabile, entro certi limiti, sovrappesare i prodotti meno volatili (fissando cioè un valore della rata iniziale superiore).
Un'ultima raccomandazione: non è opportuno diversificare eccessivamente l’investimento con strumenti finanziari poco volatili: il piano di accumulo è una strategia che ha lo scopo di limitare il rischio tramite la diversificazione temporale. Se si esagera con la diversificazione su fondi poco volatili, si rischia di creare un portafoglio con bassa potenzialità di crescita.
11.2 Aumento della percentuale di incremento del target
Per valutare la convenienza dell'aumento delle percentuali di incremento del PAC, si dovranno lanciare nuovamente le simulazioni Monte Carlo: verificheremo, approssimativamente, quali siano le percentuali e l'extra-liquidità richiesta.
Per ogni durata, dovranno essere backtestate diverse percentuali di incremento del target (ovviamente superiori all’1%), in modo da avere un’idea dei livelli medi e massimi di extra-liquidità richiesti per ognuna di esse.
Il problema di questa strategia è che, indipendentemente dall’andamento del sottostante, sovrappesa molto i versamenti che saranno effettuati nell’ultima parte di vita del piano di accumulo (soprattutto nelle durate più lunghe).
Di conseguenza, la maggior parte del capitale rimane investito per un periodo relativamente breve: l’inevitabile conseguenza è una diminuzione dei rendimenti, che saranno inferiori a quelli ottenuti con la strategia precedente.
Quello che stiamo facendo è, infatti, spostare in avanti nel tempo la maggior parte dell’investimento. Ipotizzando un mercato con un trend positivo, il costo-opportunità di questa scelta è alto.
Tra incremento percentuale del target e rendimento verrà a crearsi una proporzionalità inversa: all’aumentare del primo, diminuirà il secondo (e viceversa). La concentrazione dell’investimento nella parte finale del piano di accumulo genera anche una minore deviazione standard dei rendimenti, anch’essa inversamente proporzionale alla percentuale di incremento del target.
L’extra-liquidità richiesta, invece, seguirà l’andamento inverso: aumenterà in modo più che proporzionale al crescere della percentuale di incremento del target.
I risultati ottenuti nelle simulazioni Monte Carlo (parametriche, con media positiva) sul Value Averaging puro con rata iniziale di 300 euro sono stati condensati nella seguente tabella:
| Value Averaging No Sell - Performance su PAC brevi in caso di alti incrementi percentuali del target - 100.000 simulazioni per target | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Durata | 1,50% | 2,00% | 2,50% | 3,00% | ||||||||||||||||
| Rend. | Dev. St. | Mont. | Ex.L. Media | Ex.L. Max | Rend. | Dev. St. | Mont. | Ex.L. Media | Ex.L. Max | Rend. | Dev. St. | Mont. | Ex.L. Media | Ex.L. Max | Rend. | Dev. St. | Mont. | Ex.L. Media | Ex.L. Max | |
| 120 | 38,41% | 50,29% | 105.644 | 49.300 | 146.649 | 32,91% | 45,08% | 152.993 | 89.562 | 219.301 | 28,22% | 39,01% | 227.374 | 154.076 | 354.781 | 24,10% | 33,93% | 345.088 | 258.429 | 564.758 |
| 96 | 30,58% | 40,50% | 66.815 | 27.627 | 88.042 | 27,87% | 38,49% | 88.725 | 46.296 | 132.121 | 24,52% | 34,60% | 119.820 | 73.740 | 183.670 | 21,63% | 31,08% | 164.271 | 113.656 | 241.892 |
| 72 | 22,89% | 31,39% | 39.918 | 13.779 | 43.161 | 21,72% | 31,13% | 48.875 | 21.468 | 60.367 | 19,97% | 29,33% | 60.431 | 31.752 | 88.718 | 18,23% | 27,20% | 75.394 | 45.328 | 96.992 |
| 60 | 18,89% | 27,11% | 29.773 | 9.111 | 32.983 | 18,20% | 27,22% | 35.077 | 13.676 | 38.014 | 17,05% | 26,13% | 41.632 | 19.522 | 49.382 | 15,91% | 24,72% | 49.716 | 26.884 | 60.583 |
| 48 | 14,92% | 22,75% | 21.361 | 5.591 | 20.993 | 14,71% | 23,14% | 24.269 | 8.067 | 28.867 | 13,99% | 22,63% | 27.694 | 11.138 | 29.048 | 13,44% | 21,89% | 31.732 | 14.782 | 38.117 |
| 36 | 11,02% | 18,51% | 14.395 | 3.047 | 12.120 | 10,91% | 18,84% | 15.795 | 4.231 | 14.125 | 10,68% | 18,71% | 17.373 | 5.621 | 14.948 | 10,39% | 18,47% | 19.153 | 7.230 | 19.190 |
| 24 | 7,06% | 14,16% | 8.646 | 1.346 | 6.340 | 7,17% | 14,36% | 9.177 | 1.773 | 6.680 | 7,15% | 14,44% | 9.753 | 2.267 | 6.871 | 7,07% | 14,45% | 10.371 | 2.817 | 8.155 |
| Durata | 3,50% | 4,00% | 4,50% | 5,00% | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rend. | Dev. St. | Mont. | Ex.L. Media | Ex.L. Max | Rend. | Dev. St. | Mont. | Ex.L. Media | Ex.L. Max | Rend. | Dev. St. | Mont. | Ex.L. Media | Ex.L. Max | Rend. | Dev. St. | Mont. | Ex.L. Media | Ex.L. Max | |
| 120 | 20,85% | 29,53% | 532.585 | 426.214 | 877.407 | 18,31% | 26,44% | 833.380 | 697.720 | 1.259.775 | 16,16% | 23,65% | 1.318.255 | 1.139.410 | 1.991.769 | 14,45% | 21,72% | 2.103.411 | 1.859.908 | 3.200.482 |
| 96 | 19,35% | 28,14% | 228.147 | 171.277 | 343.002 | 17,17% | 25,35% | 320.300 | 255.506 | 494.849 | 15,37% | 23,10% | 453.811 | 378.287 | 738.275 | 13,85% | 21,25% | 647.900 | 557.786 | 966.896 |
| 72 | 16,73% | 25,35% | 94.852 | 63.151 | 138.638 | 15,31% | 23,60% | 120.211 | 86.558 | 171.704 | 14,04% | 21,84% | 153.291 | 117.252 | 216.393 | 12,91% | 20,36% | 196.662 | 157.711 | 287.601 |
| 60 | 14,89% | 23,37% | 59.716 | 36.064 | 79.605 | 13,83% | 21,91% | 72.137 | 47.608 | 101.810 | 12,91% | 20,77% | 87.564 | 62.005 | 119.723 | 11,99% | 19,56% | 106.762 | 80.031 | 145.870 |
| 48 | 12,68% | 21,09% | 36.501 | 19.211 | 44.296 | 11,95% | 19,97% | 42.141 | 24.478 | 52.163 | 11,32% | 19,15% | 48.816 | 30.743 | 59.035 | 10,71% | 18,36% | 56.729 | 38.211 | 71.389 |
| 36 | 10,09% | 18,08% | 21.161 | 9.080 | 21.526 | 9,59% | 17,35% | 23.422 | 11.203 | 24.550 | 9,22% | 16,93% | 25.981 | 13.622 | 28.898 | 8,86% | 16,32% | 28.871 | 16.358 | 32.804 |
| 24 | 6,90% | 14,23% | 11.038 | 3.427 | 8.744 | 6,70% | 14,03% | 11.760 | 4.104 | 9.803 | 6,58% | 13,79% | 12.538 | 4.831 | 11.768 | 6,40% | 13,49% | 13.379 | 5.631 | 13.602 |
Fig. 90 – Tabella riassuntiva di alcuni risultati dei PAC Value Averaging No-Sell brevi su serie storiche simulate con tecniche parametriche (media 0,50%, deviazione standard 5%), con incrementi del target 1.50-5.00%, senza massimale, filtro anti-Hayley: assente)
Per evitare di pubblicare svariate pagine di noiose tabelle, abbiamo incluso soltanto alcune delle performance generate da questi piani di accumulo.
Il grafico seguente si concentra su quelle dei PAC decennali:
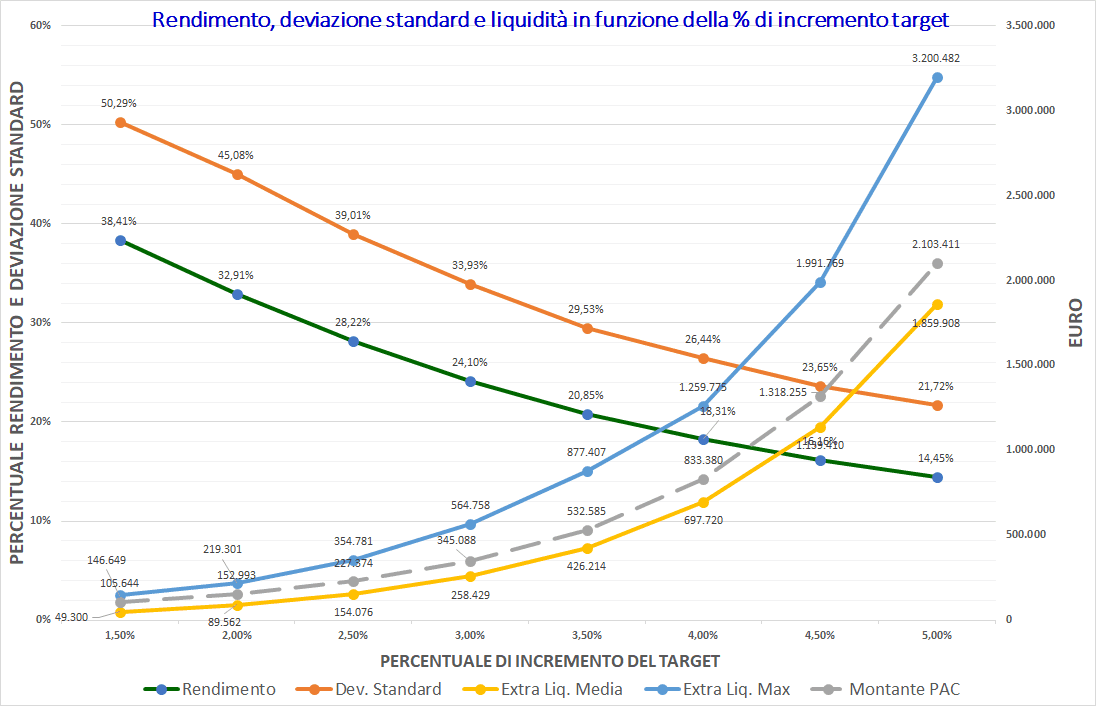
Fig. 91 – Grafico di alcuni risultati dei PAC Value Averaging No-Sell decennali su serie storiche simulate con tecniche parametriche (media 0,50%, deviazione standard 5%), con incrementi del target 1.50-5.00%, senza massimale, filtro anti-Hayley assente)
Sia i rendimenti che le deviazioni standard diminuiscono all’aumentare della percentuale di incremento del target, mentre la liquidità media e massima richiesta, così come i montanti dei PAC, crescono in modo più che proporzionale.
I risultati della tabella e del grafico sono relativi al Value Averaging No-Sell; i risultati del Value Averaging puro sono molto simili: un target che aumenta con questa velocità sarà difficilmente sopravanzato dalla crescita del mercato, riflessa nel controvalore dell’investimento (condizione necessaria a far scattare una vendita nel Value Averaging puro).
Perché scegliere questa alternativa di investimento?
Si potrebbe optare per la costruzione di un piano di accumulo Value Averaging con rata iniziale di 300 euro e un target crescente compreso tra l’1,50% e il 5% perché attratti dalla possibilità di versamenti che crescono in maniera più che proporzionale al trascorrere del tempo.
Si tratta di una valutazione soggettiva, sensata per l’investitore che preveda un periodo iniziale di decrescita o di lateralità del mercato.
Seguire una strategia del genere significa comunque scegliere sulla base di una congettura sul futuro: una scelta in conflitto con una filosofia di investimento svincolata da ogni previsione dei movimenti del mercato, tipica dei Piani di Accumulo del Capitale.
Per questo motivo, la strategia raccomandata è quella precedente: non si basa su stime future e non posticipa in maniera considerevole l’investimento. Si tratta di una strategia concettualmente più vicina al Value Averaging classico, dove l’investimento si plasma all’andamento del mercato senza volerlo anticipare o prevedere.
Concludiamo con una domanda ed una riflessione: il Value Averaging è una valida alternativa alle solite metodologie di investimento o non è altro che un piccolo ma complicato upgrade del Cost Averaging?
Può darsi che i rendimenti non impressionino più di tanto. Fin dall’inizio, però, abbiamo detto che il punto principale del Value Averaging non è la massimizzazione del rendimento.
Tutto il lavoro fin qui svolto non è finalizzato a ottenere dei rendimenti più alti. Se questo è ciò che vogliamo realizzare, sappiamo già che l’investimento lump sum – il PIC – è imbattibile: ce lo dicono 200 anni di storia dei mercati azionari.
Sappiamo anche come battere il mercato sia un’operazione difficilissima e le metodologie di investimento basate sulle previsioni del futuro, orientate quindi al market timing, sono dense di incognite e foriere di errori.
Scegliere l'investimento in un'unica soluzione (lump sum) o fare market timing si paga con un consumo di capitale psicologico molto elevato: se non si dispone di una propensione al rischio alta o di una lunga esperienza accumulata in anni di investimenti finanziari, sarà quasi inevitabile andare incontro a periodi di stress, ansia e incertezza causati dalla volatilità dei mercati azionari.
Il rischio è quello di finire per liquidare l’investimento prima del tempo previsto, probabilmente in perdita e al culmine di una crisi finanziaria.
Tutto questo, a condizione che si sia trovato il coraggio di investire.
Spesso, non succede. Non sono rari i casi in cui gli investitori rimangono alla finestra per anni, in stand-by, in attesa di uno storno dei prezzi che li convinca ad aprire una posizione d’acquisto. Anni in cui i mercati continuano a salire, a realizzare nuovi massimi, a battere record dopo record.
A volte il coraggio di investire si trova, ma sottopesando eccessivamente il comparto azionario: rinunciando così a gran parte dei potenziali guadagni.
Il Value Averaging non ha certo la pretesa di battere ogni altra strategia o di ottenere rendimenti migliori dei PIC. Col Value Averaging si vuole sfruttare, nei limiti del possibile, una modalità di investimento che vada d’accordo con la psicologia dell’investitore e non sia fonte di ansia e inquietudine.
Il piano di accumulo Value Averaging è una soluzione pensata per un investitore medio, abbastanza evoluto ma non necessariamente esperto, che può essere sfruttata in due modi:
- Come metodologia di costruzione di un capitale, esattamente come un Cost Averaging: è possibile aggirare la critica di Hayley e costruire un PAC Value Averaging senza bisogno di liquidità iniziale. I rendimenti possono essere superiori a quelli del Cost Averaging, soprattutto in mercati con trend al ribasso, ma i punti di forza del Value Averaging sono la minor volatilità, le minori perdite massime e le migliori percentuali di successo.
- Come metodologia di investimento di un capitale già esistente: il Value Averaging può essere utilizzato anche da chi disponga di un capitale da impiegare fin da subito e sia alla ricerca di un’alternativa all’investimento lump sum, senza per questo volersi addentrare in modelli econometrici di investimento troppo sofisticati o costruire un portafoglio sovraccarico di prodotti finanziari. Per chi dispone di un fondo iniziale di liquidità, il Value Averaging sia di breve che di medio/lungo termine è un’alternativa che sfrutta la diversificazione temporale relativamente semplice da capire e applicare e, perché no, sufficientemente profittevole. E quel che è più importante, evita lo stress psicologico tipico di un investimento in un’unica soluzione.
È bene ribadire che il Value Averaging non sia una soluzione adatta a tutti. Ognuno dovrebbe scegliere la metodologia di investimento che preferisce: un PAC Cost Averaging è sicuramente più semplice di un PAC Value Averaging; il PIC è senz’altro più efficiente.
Il PAC Cost Averaging e il PIC hanno però i loro limiti e i loro inconvenienti. Riteniamo che lo sviluppo di soluzioni di investimento alternative dovrebbe soddisfare maggiormente il bisogno di tranquillità psicologica dell’investitore, ancor prima di quello finanziario.
L’assioma di razionalità è un ingrediente immancabile nelle teorie economico-finanziarie finalizzate alla massimizzazione del profitto; l’uomo però, raramente si comporta in modo razionale secondo i canoni classici dell’economia.
Non potendo cambiare l’essenza degli esseri umani, si dovrebbe allora prendere atto che l’economia e la finanza personale hanno a che fare con i processi decisionali dell’uomo: processi spesso non razionali, ma psicologicamente logici e comprensibili.
12. Risposte alle critiche al Value Averaging

«What could I say to you that would be of value, except that perhaps you seek too much, that as a result of your seeking you cannot find».
Hermann Hesse
1) Mancanza di piattaforme di investimento automatizzato
Per il momento, almeno in Italia, non esistono piattaforme automatizzate e non è detto che vengano implementate in futuro. In un mondo dove ormai tutto è computerizzato, non sarebbe però così difficile per una banca congegnare un piano di accumulo Value Averaging personalizzabile e automatizzato. Oltre a offrire un ottimo servizio ai propri clienti, potrebbe essere una buona manovra di marketing strategico.
Nel frattempo, l’unico modo di superare questa mancanza è quello di gestire il Value Averaging in prima persona.
Questa critica può tuttavia essere estesa a qualsiasi strategia di investimento diversa dal piano di accumulo a rate costanti.
2) Importo dei versamenti
La critica viene neutralizzata nel momento in cui non si costituisce un fondo di liquidità all’inizio del piano di accumulo. La liquidità può accumularsi anche durante la vita del PAC, essendo alimentata dalle rate non versate (Value Averaging No-Sell) o dalle vendite delle quote in eccesso (Value Averaging puro). La maggior parte delle maxi-rate, che tendono a presentarsi in fasi avanzate della vita dei PAC, sarà quindi fronteggiata con la liquidità accumulata nel tempo.
È una critica che può trasformarsi in un punto di forza, peculiare del Value Averaging, nel momento in cui un investitore decida scientemente di sviluppare un piano di accumulo Value Averaging nonostante sia già in possesso della liquidità necessaria.
3) Importo medio delle rate (giacenza media)
Per evitare una giacenza media molto inferiore a quella del Cost Averaging, è necessario impostare un incremento crescente del target. Nei PAC più corti, le differenze sono minime; in quelli lunghi (fino a 30 anni), con un incremento dello 0,50% la giacenza media finale è quasi uguale a quella del Cost Averaging.
È molto importante aver verificato che il target crescente, entro certi limiti, non solo non inficia le percentuali di rendimento, ma riesce quasi sempre ad aumentarle (la stessa cosa avviene per le somme finali generate). Nel caso in cui non si attivi il filtro anti-Hayley, la giacenza media del Value Averaging può superare senza problemi quella del Cost Averaging.
4) Volatilità del sottostante
Affinché il Value Averaging produca i suoi frutti, è necessario che il sottostante sia volatile. La ricerca della volatilità non deve però essere estremizzata: un fondo azionario globale è sufficiente e non è necessario focalizzarsi su settori troppo rischiosi, di nicchia o – peggio ancora – singole azioni.
La scelta di diversificare – invece che concentrare – l’investimento è una misura di riduzione del rischio che vale per qualsiasi strategia, soprattutto se di medio o lungo termine.
5) Distorsioni nella modalità di calcolo del rendimento annualizzato
La critica avanzata da Hayley è corretta e molto insidiosa. Edleson e Marshall non avevano notato la distorsione provocata dall’utilizzo di extra-liquidità nel calcolo dei rendimenti del Value Averaging. Tuttavia, questa distorsione può essere aggirata evitando di costituire un fondo di liquidità iniziale e gestendo il piano di accumulo applicando il filtro anti-Hayley.
L’impatto sul rendimento è significativo, ma il Value Averaging rimane meno rischioso del Cost Averaging. Inoltre, i rendimenti continuano a essere superiori nei test sviluppati sulle serie storiche reali e quando il trend del sottostante è negativo.
La critica di Hayley può infine trasformarsi in un punto di forza se decidiamo di investire un capitale già disponibile per mezzo di un piano di accumulo Value Averaging di breve o di lungo termine. Seppure non sia la soluzione di investimento più efficiente, rimane un’alternativa molto valida in quanto offre tranquillità e diminuisce il rischio dell’investimento, senza rinunciare a un rendimento soddisfacente.
La tranquillità psicologica è senz’altro l’asset più prezioso; l’investimento ottimale e il portafoglio efficiente sono dei bei concetti, assolutamente corretti da un punto di vista teorico, ma troppo spesso intangibili, accademici e talvolta incompresi: spesso non riescono a trasferire la giusta tranquillità agli investitori. Conoscendo le modalità di funzionamento del Value Averaging, un investitore sarà consapevole di ciò che lo aspetta sia quando i prezzi salgono, sia quando si dovesse verificare la tanto temuta crisi finanziaria.
Lo stesso Hayley riconosce al Value Averaging alcuni meriti in ambito comportamentale, seppure in maniera molto blanda e approssimativa. Quella di Hayley è in realtà una critica a 360° del Value Averaging e nel portarla avanti non si pone alcun problema a raccomandare strategie più efficienti, come lo stesso Buy and Hold o altre metodologie non meglio identificate.
13. PIC Value Averaging

«The average investor's return is significantly lower than market indices due primarily to market timing».
Daniel Kahneman
Fino ad oggi, il Value Averaging è sempre stato pensato come Piano di Accumulo del Capitale: un modo più efficiente del Cost Averaging di costruire un capitale nel tempo.
Sfruttando un fondo di liquidità iniziale, abbiamo anche visto come il Value Averaging possa essere l’alternativa a un investimento lump sum: la diminuzione del rischio e la tranquillità psicologica che ne derivano sono i principali benefici offerti da questa metodologia: per alcuni investitori, saranno più che sufficienti a compensare la minor efficienza.
Il Value Averaging, però, potrebbe essere pensato come una modalità di investimento – sempre per chi disponga già di un capitale – da sviluppare in tempi molto rapidi: fino a 24 mesi. L’obiettivo sarebbe quello di diminuire il rischio insito nell’impiego del capitale in un’unica soluzione (PIC), rinunciando a una piccola parte di rendimento: definiremo questa modalità di investimento PIC Value Averaging.
Perché si dovrebbe ricorrere ad un PIC Value Averaging invece che ad un PAC Value Averaging con disponibilità di un fondo di liquidità iniziale?
Perché alcuni investitori, pur temendo di prendere posizione sui mercati azionari impiegando il proprio capitale in un’unica soluzione, potrebbero non esser disposti a spalmare il loro investimento in un periodo di tempo compreso tra i 2 e i 10 anni: vogliono farlo in tempi più brevi.
Chi decide di impiegare questa strategia, tende di solito a suddividere il capitale in 3, 6 o magari 12 rate uguali, investendole a distanza di uno o più mesi l’una dall’altra. La variante proposta è simile, ma adotta il Value Averaging per la determinazione del valore di ciascun versamento.
Un PIC Value Averaging permette di iniziare a investire subito, senza dover ricorrere al troppo rischioso PIC o al troppo lento PAC.
La distribuzione della somma iniziale dovrebbe effettuarsi sulla base delle seguenti regole:
- Un numero di versamenti non superiore a 24. Andando oltre, si entrerebbe nel territorio dei piani di accumulo Value Averaging con fondo di liquidità iniziale. Quest’ultimo è un approccio diverso, più tranquillo: l’ottica di investimento è più simile a quella del PAC.
- Rate consistenti: ad esempio, se si dispone di un capitale pari a 100.000 euro, si possono ipotizzare 10 rate da 10.000 euro, 15 rate da 6.667 euro o 20 rate da 5.000 euro ciascuna (abbiamo semplificato; in realtà, trattandosi di un Value Averaging l’importo sarà variabile).
- Modalità di investimento da utilizzare: Value Averaging No-Sell con incrementi costanti del target. Non è opportuno vendere quote in questa tipologia di investimento, che è teoricamente molto simile al PIC: ciò che varia è soltanto la modalità di sottoscrizione delle quote, diversificata temporalmente invece che concentrata in un’unica soluzione. Anche un incremento del target crescente non è giustificato da un punto di vista teorico: le rate non sono molte e, seguendo la filosofia dei PIC, si tende per quanto possibile a non posticipare l’investimento.
- Massimale ai versamenti: si può inserire ed è consigliabile adottare un valore almeno doppio di quello della rata iniziale.
- Importo versato: non deve superare quello inizialmente disponibile. Se il capitale è di 100.000 euro, una volta investita tutta la cifra i versamenti dovranno fermarsi e il PIC Value Averaging si trasformerà in un PIC classico. Le quote sottoscritte saranno mantenute fino al raggiungimento dell’orizzonte temporale d’investimento.
Anche il PIC Value Averaging può essere interpretato come una metodologia di diversificazione: non di tipo spaziale, come avviene distribuendo il capitale tra vari strumenti finanziari di diversa tipologia al tempo 0, ma temporale, ovvero generata dalla distribuzione della somma da investire al tempo 0, 1, 2, …, n−1.
I due tipi di diversificazione potrebbero comunque coesistere.
In un mercato tendenzialmente crescente, come quello azionario, un PIC Value Averaging non sarà quasi mai più efficiente di un PIC puro. Non è questo il suo scopo: ciò che interessa è una riduzione della volatilità attesa dei rendimenti; non la massimizzazione di questi ultimi.
L’obiettivo finale è supportare l’investitore e convincerlo, se necessario, a fare un passo in più: prendere posizione sul mercato.
Per confermare la bontà di un PIC Value Averaging anche da un punto di vista matematico, dovremo assicurarci che i rendimenti attesi siano meno volatili di quelli dei PIC puri.
Simuleremo questa strategia sullo stesso fondo azionario Raiffeisen analizzato in precedenza.
I parametri delle due analisi che effettueremo sono i seguenti:
- Capitale investito: 100.000 euro.
- Distribuzione del capitale: 10 versamenti (rata iniziale di 10.000 euro) e 20 versamenti (rata iniziale di 5.000 euro).
- Applicazione del Value Averaging No-Sell, con incremento del target costante.
- Massimo versamento: il doppio della rata iniziale (20.000 e 10.000 euro).
Nei PIC Value Averaging, evitiamo di calcolare il rendimento annualizzato: la critica di Hayley è valida anche adesso e il fondo di liquidità iniziale (100.000 euro nel nostro esempio) causerebbe una leggera distorsione nel calcolo.
I risultati dei PIC Value Averaging applicati al fondo Raiffeisen - Azionario Globale VT analizzato in precedenza sono i seguenti:
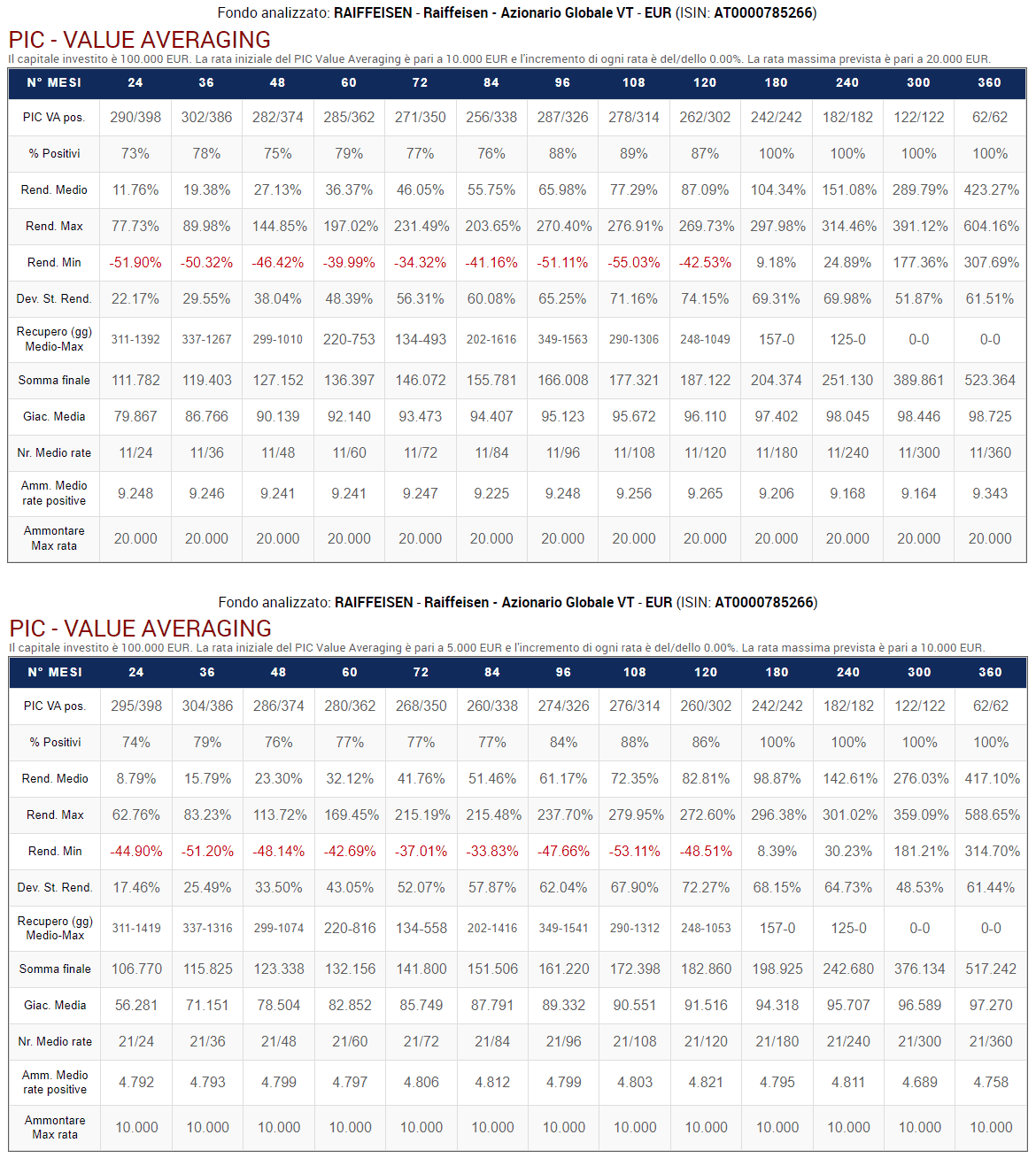
Fig. 92 – PIC Value Averaging (No-Sell) sul fondo Raiffeisen. Capitale: 100.000 euro. Rata iniziale 5.000 euro (20 versamenti) e 10.000 euro (10 versamenti). Target costante. Versamento massimo 5.000 e 10.000 euro
Questi sono invece quelli dei PIC puri (lump sum):
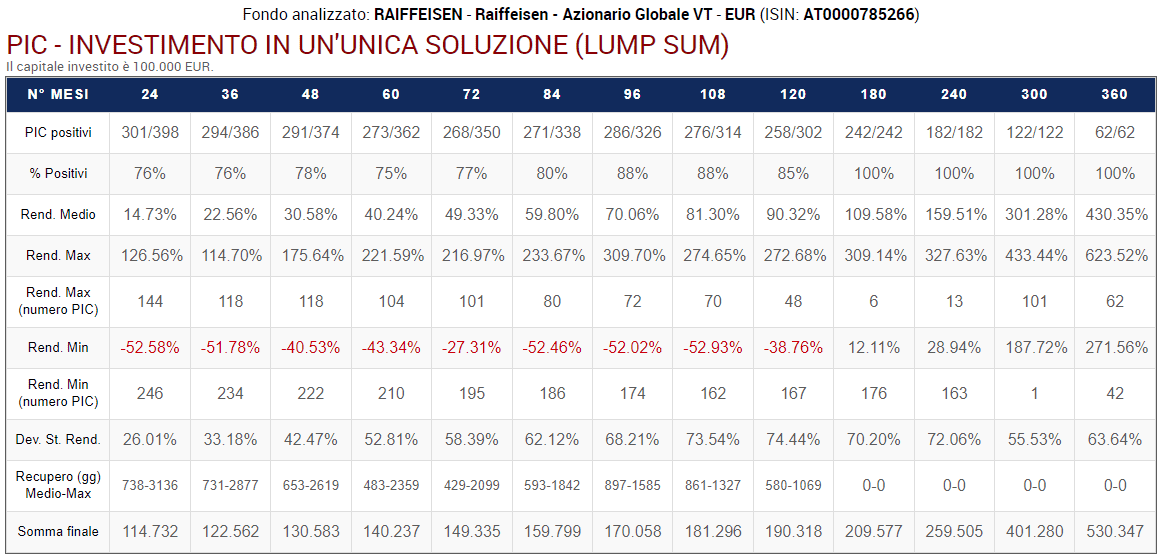
Fig. 93 – PIC puri. Capitale: 100.000 euro
I versamenti di tutti i PIC Value Averaging sono stati, in media, 11 e 21. Le diverse colonne identificano le performance dei PIC Value Averaging costruiti con le regole formulate poco sopra e mantenuti per il numero di mesi indicato nelle varie colonne.
Nella seconda figura, invece, sono rappresentate le performance dei PIC puri: investimenti effettuati in un’unica soluzione.
La deviazione standard dei rendimenti dei PIC Value Averaging è sensibilmente inferiore a quella dei PIC puri: col crescere della lunghezza del PIC, la differenza tende a diminuire. La deviazione standard è minore nella seconda tabella, quella con un numero doppio di versamenti, in quanto la diversificazione temporale è maggiore.
Una minore volatilità rispetto ad un PIC puro è ciò che desideravamo: questa strategia non offre soltanto un supporto psicologico per prendere posizione sul mercato; c’è anche la conferma statistica di una deviazione standard inferiore, ovvero un rischio minore.
Il prezzo che si paga per questa sorta di “assicurazione” è il rendimento. La minore volatilità è infatti accompagnata da un rendimento medio inferiore: tanto minore, quanto maggiore è la diversificazione temporale del PIC Value Averaging.
Il rendimento è decisamente inferiore nelle durate brevi, ma è bene ricordare che un investimento azionario dovrebbe essere sempre di medio/lungo termine (almeno 10 anni). Dai 10 anni in su, le differenze di rendimento tendono ad appiattirsi.
Se il PIC Value Averaging aiutasse davvero gli investitori a posizionarsi sul mercato fin da subito, senza perdere tempo aspettando una crisi finanziaria che potrebbe anche non verificarsi, una piccola differenza di rendimento sarebbe l’ultimo dei problemi: sarebbe stato evitato un costo opportunità molto più alto, generato dall’inutile attesa.
Verifichiamo i risultati che si sarebbero ottenuti sul fondo Aberdeen Japanese Equity Fund A Acc JPY, caratterizzato da un andamento decrescente di lungo termine.
Questi sono i risultati del PIC Value Averaging:
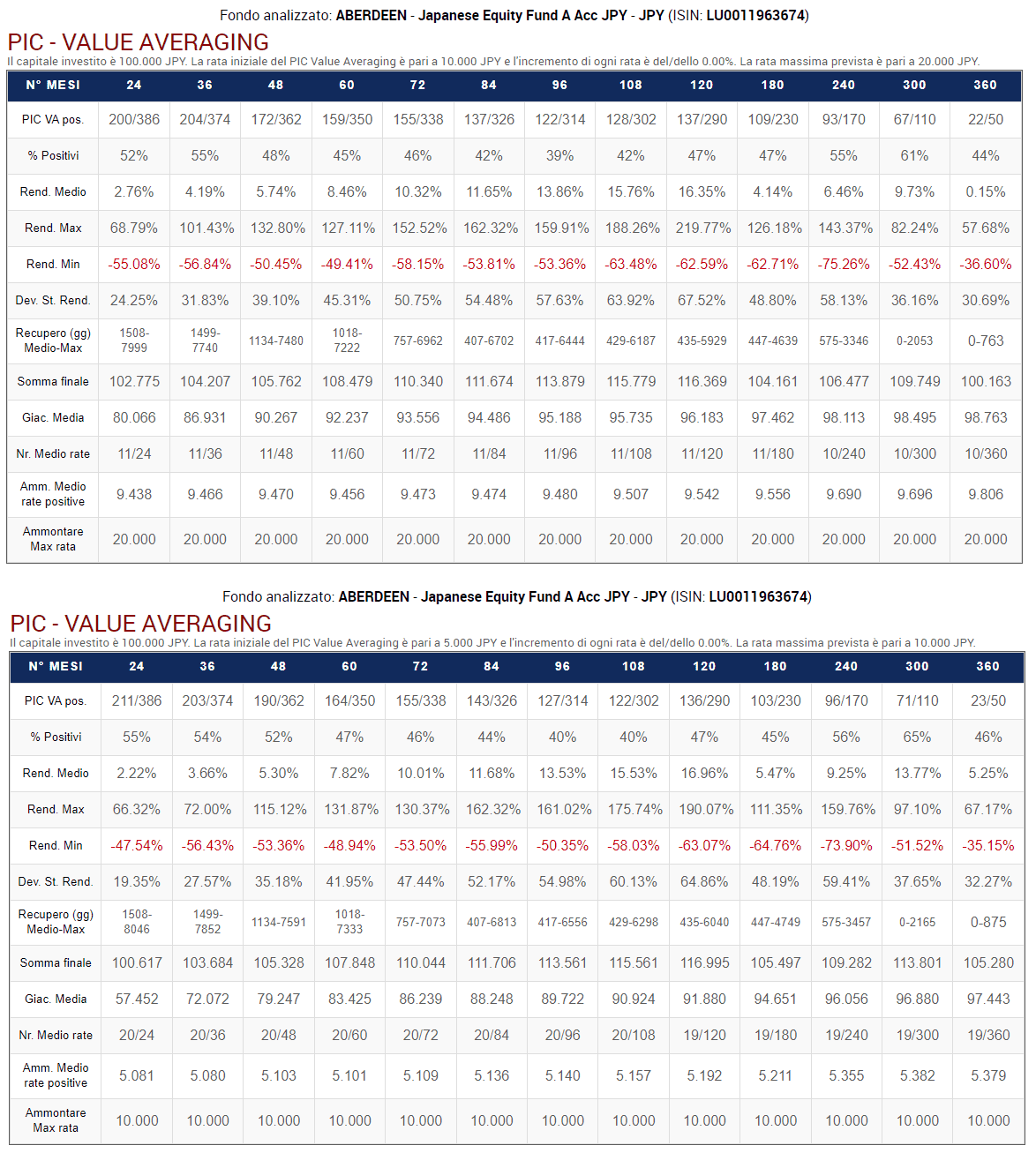
Fig. 94 – PIC Value Averaging (No-Sell) sul fondo Aberdeen. Capitale: 100.000 euro. Rata iniziale 5.000 euro (20 versamenti) e 10.000 euro (10 versamenti). Target costante. Versamento massimo 5.000 e 10.000 euro
I PIC puri hanno invece generato le performance seguenti:
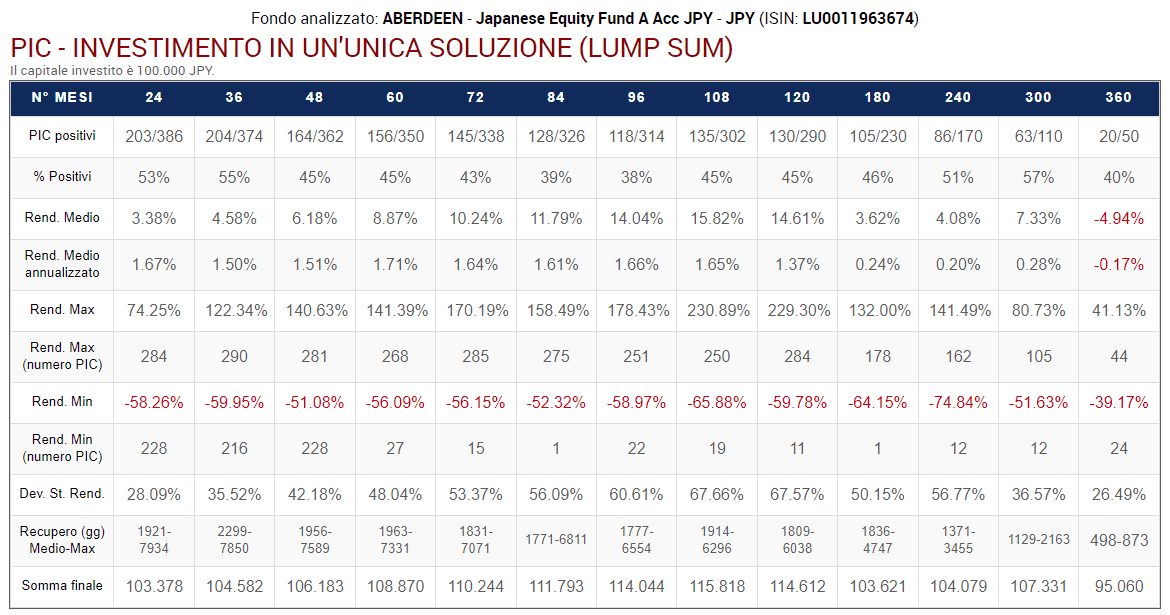
Fig. 95 – PIC puri. Capitale: 100.000 euro
La deviazione standard è, anche stavolta, inferiore nei PIC Value Averaging. Ma c’è di più: il trend decrescente ha permesso ai PIC Value Averaging di ottenere:
- Rendimenti mediamente più alti di quelli dei PIC puri sulle durate superiori ai 5 anni.
- Percentuali di PAC positivi non inferiori a quelle dei PIC puri su quasi tutte le durate (qualche eccezione si verifica in quelle più brevi).
I risultati ottenuti sembrano confermare come i PIC Value Averaging siano meno rischiosi di quelli puri.
Verifichiamo i risultati ottenuti con le simulazioni Monte Carlo.
Abbiamo di nuovo simulato 100.000 serie storiche di rendimenti mensili che seguono la distribuzione normale con media pari a 0,5% e deviazione standard del 5%.
Utilizzando 20 versamenti, i risultati ottenuti sono i seguenti:
| Media 0,50%, Deviazione standard 5% - 100.000 simulazioni | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. totale | St. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. |
| PIC | 360 | VA | 473,93% | 669,90% | 573.926 | 0 | 573.926 | 10.000 | 19.380,53% | −95,33% | 92,116% | 273,59% | 4,826 | 48,871 |
| PIC | 300 | VA | 322,96% | 424,57% | 422.963 | 0 | 422.963 | 10.000 | 14.869,49% | −94,19% | 90,123% | 197,72% | 4,075 | 43,129 |
| PIC | 240 | VA | 213,68% | 270,42% | 313.680 | 0 | 313.680 | 10.000 | 4.845,00% | −90,79% | 87,489% | 137,18% | 3,074 | 18,391 |
| PIC | 180 | VA | 132,00% | 165,57% | 231.996 | 0 | 231.996 | 10.000 | 2.581,22% | −88,83% | 83,842% | 89,11% | 2,490 | 12,357 |
| PIC | 120 | VA | 72,05% | 93,71% | 172.055 | 0 | 172.055 | 10.000 | 1.305,20% | −86,51% | 79,004% | 51,18% | 1,775 | 6,109 |
| PIC | 60 | VA | 27,86% | 43,92% | 127.857 | 2 | 127.859 | 10.000 | 466,45% | −74,20% | 71,449% | 21,46% | 1,010 | 1,856 |
| PIC | 36 | VA | 13,31% | 26,25% | 113.263 | 44 | 113.307 | 10.000 | 166,09% | −60,94% | 66,836% | 10,77% | 0,568 | 0,423 |
| PIC | 24 | VA | 6,73% | 16,16% | 105.181 | 1.547 | 106.729 | 10.000 | 83,03% | −53,48% | 64,857% | 6,20% | 0,173 | −0,120 |
| PIC | 360 | Puro | 502,75% | 723,62% | 602.752 | 0 | 602.752 | 0 | 22.053,02% | −94,37% | 92,284% | 285,13% | 5,063 | 55,156 |
| PIC | 300 | Puro | 344,83% | 461,98% | 444.831 | 0 | 444.831 | 0 | 17.368,32% | −94,35% | 90,249% | 207,70% | 4,300 | 49,274 |
| PIC | 240 | Puro | 229,30% | 293,96% | 329.297 | 0 | 329.297 | 0 | 5.896,05% | −90,17% | 87,679% | 144,95% | 3,208 | 20,393 |
| PIC | 180 | Puro | 143,87% | 183,16% | 243.866 | 0 | 243.866 | 0 | 2.988,09% | −90,66% | 84,041% | 95,08% | 2,654 | 13,937 |
| PIC | 120 | Puro | 80,93% | 105,78% | 180.928 | 0 | 180.928 | 0 | 1.369,44% | −88,35% | 79,413% | 56,14% | 1,929 | 7,092 |
| PIC | 60 | Puro | 34,33% | 53,29% | 134.335 | 0 | 134.335 | 0 | 631,40% | −80,66% | 71,940% | 25,14% | 1,236 | 2,940 |
| PIC | 36 | Puro | 19,14% | 36,04% | 119.143 | 0 | 119.143 | 0 | 295,42% | −70,00% | 67,119% | 14,22% | 0,898 | 1,431 |
| PIC | 24 | Puro | 12,16% | 27,12% | 112.156 | 0 | 112.156 | 0 | 198,08% | −64,42% | 64,237% | 9,13% | 0,701 | 0,839 |
Fig. 96 – PIC Value Averaging (No-Sell) e puro. Capitale: 100.000 euro. Rata iniziale 5.000 euro (20 versamenti). Target costante. Versamento massimo 10.000 euro. Parametri: media 0,50%, deviazione standard 5%
I risultati dei PIC con 10 versamenti, generati da 100.000 nuove simulazioni, sono invece questi:
| Media 0,50%, Deviazione standard 5% - 100.000 simulazioni (10 versamenti) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. totale | St. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. |
| PIC | 360 | VA | 487,33% | 702,90% | 587.327 | 0 | 587.327 | 20.000 | 22.397,24% | −93,17% | 92,187% | 280,03% | 5,593 | 74,075 |
| PIC | 300 | VA | 333,16% | 443,55% | 433.163 | 0 | 433.163 | 20.000 | 12.540,52% | −91,95% | 90,131% | 201,30% | 4,117 | 38,751 |
| PIC | 240 | VA | 221,38% | 281,72% | 321.377 | 0 | 321.377 | 20.000 | 4.347,08% | −93,72% | 87,713% | 141,29% | 3,079 | 17,693 |
| PIC | 180 | VA | 138,41% | 172,54% | 238.410 | 0 | 238.410 | 20.000 | 3.286,45% | −85,11% | 84,251% | 92,97% | 2,524 | 13,182 |
| PIC | 120 | VA | 76,48% | 100,05% | 176.479 | 0 | 176.479 | 20.000 | 1.964,46% | −88,04% | 79,224% | 53,73% | 1,943 | 8,134 |
| PIC | 60 | VA | 31,08% | 48,77% | 131.081 | 0 | 131.081 | 20.000 | 405,80% | −73,68% | 71,749% | 22,92% | 1,119 | 2,206 |
| PIC | 36 | VA | 16,37% | 31,57% | 116.367 | 0 | 116.367 | 20.000 | 243,80% | −64,47% | 66,929% | 12,58% | 0,781 | 1,090 |
| PIC | 24 | VA | 9,58% | 22,43% | 109.580 | 0 | 109.580 | 20.000 | 167,10% | −58,63% | 63,895% | 7,53% | 0,560 | 0,534 |
| PIC | 360 | Puro | 500,77% | 729,73% | 600.774 | 0 | 600.774 | 0 | 27.869,50% | −93,52% | 92,278% | 286,10% | 5,909 | 86,940 |
| PIC | 300 | Puro | 343,33% | 460,89% | 443.325 | 0 | 443.325 | 0 | 12.923,02% | −91,63% | 90,262% | 206,40% | 4,165 | 38,743 |
| PIC | 240 | Puro | 228,86% | 293,50% | 328.864 | 0 | 328.864 | 0 | 4.978,32% | −93,65% | 87,753% | 145,03% | 3,151 | 18,692 |
| PIC | 180 | Puro | 144,01% | 180,74% | 244.008 | 0 | 244.008 | 0 | 3.621,93% | −87,28% | 84,365% | 95,88% | 2,609 | 14,259 |
| PIC | 120 | Puro | 80,55% | 105,69% | 180.550 | 0 | 180.550 | 0 | 2.266,56% | −87,70% | 79,349% | 56,00% | 2,042 | 9,263 |
| PIC | 60 | Puro | 34,13% | 53,10% | 134.133 | 0 | 134.133 | 0 | 509,11% | −76,13% | 71,919% | 24,64% | 1,212 | 2,644 |
| PIC | 36 | Puro | 19,02% | 35,80% | 119.021 | 0 | 119.021 | 0 | 302,85% | −69,73% | 67,224% | 14,21% | 0,886 | 1,424 |
| PIC | 24 | Puro | 12,10% | 27,15% | 112.098 | 0 | 112.098 | 0 | 236,86% | −62,05% | 64,258% | 9,00% | 0,713 | 0,947 |
Fig. 97 – PIC Value Averaging (No-Sell) e puro. Capitale: 100.000 euro. Rata iniziale 10.000 euro (10 versamenti). Target costante. Versamento massimo 20.000 euro. Parametri: media 0,50%, deviazione standard 5%
Le simulazioni Monte Carlo confermano la minore deviazione standard dei PIC Value Averaging e un maggior rendimento medio dei PIC puri.
Un altro interessante risultato a favore dei PIC Value Averaging è quello del rendimento minimo dei 100.000 PIC simulati: i rendimenti del peggior PIC Value Averaging sono stati del −53,48%/−58,63% (24 mesi); quelli del peggior PIC puro sono stati rispettivamente del −64,42%/−62,05%.
Sono valori pessimi, ma dobbiamo ricordarci che sono i peggiori rendimenti delle 100.000 serie storiche simulate (la differenza tra un −53% e un −64% non è, comunque ,marginale).
Con il crescere delle durate, il gap si affievolisce ma rimane vistoso fino ai 10-15 anni. È un’ulteriore conferma che il supporto psicologico non è fine a sé stesso: il minor rischio di questa strategia non è soltanto percepito; è reale.
Verifichiamo se queste dinamiche permangono in caso di media pari a 0% (stessa deviazione standard).
Lanciamo 100.000 simulazioni parametriche con metodo Monte Carlo utilizzando 20 versamenti:
| Media 0%, Deviazione standard 5% - 100.000 simulazioni | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. totale | St. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. |
| PIC | 360 | VA | −0,16% | 117,17% | 99.841 | 0 | 99.841 | 10.000 | 7.075,18% | −98,95% | 32,125% | −35,22% | 6,335 | 167,725 |
| PIC | 300 | VA | −0,01% | 101,57% | 99.986 | 0 | 99.986 | 10.000 | 2.614,39% | −99,03% | 33,677% | −30,14% | 3,904 | 32,488 |
| PIC | 240 | VA | −0,02% | 87,38% | 99.979 | 0 | 99.979 | 10.000 | 2.079,76% | −96,79% | 35,203% | −24,61% | 3,287 | 23,373 |
| PIC | 180 | VA | −0,11% | 71,21% | 99.895 | 0 | 99.895 | 10.000 | 1.131,05% | −95,60% | 37,534% | −18,45% | 2,470 | 12,023 |
| PIC | 120 | VA | 0,11% | 55,15% | 100.111 | 0 | 100.111 | 10.000 | 742,84% | −90,55% | 40,107% | −12,29% | 1,825 | 6,622 |
| PIC | 60 | VA | 0,05% | 34,75% | 100.051 | 0 | 100.051 | 10.000 | 310,29% | −80,48% | 43,899% | −5,19% | 1,012 | 1,820 |
| PIC | 36 | VA | 0,01% | 23,74% | 100.007 | 8 | 100.015 | 10.000 | 155,59% | −64,52% | 45,744% | −2,54% | 0,631 | 0,617 |
| PIC | 24 | VA | −0,02% | 15,74% | 99.310 | 666 | 99.976 | 10.000 | 73,03% | −53,65% | 48,231% | −0,71% | 0,228 | −0,076 |
| PIC | 360 | Puro | −0,15% | 120,48% | 99.851 | 78 | 99.929 | 0 | 7.757,54% | −98,99% | 31,879% | −36,32% | 6,850 | 207,277 |
| PIC | 300 | Puro | 0,08% | 105,38% | 100.083 | 29 | 100.111 | 0 | 2.864,00% | −99,22% | 33,188% | −31,21% | 4,164 | 37,425 |
| PIC | 240 | Puro | 0,00% | 90,41% | 100.000 | 22 | 100.021 | 0 | 2.168,25% | −97,44% | 34,796% | −25,97% | 3,349 | 23,271 |
| PIC | 180 | Puro | −0,08% | 74,80% | 99.915 | 15 | 99.931 | 0 | 1.546,79% | −95,22% | 37,061% | −19,67% | 2,714 | 15,664 |
| PIC | 120 | Puro | 0,13% | 59,05% | 100.128 | 12 | 100.139 | 0 | 1.169,84% | −91,93% | 39,569% | −13,61% | 2,029 | 8,808 |
| PIC | 60 | Puro | 0,07% | 39,75% | 100.074 | 4 | 100.078 | 0 | 368,84% | −82,49% | 42,734% | −6,80% | 1,205 | 2,591 |
| PIC | 36 | Puro | 0,01% | 30,28% | 100.011 | 3 | 100.013 | 0 | 276,74% | −71,00% | 44,260% | −4,20% | 0,924 | 1,578 |
| PIC | 24 | Puro | −0,03% | 24,26% | 99.965 | 2 | 99.967 | 0 | 220,62% | −63,63% | 45,403% | −2,76% | 0,714 | 0,939 |
Fig. 98 – PIC Value Averaging (No-Sell) e puro. Capitale: 100.000 euro. Rata iniziale 5.000 euro (20 versamenti). Target costante. Versamento massimo 10.000 euro. Parametri: media 0%, deviazione standard 5%
Eseguiamo quindi altre 100.000 simulazioni parametriche col metodo Monte Carlo relative ai PIC Value Averaging con 10 versamenti:
| Media 0%, Deviazione standard 5% - 100.000 simulazioni (10 versamenti) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strat. | Rate mens. | Tipol. | Rend. totale | St. Dev. | Mont. | Liq. | Somma finale | Rata max | Rend. max | Rend. min | % Pos. | Med. | Skew. | Kurt. |
| PIC | 360 | VA | 0,11% | 118,04% | 100.107 | 0 | 100.107 | 20.000 | 2.871,73% | −98,75% | 32,185% | −35,73% | 4,727 | 45,396 |
| PIC | 300 | VA | −0,03% | 103,57% | 99.969 | 0 | 99.969 | 20.000 | 2.221,05% | −98,26% | 33,559% | −30,70% | 4,019 | 32,502 |
| PIC | 240 | VA | 0,12% | 88,50% | 100.116 | 0 | 100.116 | 20.000 | 1.860,14% | −97,04% | 35,363% | −24,95% | 3,177 | 20,031 |
| PIC | 180 | VA | 0,21% | 73,61% | 100.206 | 0 | 100.206 | 20.000 | 1.316,06% | −95,63% | 37,502% | −18,90% | 2,589 | 13,628 |
| PIC | 120 | VA | −0,38% | 56,52% | 99.624 | 0 | 99.624 | 20.000 | 554,12% | −91,53% | 39,374% | −13,33% | 1,786 | 5,668 |
| PIC | 60 | VA | 0,00% | 37,44% | 100.001 | 0 | 100.001 | 20.000 | 360,16% | −83,72% | 43,004% | −6,20% | 1,140 | 2,305 |
| PIC | 36 | VA | 0,11% | 27,23% | 100.113 | 0 | 100.113 | 20.000 | 214,45% | −74,42% | 45,054% | −3,31% | 0,789 | 1,112 |
| PIC | 24 | VA | −0,01% | 20,65% | 99.994 | 0 | 99.994 | 20.000 | 132,25% | −62,25% | 46,257% | −1,91% | 0,580 | 0,625 |
| PIC | 360 | Puro | 0,12% | 119,75% | 100.117 | 0 | 100.117 | 0 | 3.079,15% | −98,87% | 31,993% | −36,26% | 4,833 | 47,618 |
| PIC | 300 | Puro | −0,07% | 105,06% | 99.927 | 0 | 99.927 | 0 | 2.377,27% | −98,57% | 33,328% | −31,21% | 4,095 | 33,524 |
| PIC | 240 | Puro | 0,11% | 89,99% | 100.110 | 0 | 100.110 | 0 | 1.908,70% | −97,22% | 35,123% | −25,47% | 3,251 | 21,097 |
| PIC | 180 | Puro | 0,25% | 75,22% | 100.249 | 0 | 100.249 | 0 | 1.338,40% | −96,02% | 37,282% | −19,56% | 2,666 | 14,601 |
| PIC | 120 | Puro | −0,40% | 58,30% | 99.601 | 0 | 99.601 | 0 | 643,33% | −92,08% | 39,036% | −13,96% | 1,865 | 6,256 |
| PIC | 60 | Puro | 0,01% | 39,82% | 100.010 | 0 | 100.010 | 0 | 409,18% | −86,93% | 42,476% | −7,00% | 1,240 | 2,798 |
| PIC | 36 | Puro | 0,10% | 30,19% | 100.101 | 0 | 100.101 | 0 | 251,68% | −75,73% | 44,472% | −4,14% | 0,901 | 1,465 |
| PIC | 24 | Puro | 0,01% | 24,35% | 100.010 | 0 | 100.010 | 0 | 176,37% | −68,79% | 45,512% | −2,69% | 0,720 | 0,983 |
Fig. 99 – PIC Value Averaging (No-Sell) e puro. Capitale: 100.000 euro. Rata iniziale 10.000 euro (10 versamenti). Target costante. Versamento massimo 20.000 euro. Parametri: media 0%, deviazione standard 5%
La minor volatilità ci viene confermata dalla deviazione standard, minore in entrambi i PIC Value Averaging. Il minor rischio è comprovato dai migliori rendimenti minimi e, stavolta, anche da una percentuale più alta di PIC positivi.
Questi risultati sono confortanti e costituiscono un piccolo passo verso uno spostamento del focus di un investimento dal solo rendimento ad aspetti più prettamente di finanza comportamentale.
La spasmodica ricerca dell’efficienza è giustificata quando a perseguirla sono gli operatori professionali (come, ad esempio, i gestori dei fondi), che si muovono generalmente in un ambiente fortemente competitivo; diventa un ostacolo e una fonte di insicurezza, stress e logorio psicologico per l’investitore medio.
L’efficienza e la razionalità sono da secoli i principi cardine dell’economia; soltanto in tempi recenti sono stati messi in discussione: si sta pian piano diffondendo la consapevolezza che troppo spesso siano soltanto delle astrazioni teoriche.
In materia di finanza personale, tutto questo è ancora più vero e si dovrebbe perseguire ogni sforzo possibile per favorire un nuovo modo di relazionare l’investitore con i mercati finanziari: più consapevole, paziente, diligente e rilassato.
14. Conclusioni

«La conclusione è il punto dove ti sei stufato di pensare».
Arthur Bloch
I grafici e le tabelle analizzate in questo lavoro permettono di capire le differenze tra le varie modalità del Value Averaging e del Cost Averaging, nonché tra un PIC Value Averaging e un PIC puro.
I backtest sono stati inizialmente condotti su un paio di fondi azionari, ma hanno coinvolto centinaia di Piani di Accumulo del Capitale, di diverse durate, che hanno attraversato lunghi periodi e numerose crisi finanziarie: tra le principali ricordiamo il Black Monday (1987), il crollo del rublo (crisi finanziaria russa del 1998), la bolla Dot-com (2000-2003), quella dei Subprime (2007-2009) e il più recente COVID-19 (2020).
Le analisi sono proseguite con l’utilizzo del metodo Monte Carlo, grazie alla simulazione di diversi milioni di serie storiche dei rendimenti. Il Value Averaging ha confermato i risultati precedentemente ottenuti e si è dimostrato essere una valida modalità di investimento, alternativa al piano di accumulo classico (Cost Averaging).
Ci sembra che le critiche ricevute dal Value Averaging negli ultimi anni siano state troppo severe. Da una parte, hanno giustamente messo in luce una distorsione nel calcolo dei rendimenti che autori precedenti non avevano individuato; dall’altra, hanno condannato in toto questa modalità di investimento, che si è invece dimostrata migliore del Cost Averaging in molte circostanze, anche dopo aver eliminato le distorsioni evidenziate.
A partire da queste critiche, abbiamo sviluppato un nuovo modo di investire un capitale iniziale con l'ausilio di un PAC Value Averaging. Questa metodologia è un ibrido tra un PAC e un PIC: una strategia di investimento che sembra generare ottimi risultati con un rischio relativamente basso.
Per finire, abbiamo esplorato il PIC Value Averaging, una variante da utilizzarsi su durate molto brevi: un PIC trasformato da investimento in un’unica soluzione a uno in più versamenti, da effettuarsi con le logiche del Value Averaging.
Il PAC Value Averaging con un fondo di liquidità iniziale e il PIC Value Averaging non hanno la pretesa di ottenere rendimenti superiori al Buy and Hold: il loro scopo principale è quello di diminuire il rischio dell’investimento, che è spesso la causa dell’inattività degli investitori.
Talvolta, la prudenza è raccomandata anche dai consulenti finanziari. A seconda della propensione al rischio del cliente, questa prudenza è la giusta espressione di un dovere deontologico del consulente stesso, e non può che essere vista positivamente.
Altre volte, però, viene oltremodo enfatizzata – con la conseguenza che il cliente si ritrova con troppi prodotti obbligazionari in portafoglio – o, peggio ancora, la prudenza viene soltanto ostentata: al povero investitore vengono magari consigliati fondi contrarian (fondi che guadagnano se i mercati scendono) o strumenti finanziari derivati o complessi, il cui alto rischio potrebbe non essere correttamente percepito dai clienti.
Il Value Averaging può essere lo strumento giusto per superare l’immobilità e l’eccessiva cautela: aiuterà a sostituire l’attesa con l’azione e permetterà di rinunciare al market timing e alla frenetica, ma spesso sterile, ricerca dell’efficienza.
15. Bibliografia
Edleson, Value Averaging, John Wiley & Sons, 2007.
Hayley, Value Averaging and the Automated Bias of Performance Measures, 2010.
Marshall, A Statistical Comparison of Value Averaging vs. Dollar Cost Averaging and Random Investment Techniques, Journal of Financial and Strategic Decisions, Vol. 13, No. 1, Spring 2000.
Il Percorso intermedio continua con l'articolo:


