Il rischio di cambio negli investimenti finanziari
- Information
- Investimenti finanziari
- Prima pubblicazione: 06 Agosto 2023
«The true currency of life is time, not money, and we've all got a limited stock of that».
Robert Harris
I concetti discussi in questo articolo possono essere approfonditi nel libro disponibile in formato ebook e cartaceo su Amazon: Il rischio di cambio negli investimenti finanziari.
Questo articolo fa parte del Percorso per principianti, pensato per chi desidera apprendere le basi della finanza personale e degli investimenti. In fondo alla pagina, troverai il link al prossimo articolo del percorso.
Quando decido di investire in un asset denominato in una valuta diversa dall’euro e non utilizzo l’hedging, mi espongo al rischio di cambio. Questo rischio si combina con quello di mercato.
Consideriamo l’esempio di un investitore dell’area euro che acquista uno strumento finanziario quotato in dollari statunitensi. In questo caso, l’euro rappresenta la valuta domestica, mentre il dollaro è la valuta estera.
A meno che non si decida di speculare intenzionalmente sul cambio – ovvero assumersi volontariamente il rischio di cambio su una o più valute estere perché si prevede che il cambio vada in una certa direzione – il nostro investimento sarà soggetto sia al rischio di mercato che al rischio di cambio.
Di solito, siamo consapevoli di assumerci il rischio di mercato; raramente, però, è altrettanto chiaro l’impatto che il rischio di cambio potrebbe avere sul nostro investimento.
Il rischio di cambio può influenzare le performance di un investimento in tre modi:
- Impatto sul rendimento.
- Impatto sulla volatilità.
- Impatto sulle altre misure di rischio (massimo drawdown, periodo di recupero, Ulcer Index, VaR e CVaR).
L’impatto del rischio di cambio sul rendimento di un investimento si manifesta come una correzione verso l'alto o verso il basso del rendimento di mercato. La variazione sarà positiva o negativa in funzione della differenza di valore del tasso di cambio tra l’inizio e la fine dell’investimento.
Se il tasso di cambio si muove a favore dell’investitore, il rendimento complessivo dell’investimento aumenta, mentre se il tasso di cambio si muove contro l’investitore, il rendimento diminuisce.
Nel libro citato all'inizio dell'articolo, Il rischio di cambio negli investimenti finanziari, vengono approfonditi tutti questi aspetti.
Il libro è composto da 13 capitoli e 6 appendici. Di seguito è riportato l'indice completo:
Prefazione di Massimo Scolari, Presidente di Ascofind
- Introduzione
- Le valute e i tassi di cambio
- Modelli di equilibrio dei tassi di cambio, bilancia dei pagamenti e politiche economiche
- Le condizioni di parità internazionale
- Parità coperta dei tassi d’interesse
- Parità scoperta dei tassi d’interesse
- Parità del tasso forward
- Parità del potere di acquisto (Purchasing Power Parity o PPP)
- L’equazione di Fisher
- Conclusioni
- La bilancia dei pagamenti
- Le politiche economiche
- Le condizioni di parità internazionale
- Le teorie naïf dei tassi di cambio
- Letteratura sulla stima dei tassi di cambio
- L’impatto del rischio di cambio sul rendimento
- L’impatto del rischio di cambio sulla volatilità
- L’impatto del rischio di cambio sul rendimento e sulla volatilità di un portafoglio con due titoli di diverse valute estere
- Studio della varianza e covarianza con lo S&P 500 TR di alcuni tassi di cambio
- L’impatto del cambio su altre misure di rischio
- L’hedging e il suo costo
- Il rischio di cambio nei PAC a rate costanti
- Conclusioni
———————————
Appendice 1: I rendimenti sotto forma di logaritmo e la dimostrazione della formula della varianza dei rendimenti in euro con un singolo titolo
Appendice 2: Dimostrazione della formula della varianza dei rendimenti in euro con due titoli
Appendice 3: Dimostrazione della formula della varianza dei rendimenti in euro con tre titoli
Appendice 4: Dimostrazione della formula della varianza dei rendimenti in euro con due titoli in diverse valute estere
Appendice 5: La covarianza
Appendice 6: La formula della varianza di un portafoglio con due o più titoli
Bibliografia
Ringraziamenti
———————————
Pubblichiamo qui di seguito l'intero sesto capitolo del libro "Il rischio di cambio negli investimenti finanziari", intitolato "L’impatto del rischio di cambio sul rendimento", con l'auspicio che possa aiutare a capire come questo importante rischio, spesso trascurato, possa influenzare la performance di un investimento.
L'impatto del rischio di cambio sul rendimento

«When markets go down, the only thing that goes up is correlation».
Anonimo
Quando si investe in uno strumento finanziario il cui sottostante è denominato in valuta estera, il rendimento viene influenzato dall’andamento del tasso di cambio tra la valuta estera e quella locale.
Il rischio di cambio non incide solo sul rendimento, ma influisce anche sulla volatilità di un investimento in valuta estera.
In certi casi, l’impatto sulla volatilità è così significativo da poter cambiare la natura dell’investimento stesso (da poco a molto rischioso).
Gli investitori tendono a concentrarsi principalmente sul rendimento ed è su questo che ci focalizzeremo in questo capitolo.
Ipotizziamo di investire nello S&P 500 Total Return. Essendo un indice azionario statunitense, il suo rendimento è espresso in dollari. Un investitore dell’area euro dovrà quindi convertire in dollari l’importo che intende investire.
Il rendimento finale dell’investimento nello S&P 500 TR sarà anch’esso in dollari: la somma ottenuta dovrà quindi essere convertita in euro. Il rendimento in valuta locale ottenuto dall’investitore dell’area euro sarà pari alla differenza tra l’importo finale incassato e quello iniziale investito, entrambi espressi in euro.
Facciamo un esempio, ignorando per semplicità le commissioni di cambio e di transazione:
- Abbiamo investito 1.000 euro nello S&P 500 TR il 3 gennaio 2022.
- Il 3 gennaio 2022, il tasso di cambio USD/EUR era pari a 1,1294. Cambiando i nostri 1.000 euro in dollari, abbiamo ottenuto 1.000 × 1,1294 = 1.129,40 dollari.
- Abbiamo disinvestito il 30 dicembre 2022. Durante questo periodo, lo S&P 500 TR ha subito una perdita del 18,63%. I 1.129,40 dollari sono perciò diventati 918,99.
- Il 30 dicembre 2022, il tasso di cambio USD/EUR era pari a 1,0702. Cambiando i nostri 918,99 dollari in euro, abbiamo ottenuto 918,99 / 1,0702 = 858,71 euro.
- Il nostro rendimento finale è stato del −14,13%.
Nel nostro esempio, l’andamento favorevole del tasso di cambio ha permesso di ridurre la perdita dal 18,63% al 14,13%.
Apriamo una breve parentesi sui tassi di cambio: un tasso di cambio rappresenta il numero di unità di una valuta che possono essere acquistate con un’unità di un’altra valuta. La valuta al numeratore è chiamata “valuta quotata” (price currency), mentre quella al denominatore è chiamata “valuta base” (base currency).
Le valute sono solitamente rappresentate da un codice di tre lettere: ad esempio, EUR per l’euro, USD per il dollaro statunitense, GBP per la sterlina inglese e così via.
Quando si dice che il tasso di cambio USD/EUR è pari a 1,0729, significa che con un euro si possono comprare 1,0729 dollari statunitensi. In questa situazione, l’euro è la valuta base, mentre il dollaro statunitense è la valuta quotata.
Le cose sarebbero potute andare diversamente: se il tasso di cambio si fosse mosso in direzione opposta, la perdita sarebbe aumentata.
Dal punto di vista matematico, possiamo riassumere tutti i passaggi precedenti con la seguente formula:
\begin{equation} r_{€} = \frac{\frac{\rm Somma_{e}}{\rm USD/{EUR}_{t1}}\times(1+r_\$)\times {\rm USD}/{\rm EUR}_{t0}-{\rm Somma_{e}}}{\rm Somma_{e}} \end{equation}
Dove:
r€ = Rendimento in euro (valuta locale).
Somma€ = Somma investita in euro.
USD/EURt0 = Tasso di cambio tra dollaro ed euro all’inizio dell’investimento (t0).
USD/EURt1 = Tasso di cambio tra dollaro ed euro alla fine dell’investimento (t1).
r$ = Rendimento in dollari (valuta estera).
Dopo aver semplificato la formula dividendo il numeratore per Somma€ otteniamo:
\begin{equation} r_€ = \frac{\rm USD}{\rm EUR_{t1}} \times (1 + r_\$ ) \times \frac{\rm USD}{\rm EUR_{t0}} - 1 \end{equation}
Che possiamo riscrivere come:
\begin{equation} r_€ = \frac{\rm USD/{\rm EUR}_{t0}}{\rm USD/{\rm EUR}_{t1}} \times (1 + r_$ ) - 1 \end{equation}
Il rendimento in euro è quindi pari al rapporto tra il tasso di cambio al momento dell’investimento (t0) e il tasso di cambio al momento del disinvestimento (t1), moltiplicato per il rendimento dello S&P 500 TR in dollari. Al risultato ottenuto deve essere sottratto 1.
Nell’esempio precedente, avremmo potuto calcolare il rendimento in euro utilizzando la seguente formula:
\begin{equation} r_€ = \frac{1,1294}{1,0702} \times (1 - 18,63\%) - 1 = -14,13\% \end{equation}
Dobbiamo prestare molta attenzione al corretto posizionamento delle valute nel tasso di cambio: nella formula finale, potrebbe sembrare controintuitivo dividere il tasso di cambio iniziale per quello finale; sembrerebbe più logico fare il contrario. È possibile farlo, ma in quel caso dobbiamo utilizzare il reciproco del tasso di cambio precedente, ovvero EUR/USD.
Il reciproco dei tassi di cambio precedenti è pari a 1/1,1294 = 0,8854 (EUR/USDt0) e a 1/1,0702 = 0,9344 (EUR/USDt1).
Il rendimento in valuta locale può essere adesso calcolato come segue:
\begin{equation} r_€ = \frac{\rm EUR/{\rm USD}_{t1}}{\rm EUR/{\rm USD}_{t0}} \times (1 + r_$ ) - 1 = \frac{0,9344}{0,8854} \times (1 - 18,63\%) - 1 = -14,13\% \end{equation}
Questa formula è molto importante perché ci consente di capire come ciascun elemento dell’investimento contribuisce al rendimento finale.
Riscriviamo la formula generale:
\begin{equation} r_€ = \frac{\rm USD/{\rm EUR}_{t0}}{\rm USD/{\rm EUR}_{t1}} \times (1 + r_$ ) - 1 \end{equation}
La prima quantità misura l’impatto dell’andamento del tasso di cambio:
- Se è maggiore di 1, significa che l’andamento è stato favorevole all’investitore dell’area euro. Questo si verifica quando l’euro si svaluta rispetto al dollaro.
- Se è minore di 1, si verifica l’opposto.
- Se è uguale a 1, il tasso di cambio non produce alcun effetto: il rendimento finale dell’investimento in euro sarà identico a quello in dollari.
La seconda quantità, (1 + r$), misura il rendimento dell’investimento in dollari più uno: nel nostro esempio, il rendimento dello S&P 500 TR dal 3 gennaio al 30 dicembre 2022.
Qual è l’intervallo di variazione di queste due quantità?
Dato che stiamo trattando valute forti come il dollaro e l’euro, possiamo aspettarci variazioni significative, ma probabilmente comprese tra 0,5 e 2. Ad esempio, se il dollaro si deprezza rispetto all’euro, facendo passare il tasso di cambio da 1,2 a 2,4, il rapporto precedente sarà pari a 0,5; se il dollaro si rivaluta rispetto all’euro facendo passare il tasso di cambio da 1,2 a 0,6, quel rapporto sarà pari a 2.
È importante sottolineare che questo intervallo di variazione, per quanto ampio, è soltanto indicativo. Non ha niente di particolare: lo utilizzeremo, per convenienza, in alcuni esempi successivi. Nella realtà, non possiamo escludere che si possano verificare valori esterni a questa forbice.
Anche se non siamo abituati a valutare l’impatto del tasso di cambio utilizzando la formula precedente, è fondamentale comprenderla bene.
In generale, abbiamo soltanto una vaga idea di come il rischio di cambio possa impattare il rendimento del nostro investimento: se siamo fortunati, lo amplificherà; se siamo sfortunati, lo diminuirà.
Quello che spesso non comprendiamo è quanto il rischio di cambio possa davvero incidere sul rendimento del nostro investimento. In questo senso, è necessario considerare quattro scenari, che esamineremo sempre dall’ottica di un soggetto dell’area euro che investe in titoli in dollari.
Nella matrice sottostante, abbiamo quattro quadranti: ciascuno di essi è contraddistinto dal rendimento positivo o negativo dell’investimento in valuta estera (nel nostro caso dollari) e dalla favorevole o sfavorevole variazione del tasso di cambio.

I possibili scenari sono i seguenti:
- Quadrante in alto a sinistra: se il rendimento del titolo in dollari è positivo e l’andamento del tasso di cambio è favorevole, il rendimento in euro sarà sicuramente più alto di quello in dollari.
- Quadrante in basso a destra: se il rendimento del titolo in dollari è negativo e l’andamento del tasso di cambio è sfavorevole, il rendimento in euro sarà sicuramente più basso di quello in dollari.
- Negli altri due casi, il rendimento in euro potrebbe essere sia positivo che negativo e sia superiore che inferiore a quello in dollari. Il suo posizionamento dipenderà dal rendimento in dollari e dalla variazione del rendimento del tasso di cambio.
Cerchiamo di chiarire meglio la terminologia utilizzata nei tassi di cambio. Fino a ora, abbiamo parlato di andamento favorevole o sfavorevole per l’investitore dell’area euro in relazione ai potenziali movimenti del tasso di cambio USD/EUR.
Contrariamente a quanto si potrebbe pensare, un andamento favorevole per l’investitore dell’area euro si verifica quando c’è una svalutazione dell’euro rispetto al dollaro.
Un andamento sfavorevole per l’investitore dell’area euro si verifica, invece, quando l’euro si rivaluta rispetto al dollaro.
Perché la svalutazione della sua valuta è favorevole all’investitore dell’area euro?
Il motivo è semplice: perché ha già convertito la sua liquidità da euro a dollari per investire in titoli denominati in dollari. Quando il dollaro si rinforza rispetto all’euro, si verifica un vantaggio per l’investitore dell’area euro poiché, al momento del disinvestimento, ognuno dei suoi dollari permetterà di acquistare più euro di quanto aveva consentito all’inizio dell’investimento.
In altre parole, l’investitore dell’area euro ha in mano dollari con i quali, quando deciderà di disinvestire, acquisterà euro: più l’euro si sarà svalutato, più saranno gli euro che potrà ottenere in cambio dei suoi dollari.
La svalutazione dell’euro, però, è negativa per tutti coloro che desiderano acquistare dollari o beni denominati in dollari ma non li possiedono già: in questo caso, dovranno pagare più euro adesso rispetto a quanto avrebbero pagato in precedenza, quando l’euro valeva di più rispetto al dollaro.
A complicare ulteriormente la situazione, si deve fare attenzione a non cadere nell’errore di pensare che ci sia una corrispondenza diretta tra le percentuali di svalutazione e rivalutazione tra due valute. Ad esempio, se l’euro si svaluta del 20% rispetto al dollaro, non significa automaticamente che il dollaro si sia rivalutato del 20% nei confronti dell’euro. Le percentuali di svalutazione e rivalutazione tra le due valute non sono speculari.
Per comprendere questa dinamica, possiamo effettuare un semplice calcolo, partendo dall’ipotesi che al momento t0 il tasso di cambio USD/EUR sia pari a 1:
- Se al momento t1 il tasso di cambio USD/EUR è aumentato fino a 1,20, si ha una rivalutazione dell’euro del 20%.
- Il tasso di cambio EUR/USD, ovvero il reciproco del tasso USD/EUR e anch’esso uguale a 1 al momento t0, a t1 scende a 1/(USD/EUR) = 1/1,20 = 0,8333.
- Di conseguenza, la svalutazione del dollaro rispetto all’euro è stata del –16,67%.
Supponiamo ora che, sempre partendo dal valore di 1, il tasso di cambio USD/EUR salga a 1,50:
- Se al momento t1 il tasso di cambio USD/EUR è pari a 1,50, si ha una rivalutazione dell’euro del 50%.
- Il tasso di cambio EUR/USD, ancora una volta pari al reciproco del tasso USD/EUR e anch’esso 1 al momento t0, a t1 scende a 1/(USD/EUR) = 1/1,50 = 0,6667.
- La svalutazione del dollaro rispetto all’euro è quindi del −33,33%.
Questa mancanza di corrispondenza tra le percentuali di rivalutazione e svalutazione delle due valute non dovrebbe sorprendere più di tanto: si basa sullo stesso principio che si applica ai rendimenti positivi e negativi degli investimenti finanziari.
Per esempio, se un investimento perde il 33,33%, non è sufficiente un incremento del 33,33% per riportarlo al valore iniziale. Sarà necessario un incremento del 50%, proprio come abbiamo osservato nell’esempio precedente, dove un aumento del 50% nel tasso di cambio USD/EUR (rivalutazione dell’euro del 50%) corrispondeva a una diminuzione del 33,33% nel tasso di cambio EUR/USD.
La seguente tabella aiuta a comprendere le relazioni esistenti tra le percentuali di svalutazione e di rivalutazione di due valute. Come sempre, nei nostri esempi consideriamo il dollaro e l’euro:
| Svalutazione / Rivalutazione EUR | Tasso di cambio iniziale USD/EUR | Tasso di cambio finale USD/EUR | Tasso di cambio finale EUR/USD | Rivalutazione / Svalutazione USD |
|---|---|---|---|---|
| -100% | 1,0000 | 0,0000 | ∞ | ∞ |
| -90% | 1,0000 | 0,1000 | 10,0000 | 900% |
| -80% | 1,0000 | 0,2000 | 5,0000 | 400% |
| -70% | 1,0000 | 0,3000 | 3,3333 | 233% |
| -60% | 1,0000 | 0,4000 | 2,5000 | 150% |
| -50% | 1,0000 | 0,5000 | 2,0000 | 100% |
| -40% | 1,0000 | 0,6000 | 1,6667 | 67% |
| -30% | 1,0000 | 0,7000 | 1,4286 | 43% |
| -20% | 1,0000 | 0,8000 | 1,2500 | 25% |
| -10% | 1,0000 | 0,9000 | 1,1111 | 11% |
| 0% | 1,0000 | 1,0000 | 1,0000 | 0% |
| 10% | 1,0000 | 1,1000 | 0,9091 | −9,09% |
| 20% | 1,0000 | 1,2000 | 0,8333 | −16,67% |
| 30% | 1,0000 | 1,3000 | 0,7692 | −23,08% |
| 40% | 1,0000 | 1,4000 | 0,7143 | −28,57% |
| 50% | 1,0000 | 1,5000 | 0,6667 | −33,33% |
| 60% | 1,0000 | 1,6000 | 0,6250 | −37,50% |
| 70% | 1,0000 | 1,7000 | 0,5882 | −41,18% |
| 80% | 1,0000 | 1,8000 | 0,5556 | −44,44% |
| 90% | 1,0000 | 1,9000 | 0,5263 | −47,37% |
| 100% | 1,0000 | 2,0000 | 0,5000 | −50,00% |
| 150% | 1,0000 | 2,5000 | 0,4000 | −60,00% |
| 200% | 1,0000 | 3,0000 | 0,3333 | −66,67% |
| 300% | 1,0000 | 4,0000 | 0,2500 | −75,00% |
| 400% | 1,0000 | 5,0000 | 0,2000 | −80,00% |
| 500% | 1,0000 | 6,0000 | 0,1667 | −83,33% |
| 600% | 1,0000 | 7,0000 | 0,1429 | −85,71% |
| 700% | 1,0000 | 8,0000 | 0,1250 | −87,50% |
| 800% | 1,0000 | 9,0000 | 0,1111 | −88,89% |
| 900% | 1,0000 | 10,0000 | 0,1000 | −90,00% |
| 1000% | 1,0000 | 11,0000 | 0,0909 | −90,91% |
Nella prima colonna, vengono elencate le percentuali di svalutazione e di rivalutazione del tasso di cambio USD/EUR.
La seconda colonna indica il tasso di cambio iniziale, che supponiamo essere sempre 1 all’inizio dell’investimento (1 EUR = 1 USD).
La terza colonna riflette il valore del tasso di cambio USD/EUR corrispondente alla variazione percentuale della prima colonna, sempre considerando che il tasso di cambio iniziale era pari a 1.
La quarta colonna mostra il reciproco del tasso di cambio della colonna precedente: si tratta del tasso di cambio EUR/USD.
La quinta colonna, infine, rappresenta la variazione percentuale del dollaro rispetto all’euro corrispondente alla variazione percentuale dell’euro rispetto al dollaro della prima colonna.
Prendiamo, ad esempio, una svalutazione dell’euro rispetto al dollaro del 20%:
- Nella prima colonna, troviamo il valore –20% (nona riga della tabella).
- La seconda e terza colonna mostrano i valori iniziali e finali del tasso di cambio USD/EUR: 1 e 0,80. Questo perché l’euro si è svalutato del 20%.
- La quarta colonna indica il tasso di cambio finale EUR/USD, pari al reciproco di quello USD/EUR: il suo valore è 1,25.
- La quinta colonna misura la rivalutazione del dollaro corrispondente alla svalutazione dell’euro del 20%, che risulta essere del 25%.
La tabella successiva presenta il rendimento di un investimento in euro in funzione del:
- Rendimento dell’investimento in dollari, che ipotizziamo essere compreso tra –100% e +5.000%.
- Tasso di cambio USD/EUR (da una rivalutazione dell’euro del 50% a una sua svalutazione di pari entità).
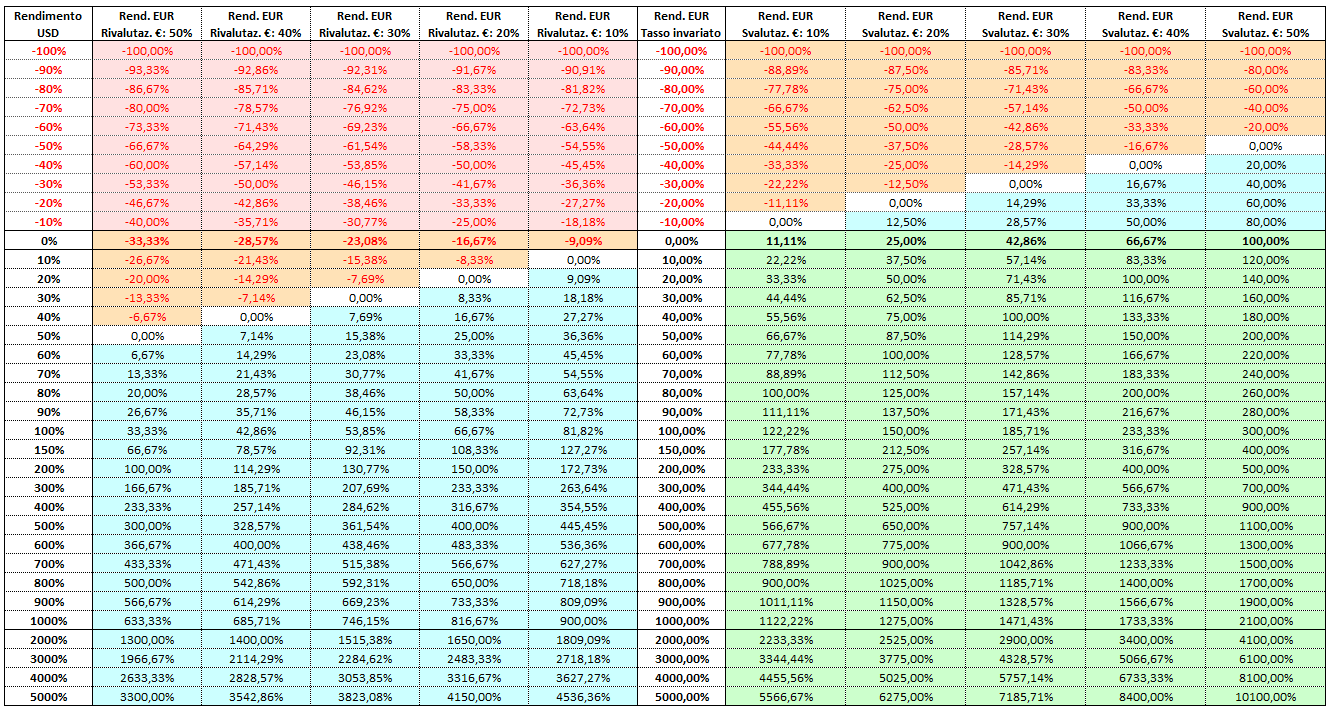
La parte della tabella con sfondo verde chiaro corrisponde al quadrante in alto a sinistra della matrice analizzata in precedenza; la parte con sfondo rosso chiaro, al quadrante in basso a destra.
La parte con sfondo arancione, bianco o blu della metà sinistra della tabella corrisponde al quadrante in alto a destra della matrice; la parte con sfondo arancione della metà destra della tabella corrisponde, infine, al quadrante in basso a sinistra.
La colonna centrale rappresenta il caso del tasso di cambio invariato: quando il tasso di cambio USD/EUR al momento del disinvestimento è identico a quello al momento dell’investimento. In questo caso, il rendimento in euro è sempre uguale a quello in dollari.
La tabella è organizzata come segue:
- La prima colonna rappresenta il rendimento dell’investimento in dollari, che varia dal −100% al +5000%.
- Dalla seconda alla sesta colonna, troviamo i rendimenti in euro nel caso in cui l’euro si sia rivalutato tra il 50% e il 10% rispetto al dollaro. Questo movimento è sfavorevole per l’investitore dell’area euro, poiché ora sono necessari più dollari per ottenere un euro rispetto all’inizio dell’investimento.
- La settima colonna rappresenta il rendimento in euro dell’investimento nel caso in cui il tasso di cambio rimanga invariato. In questo caso, il rendimento in euro corrisponde esattamente a quello in dollari.
- Dall’ottava alla dodicesima colonna, troviamo i rendimenti in euro nel caso in cui l’euro si sia svalutato tra il 10% e il 50% rispetto al dollaro. Questo movimento è favorevole all’investitore dell’area euro, poiché ora sono necessari meno dollari per ottenere un euro rispetto all’inizio dell’investimento.
Prendiamo ad esempio un investimento con un rendimento di mercato in dollari del −50%, ma con una rivalutazione dell’euro rispetto al dollaro del 50%.
In questo caso, avremmo investito 100 euro = 100 dollari. Con un rendimento del −50%, alla fine dell’investimento saremmo rimasti soltanto con 50 dollari. Tuttavia, a causa della rivalutazione dell’euro (1 EUR = 1,5 USD), quando cambiamo i nostri 50 dollari in euro, otteniamo solo 33,33 euro.
In conclusione, avevamo investito 100 euro e siamo rimasti solo con 33,33: il rendimento del nostro investimento in euro è stato del −66,67%.
Nella seconda colonna, corrispondente al −50% di rendimento dell’investimento in dollari, troviamo proprio il valore di −66,67%.
Alcuni grafici possono aiutare a capire meglio l’impatto del tasso di cambio sui rendimenti di un investimento.
Nel grafico seguente, vengono visualizzate undici linee: cinque sopra e cinque sotto la linea centrale blu. Tutte queste linee rappresentano i possibili rendimenti di mercato in dollari di un investimento: dal −100% al +100%.
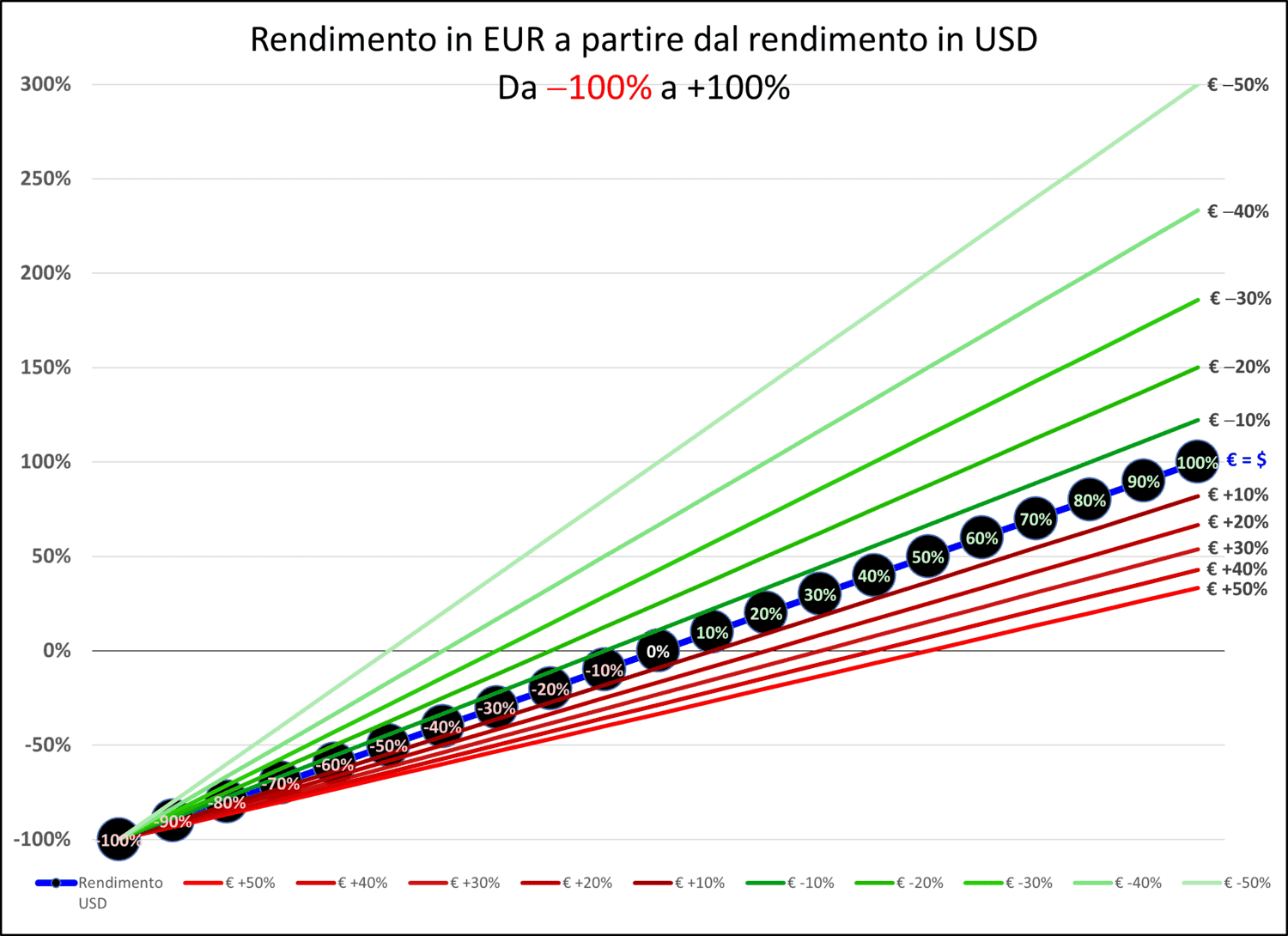
Nel caso in cui si perda l’intero capitale investito, ci ritroviamo con zero dollari alla fine dell’investimento. Indipendentemente dall’andamento del tasso di cambio, corrisponderanno a zero euro. Questo è il punto più in basso a sinistra nel grafico, da cui partono tutte le linee.
Se ci spostiamo verso destra, troviamo un rendimento di mercato in dollari del −90%. In questo punto, l’impatto del tasso di cambio inizia a manifestarsi, per quanto ancora modesto. Ciò è dovuto al fatto che quando si perde il 90% del capitale, qualsiasi beneficio derivante da una svalutazione dell’euro sarà minimo, dato che il capitale residuo è solo un decimo di quello iniziale. La maggior parte del capitale è stata persa.
In termini numerici, un rendimento di mercato del −90% si trasformerà in un −93,33% nel caso di una rivalutazione dell’euro del 50% (il caso più negativo considerato nella tabella, rappresentato dalla linea rossa più in basso) e in un −80% nel caso di una svalutazione dell’euro del 50% (il caso più positivo tra quelli presenti nella tabella, rappresentato dalla linea verde più in alto).
Nel grafico, man mano che ci spostiamo verso destra, l’impatto del tasso di cambio diventa sempre più significativo. Ad esempio, se il rendimento di mercato in dollari è dello 0%, il rendimento in euro varierà tra:
⇒ −33,33%, nel caso di una rivalutazione dell’euro del 50%:
- Supponiamo di aver investito 1.000 euro a t0, quando il tasso di cambio USD/EUR era pari a 1: abbiamo investito 1.000 × 1 = 1.000 dollari.
- Il rendimento di mercato è stato dello 0% e i nostri 1.000 dollari sono rimasti invariati alla fine dell’investimento.
- Adesso, però, il tasso di cambio è salito a 1,5 dollari per ottenere 1 euro: l’euro si è rivalutato del 50%. Come abbiamo visto in precedenza, la rivalutazione del 50% di una valuta corrisponde alla svalutazione del 33,33% dell’altra.
- Cambiando i nostri 1.000 dollari in euro otteniamo 1.000 / 1,5 = 666,67 euro.
- Il rendimento finale è (666,67 − 1.000) / 1.000 = −0,3333 = −33,33%.
⇒ +100%, nel caso di una svalutazione dell’euro del 50%:
- Supponiamo di aver investito 1.000 euro a t0, quando il tasso di cambio USD/EUR era pari a 1: abbiamo investito 1.000 × 1 = 1.000 dollari.
- Il rendimento di mercato è stato dello 0% e i nostri 1.000 dollari sono rimasti invariati alla fine dell’investimento.
- Adesso, però, il tasso di cambio è sceso a 0,5 dollari per ottenere 1 euro: l’euro si è svalutato del 50%.
- Cambiando i nostri 1.000 dollari in euro otteniamo 1.000 / 0,5 = 2.000 euro.
- Il rendimento finale è (2.000 − 1.000) / 1.000 = 1 = 100%.
Il grafico che segue è la continuazione del precedente e mostra di nuovo undici linee: cinque sopra e cinque sotto la linea centrale blu. Tutte queste linee rappresentano i possibili rendimenti di mercato in dollari di un investimento: dal +100% al +1.000%.
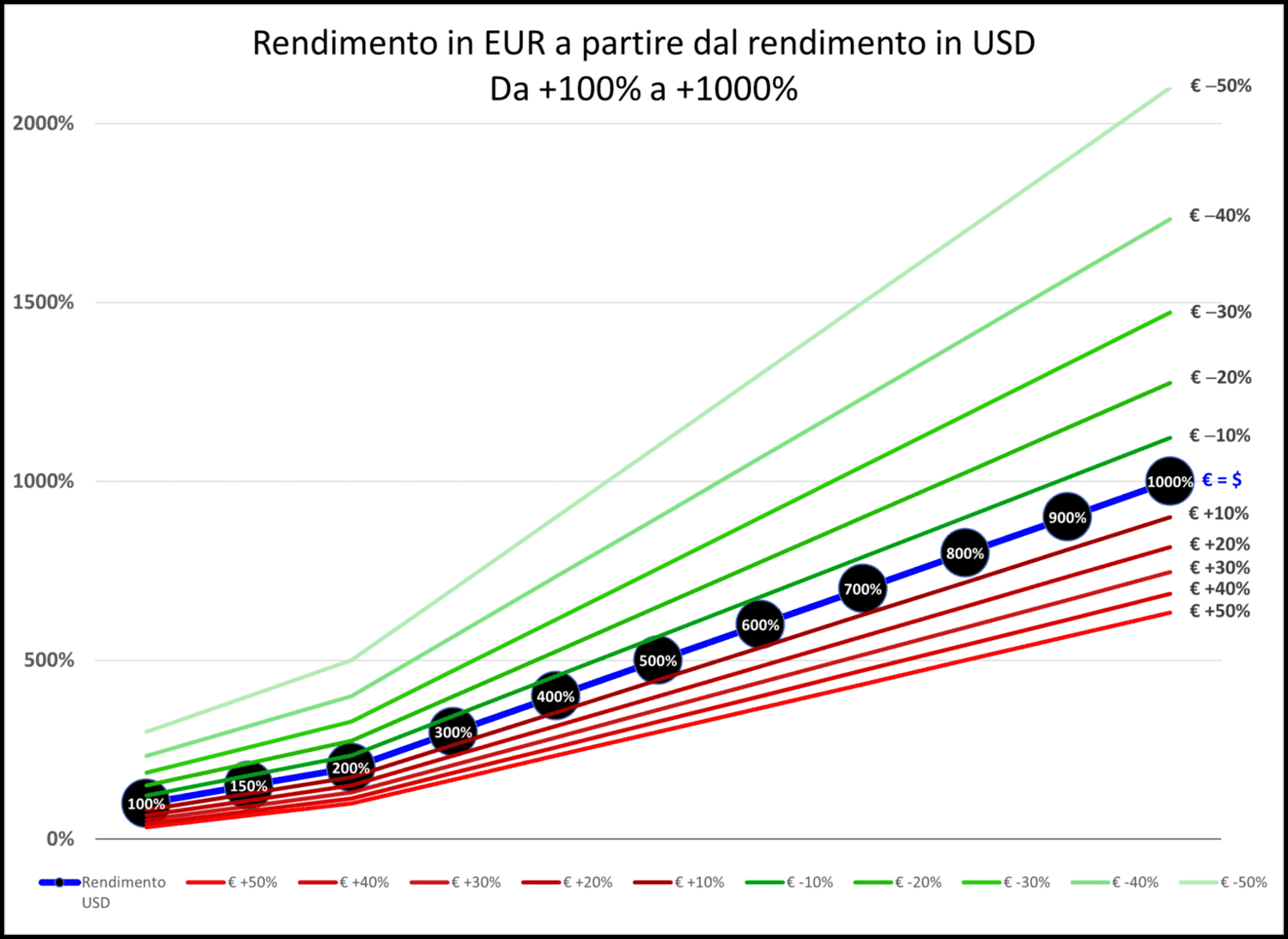
Nel grafico, man mano che ci spostiamo verso destra, l’impatto del tasso di cambio diventa sempre più significativo.
Ad esempio, se il rendimento in dollari è del 100% (punto più in basso a sinistra), il rendimento in euro può variare dal 33,33% (nel caso di una rivalutazione dell’euro del 50%, linea rossa più in basso) al 300% (nel caso di una svalutazione dell’euro del 50%, linea verde più in alto). Il rendimento massimo nel grafico, 1.000%, si trasforma in valori compresi tra 633,33% e 2.100%.
Prendiamo ad esempio il rendimento dell’investimento in dollari del 500%. In questo caso, il rendimento in euro sarà:
⇒ +300%, nel caso di una rivalutazione dell’euro del 50%:
- Supponiamo di aver investito 1.000 euro a t0, quando il tasso di cambio USD/EUR era pari a 1: abbiamo investito 1.000 × 1 = 1.000 dollari.
- Il rendimento di mercato è stato del 500% e i nostri 1.000 dollari sono diventati 6.000.
- Adesso, però, il tasso di cambio è salito a 1,5 dollari per ottenere 1 euro: l’euro si è rivalutato del 50%.
- Cambiando i nostri 6.000 dollari in euro otteniamo 6.000 / 1,5 = 4.000 euro.
- Il rendimento finale è (4.000 − 1.000) / 1.000 = 3.000 / 1.000 = 3 = 300%.
⇒ +1.100%, in caso di svalutazione dell’euro del 50%:
- Supponiamo di aver investito 1.000 euro a t0, quando il tasso di cambio USD/EUR era pari a 1: abbiamo investito 1.000 × 1 = 1.000 dollari.
- Il rendimento di mercato è stato del 500% e i nostri 1.000 dollari sono diventati 6.000.
- Adesso, però, il tasso di cambio è sceso a 0,5 dollari per ottenere 1 euro: l’euro si è svalutato del 50%.
- Cambiando i nostri 6.000 dollari in euro otteniamo 6.000 / 0,5 = 12.000 euro.
- Il rendimento finale è (12.000 − 1.000) / 1.000 = 11.000 / 1.000 = 11 = 1.100%.
Nel capitolo 3.1.2, avevamo analizzato un esempio che ci aveva fatto concludere che, dopo un anno, il tasso di cambio USD/GBP che avrebbe assicurato la parità scoperta dei tassi di interesse sarebbe stato di 1,3451 (un anno prima era 1,37).
Ora che abbiamo capito la formula che determina l’impatto del rischio di cambio sul rendimento di un investimento in valuta estera, vediamo come abbiamo ottenuto il valore di 1,3451.
Data l’equazione:
\begin{equation} r_$ = \frac{\rm USD/{GBP}_{t1}}{\rm USD/{GBP}_{t0}} \times (1 + r_£ ) - 1 = \frac{\rm USD/{GBP}_{t1}}{1,37} \times (1 + 10\%) - 1 \end{equation}
Possiamo risolverla come segue:
\begin{equation} \frac{\rm USD/{GBP}_{t1}}{1,37} \times (1 + 10\%) = 1,08 \end{equation}
\begin{equation} \frac{\rm USD/{GBP}_{t1}}{1,37} = \frac{1,08}{1,10} = 0,9818 \end{equation}
\begin{equation} \rm USD/{GBP}_{t1} = 0,9818 \times 1,37 = 1,3451 \end{equation}
Come abbiamo osservato, l’impatto del rischio di cambio sul rendimento può essere molto significativo: può letteralmente far schizzare in alto o in basso il rendimento finale di un investimento.
Per concludere questo capitolo, vorrei ribadire quanto sia fuorviante l’idea diffusa tra gli investitori che la copertura del rischio di cambio sia necessaria solo per gli investimenti a breve termine. I motivi sono i seguenti:
- Molti sostengono che nel lungo termine il tasso di cambio ritornerà ai suoi valori medi, minimizzando l’impatto sul rendimento. Tuttavia, come abbiamo visto nel quarto capitolo, non è detto che ciò avvenga o che si verifichi nei tempi utili all’investitore. Quello che ci dobbiamo aspettare, invece, è che la valuta locale si svaluti o si rivaluti: se si rivaluta, l’impatto del tasso di cambio sarà negativo.
- Quando parliamo di investimenti finanziari di lungo termine, di solito si verificano le seguenti situazioni:
- Più un portafoglio è rischioso, più alto è il suo rendimento di mercato atteso.
- Più il rendimento di mercato è alto, maggiore sarà l’impatto del rischio di cambio.
- Se l’impatto è negativo, il rischio di cambio si trasformerà in un costo per l’investitore: costo che sarà tanto maggiore quanto più alto sarà stato il rendimento di mercato dell’investimento.
- Molti sconsigliano energicamente la copertura del rischio di cambio sostenendo che l’hedging, nel lungo termine, comporti un costo insostenibile. Questa affermazione, però, non è corretta per due motivi:
- Prima di tutto, l’hedging non è necessariamente un costo. In alcune circostanze, potrebbe addirittura rappresentare un “guadagno”, ovvero un extra-rendimento per l’investitore. Questo argomento sarà approfondito nel capitolo 11.
- In secondo luogo, anche se l’hedging dovesse comportare un costo per l’investitore, questo costo verrebbe sostenuto per una ragione molto precisa: neutralizzare il rischio di cambio. L’hedging può essere visto come un “servizio di assicurazione” a cui l’investitore decide di accedere: per usufruire di questo servizio (ovvero evitare il rischio di cambio), si deve pagare un costo. Tuttavia, il costo sostenuto potrebbe essere molto inferiore al beneficio ottenuto nel caso in cui si verifichi l’evento contro cui ci si è assicurati: le assicurazioni funzionano proprio in base a questo principio. La cosa interessante, nel caso dell’hedging, è che in alcuni casi l’investitore potrebbe addirittura essere remunerato per aver stipulato questa “assicurazione”.
Per convincerci che il rischio di cambio non viene necessariamente eliminato nel lungo termine, possiamo calcolare il rendimento rolling a 20 e 30 anni dello S&P 500 TR sia in dollari che in euro.
Il grafico che segue rappresenta il rendimento rolling a 20 anni:
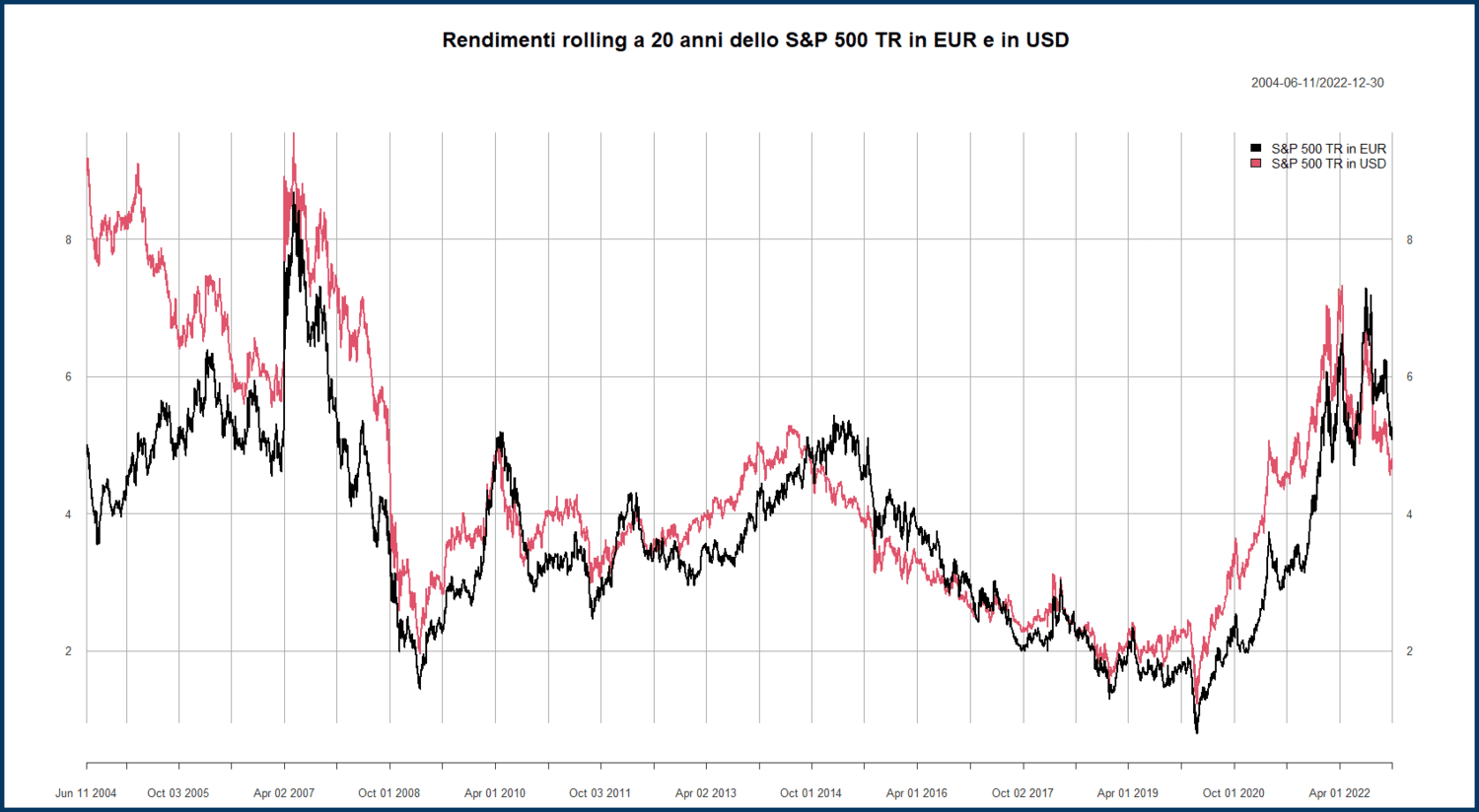
Questo è invece il grafico del rendimento rolling a 30 anni:
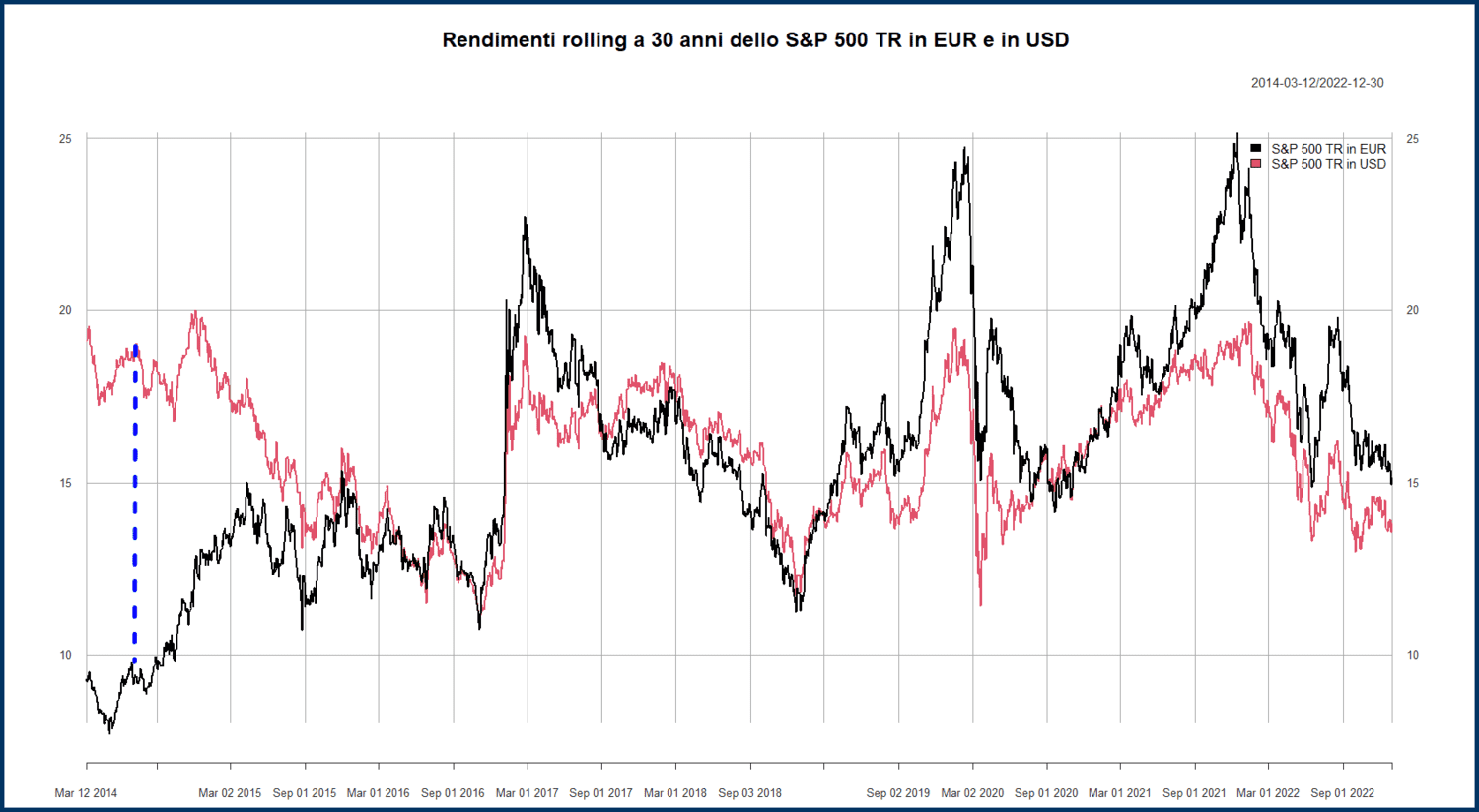
Ogni punto sulla linea rossa indica il rendimento in dollari ottenuto nel trentennio che termina alla data corrispondente a quel punto. Analogamente, la linea nera rappresenta il rendimento dello S&P 500 TR in euro nello stesso periodo.
In molti casi, le due linee sono vicine. Bisogna però fare attenzione alla scala dell’asse delle ordinate: 10, 15, 20 rappresentano rendimenti del 1.000%, 1.500% e 2.000%. Anche se le differenze possono sembrare piccole, in realtà spesso corrispondono a decine o centinaia di punti percentuali.
Esaminiamo più attentamente i rendimenti del trentennio conclusosi il 14 luglio 2014. I rendimenti in dollari e in euro sono collegati dalla linea blu tratteggiata: il rendimento in dollari è stato del 1.902,89%; quello in euro, del 935,49%.
La differenza è enorme: la significativa variazione del tasso di cambio tra l’inizio e la fine del trentennio avrebbe avuto un impatto negativo sugli investitori dell’area euro, che avrebbero lasciato per strada un rendimento di quasi il 1.000%!
Ora che conosciamo la formula per calcolare il rendimento in euro in funzione di quello in dollari e del tasso di cambio EUR/USD, possiamo utilizzarla per un’ulteriore verifica.
Il trentennio che stiamo esaminando va dal 2 maggio 1985 al 14 luglio 2014:
- Il 2 maggio 1985, lo S&P 500 TR era quotato a 179,01 punti e l’EUR/USD era pari a 1,4203.
- Il 14 luglio 2014, lo S&P 500 TR era quotato a 3.585,37 punti e l’EUR/USD era pari a 0,7343.
Sostituiamo questi valori nella formula:
\begin{equation} r_€ = \frac{\rm EUR/{\rm USD}_{t1}}{\rm EUR/{\rm USD}_{t0}} \times (1 + r_$ ) - 1 \end{equation}
\begin{equation} r_€ = \frac{0,7343}{1,4203} \times (1 + 1.902,89\%) - 1 \end{equation}
\begin{equation} r_€ = 0,5170 \times 2.002,89\% -1 = 1.035,49\% - 100\% = 935,49\% \end{equation}
Purtroppo, un periodo di tempo molto lungo non elimina necessariamente il rischio di cambio. Anzi, l’impatto sul rendimento in valuta locale può essere significativo. Nonostante un rendimento eccezionale pari al 935% (che equivale all’incirca a decuplicare il capitale investito), non si può ignorare una perdita di rendimento altrettanto considerevole.
Naturalmente, in altri periodi si sarebbero verificati risultati opposti. Come dimostra il grafico precedente, in diverse occasioni il rendimento dello S&P 500 TR in euro ha superato quello dello S&P 500 TR in dollari, a volte anche di percentuali superiori al 500%.
L’essenza del rischio di cambio è quella di influire sul rendimento finale: all’inizio di un investimento, non possiamo prevedere né la direzione, né l’entità del suo impatto. Assumersi questo rischio equivale a introdurre un elemento di casualità nell’investimento: a volte andrà bene, altre volte male e, in certi casi, avrà un impatto minimo o nullo sul rendimento.
Quello che è certo, però, è che l’affermazione secondo cui questo rischio diventi trascurabile investendo nel lungo termine è sbagliata.
La lettura di un singolo capitolo potrebbe portare a conclusioni diverse rispetto a quelle che si potrebbero trarre dall'analisi completa del libro, che esamina in dettaglio anche l'impatto del rischio di cambio sulla volatilità e su altre importanti misure di rischio degli investimenti finanziari.
Inoltre, si deve tenere in considerazione come l'impatto del rischio di cambio su un titolo azionario sia molto diverso da quello su un titolo obbligazionario.
Per questo motivo e per evitare fraintendimenti, desidero riportare alcune frasi del capitolo conclusivo del libro, del quale si consiglia una lettura integrale per una comprensione più completa:
- Il fatto che esista il rischio di cambio negli investimenti non significa che l’obiettivo debba sempre essere quello di eliminarlo.
- L'obiettivo di questo studio è stato sensibilizzare gli investitori sull'importanza e sulle potenziali ripercussioni del rischio di cambio. Se c’è consapevolezza, si può decidere più efficacemente quanto di quel rischio si è disposti ad accettare.
- L’esistenza del rischio di cambio non significa, quindi, cercare di evitarlo a ogni costo, così come l’esistenza del rischio di mercato non ci impedisce di investire. Al contrario, il rischio di mercato e il rischio di cambio, se compresi e gestiti correttamente, offrono opportunità di rendimento che sono inaccessibili nei mercati privi di rischio.
- In conclusione, non esiste una risposta universalmente accettata sulla copertura del rischio di cambio. Come abbiamo avuto modo di ripetere più volte, le scelte dipendono dalle preferenze individuali e dagli obiettivi di investimento.
La collezione di articoli "IL COMPENDIO DELL'INVESTITORE" contiene:
Diversificazione: mitigare il rischio di un investimento
Capire gli strumenti finanziari che si utilizzano
L'orizzonte temporale di investimento
La propensione al rischio dell'investitore
I REITs tra mito e realtà: possiamo considerarli come una asset class a sé stante?
I rendimenti passati non sono indicativi di quelli futuri
È meglio investire nel mercato azionario o in quello obbligazionario?
15 errori da evitare e 10 consigli utili per investire
L'illusione di saper prevedere i mercati finanziari
Attualità? Molto rumore per nulla
Bitcoin e mercato azionario: un'analisi su rischio, correlazione e diversificazione


