Lazy portfolios
- Information
- Lazy portfolios
- Prima pubblicazione: 25 Gennaio 2019
«L’ambizione è la misera scusa di chi non ha abbastanza coraggio di esser pigro».
Milan Kundera
L'ebook dell'articolo e il libro in forma cartacea sono disponibili su Amazon: Lazy portfolios: Un'analisi approfondita e una guida pratica a una modalità di investimento semplice ed efficiente.
L'ebook e il libro in forma cartacea includono sia l'articolo principale che i 31 articoli di approfondimento dei 40 Lazy portfolios (capitoli 13.3.1-13.3.31).
Questo articolo fa parte del Percorso intermedio, pensato per chi possiede già le basi e vuole approfondire strategie di investimento e concetti teorici per una comprensione più approfondita della finanza. In fondo alla pagina, troverai il link al prossimo articolo del percorso.
I Lazy portfolios, detti portafogli pigri in italiano, sono una modalità di investimento che ha lo scopo di replicare un mix di indici attraverso gli ETF, mirando al raggiungimento della massima efficienza grazie al contenimento dei costi.
I Lazy portfolios, quindi, non pretendono di battere il mercato, ma si limitano a replicarlo sulla base di un asset allocation la cui rischiosità deve essere coerente con le caratteristiche e le esigenze dell'investitore.
Questo articolo, costituito da 21 capitoli (alcuni dei quali suddivisi in sottocapitoli) ha i seguenti obiettivi:
- Presentare i vantaggi e gli svantaggi dei Lazy portfolios.
- Approfondire il rischio di cambio dei Lazy portfolios.
- Analizzare i Lazy portfolios attraverso backtest con ribilanciamenti annuali (in basso troverete i link ai 31 articoli di approfondimento):
- Su tre diversi periodi: 1985-2020, 2000-2020 e 2010-2020.
- Utilizzando 40 Lazy portfolios, la maggior parte dei quali molto conosciuti.
- Backtestando i Lazy portfolios originali in USD, in USD→EUR (applicando la conversione in base ai valori giornalieri del tasso di cambio) e in EUR: una versione creata appositamente per gli investitori dell'area euro.
- Effettuati sulla base di 11 modelli di ottimizzazione dei pesi degli ETF (2 statici, 5 dinamici vincolati e 4 dinamici non vincolati).
- Verificare se l'applicazione di modelli di ribilanciamento dinamico vincolato e non vincolato riesca a produrre risultati migliori del ribilanciamento statico.
- Aggiornare mensilmente i pesi ottimali dei 40 Lazy portfolios modello.
- Analizzare i rendimenti rolling a 5 e 10 anni dei Lazy portfolios.
- Quantificare l'impatto del costo della consulenza finanziaria e della gestione attiva.
- Confrontare i Lazy portfolios con i fondi flessibili a gestione attiva.
- Confrontare i Lazy portfolios con gli ETF Vanguard LifeStrategy.
Si tratta di un articolo molto lungo: è focalizzato sui portafogli pigri ma alcune parti sono applicabili anche ad altre modalità di investimento (ad esempio, il rischio di cambio, il costo della consulenza e così via).
Non c'è niente di sbagliato nel saltare subito alla lettura del capitolo 19 – dove si discutono le modalità di scelta del Lazy portfolio – o delle conclusioni. Il rischio, però, è quello di non comprendere appieno i vantaggi e i rischi dei portafogli pigri: quando si tratta di investire i propri soldi, è importante cercare di capire il più possibile e non improvvisare niente.
Si consiglia la lettura dei capitoli nell'ordine proposto. Dall’indice è comunque possibile accedere direttamente a ciascuno di essi.
Indice
- Introduzione
- Vantaggi e svantaggi
- Integrazione delle serie storiche degli ETF con gli indici
- Il rischio di cambio
- Elenco dei principali Lazy portfolios (in USD e in EUR) e degli ETF che li costituiscono
- Criteri di scelta degli ETF
- Perché esistono così tanti Lazy portfolios?
- Limiti dell’approccio di ottimizzazione classico (Markowitz) e Hierarchical Risk Parity
- Procedura e modelli di ottimizzazione. Il ribilanciamento
- La strategia 1/N
- Lazy portfolios modello
- Classifiche finali: per portafoglio e per modello di ottimizzazione
- Analisi dei Lazy portfolios e presentazione dei risultati dei backtest
- Considerazioni generali sui Lazy portfolios e sulla diversificazione
- Primo e secondo livello di diversificazione
- Composizione, caratteristiche e risultati dei backtest di ogni Lazy portfolio
- World Bond
- World Stocks
- Two funds portfolios
- Warren Buffett
- Simple Path to Wealth
- Couch Potato
- Three Funds Bogleheads
- Second Grader’s Starter
- Talmud
- Margaritaville
- Andrew Tobias
- Gyroscopic Investing Desert
- Permanent
- Core Four
- Bogleheads Four Funds
- No Brainer
- Larry
- Golden Butterfly
- All Weather
- Ivy
- Dynamic 60/40 Income
- Dynamic 40/60 Income
- Five Asset
- David Swensen Lazy Portfolio
- Coffee House
- Rob Arnott
- Ultimate Buy and Hold Strategy
- Ultimate Buy & Hold
- Dedalo Three
- Dedalo Four
- Dedalo Eleven
- Rendimenti rolling dei Lazy portfolios a 5 e 10 anni
- L’impatto del costo della consulenza finanziaria e della gestione attiva
- Confronto tra fondi flessibili a gestione attiva e i Two funds Lazy portfolios
- ETF Vanguard LifeStrategy
- La gestione della parte obbligazionaria e della liquidità
- La scelta del Lazy portfolio
- Conclusioni
- Bibliografia
1. Introduzione

«I like the word 'indolence'. It makes my laziness seem classy».
Bernard Williams
I Lazy portfolios sono una soluzione d’investimento che consiste nella replica di una certa asset allocation utilizzando pochi ETF.
I vantaggi dei Lazy portfolios verranno approfonditi nel secondo capitolo, ma le loro caratteristiche principali sono la replica passiva del mercato, i costi molto contenuti e la facilità nella loro costruzione e gestione.
In italiano vengono definiti portafogli pigri e il loro nome prende spunto dall'essere concepiti come strumenti di investimento a lungo termine, con pochi ribilanciamenti da effettuare periodicamente: di solito, non più di una volta all'anno.
I Lazy portfolio si sono sviluppati a partire dagli anni ’70 del secolo scorso, quando John Bogle ebbe l’idea di creare gli “Index funds”, ovvero dei fondi indicizzati che replicano un indice di riferimento (benchmark).
La replica implicava la rinuncia a ogni tentativo di far meglio del benchmark: John Bogle aveva appena inventato la gestione passiva degli investimenti finanziari.
Gli ETF sono stati l’evoluzione naturale degli index funds, con i quali condividono l'approccio passivo, ma vengono quotati in negoziazione continua in molti mercati borsistici, esattamente come le azioni.
Gli ETF possono essere comprati o venduti durante tutto l’arco di apertura di una sessione borsistica, a prezzi che non sono necessariamente uguali al loro NAV.
Il passaggio dai fondi comuni a gestione attiva a quelli a gestione passiva sembra scontato, oggi. Anzi, viene da chiedersi perché si sia dovuto aspettare fino alla metà degli anni ’70 per vedere la nascita dei primi fondi indicizzati.
In realtà, fu un vero e proprio cambio di paradigma: nel 1975 John Bogle fondò “The Vanguard Group” e dette vita al “The Vanguard Experiment”, che aveva lo scopo di lanciare la gestione passiva dei fondi comuni d’investimento.
Questa novità fu accolta con molto scetticismo. Molte furono le critiche ricevute, tra le quali le accuse di essere antiamericano e di incentivare la mediocrità.
Il tempo ha dimostrato che John Bogle aveva ragione.
Gli strumenti oggi di gran lunga più utilizzati nei portafogli pigri sono gli ETF.
Esistono molti tipi di portafogli pigri: i più semplici sono composti da uno o due soli ETF; i più complessi arrivano fino a 12 ETF (che sembra essere la soglia massima, anche se ovviamente ciascuno è libero di includerne un numero maggiore nel suo portafoglio).
Definire un portafoglio con l’aggettivo “pigro” non lo rende molto accattivante.
Nella nostra società, la pigrizia è considerata un atteggiamento negativo: le persone pigre sono quelle che non hanno troppa voglia di studiare, lavorare o fare qualcosa in generale. In un certo senso, pigrizia è sinonimo di insuccesso.
Nei mercati finanziari non è così. I mercati finanziari funzionano in maniera diametralmente opposta: meno l’investitore interferisce, meglio è.
Le uniche eccezioni sono costituite dagli investitori professionali, che comunque non hanno vita facile per battere il mercato.
Intesa nel senso di rinuncia a intervenire o a modificare il proprio portafoglio prima del raggiungimento dell’orizzonte temporale d’investimento stabilito, la pigrizia è una qualità positiva ed estremamente rara.
Non è un concetto banale. I mercati finanziari sono controintuitivi ed è per questo che gli investitori non riescono, generalmente, a ottenere gli stessi rendimenti del mercato: non agiscono seguendo la strada più semplice e – nei mercati finanziari – semplice è molto spesso sinonimo di efficiente.
Aspettare senza far niente è ciò che una corretta gestione degli investimenti finanziari richiede.
Se arriva un’improvvisa crisi finanziaria, l’investitore non si deve comportare come un imprenditore: l’imprenditore deve reagire, rispondere alle mutate condizioni del mercato in fretta, prendere le contromisure più adatte per la sua azienda.
L’investitore no: deve limitarsi a non interferire e aspettare che la tempesta sia passata. Nel caso in cui agisca in modo improvvisato, senza rispettare la strategia iniziale, rischia di mandare all'aria ciò che di buono ha fatto fino a quel momento.
Come questa analisi cercherà di dimostrare, i portafogli pigri sono uno dei più potenti strumenti a disposizione degli investitori per raggiungere i loro obiettivi di investimento.
2. Vantaggi e svantaggi

«Un uomo che non legge buoni libri non ha alcun vantaggio rispetto a quello che non sa leggere».
Mark Twain
I principali vantaggi degli ETF sono:
- Semplicità
- Basso costo
- Diversificazione
Semplicità
Comprare un paio di ETF ed effettuare un ribilanciamento una volta all’anno è semplice. Gli ETF potrebbero essere anche qualcuno in più e la mole di lavoro non crescerebbe granché.
Questo vantaggio non è peculiare dei Lazy portfolios: vale anche per gli investitori che utilizzano i fondi a gestione attiva.
Presi singolarmente, i vantaggi elencati non sono esclusivi dei Lazy portfolios: tutti insieme, però, li possiamo trovare soltanto in questa tipologia di portafogli.
Basso costo
Il costo degli ETF è molto più basso di quello dei fondi a gestione attiva. Non si tratta di una piccola differenza: gli ETF costano circa 10 volte meno.
Un risparmio dell’1% di costi all’anno potrebbe non essere rilevante se le cifre in gioco sono piccole o se l’investimento è di breve termine. Nel lungo periodo, però, il costo totale non è uguale al numero di anni moltiplicato 1%: se il trend del mercato è crescente, può essere molto più grande, perché il costo-opportunità di ogni 1% pagato (e, di conseguenza, non reinvestito) è pari al suo controvalore capitalizzato per il numero di anni dell’investimento (capitalizzazione effettuata al tasso di rendimento annualizzato dell’investimento stesso).
Un esempio aiuterà a capire meglio: ipotizziamo che un capitale di 100.000 euro venga investito su un fondo a gestione attiva per 20 anni, con commissioni di gestione pari all’1,20% all’anno. Alternativamente, si potevano investire i 100.000 euro su un ETF della stessa categoria con commissioni di gestione pari allo 0,20% all’anno (sempre per 20 anni). Esattamente un 1% di differenza.
Ipotizziamo, inoltre, che se le commissioni non fossero state conteggiate e addebitate direttamente sui NAV dei due fondi, entrambi avrebbero generato un rendimento del 5%. Questo significherebbe, una volta sottratte le commissioni di gestione, un rendimento del 3,8% e del 4,8% all’anno.
Quanto ci è costato, in tutto, questo 1% di commissioni in più all’anno?
Molto: per la precisione, 44.565,68 euro. Ben più di 1.000 euro all’anno (1% di 100.000 euro) per 20 anni: questo maggior costo è dovuto al rendimento perso a causa del mancato reinvestimento di quell’1% all’anno.
Se invece dell’1% o di un periodo di 20 anni avessimo scelto dei valori superiori, come ad esempio 1,5% e 30 anni, il costo totale sarebbe salito rispettivamente a 66.974,37 euro (1,5% per 20 anni), 102.027,18 euro (1% per 30 anni) e 143.311,66 euro (1,5% per 30 anni).
Vediamo graficamente l’ipotesi di un 1% di differenza nei costi:
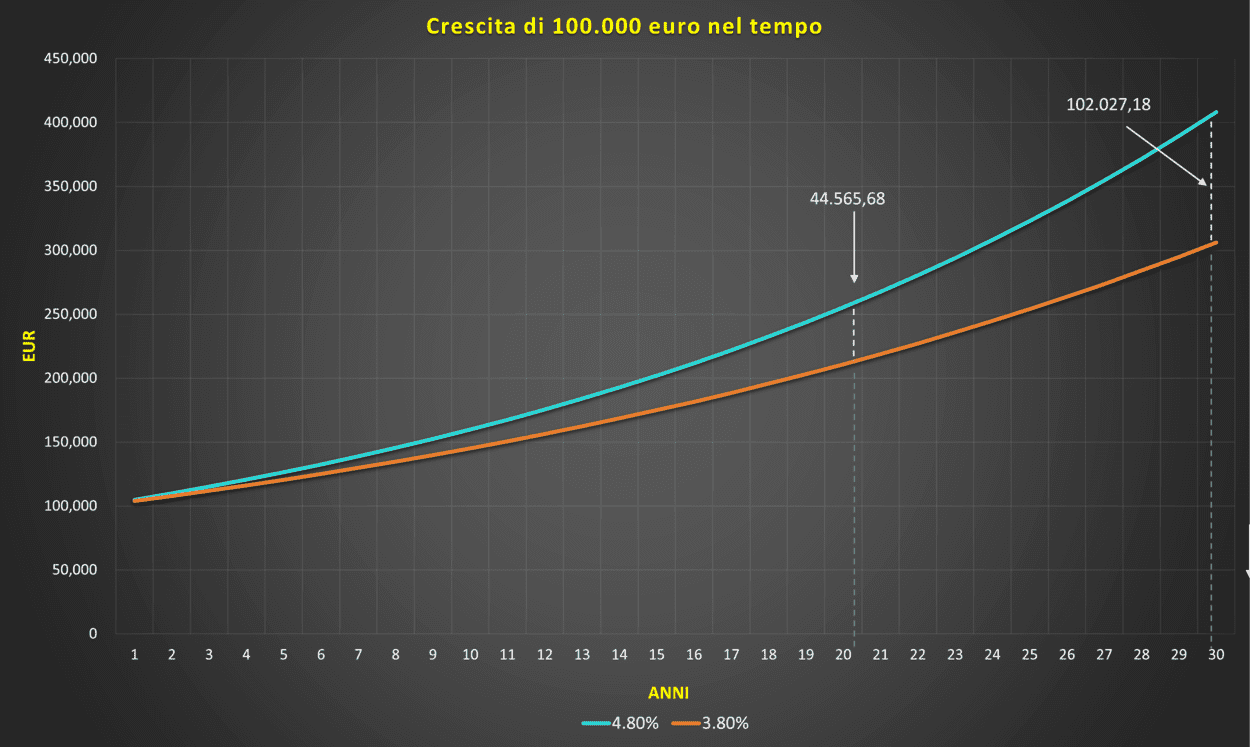
Sono cifre notevoli, che crescerebbero ancora se, invece di un rendimento del 5% al lordo dei costi, ne ipotizzassimo uno superiore (e viceversa).
Il vecchio adagio che recita “i costi sono certi, i rendimenti no” è valido più che mai.
Vedremo ancora meglio nel capitolo 15 quanto le spese correnti o il costo della consulenza impattino sui rendimenti dei Lazy portfolios che esamineremo.
La minimizzazione dei costi è la condizione che, nel lungo termine, permetterà di ottenere un rendimento finale più alto.
Diversificazione
La diversificazione è una regola fondamentale negli investimenti.
Diversificare significa investire il capitale in più asset, possibilmente utilizzando più strumenti finanziari: la diversificazione serve a diminuire il rischio di una grossa perdita dovuta a una forte riduzione del prezzo dell'unico asset o dell'unico titolo in portafoglio.
In altre parole, significa non mettere tutte le uova nello stesso paniere: vecchia saggezza popolare applicata alla finanza.
Avevamo detto che, in un portafoglio pigro, potevamo avere anche uno o due soli ETF: di che diversificazione stiamo allora parlando?
In primis, di quella fornita dagli stessi ETF: strumenti finanziari che contengono al loro interno decine, centinaia o migliaia di azioni o di obbligazioni.
Possedere anche una sola quota di un ETF significa detenere una piccola percentuale di ognuna di esse.
La diversificazione non è soltanto espressione di buon senso: in ambito finanziario ne è stata dimostrata l'utilità, anche matematicamente, fin dal 1952, quando Harry Markowitz pubblicò il suo primo importante contributo nell’articolo intitolato Portfolio Selection, che dette origine alla Teoria Moderna del Portafoglio.
Il concetto di diversificazione verrà ripreso nel capitolo 13.2.
I Lazy portfolios hanno anche alcuni inconvenienti:
- Alta volatilità
- Inefficienza fiscale degli ETF
Alta volatilità
Nonostante l’elevata diversificazione, molti portafogli pigri sono volatili.
Affronteremo la volatilità nelle nostre analisi e vedremo se e come sia possibile mitigarla, senza rinunciare a un livello eccessivo di rendimento atteso.
Perseguiremo questo obiettivo in vari modi; anche rendendo flessibili le percentuali delle asset class che compongono i Lazy portfolios.
Inefficienza fiscale degli ETF
Il problema dell’inefficienza fiscale non riguarda soltanto gli ETF, ma gli OICR in generale.
Verrebbe naturale pensare che una minusvalenza e una plusvalenza realizzate con due ETF diversi o, addirittura, con lo stesso ETF, possano essere compensate.
In realtà, a causa del regime fiscale che è stato riservato loro dal legislatore, questa semplice operazione non è possibile: non è ammessa la compensazione tra minusvalenze e plusvalenze perché le prime sono assimilate a redditi diversi e le seconde a redditi di capitale.
Vediamo meglio che cosa viene considerato reddito di capitale o reddito diverso:
- Reddito di capitale:
- Plusvalenze generate dalla differenza positiva tra prezzo di vendita e di acquisto degli ETF.
- Proventi erogati dagli ETF a distribuzione.
- Reddito diverso:
- Minusvalenze generate dalla differenza negativa tra prezzo di vendita e di acquisto degli ETF.
Le minusvalenze non possono perciò essere compensate né con le plusvalenze né con i proventi erogati dagli ETF a distribuzione, proprio a causa della diversa natura del reddito che generano.
Le minusvalenze costituiscono un credito d’imposta che può abbattere altri redditi diversi positivi nell’anno in cui sono state realizzate o nei 4 anni successivi.
Questo discutibile regime fiscale è all’origine di inefficienze forse peggiori: esse si producono quando gli investitori vogliono a tutti i costi inserire nei loro portafogli strumenti finanziari le cui plusvalenze siano considerate “Reddito diverso” per poter compensare le eventuali minusvalenze degli ETF.
Rientrano tra queste le plusvalenze generate dalla negoziazione di:
- Azioni
- Obbligazioni
- Derivati
- ETC ed ETN
- Certificati
Sono tutti prodotti che aumentano la concentrazione del portafoglio (azioni e obbligazioni) e/o la sua rischiosità: i derivati e i certificati sono strumenti finanziari complessi e dovrebbero essere trattati soltanto da professionisti; purtroppo, sempre più spesso si trovano anche nei portafogli dei normali investitori che, in molti casi, non hanno compreso fino in fondo il rischio che si stanno assumendo.
Gli ETC e gli ETN sono concettualmente simili agli ETF ma, rispetto a questi, sono più pericolosi a causa della presenza del rischio emittente: in caso di fallimento della società che li ha emessi, l’investitore corre il rischio di perdere una parte o tutto il capitale in essi investito.
La differenza tra gli ETC e gli ETN è che mentre i primi hanno come sottostante le materie prime, gli ETN replicano l’andamento di indici azionari, obbligazionari, valute e così via.
Gli ETC, in particolare, non sono necessariamente da evitare e, in certi casi, sono l’unico strumento finanziario a disposizione dell’investitore: ad esempio, se si vuole includere l’oro nel portafoglio, gli ETC a replica fisica sono lo strumento migliore da utilizzare (come vedremo, gli ETC saranno inseriti anche in alcuni dei Lazy portfolios che analizzeremo).
L’inefficienza fiscale degli ETF non deve essere vista come un ostacolo: in particolare, l’approccio passivo all’investimento punta all’ottenimento di rendimenti positivi di lungo termine e le eventuali minusvalenze – di importo non eccessivo – dovrebbero generarsi soltanto in fase di ribilanciamento del portafoglio.
3. Integrazione delle serie storiche degli ETF con gli indici

«Great things are done by a series of small things brought together».
Vincent van Gogh
Quando si analizzano le performance passate dei portafogli pigri, sarebbe importante effettuare i backtest di strumenti finanziari dalle serie storiche molto lunghe.
Purtroppo, gli ETF sono prodotti finanziari relativamente recenti e, soprattutto in Italia, hanno raggiunto la notorietà soltanto nel primo decennio di questo secolo. Di conseguenza, la maggior parte di essi non dispone di serie storiche lunghe a sufficienza.
Per ovviare a questo problema, per le date antecedenti a quelle di lancio di ciascun ETF sfrutteremo i rendimenti di indici molto simili a quelli che gli stessi ETF hanno lo scopo di replicare.
È una soluzione di comodo, largamente utilizzata da numerosi servizi e siti finanziari. In realtà, spesso ne viene fatto un uso improprio, dal momento che gli indici non dovrebbero essere impiegati per prolungare le serie storiche di fondi a gestione attiva: l’andamento del mercato potrebbe essere stato anche molto diverso da quello di un fondo composto da un campione di titoli sovra o sottopesati a discrezione del gestore.
Questo tipo di utilizzo ha molto più senso con i portafogli pigri, perché la differenza tra i valori degli indici e degli ipotetici ETF che avrebbero dovuto replicarli sarebbe stata minima.
Tuttavia, l’uso delle serie storiche pure degli indici altera l’analisi: gli indici non includono le spese correnti, mentre gli ETF sì (per quanto basse). Per eliminare questa distorsione, applicheremo artificiosamente i costi di ciascun ETF anche ai rispettivi indici.
Quello che faremo, cioè, sarà ridurre il rendimento giornaliero di ciascun indice per la quota parte giornaliera della percentuale annuale di spese correnti applicate all’ETF.
Non è una soluzione perfetta, ma è sempre meglio di niente: si tratta di un modo per rendere le simulazioni ancora più realistiche.
Tutti gli indici sono utilizzati in versione Total Return: letteralmente, Total Return significa “rendimento complessivo”, dato che include sia la rivalutazione del capitale che il reinvestimento dei proventi derivanti da dividendi o cedole.
Con l’integrazione delle serie storiche degli ETF e quelle degli indici e con l’applicazione delle spese correnti degli ETF anche agli indici, i backtest dei portafogli pigri – nonché eventuali confronti con altre strategie – saranno più robusti.
L’elenco degli indici impiegati nelle nostre analisi è il seguente:
- Azionari Area Asia/Pacifico (Giappone escluso)
- Azionari Area Euro Large Cap
- Azionari Area Euro Mid Cap
- Azionari Area Euro Settore Immobiliare
- Azionari Europa Large Cap Value
- Azionari Europa Small Cap
- Azionari Giappone Large Cap
- Azionari Internazionali Large Cap Blend
- Azionari Internazionali Large Cap Value
- Azionari Internazionali Small/Mid Cap
- Azionari Paesi Emergenti
- Azionari Svizzera
- Azionari UK Large Cap
- Azionari USA – Wilshire 5000
- Azionari USA Small Cap – Wilshire US Small Cap
- Azionari USA Small Cap Value – Wilshire US Small Cap Value
- Azionari USA Large Cap – Wilshire US Large Cap
- Azionari USA Large Cap Value – Wilshire US Large Cap Value
- Azionari USA Settore Immobiliare – Wilshire US REIT
- Monetari Breve Termine
- Obbligazionari Corporate EUR
- Obbligazionari Globali
- Obbligazionari Globali EUR Hedged
- Obbligazionari Governativi Breve Termine EUR
- Obbligazionari Governativi EUR
- Obbligazionari High Yield EUR
- Obbligazionari Inflation-Linked EUR
- Obbligazionari Paesi emergenti EUR
- Obbligazionari USA Corporate – ICE BofA US Corporate Index
- Obbligazionari USA Diversificati Breve Termine
- Obbligazionari USA High Yield – ICE BofA US High Yield Index
- S&P 500
- S&P US Preferred Stocks
4. Il rischio di cambio

«The first panacea for a mismanaged nation is inflation of the currency; the second is war. Both bring a temporary prosperity; both bring a permanent ruin. But both are the refuge of political and economic opportunists».
Ernest Hemingway
Come è noto, le valute più importanti e più utilizzate al mondo sono il dollaro (USD) e l’euro (EUR). Sono anche le più scambiate in assoluto.
Esistono però anche altre valute di grande rilevanza internazionale: lo yen giapponese (JPY), la sterlina inglese (GBP), il franco svizzero (CHF), il dollaro australiano (AUD) e canadese (CAD), il renminbi cinese (CNH), la corona svedese (SEK) e così via.
La realizzazione di backtest che non tengano conto delle differenze valutarie è molto comune: in fin dei conti, le serie storiche dei rendimenti sono una sequenza di numeri puri ed è facile dimenticarsi che quei rendimenti sono, in realtà, l’espressione di un incremento o un decremento di un prezzo espresso in una specifica valuta.
Se questa valuta non è quella utilizzata dall’investitore, c’è il rischio di perdita del potere di acquisto della valuta locale: in altre parole, siamo in presenza del rischio di cambio.
Un esempio aiuterà a capire meglio l’impatto che il rischio di cambio può avere sul rendimento di un investimento.
Ipotizziamo di comprare 10 quote di un ETF composto da titoli azionari statunitensi, al prezzo di 100 USD dollari ciascuna. L’ETF è quotato in USD e la spesa totale per questo investimento (ignoriamo per semplicità le commissioni di transazione) è pari a 1.000 USD. Supponiamo che il tasso di cambio EUR/USD sia pari a 1. Il controvalore in euro sarà, ovviamente, pari a 1.000 EUR.
Dopo un certo periodo di tempo vendiamo le nostre 10 quote. Ipotizziamo che il valore di ciascuna quota sia rimasto invariato a 100 USD, mentre il tasso di cambio EUR/USD, invece, si sia deteriorato a sfavore del dollaro, essendo adesso pari a 0,909 (1 USD = 0,909 EUR ovvero 1 EUR = 1,10 USD).
Il flusso di cassa originato dalla vendita delle quote sarà quindi pari a 1.000 USD = 909 EUR. Sebbene il rendimento puro del fondo sia stato dello 0% (il prezzo di ciascuna quota è rimasto invariato), abbiamo subito una perdita del 9,09%.
Lo stesso ETF quotato in euro avrebbe prodotto lo stesso risultato. L’unica differenza sarebbe stata nel suo prezzo, già convertito in euro: al momento della vendita, avremmo ricavato gli stessi 909 euro, generati da 10 quote del valore di 90,9 euro ciascuna.
Ovviamente, il tasso di cambio EUR/USD poteva modificarsi a nostro favore: se avessimo avuto fortuna e il tasso di cambio fosse salito a 1,10, al momento della vendita delle quote dell’ETF avremmo incassato 1.100 euro (1 EUR = 0,909 USD → 1 USD = 1,10 EUR), con un rendimento positivo del 10%.
Il rischio di cambio, se presente, aumenta la rischiosità di un investimento. Nel nostro esempio, e in generale in tutti gli investimenti finanziari in cui è presente, il rischio di cambio si aggiunge al rischio di mercato.
Se l’orizzonte temporale dell’investimento è di lungo termine, un’opinione molto diffusa è che non ci si debba preoccupare troppo del rischio di cambio tra dollaro ed euro: il cambio tenderebbe sempre a tornare verso un ipotetico valore medio.
Premesso che non esistono conferme scientifiche di questa affermazione, proviamo a verificarne la validità graficamente, analizzando l’andamento del tasso di cambio USD/EUR dal 1° gennaio 1985 al 31 dicembre 2020:
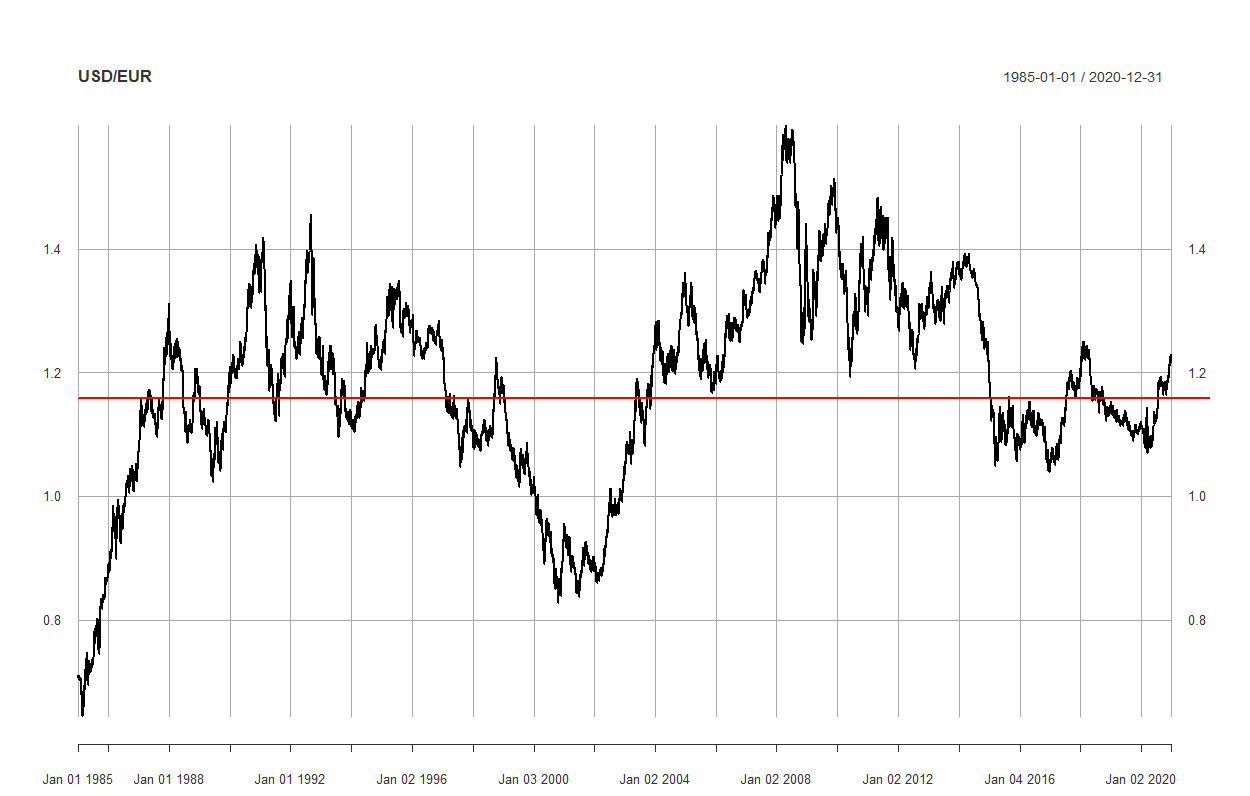
La media si colloca intorno a 1,18 (1 euro = 1,18 dollari) ed è rappresentata dalla linea orizzontale rossa. Effettivamente, si può vedere come questo valore sia stato incrociato più volte, verso l’alto e verso il basso.
Il problema è che negli anni il tasso di cambio è oscillato molto, con il minimo raggiunto nel febbraio 1985 (0,6444) e il massimo ad aprile 2008 (1,5990). La volatilità delle oscillazioni (deviazione standard annualizzata) è stata pari a 0,5490: un valore elevato (0,1585 è la volatilità non annualizzata).
Sono fluttuazioni importanti: nell’esempio fatto in precedenza, se le 10 quote dell’ETF a 100 dollari ciascuna fossero state acquistate il 25 ottobre 2000, il loro controvalore per un investitore dell’area euro sarebbe stato pari a 1.209,48 euro (il valore del tasso di cambio USD/EUR di quel giorno era pari a 0,8268).
Ipotizzando la vendita delle stesse 10 quote il 22 aprile 2008 (per assurdo, supponiamo che il prezzo di ogni quota fosse ancora esattamente 100 dollari), il controvalore dei 1.000 dollari sarebbe stato stavolta pari a soli 625,39 euro.
L’investimento si sarebbe chiuso con una perdita del 48,29%, da addebitarsi interamente al rischio di cambio.
L’esempio appena fatto rappresenta un caso estremo. Tuttavia, pensare di sterilizzare il rischio di cambio semplicemente assumendo che al momento dell’acquisto esso sia più o meno uguale a quello della vendita – che potrebbe potenzialmente avvenire a molti anni o addirittura decenni di distanza – è una palese forzatura.
Se le cose non andassero nella direzione giusta, il rischio di cambio potrebbe costare molto caro.
Vediamo quante volte, nell’arco di 5, 10, 15, 20, 25 e 30 anni, il cambio USD/EUR è stato favorevole o sfavorevole all’investitore tra il 1985 e la fine del 2020.
La tabella seguente ci fornisce le risposte cercate:
| Casi favorevoli e sfavorevoli all'investitore in euro | ||||||
|---|---|---|---|---|---|---|
| Differenza tra il tasso di cambio USD/EUR di fine e inizio investimento | ||||||
| N | 5 anni | 10 anni | 15 anni | 20 anni | 25 anni | 30 anni |
| N | 8,057 | 6,797 | 5,537 | 4,277 | 3,017 | 1,757 |
| Casi favorevoli | 4,003 | 3,494 | 1,790 | 930 | 1,384 | 742 |
| % | 49.68% | 51.41% | 32.33% | 21.74% | 45.87% | 42.23% |
| Casi sfavorevoli | 4,054 | 3,303 | 3,747 | 3,347 | 1,633 | 1,015 |
| % | 50.32% | 48.59% | 67.67% | 78.26% | 54.13% | 57.77% |
Indipendentemente dalla lunghezza dell’investimento, negli ultimi 35 anni il cambio è stato favorevole non più del 50% delle volte.
Il Forex è il mercato più grande e, forse, più efficiente del mondo: all’interno del Forex, la coppia di valute euro/dollaro è quella più scambiata in assoluto. I risultati riportati nella tabella non ci devono perciò sorprendere (possiamo associare al caso le basse percentuali di casi favorevoli nei periodi dai 15 anni in su).
Nel grafico seguente viene visualizzata la distribuzione delle frequenze delle variazioni del tasso di cambio in base alla durata dell’investimento:
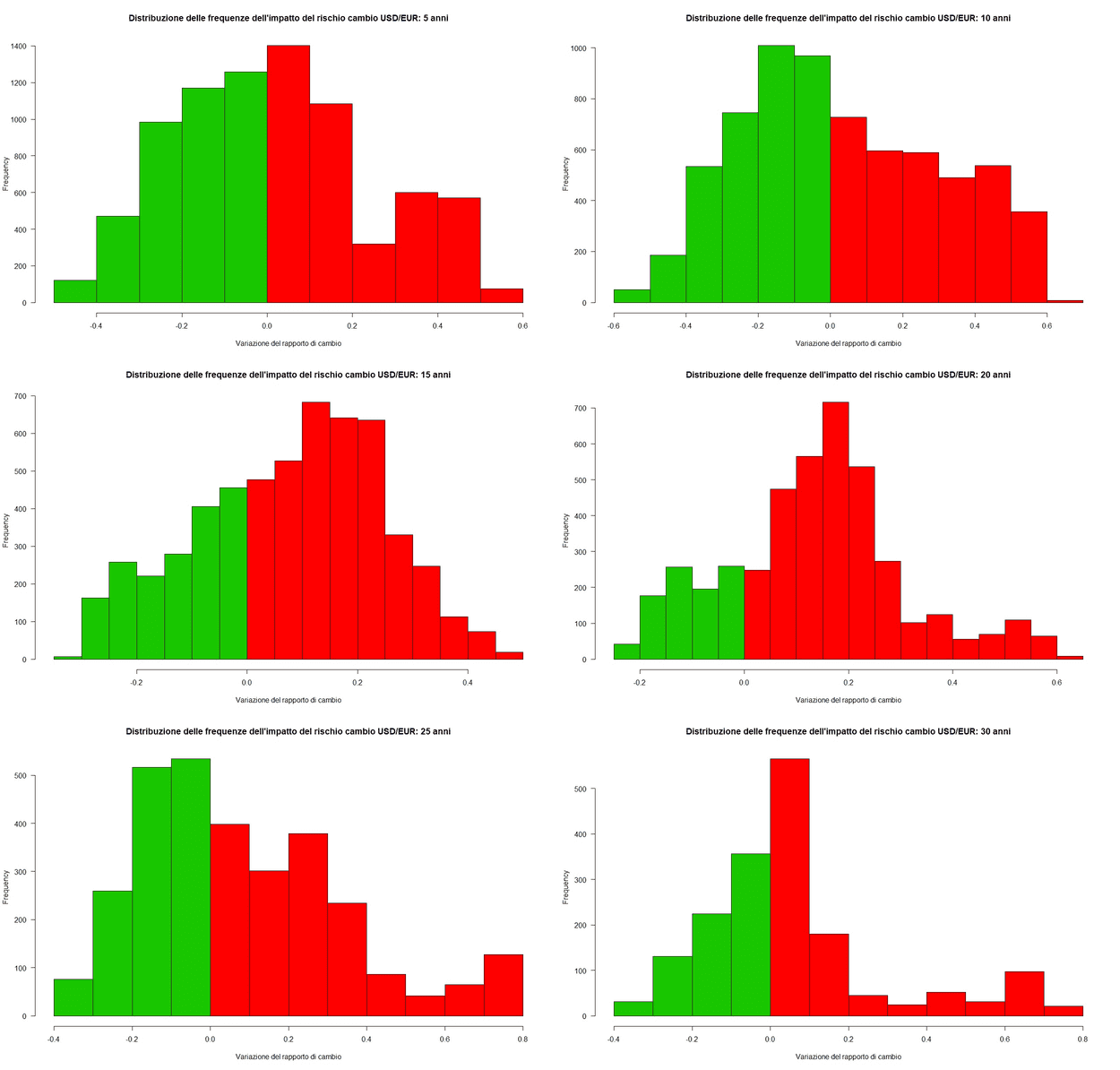
Gli istogrammi rossi rappresentano le densità di frequenza del cambio sfavorevole all’investitore: più l’istogramma è a destra, maggiore è stato l’impatto negativo.
Gli istogrammi verdi sono invece quelli relativi alle densità di frequenza del cambio favorevole all’investitore: più l’istogramma è a sinistra, maggiore è stato l’impatto positivo.
Anche se, per pura coincidenza, il tasso di cambio fosse lo stesso al momento di inizio e di fine investimento, c’è un’altra importante misura statistica – quasi sempre ignorata nel contesto di questa analisi – che verrebbe influenzata pesantemente: la volatilità.
Durante la vita dell’investimento, infatti, il tasso di cambio ha un impatto sui rendimenti del sottostante, amplificandoli o diminuendoli, e la volatilità aumenta di conseguenza.
Nei capitoli 13.3 e 14 questo fenomeno sarà approfondito con l’ausilio di numerosi grafici.
Il tasso di cambio tra due valute dipende da molti fattori macroeconomici che caratterizzano gli Stati in cui circolano tali valute: tra i più importanti troviamo il differenziale tra i tassi di inflazione, quello tra i tassi di interesse, i deficit di bilancio, il debito pubblico, la bilancia dei pagamenti, l’andamento economico e così via.
La prevedibilità dei tassi di cambio è oggetto di studio da molti decenni. Nel seguito di questo capitolo analizzeremo alcune teorie che definiremo “Naif”, in quanto abbastanza note tra gli investitori ma che non si basano su rigorosi studi o sulla pubblicazione di articoli scientifici. Daremo poi un’occhiata agli orientamenti più diffusi tra quelli che – in materia di prevedibilità dei tassi di cambio – circolano nella letteratura accademica e scientifica.
1° TEORIA NAIF → Se il dollaro si svaluta nei confronti dell’euro, la borsa americana cresce di più
Una delle teorie utilizzate per giustificare l’utilizzo di titoli in dollari (o di altre valute diverse dall’euro) nei portafogli finanziari degli investitori dell’area euro sostiene che se il dollaro si svaluta nei confronti dell’euro, le aziende americane ne beneficiano perché – sfruttando la debolezza relativa del dollaro – possono aumentare le loro esportazioni.
Le maggiori esportazioni implicano un aumento delle vendite, dei ricavi e quindi dei profitti aziendali: si verificherebbe allora una crescita del mercato azionario statunitense superiore a quella che ci sarebbe stata se il dollaro fosse stato più forte.
L’investitore dell’area euro, pur essendo sfavorito dalla svalutazione del dollaro, otterrebbe un beneficio in termini di rendimento dei titoli in dollari presenti nel suo portafoglio.
Se questo fosse vero, dovremmo riscontrare una stabile correlazione lineare negativa tra l’andamento dell’USD/EUR e quello del mercato azionario americano.
I grafici seguenti mostrano la correlazione lineare rolling a 5, 10, 15, 20, 25 e 30 anni tra l’USD/EUR e l’indice S&P 500 Total Return nel periodo compreso tra gennaio 1985 e dicembre 2020:
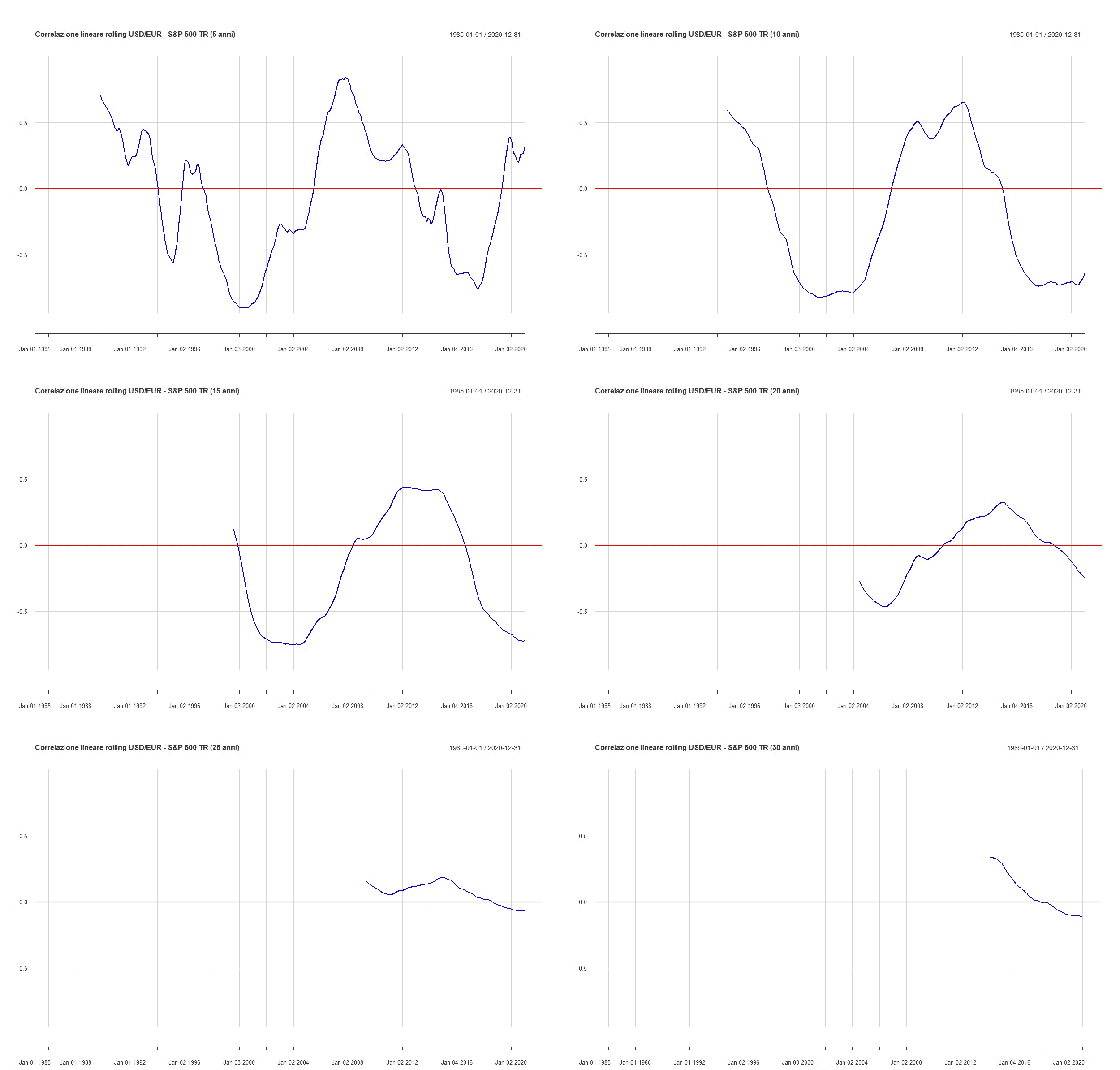
La correlazione lineare varia nel tempo: è negativa per una buona parte di esso ma non sempre; soprattutto, lo è sempre di meno con l’aumentare del suo periodo di calcolo.
Molte volte la correlazione lineare è positiva e lo rimane per numerosi anni di fila.
2° TEORIA NAIF → Se il dollaro si svaluta nei confronti dell’euro, basta allungare l’orizzonte temporale d’investimento
Qualcuno ritiene che, nel caso in cui il rapporto di cambio non sia favorevole, si debba aspettare un po’ di tempo in più prima di liquidare l’investimento: nel nostro esempio, siccome il cambio USD/EUR tende a regredire verso la media, prima o poi esso tornerebbe intorno a 1,18.
Questa maggiore attesa potrebbe scontrarsi con l’orizzonte temporale dell’investimento:
- Non è detto che l’investitore si possa permettere di aspettare.
- Non è detto che l’ipotetica regressione verso la media del tasso di cambio si verifichi nei tempi e nei modi auspicati dall’investitore.
Il temporeggiamento come strategia di uscita viene suggerito anche negli investimenti azionari: è vero che il rischio di ottenere un rendimento negativo è tanto più grande quanto più l’orizzonte temporale di investimento è breve, ma basta poter aspettare fino a 3-4 anni in più e, molto probabilmente, il risultato tornerà a essere positivo.
Una certa flessibilità nella lunghezza dell’orizzonte temporale sarebbe cioè un’arma in più, pronta per essere utilizzata quando le cose non vanno nella direzione giusta.
Se per i mercati azionari questa strategia è plausibile, quando di mezzo ci sono i tassi di cambi la questione rischia di prendere una brutta piega: i tassi di cambio non hanno una tendenza crescente nel lungo periodo come i mercati azionari e non è assolutamente detto che una maggiore attesa favorisca il ritorno del segno più nel rendimento di un investimento.
3° TEORIA NAIF → La diversificazione valutaria è un fattore positivo
Un’altra giustificazione all’assunzione del rischio di cambio è quella della maggior diversificazione del portafoglio, accentuata dalla presenza di altre valute: l’affermazione è corretta in linea teorica, ma la diversificazione valutaria aumenta o diminuisce il rischio complessivo dell’investimento?
Dai grafici e dalla tabella precedente, sembra proprio che l’investitore si assuma un rischio maggiore: forse si parla con troppa nonchalance di “effetto benefico della diversificazione valutaria”.
Ci sono troppe domande alle quali questa teoria non fornisce risposte:
- Basta un’altra valuta o è meglio avere più di due valute in portafoglio?
- Va bene qualsiasi valuta o è un discorso valido solo per le valute forti?
- L’impatto è positivo nel breve o nel medio/lungo termine?
- Come si dimostra che la diversificazione valutaria abbia effetti benefici in termini di rendimento e di volatilità dell’investimento superiori a quelli negativi generati da tassi di cambio che vanno nella direzione sfavorevole all’investitore?
- Qual è la giusta percentuale di portafoglio che dovrebbe essere lasciata in balia del rischio di cambio?
Un po’ di diversificazione valutaria forse non guasta ma, se si esagera, gli effetti negativi non tarderanno a manifestarsi.
Nei capitoli 13.3 e 14 approfondiremo l’analisi dell’impatto del rischio di cambio sulle performance dei 40 Lazy portfolios che saranno studiati.
Letteratura sulla stima dei tassi di cambio
Esistono numerosissimi articoli accademici e scientifici che trattano la stima dei tassi di cambio: le opinioni sono, ancora oggi, contrastanti.
Uno dei più importanti contributi in materia è stato l’articolo del 1982 di Meese e Rogoff: Empirical exchange rate models of the seventies: Do they fit out of sample?
Gli autori sostengono che sia impossibile prevedere l’andamento dei tassi di cambio: il modello random walk non produrrebbe risultati peggiori di quelli generati dalle stime ottenute da modelli di serie storiche univariate, modelli autoregressivi vettoriali o modelli strutturali costruiti su tre importanti tassi di cambio (dollaro/marco tedesco, dollaro/sterlina inglese e dollaro/yen).
Sulla stessa linea di Meese e Rogoff si sono schierati molti altri studiosi, tra i quali ricordiamo Kilian e Taylor, Rossi, Rashid, Moosa e Burns, Marçal e Hadad Junior.
È abbastanza numerosa anche la schiera di coloro che la pensano in maniera diversa: tra questi, Canova, Engel, Mark e West, Lam, Fung e Yu.
Ritenere che i tassi di cambio non siano casuali (generati cioè da un modello random walk) non significa affatto che siano facilmente prevedibili: i modelli che secondo alcuni autori riescono a ottenere risultati migliori del random walk sono molto complicati e funzionano soltanto su alcune coppie di valute: siamo molto lontani dall’aver trovato una risposta universale e gli stessi promotori suggeriscono di utilizzare le previsioni dei tassi di cambio generate dai modelli studiati con cautela.
In conclusione, non è detto che assumersi un certo grado di rischio di cambio negli investimenti finanziari sia per forza da evitare ma, se si vogliono evitare spiacevoli sorprese, il rischio di cambio è un fattore da prendere in considerazione, adottando le giuste contromisure.
L’investitore dell’area euro che decide di crearsi un portafoglio multi-valuta dovrebbe esserne consapevole e pronto a subirne le conseguenze se le cose non dovessero andare nel verso giusto.
5. Elenco dei principali Lazy portfolio (in USD e in EUR) e degli ETF che li costituiscono

«Lists today are a way of trying to get through the day, because we are losing a sense of time».
David Viscott
Il numero di portafogli pigri che si possono costruire è illimitato: gli ETF sono tantissimi e di uno stesso portafoglio si possono creare molte varianti anche semplicemente modificando i pesi degli ETF stessi.
Il numero di ETF che compongono un Lazy portfolio è variabile: si va generalmente dal singolo ETF ai 12 ETF.
Nella tabella seguente saranno elencati i Lazy portfolios che analizzeremo: il loro studio ci servirà a capire le caratteristiche e le performance di ciascuno di essi.
Di questi Lazy portfolios, forniremo i pesi ottimali su base mensile (i pesi verranno generati da alcuni modelli di ottimizzazione di cui parleremo nei capitoli successivi).
I pesi ottimali più recenti possono essere consultati al seguente link (per avere accesso è necessario sottoscrivere un abbonamento PRO): Lazy portfolios modello.
I Lazy portfolios sono nati negli Stati Uniti e la loro composizione originaria è pensata per l’investitore americano: la valuta predominante è il dollaro e l’area geografica di riferimento della maggioranza degli ETF, sia azionari che obbligazionari, è quella statunitense.
Purtroppo, la loro composizione non è ideale per un investitore appartenente a un’area geografica dove circola una valuta diversa dal dollaro.
Gli ETF che costituiscono questi Lazy portfolios, inoltre, sono tutti non armonizzati. Gli ETF non armonizzati sono quelli non conformi alle regolamentazioni dell’Unione Europea (UCITS) e sono caratterizzati da un regime fiscale sfavorevole.
Per ovviare a questi inconvenienti, analizzeremo sia la variante originaria di ciascun portafoglio, sia quella adattata a un investitore dell’eurozona. Questa seconda variante sarà denominata in euro e, laddove possibile, il mercato statunitense sarà sostituito con quello dell’eurozona o, per sfruttare una maggiore diversificazione, dal mercato europeo o globale.
Ecco la lista dei Lazy portfolio che saranno oggetto del nostro studio:
| Asset allocation dei Lazy portfolios1 | ||||||
|---|---|---|---|---|---|---|
| Composizione dei Lazy portfolios e nome degli ETF che li compongono (USD e EUR) | ||||||
| Asset allocation | ETF e Indici replicati | |||||
| Azioni | Bond | Comm. | Asset Class | ETF (USD) | ETF (EUR) | Peso |
| World Bond: 1 ETF | ||||||
| 0% | 100% | 0% | U.S., Intermediate-Term | iShares 7-10 Year Treasury Bond (IEF) | Xtrackers II Eurozone Gov. Bond 7-10 1C EUR (X710) | 100% |
| World Stocks: 1 ETF | ||||||
| 100% | 0% | 0% | Developed Markets, Large Cap | Vanguard Total World Stock (VT) | Lyxor MSCI All Country World UCITS ETF Acc EUR (ACWI) | 100% |
| Two funds 10/90: 2 ETF | ||||||
| 10% | 90% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 10% |
| 10% | 90% | 0% | U.S., All-Term | Vanguard Total Bond Market (BND) | WisdomTree EUR Aggr. Bond Enh. Yield EUR Acc (EYLD) | 90% |
| Two funds 20/80: 2 ETF | ||||||
| 20% | 80% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 20% |
| 20% | 80% | 0% | U.S., All-Term | Vanguard Total Bond Market (BND) | WisdomTree EUR Aggr. Bond Enh. Yield EUR Acc (EYLD) | 80% |
| Two funds 30/70: 2 ETF | ||||||
| 30% | 70% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 30% |
| 30% | 70% | 0% | U.S., All-Term | Vanguard Total Bond Market (BND) | WisdomTree EUR Aggr. Bond Enh. Yield EUR Acc (EYLD) | 70% |
| Two funds 40/60: 2 ETF | ||||||
| 40% | 60% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 40% |
| 40% | 60% | 0% | U.S., All-Term | Vanguard Total Bond Market (BND) | WisdomTree EUR Aggr. Bond Enh. Yield EUR Acc (EYLD) | 60% |
| Two funds 50/50: 2 ETF | ||||||
| 50% | 50% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 50% |
| 50% | 50% | 0% | U.S., All-Term | Vanguard Total Bond Market (BND) | WisdomTree EUR Aggr. Bond Enh. Yield EUR Acc (EYLD) | 50% |
| Two funds 60/40: 2 ETF | ||||||
| 60% | 40% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 60% |
| 60% | 40% | 0% | U.S., All-Term | Vanguard Total Bond Market (BND) | WisdomTree EUR Aggr. Bond Enh. Yield EUR Acc (EYLD) | 40% |
| Two funds 70/30: 2 ETF | ||||||
| 70% | 30% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 70% |
| 70% | 30% | 0% | U.S., All-Term | Vanguard Total Bond Market (BND) | WisdomTree EUR Aggr. Bond Enh. Yield EUR Acc (EYLD) | 30% |
| Two funds 80/20: 2 ETF | ||||||
| 80% | 20% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 80% |
| 80% | 20% | 0% | U.S., All-Term | Vanguard Total Bond Market (BND) | WisdomTree EUR Aggr. Bond Enh. Yield EUR Acc (EYLD) | 20% |
| Two funds 90/10: 2 ETF | ||||||
| 90% | 10% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 90% |
| 90% | 10% | 0% | U.S., All-Term | Vanguard Total Bond Market (BND) | WisdomTree EUR Aggr. Bond Enh. Yield EUR Acc (EYLD) | 10% |
| Warren Buffett: 2 ETF | ||||||
| 90% | 10% | 0% | U.S. Large Cap | Vanguard Large-Cap (VV) | iShares MSCI EMU Large Cap UCITS ETF (EMUL) | 90% |
| 90% | 10% | 0% | U.S., Short Term | iShares 1-3 Year Treasury Bond (SHY) | Lyxor Euro Government Bond 1-3Y DR UCITS ETF Acc (EM13) | 10% |
| Simple Path to Wealth: 2 ETF | ||||||
| 75% | 25% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 75% |
| 75% | 25% | 0% | U.S., All-Term | Vanguard Total Bond Market (BND) | WisdomTree EUR Aggr. Bond Enh. Yield EUR Acc (EYLD) | 25% |
| Couch Potato: 2 ETF | ||||||
| 50% | 50% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 50% |
| 50% | 50% | 0% | U.S., All-Term | iShares TIPS Bond (TIP) | Lyxor Euro Gov. Inflation Linked Bond DR UCITS ETF Acc (EMI) | 50% |
| Three Funds Bogleheads: 3 ETF | ||||||
| 80% | 20% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 50% |
| 80% | 20% | 0% | Global ex-US, Large Cap | Vanguard FTSE All-World ex-US (VEU) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) | 30% |
| 80% | 20% | 0% | U.S., All-Term | Vanguard Total Bond Market (BND) | WisdomTree EUR Aggr. Bond Enh. Yield EUR Acc (EYLD) | 20% |
| Second Grader's Starter: 3 ETF | ||||||
| 90% | 10% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 60% |
| 90% | 10% | 0% | Global ex-US, Large Cap | Vanguard FTSE All-World ex-US (VEU) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) | 30% |
| 90% | 10% | 0% | U.S., All-Term | Vanguard Total Bond Market (BND) | WisdomTree EUR Aggr. Bond Enh. Yield EUR Acc (EYLD) | 10% |
| Talmud: 3 ETF | ||||||
| 67% | 33% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 34% |
| 67% | 33% | 0% | Real Estate, U.S. | Vanguard Real Estate (VNQ) | Xtrackers FTSE EPRA/NAREIT Dev. Europe Real Estate 1C (XDER) | 33% |
| 67% | 33% | 0% | U.S., All-Term | Vanguard Total Bond Market (BND) | WisdomTree EUR Aggr. Bond Enh. Yield EUR Acc (EYLD) | 33% |
| Margaritaville: 3 ETF | ||||||
| 67% | 33% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 34% |
| 67% | 33% | 0% | Real Estate, U.S. | Vanguard FTSE All-World ex-US (VEU) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) | 33% |
| 67% | 33% | 0% | U.S., All-Term | iShares TIPS Bond (TIP) | Lyxor Euro Gov. Inflation Linked Bond DR UCITS ETF Acc (EMI) | 33% |
| Andrew Tobias: 3 ETF | ||||||
| 67% | 33% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 34% |
| 67% | 33% | 0% | EAFE, Large Cap | iShares MSCI EAFE (EFA) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) | 33% |
| 67% | 33% | 0% | U.S., Short Term | iShares 1-3 Year Treasury Bond (SHY) | Lyxor Euro Government Bond 1-3Y DR UCITS ETF Acc (EM13) | 33% |
| Gyroscopic Investing Desert: 3 ETF | ||||||
| 30% | 60% | 10% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 30% |
| 30% | 60% | 10% | U.S., Intermediate-Term | iShares 3-7 Year Treasury Bond (IEI) | Lyxor Euro Government Bond 5-7Y DR UCITS ETF Acc (EM57) | 60% |
| 30% | 60% | 10% | Gold | SPDR Gold Trust (GLD) | Xtrackers Physical Gold EUR Hedged ETC (XAD1) | 10% |
| Permanent: 4 ETF | ||||||
| 25% | 50% | 25% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 25% |
| 25% | 50% | 25% | U.S., Ultra Short Term | SPDR Blmbg Barclays 1-3 Mth T-Bill (BIL) | Amundi ETF Govies 0-6 Mts EuroMTS Inv. Gr. DR EUR (C3M) | 25% |
| 25% | 50% | 25% | U.S., Long-Term | iShares 20+ Year Treasury Bond (TLT) | Xtrackers Eurozone Government Bond 15+ UCITS ETF 1C (X15E) | 25% |
| 25% | 50% | 25% | Gold | SPDR Gold Trust (GLD) | Xtrackers Physical Gold EUR Hedged ETC (XAD1) | 25% |
| Core Four: 4 ETF | ||||||
| 80% | 20% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 48% |
| 80% | 20% | 0% | Global ex-US, Large Cap | Vanguard FTSE All-World ex-US (VEU) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) | 24% |
| 80% | 20% | 0% | Real Estate, U.S. | Vanguard Real Estate (VNQ) | Xtrackers FTSE EPRA/NAREIT Dev. Europe Real Estate 1C (XDER) | 8% |
| 80% | 20% | 0% | U.S., All-Term | Vanguard Total Bond Market (BND) | WisdomTree EUR Aggr. Bond Enh. Yield EUR Acc (EYLD) | 20% |
| Bogleheads Four Funds: 4 ETF | ||||||
| 80% | 20% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 50% |
| 80% | 20% | 0% | Global ex-US, Large Cap | Vanguard FTSE All-World ex-US (VEU) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) | 30% |
| 80% | 20% | 0% | U.S., All-Term | iShares TIPS Bond (TIP) | Lyxor Euro Gov. Inflation Linked Bond DR UCITS ETF Acc (EMI) | 10% |
| 80% | 20% | 0% | U.S., All-Term | Vanguard Total Bond Market (BND) | WisdomTree EUR Aggr. Bond Enh. Yield EUR Acc (EYLD) | 10% |
| No Brainer: 4 ETF | ||||||
| 75% | 25% | 0% | U.S., Small Cap | iShares Core S&P Small-Cap (IJR) | iShares MSCI EMU Small Cap UCITS ETF Acc (CSEMUS) | 25% |
| 75% | 25% | 0% | Global ex-US, Large Cap | Vanguard FTSE All-World ex-US (VEU) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) | 25% |
| 75% | 25% | 0% | U.S., Large Cap | Vanguard Large-Cap (VV) | iShares MSCI EMU Large Cap UCITS ETF (EMUL) | 25% |
| 75% | 25% | 0% | U.S., Short Term | iShares 1-3 Year Treasury Bond (SHY) | Lyxor Euro Government Bond 1-3Y DR UCITS ETF Acc (EM13) | 25% |
| Larry: 4 ETF | ||||||
| 30% | 70% | 0% | U.S., Small Cap Value | iShares S&P Small-Cap 600 Value (IJS) | iShares MSCI EMU Small Cap UCITS ETF Acc (CSEMUS) | 15% |
| 30% | 70% | 0% | Developed Markets, Small Cap, Value | WisdomTree International SmallCp Div (DLS) | SPDR MSCI World Small Cap UCITS ETF (ZPRS) | 8% |
| 30% | 70% | 0% | Emerging Markets, Large Cap | iShares MSCI Emerging Markets (EEM) | Lyxor MSCI Emerging Markets UCITS ETF Acc EUR (EMKT) | 8% |
| 30% | 70% | 0% | U.S., Intermediate-Term | iShares 3-7 Year Treasury Bond (IEI) | Lyxor Euro Government Bond 5-7Y DR UCITS ETF Acc (EM57) | 70% |
| Golden Butterfly: 5 ETF | ||||||
| 40% | 40% | 20% | U.S., Small Cap Value | iShares S&P Small-Cap 600 Value (IJS) | iShares MSCI EMU Small Cap UCITS ETF Acc (CSEMUS) | 20% |
| 40% | 40% | 20% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 20% |
| 40% | 40% | 20% | U.S., Short Term | iShares 1-3 Year Treasury Bond (SHY) | Lyxor Euro Government Bond 1-3Y DR UCITS ETF Acc (EM13) | 20% |
| 40% | 40% | 20% | U.S., Long-Term | iShares 20+ Year Treasury Bond (TLT) | Xtrackers Eurozone Government Bond 15+ UCITS ETF 1C (X15E) | 20% |
| 40% | 40% | 20% | Gold | SPDR Gold Trust (GLD) | Xtrackers Physical Gold EUR Hedged ETC (XAD1) | 20% |
| All Weather: 5 ETF | ||||||
| 30% | 55% | 15% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 30% |
| 30% | 55% | 15% | U.S., Long-Term | iShares 20+ Year Treasury Bond (TLT) | Xtrackers Eurozone Government Bond 15+ UCITS ETF 1C (X15E) | 40% |
| 30% | 55% | 15% | U.S., Intermediate-Term | iShares 3-7 Year Treasury Bond (IEI) | Lyxor Euro Government Bond 5-7Y DR UCITS ETF Acc (EM57) | 15% |
| 30% | 55% | 15% | Gold | SPDR Gold Trust (GLD) | Xtrackers Physical Gold EUR Hedged ETC (XAD1) | 8% |
| 30% | 55% | 15% | Broad Diversified | iShares S&P GSCI Commodity Indexed Trust (GSG) | Lyxor Comm. Thomson Reuters/CoreComm. CRB TR Acc (CRB) | 8% |
| Ivy: 5 ETF | ||||||
| 60% | 20% | 20% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 20% |
| 60% | 20% | 20% | Global ex-US, Large Cap | Vanguard FTSE All-World ex-US (VEU) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) | 20% |
| 60% | 20% | 20% | Real Estate, U.S. | Vanguard Real Estate (VNQ) | Xtrackers FTSE EPRA/NAREIT Dev. Europe Real Estate 1C (XDER) | 20% |
| 60% | 20% | 20% | U.S., All-Term | Vanguard Total Bond Market (BND) | WisdomTree EUR Aggr. Bond Enh. Yield EUR Acc (EYLD) | 20% |
| 60% | 20% | 20% | Broad Diversified | iShares S&P GSCI Commodity Indexed Trust (GSG) | Lyxor Comm. Thomson Reuters/CoreComm. CRB TR Acc (CRB) | 20% |
| Dynamic 60/40 Income: 5 ETF | ||||||
| 60% | 40% | 0% | Preferred Stock, U.S. | iShares Preferred and Income Securities ETF (PFF) | Invesco Preferred Shares UCITS ETF A (PRAC) | 20% |
| 60% | 40% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 20% |
| 60% | 40% | 0% | Real Estate, U.S. | Vanguard Real Estate (VNQ) | Xtrackers FTSE EPRA/NAREIT Dev. Europe Real Estate 1C (XDER) | 20% |
| 60% | 40% | 0% | U.S., Short Term | iShares 1-3 Year Treasury Bond (SHY) | Lyxor Euro Government Bond 1-3Y DR UCITS ETF Acc (EM13) | 20% |
| 60% | 40% | 0% | U.S., Intermediate-Term | iShares iBoxx $ High Yield Corporate Bond (HYG) | PIMCO Euro Short-Term High Yield Corp. Bond Index Acc (EUHA) | 20% |
| Dynamic 40/60 Income: 5 ETF | ||||||
| 40% | 60% | 0% | Preferred Stock, U.S. | iShares Preferred and Income Securities ETF (PFF) | Invesco Preferred Shares UCITS ETF A (PRAC) | 20% |
| 40% | 60% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 20% |
| 40% | 60% | 0% | Emerging Markets, All-Term | iShares JP Morgan USD Em Mkts Bd (EMB) | Em. Mkts. USD Gov. and Gov.-Rel. Bond Select 1C EUR H (XEMB) | 20% |
| 40% | 60% | 0% | U.S., Short Term | iShares 1-3 Year Treasury Bond (SHY) | Lyxor Euro Government Bond 1-3Y DR UCITS ETF Acc (EM13) | 20% |
| 40% | 60% | 0% | U.S., Intermediate-Term | iShares iBoxx $ High Yield Corporate Bond (HYG) | PIMCO Euro Short-Term High Yield Corp. Bond Index Acc (EUHA) | 20% |
| Five Asset: 6 ETF | ||||||
| 60% | 20% | 20% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 20% |
| 60% | 20% | 20% | Global ex-US, Large Cap | Vanguard FTSE All-World ex-US (VEU) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) | 20% |
| 60% | 20% | 20% | Real Estate, U.S. | Vanguard Real Estate (VNQ) | Xtrackers FTSE EPRA/NAREIT Dev. Europe Real Estate 1C (XDER) | 20% |
| 60% | 20% | 20% | U.S., All-Term | Vanguard Total Bond Market (BND) | WisdomTree EUR Aggr. Bond Enh. Yield EUR Acc (EYLD) | 14% |
| 60% | 20% | 20% | Developed Markets, All-Term | Vanguard Total International Bond (BNDX) | Amundi ETF Barclays Global Aggregate 500m DR (GAGG) | 6% |
| 60% | 20% | 20% | Broad Diversified | Invesco DB Commodity Tracking (DBC) | Lyxor Comm. Thomson Reuters/CoreComm. CRB TR Acc (CRB) | 20% |
| David Swensen Lazy Portfolio: 6 ETF | ||||||
| 70% | 30% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) | 30% |
| 70% | 30% | 0% | Real Estate, U.S. | Vanguard Real Estate (VNQ) | Xtrackers FTSE EPRA/NAREIT Dev. Europe Real Estate 1C (XDER) | 20% |
| 70% | 30% | 0% | Global ex-US, Large Cap | Vanguard FTSE All-World ex-US (VEU) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) | 15% |
| 70% | 30% | 0% | Emerging Markets, Large Cap | iShares MSCI Emerging Markets (EEM) | Lyxor MSCI Emerging Markets UCITS ETF Acc EUR (EMKT) | 5% |
| 70% | 30% | 0% | U.S., Intermediate-Term | iShares 3-7 Year Treasury Bond (IEI) | Lyxor Euro Government Bond 5-7Y DR UCITS ETF Acc (EM57) | 15% |
| 70% | 30% | 0% | U.S., All-Term | iShares TIPS Bond (TIP) | Lyxor Euro Gov. Inflation Linked Bond DR UCITS ETF Acc (EMI) | 15% |
| Coffee House: 7 ETF | ||||||
| 60% | 40% | 0% | U.S., Small Cap | iShares Core S&P Small-Cap (IJR) | iShares MSCI EMU Small Cap UCITS ETF Acc (CSEMUS) | 10% |
| 60% | 40% | 0% | U.S., Small Cap Value | iShares S&P Small-Cap 600 Value (IJS) | iShares MSCI EMU Small Cap UCITS ETF Acc (CSEMUS) | 10% |
| 60% | 40% | 0% | U.S., Large Cap Value | Vanguard Value (VTV) | Xtrackers MSCI Europe Value Factor UCITS ETF 1C (D5BL) | 10% |
| 60% | 40% | 0% | Global ex-US, Large Cap | Vanguard FTSE All-World ex-US (VEU) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) | 10% |
| 60% | 40% | 0% | Real Estate, U.S. | Vanguard Real Estate (VNQ) | Xtrackers FTSE EPRA/NAREIT Dev. Europe Real Estate 1C (XDER) | 10% |
| 60% | 40% | 0% | U.S., Large Cap | Vanguard Large-Cap (VV) | iShares MSCI EMU Large Cap UCITS ETF (EMUL) | 10% |
| 60% | 40% | 0% | U.S., All-Term | Vanguard Total Bond Market (BND) | WisdomTree EUR Aggr. Bond Enh. Yield EUR Acc (EYLD) | 40% |
| Rob Arnott: 8 ETF | ||||||
| 30% | 60% | 10% | Global ex-US, Large Cap | Vanguard FTSE All-World ex-US (VEU) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) | 10% |
| 30% | 60% | 10% | Real Estate, U.S. | Vanguard Real Estate (VNQ) | Xtrackers FTSE EPRA/NAREIT Dev. Europe Real Estate 1C (XDER) | 10% |
| 30% | 60% | 10% | U.S., Large Cap | Vanguard Large-Cap (VV) | iShares MSCI EMU Large Cap UCITS ETF (EMUL) | 10% |
| 30% | 60% | 10% | Developed Markets, All-Term | Vanguard Total International Bond (BNDX) | Amundi ETF Barclays Global Aggregate 500m DR (GAGG) | 20% |
| 30% | 60% | 10% | U.S., All-Term | iShares Investment Grade Corporate Bond (LQD) | Xtrackers EUR Corporate Bond UCITS ETF 1C (XBLC) | 20% |
| 30% | 60% | 10% | U.S., Long-Term | iShares 20+ Year Treasury Bond (TLT) | Xtrackers Eurozone Government Bond 15+ UCITS ETF 1C (X15E) | 10% |
| 30% | 60% | 10% | U.S., All-Term | iShares TIPS Bond (TIP) | Lyxor Euro Gov. Inflation Linked Bond DR UCITS ETF Acc (EMI) | 10% |
| 30% | 60% | 10% | Broad Diversified | Invesco DB Commodity Tracking (DBC) | Lyxor Comm. Thomson Reuters/CoreComm. CRB TR Acc (CRB) | 10% |
| Ultimate Buy and Hold Strategy: 10 ETF | ||||||
| 100% | 0% | 0% | Emerging Markets, Large Cap | iShares MSCI Emerging Markets (EEM) | Lyxor MSCI Emerging Markets UCITS ETF Acc EUR (EMKT) | 10% |
| 100% | 0% | 0% | U.S., Small Cap | iShares Core S&P Small-Cap (IJR) | iShares MSCI EMU Small Cap UCITS ETF Acc (CSEMUS) | 10% |
| 100% | 0% | 0% | U.S., Small Cap Value | iShares S&P Small-Cap 600 Value (IJS) | iShares MSCI EMU Small Cap UCITS ETF Acc (CSEMUS) | 10% |
| 100% | 0% | 0% | Developed Markets, Small Cap, Value | WisdomTree International SmallCp Div (DLS) | SPDR MSCI World Small Cap UCITS ETF (ZPRS) | 10% |
| 100% | 0% | 0% | U.S., Large Cap | SPDR S&P 500 (SPY) | Xtrackers STOXX Europe 600 UCITS ETF 1C (XSX6) | 10% |
| 100% | 0% | 0% | Developed Markets, Large Cap | Vanguard Total World Stock (VT) | Lyxor MSCI All Country World UCITS ETF Acc EUR (ACWI) | 10% |
| 100% | 0% | 0% | U.S., Large Cap | Vanguard Value (VTV) | Xtrackers MSCI Europe Value Factor UCITS ETF 1C (D5BL) | 10% |
| 100% | 0% | 0% | EAFE, Small Cap | iShares MSCI EAFE Small-Cap (SCZ) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) | 10% |
| 100% | 0% | 0% | EAFE, Large Cap, Value | iShares MSCI EAFE Value (EFV) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) | 10% |
| 100% | 0% | 0% | Real Estate, U.S. | Vanguard Real Estate (VNQ) | Xtrackers FTSE EPRA/NAREIT Dev. Europe Real Estate 1C (XDER) | 10% |
| Ultimate Buy & Hold: 12 ETF | ||||||
| 60% | 40% | 0% | Developed Markets, Small Cap, Value | WisdomTree International SmallCp Div (DLS) | SPDR MSCI World Small Cap UCITS ETF (ZPRS) | 12% |
| 60% | 40% | 0% | U.S., Small Cap | iShares Core S&P Small-Cap (IJR) | iShares MSCI EMU Small Cap UCITS ETF Acc (CSEMUS) | 6% |
| 60% | 40% | 0% | U.S., Small Cap Value | iShares S&P Small-Cap 600 Value (IJS) | iShares MSCI EMU Small Cap UCITS ETF Acc (CSEMUS) | 6% |
| 60% | 40% | 0% | Emerging Markets, Large Cap | iShares MSCI Emerging Markets (EEM) | Lyxor MSCI Emerging Markets UCITS ETF Acc EUR (EMKT) | 6% |
| 60% | 40% | 0% | U.S., Large Cap, Value | Vanguard Value (VTV) | Xtrackers MSCI Europe Value Factor UCITS ETF 1C (D5BL) | 6% |
| 60% | 40% | 0% | EAFE, Large Cap | Vanguard FTSE Developed Markets (VEA) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) | 6% |
| 60% | 40% | 0% | EAFE, Large Cap, Value | iShares MSCI EAFE Value (EFV) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) | 6% |
| 60% | 40% | 0% | Real Estate, U.S. | Vanguard Real Estate (VNQ) | Xtrackers FTSE EPRA/NAREIT Dev. Europe Real Estate 1C (XDER) | 6% |
| 60% | 40% | 0% | U.S., Large Cap | Vanguard Large-Cap (VV) | iShares MSCI EMU Large Cap UCITS ETF (EMUL) | 6% |
| 60% | 40% | 0% | U.S., Intermediate-Term | iShares 3-7 Year Treasury Bond (IEI) | Lyxor Euro Government Bond 5-7Y DR UCITS ETF Acc (EM57) | 20% |
| 60% | 40% | 0% | U.S., Short Term | iShares 1-3 Year Treasury Bond (SHY) | Lyxor Euro Government Bond 1-3Y DR UCITS ETF Acc (EM13) | 12% |
| 60% | 40% | 0% | U.S., All-Term | iShares TIPS Bond (TIP) | Lyxor Euro Gov. Inflation Linked Bond DR UCITS ETF Acc (EMI) | 8% |
| Dedalo Three: 3 ETF | ||||||
| 100% | 0% | 0% | All Country World | Vanguard Total World Stock (VT) | MSCI ACWI UCITS ETF Acc (IUSQ) | 30% |
| 100% | 0% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | MSCI USA hedged EUR UCITS A-acc (USEUWH) | 40% |
| 100% | 0% | 0% | Europe, Large-Mid Cap | Vanguard Total Stock Market (VTI) | MSCI EMU UCITS ETF EUR Acc (CSEMU) | 30% |
| Dedalo Four: 4 ETF | ||||||
| 80% | 20% | 0% | All Country World | Vanguard Total World Stock (VT) | MSCI ACWI UCITS ETF Acc (IUSQ) | 25% |
| 80% | 20% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | MSCI USA hedged EUR UCITS A-acc (USEUWH) | 30% |
| 80% | 20% | 0% | Europe, Large-Mid Cap | Vanguard Total Stock Market (VTI) | MSCI EMU UCITS ETF EUR Acc (CSEMU) | 25% |
| 80% | 20% | 0% | International, All-Term | Vanguard Total International Bond (BNDX) | Global Aggr. Bond UCITS EUR Hedged Acc (AGGH) | 20% |
| Dedalo Eleven: 11 ETF | ||||||
| 80% | 20% | 0% | Europe, Large-Mid Cap | Vanguard Total Stock Market (VTI) | MSCI EMU UCITS ETF EUR Acc (CSEMU) | 24% |
| 80% | 20% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | MSCI USA Swap UCITS ETF 1C (XMUS) | 20% |
| 80% | 20% | 0% | U.S., Large Cap | Vanguard Total Stock Market (VTI) | MSCI USA hedged EUR UCITS A-acc (USEUWH) | 12% |
| 80% | 20% | 0% | Emerging Markets | iShares MSCI Emerging Markets (EEM) | MSCI Emerging Markets UCITS ETF Acc (EMKT) | 8% |
| 80% | 20% | 0% | UK, Large-Mid Cap | iShares MSCI United Kingdom (EWU) | MSCI UK UCITS ETF (CU1) | 4% |
| 80% | 20% | 0% | Switzerland, Large Cap | iShares MSCI Switzerland (EWL) | MSCI Switzerland 20/35 UCITS ETF A-acc (SW2CHB) | 4% |
| 80% | 20% | 0% | Japan, Large Cap | iShares MSCI Japan (EWJ) | MSCI Japan UCITS ETF 1C (XMJP) | 4% |
| 80% | 20% | 0% | Pacific ex Japan, Large Cap | iShares MSCI All Country Asia ex Japan (AAXJ) | MSCI Pacific ex Japan UCITS ETF Acc (CSPXJ) | 4% |
| 80% | 20% | 0% | International Gov. Develop., All-Term | Vanguard Total International Bond (BNDX) | Global Gover. Bond UCITS EUR Hedged (XGSH) | 7% |
| 80% | 20% | 0% | Inter. Infl.-Linked Develop., All-Term | SPDR FTSE Inter. Gvt. Infl.-Protected Bond (WIP) | Global Infl.-Linked Bond UCITS EUR hedged (XGIN) | 7% |
| 80% | 20% | 0% | Government Em. Markets, All-Term | Vanguard Total Bond Market (BND) | USD Em. Mkt. Sovereign UCITS Hedged Acc (SBEME) | 6% |
| Fonte (solo per i Lazy portfolios in USD): Lazy Portfolio ETF | ||||||
|
1 Maggiori informazioni sono disponibili nel capitolo 13. |
||||||
Nella tabella seguente, vengono elencati gli ETF utilizzati nei backtest: quelli in blu, sia nella colonna di sinistra (30) che di destra (9), sono gli ETF dei Lazy portfolios originariamente creati per gli investitori in dollari (sinistra) e in euro (destra).
Gli ETF in nero che si trovano nella colonna di destra sono gli equivalenti in euro degli ETF originari in dollari; quelli in nero nella colonna di sinistra sono gli equivalenti in dollari degli ETF originari in euro.
| Lista degli ETF1 | ||
|---|---|---|
| ETF utilizzati nei backtest in USD e in EUR | ||
| N° | ETF (USD) | ETF (EUR) |
| 1 | Invesco DB Commodity Tracking (DBC) | Lyxor Commodities Refinitiv/CoreCommodity CRB TR UCITS ETF Acc (CRB) |
| 2 | iShares 1-3 Year Treasury Bond (SHY) | Lyxor Euro Government Bond 1-3Y (DR) UCITS ETF Acc (EM13) |
| 3 | iShares 20+ Year Treasury Bond (TLT) | Xtrackers Eurozone Government Bond 15-30 UCITS ETF 1C (X15E) |
| 4 | iShares 3-7 Year Treasury Bond (IEI) | Lyxor Euro Government Bond 5-7Y (DR) UCITS ETF Acc (EM57) |
| 5 | iShares 7-10 Year Treasury Bond (IEF) | Xtrackers Eurozone Government Bond 7-10 UCITS ETF 1C (X710) |
| 6 | iShares Core S&P Small-Cap (IJR) | iShares MSCI EMU Small Cap UCITS ETF Acc (CSEMUS) |
| 7 | iShares iBoxx $ High Yield Corporate Bond (HYG) | PIMCO Euro Short-Term High Yield Corporate Bond Index UCITS ETF Acc (EUHA) |
| 8 | iShares Investment Grade Corporate Bond (LQD) | Xtrackers EUR Corporate Bond UCITS ETF 1C (XBLC) |
| 9 | iShares JP Morgan USD Em Mkts Bd (EMB) | Xtrackers Emerging Markets USD Government and Government-Related Bond Select UCITS ETF 1C EUR Hedged (XEMB) |
| 10 | iShares MSCI EAFE (EFA) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) |
| 11 | iShares MSCI EAFE Small-Cap (SCZ) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) |
| 12 | iShares MSCI EAFE Value (EFV) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) |
| 13 | iShares MSCI Emerging Markets (EEM) | Lyxor MSCI Emerging Markets UCITS ETF Acc EUR (EMKT) |
| 14 | iShares Preferred and Income Securities ETF (PFF) | Invesco Preferred Shares UCITS ETF A (PRAC) |
| 15 | iShares S&P GSCI Commodity Indexed Trust (GSG) | Lyxor Commodities Refinitiv/CoreCommodity CRB TR UCITS ETF Acc (CRB) |
| 16 | iShares S&P Small-Cap 600 Value (IJS) | iShares MSCI EMU Small Cap UCITS ETF Acc (CSEMUS) |
| 17 | iShares TIPS Bond (TIP) | Lyxor Euro Government Inflation Linked Bond (DR) UCITS ETF Acc (EMI) |
| 18 | SPDR Blmbg Barclays 1-3 Mth T-Bill (BIL) | Amundi ETF Govies 0-6 Months EuroMTS Investment Grade UCITS ETF EUR C (C3M) |
| 19 | SPDR Gold Trust (GLD) | Xtrackers Physical Gold EUR Hedged ETC (XAD1) |
| 20 | SPDR S&P 500 (SPY) | Xtrackers STOXX Europe 600 UCITS ETF 1C (XSX6) |
| 21 | Vanguard FTSE All-World ex-US (VEU) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) |
| 22 | Vanguard FTSE Developed Markets (VEA) | Amundi ETF MSCI World ex EMU UCITS ETF EUR C (CM9) |
| 23 | Vanguard Large-Cap (VV) | iShares MSCI EMU Large Cap UCITS ETF (EMUL) |
| 24 | Vanguard Real Estate (VNQ) | Xtrackers FTSE EPRA/NAREIT Developed Europe Real Estate UCITS ETF 1C (XDER) |
| 25 | Vanguard Total Bond Market (BND) | WisdomTree EUR Aggregate Bond Enhanced Yield UCITS ETF EUR Acc (EYLD) |
| 26 | Vanguard Total International Bond (BNDX) | Amundi Index Barclays Global Aggregate 500m UCITS ETF DR C (GAGG) |
| 27 | Vanguard Total Stock Market (VTI) | iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU) |
| 28 | Vanguard Total World Stock (VT) | Lyxor MSCI All Country World UCITS ETF Acc EUR (ACWI) |
| 29 | Vanguard Value (VTV) | Xtrackers MSCI Europe Value UCITS ETF 1C (D5BL) |
| 30 | WisdomTree International SmallCp Div (DLS) | SPDR MSCI World Small Cap UCITS ETF (ZPRS) |
| 31 | iShares MSCI United Kingdom (EWU) | Amundi ETF MSCI UK UCITS ETF EUR C (CU1) |
| 32 | iShares MSCI Switzerland (EWL) | UBS MSCI Switzerland 20/35 UCITS ETF CHF A-acc EUR (SW2CHB) |
| 33 | iShares MSCI Japan (EWJ) | Xtrackers MSCI Japan UCITS ETF 1C (XMJP) |
| 34 | iShares MSCI All Country Asia ex Japan (AAXJ) | iShares Core MSCI Pacific ex Japan UCITS ETF Acc (CSPXJ) |
| 35 | SPDR FTSE Inter. Gvt. Infl.-Protected Bond (WIP) | Xtrackers Global Inflation-Linked Bond UCITS ETF 1C EUR Hedged (XGIN) |
| 36 | Vanguard Total International Bond (BNDX) | Xtrackers Global Government Bond UCITS ETF 1C EUR Hedged (XGSH) |
| 37 | Vanguard Total Bond Market (BND) | UBS USD Emerging Markets Sovereign UCITS EUR Hedged (SBEME) |
| 38 | Vanguard Total World Stock (VT) | iShares MSCI ACWI UCITS ETF Acc (IUSQ) |
| 39 | Vanguard Total International Bond (BNDX) | iShares Core Global Aggregate Bond UCITS ETF EUR Hedged Acc (AGGH) |
|
1 Maggiori informazioni sono disponibili nel capitolo 13. |
||
Gli ETF elencati possono essere rimpiazzati senza problemi, a condizione che l’indice replicato sia il medesimo o uno simile. Se così non fosse, si stravolgerebbe l’asset allocation del Lazy portfolio.
Un ETF in EUR può sostituire più di un ETF tra quelli utilizzati per i Lazy portfolios in USD (e viceversa), dato che l’investitore dell’area euro – in particolare – non dispone di alcune categorie di ETF accessibili agli investitori americani (ad esempio, al momento non esistono ETF che investono in società a bassa capitalizzazione a livello globale ma con l’esclusione della zona euro).
Un elenco indicativo degli ETF che possono essere impiegati al posto di quelli utilizzati nei backtest è disponibile nei vari sotto-capitoli del capitolo 13.3, ognuno dedicato a uno specifico portafoglio pigro.
6. Criteri di scelta degli ETF

«L’uomo non può prendere due sentieri alla volta».
Proverbio africano
Gli ETF elencati nel capitolo precedente sono stati selezionati sulla base di molte variabili, tre delle quali sono comuni a tutti: la valuta di negoziazione (euro), l’accumulazione dei proventi e la negoziazione da parte di Borsa Italiana.
Le altre caratteristiche prese in considerazione sono:
- Data di lancio: sono stati preferiti gli ETF più longevi, perché dispongono di una serie storica dei rendimenti più lunga.
- Indice replicato: nei limiti del possibile, si è cercato di rispecchiare gli indici seguiti dagli ETF che compongono i Lazy portfolios originali, sostituendo il mercato statunitense con – in ordine di preferenza – mercato dell’area euro, mercato europeo e mercato globale.
- Commissioni: la filosofia dei Lazy portfolios impone la scelta di ETF economici. Talvolta, abbiamo preferito dare la precedenza alla lunghezza della serie storica o ad altre variabili piuttosto che alle commissioni ma, in generale, l’investitore dovrebbe cercare sempre di minimizzare il costo di gestione dei prodotti scelti.
- Modalità di replica. Si distingue in:
- Fisica:
- Totale: permette di replicare l’indice di riferimento nel modo più accurato possibile. Nella replica fisica totale, l’ETF è costituito da tutti gli strumenti finanziari che compongono l’indice stesso.
- Campionamento: in certi casi, replicare l’intero indice di riferimento può essere complicato o troppo costoso. Si preferisce allora inserire in un ETF soltanto alcuni tra gli strumenti finanziari che costituiscono l’indice (di solito, quelli più rilevanti o più liquidi). Una possibile alternativa è il cosiddetto campionamento ottimizzato che, attraverso l’uso di modelli quantitativi, permette di selezionare gli strumenti finanziari che hanno il maggior impatto sulla performance dell’indice.
- Sintetica: la replica dell’indice di riferimento viene effettuata tramite un’operazione finanziaria denominata swap. Lo swap è un contratto stipulato tra l’ETF e un intermediario finanziario che si impegna, dietro al pagamento di una commissione, a consegnare all’ETF il rendimento dell’indice di riferimento.
La replica sintetica è generalmente più economica di quella fisica, ma comporta il rischio di controparte, mitigato negli ultimi anni da varie misure che sono state imposte per aumentarne la sicurezza: le direttive europee (UCITS), le controparti multiple, la reimpostazione dello swap, la sovracollateralizzazione e la miglior qualità del collaterale.
- Fisica:
- Copertura valutaria: tutti gli ETF sono negoziati in euro, ma non è detto che gli strumenti finanziari che li compongono siano denominati nella stessa valuta. Un ETF azionario globale, ad esempio, sarà costituito da una moltitudine di azioni quotate in vari mercati: tra questi, avremo quello americano, denominato in dollari e quello europeo, denominato sia in euro che in sterline inglesi, franchi svizzeri e molte altre valute che circolano in Europa.
Per eliminare il rischio di cambio valutario (approfondito nel quarto capitolo), è possibile utilizzare un ETF Hedged. Gli ETF hedgiati potrebbero avere delle spese correnti leggermente superiori a quelli non hedgiati. - Dimensione del fondo: un fondo di grandi dimensioni è preferibile, in quanto la possibilità che l’ETF venga liquidato è remota. Il delisting di un ETF non è un problema in sé: le somme incassate possono essere reinvestite in un ETF simile. L’unico inconveniente – non di poco conto – è che in caso di plusvalenza dovranno essere pagate le imposte sul capital gain.
Gli ETF di piccole dimensioni sono teoricamente più soggetti a una liquidazione anticipata, dal momento che le basse commissioni di gestione dall’ETF potrebbero renderli poco redditizi per l’emittente.
Quali sono le differenze nelle performance tra ETF della stessa categoria?
Possiamo lanciare un’analisi di correlazione lineare tra le serie storiche dei rendimenti di due ETF simili. Partiamo da due ETF azionari:
- iShares Core MSCI EMU UCITS ETF EUR (Acc) – CSEMU (ISIN: IE00B53QG562)
- SPDR MSCI EMU UCITS ETF (EUR) – EURO (ISIN: IE00B910VR50)
Il primo sarà utilizzato in diversi portafogli pigri; il secondo replica lo stesso indice (MSCI EMU). Entrambi sono ETF a replica fisica totale.
Vediamo il grafico della correlazione lineare rolling tra questi due strumenti calcolata su un periodo di circa un anno solare (252 giorni borsistici):
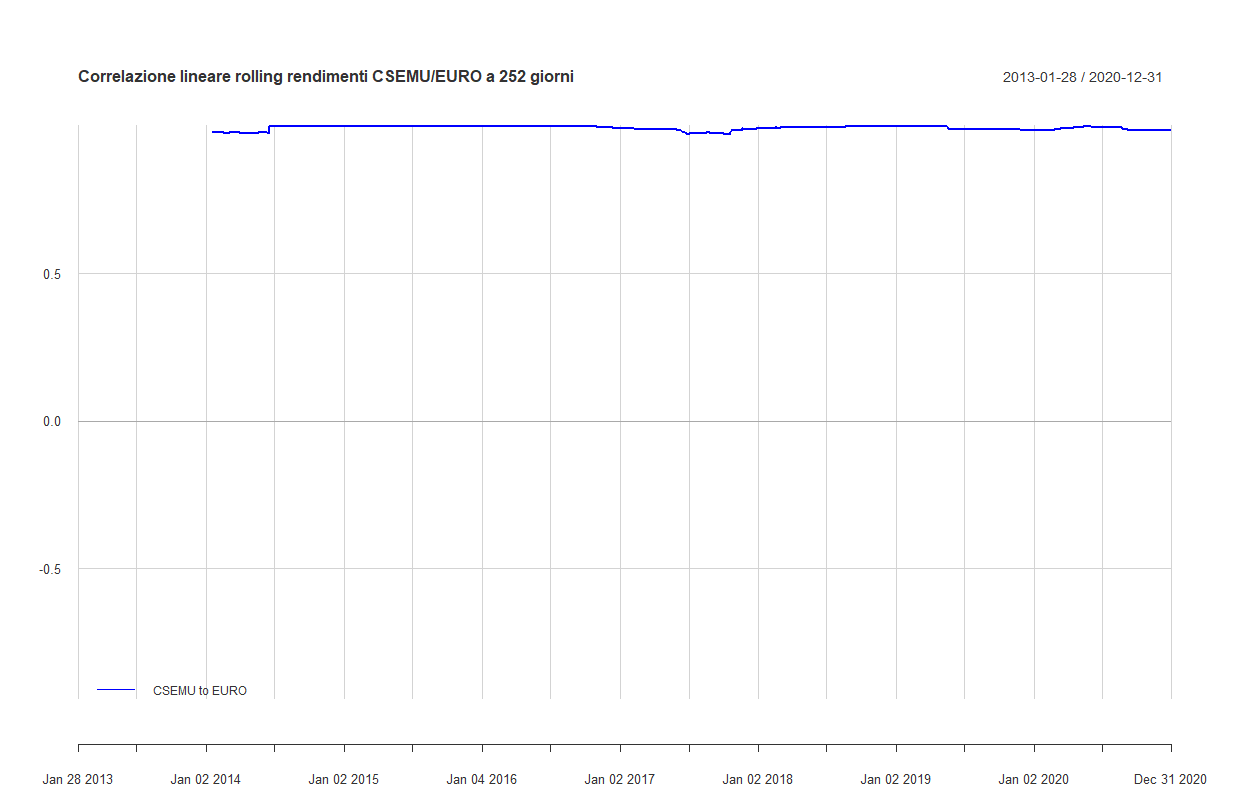
La correlazione è molto vicina a 1 indipendentemente dal periodo sul quale viene misurata (correlazione media = 0,993).
Vediamo se, aumentando il periodo di calcolo a 5 anni (1260 giorni borsistici), si verifica qualche cambiamento:
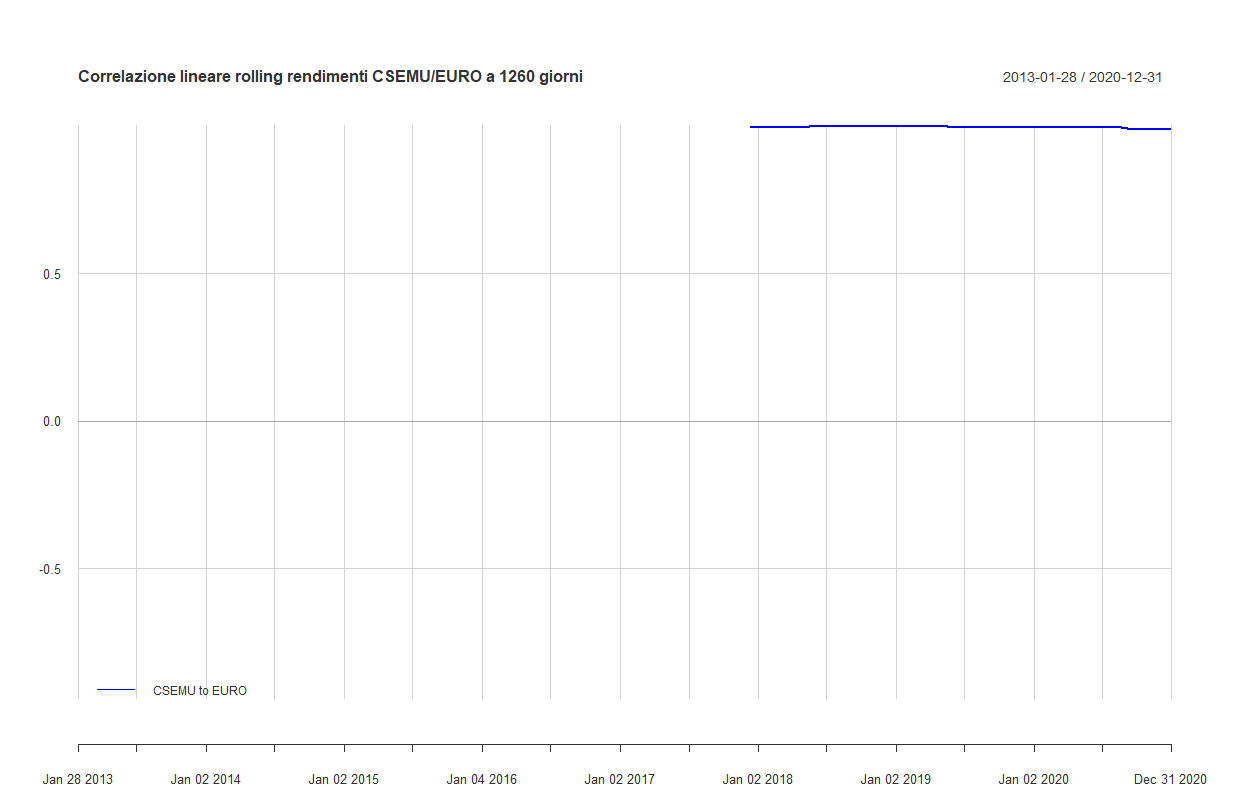
Di nuovo, la correlazione lineare è vicinissima a 1 in tutti i periodi sui quali è stata calcolata (correlazione media = 0,995).
Effettuiamo adesso la stessa analisi su due ETF obbligazionari governativi (area euro):
- Xtrackers II Eurozone Government Bond 7-10 UCITS ETF 1C (EUR) – X710 (ISIN: LU0290357259)
- Amundi ETF Government Bond EuroMTS Broad Investment Grade 7-10 UCITS ETF DR (EUR) – C73 (ISIN: FR0010754184)
Questi due ETF non replicano lo stesso indice: il primo segue l’indice Markit iBoxx® EUR Eurozone 7-10; il secondo l’indice FTSE MTS Eurozone Government Broad Investment Grade 7-10 (sono indici simili ma non identici).
La modalità di replica non è la stessa: l’Amundi effettua una replica fisica totale dell’indice; lo Xtrackers una replica fisica a campionamento.
Vediamo il grafico della correlazione lineare rolling a 252 giorni:
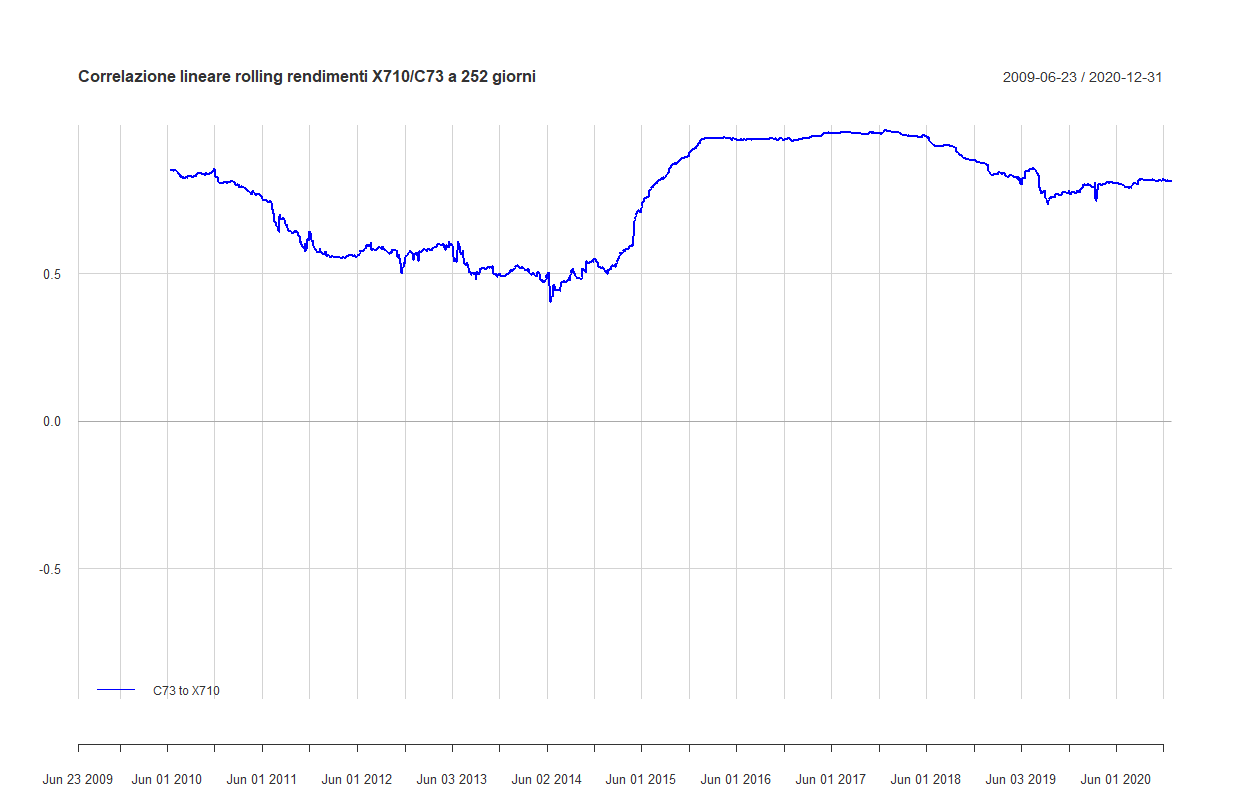
Questa invece è la correlazione lineare rolling a 5 anni:
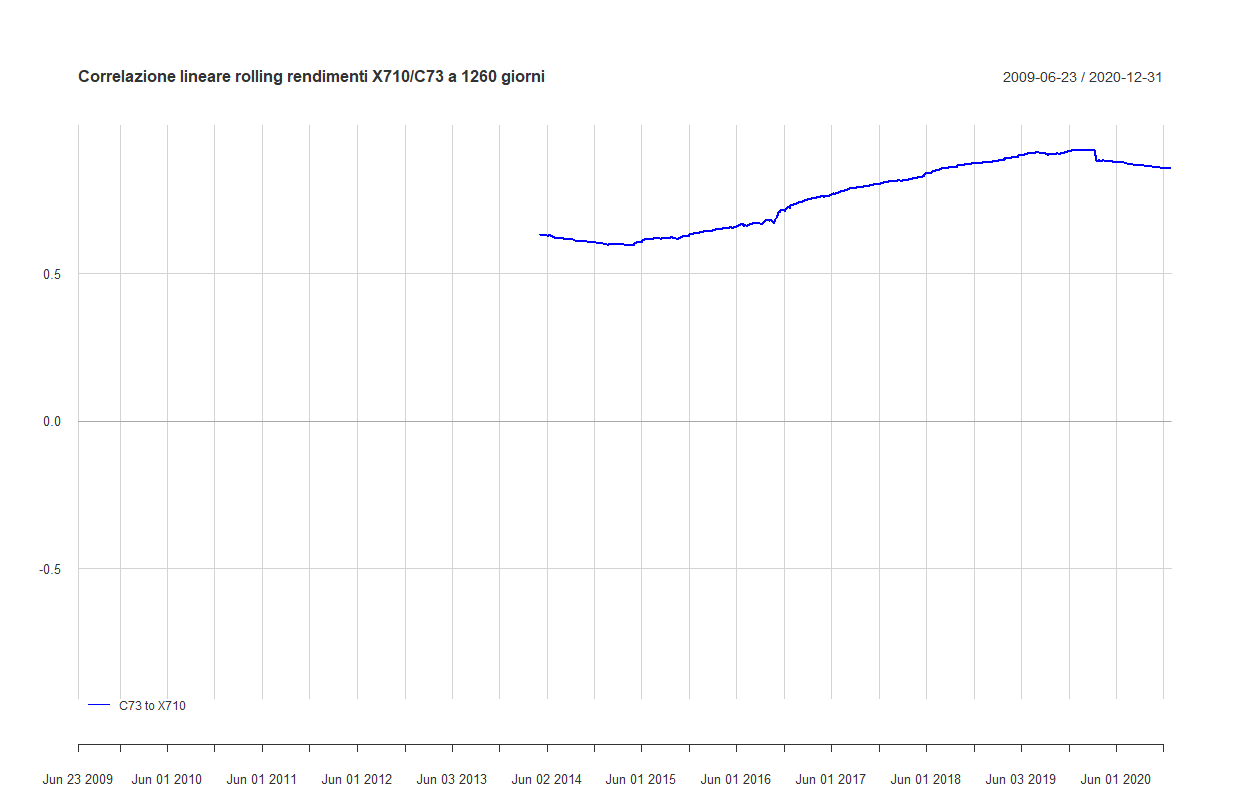
Questa volta, la correlazione lineare non è vicinissima a 1 come nel caso degli ETF azionari. Tuttavia, si mantiene sempre su valori molto alti: la correlazione media è di 0,758 se calcolata su un periodo di un anno e di 0,763 se calcolata su 5 anni.
Di quanto si discostano le equity lines dei due ETF obbligazionari nell’arco di tempo analizzato?
Lo possiamo osservare nel grafico seguente, che ci mostra un andamento quasi identico:
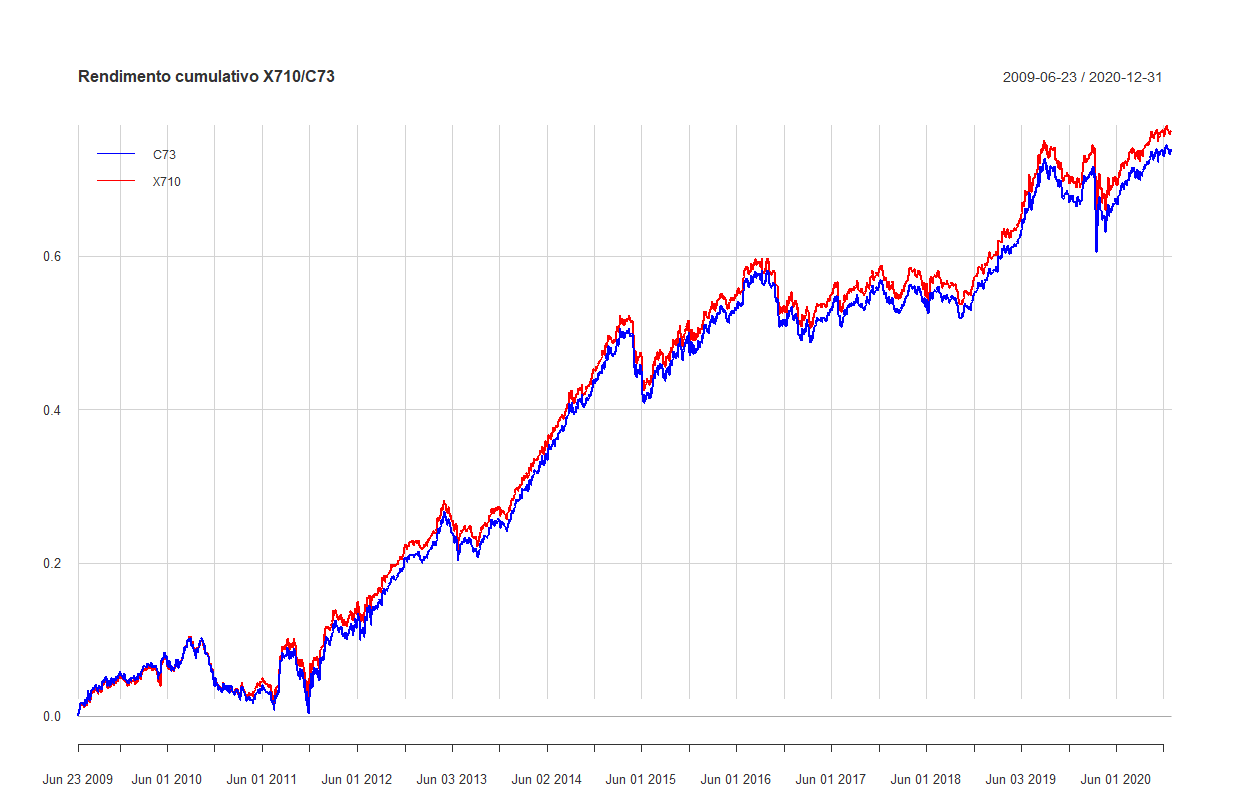
In definitiva, in un Lazy portfolio la scelta di un ETF rispetto a un altro non deve essere fatta guardando al rendimento: i fondi a gestione passiva, se appartenenti alla stessa categoria, otterranno delle performance molto simili.
È una conferma di come le variabili da prendere in considerazione nella costruzione dei portafogli pigri siano altre: le più importanti le abbiamo elencate all’inizio di questo capitolo.
7. Perché esistono così tanti Lazy portfolios?

«I choose a Lazy person to do a hard job. Because a Lazy person will find an easy way to do it».
Bill Gates
Esistono centinaia di Lazy portfolios.
Perché così tanti? Non ne basterebbe uno composto da due soli ETF, uno azionario e uno obbligazionario?
In fin dei conti, il CAPM ci insegna che ogni investitore ha bisogno di un solo ETF – il più diversificato possibile – sul quale dovrebbe essere investita una certa percentuale della disponibilità finanziaria totale.
Questa percentuale oscillerebbe tra lo 0% (minima propensione al rischio dell’investitore) e il 100% (propensione al rischio massima). La parte residua verrebbe semplicemente investita al tasso privo di rischio.
Troppo semplice per essere vero?
Forse. In finanza personale, però, la strada più semplice è spesso la più efficiente.
Riconoscere che semplicità sia sinonimo di efficienza è controintuitivo e molti investitori non riescono ad accettarlo.
Questo è, probabilmente, il principale motivo per cui continuano a proliferare derivati e strumenti finanziari complessi, altamente speculativi, a volte molto costosi e quasi sempre incomprensibili ai non addetti ai lavori.
Invece di evitarli, l’investitore medio tende a sottoscriverli e inserirli nel proprio portafoglio, confortato dall’illusione che la complessità degli strumenti sia funzionale all’ottenimento di previsioni dei mercati finanziari più accurate.
Il discorso cambia nel caso di un investitore professionale. Quest’ultimo è libero di complicare il modello d’investimento quanto vuole, perché si presume che sappia quello che sta facendo e sia consapevole del rischio associato a ogni sua scelta.
Un professionista dedica ogni sua giornata lavorativa ad analizzare il mercato, le società e le strategie di investimento. È pagato proprio per questo.
Un investitore normale, che sarebbe in grado di comprendere senza troppe difficoltà il funzionamento dei portafogli pigri, dovrebbe mettere in conto il maggior costo derivante dalla complicazione del suo modello di investimento.
Questo maggior costo può essere espresso in due modi:
- Tempo: serve tempo per approfondire la conoscenza della materia in prima persona, studiando il funzionamento del mercato finanziario, gli strumenti, i modi di misurare il rischio e così via. Una cognizione di base è auspicabile per chiunque decida di approcciare il mercato ma chi volesse investire utilizzando strumenti più complicati non dovrebbe limitarsi a questo livello minimo di conoscenze.
- Soldi: servono soldi per farsi assistere in maniera continuativa da un consulente finanziario che abbia il compito di costruire una strategia di investimento su misura per l’investitore.
Il costo principale è quello delle spese correnti dei fondi attivi – generalmente molto alte – o quello applicato in percentuale sul patrimonio nella consulenza continuativa autonoma. Nel capitolo 15, cercheremo di quantificare questi costi.
Un maggior costo è poi imputabile alle commissioni di transazione di un maggior numero di titoli o alla bassa liquidità di certi strumenti.
Anche quando un investitore decide di optare per un portafoglio pigro, la tendenza a cercare sicurezza nella complicazione conduce spesso all’elaborazione di Lazy portfolios composti da troppi ETF, ETF poco diversificati geograficamente, ETF settoriali, tematici o che replicano strategie discutibili.
C’è poi un ulteriore costo – molto alto – che l’investitore si troverebbe a dover pagare se decidesse di creare e gestire il proprio portafoglio finanziario in prima persona ma senza prepararsi in modo adeguato ad affrontare i mercati finanziari: le sue scelte potrebbero non essere in sintonia con l’obiettivo del suo investimento, con il suo orizzonte temporale o con la sua propensione al rischio.
In tal caso, non tarderebbero a verificarsi delle situazioni di mercato stressanti (paura di perdere i soldi durante una crisi, nervosismo derivante da scelte troppo conservative in fasi di crescita e così via), che potrebbero portarlo a interrompere l’investimento in un momento poco appropriato.
L’illusoria ed estenuante convinzione che esista un portafoglio migliore è un’altra possibile ragione alla base del proliferarsi dei Lazy portfolios: ottimizzando a posteriori, è sempre possibile trovarne uno che avrebbe ottenuto delle performance superiori a quello che si possiede.
È uno dei più comuni errori degli investitori: guardo indietro e, tra i possibili portafogli pigri che avrei potuto selezionare, identifico il migliore. Lo ottimizzo ulteriormente, magari aggiungendo o sostituendo uno o più ETF.
Alcuni consulenti e siti finanziari propongono in continuazione nuovi portafogli seguendo proprio l’approccio della loro ottimizzazione nel passato: ne segue una qualche forma di pubblicizzazione, in cui vengono messe in luce le sue strabilianti qualità e la meravigliosa performance che avrebbe ottenuto negli ultimi X mesi o anni.
Si condisce il tutto con un nome accattivante e il gioco è fatto: un nuovo Lazy portfolio è nato.
Purtroppo, non sarà mai un portafoglio che, in futuro, performerà altrettanto bene, essendo nato sulla base di uno dei bias più comuni e insidiosi: il Look-back bias.
Non c’è niente di male a ideare dei nuovi portafogli pigri ma, se questa fosse davvero la procedura seguita per la loro creazione, le performance future sarebbero pessime.
Come vedremo, alcuni Lazy portfolio hanno l’obiettivo di massimizzare il rendimento di lungo termine, mentre altri sono più finalizzati a minimizzare la volatilità.
Uno dei compiti più ostici per l’investitore è proprio quello di decidere quale sia il Lazy portfolio più adatto alle proprie esigenze.
L’obiettivo della nostra indagine è anche quello di rendere l’investitore più consapevole di ciò che sta facendo quando si troverà di fronte a questa inevitabile scelta.
Torneremo su questo punto più avanti e, in particolare, nel capitolo 19.
8. Limiti dell’approccio di ottimizzazione classico (Markowitz) e Hierarchical Risk Parity

«Every man takes the limits of his own field of vision for the limits of the world».
Arthur Schopenhauer
I Lazy portfolios classici non hanno bisogno di ottimizzazioni: il capitale da investire viene distribuito tra i vari ETF che li compongono sulla base di pesi prestabiliti. Il ribilanciamento periodico dei Lazy portfolios è l’unico intervento richiesto all’investitore nella loro gestione.
Come vengono assegnati i pesi agli ETF?
Non esiste una risposta univoca: così è stato deciso dagli ideatori dei vari portafogli pigri.
Non si tratta tuttavia di percentuali casuali: anche se sono il frutto di valutazioni soggettive, vengono di solito scelte in funzione dell’obiettivo perseguito. Ad esempio, un Lazy portfolio che punta a massimizzare il rendimento di lungo termine avrà un’alta percentuale di azionario.
Un portafoglio pigro conservativo sarà invece composto da molto obbligazionario e, talvolta, da una percentuale di commodities, che avranno lo scopo di mitigare la volatilità e i cali di rendimento durante le crisi finanziarie più gravi.
Ipotizziamo che la percentuale di azionario del primo portafoglio pigro sia stata dell’80%. A un investitore con una minore propensione al rischio, questa percentuale azionaria potrebbe essere sembrata troppo alta: perché, ad esempio, non optare per un portafoglio pigro dal peso azionario del 40%?
Seguendo lo stesso ragionamento, altri potrebbero aver scelto un 50/50, un 20/80, e così via fino a coprire tutte le possibili alternative.
Alcuni investitori preferiscono un’equa distribuzione dei pesi:
- 50% per ognuno dei 2 ETF che compongono i portafogli formati da un ETF azionario e un ETF obbligazionario.
- 33,33% per ognuno degli ETF che compongono i portafogli formati da 3 ETF.
- 25% per ogni ETF nel caso di portafogli costituiti da 4 ETF e così via.
In fin dei conti, perché limitarsi a 2 ETF, se si può aumentare la diversificazione aggiungendo qualche ETF in più?
Vedremo più avanti come l’equidistribuzione dei pesi sia una vera e propria strategia di investimento.
Nei capitoli seguenti analizzeremo anche una modalità innovativa di selezione dei pesi: partendo da quelli standard, li genereremo dinamicamente attraverso la procedura di ottimizzazione ideata da Markowitz nel 1952.
Markowitz ebbe un’intuizione geniale: fu il primo a capire che diversi livelli di rischiosità possono essere associati a diversi portafogli ottimali, scelti dall’investitore in base alla propria propensione al rischio.
Il lavoro di Markowitz introdusse un concetto rivoluzionario: la “frontiera efficiente”.
La nuova metodologia di costruzione del portafoglio – basata sull’ottimizzazione rischio/rendimento – dimostrò come raramente il portafoglio ottimale sarebbe stato quello che avrebbe permesso la massimizzazione del rendimento atteso dell’investitore: molto più spesso, sfruttando le proprietà della covarianza tra i rendimenti dei titoli, la soluzione ottimale si sarebbe ottenuta con un portafoglio diversificato.
Nonostante la brillantezza dell’intuizione di Markowitz, la procedura matematica di ottimizzazione comporta diversi problemi di ordine pratico: il principale è legato al fatto che piccole differenze nel forecast dei rendimenti attesi producono dei portafogli molto diversi tra loro.
Considerando che stimare i rendimenti futuri richiede procedure abbastanza complicate, è inevitabile che esisteranno delle differenze tra i rendimenti stimati e quelli effettivi.
I portafogli ottimali generati dai forecast, quindi, potrebbero non rivelarsi tali alla luce dei fatti.
Perché piccole differenze nel forecast dei rendimenti attesi producono dei portafogli molto diversi tra loro?
Essenzialmente perché la procedura di calcolo dei pesi dei titoli in portafoglio proposta da Markowitz si basa sull’ottimizzazione quadratica: a un certo punto, si richiede di invertire la matrice di covarianza dei rendimenti (una matrice che deve essere definita positiva).
L’inversione è alla fonte degli errori di stima quando la matrice di covarianza dei rendimenti ha un numero condizionale alto.
Il numero condizionale di una matrice di covarianza (o di correlazione) viene definito come il valore assoluto del rapporto tra il più alto e il più basso autovalore della matrice.
Il numero condizionale cresce all’aumentare della correlazione tra i titoli del portafoglio. Più è alto il numero di titoli in portafoglio e più è alta la correlazione tra loro; più è alta la correlazione tra i titoli e più la matrice di covarianza inversa diventa instabile: piccole differenze nei valori in ingresso produrranno matrici inverse molto differenti tra loro.
Marcos Lopez de Prado, uno dei maggiori esperti di Machine Learning, definisce questa difficoltà “maledizione di Markowitz”: più i titoli sono correlati, più c’è bisogno di diversificazione e più alta sarà la probabilità di ottenere un risultato instabile.
In altre parole, la maledizione di Markowitz si concretizza con l’annullamento totale o parziale dei benefici della diversificazione a causa degli errori di stima che si ripercuotono nella matrice di covarianza dei rendimenti.
Per ovviare alla maledizione di Markowitz, Marcos Lopez de Prado propone di introdurre nel modello il concetto di gerarchia: un’ottimizzazione strutturata su vari livelli gerarchici in cui i pesi vengono distribuiti con un approccio top-down.
Le strutture gerarchiche permetterebbero di ottenere risultati più stabili e intuitivi.
Il metodo di ottimizzazione creato da Marcos Lopez de Prado, detto Hierarchical Risk Parity (HRP), utilizza le informazioni contenute nella matrice di covarianza senza che questa debba necessariamente essere definita positiva o invertibile.
L’algoritmo di ottimizzazione si sviluppa in tre fasi: tree clustering, quasi-diagonalizzazione e bisezione ricorsiva.
Chi fosse interessato ad approfondire l’argomento può trovare una spiegazione dettagliata di questo metodo nel libro Advances in Financial Machine Learning.
Utilizzeremo anche noi questo innovativo approccio di ottimizzazione dei pesi dei Lazy portfolios: il modello Hierarchical Risk Parity (HRP) sarà uno di quelli che studieremo.
Nell’HRP e in altri 3 modelli che vedremo in seguito, lasceremo l’algoritmo libero di calcolare i pesi ideali di ciascun ETF: in alcuni casi, essi potranno essere molto diversi da quelli standard, ovvero quelli assegnati a ciascun strumento finanziario dagli ideatori dei vari Lazy portfolios.
9. Procedura e modelli di ottimizzazione. Il ribilanciamento
«They are sick that surfeit with too much, as they that starve with nothing».
William Shakespeare
L’analisi effettuata non utilizzerà soltanto il modello HRP presentato nel capitolo precedente: ottimizzeremo i portafogli pigri anche col metodo di Markowitz.
Adotteremo due modelli di ottimizzazione: vincolati e non vincolati. L’approccio non vincolato permetterà ai pesi di fluttuare liberamente tra 0% e 100%; quello vincolato avrà un margine di manovra inferiore: i pesi dovranno muoversi all’interno di una forbice pari al ± 5% dei pesi standard.
Perché utilizzare la procedura di Markowitz, visti i limiti di cui abbiamo discusso nel capitolo precedente?
Essenzialmente per i seguenti motivi:
- Poter valutare le differenze tra il modello di Markowitz, quello HRP e i due modelli statici: verranno tutti backtestati su serie storiche molto lunghe e su molti portafogli pigri diversi tra loro.
- Come abbiamo visto, l’instabilità del modello di Markowitz è direttamente proporzionale al numero di titoli in portafoglio e alla loro correlazione lineare: molti dei Lazy portfolios analizzati, però, sono costituiti da pochi ETF non molto correlati tra loro (come – ad esempio – il Two funds, composto da un ETF azionario e uno obbligazionario).
- Nei modelli vincolati, i pesi sono liberi di oscillare soltanto di un ± 5% rispetto a quelli standard: in questo caso il confronto non sarà tanto con i modelli non vincolati quanto con il modello standard.
Tutte l’analisi è stata effettuata con l’ausilio di R.
R è un ambiente di sviluppo utilizzato principalmente per l’analisi statistica di dati. R è anche un linguaggio di programmazione ed è un software disponibile in modo gratuito, essendo distribuito con la licenza GNU GPL.
Le caratteristiche della procedura di ottimizzazione sono le seguenti:
- L’ottimizzazione si basa su vincoli e obiettivi. I vincoli presenti in tutti i portafogli sono quelli di full investment (l’intera somma disponibile deve essere investita) e long only (solo posizioni lunghe; le vendite allo scoperto non sono consentite).
- Alcuni modelli hanno l’ulteriore vincolo costituito dalle percentuali di investimento minime e massime su ogni ETF (box constraints): ± 5% dei pesi standard.
- Per la stima dei rendimenti attesi e delle matrici di varianza/covarianza verrà utilizzato:
- Il modello fattoriale di Kris Boudt (disponibile nel package PortfolioAnalytics.)
- La stima robusta delle matrici di varianza/covarianza assumendo che i dati siano generati da una distribuzione multivariata t.
- L’approccio naif, basato su rendimenti attesi e matrici di varianza/covarianza calcolate sui rendimenti passati.
- Ottimizzazioni e ribilanciamenti periodici.
Oltre al modello di stima dei momenti (rendimenti attesi e matrice delle varianze/covarianze attese), in fase di ottimizzazione l’analista si trova di fronte a un’altra importante scelta: nell’universo dei portafogli possibili, quale asset allocation scegliere?
Nell’universo dei portafogli possibili, la scelta deve essere effettuata tra i portafogli situati sulla frontiera efficiente, che è formata da tutti i portafogli efficienti.
Un portafoglio efficiente non può essere migliorato sia a livello di rendimento atteso che di rischio: possono essere individuati portafogli con un rendimento atteso superiore, ma dal rischio più elevato. Alternativamente, si possono identificare portafogli con un rischio più basso, ma dal rendimento atteso minore.
Un portafoglio efficiente è quindi caratterizzato da un grado minimo di rischio per ogni dato livello di rendimento atteso.
Tra tutti i portafogli efficienti, quale dovrebbe essere selezionato?
La scelta finale dipenderà essenzialmente da fattori soggettivi quali la propensione individuale al rischio e l’aspettativa di rendimento.
In base all’approccio di Markowitz, di solito un investitore opterà per uno dei seguenti portafogli efficienti:
- Minimum Variance Portfolio (MVP): è il portafoglio che minimizza la varianza attesa.
- Highest Sharpe Ratio (HSR): è il portafoglio che massimizza l’indice di Sharpe atteso.
Si tende a evitare la scelta del portafoglio che massimizza il rendimento atteso disinteressandosi della volatilità attesa perché, di solito, è molto poco diversificato e concentra l’investimento su un solo titolo in portafoglio.
Vediamo graficamente la differenza tra i portafogli Minimum Variance e Highest Sharpe Ratio.
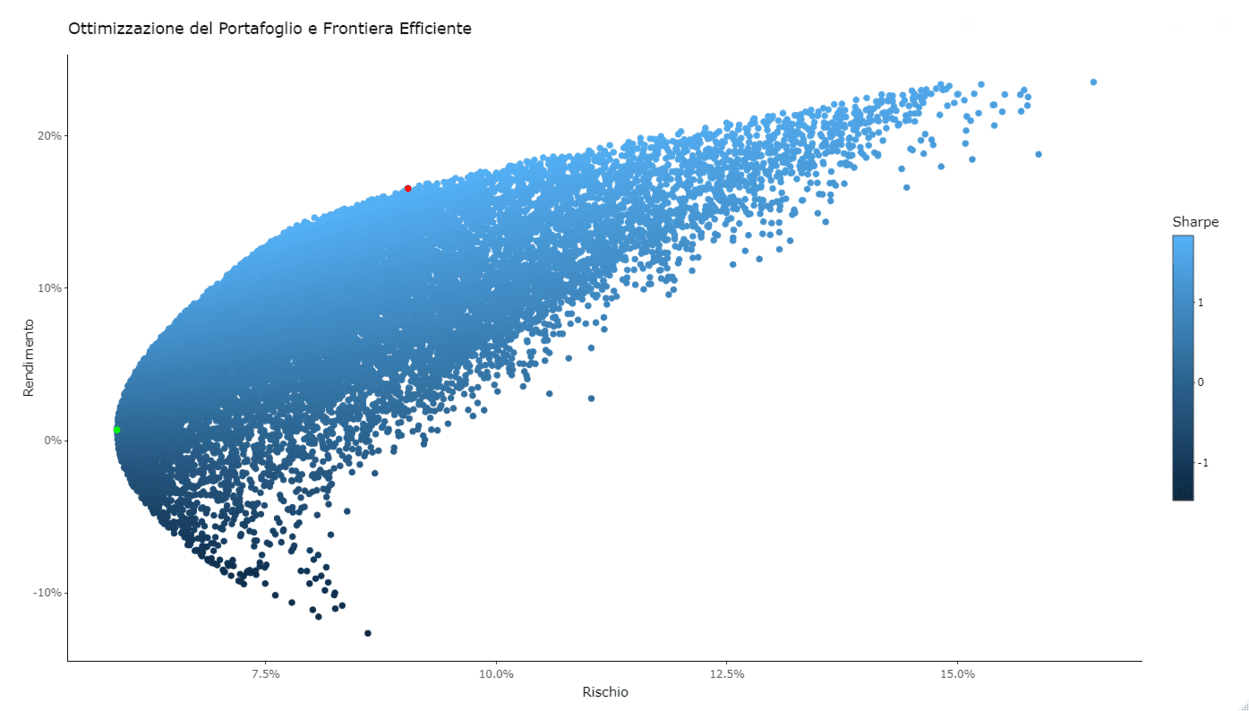
In questo esempio, i punti blu sono 20.000 e rappresentano le combinazioni Rischio/Rendimento di altrettanti portafogli random, generati in fase di ottimizzazione del “Permanent” Lazy portfolio.
Il punto verde, situato sull’estrema sinistra dell’insieme dei portafogli possibili, rappresenta il Minimum Variance Portfolio.
Il punto rosso, situato verso la metà della frontiera efficiente, individua invece il portafoglio col più alto indice di Sharpe. Viene anche definito Portafoglio Tangente.
Il Permanent Lazy portfolio è costituito da 4 ETF e la sua asset allocation è composta per il 25% da azioni Large Cap statunitensi (ETF VTI), per il 25% da obbligazioni governative statunitensi di brevissimo termine (ETF BIL), per il 25% da obbligazioni governative statunitensi di lungo termine (superiori a 20 anni, ETF TLT), e per il rimanente 25% da una specifica commodity: l’oro.
Vediamo quali sono i pesi assegnati in fase di ottimizzazione agli ETF del Minimum Variance Portfolio:
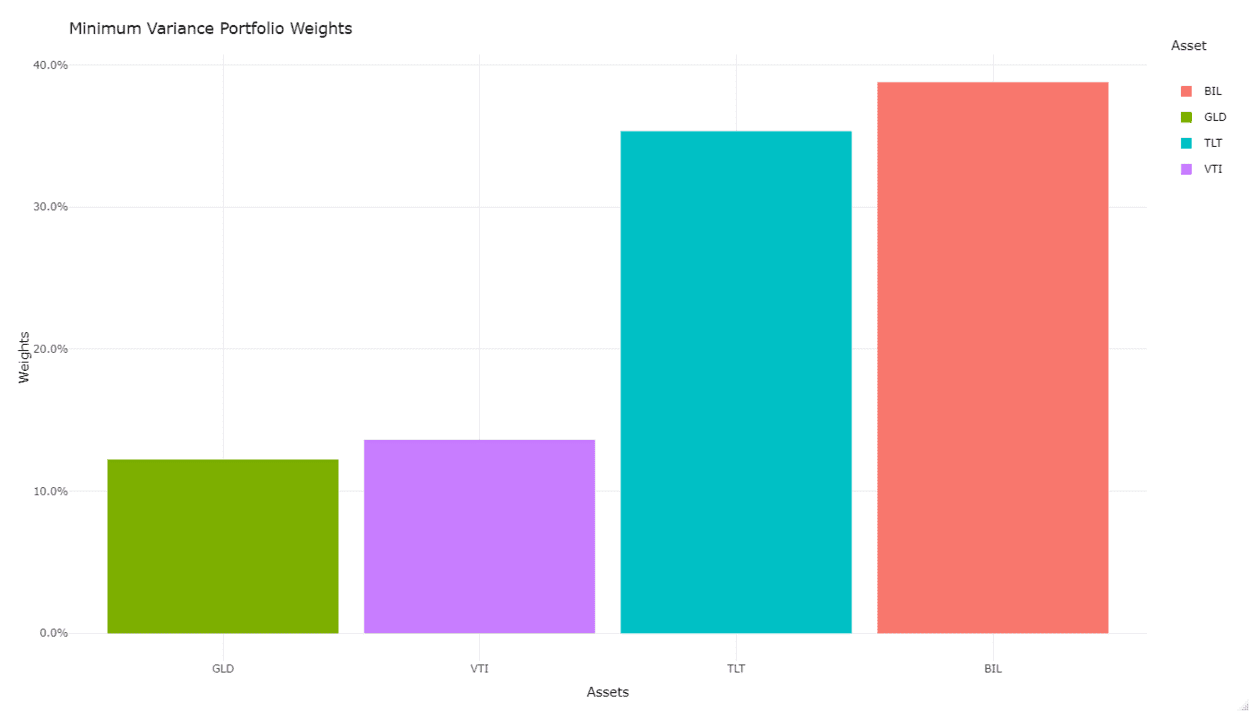
L’ETF BIL, che replica un indice obbligazionario statunitense di brevissimo termine, è quello con il peso più alto: quasi il 40%. Seguono il TLT, un ETF che replica un indice obbligazionario statunitense di lungo termine, con un peso intorno al 35%; il VTI, un ETF che replica un indice azionario Large Cap statunitense, con un peso del 14% circa e, per finire, l’oro con un peso poco superiore al 10%.
Scegliere di investire nel Minimum Variance Portfolio significa voler minimizzare la varianza del portafoglio, ovvero il rischio. Non è un caso che i pesi maggiori siano quelli degli ETF obbligazionari.
I pesi assegnati in fase di ottimizzazione agli ETF del portafoglio con il più alto indice di Sharpe sono invece i seguenti:
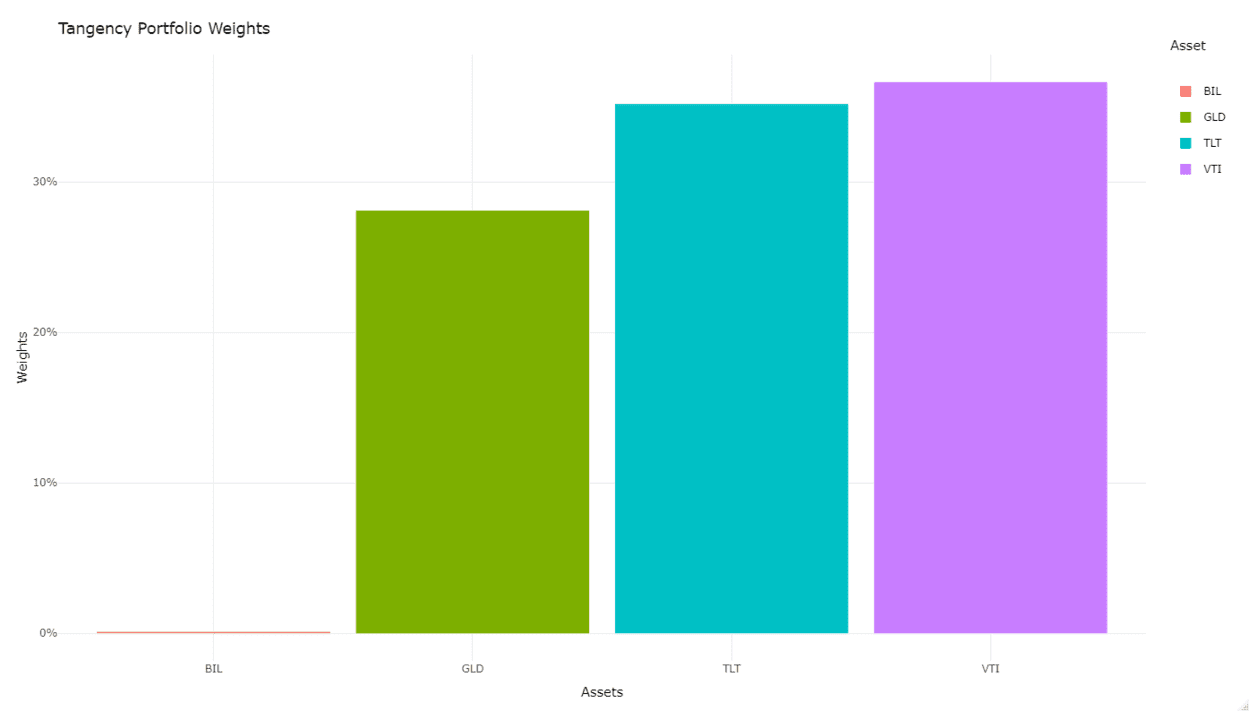
In questo caso, l’ETF VTI, che replica un indice azionario Large Cap statunitense, ha il peso più alto, con un 37,50% circa, seguito a breve distanza dal TLT, che replica un indice obbligazionario statunitense di lungo termine, e dall’oro. È invece nullo il contributo dell’ETF BIL, che replica un indice obbligazionario di brevissimo termine.
Il risultato è in linea con le aspettative, dato che il portafoglio che massimizza l’indice di Sharpe, nel nostro esempio, si trova verso la metà della frontiera efficiente: dagli stessi grafici si può notare come il rischio atteso di questo portafoglio sia molto più alto di quello del Minimum Variance Portfolio.
L’uni-periodicità del modello di Markowitz – ovvero il non considerare alcuna movimentazione del portafoglio tra l’inizio e la fine del periodo di analisi – è considerato un limite di questa teoria.
Per superarlo, a intervalli periodici e in concomitanza con il ribilanciamento dei portafogli, effettueremo una nuova ottimizzazione, che permetterà di riportare i pesi dei titoli in portafoglio ai valori ideali.
Trasformeremo cioè l’analisi da uniperiodale a multi-periodale, sempre facendo attenzione a non commettere errori di Look-Ahead Bias: nei nostri backtest, i rendimenti e la volatilità attesa sono sempre stati stimati sulla base delle informazioni disponibili al momento del ribilanciamento, senza “sbirciare nel futuro”.
L’intero periodo backtestato viene diviso in sottoperiodi di 252 giorni borsistici ciascuno (approssimativamente pari a un anno solare).
Prendiamo ad esempio il sottoperiodo compreso tra il 1° gennaio e il 31 dicembre 2018. Il 2 gennaio 2019 utilizzeremo le serie storiche dei rendimenti degli ETF del 2018 per l’ottimizzazione dei pesi relativi: ciascun modello di ottimizzazione, in base ai vincoli applicati, genererà i pesi ottimali di ogni Lazy portfolio.
Il backtest vero e proprio, cioè la misurazione delle performance ottenute, viene effettuato sui portafogli così ottenuti nel periodo compreso tra il 2 gennaio 2019 e il 31 dicembre 2019. Il 2 gennaio 2020 verrà effettuata una nuova ottimizzazione e saranno generati i nuovi pesi ottimali dei Lazy portfolios.
In fase di backtest, è fondamentale che le performance non vengano mai calcolate sui rendimenti dei portafogli nei periodi impiegati per l’ottimizzazione dei pesi: l’intervallo di tempo che va dal 1° gennaio al 31 dicembre 2018 sarà utilizzato per l’ottimizzazione dei pesi, mentre le performance dei Lazy portfolios costruiti con quei pesi saranno calcolate sui rendimenti del periodo successivo (1° gennaio – 31 dicembre 2019).
Si tratta di una procedura ciclica, che permette di superare l’uni-periodicità del modello di Markowitz e delle altre strategie di ottimizzazione.
Essa ci permetterà di ottenere la serie storica completa dei rendimenti di ciascun portafoglio, costruita nel modo descritto, di lunghezza pari alla totalità del periodo scelto (con la sola eccezione dei primi 252 giorni borsistici, utilizzati soltanto per l’ottimizzazione dei pesi nella fase iniziale del backtest).
Questa procedura non va in alcun modo confusa con i rendimenti di uno strumento finanziario o di un portafoglio di titoli presentati in molti siti finanziari: a meno che non venga dichiarato il contrario, si tratta di un’analisi ex-post, che potrebbe essere stata effettuata su un portafoglio di cui a posteriori sappiamo già la performance che ha ottenuto.
La nostra analisi è invece svolta su portafogli generati sulla base delle sole informazioni disponibili al momento della loro costruzione, non quelli generati col “senno di poi”.
La differenza non viene sempre percepita con facilità, soprattutto dagli investitori meno esperti, ma è fondamentale.
Ipotizziamo di essere all’inizio del 2022 e di pubblicizzare un portafoglio che ha ottenuto un rendimento del 30% nel 2021. Potremmo proporlo come il portafoglio ideale per il 2022, giustificando la scelta con le ottime performance ottenute l’anno precedente, che sono facilmente verificabili.
Quello che stiamo facendo, però, è selezionare un portafoglio sulla base di informazioni passate (il rendimento ottenuto l’anno precedente); una scelta ex-post, quindi.
Sapere che ha ottenuto un rendimento del 30% l’anno precedente non mi garantisce in alcun modo che quel rendimento possa essere prodotto di nuovo.
Di conseguenza:
- Il rendimento dell’anno scorso, pari al 30%, non può essere inserito nei risultati dei backtest (se esistenti) della strategia che pubblicizza quel portafoglio, dato che la raccomandazione è avvenuta soltanto oggi, quando quel rendimento era stato già prodotto.
- Il rendimento di quest’anno, che sarebbe il primo valore attendibile della strategia suggerita, lo conosceremo soltanto a fine anno.
Il backtest di questa strategia dovrebbe perciò, oggi, prendere in considerazione il rendimento del portafoglio raccomandato l’anno scorso, se una raccomandazione del genere era stata fatta.
L’anno prossimo sarà aggiunto il rendimento del portafoglio che è stato suggerito all’inizio di quest’anno. E così via, anno dopo anno.
Di nuovo, quel 30% iniziale non rientra nella performance della strategia, anche se farebbe tanto comodo inserircelo. Purtroppo, molto spesso viene conteggiato.
Potrebbero sembrare dei concetti scontati, ma nei backtest è fin troppo frequente l’errore che consiste nell’utilizzo ex-post di informazioni che non sarebbero state disponibili all’inizio del periodo che si vuole analizzare.
Un fenomeno in un certo senso simile è quello delle raccomandazioni di investimento a favore di uno strumento finanziario sulla base di stelle, ratings, punti e quant’altro: tutte assegnate ex-post, in seguito a classifiche costruite a partire dalle performance passate.
Queste quantificazioni a posteriori sono all’origine del fenomeno del return chasing, che inganna non soltanto gli investitori ma anche molti consulenti finanziari.
Nella speranza di ottenere rendimenti più alti di quelli del mercato o di un portafoglio già in essere, si switchano in continuazione gli strumenti finanziari meno performanti con quelli col massimo numero di stelle o con il miglior rating: strumenti che sono andati molto bene in passato, ma di cui non si ha alcuna garanzia per quanto riguarda il futuro.
Il return chasing è una vera e propria rincorsa dei rendimenti: una forma di market timing che nel lungo termine peggiorerà la performance complessiva.
Proporre strategie conteggiando rendimenti a posteriori o consigliare strumenti finanziari sulla base delle ottime performance passate non implica necessariamente malafede: spesso si procede in questo modo a causa di una scarsa comprensione del fenomeno conosciuto come Look-Back Bias (spesso condito da altri errori metodologici come l’overfitting e il Look-Ahead Bias).
Questi errori generano delle irrealistiche aspettative di rischio e rendimento; un'illusione che non durerà a lungo: la realtà non tarderà a manifestarsi e – si spera – a convincere l'investitore o l'analista che c'è qualcosa che non va.
Tornando alla nostra analisi, essa consisterà nel backtest delle performance dei Lazy portfolios e dei diversi modelli di ottimizzazione utilizzati.
I modelli statici sono quelli che non hanno bisogno di alcuna ottimizzazione, perché i pesi degli strumenti finanziari rimangono costanti: stiamo parlando del modello 1/N e del modello standard.
In questi due casi, in realtà, non ha neppure senso parlare di ottimizzazione: si tratta di semplice ribilanciamento periodico.
Per gli altri modelli, invece, effettueremo delle vere e proprie ottimizzazioni (vincolate e non vincolate).
Al termine di ciascun periodo, misureremo le performance ottenute dai portafogli ottimali di volta in volta generati.
Considerando che:
- le serie storiche giornaliere degli ETF analizzati, completate con i valori degli indici di categoria come descritto nel terzo capitolo, sono disponibili a partire dal 1° gennaio 1985;
- per le stime dei rendimenti e della matrice di varianza/covarianza attesi sono state utilizzate le serie storiche dei rendimenti dell’ultimo anno di ciascun ETF, pari a circa 252 giorni borsistici;
l’analisi effettuata ha coperto un periodo di 36 anni (da inizio 1985 a fine 2020), durante il quale per ognuno dei 40 Lazy portfolios analizzati sono state effettuate 35 ottimizzazioni o ribilanciamenti per ciascuna delle 11 strategie utilizzate.
Perché è necessario ribilanciare periodicamente i portafogli pigri e, più in generale, ogni portafoglio?
Il ribilanciamento ha lo scopo di riportare i pesi dei titoli ai loro valori originari o a quelli ottimizzati.
È un’operazione necessaria perché l’andamento del mercato determina la deriva (drift) dei pesi dai valori scelti inizialmente. Senza ribilanciamento, col tempo si modifica l’asset allocation del portafoglio.
Anche quando si parla di portafoglio equipesato o di pesi standard si fa sempre riferimento a un istante ben preciso: quello del momento iniziale dell’investimento o di quando si esegue un ribilanciamento. Subito dopo, le variazioni di prezzo dei titoli modificheranno il peso delle quote di ciascun ETF.
Vediamo un semplice esempio numerico, che dovrebbe aiutare a capire come funzionano i ribilanciamenti: ipotizziamo un portafoglio composto da 100 quote di un ETF azionario e 100 quote di un ETF obbligazionario. Al momento del loro acquisto, le quote hanno un prezzo di 5 euro ciascuna.
L’investitore avrà speso 1000 euro per sottoscrivere le 200 quote. Il peso dell’azionario e dell’obbligazionario è del 50% ciascuno.
Supponiamo che dopo un anno l’ETF azionario abbia raddoppiato il suo valore (10 euro a quota), mentre il prezzo delle quote dell’ETF obbligazionario sia rimasto invariato.
Il valore del portafoglio sarà quindi pari a 1000 + 500 = 1500 euro, con un rendimento complessivo del 50%.
Il peso dell’ETF azionario è però aumentato: adesso è pari a 1000/1500 = 66,67%. Il peso dell’ETF obbligazionario è invece sceso al 33,33%.
Ribilanciare significa riportare i pesi dei due ETF ai valori iniziali, pari al 50%: il valore delle quote dei due ETF in portafoglio dovrebbe essere di 750 euro ciascuno.
Il ribilanciamento consisterà quindi nella vendita di 25 quote dell’ETF azionario al prezzo di 10 euro ciascuna, e nell’acquisto di 50 quote dell’ETF obbligazionario al prezzo di 5 euro ciascuna.
Al termine del ribilanciamento, del quale per semplicità abbiamo ignorato sia le commissioni di transazione che le imposte sul capital gain, il portafoglio sarà così composto:
- 75 quote dell’ETF azionario al valore di 10 euro ciascuna = 750 euro.
- 150 quote dell’ETF obbligazionario al valore di 5 euro ciascuna = 750 euro.
Il valore del portafoglio sarà di 1500 euro e i pesi di ciascun ETF saranno di nuovo pari al 50% ciascuno.
Il ribilanciamento è importante per tenere sotto controllo la volatilità: serve a riportare il rischio del portafoglio nei limiti stabiliti e tollerati dall’investitore.
Il dibattito sulla frequenza dei ribilanciamenti è acceso ancora oggi: è meglio ribilanciare a intervalli periodici o in funzione di soglie percentuali di allontanamento dei pesi da quelli iniziali?
Nel primo caso, qual è la migliore periodicità di ribilanciamento? Nel secondo, qual è la soglia più efficiente?
Non essendo mai stata data una risposta definitiva a questi quesiti, nelle nostre analisi effettueremo dei ribilanciamenti annuali: questa scelta sembra essere un ottimo compromesso tra la ricerca della massima efficienza (maggior frequenza dei ribilanciamenti) e del minimo costo (minor frequenza dei ribilanciamenti).
La lista completa delle strategie e dei modelli di ottimizzazione utilizzati è la seguente:
| Lista e caratteristiche dei modelli di ottimizzazione | |||||
|---|---|---|---|---|---|
| Nome | Modello | R package/Risolutore | Algoritmo/Stima | Misura di rischio | Vincoli |
| Standard | Standard | Nessuno | Nessuna | Nessuna | In base al Lazy portfolio |
| 1/N | 1/N | Nessuno | Nessuna | Nessuna | 1/N |
| Boudt SD ROI | Ottimizzazione rischio/rendimento | PortfolioAnalytics - ROI | Boudt | Deviazione standard | Pesi standard ± 5% |
| Boudt SD Random | Ottimizzazione rischio/rendimento | PortfolioAnalytics - Portafogli random | Boudt | Deviazione standard | Pesi standard ± 5% |
| Boudt CVaR ROI | Ottimizzazione rischio/rendimento | PortfolioAnalytics - ROI | Boudt | CVaR | Pesi standard ± 5% |
| TCOV ROB | Ottimizzazione rischio/rendimento | PortfolioAnalytics/MASS - ROI | Stima robusta t di Student | Varianza | Pesi standard ± 5% |
| Naif | Ottimizzazione rischio/rendimento | PortfolioAnalytics - ROI | Naif (momenti passati) | Deviazione standard | Pesi standard ± 5% |
| Boudt SD No-Box | Ottimizzazione rischio/rendimento | PortfolioAnalytics - ROI | Boudt | Deviazione standard | Nessuno |
| Hier. Risk Parity (HRP) | Ottimizzazione rischio/rendimento | Codice customizzato | Tree clustering, quasi-diag. e bisez. ricorsiva | Nessuna | Nessuno |
| Boudt Random MVP | Minimum Variance Portfolio (MVP) | PortfolioAnalytics - Portafogli random | Boudt | Deviazione standard | Nessuno |
| Boudt Random HS | Highest Sharpe Ratio (HS) | PortfolioAnalytics - Portafogli random | Boudt | Deviazione standard | Nessuno |
La fase più critica dell’intero processo è l’applicazione dell’algoritmo di ottimizzazione finalizzato alla scelta dei pesi ottimali, in funzione dei vincoli e dell’obiettivo prefissato.
Per l’ottimizzazione rischio/rendimento di Markowitz, abbiamo utilizzato:
- Un risolutore disponibile nel package di R chiamato PortfolioAnalytics (ROI) e/o la metodologia dei portafogli random.
- Codice R scritto appositamente per il modello Hierarchical Risk Parity.
ROI, acronimo di R Optimization Infrastructure, è un risolutore molto flessibile che può essere utilizzato con modelli lineari e quadratici (massimizzazione del rendimento, minimizzazione della varianza/deviazione standard o del CVaR, ecc.).
I portafogli random (Random Portfolios) nascono da un’intuizione di Patrick Burns e costituiscono un campione estratto dall’universo di portafogli che rispettano tutti i vincoli richiesti.
L’idea è presentata in un articolo pubblicato nel 2010 nel libro Optimisation, Econometric and Financial Analysis.
Quello dei portafogli random è un approccio versatile, implementato sia nel package PortfolioAnalytics che direttamente in codice R.
Al di là della metodologia di ottimizzazione, dei vincoli e degli obiettivi, è bene ricordare il limite principale dell’approccio di Markowitz, già discusso nel capitolo 8: la qualità delle stime dei rendimenti attesi e della matrice di varianza/covarianza.
A questo riguardo:
- Tanto più esatte saranno le stime, tanto più efficiente sarà l’ottimizzazione.
- Tanto più efficiente sarà l’ottimizzazione, tanto più alto sarà il rendimento ottenuto dall’investitore per ogni unità di rischio assunto (e viceversa).
Una volta all’anno, i pesi dei Lazy portfolios vengono ricalcolati secondo gli algoritmi degli 11 modelli di ottimizzazione elencati nella tabella precedente.
Per ogni periodo, la serie dei rendimenti di ciascun Lazy portfolio per ogni modello di ottimizzazione viene costruita in base ai pesi degli ETF calcolati all’inizio di ogni periodo.
Alla fine (dicembre 2020 per tutti i backtest), i rendimenti così calcolati in ogni periodo di analisi vengono uniti in modo da formare un’unica serie storica dei rendimenti che parte dal 253° giorno borsistico del periodo analizzato e termina il 31 dicembre 2020.
I backtest vengono quindi eseguiti – alla fine di ogni periodo – sui rendimenti dei Lazy portfolios generati dai pesi degli ETF calcolati all’inizio di ogni periodo.
10. La strategia 1/N

«Sticking with a plan when you are winning sounds simple, but it's easy to become overconfident and get caught up in events. Long-term success is impossible if you let your heat-of-the-moment reactions trump careful planning».
Garri Kasparov
Oltre a modelli sofisticati come il Hierarchical Risk Parity, introdotto da Marcos Lopez de Prado e analizzato nel capitolo 8, la maledizione di Markowitz ha portato anche alla riscoperta di strategie di Asset Allocation conosciute fin dall’antichità ma che, con l’avvento della Teoria Moderna del Portafoglio e del Capital Asset Pricing Model, sembravano superate per sempre.
Tra queste, l’approccio più utilizzato è l’equidistribuzione del capitale tra i titoli in portafoglio. Il peso di ciascuno strumento finanziario è pari a 1/N, dove N rappresenta il numero di titoli.
L’idea alla base di questa strategia è la mancanza di preferenze aprioristiche per i titoli che compongono il portafoglio: per questa ragione, si assegna a ciascuno di essi lo stesso peso.
Questa modalità di investimento era già conosciuta molti secoli fa: “Ogni uomo divida il suo denaro in tre parti e ne investa un terzo in una proprietà terriera, un terzo in un’attività commerciale e un terzo lo tenga come riserva” è una citazione contenuta nel Talmud babilonese, che risale addirittura al IV secolo d.C. e sembra appartenere al rabbino Isaac bar Aha.
Si tratta di uno dei primi riferimenti documentati alla strategia di investimento 1/N.
Il più grande vantaggio di questa metodologia di investimento è la semplicità; non ha bisogno di informazioni per essere applicata: non servono serie storiche, non servono stime dei rendimenti attesi e della matrice di varianza/covarianza attesa, non serve alcun modello di ottimizzazione.
La strategia 1/N è stata analizzata da molti studiosi di finanza e diversi articoli sono stati pubblicati al riguardo. Tra questi, procedendo in ordine cronologico, troviamo ”Naive Diversification Strategies in Defined Contribution Saving Plans”, di Benartzi e Thaler (pubblicato nel 2001).
Nel loro articolo, gli autori affermano che la strategia 1/N può comportare degli alti costi – intesi nel senso di minor rendimento – rispetto ad altre strategie più dinamiche, se applicata su piani di risparmio/accumulo di lungo o lunghissimo periodo con finalità pensionistiche.
Nell’articolo del 2009 intitolato ”Optimal Versus Naive Diversification: How Inefficient is the 1/N Portfolio Strategy?”, DeMiguel, Garlappi e Uppal analizzano 14 diversi portafogli ottimali, ottenuti in base ad altrettanti modelli, e li confrontano con il portafoglio 1/N, utilizzato come benchmark di riferimento.
L’indagine viene portata avanti sulla base di 7 dataset composti da serie storiche reali e sintetiche. Il risultato è sorprendente: il classico portafoglio efficiente generato dal modello di ottimizzazione media/varianza ha sempre un indice di Sharpe out-of-sample inferiore a quello del benchmark 1/N.
Nessun modello di ottimizzazione – nemmeno il più sofisticato – riesce a sovraperformare il portafoglio naif: sembra che gli errori di stima della matrice di varianza/covarianza erodano tutto il vantaggio generato dal processo di ottimizzazione.
Gli autori concludono che, per compensare questo svantaggio, le serie storiche utilizzate nel processo di ottimizzazione dovrebbero essere molto più lunghe di quelle normalmente disponibili: per un portafoglio di 25 titoli, servirebbero più di 3000 mesi di dati, mentre per uno di 50 titoli, più di 6000 (contro i circa 60-120 mesi che vengono solitamente utilizzati).
È sempre del 2009 il contributo di Duchin e Levy “Markowitz Versus the Talmudic Portfolio Diversification Strategies”. In questo articolo, gli autori sostengono che la strategia 1/N sovraperforma l’ottimizzazione di Markowitz quando i portafogli contengono pochi titoli. All’aumentare di N, però, la situazione cambia e il vantaggio si sposta dalla parte di Markowitz.
È del 2010 l’articolo ”In Defense of Optimization: The Fallacy of 1/N” di Kritzman, Page e Turkington. Secondo gli autori, l’apparente superiorità della strategia 1/N non è dovuta alle problematiche di ottimizzazione, quanto all’uso di serie storiche troppo corte nella stima dei rendimenti attesi. Utilizzando serie storiche più lunghe, si otterrebbe il risultato opposto: una sovra-performance dei portafogli ottimizzati sugli 1/N.
Lo studio utilizza 13 dataset composti da 1028 serie storiche, con le quali vengono costruiti più di 50.000 portafogli ottimizzati, poi confrontati out-of-sample con il portafoglio di mercato e i portafogli 1/N.
La più importante differenza rispetto agli studi precedenti concerne la stima dei rendimenti attesi: invece di utilizzare serie storiche di pochi anni, gli autori preferiscono basarsi su previsioni ragionevoli legate a variabili economiche.
Le conclusioni sono nette: anche senza particolari abilità nella realizzazione dei forecast dei rendimenti attesi, l’ottimizzazione basata sulla sola matrice di varianza/covarianza produce risultati superiori. La strategia 1/N non sarebbe, perciò, un’alternativa preferibile a un’ottimizzazione ben formulata: piuttosto, adottarla significherebbe "darla vinta ai cinici".
Tu e Zhou tentano invece di unire le due strategie e propongono un approccio che combina la stima dei parametri in linea col modello di Markowitz e la strategia 1/N.
Questo approccio permetterebbe di mitigare gli errori e di giungere a una soluzione migliore, che sovraperforma la semplice strategia 1/N anche quando N è piccolo.
In conclusione, gli autori ritengono che la teoria proposta da Markowitz sia efficace e, sebbene utilizzata in una forma ibrida, permetta di ottenere risultati superiori alla strategia 1/N anche in presenza di errori di stima.
Nel 2013, Escobar, Mitterreiter, Saunders, Seco e Zagst introducono un ulteriore elemento di analisi: il contesto di mercato.
Gli autori distinguono i periodi di tranquillità da quelli di turbolenza dei mercati: in periodi di relativa calma, un portafoglio equidistribuito sovraperformerebbe uno ottimizzato; durante i periodi turbolenti, gli investitori dovrebbero concentrarsi sui portafogli efficienti, in quanto ridurrebbero il rischio e produrrebbero risultati migliori.
Entrerebbe perciò in gioco una nuova grandezza, la variabilità del mercato, che deve essere misurata: per farlo, gli autori si basano su dati macroeconomici, ma sostengono che ottimi risultati si ottengono anche col modello introdotto da Hauptmann et al., che permette di individuare tre differenti stati del mercato.
È del 2018, invece, l’articolo ”Asset allocation strategies, data snooping, and the 1/N rule”, i cui autori sono Hsu, Han, Wu e Cao.
Lo studio giunge alla conclusione che l’eventuale superiorità delle strategie di ottimizzazione dei portafogli sarebbe puramente casuale. Per dimostrare questo assunto, gli autori applicano alcuni processi econometrici ai dati utilizzati nell’analisi, che hanno lo scopo di eliminare le distorsioni causate dal data-snooping.
In definitiva, la strategia 1/N, semplice ed economica, sembrerebbe ottenere le stesse performance delle più complicate strategie di ottimizzazione del portafoglio.
Questa breve panoramica include soltanto alcuni dei numerosi contributi che hanno analizzato l’efficienza dei portafogli equipesati rispetto a quelli generati con più o meno sofisticate tecniche di ottimizzazione.
Nelle nostre analisi sui Lazy portfolios, calcoleremo anche i risultati generati dalla strategia 1/N, che sarà uno dei due modelli statici impiegati nei nostri backtest.
Bisogna riconoscere come la strategia 1/N sia ancora oggi molto apprezzata e utilizzata: non è un caso se gli stessi autori di molti portafogli pigri hanno impostato i pesi standard degli ETF utilizzati seguendo proprio questa filosofia d’investimento.
11. Lazy portfolios modello

«Noi non imitiamo, ma siamo modelli per gli altri».
Pericle
I Lazy portfolio modello hanno lo scopo di migliorare le performance dei Lazy portfolios standard: quelli che vengono regolarmente ribilanciati in modo da riportare il peso di ciascun ETF al suo valore iniziale.
I Lazy portfolios con ribilanciamento periodico dei pesi degli ETF ai loro valori standard sono uno dei due modelli statici che abbiamo backtestato.
Indipendentemente dal modello di ottimizzazione scelto, gli investitori che – convinti della validità dei portafogli pigri – decidano di utilizzarli operativamente, entrano a far parte di un club ristretto: quello degli investitori evoluti.
Coloro che replicano i Lazy portfolios sono generalmente investitori fai da te: persone che non hanno bisogno del supporto di un consulente finanziario.
La maggior parte di loro:
- Conosce i principi di funzionamento dei mercati finanziari e degli ETF.
- Ha un chiaro obiettivo di investimento.
- È consapevole della propria propensione al rischio e del proprio orizzonte temporale di investimento.
- È consapevole degli alti costi dei fondi a gestione attiva, che spesso compromettono il rendimento dell’investimento nel lungo termine.
- Ha seguito un percorso di approfondimento dei concetti base di finanza personale e, spesso, ha frequentato almeno saltuariamente un forum finanziario online dove si discute di finanza e investimenti.
Gli investitori evoluti non disprezzano un confronto su questi temi con i consulenti finanziari, ma raramente vengono in contatto con loro: sanno che la strada dell’investimento passivo, perseguito attraverso gli ETF e i portafogli pigri, non è molto gradita negli istituti finanziari e a molti consulenti stessi, fatta eccezione per i Consulenti Finanziari Autonomi.
I Lazy portfolios modello costituiscono quindi una soluzione alternativa per:
- Gli investitori evoluti che gestiscono in prima persona i loro portafogli finanziari e li preferiscono ai portafogli pigri standard.
- I consulenti finanziari che sono consapevoli dei vantaggi dei Lazy portfolios ma che, per motivi di bassa remunerazione o per paura di perdere i loro clienti, non possono proporli.
Per alcuni, la paura è che i clienti, una volta capite le logiche di funzionamento dei Lazy portfolios, decidano di gestirli per conto proprio.
Per altri, la paura è che i clienti – non percependo il valore di questo tipo di approccio – potrebbero erroneamente credere che il lavoro del consulente (e la sua remunerazione) non sia giustificato da un approccio “troppo passivo”.
Per ogni Lazy portfolio, verranno mensilmente pubblicati i pesi ottimizzati di tutte strategie di ottimizzazione dei Lazy portfolios modello:
- Modelli dinamici vincolati (pesi standard ottimizzati col vincolo del ± 5%):
- Boudt SD ROI
- Boudt SD Random
- Boudt CVaR ROI
- TCOV Robusta
- NAIF
- Modelli dinamici non vincolati (senza vincoli sui pesi):
- Boudt SD No-Box: è il portafoglio ottimale in base all’ottimizzazione di Markowitz. Questo approccio è adatto agli investitori con un’alta propensione al rischio in senso relativo (i concetti di propensione al rischio in senso relativo e assoluto saranno approfonditi in seguito), dal momento che anche un portafoglio pigro prudente nella sua versione standard, potrebbe essere rivoluzionato e diventare un portafoglio con il 100% del peso su un unico ETF (potenzialmente, proprio il più rischioso).
- HRP: è l’approccio analizzato nel capitolo 8. Questa strategia di ottimizzazione si è dimostrata conservativa e, come approfondiremo nel capitolo 19, è adatta agli investitori con una bassa propensione al rischio in senso relativo.
- Minimum Variance Portfolio (MVP): è il portafoglio che, in seguito all’ottimizzazione di Markowitz, ha la più bassa varianza attesa. Anche questa scelta è adatta agli investitori con una bassa propensione al rischio in senso relativo.
- Higher Sharpe Ratio (HS): è il portafoglio che, in seguito all’ottimizzazione di Markowitz, ha il più alto indice di Sharpe atteso. Questa scelta – in teoria – dovrebbe essere adatta agli investitori con una propensione al rischio in senso relativo media.
In realtà, i nostri backtest dimostreranno come questo modello generi risultati molto rischiosi, imprevedibili e instabili. Senz’altro, è il modello dinamico non vincolato che sconsigliamo di utilizzare (i pesi degli ETF generati con questo modello vengono comunque forniti).
- Modelli statici
- 1/N
- Standard
I modelli statici vengono pubblicati per completezza: trattandosi di semplici ribilanciamenti periodici, i pesi sono sempre gli stessi.
Per propensione al rischio in senso relativo intendiamo il livello di rischiosità scelto dall’investitore in fase di ottimizzazione: ad esempio, il Minimum Variance Portfolio è meno rischioso dell’Highest Sharpe Ratio Portfolio.
Tuttavia, un portafoglio pigro contenente soltanto ETF azionari sarà molto rischioso indipendentemente dalla strategia di ottimizzazione scelta: non sarà perciò adatto a un investitore con una bassa propensione al rischio in senso assoluto.
Nel capitolo 19 approfondiremo la propensione al rischio relativa e assoluta e vedremo il ruolo che assumono questi due elementi in una potenziale strategia di scelta del Lazy portfolio e del modello di ottimizzazione.
Potete trovare i Lazy portfolios modello al seguente link (per avere accesso è necessario sottoscrivere un abbonamento PRO): Lazy portfolios modello.
12. Classifiche finali: per portafoglio e per modello di ottimizzazione

«Più bravi di Boskov sono quelli che stanno sopra di lui in classifica».
Vujadin Boškov
Non è facile classificare 40 portafogli pigri – ribilanciati e ottimizzati periodicamente con 11 diversi modelli – sulla base di 12 misure di performance.
Da una parte, è necessaria una sintesi dei risultati ottenuti affinché siano comprensibili; dall’altra, tutte le informazioni generate dai backtest sono importanti: non se ne vogliono perdere troppe nel processo di semplificazione.
Le 12 misure statistiche utilizzate sono le seguenti:
- Rendimento annualizzato
- Volatilità (deviazione standard)
- Indice di Sharpe
- Rendimento cumulato
- Massimo drawdown
- Drawdown medio
- Durata media dei drawdown (in giorni)
- Periodo medio di recupero
- Coefficiente di Hurst
- VaR
- CVaR
- Indice di Sortino
Dato che alcune misure sono molto simili tra loro, dato che quantificano gli stessi fenomeni (ad esempio l’Indice di Sharpe e quello di Sortino, il rendimento annualizzato e quello cumulato, ecc.), mentre altre sono di difficile interpretazione (Coefficiente di Hurst), per misurare la bontà dei Lazy portfolios e confrontarli tra di loro ci limiteremo a utilizzarne 5:
- Rendimento annualizzato
- Volatilità (deviazione standard)
- Indice di Sharpe
- Massimo drawdown
- CVaR
La prima di queste 5 misure statistiche è l’unica che quantifica la redditività di un portafoglio pigro; le altre 4 sono misure di rischio.
L’analisi effettuata non ha soltanto lo scopo di verificare le performance dei Lazy portfolios: permetterà di valutare anche i pro e i contro di ogni modello di ottimizzazione dei pesi nelle fasi di ribilanciamento, con o senza vincoli, e dei due modelli statici utilizzati (1/N e standard).
Inoltre, l’intera analisi sarà svolta su 3 diversi periodi:
- Dal 1° gennaio 1985 al 31 dicembre 2020.
- Dal 1° gennaio 2000 al 31 dicembre 2020.
- Dal 1° gennaio 2010 al 31 dicembre 2020.
L'utilizzo di tre differenti periodi nasce dalla volontà di verificare le performance di ciascun Lazy portfolio in diverse condizioni di mercato. Il primo e più lungo periodo, che copre ben 36 anni, è importante per più motivi:
- Mette a dura prova la robustezza di ciascun portafoglio. In un periodo di questa lunghezza si sono verificate molte crisi finanziarie, alternate a periodi di rapida crescita dei mercati, ed è improbabile che accadano eventi futuri che differiscano molto da quanto successo in questi 36 anni. Difficile, ma non impossibile: per quanto nessuno se lo auguri, non si può sapere se e quando i mercati finanziari attraverseranno una nuova Grande Depressione o una crisi addirittura peggiore.
- Enfatizza l’importanza di investire il più a lungo possibile. Certi rendimenti sembreranno irreali, mentre non sono altro che l’effetto prodigioso della capitalizzazione composta e della crescita dei mercati nel lunghissimo termine.
Gli altri 2 periodi sono più corti e più vicini ai giorni nostri:
- Quello che parte dal 2000, lungo 21 anni, è particolarmente interessante, perché vede la sua prima metà caratterizzata da due gravi finanziarie, la dotcom e la subprime; la seconda metà è invece contraddistinta da una poderosa crescita dei mercati, come raramente accaduto prima.
- Il periodo più breve, lungo 11 anni, è quello a noi più prossimo. Si è trattato di un decennio in cui i mercati finanziari sono cresciuti quasi senza sosta. Neppure la grave ma breve crisi di inizio 2020, scatenata dal COVID-19, è riuscita ad arginarne la crescita: dopo pochi mesi, i mercati hanno ripreso il loro cammino al rialzo.
L’analisi si complica ulteriormente prendendo in considerazione le valute.
Quasi tutti i portafogli pigri analizzati nascono per soddisfare le esigenze di un investitore americano. Gli ETF consigliati, quindi, sono denominati in USD e il mercato di riferimento è in gran parte quello statunitense.
Molti di questi Lazy portfolios sono diventati molto conosciuti anche nel resto del mondo e, ovviamente, anche in Europa e in Italia.
Gli investitori dell’area euro devono fronteggiare due grossi problemi:
- Il dollaro non è la loro valuta di riferimento. Le performance generate dai Lazy portfolios, quindi, non sono quelle effettive, perché il tasso di cambio tra euro e dollaro ha un impatto sia sul rendimento che sul rischio di tutti i portafogli pigri.
- Gli ETF che compongono i Lazy portfolios originali non sono armonizzati e non possono perciò essere utilizzati dagli investitori italiani.
Per ovviare a queste difficoltà, ogni analisi viene ripetuta tre volte:
- Utilizzando ETF in dollari e, per i periodi antecedenti al lancio di ciascun ETF, indici rappresentativi delle categorie replicate: le performance delle analisi sono quelle effettive per un investitore statunitense.
Questa tipologia di analisi/portafogli sarà identificata come “USD”. - Utilizzando ETF in dollari, ma con le serie storiche convertite in euro: i prezzi giornalieri degli ETF e, per i periodi antecedenti al lancio di ciascun ETF, degli indici rappresentativi delle categorie replicate, sono convertiti in euro su base giornaliera in funzione del tasso di cambio corrente. Le performance delle analisi sono quelle effettive per gli investitori dell’area euro.
Le differenze tra i risultati di questa e della precedente analisi misurano l’impatto del rischio di cambio.
Questa tipologia di analisi/portafogli sarà identificata come “USD→EUR”. - Utilizzando ETF in euro e, per i periodi antecedenti al lancio di ciascun ETF, degli indici rappresentativi delle categorie replicate. Il focus viene spostato dagli USA all’area euro. I mercati azionari e obbligazionari americani vengono sostituiti da quelli dell’area euro (o europei/globali, in mancanza di ETF dell’area euro in categorie specifiche).
Le performance delle analisi sono quelle effettive per gli investitori dell’area euro e il rischio di cambio è ridotto al minimo.
Questa tipologia di analisi/portafogli sarà identificata come “EUR”.
Disclaimer
Queste classifiche possono essere utili, ma la scelta del Lazy portfolio più adatto per un investitore non deve essere effettuata semplicemente scorrendo l’elenco dall’alto verso il basso per diversi motivi.
Ne elenchiamo alcuni:
- L’ordinamento cambia al variare del periodo di analisi: è molto difficile che un portafoglio pigro posizionato al primo posto nei backtest della durata più lunga finisca all’ultimo posto in una durata più breve, ma è altrettanto improbabile che rimanga sempre al vertice (e questo vale per ogni posizione in classifica).
- Un Lazy portfolio situato a metà/bassa classifica potrebbe comunque essere un’ottima scelta per molti investitori: può darsi che in passato abbia generato un rendimento minore di altri portafogli dalla rischiosità simile o sia stato più rischioso di altri portafogli dal rendimento simile, ma potrebbe tuttavia essere la scelta preferita per alcuni in ragione della propria asset allocation. Ad esempio, lo potrei preferire perché include (o meno) l’oro, che ritengo essere una componente imprescindibile (o meno) di un portafoglio ben strutturato.
- I parametri selezionati per la classificazione dei Lazy portfolios sono universamente riconosciuti come validi (rendimento e rischio) ma, cambiando i pesi assegnati a ciascuna delle componenti scelte per la misurazione del rischio (volatilità, indice di Sharpe, massimo drawdown, CVaR) o a quello del rendimento annualizzato, l’ordinamento verrebbe modificato.
- Nei prossimi 10, 20 o 35 anni, i mercati finanziari potrebbero seguire dei trend molto diversi da quelli degli anni passati: è vero che il trend di crescita di lungo periodo va avanti da oltre 200 anni, ma non possiamo escludere che le cose cambino in futuro (a maggior ragione nel periodo più breve) .
Vedremo in seguito altre analisi dei risultati ottenuti, da valutare insieme a queste: le heatmaps e i rendimenti rolling, ad esempio. Inoltre, ogni Lazy portfolio verrà approfondito e tutte le performance saranno visualizzate in forma tabellare. Infine, nel capitolo 19 verrà proposto un possibile metodo di scelta del Lazy portfolio più adatto per un investitore.
12.1 Lazy portfolios

«Invention, in my opinion, arises directly from idleness, possibly also from laziness - to save oneself trouble».
Agatha Christie
Il procedimento utilizzato per stilare la classifica dei 40 Lazy portfolios è il seguente:
- Calcolo del rendimento annualizzato, della volatilità, dell’Indice di Sharpe, del massimo drawdown e del CVaR di ogni portafoglio pigro, ribilanciato annualmente in base agli 11 modelli di ottimizzazione.
- Per ognuna delle misure statistiche elencate al punto 1), calcolo del valore medio per ogni portafoglio pigro: si trasformano 11 risultati – uno per ogni modello utilizzato – in un'unica quantità, pari alla loro media.
- Calcolo del rango dei valori medi delle 5 misure statistiche. Il rango è la posizione occupata da ciascuna delle 40 medie delle 5 misure computate al punto precedente.
Ogni Lazy portfolio sarà perciò caratterizzato da 5 diversi ranghi, tutti compresi da 1 a 40: uno per ogni misura statistica di cui al punto 1).
Ad esempio, il rango pari a 1 individuerà il miglior valor medio delle 5 misure statistiche tra tutte quelli dei 40 Lazy portfolios: sarà il valore più alto nel caso del rendimento annualizzato, dell’Indice di Sharpe e del massimo drawdown; il più basso, nel caso della volatilità e del CVaR. - Calcolo della media ponderata dei ranghi: il rango del rendimento annualizzato ha un peso 5 volte superiore a quello dell’Indice di Sharpe, del massimo drawdown e del CVAR. Il peso della volatilità, invece, è pari a 2.
In questo modo, le misure di rendimento e di rischio hanno, nel loro insieme, un peso pari al 50% ciascuno. - Ordinamento crescente dei 40 ranghi ponderati. I portafogli con i valori più bassi saranno quelli che hanno performato meglio (e viceversa).
Vediamo dunque le classifiche dei 40 Lazy portfolios (USD, USD→EUR e EUR).
Le tabelle che seguono sono in ordine alfabetico mentre i grafici seguenti sono in ordine di classifica.
PERIODO 1985-2020
| Ordinamento dei Lazy portfolios | ||||||
|---|---|---|---|---|---|---|
| Backtest del periodo 01/01/1985 - 31/12/2020 | ||||||
| Lazy portfolio | USD | USD→EUR | EUR | |||
| Media ponderata | Rango | Media ponderata | Rango | Media ponderata | Rango | |
| All Weather | 23.4 | 30 | 29.1 | 36 | 20.2 | 20 |
| Andrew Tobias | 24.5 | 32 | 24.0 | 30.5 | 27.3 | 38.5 |
| Coffee House | 15.3 | 3 | 15.3 | 6 | 14.7 | 4 |
| Core Four | 15.9 | 5 | 15.2 | 4.5 | 18.3 | 14 |
| Couch Potato | 14.9 | 2 | 13.3 | 3 | 25.5 | 36 |
| David Swensen Lazy Portfolio | 20.5 | 22 | 15.9 | 7 | 22.1 | 28.5 |
| Dedalo Eleven | 21.9 | 29 | 17.6 | 13 | 13.7 | 1 |
| Dedalo Four | 18.0 | 13 | 10.8 | 1 | 17.4 | 13 |
| Dedalo Three | 18.8 | 16 | 17.2 | 11.5 | 20.4 | 22 |
| Desert | 27.6 | 36.5 | 31.9 | 39 | 21.9 | 27 |
| Dynamic 40-60 Income | 13.8 | 1 | 11.6 | 2 | 16.9 | 8 |
| Dynamic 60-40 Income | 18.9 | 17 | 24.3 | 32 | 17.3 | 12 |
| Five Asset | 25.3 | 35 | 20.5 | 26 | 26.8 | 37 |
| Four Funds Bogleheads | 21.1 | 28 | 15.2 | 4.5 | 23.9 | 33 |
| Golden Butterfly | 16.8 | 7 | 20.7 | 27 | 13.8 | 2 |
| Ivy | 29.4 | 40 | 27.1 | 34 | 27.3 | 38.5 |
| Larry | 27.6 | 36.5 | 29.2 | 37 | 21.2 | 25 |
| Margaritaville | 23.8 | 31 | 16.0 | 8 | 23.8 | 32 |
| No Brainer | 20.6 | 24 | 17.9 | 14 | 25.2 | 35 |
| Permanent | 25.0 | 34 | 26.9 | 33 | 19.0 | 16.5 |
| Rob Arnott | 16.4 | 6 | 17.1 | 10 | 20.7 | 23 |
| Second Grader's Starter | 20.6 | 24 | 19.7 | 24 | 23.0 | 31 |
| Simple Path to Wealth | 18.4 | 14.5 | 18.5 | 20 | 21.2 | 25 |
| Talmud | 19.3 | 20 | 20.4 | 25 | 14.2 | 3 |
| Three Funds Bogleheads | 20.6 | 24 | 18.9 | 22 | 22.9 | 30 |
| Two funds 10-90 | 24.7 | 33 | 31.5 | 38 | 20.0 | 19 |
| Two funds 20-80 | 21.0 | 27 | 28.8 | 35 | 17.1 | 9.5 |
| Two funds 30-70 | 19.0 | 18 | 24.0 | 30.5 | 15.6 | 5 |
| Two funds 40-60 | 17.1 | 9 | 22.2 | 28 | 16.0 | 6 |
| Two funds 50-50 | 17.0 | 8 | 18.4 | 18 | 17.1 | 9.5 |
| Two funds 60-40 | 15.8 | 4 | 18.5 | 20 | 19.0 | 16.5 |
| Two funds 70-30 | 17.9 | 12 | 18.5 | 20 | 20.3 | 21 |
| Two funds 80-20 | 18.4 | 14.5 | 18.3 | 16.5 | 21.2 | 25 |
| Two funds 90-10 | 19.6 | 21 | 18.3 | 16.5 | 22.1 | 28.5 |
| Two funds Dinamico | 17.8 | 11 | 19.3 | 23 | 18.5 | 15 |
| Ultimate Buy & Hold | 20.8 | 26 | 18.2 | 15 | 17.2 | 11 |
| Ultimate Buy and Hold Strategy | 19.2 | 19 | 17.2 | 11.5 | 19.8 | 18 |
| Warren Buffett | 17.2 | 10 | 16.3 | 9 | 36.1 | 40 |
| World Bond | 28.1 | 39 | 33.4 | 40 | 16.5 | 7 |
| World Stocks | 28.0 | 38 | 22.8 | 29 | 24.8 | 34 |
I grafici delle classifiche finali, ottenute riordinando in base al rango i Lazy portfolios in USD, USD→EUR e EUR, sono i seguenti:
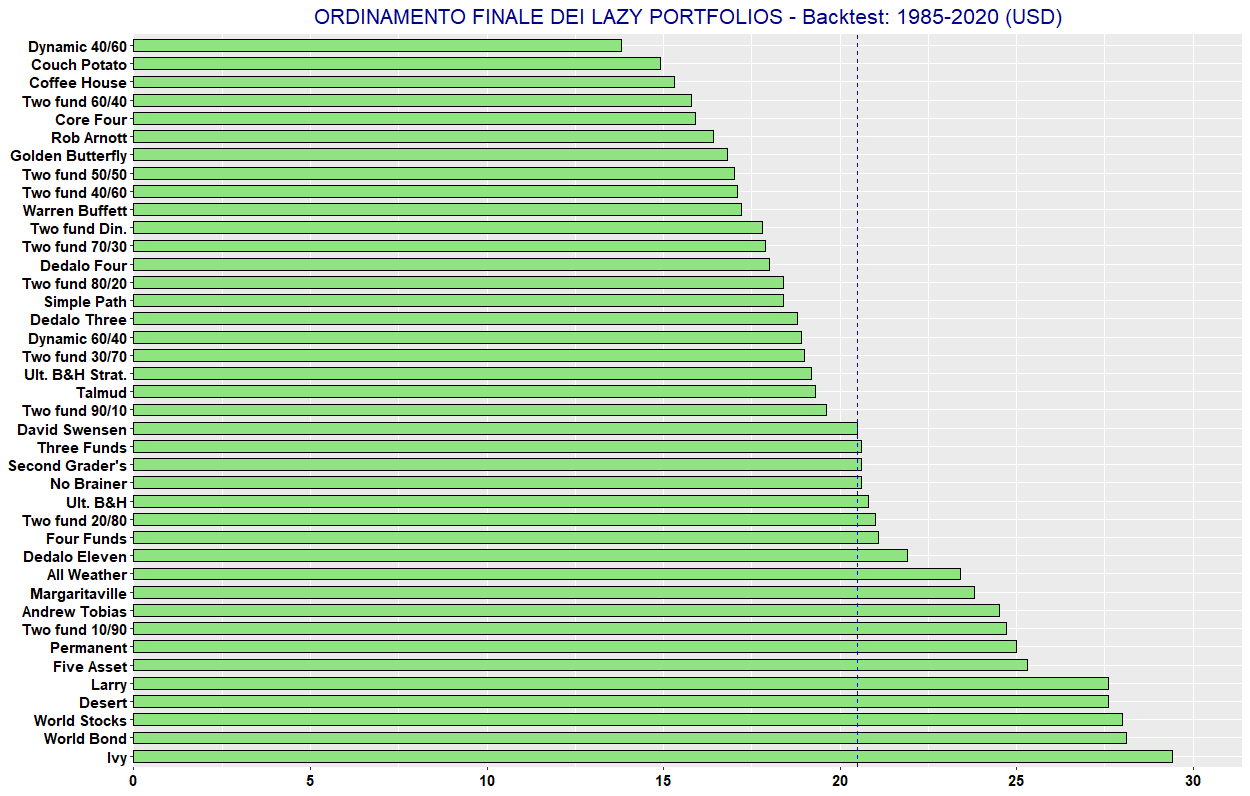
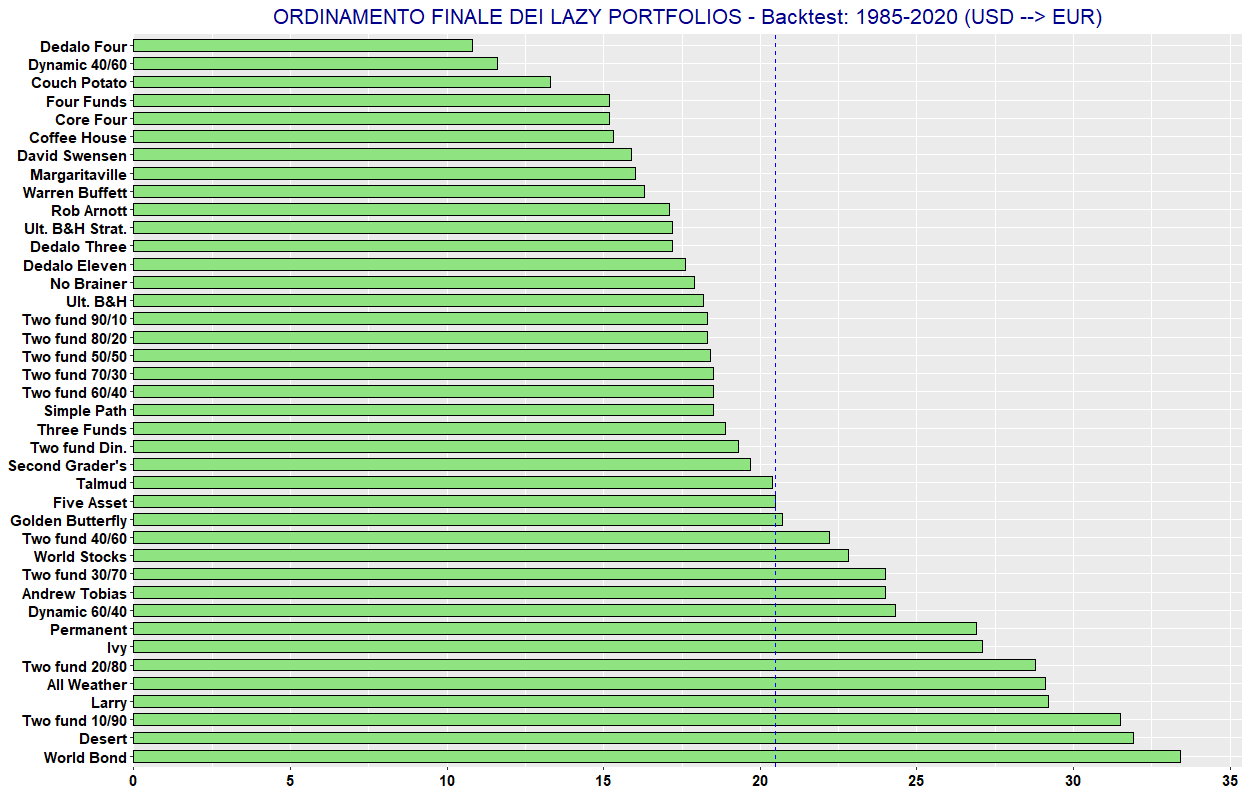
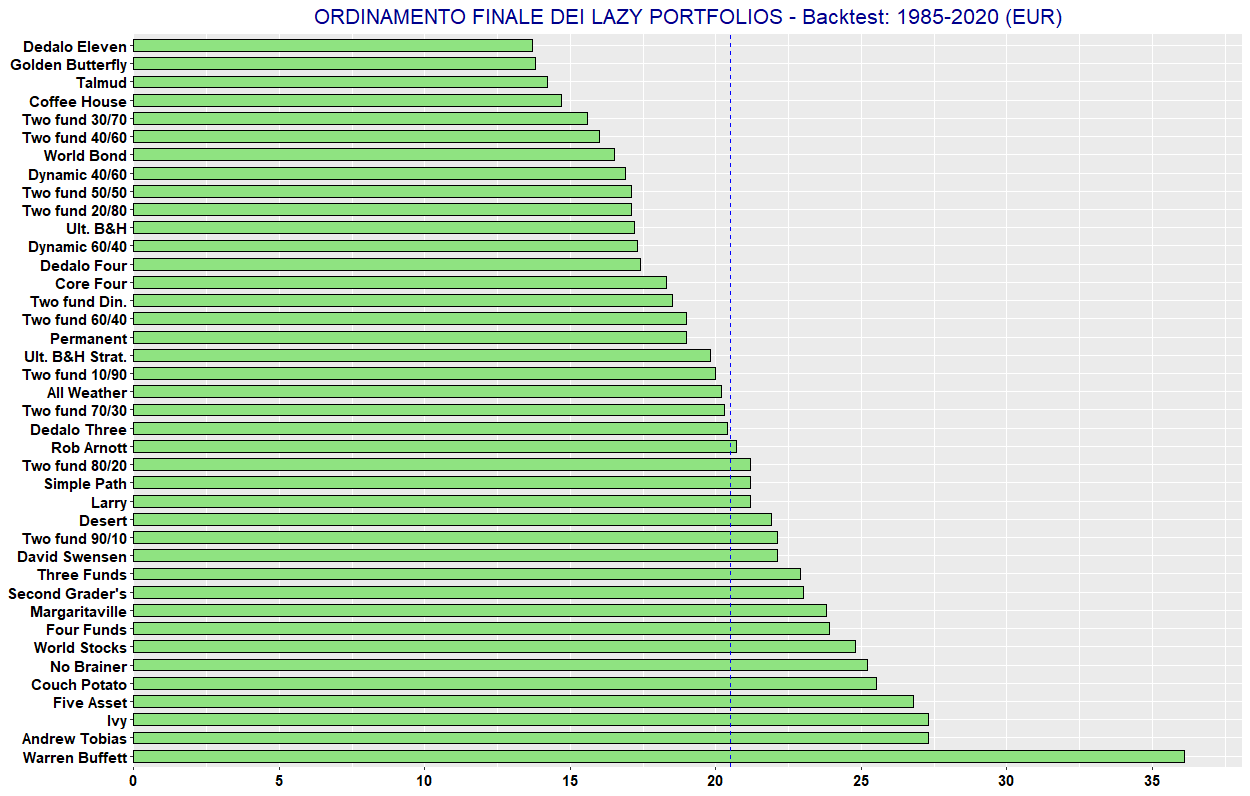
PERIODO 2000-2020
| Ordinamento dei Lazy portfolios | ||||||
|---|---|---|---|---|---|---|
| Backtest del periodo 01/01/2000 - 31/12/2020 | ||||||
| Lazy portfolio | USD | USD→EUR | EUR | |||
| Media ponderata | Rango | Media ponderata | Rango | Media ponderata | Rango | |
| All Weather | 11.1 | 4 | 8.2 | 6 | 11.3 | 5 |
| Andrew Tobias | 30.7 | 39 | 30.7 | 37 | 25.0 | 30 |
| Coffee House | 18.6 | 15 | 21.0 | 19 | 13.6 | 8 |
| Core Four | 20.5 | 19 | 20.4 | 17 | 17.6 | 16 |
| Couch Potato | 8.6 | 3 | 4.0 | 2 | 21.2 | 22.5 |
| David Swensen Lazy Portfolio | 12.3 | 5.5 | 8.6 | 7 | 13.9 | 9 |
| Dedalo Eleven | 16.4 | 9 | 12.8 | 11 | 15.5 | 12 |
| Dedalo Four | 16.8 | 12.5 | 11.6 | 9 | 21.3 | 24 |
| Dedalo Three | 19.8 | 16 | 19.2 | 16 | 23.0 | 27 |
| Desert | 16.5 | 10 | 13.6 | 12 | 17.1 | 15 |
| Dynamic 40/60 Income | 14.3 | 7 | 9.3 | 8 | 16.1 | 13 |
| Dynamic 60/40 Income | 20.3 | 18 | 23.3 | 21 | 15.2 | 10.5 |
| Five Asset | 22.8 | 23 | 20.7 | 18 | 19.1 | 18.5 |
| Four Funds Bogleheads | 16.7 | 11 | 12.7 | 10 | 22.9 | 26 |
| Golden Butterfly | 7.6 | 1 | 3.0 | 1 | 5.7 | 2 |
| Ivy | 33.9 | 40 | 31.2 | 38.5 | 16.9 | 14 |
| Larry | 21.0 | 21 | 21.2 | 20 | 15.2 | 10.5 |
| Margaritaville | 15.0 | 8 | 8.0 | 5 | 19.1 | 18.5 |
| No Brainer | 29.2 | 38 | 28.6 | 32 | 21.2 | 22.5 |
| Permanent | 12.3 | 5.5 | 6.2 | 3 | 8.2 | 3 |
| Rob Arnott | 7.8 | 2 | 7.5 | 4 | 9.0 | 4 |
| Second Grader's Starter | 27.0 | 35 | 26.1 | 25 | 29.5 | 35 |
| Simple Path to Wealth | 21.9 | 22 | 26.6 | 26 | 34.4 | 37 |
| Talmud | 16.8 | 12.5 | 17.8 | 14 | 12.9 | 7 |
| Three Funds Bogleheads | 27.6 | 36 | 26.0 | 24 | 26.6 | 32 |
| Two funds 10/90 | 25.4 | 34 | 32.5 | 40 | 21.8 | 25 |
| Two funds 20/80 | 24.3 | 30 | 31.2 | 38.5 | 20.3 | 20 |
| Two funds 30/70 | 23.6 | 25 | 30.2 | 36 | 20.6 | 21 |
| Two funds 40/60 | 23.9 | 27 | 29.1 | 33 | 23.2 | 28 |
| Two funds 50/50 | 24.1 | 29 | 28.1 | 30 | 25.3 | 31 |
| Two funds 60/40 | 23.8 | 26 | 28.4 | 31 | 28.4 | 34 |
| Two funds 70/30 | 23.3 | 24 | 27.6 | 29 | 32.5 | 36 |
| Two funds 80/20 | 23.9 | 28 | 26.8 | 27 | 36.2 | 39 |
| Two funds 90/10 | 25.2 | 32 | 26.9 | 28 | 38.1 | 40 |
| Two funds Dinamico | 25.1 | 31 | 29.5 | 35 | 23.6 | 29 |
| Ultimate Buy & Hold | 18.1 | 14 | 13.8 | 13 | 12.7 | 6 |
| Ultimate Buy and Hold Strategy | 20.1 | 17 | 18.7 | 15 | 19.0 | 17 |
| Warren Buffett | 27.7 | 37 | 29.2 | 34 | 34.6 | 38 |
| World Bond | 20.7 | 20 | 24.1 | 22 | 5.1 | 1 |
| World Stocks | 25.3 | 33 | 25.6 | 23 | 27.1 | 33 |
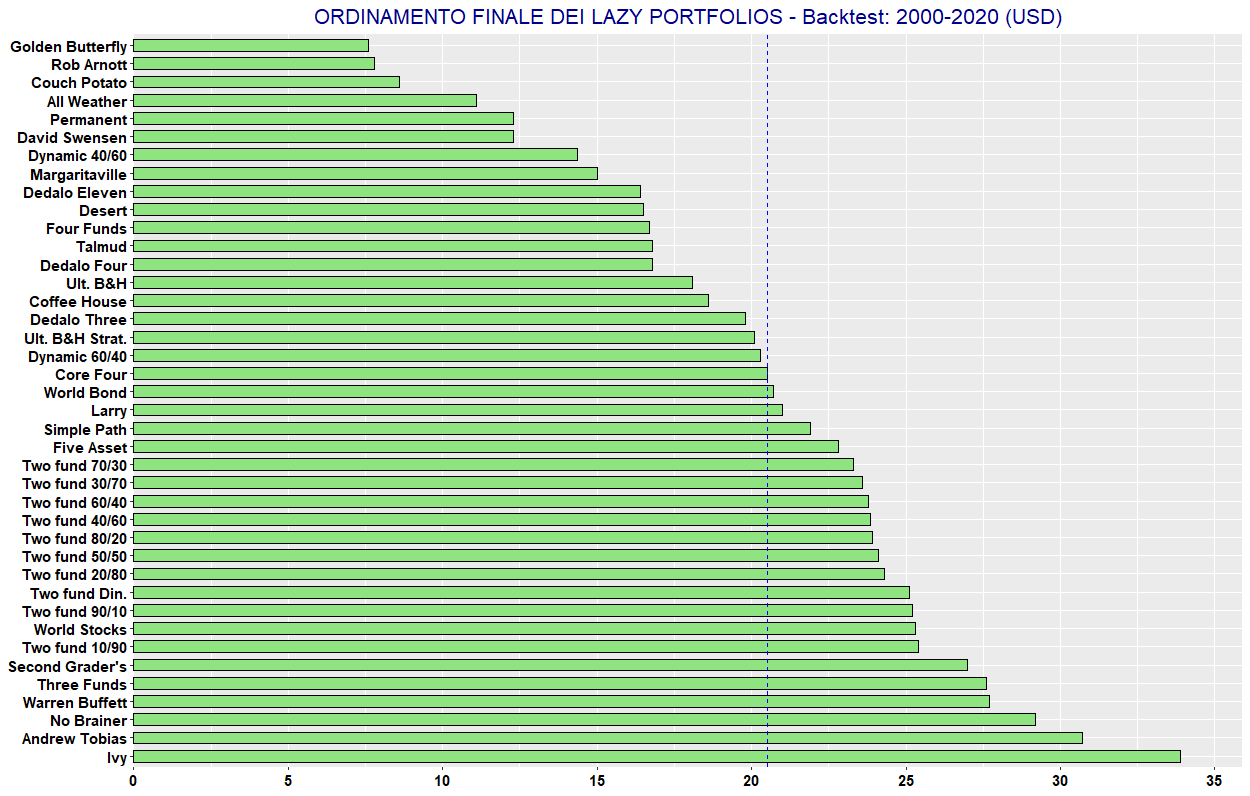
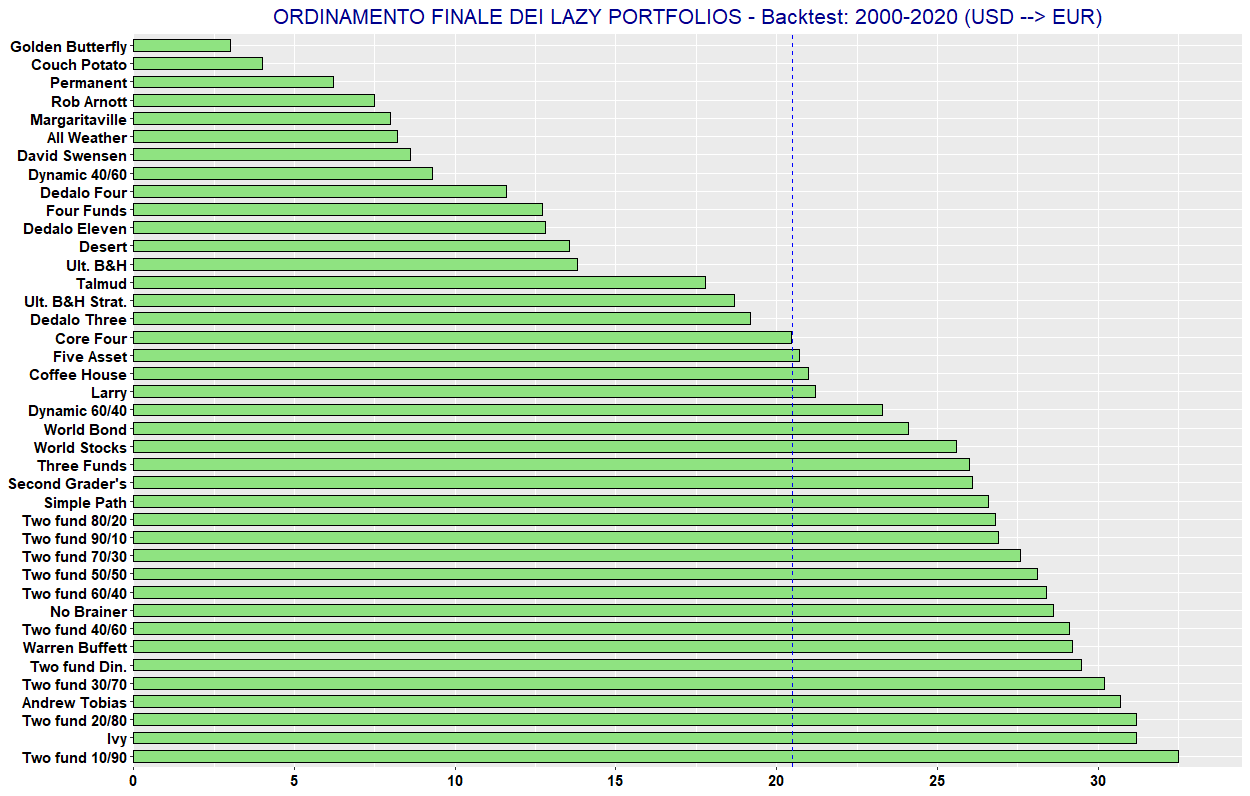
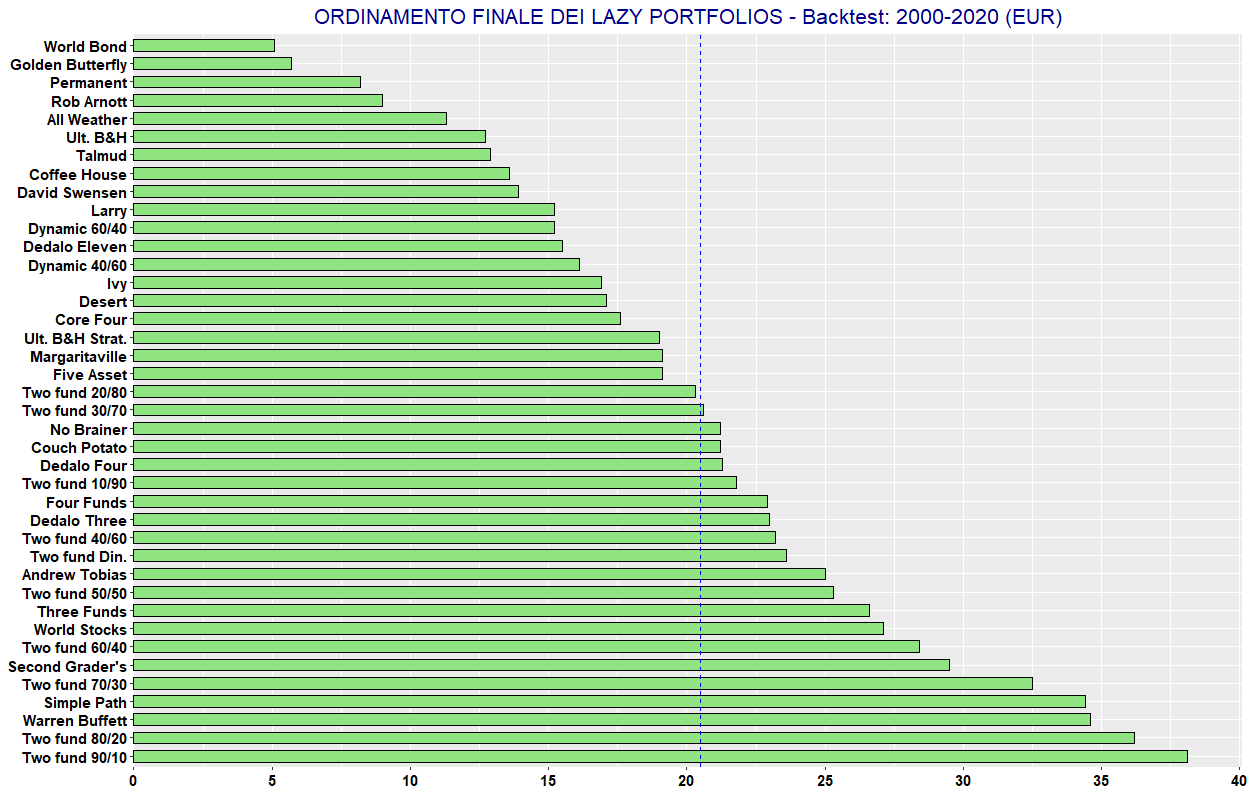
PERIODO 2010-2020
| Ordinamento dei Lazy portfolios | ||||||
|---|---|---|---|---|---|---|
| Backtest del periodo 01/01/2010 - 31/12/2020 | ||||||
| Lazy portfolio | USD | USD→EUR | EUR | |||
| Media ponderata | Rango | Media ponderata | Rango | Media ponderata | Rango | |
| All Weather | 16.7 | 13 | 16.9 | 14 | 16.5 | 6.5 |
| Andrew Tobias | 27.2 | 36.5 | 27.6 | 35 | 20.2 | 21.5 |
| Coffee House | 22.9 | 29 | 24.7 | 31 | 16.5 | 6.5 |
| Core Four | 24.0 | 31.5 | 23.4 | 26 | 19.6 | 17 |
| Couch Potato | 13.7 | 3.5 | 12.4 | 4 | 27.9 | 37 |
| David Swensen Lazy Portfolio | 22.8 | 28 | 24.6 | 30 | 20.2 | 21.5 |
| Dedalo Eleven | 22.7 | 27 | 24.9 | 32 | 12.3 | 3 |
| Dedalo Four | 19.4 | 18.5 | 18.8 | 18 | 12.1 | 2 |
| Dedalo Three | 19.4 | 18.5 | 18.2 | 16 | 18.5 | 14 |
| Desert | 15.9 | 10 | 15.5 | 10 | 25.6 | 34.5 |
| Dynamic 40/60 Income | 24.0 | 31.5 | 26.3 | 33 | 22.2 | 28 |
| Dynamic 60/40 Income | 24.2 | 33 | 27.7 | 36 | 21.3 | 23 |
| Five Asset | 31.2 | 39 | 32.4 | 39 | 28.1 | 38 |
| Four Funds Bogleheads | 21.9 | 23 | 22.0 | 25 | 17.7 | 11.5 |
| Golden Butterfly | 16.8 | 14 | 12.0 | 2 | 15.7 | 5 |
| Ivy | 36.0 | 40 | 36.4 | 40 | 30.1 | 39 |
| Larry | 24.9 | 34 | 23.8 | 27 | 22.6 | 30 |
| Margaritaville | 23.6 | 30 | 23.9 | 28 | 17.3 | 10 |
| No Brainer | 27.2 | 36.5 | 28.6 | 38 | 17.2 | 9 |
| Permanent | 17.1 | 16 | 17.3 | 15 | 19.2 | 16 |
| Rob Arnott | 20.8 | 21 | 21.9 | 24 | 15.2 | 4 |
| Second Grader's Starter | 22.6 | 26 | 21.6 | 22.5 | 18.3 | 13 |
| Simple Path to Wealth | 14.9 | 5 | 13.3 | 6 | 24.6 | 33 |
| Talmud | 20.7 | 20 | 19.0 | 19 | 20.0 | 19 |
| Three Funds Bogleheads | 22.4 | 25 | 21.6 | 22.5 | 17.0 | 8 |
| Two funds 10/90 | 18.2 | 17 | 19.9 | 20 | 22.1 | 27 |
| Two funds 20/80 | 16.9 | 15 | 18.3 | 17 | 21.5 | 24.5 |
| Two funds 30/70 | 15.3 | 6.5 | 15.7 | 12 | 22.4 | 29 |
| Two funds 40/60 | 15.4 | 8.5 | 13.7 | 7 | 21.5 | 24.5 |
| Two funds 50/50 | 13.4 | 2 | 11.4 | 1 | 20.1 | 20 |
| Two funds 60/40 | 13.3 | 1 | 12.2 | 3 | 21.8 | 26 |
| Two funds 70/30 | 13.7 | 3.5 | 12.6 | 5 | 23.1 | 31 |
| Two funds 80/20 | 15.3 | 6.5 | 14.1 | 9 | 25.6 | 34.5 |
| Two funds 90/10 | 16.5 | 12 | 15.6 | 11 | 25.8 | 36 |
| Two funds Dinamico | 15.4 | 8.5 | 14.0 | 8 | 23.4 | 32 |
| Ultimate Buy & Hold | 27.8 | 38 | 27.1 | 34 | 17.7 | 11.5 |
| Ultimate Buy and Hold Strategy | 22.3 | 24 | 24.3 | 29 | 19.9 | 18 |
| Warren Buffett | 16.3 | 11 | 16.8 | 13 | 33.9 | 40 |
| World Bond | 26.1 | 35 | 28.3 | 37 | 6.7 | 1 |
| World Stocks | 21.1 | 22 | 21.1 | 21 | 18.6 | 15 |
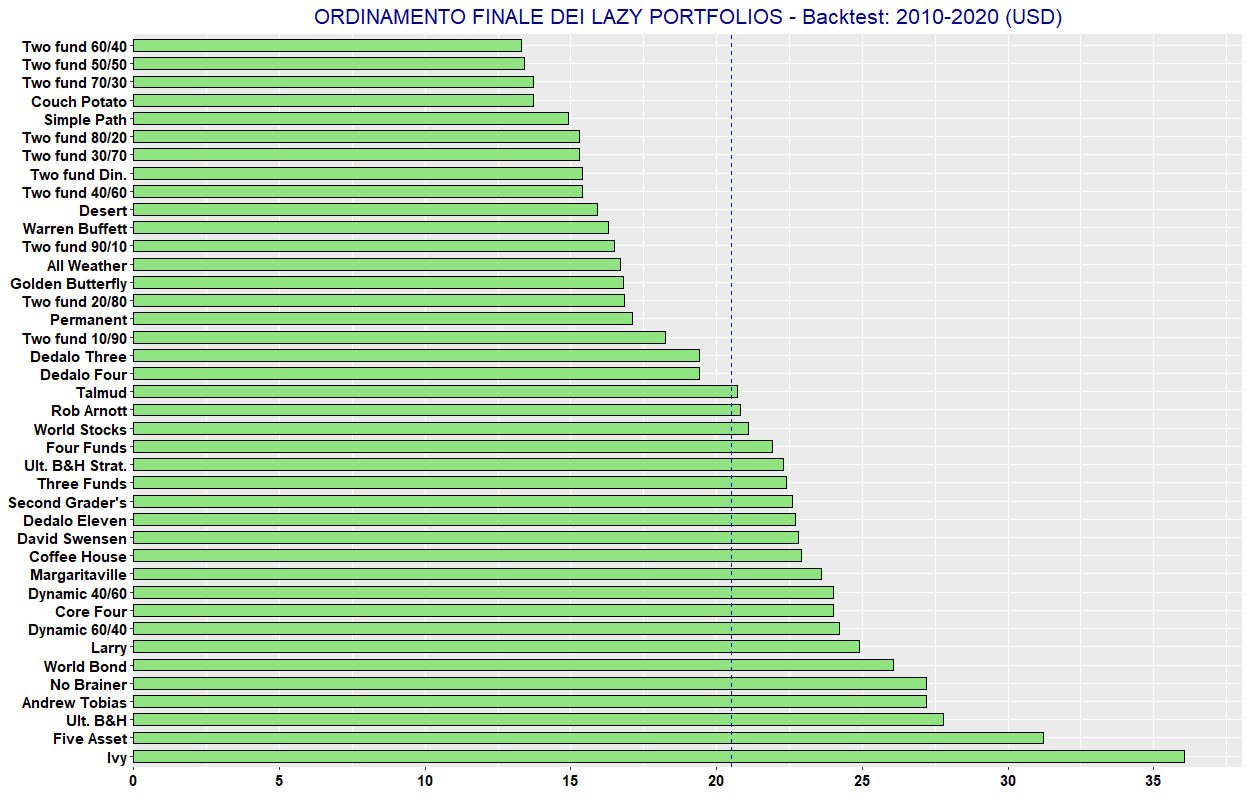

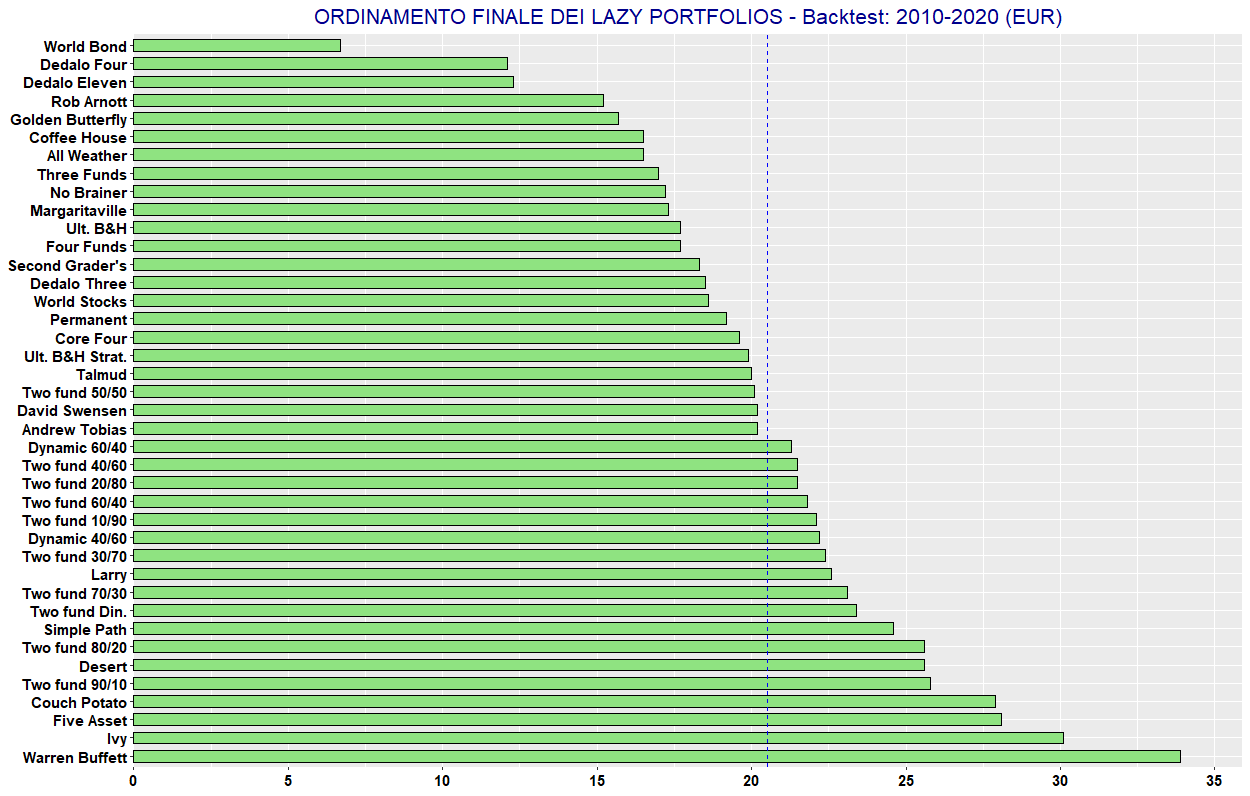
La mole di informazioni visualizzate è imponente, ma rappresenta soltanto la sintesi di un volume di dati grande almeno dieci volte tanto: in base a ogni modello di ottimizzazione, le misure statistiche calcolate per ogni Lazy portfolio saranno pubblicate nei capitoli 13.3.1-13.3.31, dove ciascuno di essi verrà analizzato in dettaglio.
Nelle tabelle, sono stati contrassegnati in blu i 10 migliori Lazy portfolios per durata e valuta. In rosso, invece, sono stati evidenziati i 10 peggiori.
I backtest possono essere divisi in 2 gruppi:
- Primo gruppo: include le analisi dei portafogli in valuta USD e USD→EUR.
- Secondo gruppo: include i soldi portafogli in valuta EUR.
Il confronto diretto tra questi due aggregati non sarebbe molto significativo: seppure ogni Lazy portfolio condivida la stessa filosofia di investimento indipendentemente dalla valuta, quelli in EUR nascono con strumenti finanziari diversi, focalizzati sull’area euro e/o sull’Europa piuttosto che sugli Stati Uniti.
Nonostante l’alta correlazione che li caratterizza, le performance dei mercati azionari e obbligazionari americani ed europei sono spesso differenti tra loro.
Inoltre, per quanto sia stato fatto ogni sforzo di omogeneizzazione, in certi casi le categorie di investimento replicate dagli ETF non sono le stesse.
Tutti questi motivi portano talvolta a risultati diversi: lo stesso Lazy portfolio potrebbe aver ottenuto delle ottime performance in USD o in USD→EUR e delle pessime performance in EUR (e viceversa).
Da qui in avanti, quindi, eviteremo di fare confronti diretti tra i due gruppi di portafogli (di nuovo, da una parte quelli in USD e USD→EUR e dall’altra quelli in EUR).
Il confronto tra USD e USD→EUR, invece, è particolarmente interessante perché ci permette di quantificare l’impatto del rischio di cambio per un investitore basato in area euro su un portafoglio in USD, che nasce per soddisfare le esigenze di un investitore statunitense.
A questo proposito, prendiamo il periodo di analisi più lungo e confrontiamo la media di ogni misura statistica calcolata su ognuno dei 40 Lazy portfolios con gli 11 diversi modelli di ottimizzazione (media di 40 x 11 = 440 backtest).
Ecco i risultati:
| MISURE STATISTICHE MEDIE | |||
|---|---|---|---|
| Analisi del periodo 1985-2020: 40 Lazy portfolios x 11 modelli di ottimizzazione | |||
| Misura statistica | USD | USD→EUR | Variazione |
| Return | 7.43% | 6.79% | −8.61% |
| Indice di Sharpe | 0.859 | 0.535 | −37.77% |
| Cumulative Return | 1,345.52% | 1,066.27% | −20.75% |
| Indice di Sortino | 1.248 | 0.830 | −33.51% |
| Indice di Hurst | 0.348 | 0.320 | −8.13% |
| Standard Deviation | 9.21% | 13.20% | 43.32% |
| Worst Drawdown | 30.15% | 42.97% | 42.52% |
| Average Drawdown | 1.17% | 2.52% | 115.38% |
| Average Length | 19.60 | 40.95 | 108.94% |
| Average Recovery | 10.69 | 21.72 | 103.07% |
| VaR (daily) | −0.81% | −1.26% | 55.56% |
| CVaR (daily) | −1.16% | −2.15% | 85.34% |
È importante ribadire che i risultati dei backtest in USD→EUR derivano dalla conversione in euro del valore giornaliero dei NAV dei portafogli pigri utilizzati, sulla base del tasso di cambio USD/EUR del periodo considerato.
Tutte le variazioni hanno un impatto negativo per l’investitore dell’area euro:
- Le misure di rendimento hanno subito una diminuzione, talvolta molto marcata (facciamo rientrare in questa categoria anche gli indici di Sharpe e di Sortino).
- Le misure di rischio sono aumentate sensibilmente.
L’utilizzo di strumenti finanziari non hedgiati in valuta diversa da quella del paese dove vive l’investitore aggiunge il rischio di cambio a quello di mercato: in questo caso, è evidente come la maggiore rischiosità abbia avuto un impatto negativo.
Non sempre è così: in altri frangenti, o in determinati sottoperiodi di questo lungo arco di tempo analizzato, le cose potrebbero essere andate in modo diverso; l’effetto potrebbe essere stato positivo.
Indipendentemente dalla lunghezza dell’investimento, il rischio di cambio è sempre presente: ignorarlo o ritenere che nel lungo periodo venga neutralizzato da una ipotetica regressione dei tassi di cambio verso la media è molto pericoloso.
Vediamo il secondo dei periodi analizzati: dall’01/01/2000 al 31/12/2020.
La tabella dei risultati è la seguente:
| MISURE STATISTICHE MEDIE | |||
|---|---|---|---|
| Analisi del periodo 2000-2020: 40 Lazy portfolios x 11 modelli di ottimizzazione | |||
| Misura statistica | USD | USD→EUR | Variazione |
| Return | 5.56% | 4.50% | −19.06% |
| Indice di Sharpe | 0.649 | 0.364 | −43.86% |
| Cumulative Return | 214.60% | 153.81% | −28.33% |
| Indice di Sortino | 0.962 | 0.594 | −38.32% |
| Indice di Hurst | 0.355 | 0.322 | −9.11% |
| Standard Deviation | 9.72% | 12.84% | 32.10% |
| Worst Drawdown | 30.64% | 39.88% | 30.16% |
| Average Drawdown | 1.16% | 2.22% | 91.38% |
| Average Length | 20.53 | 48.05 | 134.05% |
| Average Recovery | 11.66 | 25.87 | 121.87% |
| VaR (daily) | −0.84% | −1.25% | 48.81% |
| CVaR (daily) | −1.21% | −2.07% | 71.07% |
Ancora una volta, il rischio di cambio ha avuto un impatto negativo su tutti i fronti.
Le misure di rendimento hanno subito un calo rilevante, mentre quelle di rischio hanno fatto un bel balzo verso l’alto.
Non ci resta che dare un’occhiata al terzo dei periodi analizzati, il più corto di tutti: dall’01/01/2010 al 31/12/2020.
Questi sono stati i risultati ottenuti:
| MISURE STATISTICHE MEDIE | |||
|---|---|---|---|
| Analisi del periodo 2010-2020: 40 Lazy portfolios x 11 modelli di ottimizzazione | |||
| Misura statistica | USD | USD→EUR | Variazione |
| Return | 6.73% | 7.89% | 17.24% |
| Indice di Sharpe | 0.897 | 0.710 | −20.89% |
| Cumulative Return | 100.49% | 122.66% | 22.06% |
| Indice di Sortino | 1.262 | 1.048 | −17.00% |
| Indice di Hurst | 0.390 | 0.359 | −7.88% |
| Standard Deviation | 8.44% | 11.17% | 32.35% |
| Worst Drawdown | 18.46% | 20.59% | 11.54% |
| Average Drawdown | 0.95% | 1.74% | 83.16% |
| Average Length | 15.41 | 25.92 | 68.18% |
| Average Recovery | 8.40 | 13.91 | 65.71% |
| VaR (daily) | −0.83% | −1.07% | 28.92% |
| CVaR (daily) | −1.64% | −2.09% | 27.44% |
Finalmente qualche notizia positiva: il rendimento è aumentato grazie al contributo favorevole del tasso di cambio.
A differenza di prima, però, quando le misure di rischio erano andate in senso contrario al rendimento, adesso si muovono nella stessa direzione: sono aumentate anch’esse, mitigando quindi il beneficio procurato dal maggior rendimento. Quest’ultimo, essendo cresciuto in maniera inferiore alla deviazione standard, ha determinato una diminuzione degli indici di Sharpe e di Sortino.
Stavolta, il rischio di cambio non avrebbe arrecato soltanto danni: anzi, l’investitore dell’area euro sarebbe stato ben felice di vedere una crescita del rendimento del proprio portafoglio superiore a quella del suo omologo statunitense.
I risultati dei numerosi backtest effettuati sono la riprova di come il rischio di cambio sia una minaccia seria, che un investitore dovrebbe fronteggiare.
I backtest evidenziano anche alcuni effetti collaterali del rischio di cambio, generalmente ignorati: se, per puro caso, il tasso di cambio fosse lo stesso all’inizio e alla fine dell’investimento (rendimento finale identico dei portafogli in USD e in USD→EUR), si potrebbero comunque manifestare altre spiacevoli conseguenze: una maggiore volatilità dell’investimento e, in generale, una maggiore rischiosità, sottolineata anche dal più alto valore medio dei drawdown, dalla loro più lunga durata e da VaR e CVaR più alti.
Nel lungo termine, accade spesso che l’impatto del rischio di cambio, anche se penalizzante, non venga percepito correttamente dall’investitore perché il rendimento è comunque molto elevato: nell’esempio relativo al periodo che parte nel 1985, il rendimento in dollari è stato pari al 1304% e quello in euro al 1047%; si tratta di un 256% in meno in termini assoluti, un’enormità.
In termini relativi, il rendimento in euro è di quasi il 20% inferiore a quello in dollari ma, essendo comunque estremamente alto, potrebbe essere trascurato.
Nei backtest di durata inferiore, invece, la differenza in valore assoluto è stata molto più bassa, mentre quella in termini relativi più alta.
In conclusione, il tempo non neutralizza il rischio di cambio: soltanto la scelta di strumenti finanziari hedgiati, o il cui sottostante sia rappresentato da titoli nella stessa valuta di quella vigente nell’area geografica in cui risiede l’investitore, permettono di farlo.
I pesi ottimali più recenti dei Lazy portfolios possono essere consultati al seguente link (per avere accesso è necessario sottoscrivere un abbonamento PRO): Lazy portfolios modello.
12.2 Modelli di ottimizzazione

«In my opinion, no single design is apt to be optimal for everyone».
Donald Norman
Il procedimento utilizzato per stilare la classifica degli 11 modelli di ottimizzazione (9 dinamici, vincolati e non vincolati, e 2 statici) è il seguente:
- Calcolo del rendimento annualizzato e della volatilità di ogni portafoglio pigro ribilanciato annualmente in base agli 11 modelli di ottimizzazione dei pesi degli ETF.
- Per ogni modello di ottimizzazione e per ogni portafoglio pigro, calcolo del rango di ciascuna delle 2 misure statistiche (che sarà compreso tra 1 e 11).
- Per ogni modello di ottimizzazione, calcolo del valore medio dei ranghi dei 40 portafogli pigri (per ciascuna delle 2 misure statistiche).
- Calcolo della media dei ranghi di cui al punto precedente: il peso del rendimento e della volatilità (quindi delle misure di rendimento e di rischio) è pari al 50% ciascuno.
- Ordinamento crescente degli 11 ranghi ponderati. I modelli con i valori più bassi saranno quelli che hanno performato meglio (e viceversa).
Nei modelli di ottimizzazione abbiamo preferito basarci soltanto sui due classici valori del rendimento e della volatilità (deviazione standard dei rendimenti), dal momento che è proprio su queste due misure che si basa l’ottimizzazione di Markowitz.
Gli unici due modelli per cui questa scelta potrebbe essere discutibile sono il Boudt CVaR ROI, che utilizza il CVaR al posto della deviazione standard e il modello HRP che, come abbiamo visto nel capitolo 8, ha una logica di funzionamento diversa.
Dovendo però fare una sintesi, crediamo che la scelta del rendimento e della deviazione standard sia la più corretta.
Ecco le classifiche degli 11 modelli di ottimizzazione dei pesi dei Lazy portfolios (USD, USD→EUR e EUR). Le tabelle che seguono sono in ordine alfabetico mentre i grafici seguenti sono in ordine di classifica.
PERIODO 1985-2020
| ORDINAMENTO DEI MODELLI DI OTTIMIZZAZIONE | ||||||
|---|---|---|---|---|---|---|
| Backtest del periodo 01/01/1985 - 31/12/2020 | ||||||
| Modello | USD | USD→EUR | EUR | |||
| Media ponderata | Rango | Media ponderata | Rango | Media ponderata | Rango | |
| 1/N | 6.24 | 9 | 6.44 | 9 | 6.66 | 8 |
| Standard | 6.55 | 11 | 7.08 | 11 | 7.16 | 11 |
| Boudt SD ROI | 6.26 | 10 | 6.29 | 7 | 5.40 | 3 |
| Boudt SD Random | 6.16 | 8 | 6.60 | 10 | 5.86 | 6 |
| Boudt SD No-box | 5.63 | 1 | 4.62 | 1 | 4.78 | 1 |
| Boudt CVaR ROI | 5.77 | 3 | 5.68 | 4 | 6.83 | 9 |
| TCOV ROB | 5.99 | 6 | 6.03 | 5 | 5.91 | 7 |
| Naif | 5.86 | 5 | 6.10 | 6 | 5.63 | 5 |
| HRP | 5.69 | 2 | 5.60 | 3 | 5.38 | 2 |
| Boudt Random MVP | 5.80 | 4 | 5.25 | 2 | 5.43 | 4 |
| Boudt Random High. Sharpe | 6.05 | 7 | 6.32 | 8 | 6.97 | 10 |
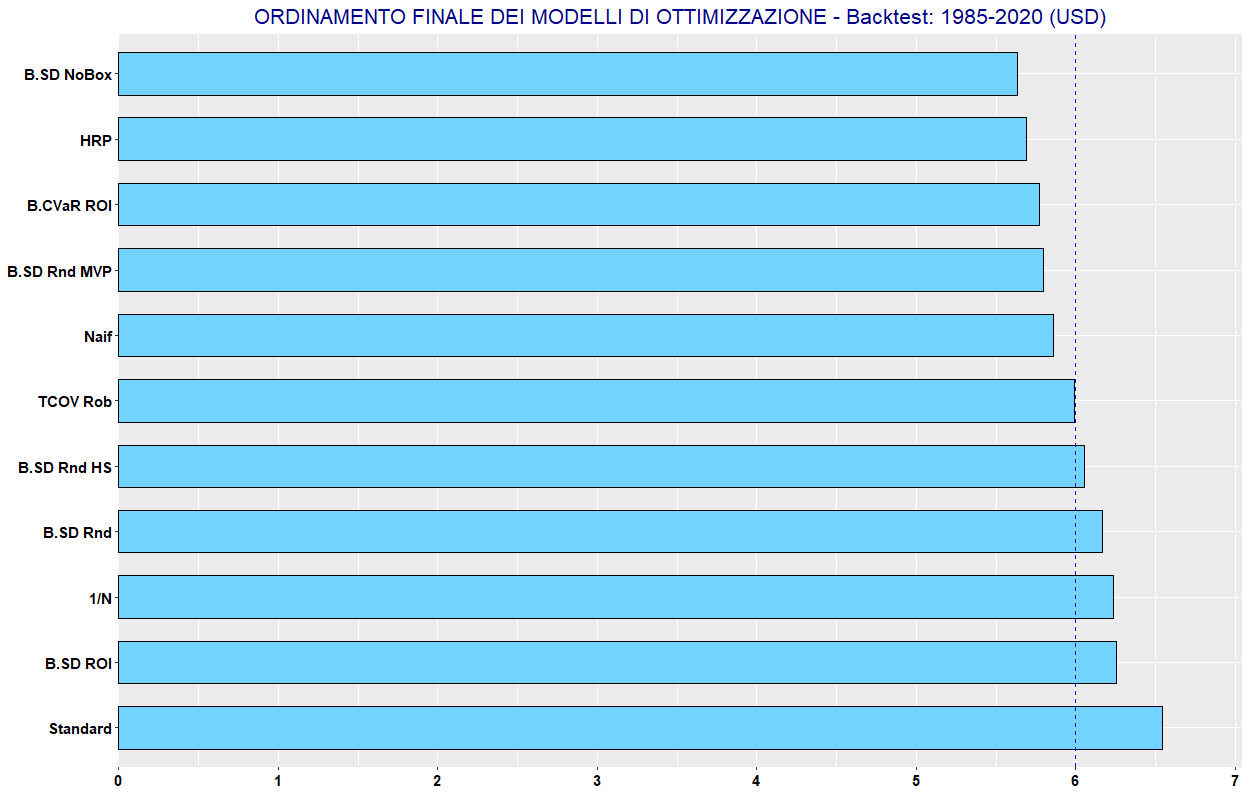
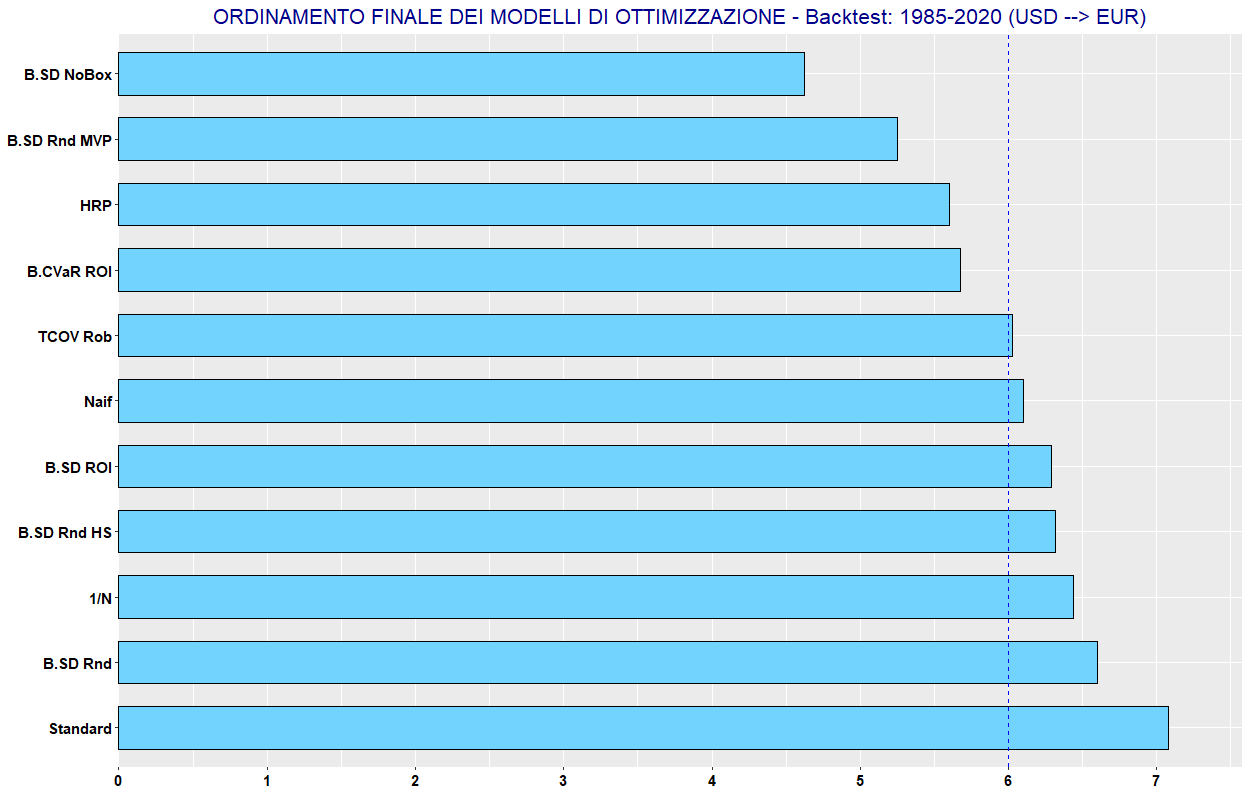
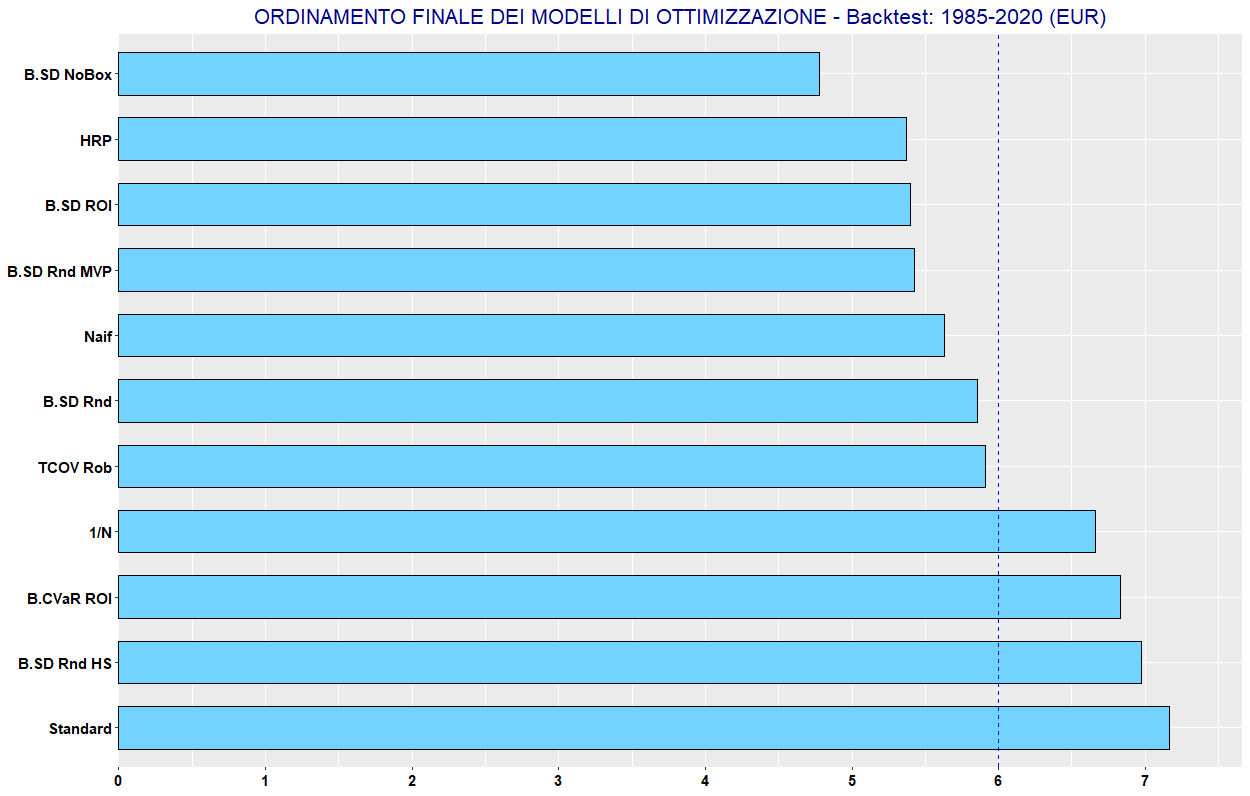
PERIODO 2000-2020
| ORDINAMENTO DEI MODELLI DI OTTIMIZZAZIONE | ||||||
|---|---|---|---|---|---|---|
| Backtest del periodo 01/01/2000 - 31/12/2020 | ||||||
| Modello | USD | USD→EUR | EUR | |||
| Media ponderata | Rango | Media ponderata | Rango | Media ponderata | Rango | |
| 1/N | 6.43 | 9 | 6.70 | 10 | 6.88 | 9 |
| Standard | 6.90 | 11 | 7.30 | 11 | 8.57 | 11 |
| Boudt SD ROI | 5.88 | 5 | 5.82 | 4 | 5.62 | 5 |
| Boudt SD Random | 6.57 | 10 | 6.61 | 9 | 6.60 | 8 |
| Boudt SD No-box | 5.11 | 1 | 4.42 | 1 | 3.26 | 1 |
| Boudt CVaR ROI | 5.79 | 3 | 6.19 | 7 | 7.06 | 10 |
| TCOV ROB | 5.83 | 4 | 6.14 | 5 | 6.14 | 7 |
| Naif | 6.09 | 8 | 6.15 | 6 | 5.94 | 6 |
| HRP | 6.08 | 7 | 4.68 | 2 | 5.25 | 2 |
| Boudt Random MVP | 5.36 | 2 | 5.68 | 3 | 5.34 | 4 |
| Boudt Random High. Sharpe | 5.95 | 6 | 6.32 | 8 | 5.34 | 3 |
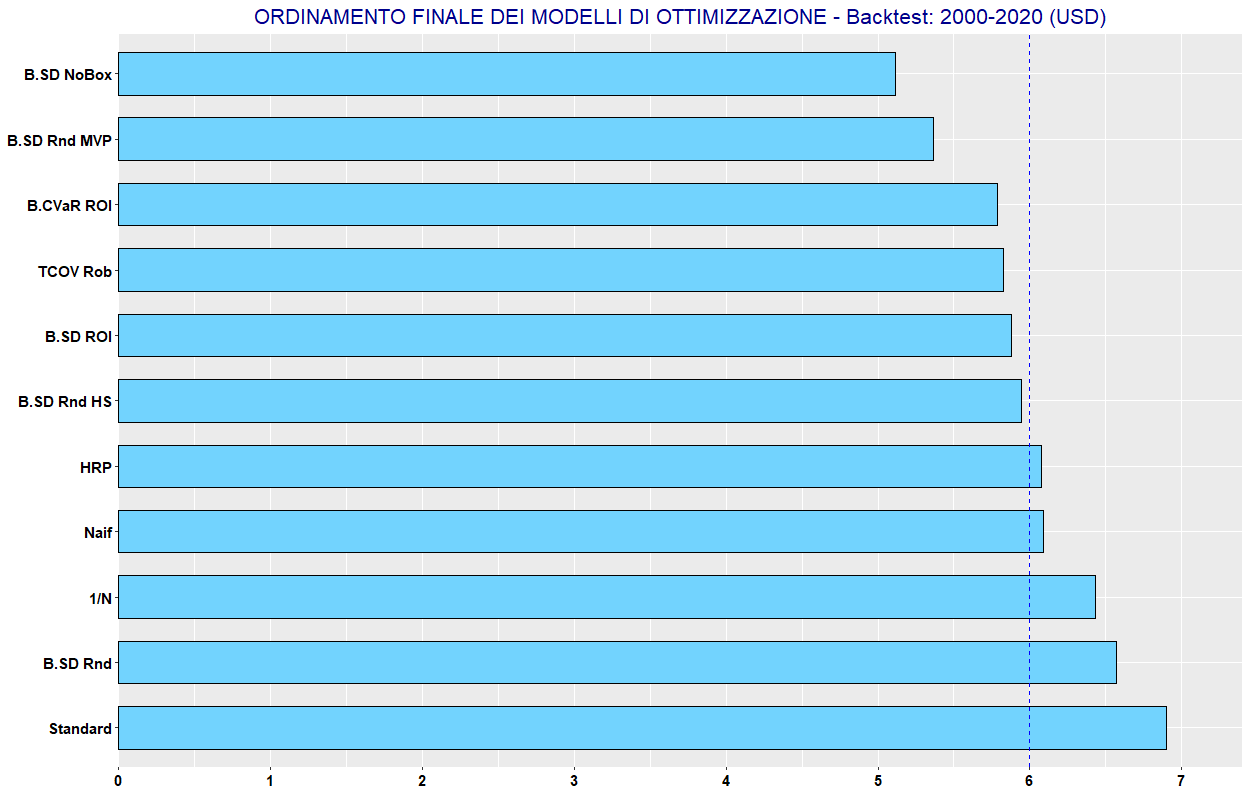
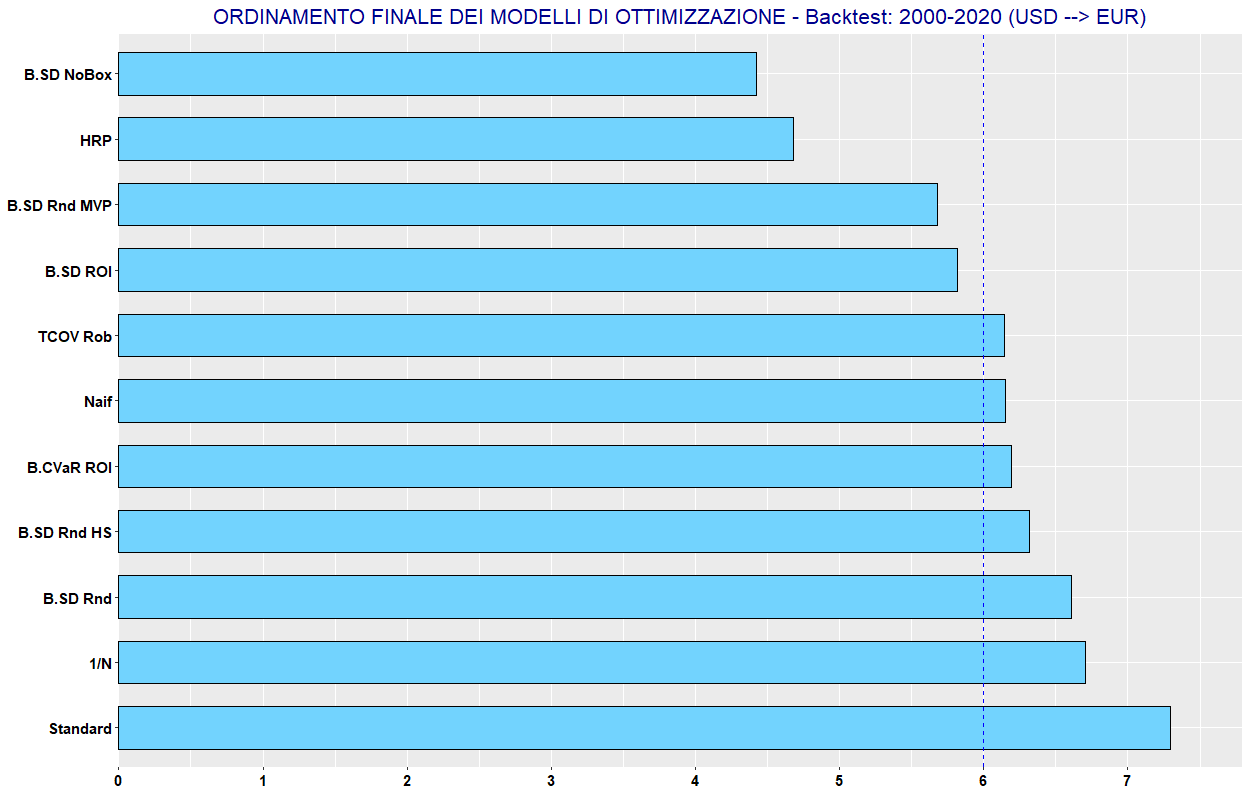
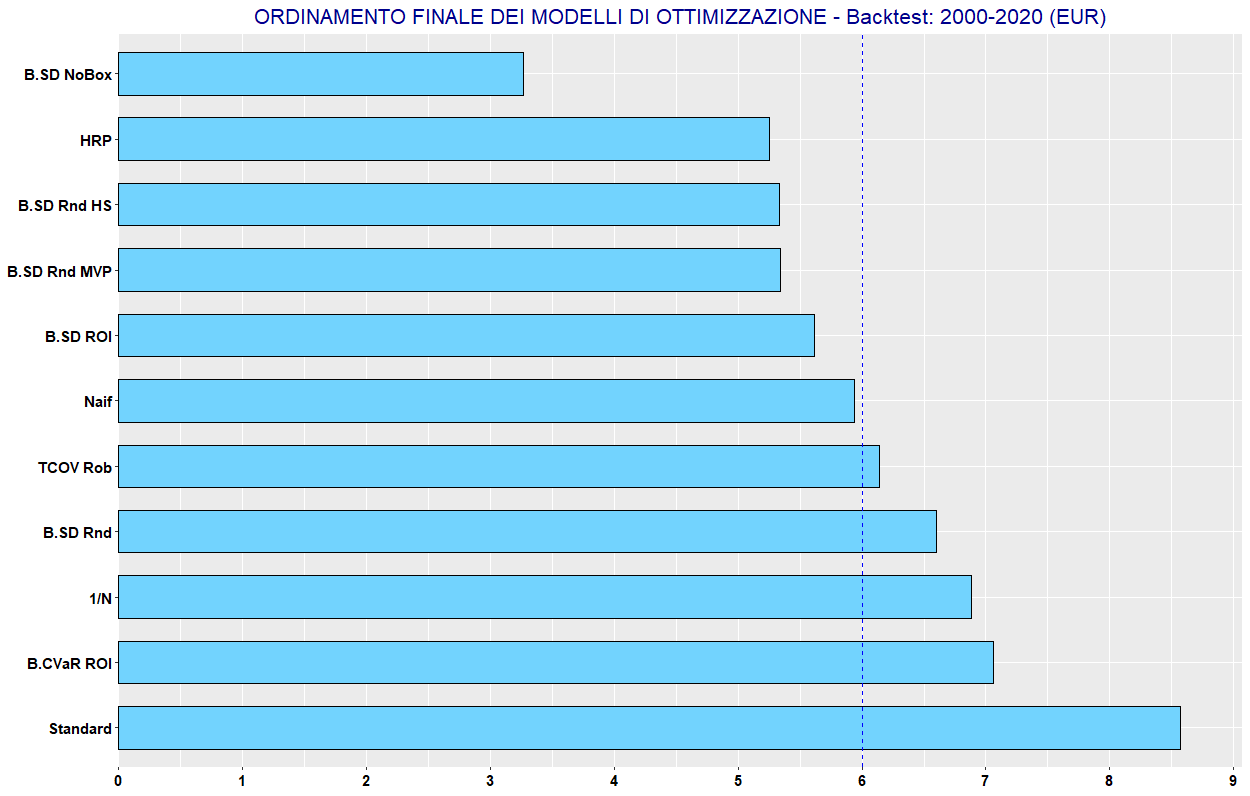
PERIODO 2010-2020
| ORDINAMENTO DEI MODELLI DI OTTIMIZZAZIONE | ||||||
|---|---|---|---|---|---|---|
| Backtest del periodo 01/01/2010 - 31/12/2020 | ||||||
| Modello | USD | USD→EUR | EUR | |||
| Media ponderata | Rango | Media ponderata | Rango | Media ponderata | Rango | |
| 1/N | 6.30 | 10 | 6.26 | 10 | 6.08 | 7 |
| Standard | 6.06 | 8 | 6.38 | 11 | 6.07 | 6 |
| Boudt SD ROI | 5.55 | 1 | 5.57 | 1 | 5.13 | 2 |
| Boudt SD Random | 5.99 | 6 | 5.92 | 4 | 5.38 | 4 |
| Boudt SD No-box | 5.77 | 4 | 5.68 | 2 | 5.89 | 5 |
| Boudt CVaR ROI | 6.03 | 7 | 5.72 | 3 | 6.96 | 10 |
| TCOV ROB | 5.97 | 5 | 6.22 | 8 | 6.09 | 8 |
| Naif | 5.59 | 2 | 6.04 | 7 | 5.32 | 3 |
| HRP | 6.24 | 9 | 6.04 | 6 | 6.21 | 9 |
| Boudt Random MVP | 5.70 | 3 | 5.95 | 5 | 4.91 | 1 |
| Boudt Random High. Sharpe | 6.80 | 11 | 6.22 | 9 | 7.97 | 11 |
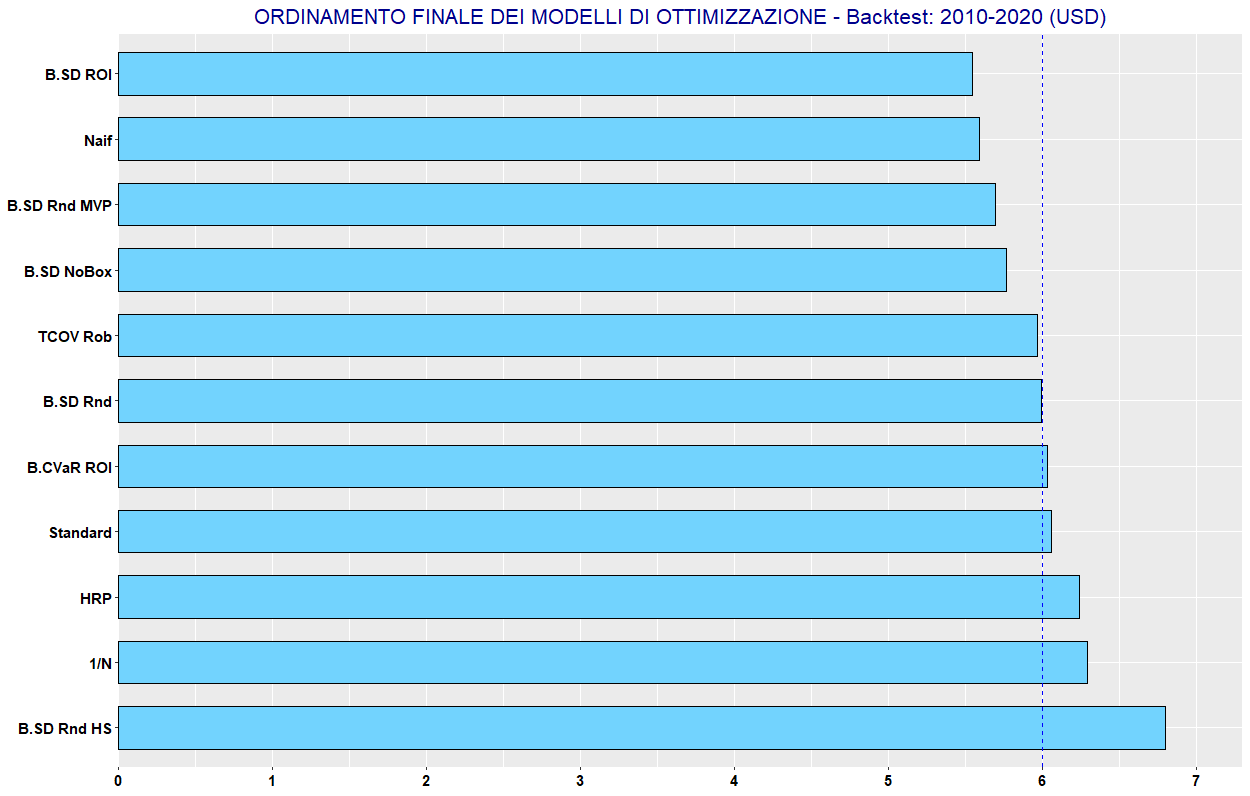
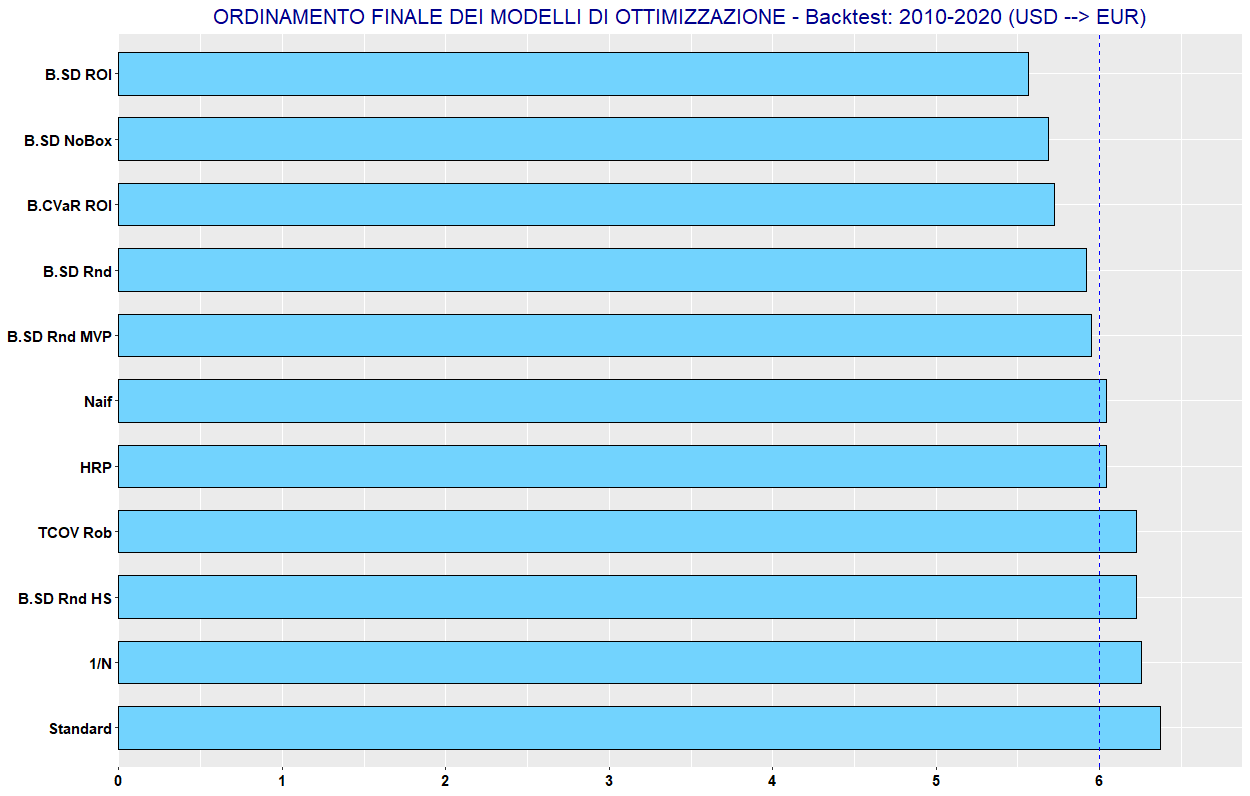
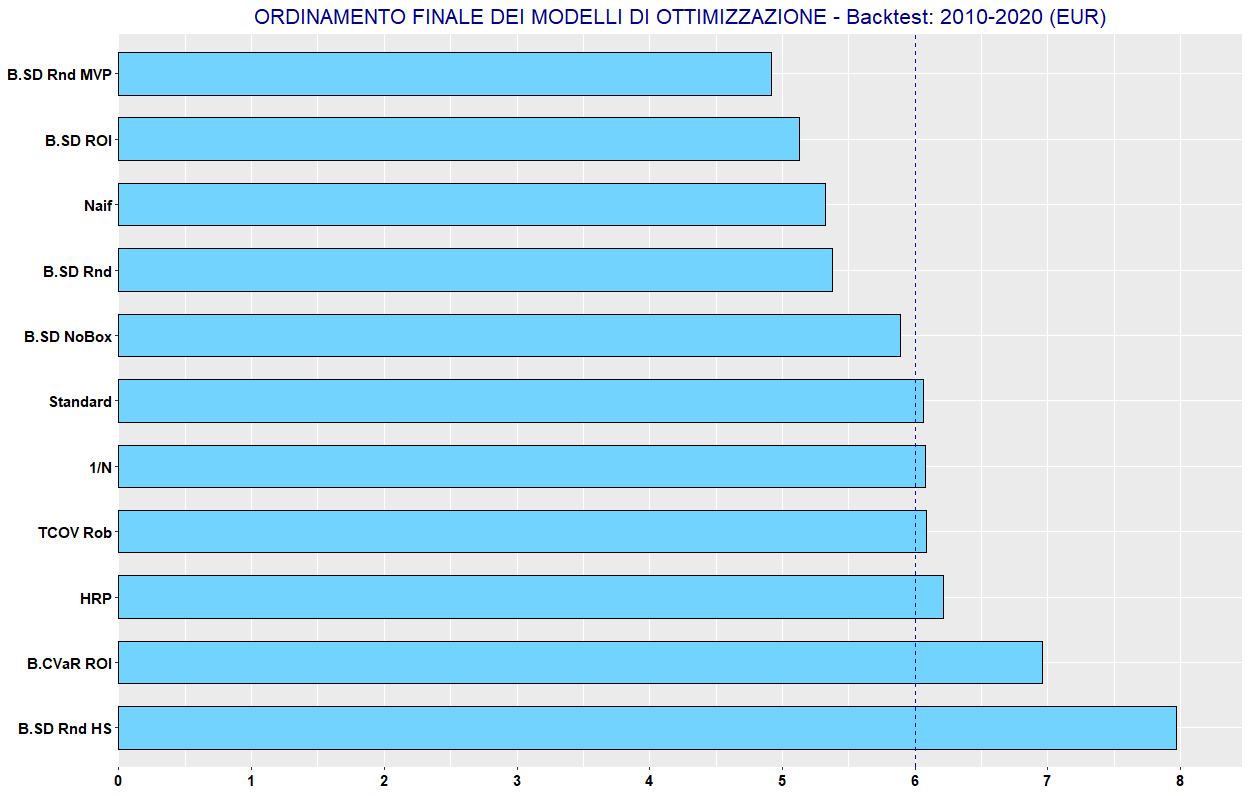
Anche sui modelli di ottimizzazione sono state visualizzate una grande quantità di informazioni che rappresentano, tuttavia, soltanto la sintesi di un volume di dati almeno dieci volte più grande: in base a ognuno di essi, le misure statistiche calcolate per ogni Lazy portfolio saranno pubblicate nei capitoli 13.3.1-13.3.31, dove ciascuno di essi verrà analizzato in dettaglio.
Nelle tabelle precedenti sono stati evidenziati in blu i 3 modelli migliori per ogni durata dei backtest e per ogni valuta dei portafogli. In rosso, invece, sono stati contrassegnati i 3 modelli peggiori.
Nel caso dei modelli di ottimizzazione, raggruppare i risultati in base alle valute (USD e USD→EUR da una parte e EUR dall’altra) non sembra essere importante come nel caso dell’ordinamento dei Lazy portfolios.
I modelli di ottimizzazione, infatti, si applicano su ogni serie storica dei rendimenti indipendentemente dalle valute: in teoria, il miglior modello dovrebbe ottimizzare al meglio qualsiasi serie storica, a prescindere dalle caratteristiche di quest’ultima. Il secondo miglior modello dovrebbe posizionarsi subito dopo e così via, fino al peggior modello di ottimizzazione.
In pratica, le cose sono un po’ più complicate.
Vediamo la tabella finale, con i risultati medi finali per valuta e quelli complessivi.
| ORDINAMENTO DEI MODELLI DI OTTIMIZZAZIONE | ||||||||
|---|---|---|---|---|---|---|---|---|
| Media di tutti i backtest per valuta | ||||||||
| Modello | USD | USD→EUR | EUR | Media complessiva | ||||
| Media ponderata | Rango | Media ponderata | Rango | Media ponderata | Rango | Media ponderata | Rango | |
| 1/N | 6.32 | 10 | 6.47 | 10 | 6.54 | 8 | 6.44 | 10 |
| Standard | 6.50 | 11 | 6.92 | 11 | 7.27 | 11 | 6.90 | 11 |
| Boudt SD ROI | 5.89 | 5 | 5.89 | 5 | 5.38 | 3 | 5.72 | 4 |
| Boudt SD Random | 6.24 | 8 | 6.38 | 9 | 5.94 | 6 | 6.19 | 7 |
| Boudt SD No-box | 5.50 | 1 | 4.91 | 1 | 4.64 | 1 | 5.02 | 1 |
| Boudt CVaR ROI | 5.86 | 4 | 5.86 | 4 | 6.95 | 10 | 6.23 | 8 |
| TCOV ROB | 5.93 | 6 | 6.13 | 7 | 6.04 | 7 | 6.04 | 6 |
| Naif | 5.85 | 3 | 6.10 | 6 | 5.63 | 5 | 5.86 | 5 |
| HRP | 6.00 | 7 | 5.44 | 2 | 5.61 | 4 | 5.68 | 3 |
| Boudt Random MVP | 5.62 | 2 | 5.62 | 3 | 5.23 | 2 | 5.49 | 2 |
| Boudt Random High. Sharpe | 6.27 | 9 | 6.29 | 8 | 6.76 | 9 | 6.44 | 9 |
Questo è il grafico della media complessiva per valuta, che permette di apprezzare meglio l’entità delle distanze tra le varie posizioni in classifica:
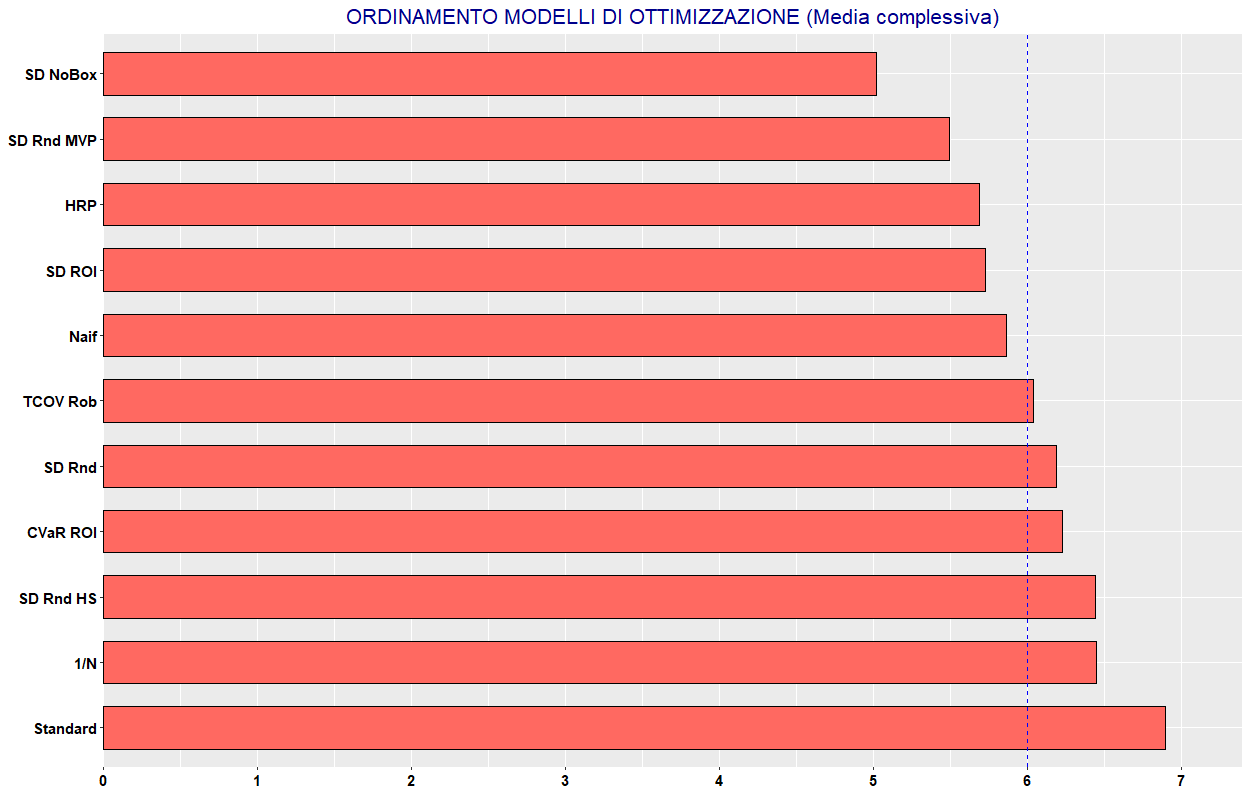
Prima di analizzare i risultati è opportuno suddividere i modelli di ottimizzazione nel modo seguente:
- Modelli dinamici: sono quelli per cui l’algoritmo di ottimizzazione è libero di scegliere i pesi appropriati in funzione delle serie storiche dei rendimenti degli ETF di ciascun Lazy portfolio.
- Modelli statici: non necessitano di una vera e propria ottimizzazione ma di un semplice ribilanciamento dei pesi alle percentuali stabilite inizialmente. I modelli statici utilizzati nelle nostre analisi sono due: standard e 1/N.
Nel primo, il ribilanciamento dei Lazy portfolios si effettua riportando i pesi a quelli tipici di ciascun portafoglio pigro; nel secondo, la strategia utilizzata è quella dell’equidistribuzione del capitale tra tutti gli ETF che compongono il portafoglio: ciascun ETF ha un peso pari a 1/N.
I modelli dinamici hanno il vantaggio di essere molto più flessibili, adattandosi meglio ai vari contesti di mercato, fedelmente replicati dalle serie storiche dei rendimenti degli ETF.
Oltre alla semplicità, i modelli statici hanno invece il vantaggio di mantenere le stesse proporzioni tra i pesi degli ETF nel tempo, rispecchiando meglio la propensione al rischio dell’investitore.
I modelli dinamici si distinguono a loro volta in:
- Modelli non vincolati: l’algoritmo di ottimizzazione è libero di scegliere i pesi appropriati. Con l’eccezione del divieto di vendite allo scoperto (operazioni short o short selling), non c’è alcun vincolo da rispettare: nessun peso minimo o massimo. Tuttavia, deve essere impiegata la totalità del capitale disponibile (non viene cioè prevista la possibilità di lasciare inutilizzata – liquida – alcuna percentuale del capitale.)
- Modelli vincolati: oltre al divieto di vendita allo scoperto e/o di mantenere una parte di capitale inutilizzato, devono rispettare alcuni vincoli che impongono dei limiti minimi e massimi al peso di ciascun ETF.
Nella nostra analisi, i pesi assegnati dall’algoritmo di ottimizzazione non potranno allontanarsi più del ± 5% dai pesi standard di ciascun portafoglio pigro, in modo da non modificare troppo la rischiosità del portafoglio nel tempo.
Ricordiamo infine che nella nostra analisi i ribilanciamenti sia dei modelli statici che di quelli dinamici avvengono annualmente.
Sempre della lunghezza di un anno è, infine, la durata delle serie storiche dei rendimenti utilizzate dagli algoritmi di ottimizzazione di tutti i modelli dinamici (vincolati e non).
Possiamo a questo punto analizzare i risultati ottenuti:
- I 3 modelli di ottimizzazione migliori sono tutti dinamici non vincolati.
È un esito che ci aspettavamo di conseguire: i vincoli restringono inesorabilmente il numero dei portafogli ammissibili e, se l’ottimizzazione non sortisse alcun effetto positivo sui risultati, scegliere un portafoglio ammissibile vincolato o non vincolato dovrebbe essere indifferente.
I backtest hanno confermato le nostre aspettative.
Vediamo questa differenza graficamente:
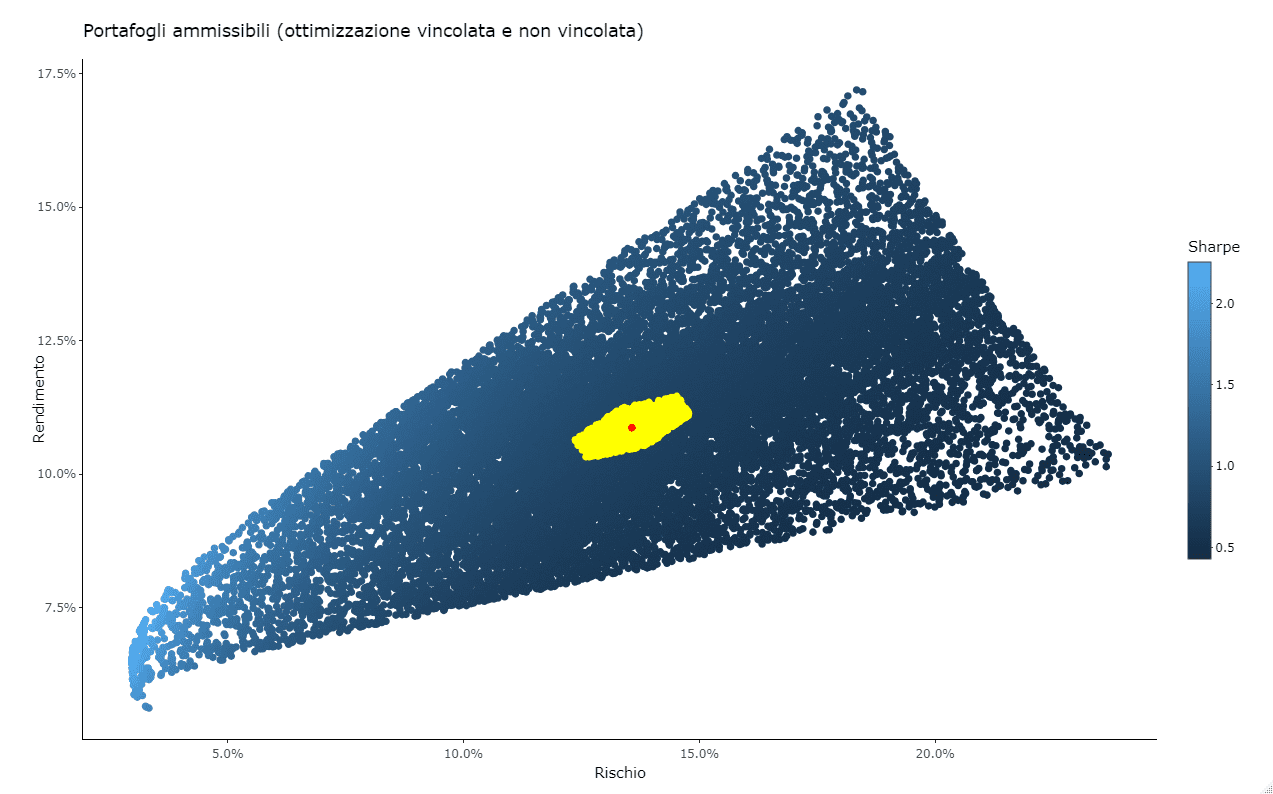
L’insieme dei punti blu comprende tutti i portafogli ammissibili di un’ipotetica ottimizzazione non vincolata di un portafoglio costituito da 3 ETF. L’asse delle X misura il Rischio, quello delle Y il Rendimento.
I punti che si trovano più in alto per ogni livello di rischio (o più a sinistra per ogni livello di rendimento) sono quelli che compongono la famosa frontiera efficiente: se fossimo sicuri che le stime del rendimento e della volatilità attesa fossero esatte, la scelta finale dovrebbe senz’altro ricadere su un portafoglio situato sulla frontiera efficiente.
L’area gialla comprende invece i soli portafogli ammissibili di un’ottimizzazione vincolata: come si vede, sono una piccola parte del totale. Tra questi, il punto rosso rappresenta il portafoglio con i pesi standard.
- Possiamo considerare l’area gialla come il margine di discrezionalità nella scelta dei pesi degli ETF che lasciamo gestire all’algoritmo. In altre parole, non ci vogliamo limitare a selezionare il punto rosso (ribilanciamento classico che riporta i pesi degli ETF a quelli standard), ma non vogliamo neppure stravolgere il rapporto rischio/rendimento del portafoglio: il ± 5% di oscillazione dei pesi che ci siamo concessi ha trasformato la regione dei portafogli ammissibili da un punto (un solo portafoglio) a un’area (una molteplicità di portafogli).
- I 2 modelli di ottimizzazione peggiori sono proprio i due modelli statici.
In particolare, il modello standard, che prevede il semplice ribilanciamento periodico dei pesi, si colloca sempre in ultima posizione, anche al di sotto del modello 1/N.
Si tratta di un’informazione molto importante: ci dice che tutti i modelli di ottimizzazione dinamici, vincolati e non vincolati, riescono a fare meglio del ribilanciamento dei pesi ai livelli arbitrariamente scelti all’inizio dell’investimento. Anche questo è un risultato che ci aspettavamo di ottenere: come si vede dal grafico precedente, è molto improbabile che i portafogli standard o equipesati corrispondano a quello selezionato dall’algoritmo tra tutti i portafogli ammissibili (vincolati e non vincolati). - Le distanze tra il migliore e il secondo miglior modello, come pure quella tra il peggiore e il penultimo modello di ottimizzazione, sono molto maggiori di quelle esistenti tra due portafogli adiacenti nelle posizioni comprese tra la seconda e la penultima. Questo significa che l’analisi ha sancito un vincitore e uno sconfitto indiscussi, mentre tra il secondo e il nono posto la situazione è più fluida e i modelli di ottimizzazione generano dei risultati non troppo dissimili.
I pesi ottimali dei Lazy portfolios generati da ciascun modello possono essere consultati al seguente link (per avere accesso è necessario sottoscrivere un abbonamento PRO): Lazy portfolios modello.
12.3 Heatmaps dei Lazy portfolios – Modelli di ottimizzazione
«I’ve always been fascinated by maps and cartography. A map tells you where you’ve been, where you are, and where you’re going — in a sense it’s three tenses in one».
Peter Greenaway
Una heatmap è una rappresentazione grafica di una matrice di dati attraverso i colori.
Una heatmap offre una panoramica dei dati analizzati e permette di riconoscere con una certa facilità determinati pattern, se presenti.
Se affiancata dalla cluster analysis, una heatmap aiuta anche a suddividere i dati in gruppi dalle caratteristiche simili.
La cluster analysis – o analisi dei gruppi in italiano – è un metodo esplorativo che consiste nella ricerca di gruppi di unità tra loro simili: l’obiettivo è quello di riconoscere gruppi che appaiono con “naturalezza” nelle osservazioni.
I risultati della cluster analysis vengono rappresentati con i dendrogrammi, posizionati di solito sopra e sulla destra (o sinistra) di una heatmap.
Il dendrogramma è una rappresentazione grafica simile a un albero stilizzato che permette di visualizzare efficacemente la famiglia di partizioni in funzione dei livelli di distanza.
La cluster analysis e i dendrogrammi ci permetteranno di raggruppare i Lazy portfolios e i modelli di ottimizzazione in gruppi dalle caratteristiche simili.
Le heatmaps che saranno visualizzate sono costruite a partire da alcune misure statistiche dei Lazy portfolios analizzati e dei modelli di ottimizzazione utilizzati:
- Rendimento (Return)
- Volatilità (St. Dev.)
- Indice di Sharpe (Sharpe)
- Worst drawdown (Worst D.)
- CVaR (CVaR)
Al colore verde corrisponderà una misura statistica favorevole all’investitore (rendimento più alto o misura di rischio più bassa), mentre al colore rosso verrà associata una misura statistica sfavorevole.
Generalmente, i Lazy portfolios e i modelli di ottimizzazione saranno divisi in 2 o 3 gruppi.
Visualizzeremo le heatmaps delle performance dei portafogli pigri e dei modelli di ottimizzazione generate dai backtest di tutte e tre le durate analizzate (1985-2020, 2000-2020 e 2010-2020), nelle due valute USD e EUR.
Partiamo dalle heatmaps dei Lazy portfolios in USD in funzione dei vari modelli di ottimizzazione.
RENDIMENTO ANNUALIZZATO
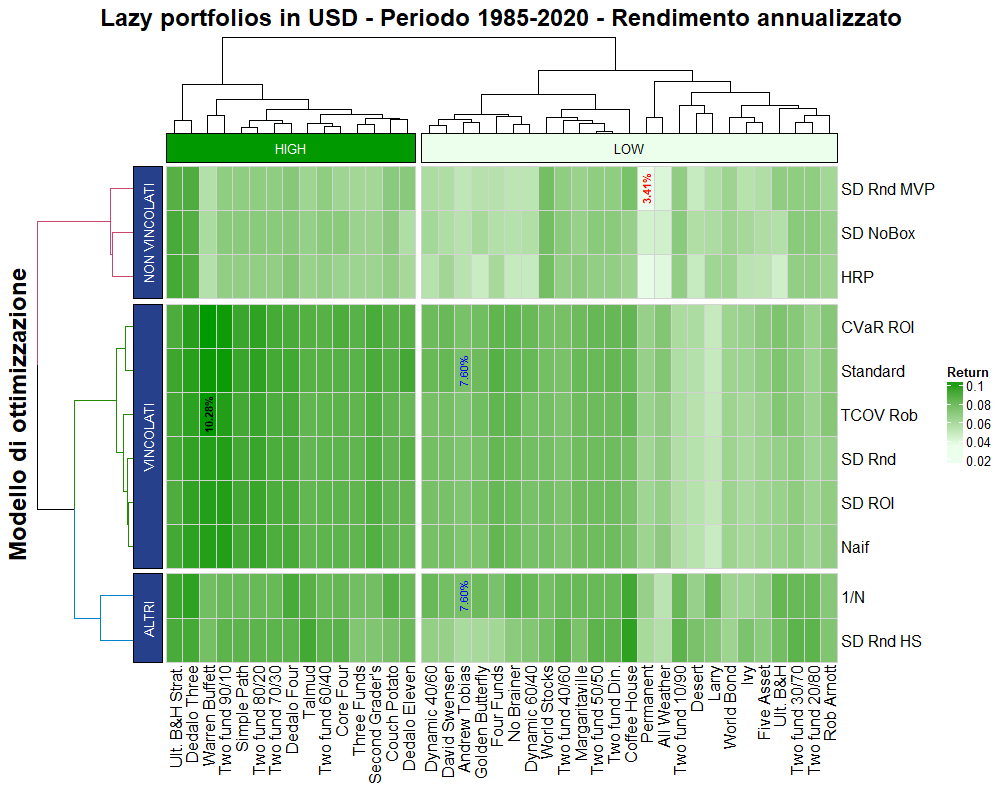
Come specificato nella legenda sulla destra, i rendimenti annualizzati più elevati sono contraddistinti da un colore verde più intenso.
Riportare tutti i rendimenti sulle heatmaps le renderebbe illeggibili: per questo motivo, su questa e sulla heatmap che misura l’indice di Sharpe potrete trovare il valore massimo in nero, il valore minimo in rosso e quello mediano in blu.
Sulle heatmaps della deviazione standard, del massimo drawdown (worst drawdown) e del CVaR – a sfondo rosso – i valori massimi saranno riportati in bianco, i valori minimi in verde e i valori mediani sempre in blu.
Abbiamo preferito visualizzare il valore mediano e non quello medio perché la mediana individua il valore che sta in mezzo alla distribuzione: essendo un indice di posizione, la mediana è meno influenzata dagli outliers della distribuzione o dell’insieme di dati analizzati.
Possiamo perciò osservare che i rendimenti annualizzati dei 40 Lazy portfolios in funzione degli 11 modelli di ottimizzazione sono compresi tra il valore minimo del 3,41% (Permanent Lazy portfolio ottimizzato col modello MVP) e il valore massimo del 10,28% (Warren Buffett Lazy portfolio ottimizzato col modello TCOV Rob).
Il valore mediano è pari al 7,60%, rilevato nell’Andrew Tobias Lazy portfolio ottimizzato col modello standard o con l’1/N.
Tornando alla heatmap, la cluster analysis ha generato 2 gruppi di Lazy portfolios e 3 gruppi di modelli di ottimizzazione.
Il dendrogramma al di sopra e sulla sinistra della heatmap permette di capire il livello di dissimilarità tra i gruppi e, all’interno di questi, degli elementi che li compongono.
I tre gruppi dei modelli di ottimizzazione sono i seguenti:
- Modelli non vincolati.
- Modelli vincolati.
- Altri: questo gruppo comprende il modello statico 1/N e il modello dinamico non vincolato che seleziona il portafoglio efficiente massimizzando l’indice di Sharpe atteso.
I due modelli appartenenti al gruppo “Altri” sembrano avere delle caratteristiche diverse dai 9 modelli rimanenti e li troveremo spesso separati da questi (in particolar modo il modello che massimizza l’indice di Sharpe atteso).
La heatmap ci permette di fare alcune osservazioni:
- I modelli vincolati e non vincolati rispecchiano due approcci molto diversi della pesatura degli ETF e la cluster analysis applicata ai rendimenti ce lo conferma.
I 2 portafogli statici dovrebbero idealmente far parte di uno o due gruppi separati. In pratica, questo non avverrà mai per il modello standard, dal momento che è quello che detta i pesi di partenza ai modelli vincolati, che dal primo non possono allontanarsi più di tanto: la logica conseguenza è che il modello standard entrerà sempre nel gruppo dei modelli vincolati.
Per il modello 1/N, invece, questo discorso vale soltanto per i portafogli che hanno pesi standard equidistribuiti (dove modello standard e 1/N sono la stessa cosa), ma non per gli altri.
Questa sua eterogeneità è il motivo per cui talvolta il modello 1/N costituisce un gruppo a sé o si trova, comunque, in un gruppo separato da quello dei modelli vincolati. - Alla base della heatmap, partendo da sinistra troviamo due portafogli pigri, contraddistinti da un verde intenso indipendentemente dal modello di ottimizzazione scelto: sono l’Ultimate Buy & Hold Strategy e il Dedalo Three.
Il più alto rendimento è dovuto essenzialmente alla loro composizione: 100% azionaria.
Esiste anche un altro portafoglio dalla composizione interamente azionaria: il World Stocks. Esso si trova, tuttavia, nel gruppo dei portafogli dai rendimenti più bassi: un gruppo, tra l’altro, molto eterogeneo. È difficile dire perché, rispetto agli altri due portafogli totalmente azionari, la sua redditività sia più bassa: si potrebbe supporre che il motivo sia una diversificazione minore, essendo il World Stocks composto da un solo ETF. Le ragioni potrebbero anche essere altre ma, almeno in questa fase della nostra analisi, non ci interessa individuarle. - La lunghezza delle linee verticali del dendrogramma superiore, relative ai Lazy portfolios e quella delle linee orizzontali del dendrogramma sul lato sinistro, relative ai modelli di ottimizzazione, è proporzionale alla dissimilarità esistente tra i gruppi stessi.
Ad esempio, le linee orizzontali della parte più in basso del dendrogramma laterale – che individua il gruppo “ALTRI” tra i vari modelli di ottimizzazione – sono molto più lunghe delle linee finali dei portafogli vincolati: questo significa che i modelli di ottimizzazione “1/N” e “SD Rnd HS”, che compongono il gruppo “ALTRI”, sono più dissimili tra loro di due qualsiasi modelli appartenenti al gruppo dei modelli vincolati.
Passiamo all’analisi dei portafogli in euro:
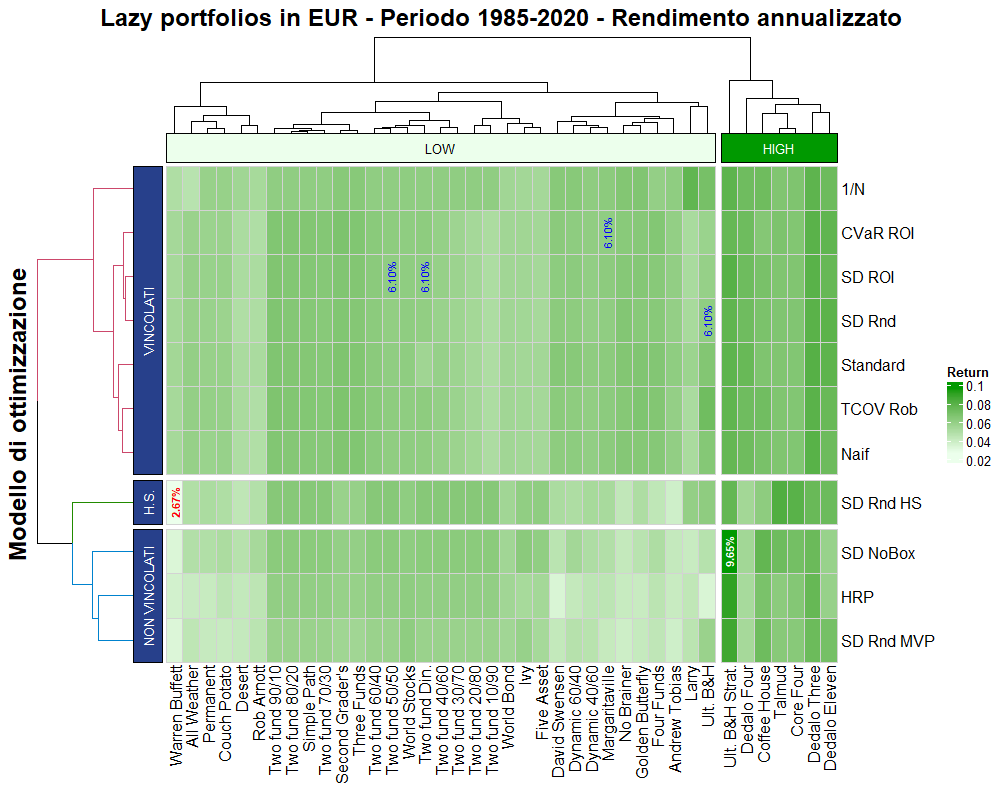
Notiamo innanzitutto che i portafogli più performanti sono situati, stavolta, sulla destra, e sono in numero minore rispetto ai portafogli in USD.
Il rendimento più alto è stato ottenuto dall’Ultimate Buy and Hold Strategy Lazy portfolio ottimizzato col modello non vincolato No-Box: 9,65% annualizzato.
Il rendimento più basso è stato invece realizzato dal Warren Buffett: un risultato apparentemente molto strano, dal momento che il Warren Buffett è un Lazy portfolio composto da 2 soli ETF e – nella sua versione standard – il peso è del 90% per l’azionario e del solo 10% per l’obbligazionario.
Il modello di ottimizzazione che ha generato il 2,67%, però, è l’Highest Sharpe: un modello non vincolato, libero quindi pesare la componente azionaria e quella obbligazionaria a piacimento. Per generare un risultato del genere, il peso medio dell’obbligazionario deve essere stato – in media – molto superiore a quello dell’azionario.
Il rendimento mediano è stato del 6,10%, ottenuto da 4 portafogli ottimizzati utilizzando 3 modelli diversi.
In generale, negli oltre 35 anni analizzati i portafogli pigri in USD hanno ottenuto dei rendimenti annualizzati superiori a quelli in EUR: lo dimostrano i valori massimi, minimi, mediani e, soprattutto, il verde più intenso diffuso su tutta la heatmap.
VOLATILITÀ
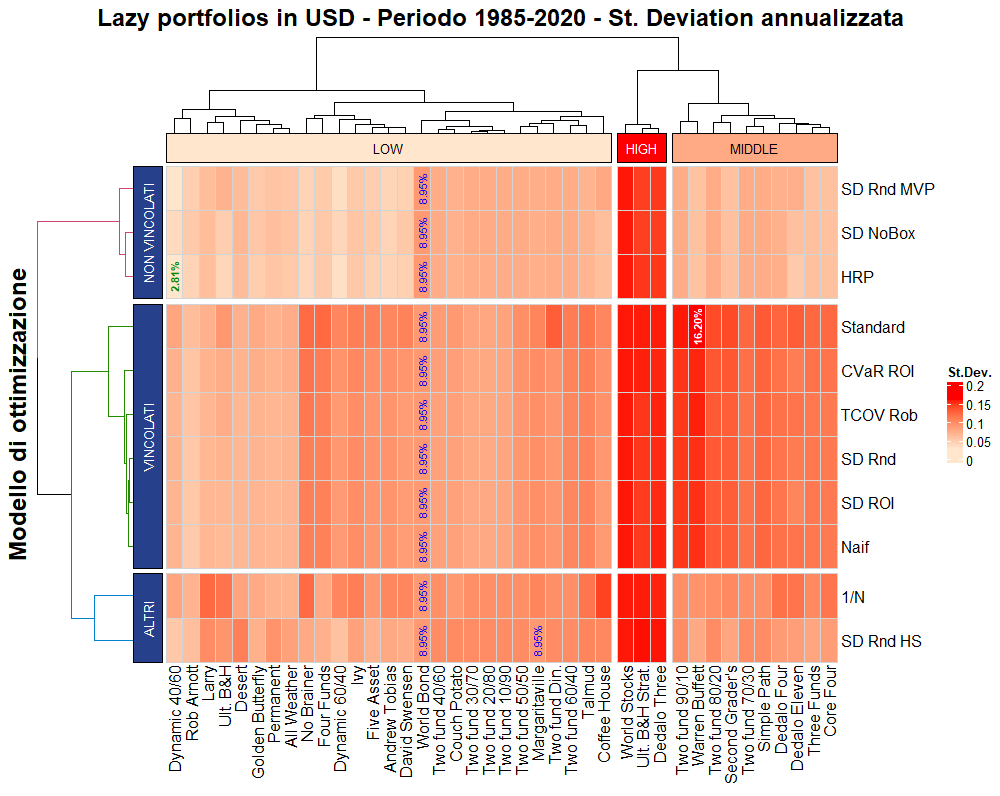
Il rosso più intenso identifica una volatilità maggiore: la volatilità è la deviazione standard annualizzata dei rendimenti di un investimento ed è una misura di rischio.
Il portafoglio più rischioso è il Warren Buffett ottimizzato col modello standard, con una volatilità del 16,20%. Pur avendo il 90% di componente azionaria, è risultato addirittura più volatile dei portafogli interamente azionari, appartenenti al gruppo “HIGH”.
Il Warren Buffett Lazy portfolio in USD – ottimizzato però con il modello TCOV Rob – aveva ottenuto anche il rendimento più alto: un’ulteriore dimostrazione, se ce ne fosse bisogno, che rischio e rendimento sono sempre direttamente proporzionali.
La volatilità più bassa è stata ottenuta dal Dynamic 40/60 Income ottimizzato col modello HRP: 2,81%.
La volatilità mediana, infine, è stata ottenuta dal World Bond – indipendentemente dal modello di ottimizzazione, dal momento che è composto da un solo ETF – e dal Margaritaville ottimizzato col modello Highest Sharpe: 8,95%.
È interessante notare come il World Bond, l’unico portafoglio totalmente obbligazionario, sia stato proprio quello che ha registrato la volatilità mediana: senz’altro, non tra le più basse. Ci saremmo aspettati il contrario, dato che il mercato obbligazionario è – per definizione – meno volatile di quello azionario o delle commodities.
Non si deve tuttavia dimenticare che le dinamiche dei mercati obbligazionari degli ultimi 35/36 anni sono state molto diverse da quelle dell’ultimo decennio e saranno sicuramente diverse da quelle del prossimo decennio: se è vero che il passato tende a ripetersi, non lo fa mai in maniera identica.
Ecco le heatmaps dei portafogli in EUR:
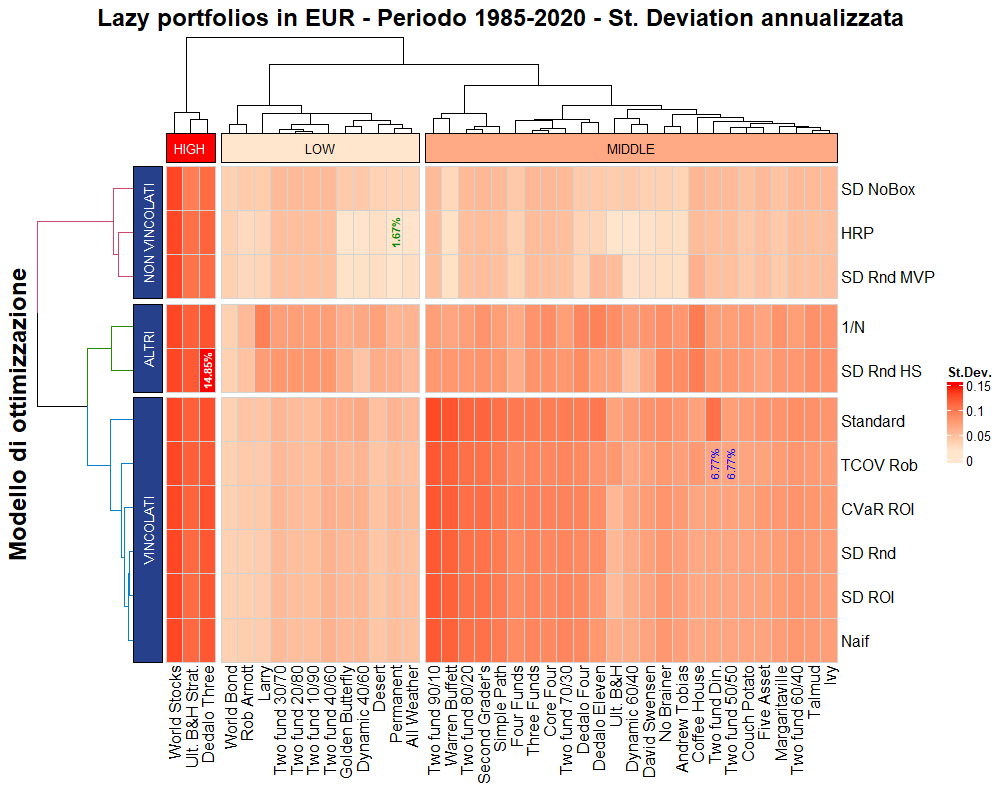
Il portafoglio pigro più volatile è stato il Dedalo Three ottimizzato col modello HS: 14,85%.
Il meno volatile è stato invece il Permanent Lazy portfolio ottimizzato col modello HRP: 1,67%.
La volatilità mediana è stata del 6,77%, ottenuta dal Two funds Dinamico e dal Two funds 50/50 ottimizzati col modello TCOV Rob.
Dividendo i Lazy portfolios in 3 gruppi, quelli contraddistinti da un rosso intenso sono stati ovviamente i portafogli col 100% di componente azionaria.
Sugli altri Lazy portfolios, i modelli non vincolati hanno invece mediamente generato delle allocazioni molto meno volatili.
INDICE DI SHARPE
L’indice di Sharpe, detto Sharpe ratio in inglese, è un coefficiente che quantifica la performance in termini di rendimento corretta per il rischio di un portafoglio.
La sua formula è molto semplice: si sottrae dal rendimento del portafoglio il tasso di rendimento a rischio zero e si divide il risultato ottenuto per la volatilità del portafoglio.
Un portafoglio con un alto indice di Sharpe è invitante per l’investitore, in quanto esprime un buon rapporto rendimento/rischio. L’indice di Sharpe viene anche definito come il rendimento ottenuto per ogni unità di rischio.
Non è comunque mai consigliabile basarsi esclusivamente sull’indice di Sharpe nella scelta di un portafoglio, in quanto il solo indice di Sharpe non permette di capirne la vera rischiosità: un valore alto dell’indice potrebbe essere originato sia dalla combinazione di valori elevati di rendimento e volatilità che da una combinazione di valori bassi.
Ecco la heatmap:
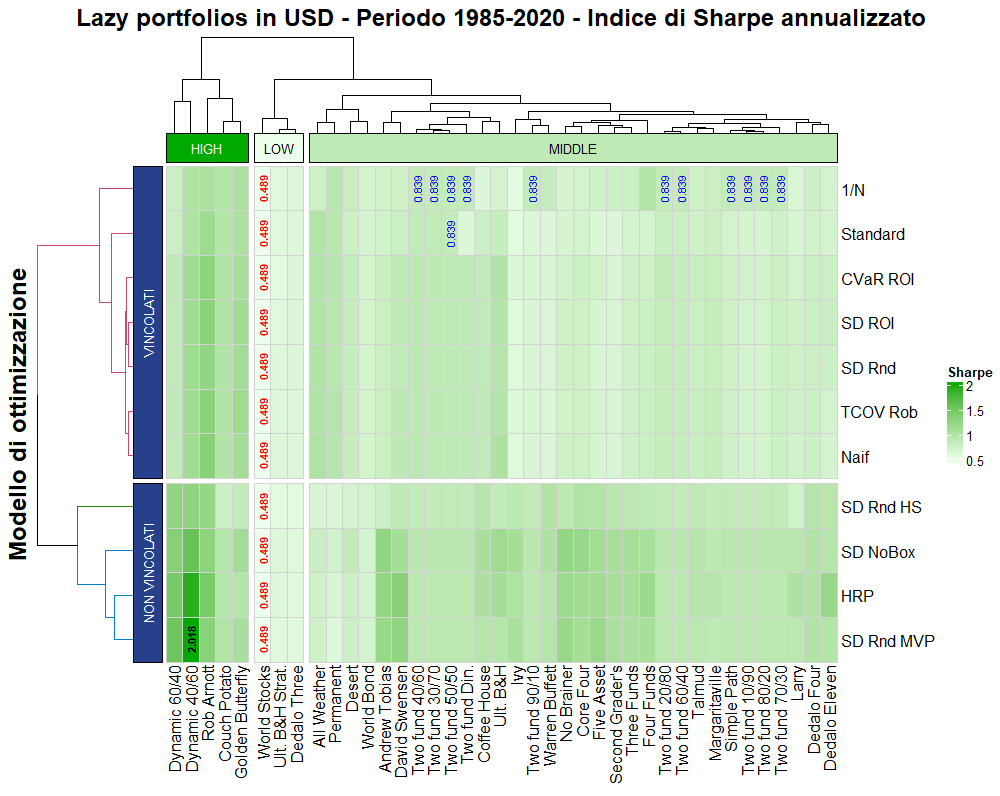
Il valore più alto è stato ottenuto dal Dynamic 40/60 Income Lazy portfolio ottimizzato col modello MVP: 2,018. Il più basso, dal World Stock: 0,489.
L’indice di Sharpe mediano, pari a 0,839, è stato invece ottenuto dal Two Fund portfolio ottimizzato con la strategia 1/N, che ha ovviamente generato portafogli uguali, con il peso degli ETF sempre pari al 50% ciascuno.
Si può osservare come i portafogli azionari al 100% abbiano ottenuto indici di Sharpe più bassi: non è un caso. Molto spesso, col crescere del rendimento atteso di un portafoglio, la sua volatilità aumenta in modo più che proporzionale, abbassando perciò l’indice di Sharpe.
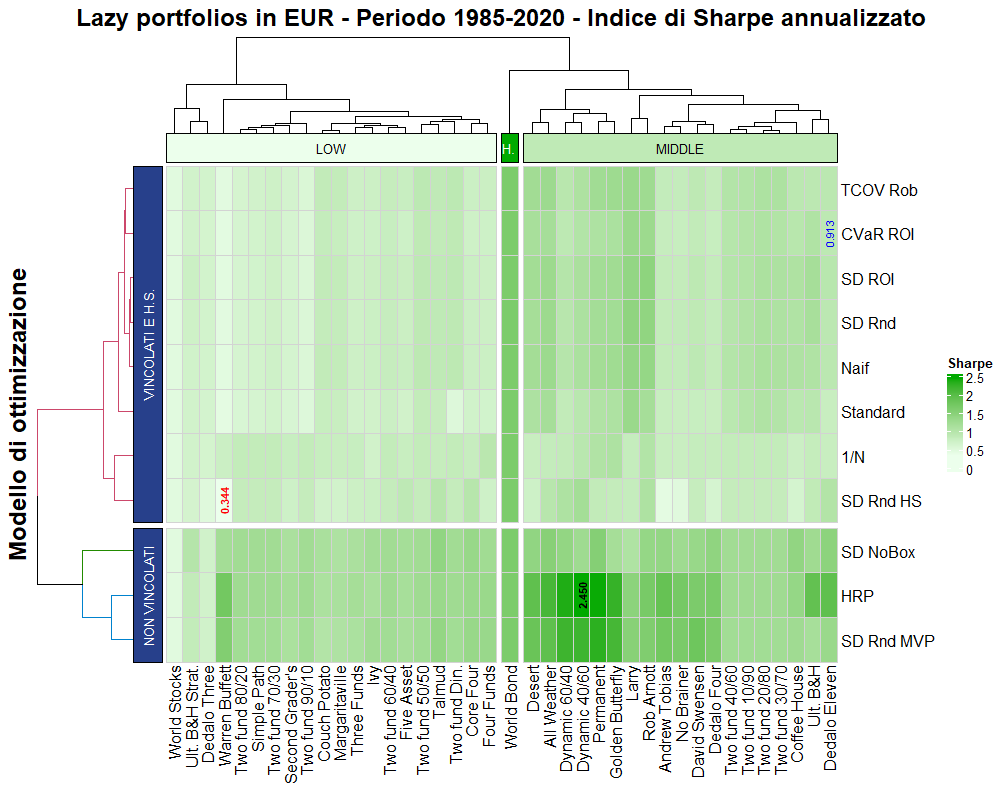
Anche tra i portafogli in euro, quello con l’indice di Sharpe più alto è il Dynamic 40/60 Income ottimizzato col modello HRP: 2,450. Quello con l’indice più basso è il Warren Buffett ottimizzato col modello HS: 0,344. Il portafoglio con l’indice di Sharpe mediano, infine, è il Dedalo Eleven ottimizzato con il modello CVaR ROI: 0,913.
MASSIMO DRAWDOWN
Il massimo drawdown è la massima perdita in termini percentuali verificatasi tra un punto di massimo rendimento e un successivo punto di minimo.
Il massimo drawdown ci permette di capire quanto, storicamente, è stata la perdita massima percentuale – calcolata a partire da un valore massimo – subita da un certo investimento.
Vediamo la heatmap:
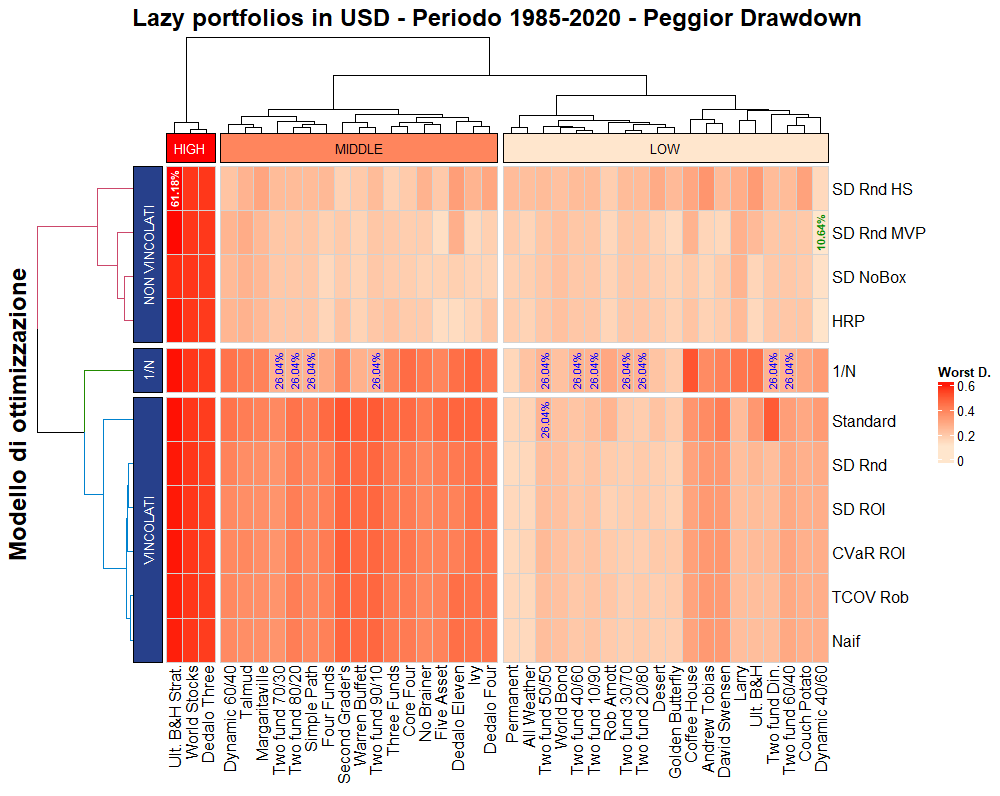
Di nuovo, il gruppo dei portafogli a più alto rischio comprende i 3 Lazy portfolios 100% azionari. Tra questi, il massimo drawdown più elevato è quello subito dall’Ultimate Buy & Hold Strategy ottimizzato col modello HS: 61,18%.
Il massimo drawdown più contenuto è stato quello del Dynamic 40/60 Income Lazy portfolios ottimizzato col modello MVP: soltanto il 10,64%.
Il massimo drawdown mediano, invece, è stato realizzato dai Two funds portfolios ottimizzati col modello 1/N: 26,04%.
I modelli non vincolati, in genere, hanno generato delle allocazioni meno rischiose, dato che hanno avuto maggior libertà nella scelta dei pesi degli ETF.
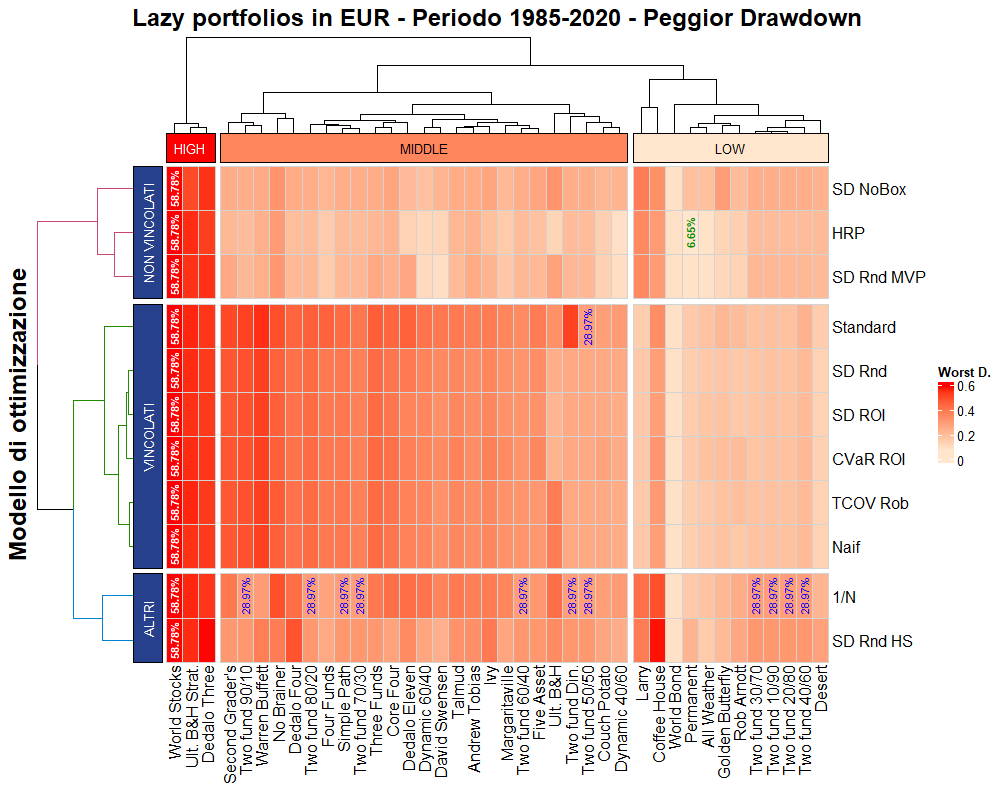
Tra i Lazy portfolios in EUR, il massimo drawdown più elevato è stato quello del World Stock: 58.78%. Il più piccolo è stato realizzato dal Permanent Lazy portfolio ottimizzato col modello HRP: 6,55%. Il massimo drawdown mediano, infine, è stato quello dei Two funds pesati con la strategia 1/N (in altre parole, del Two funds 50/50).
CVAR
Il Conditional Value at Risk (CVaR), detto anche Expected Shortfall (ES) o Expected Tail Loss (ETL), misura il valore atteso della perdita che si registrerà qualora questa ecceda il VaR calcolato al livello di confidenza α.
Il CVaR è sempre maggiore del VaR e ci fornisce un’informazione più completa.
Come il VaR, anche Il CVaR è caratterizzato da due parametri: il livello di confidenza α e l’orizzonte temporale di rischio in base al quale viene calcolato.
Il CVaR fornisce un’informazione molto importante: se, ad esempio, α è pari al 5%, il CVaR ci dà un’idea di quanto possiamo aspettarci di perdere in media in quel 5% di casi in cui la perdita ecceda il VaR.
Dobbiamo fare attenzione a non confondere il CVaR con una perdita massima, che potrebbe essere ad esso superiore.
L’orizzonte temporale per il calcolo del CVaR visualizzato nelle nostre heatmaps è quello giornaliero:
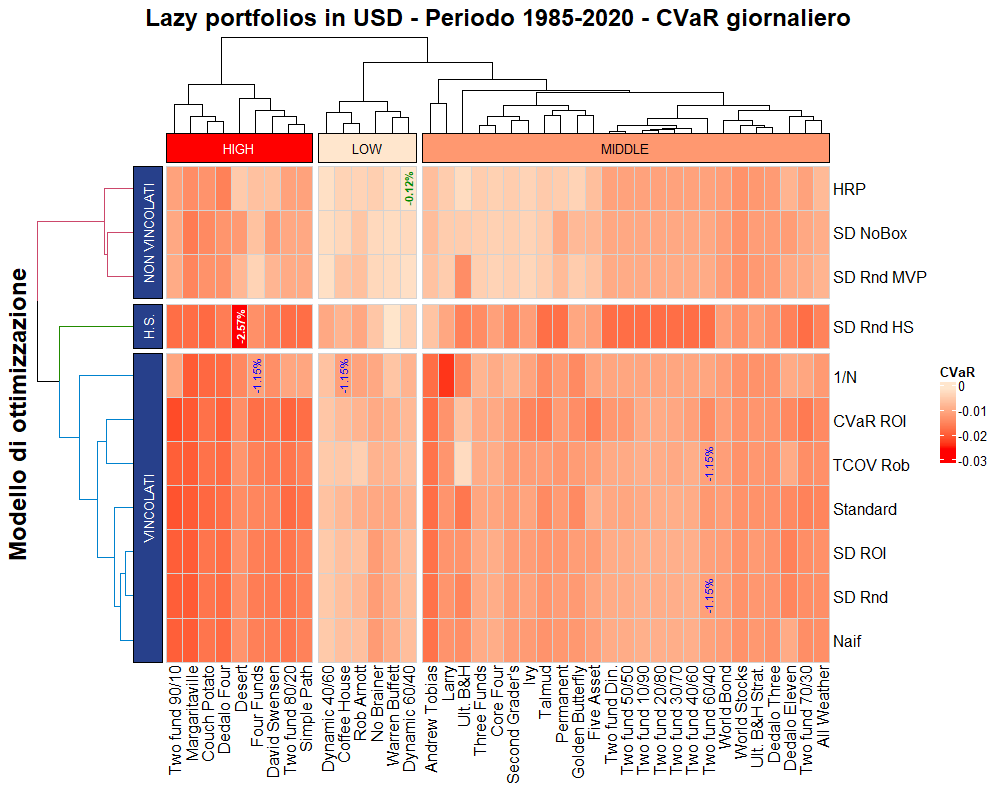
Per trasformare il CVaR da giornaliero a mensile o annuale, deve essere moltiplicato per √22 o √256: il CVaR giornaliero del −2,57% corrisponde al −12,05% mensile e al −41,12% annuale.
Il più alto CVaR è stato quello del Desert Lazy portfolio ottimizzato col modello HS: −2.57%. Il più piccolo è stato realizzato dal portafoglio Dynamic 60/40 Income ottimizzato col modello HRP: −0,12%, corrispondente al −1,92% annuale. Il CVaR mediano, infine, è stato quello dei portafogli Four Funds e Rob Arnott pesati con le strategie 1/N e del Two funds 60/40 ottimizzato coi modelli vincolati Rnd e TCOV Rob: −1,15% (−18,40% annuale).
Questa è la heatmap dei Lazy portfolios in EUR:
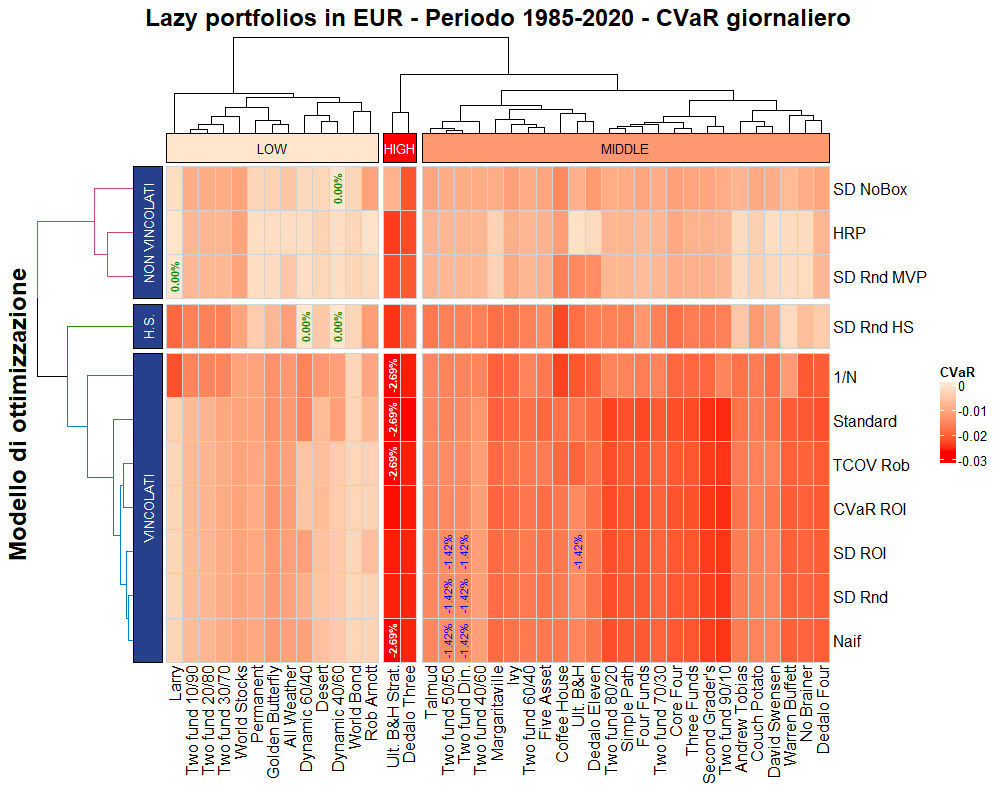
È ormai chiaro come si distinguono i valori più alti, bassi e mediani del CVaR dei portafogli pigri in EUR.
Il valore minimo, pari a 0, merita forse un commento: questo valore nullo, in realtà, proviene da un mancato calcolo del VaR e del CVaR del package PerformanceAnalytics, utilizzato nei nostri calcoli.
La ragione più probabile è che la bassa frequenza di rendimenti negativi abbia portato a un risultato positivo del CVaR e, di conseguenza, non sia stato considerato un esito affidabile dell’analisi.
Passiamo adesso alla visualizzazione delle heatmaps dei Lazy portfolios in USD e EUR in base ai 5 indicatori statistici appena analizzati nel periodo 2000-2020.
Non le commenteremo una per una come abbiamo fatto in precedenza, a meno che non ci siano particolari spunti di riflessione.
RENDIMENTO ANNUALIZZATO
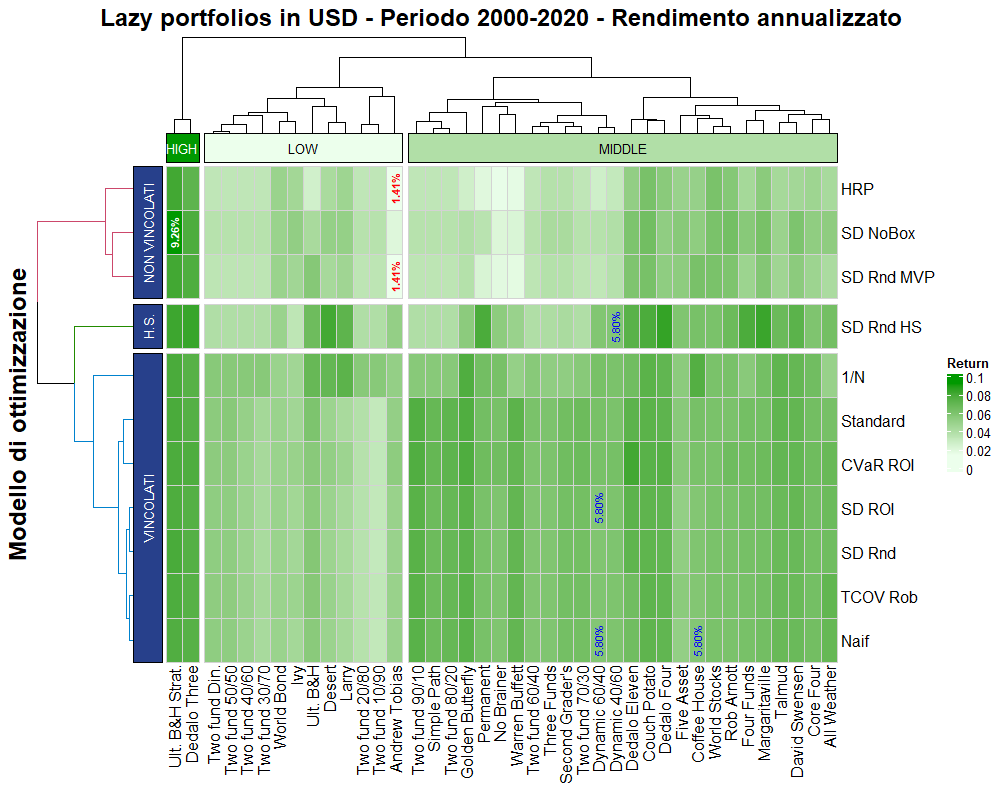
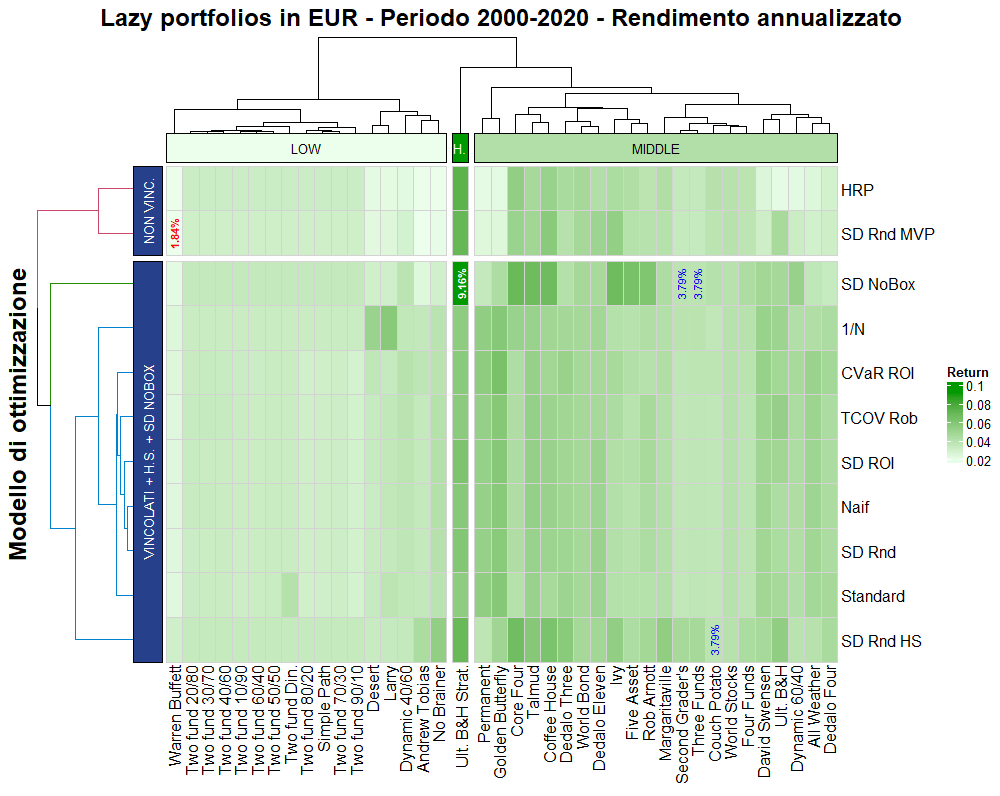
VOLATILITÀ
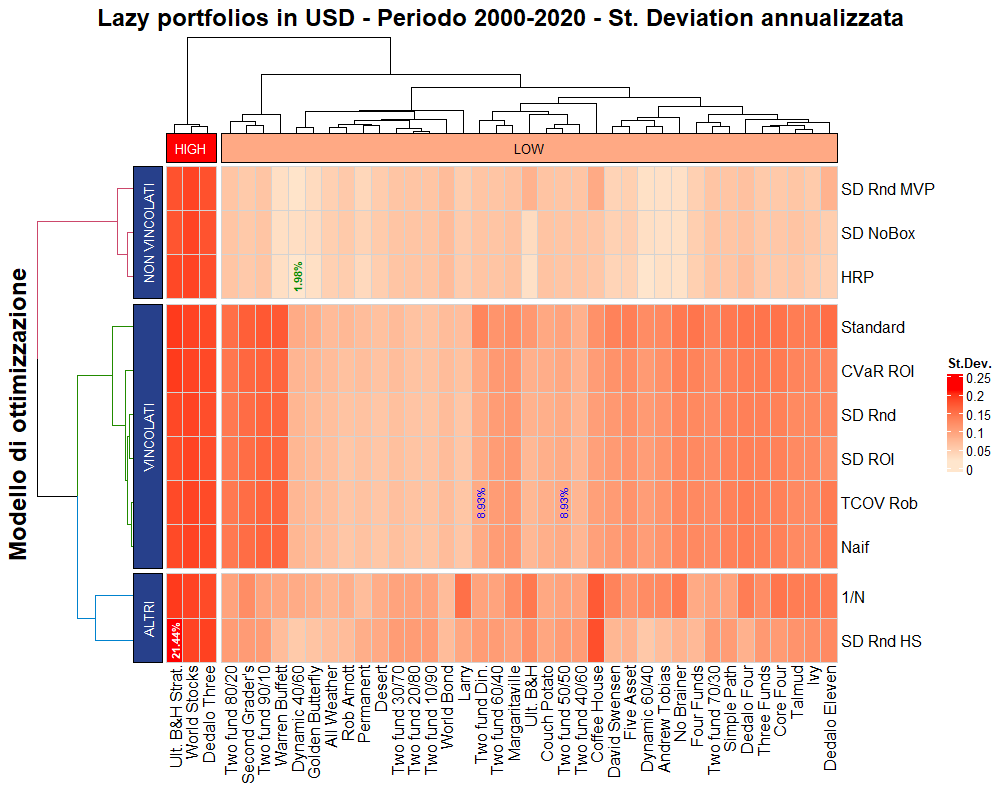
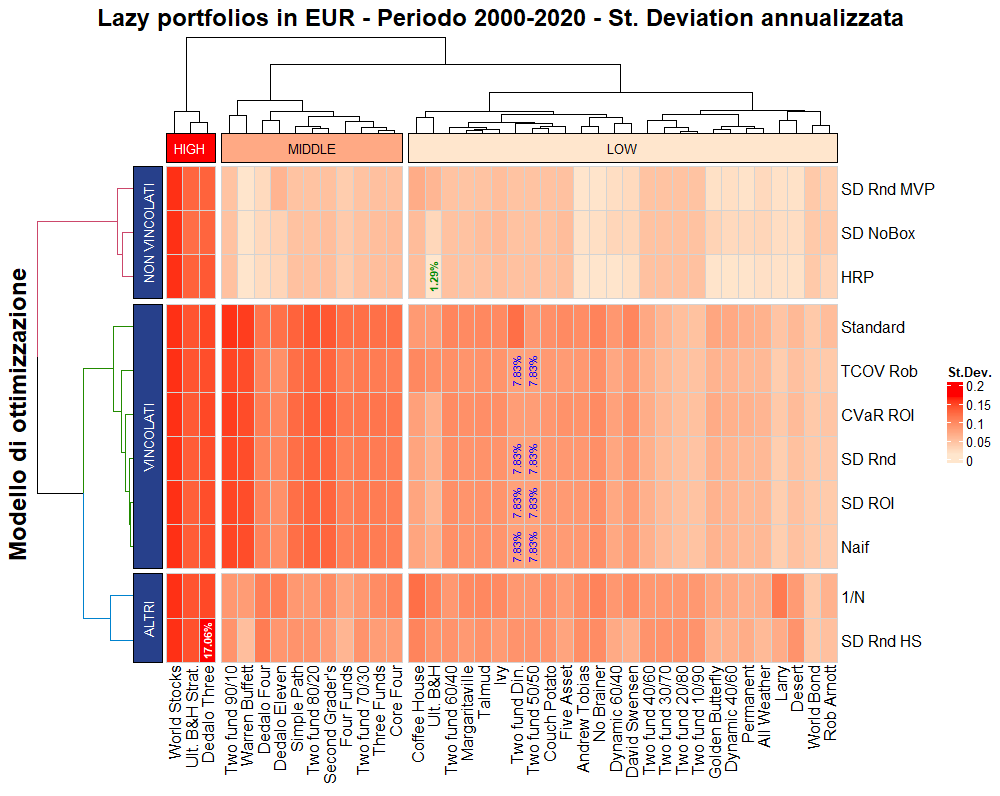
INDICE DI SHARPE
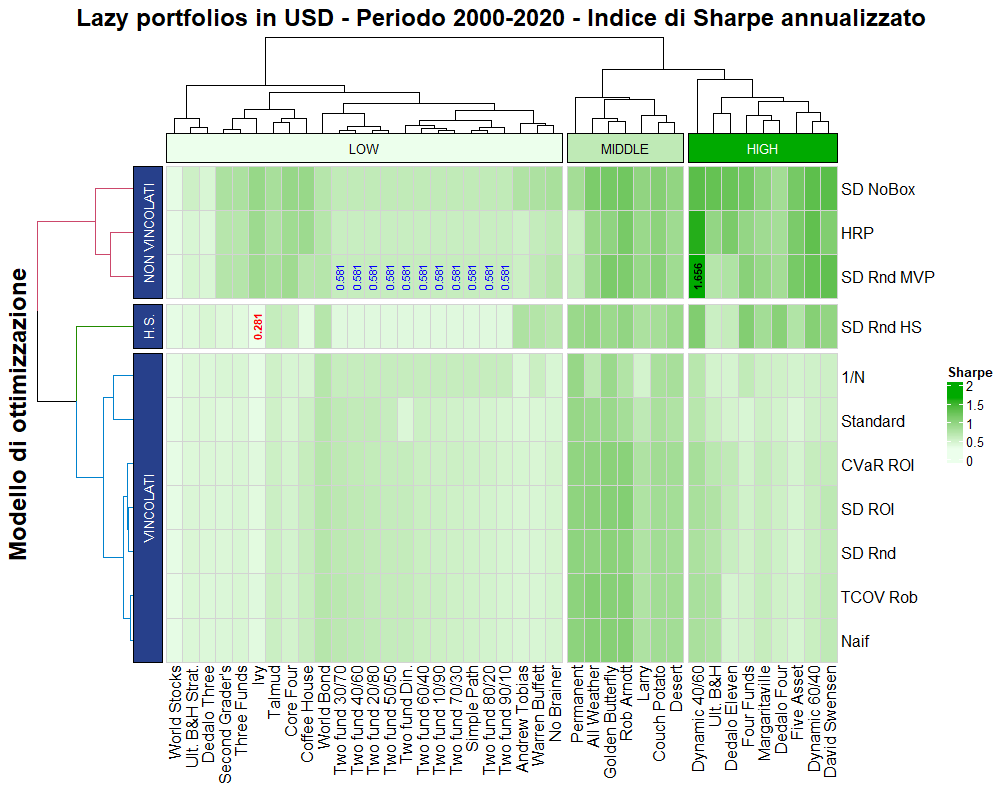
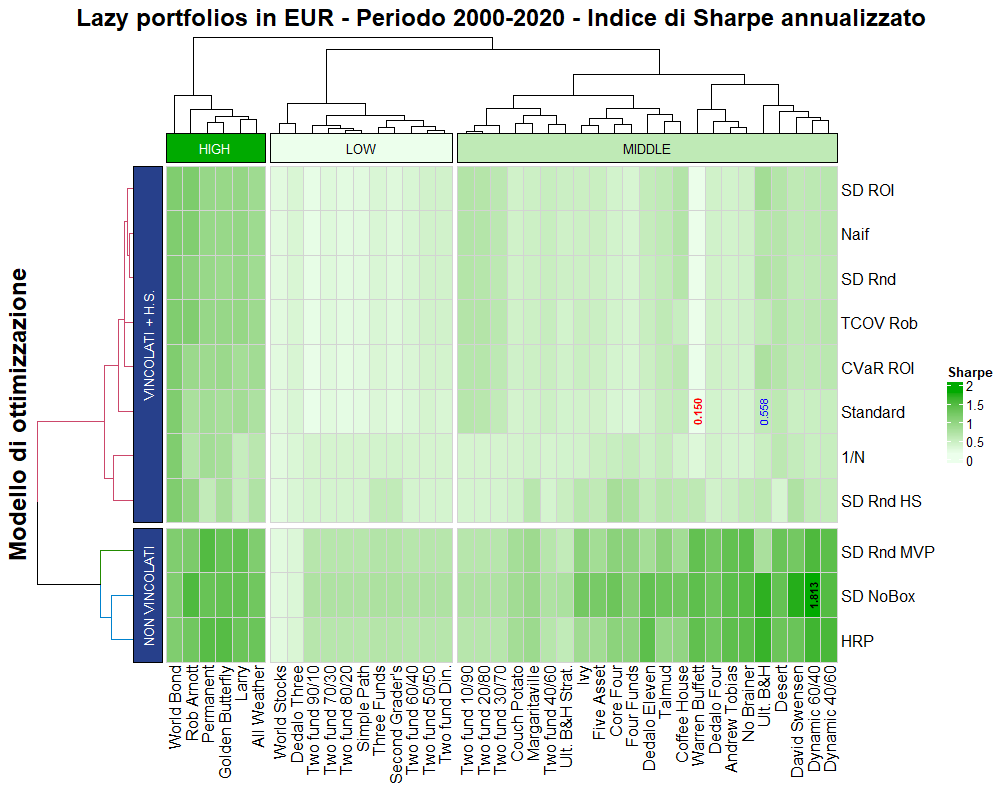
MASSIMO DRAWDOWN
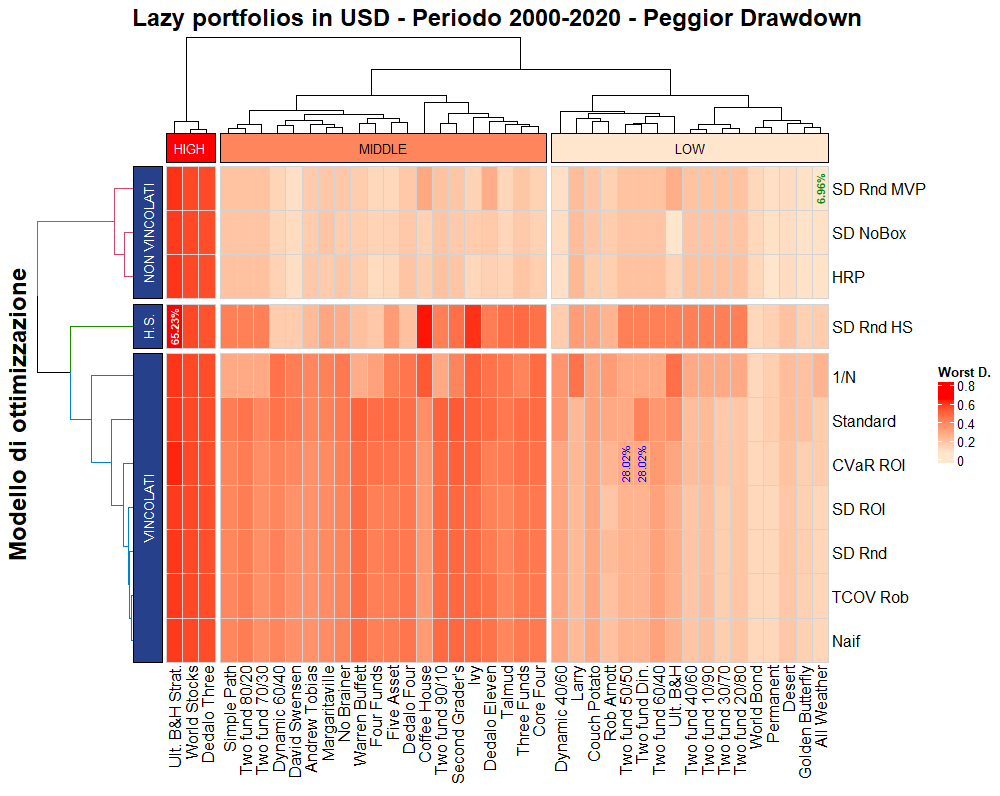
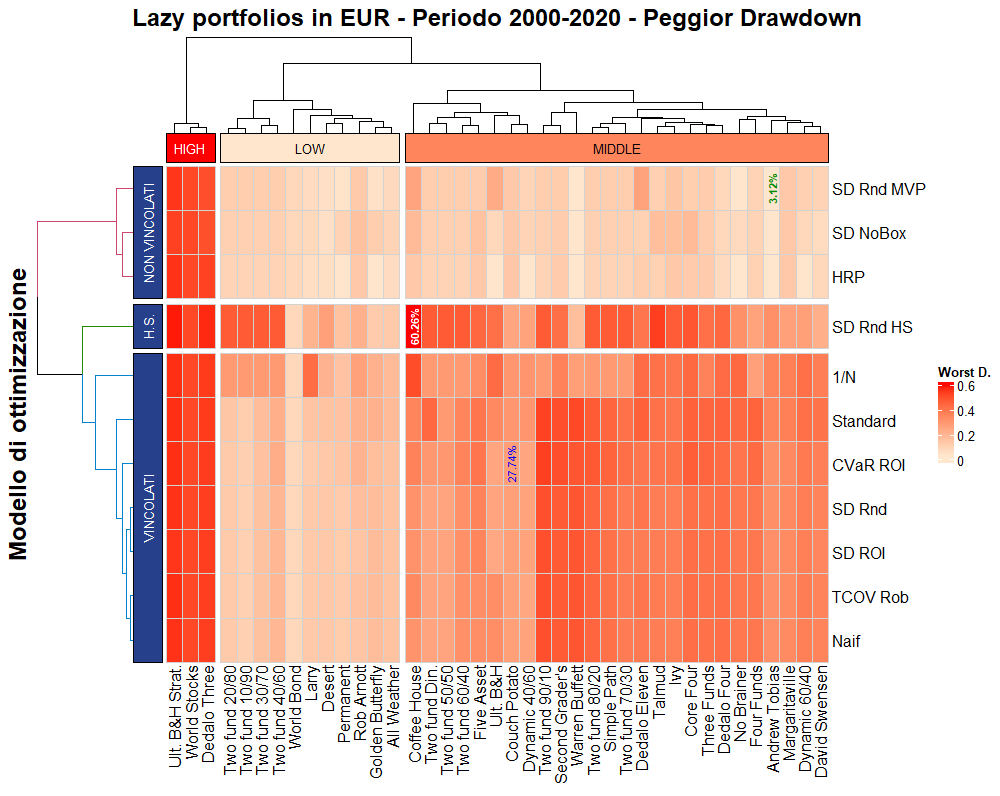
CVAR
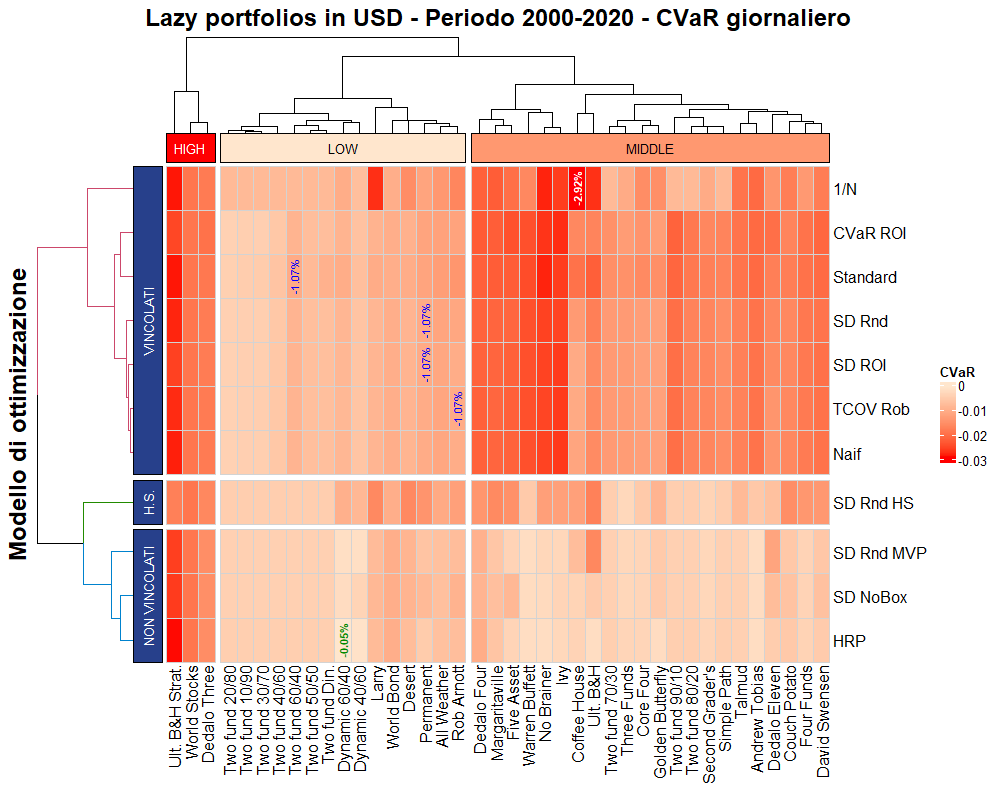
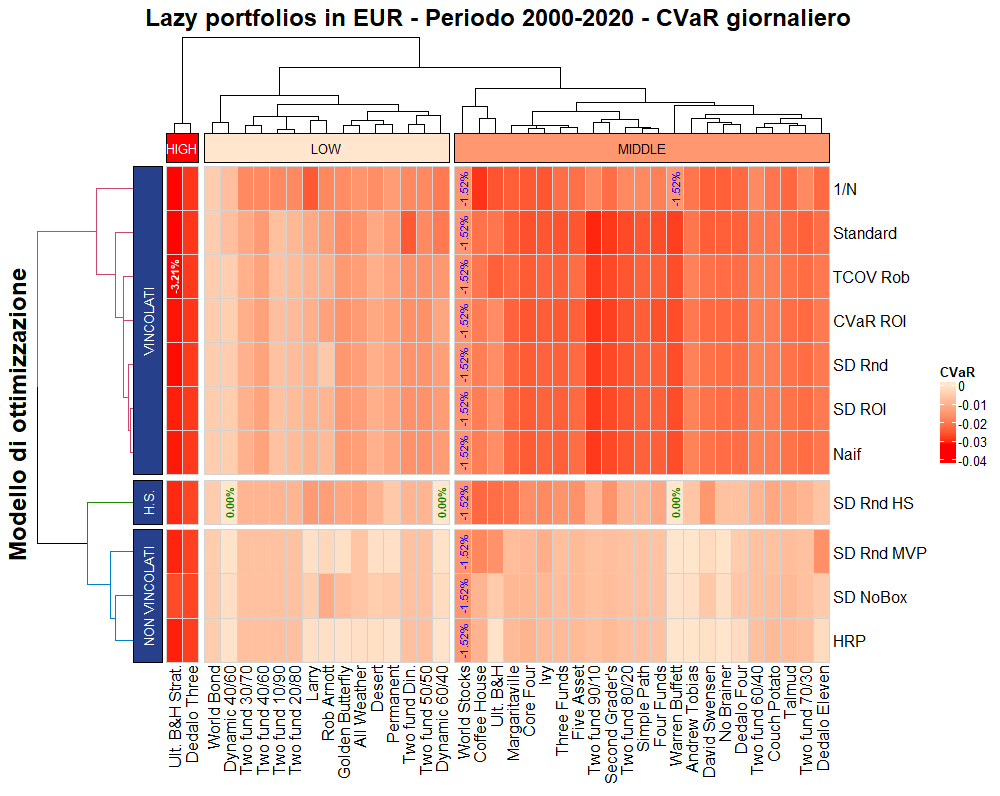
Infine, visualizziamo le heatmaps dei Lazy portfolios in USD e EUR in base ai soliti 5 indicatori statistici relative al periodo 2010-2020.
RENDIMENTO ANNUALIZZATO
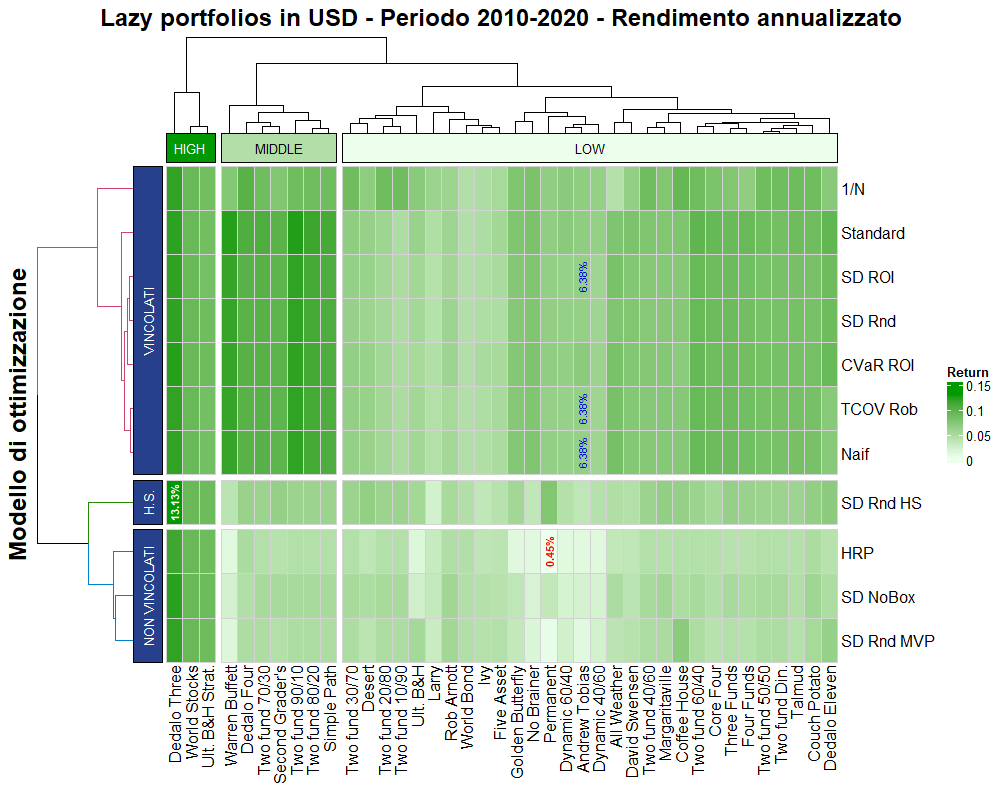
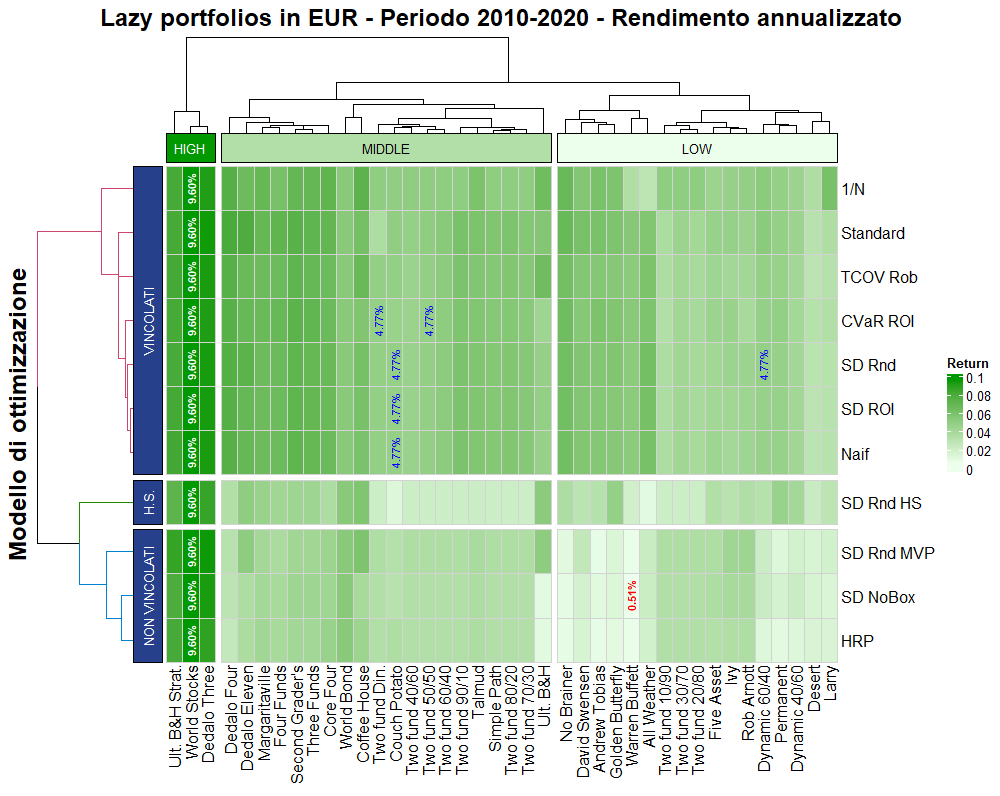
VOLATILITÀ
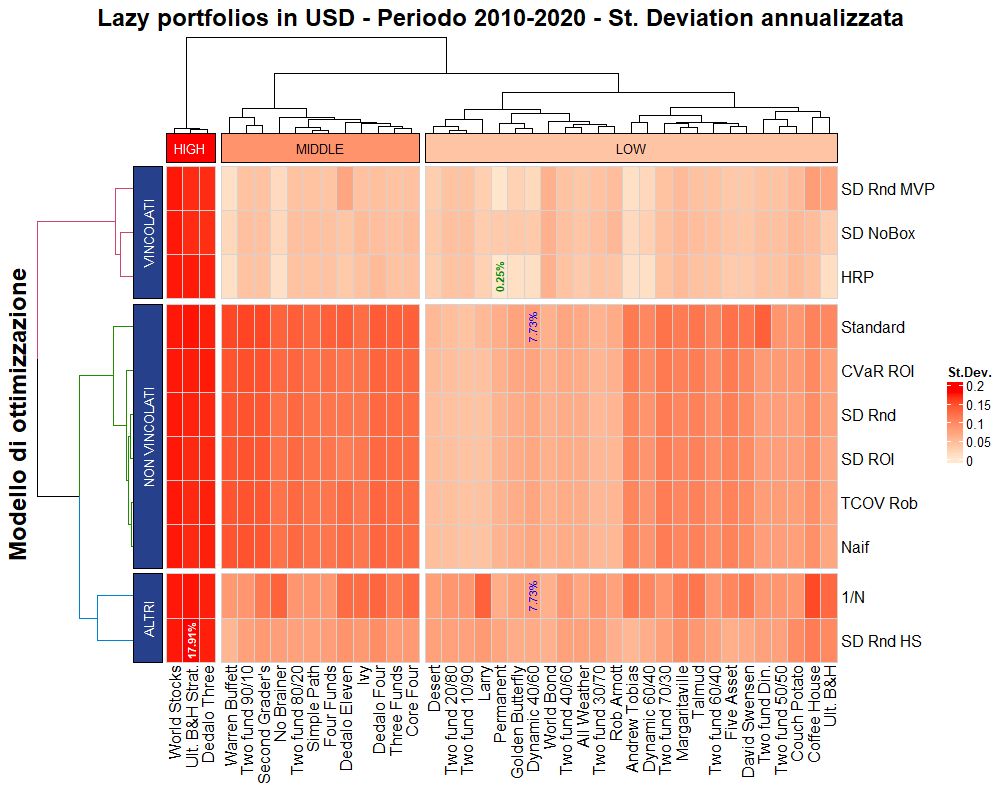
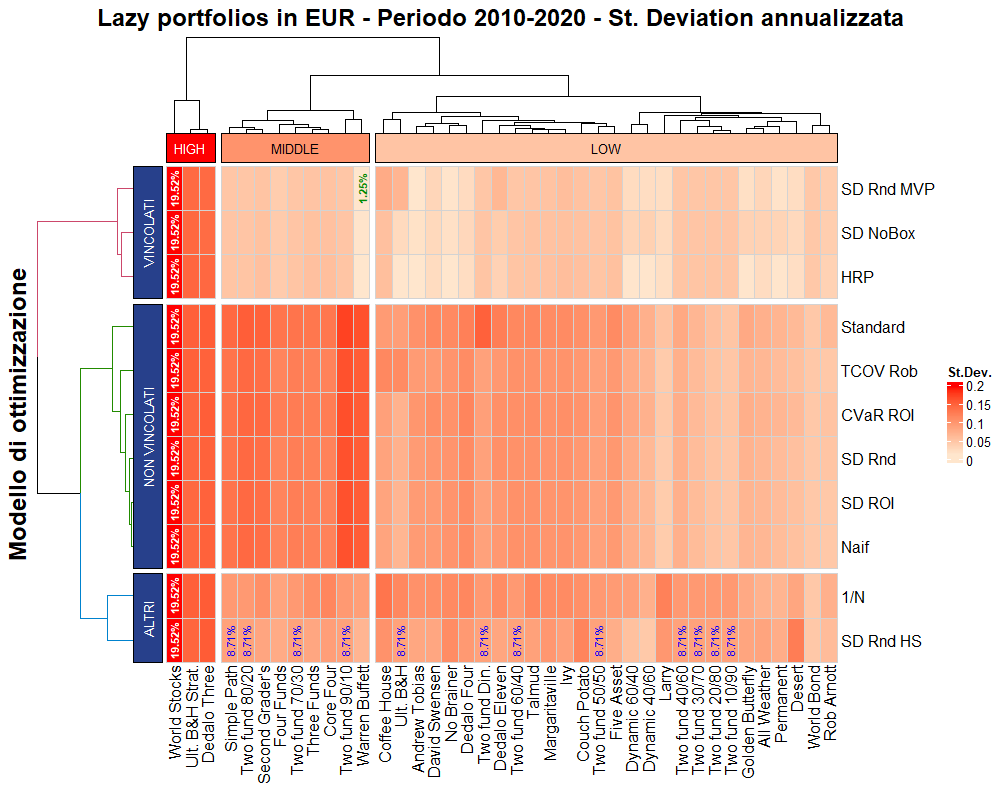
INDICE DI SHARPE
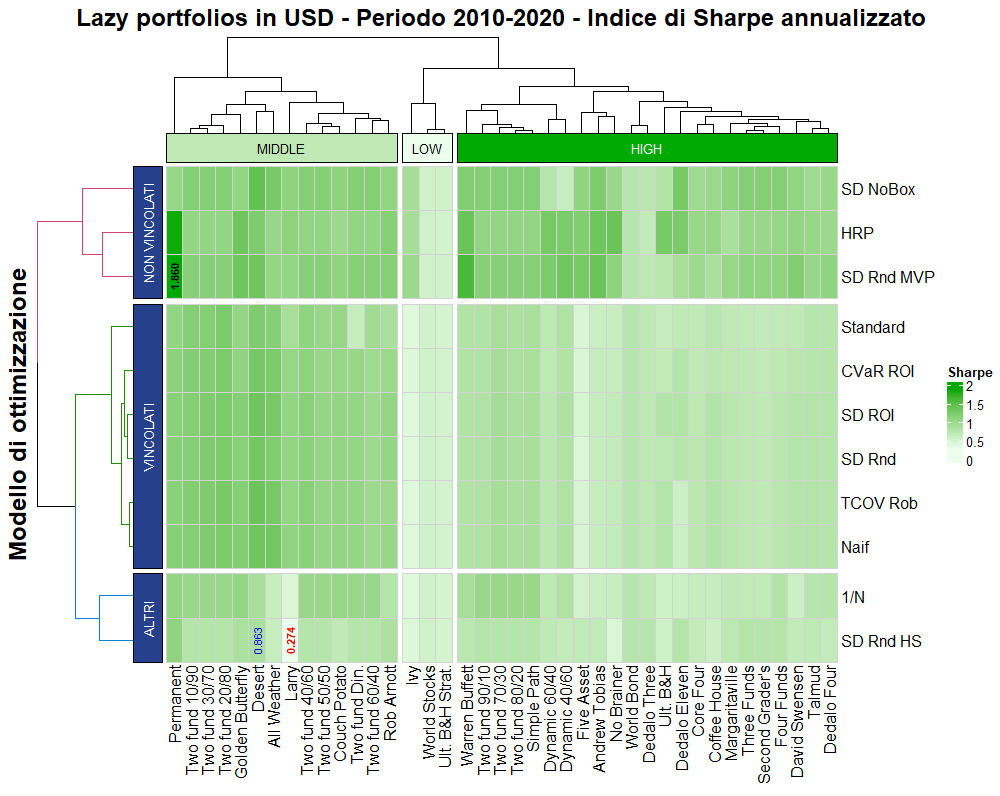
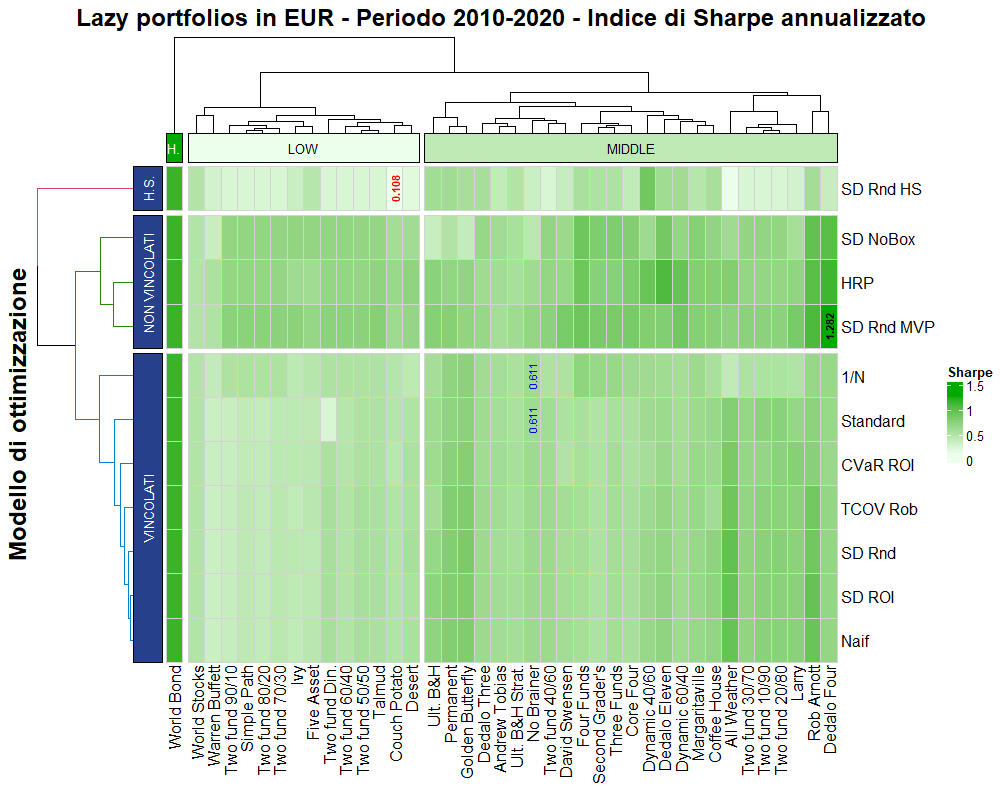
MASSIMO DRAWDOWN
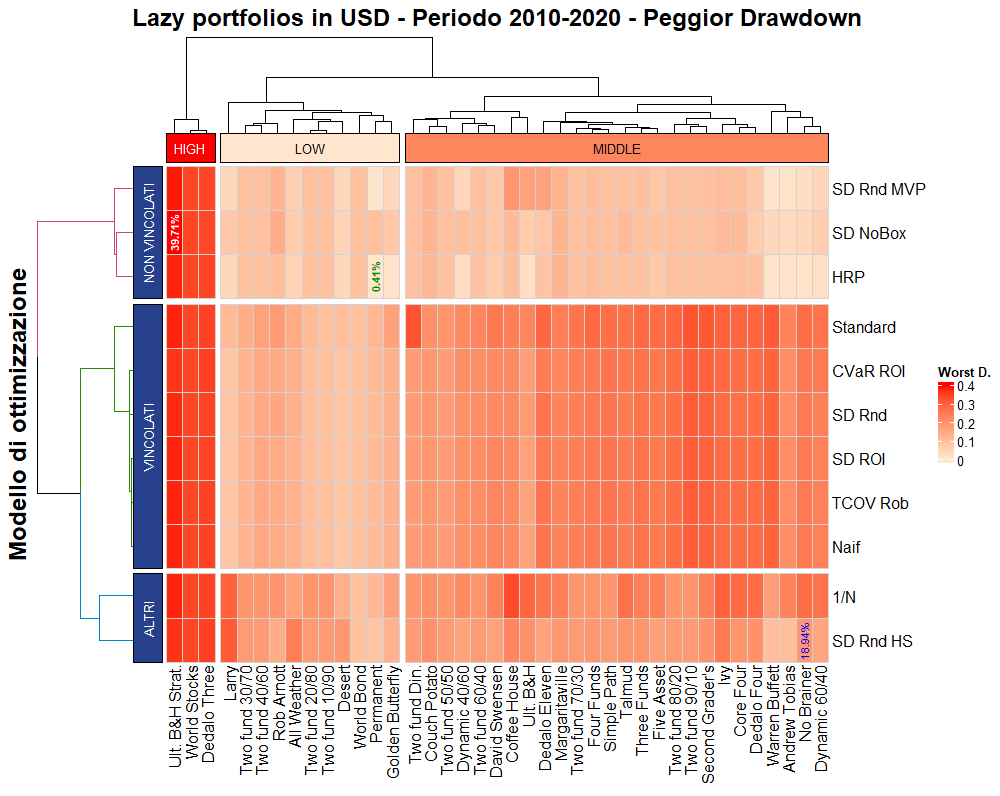
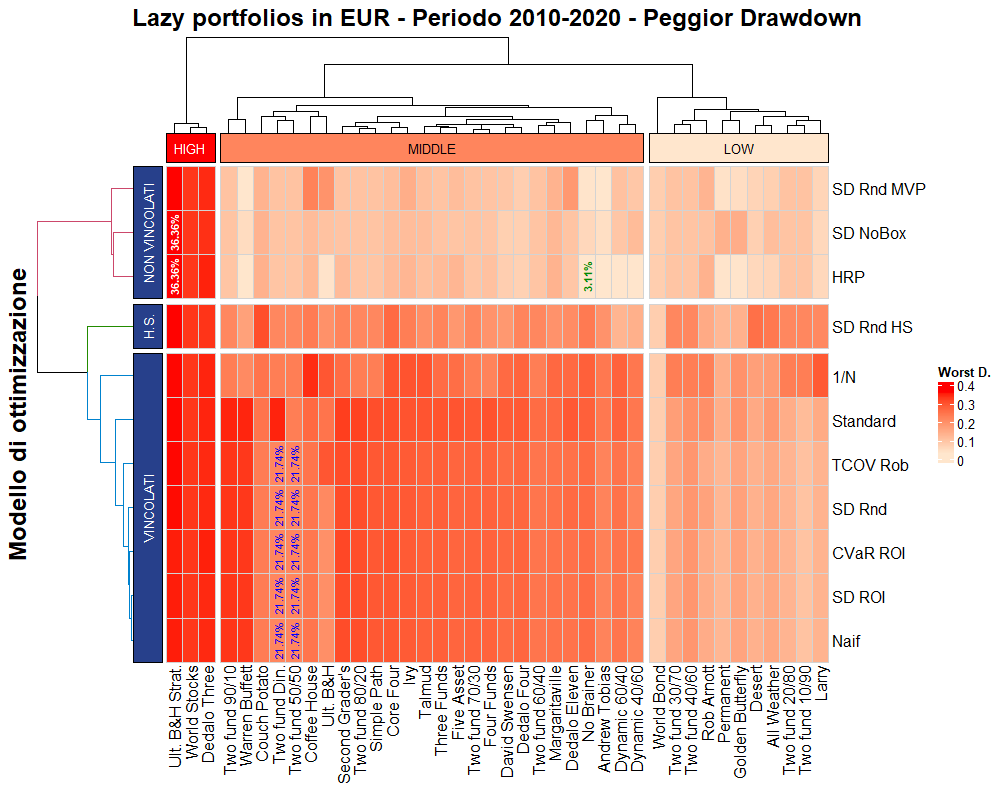
CVAR
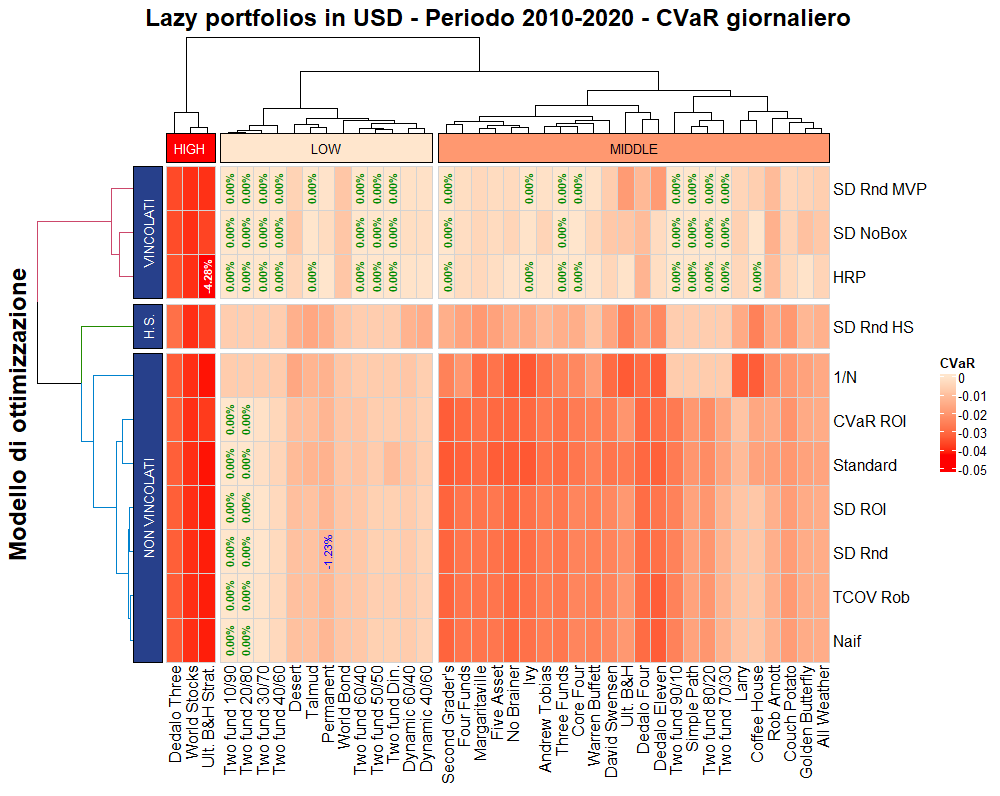
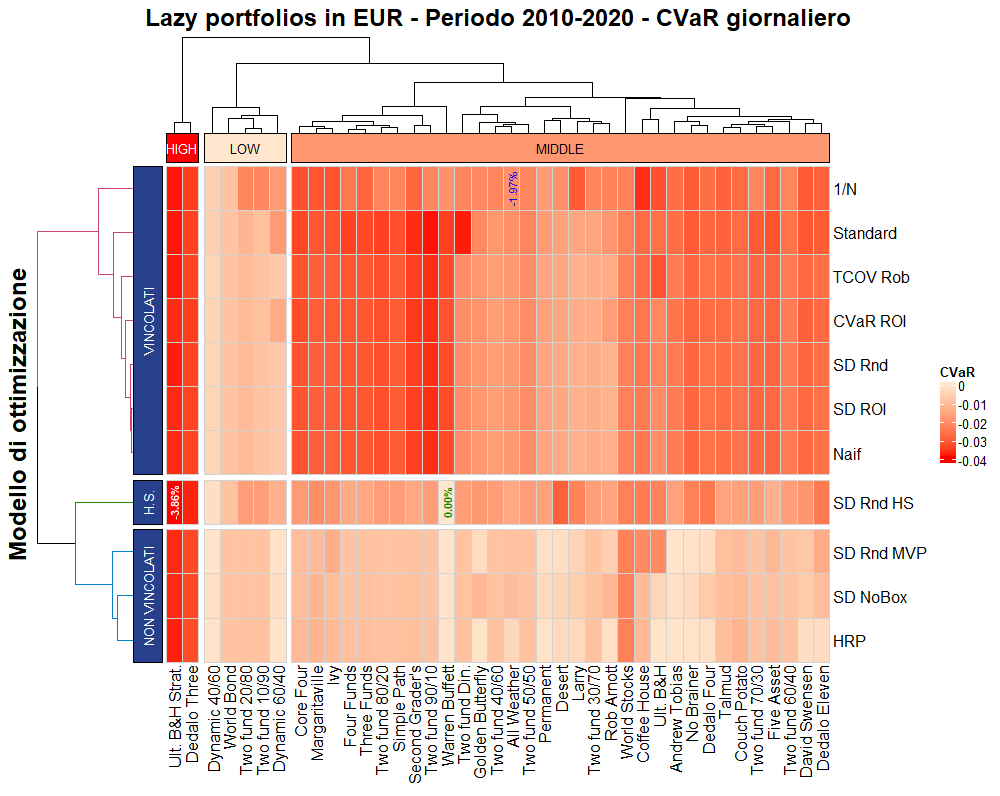
12.4 Correlazione lineare tra i Lazy portfolios

«Correlation is not cause, it is just a 'music of chance'».
Siri Hustvedt
L’analisi della correlazione lineare può rivelare informazioni molto utili, anche se purtroppo sempre più spesso viene abusata o male interpretata.
L’analisi della correlazione lineare tra i Lazy portfolios non ha lo scopo di fornire una risposta alla domanda sul portafoglio da scegliere, ma può essere utile a capire quali siano i gruppi di portafogli dai rendimenti che si muovono in maniera analoga.
Se con le heatmaps dei rendimenti annualizzati abbiamo verificato le relazioni tra i rendimenti finali dei Lazy portfolios, le matrici di correlazione che esamineremo adesso si concentrano sull’andamento dei rendimenti nell’arco di tempo analizzato.
Naturalmente, di ogni Lazy portfolio disponiamo di una serie di rendimenti diversa per ognuno dei modelli di ottimizzazione utilizzati: potremmo perciò visualizzare 11 matrici di correlazione tra i rendimenti di ogni Lazy portfolio, una per ognuno degli 11 modelli di ottimizzazione.
Abbiamo perciò deciso di semplificare questo eccesso di informazioni calcolando, per ogni Lazy portfolio, il rendimento medio ottenuto dagli 11 modelli.
Quando si parla di correlazione ci si riferisce generalmente al grado di relazione tra due variabili.
La più importante tipologia di correlazione è proprio quella lineare, che viene misurata dall’indice di correlazione di Pearson o indice di correlazione lineare.
Esso può assumere valori compresi tra −1 e +1:
- Quando è positivo, esiste una correlazione lineare diretta tra le due variabili osservate; la correlazione diretta è massima al raggiungimento del valore di +1.
- Quando è negativo, esiste una correlazione lineare inversa tra le due variabili osservate; la correlazione inversa è massima al raggiungimento del valore di −1.
- Quando è uguale a 0, le due variabili osservate non presentano alcuna correlazione lineare (non sono linearmente correlate).
Il coefficiente di correlazione lineare è una misura statistica simile alla covarianza, ma con alcune importanti differenze.
Entrambe misurano il livello di relazione esistente tra due variabili e la correlazione lineare è una funzione della covarianza, in quanto si ottiene dividendo la covarianza delle due variabili per il prodotto delle deviazioni standard delle stesse due variabili.
Chiamiamo A la serie storica dei rendimenti del Lazy portfolio x e B quella del Lazy portfolio y. La formula dell’indice di correlazione lineare è la seguente:
ρ = cov(A,B) / σAσB
Dove cov(A,B) rappresenta la covarianza tra A e B, mentre σA e σB sono, rispettivamente, le deviazioni standard di A e B.
La correlazione lineare fornisce quindi un’informazione in più rispetto alla covarianza: mentre quest’ultima indica soltanto la direzione della relazione lineare tra due variabili, la correlazione lineare ne indica la direzione e ne misura l’intensità.
È per questo motivo che la correlazione lineare è molto più conosciuta e utilizzata della covarianza: i suoi valori sono compresi in un intervallo ben definito, che va da −1 a +1.
Sono valori standardizzati e di più facile comprensione di quelli della covarianza, che può invece variare da meno infinito a più infinito.
Iniziamo la nostra analisi con la visualizzazione della matrice di correlazione dei Lazy portfolio in USD del periodo 1985-2020:
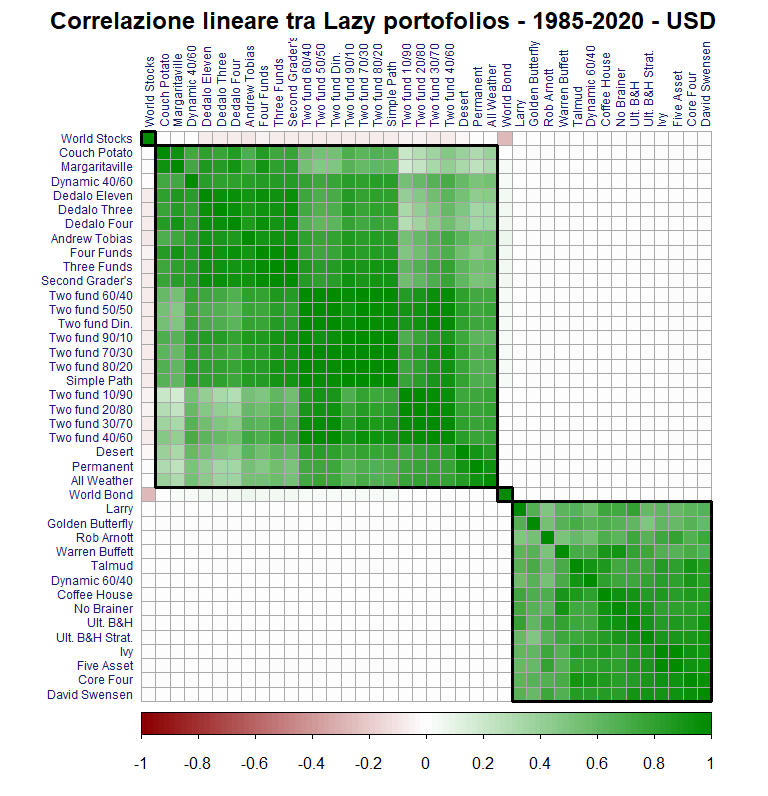
Come da legenda posizionata sotto alla matrice, il colore verde identifica le correlazioni lineari positive mentre il colore rosso identifica quelle negative.
Il verde più intenso significa che la correlazione è più elevata: i valori sulla diagonale, ad esempio, sono tutti pari a 1 dato che fanno riferimento alle correlazioni di ciascun Lazy portfolio con sé stesso.
I Lazy portfolios vengono anche suddivisi in gruppi, generati ancora una volta dalla cluster analysis:
- Esistono due gruppi formati da un solo portafoglio pigro: sono il World Stocks e il World Bond. Non a caso, sono gli unici Lazy portfolios costituiti da un singolo ETF.
La correlazione lineare tra questi due portafogli è negativa, come si può osservare nei due quadratini dal colore rosa.
La loro correlazione lineare con gli altri Lazy portfolios, invece, e molto vicina a 0: lo sfondo bianco di gran parte di questa matrice di correlazione lo testimonia. - Gli altri due gruppi, uno composto da 24 e uno da 14 Lazy portfolios, comprendono portafogli che sono più o meno correlati tra di loro e non correlati con quelli al di fuori dei rispettivi gruppi.
La matrice di correlazione dei portafogli pigri in EUR è la seguente:
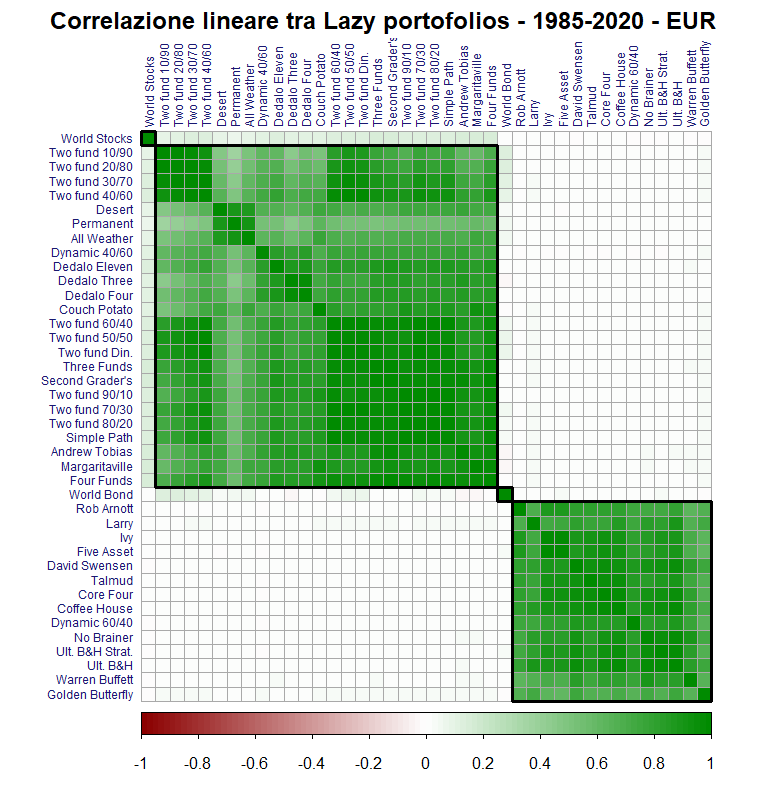
I risultati sono quasi identici ai precedenti in USD: se è vero che le differenze tra i rendimenti finali dei portafogli pigri in USD e gli equivalenti in EUR possono essere importanti, così non è per quanto riguarda le dinamiche degli stessi rendimenti durante il periodo dell’investimento.
Vediamo come cambiano le cose analizzando soltanto il periodo che va dal 2000 al 2020.
Partiamo dai Lazy portfolios in USD:
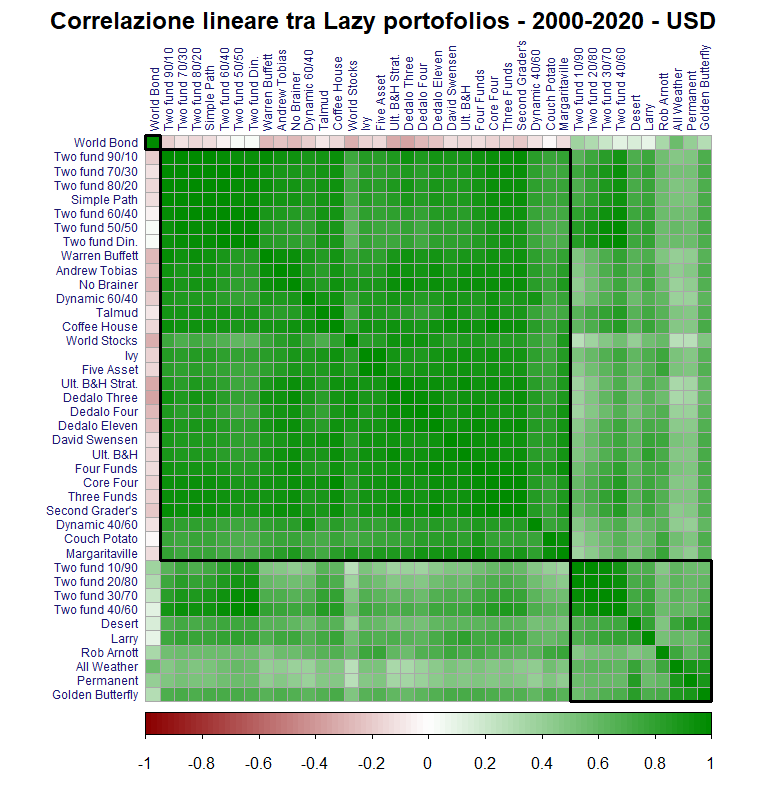
Si nota fin da subito che le ampie zone bianche sono quasi sparite. I gruppi sono 3 e non più 4, dal momento che il World Stocks si è integrato abbastanza bene nel gruppo più grande, formato adesso da 29 portafogli.
Gli altri due gruppi sono quello formato soltanto dal World Bond e il gruppo dei 10 Lazy portfolios residui.
Vediamo la matrice di correlazione dei portafogli in EUR:
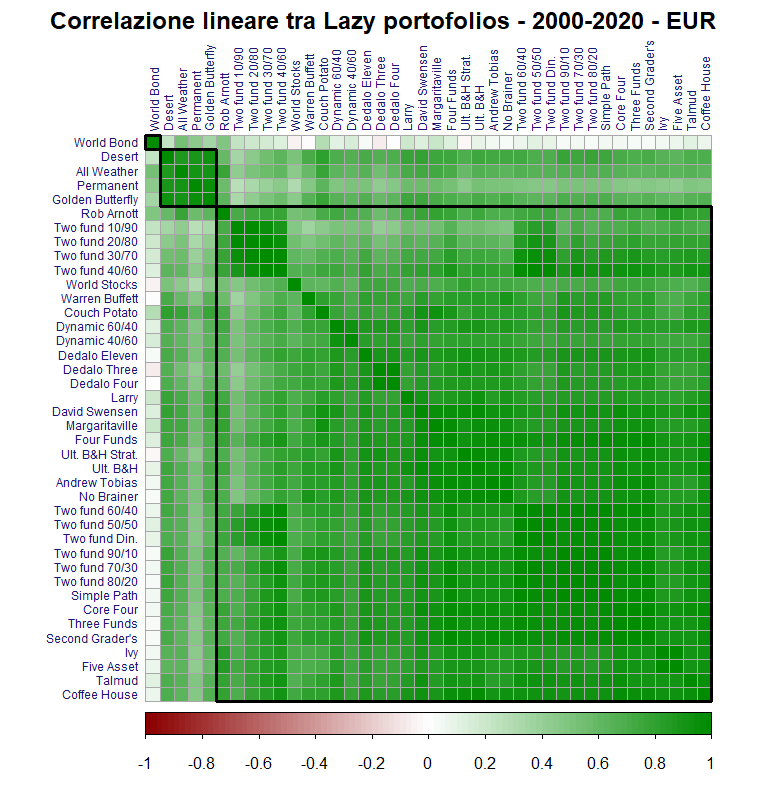
La matrice è simile a quella dei portafogli in USD, anche se il gruppo più grande è costituito da ben 35 e quello più piccolo soltanto da 4 Lazy portfolios.
Il terzo gruppo, di nuovo, è composto soltanto dal World Bond.
Per finire, vediamo la matrice di correlazione dei portafogli in USD del periodo 2010-2020:
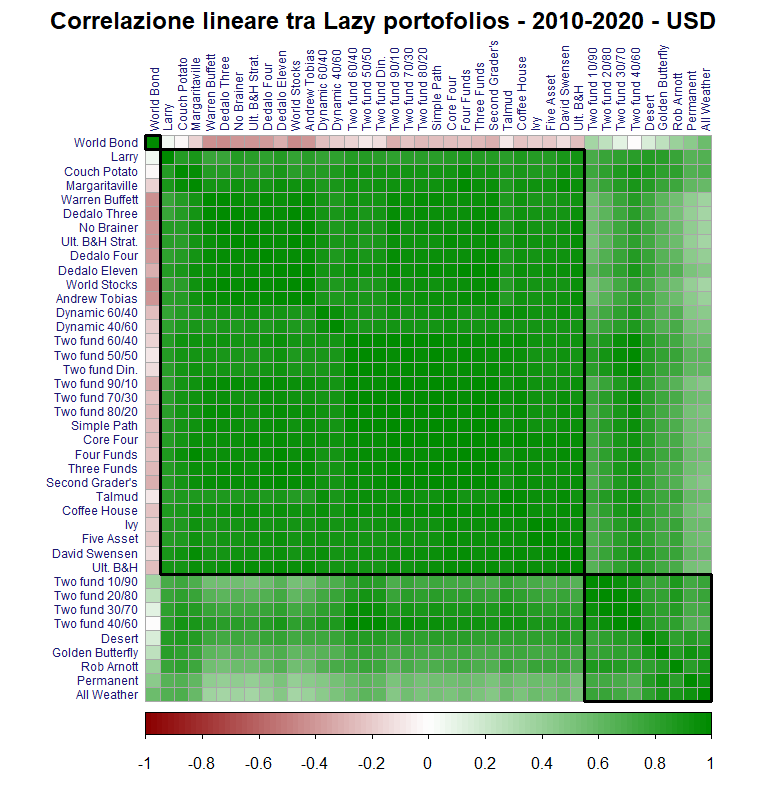
Le cose sono cambiate poco rispetto a prima:
- Nessuna zona bianca significativa (portafogli non correlati).
- Soliti 3 gruppi.
- La correlazione lineare inversa tra il World Bond e gli altri portafogli – soprattutto quelli del gruppo più grande – è molto più marcata rispetto a prima.
La matrice dei Lazy portfolios in EUR è la seguente:
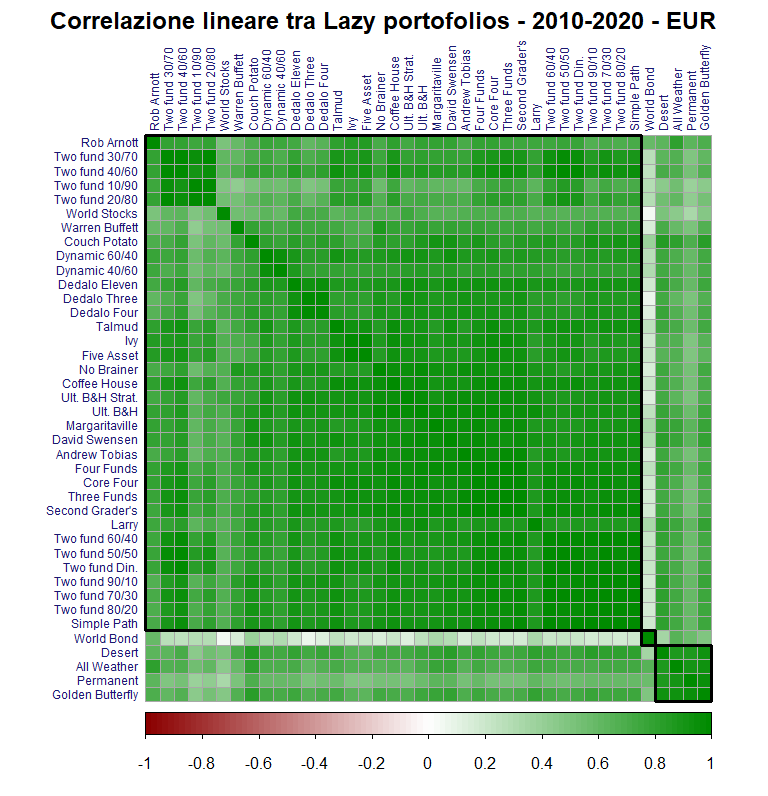
I risultati sono molto simili. Rispetto alla matrice di correlazione dei portafogli in USD, il World Bond tende a essere non correlato o poco correlato con i Lazy portfolios del gruppo più grande (invece che essere correlato inversamente).
A che cosa può servire l’analisi di correlazione lineare tra i Lazy portfolios?
In primo luogo, a conoscerli meglio. Ci permette di capire in quale “grande famiglia” (gruppo) si colloca ciascun Lazy portfolio: ad esempio, se siamo interessati al periodo più corto (2010-2020) e ai portafogli in EUR (ultima matrice visualizzata), ne troviamo uno che si discosta molto da tutti gli altri (World Bond, non a caso l’unico portafoglio la cui asset allocation è 100% obbligazionaria); i rimanenti appartengono o alla piccola famiglia di portafogli che potremmo definire “prudenti”, quelli cioè che cercano di limitare la volatilità e portare un po’ di rendimento in ogni situazione di mercato (Desert, All Weather, Permanent e Golden Butterfly), oppure alla grande famiglia che contiene la maggior parte dei Lazy portfolios analizzati, molto variegata.
L’analisi di correlazione lineare tra i Lazy portfolios potrebbe essere utile anche a chi decidesse di investire su due o più portafogli pigri, destinati magari al raggiungimento di obiettivi di investimento distinti o con orizzonti temporali diversi tra loro.
13. Analisi dei Lazy portfolios e presentazione dei risultati dei backtest
13.1 Considerazioni generali sui Lazy portfolios e sulla diversificazione

«Diversification is a safety factor that is essential because we should be humble enough to admit we can be wrong».
John Templeton
Nei capitoli 13.3.1-13.3.31, di ogni Lazy portfolio analizzeremo l’asset allocation, gli ETF che li compongono e alcune possibili alternative, le equity lines e le performance di tutte le nostre analisi.
Con l’ausilio delle matrici di correlazione, saranno anche visualizzati e commentati gli indici di correlazione tra gli ETF di ciascun portafoglio in USD e in EUR in tutti e tre i periodi che abbiamo analizzato.
Gli ETF dei portafogli in USD saranno situati nella parte sinistra dell’immagine; quelli in EUR, nella parte destra.
Nella parte alta verranno visualizzate le correlazioni tra gli ETF nei backtest del periodo più lungo (1985-2000); nella parte centrale, quelle del periodo medio (2000-2020); nella parte inferiore, quelle del periodo più corto (2010-2020).
Nella diagonale principale i valori delle correlazioni saranno sempre pari a 1: la correlazione lineare di una serie di valori con sé stessa è sempre 1.
A titolo di esempio, la figura seguente mostra la matrice di correlazione lineare tra gli ETF VTI e BND del Two funds portfolio in USD costruita sui rendimenti del periodo più lungo: 1985-2020.
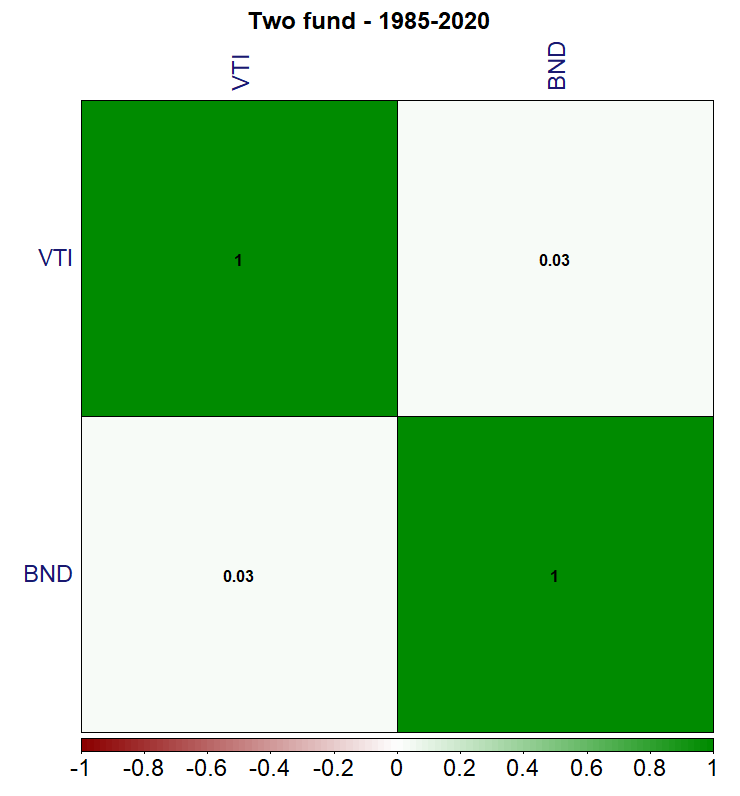
Più alta e tendente a 1 è la correlazione lineare, più intenso è il colore verde. Più la correlazione è bassa e tendente a −1, più intenso è il colore rosso. Più la correlazione è prossima a 0, più intenso è il colore bianco.
Nell’immagine di cui sopra, i valori sulla diagonale principale sono pari a 1 (correlazioni lineare di ciascun ETF con sé stesso); quelle sull’altra diagonale sono pari a 0,03: il colore è bianco e questo significa che gli ETF VTI e BND non sono stati correlati nel periodo esaminato.
La correlazione lineare tra gli ETF che compongono il Lazy portfolio è stata calcolata sull’interezza dei periodi analizzati: 1985-2020, 2000-2020 e 2010-2020. La stessa grandezza misurata su dei sottoperiodi avrebbe potuto portare a conclusioni diverse.
L’analisi effettuata fornisce anche altre informazioni. Nei portafogli con 3 o più ETF, viene eseguita anche una cluster analysis gerarchica (Hierarchical cluster analysis) e la matrice di correlazione diventa più elaborata: fanno la loro comparsa i clusters, ovvero gruppi di ETF dalle caratteristiche simili.
Vediamo un altro esempio, relativo alla matrice di correlazione degli ETF che compongono il Dedalo Eleven Lazy portfolio in EUR (periodo 2010-2020):
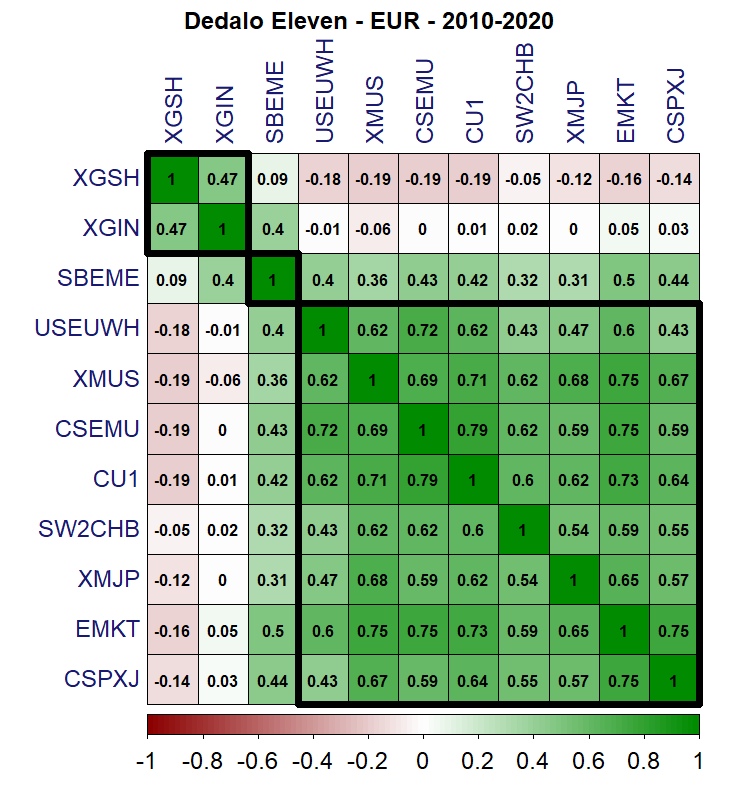
Si possono notare 3 gruppi di ETF, ciascuno dei quali delimitato da un bordo nero più spesso: partendo dall’angolo in alto a sinistra, troviamo il primo cluster formato dagli ETF XGSH e XGIN. Sono 2 ETF obbligazionari governativi globali, entrambi euro hedged (il secondo è Inflation-Linked): pur avendo una correlazione positiva tra di loro (0,47), sono molto poco correlati o correlati negativamente con tutti gli altri ETF.
Il secondo cluster comprende un solo ETF: SBEME. Questo ETF presenta una correlazione medio/bassa sia con i 2 ETF precedenti che con i rimanenti 8 ETF azionari.
Il terzo e ultimo gruppo è invece composto dagli 8 ETF azionari del portafoglio Dedalo Eleven: la correlazione lineare tra questi due ETF è medio/alta, mentre è nulla o leggermente negativa quella con i 2 ETF del primo gruppo e medio/bassa quella con l’ETF del secondo gruppo.
La cluster analysis permette di apprezzare l’apporto in termini di diversificazione di ciascun ETF ma, di nuovo, non si dovrebbe valutare la bontà degli ETF o dei portafogli pigri soltanto in base alla correlazione.
In particolare:
- Non è detto che un portafoglio pigro composto da ETF non correlati tra di loro sia migliore di uno con uno o due soli ETF non correlati con gli altri: in generale, possiamo ritenere che il primo sia più diversificato e meno rischioso del secondo, ma un’alta diversificazione implica – probabilmente – un rendimento atteso minore. Gli investitori con un’alta propensione al rischio potrebbero preferire il secondo Lazy portfolio.
- Il numero di cluster in cui viene suddiviso ciascun Lazy portfolio è arbitrario: non esiste il numero ideale di cluster, seppure esso sia in qualche modo dipendente dal numero di ETF presenti nel portafoglio.
Nella matrice di correlazione appena analizzata avremmo potuto optare per 2 soli cluster (e in tal caso lo SBEME sarebbe stato accorpato al primo gruppo), così come avremmo potuto scegliere 4 o più cluster (col rischio però di frammentare troppo il portafoglio).
La suddivisione in 3 gruppi ci è sembrata la soluzione più valida. - Come è noto, i mercati finanziari sono positivamente correlati tra di loro e, in generale, è molto più facile trovare strumenti finanziari correlati positivamente che negativamente.
Non ci si deve meravigliare che il colore dominante delle matrici di correlazione sia il verde, con qualche sfumatura di bianco (assenza di correlazione lineare) e di rosa (correlazione negativa).
Un’analisi approfondita della correlazione lineare dovrebbe prevedere una misurazione rolling: se nei Lazy portfolios composti da pochi ETF uno studio del genere è fattibile, il compito diventerebbe proibitivo per i portafogli pigri più complessi.
La correlazione lineare tra i rendimenti degli strumenti finanziari svolge un ruolo fondamentale nel processo di asset allocation di un portafoglio finanziario: tanto più è negativa o tendente a 0, tanto maggiore è la diversificazione del portafoglio.
Più il portafoglio è diversificato, minore è il suo rischio. Questa semplice conclusione, oggi pressoché unanimemente riconosciuta come una delle regole fondamentali da rispettare negli investimenti, fu proposta per la prima volta nel già citato articolo Portfolio Selection, pubblicato nel 1952 da Harry Markowitz.
Markowitz dimostrò come, scegliendo la giusta combinazione di pesi dei titoli nella costruzione di un portafoglio, fosse addirittura possibile ridurne il rischio senza modificarne il rendimento atteso o, alternativamente, aumentarne il rendimento atteso a parità di rischio: l’insieme di combinazioni ottimali venne definito frontiera efficiente.
Un portafoglio efficiente è quindi quello caratterizzato dal minimo grado di rischio per ogni livello di rendimento atteso.
La scelta di un portafoglio efficiente rispetto a un altro dipenderà essenzialmente da fattori soggettivi, quali la propensione individuale al rischio e il rendimento atteso.
Il portafoglio efficiente per un determinato investitore sarà quello che giace sulla frontiera efficiente e corrisponde al suo specifico livello di tolleranza al rischio.
Nella realtà, i mercati azionari sono molto correlati tra loro e, durante le crisi finanziarie, si registra spesso un aumento di correlazione tra mercati azionari e obbligazionari: anche una correlazione positiva inferiore a 1, tuttavia, permette di ottenere dei benefici dalla diversificazione.
Questo risultato è dovuto alla modalità di calcolo della varianza dei rendimenti del portafoglio: a differenza del rendimento atteso, che è la media ponderata per i pesi dei rendimenti attesi di ciascuno strumento finanziario, nel calcolo della varianza del portafoglio entra in gioco la covarianza tra gli strumenti finanziari, che può essere positiva, negativa o nulla, a seconda di come gli strumenti finanziari co-variano tra loro.
Soltanto nel caso in cui la correlazione lineare tra tutti gli strumenti finanziari del portafoglio sia pari a 1, anche il calcolo della varianza del portafoglio – così come quello del rendimento atteso – diventa una semplice media ponderata delle varianze degli strumenti finanziari che lo compongono.
In conclusione, un portafoglio composto da ETF poco correlati o negativamente correlati tra di loro aumenta il livello di diversificazione e diminuisce il rischio dell’investimento.
Dato che il rischio, come abbiamo già detto a più riprese, è soltanto una delle due variabili che contraddistinguono gli investimenti (l’altra è il rendimento), ogni investitore dovrà selezionare il portafoglio pigro più adatto a lui in seguito a una scelta soggettiva, basata essenzialmente su 3 elementi fondamentali:
- L’intenzione del suo investimento (obiettivo dell’investimento).
- La volontà di sopportazione del rischio (propensione al rischio).
- La capacità di sopportazione del rischio, a sua volta funzione di 3 elementi molto importanti: l’orizzonte temporale dell’investimento, il reddito atteso e il patrimonio netto dell’investitore.
Considerazioni sull’uso degli ETF che hanno come sottostante azioni e obbligazioni dell’area euro
I Lazy portfolios in EUR che abbiamo utilizzato nei nostri backtest sono composti da molti ETF che hanno come sottostante azioni e obbligazioni dell’area euro.
Come abbiamo più volte ripetuto, l’idea è quella di mitigare o – se possibile – eliminare il rischio di cambio.
Alcuni investitori potrebbero storcere il naso all’idea di sostituire l’azionario americano con quello dell’area euro, ma la composizione dei Lazy portfolios backtestati non è scolpita nella pietra: può essere tranquillamente modificata.
I risultati dei backtest dei portafogli pigri in EUR possono essere considerati prudenziali: in passato, come vedremo, il mercato azionario americano ha ottenuto un rendimento mediamente superiore di quello europeo e – per quanto il futuro sia sconosciuto – è comprensibile che molti preferiscano non escludere l'azionario statunitense (è anche un mercato molto più grande di quello dell’area euro).
In quest’ottica, nei capitoli relativi a ciascun Lazy portfolio saranno suggeriti degli ETF alternativi, di solito più diversificati di quelli utilizzati. Inoltre, ogni investitore è libero di sostituire l’azionario dell’area euro con quello statunitense o globale.
In generale, però, si consiglia di creare un asset allocation che rispetti le seguenti condizioni:
- Comparto azionario: almeno il 50% hedgiato o area euro.
- Comparto obbligazionario: 100% hedgiato o area euro.
- Commodities: almeno il 50% hedgiato.
I motivi di queste scelte saranno più chiari dopo la lettura dei capitoli seguenti.
13.2 Primo e secondo livello di diversificazione

«In choosing a portfolio, investors should seek broad diversification. Further, they should understand that equities - and corporate bonds also - involve risk; that markets inevitably fluctuate; and their portfolio should be such that they are willing to ride out the bad as well as the good times».
Harry Markowitz
La diversificazione di cui abbiamo parlato nel capitolo precedente può essere definita come “primo livello di diversificazione”.
È quella che si ottiene inserendo nel portafoglio degli strumenti finanziari che replicano mercati che non sono correlati, sono correlati negativamente o, in ultima istanza, sono il meno possibile correlati positivamente tra loro.
Possiamo individuare anche un “secondo livello di diversificazione”, che si realizza grazie alla natura degli strumenti finanziari – gli ETF – che compongono i Lazy portfolios.
Ogni ETF è costituito da decine, centinaia o addirittura migliaia di titoli: azioni, obbligazioni, commodities o, negli ETF a replica sintetica, strumenti derivati che riflettono l’andamento dei primi tre.
Il possesso anche di una sola quota di un ETF, quindi, equivale al possesso di una piccola percentuale di ognuno dei suddetti titoli.
Il secondo livello di diversificazione permette la minimizzazione dei danni causati dal fallimento di una o più società o dal default di una o più delle obbligazioni detenute in portafoglio.
In altre parole, gli ETF minimizzano il rischio specifico di un investimento finanziario. L’investitore in ETF si accolla soltanto il rischio sistematico: il rischio associato all'andamento del mercato nel suo complesso.
Il rischio sistematico è ineliminabile. L’unica cosa che l’investitore può fare è mixare vari rischi sistematici – mercato azionario, obbligazionario o delle commodities – in modo tale da raggiungere un rischio medio il più possibile corrispondente a quello desiderato.
Questo è quello che avviene con il primo livello di diversificazione.
Il processo di investimento classico si ferma, di solito qui. Si sceglie un Lazy portfolio e lo si ribilancia periodicamente in base ai pesi di partenza di ciascun ETF.
Con le ottimizzazioni periodiche in base ai modelli vincolati e non vincolati, abbiamo fatto un ulteriore passo in avanti: lo scopo delle ottimizzazioni periodiche è stato proprio quello di modificare a intervalli regolari il rischio sistematico complessivo dei Lazy portfolios, per renderlo più adatto all’andamento dei mercati sottostanti.
Queste modifiche sono state realizzate in base ai modelli matematici presentati nel capitolo 9 e in nessun modo sulla base di views o previsioni soggettive sull’andamento dei mercati.
Pesi degli ETF
Conoscere i pesi che ogni modello di ottimizzazione ha assegnato a ogni ETF dei vari Lazy portfolios in ciascun sottoperiodo analizzato è possibile: sono informazioni disponibili, tracciate dagli algoritmi utilizzati in questo studio.
La visualizzazione di queste informazioni richiederebbe tuttavia centinaia di pagine sottoforma di tabelle: un’enorme mole di dati che sarebbe poco utile ai fini pratici.
Possiamo comunque fare qualche considerazione su quanto avvenuto in passato.
In generale, nei modelli vincolati il peso dell’ETF o degli ETF obbligazionari è stato spinto verso il limite massimo, pari alla percentuale prevista in ogni portafoglio standard, più il 5% discrezionale che abbiamo permesso all’algoritmo di aggiungere (o togliere).
Questo risultato si vede molto bene soprattutto nei Two funds portfolios, dove quasi in ogni variante la percentuale dell’ETF obbligazionario è stata del 5% più alta di quella prevista dal modello standard (e, di conseguenza, l’ETF azionario è stato mediamente un 5% più basso).
Anche i modelli non vincolati hanno in molte occasioni previsto alte percentuali di strumenti obbligazionari: in media, più alte di quelle che i pesi standard di ciascun Lazy portfolio avevano previsto.
Meno azionario e più obbligazionario, dunque, negli ultimi decenni e in particolar modo negli ultimi 20 anni.
Sarà così anche in futuro?
Nessuno può saperlo. Storicamente, i rendimenti obbligazionari sono sempre stati soddisfacenti, almeno nominalmente, soprattutto negli anni ’80 del secolo scorso (con valori spesso a due cifre). Essendo anche il tasso d’inflazione molto elevato, il rendimento reale obbligazionario era però parecchio inferiore a quello nominale.
Nello stesso tempo, la volatilità del mercato obbligazionario è sempre stata inferiore a quella del mercato azionario e il rapporto rischio/rendimento è stato, in passato, spesso a favore del primo.
Il tasso d’inflazione non è una variabile che viene presa in considerazione nelle ottimizzazioni periodiche dei Lazy portfolios: in futuro, i bassi rendimenti nominali e reali che stanno contraddistinguendo il mercato obbligazionario potrebbero modificare le proporzioni nei pesi risultanti dalle ottimizzazioni, con la possibilità che il 5% di sovrappeso nei modelli vincolati e oltre il 50% del peso totale in quelli non vincolati si spostino verso l’azionario.
Nello stesso tempo, un ritorno dell’inflazione a percentuali superiori a quelle attese o programmate non è da escludersi: la cosa migliore da fare è quella di non sbilanciarsi in previsioni – che vengono quasi sempre disattese – e di lasciar lavorare gli algoritmi di ottimizzazione anche in futuro.
13.3 Composizione, caratteristiche e risultati dei backtest di ogni Lazy portfolio

«Backtesting while researching is like drinking and driving. Do not research under the influence of a backtest».
Marcos Lopez de Prado
In questo capitolo passeremo in rassegna tutti i 40 Lazy portfolios che sono stati esaminati.
Dopo averne descritto brevemente la composizione e l’obiettivo, di ogni Lazy portfolio verranno mostrati i risultati completi dei backtest effettuati con tutti gli 11 modelli di ottimizzazione utilizzati.
Soltanto per i portafogli in EUR, verranno anche suggerite delle possibili alternative agli ETF che compongono il Lazy portfolio.
Dato che abbiamo svolto backtest in USD, USD→EUR e EUR su tre diverse durate (dal 1985, dal 2000 e dal 2010 al 2020), i risultati di ogni Lazy portfolio dovrebbero essere visualizzati con l’ausilio di 9 tabelle, ognuna delle quali composta da 12 righe (una per ogni misura statistica) e 11 colonne (11 modelli di ottimizzazione).
Per una maggiore facilità di lettura, comunque, ogni tabella sarà suddivisa in due più piccole:
- La prima, formata da 6 colonne: una con i risultati del modello statico "Standard" e 5 con quelli dei "Modelli dinamici vincolati".
- La seconda, formata da 5 colonne: una con i risultati del modello statico "1/N" e 4 con quelli dei "Modelli dinamici non vincolati".
Le 12 misure statistiche calcolate sono:
- Rendimento annualizzato (return)
- Standard deviation (deviazione standard)
- Indice di Sharpe (Sharpe ratio)
- Rendimento cumulato
- Massimo drawdown (worst drawdown)
- Drawdown medio (average drawdown)
- Durata media dei drawdown in giorni (average length)
- Periodo di recupero medio (average recovery)
- Esponente di Hurst (Hurst index)
- VaR
- CVaR
- Indice di Sortino (Sortino ratio)
Anche se, come già discusso nei capitoli precedenti, soltanto 5 misure statistiche sono state utilizzate per stilare le classifiche dei portafogli pigri e soltanto 2 per quelle dei modelli di ottimizzazione, per completezza verranno visualizzati i risultati di tutte le 12 misure statistiche di ogni Lazy portfolio.
La quantità di informazioni generata dall’analisi è imponente: al di là delle classifiche pubblicate nei capitoli 12.1 e 12.2, il consiglio è quello di non focalizzarsi troppo sui dati di questa o quella misura statistica; non prima, se non altro, di aver capito bene la composizione e la logica di funzionamento di ciascun portafoglio, con i suoi punti forti e le sue eventuali debolezze.
Un elemento di cui bisogna tener conto è che le analisi partono in date antecedenti all’esistenza degli ETF che compongono i Lazy portfolios (soprattutto nei backtest che iniziano nel 1985 ma, in alcuni casi, anche in quelli cominciati nel 2000 o nel 2010): come abbiamo specificato nel terzo capitolo, gli indici utilizzati in sostituzione agli ETF sono stati “assimilati” a questi ultimi, applicando loro artificiosamente i costi dell’ETF.
Tuttavia, non è detto che gli indici siano lo specchio fedele di ciò che sarebbero stati gli ETF se fossero esistiti: le differenze non dovrebbero tuttavia essere rilevanti, dato che stiamo parlando di ETF e non di fondi a gestione attiva.
Per ogni portafoglio pigro saranno suggeriti alcuni ETF come possibili alternative di quelli utilizzati. Non dovrebbero essere considerati peggiori o delle seconde scelte: certi ETF sono stati infatti inseriti nei portafogli in ragione delle loro più lunghe serie storiche, molto utili nei backtest.
Un investitore potrebbe optare per gli ETF alternativi senza problemi, specialmente nel caso in cui l’indice replicato sia lo stesso (o uno molto simile) e/o il TER sia più basso.
Nei capitoli successivi saranno esaminati – uno a uno – tutti i 40 Lazy portfolios presentati e backtestati in precedenza.
Una parte importante dell’analisi è costituita dalla visualizzazione dei grafici delle equity line e dei drawdown di ciascun portafoglio: avendo backtestato 11 modelli di ottimizzazione, la scelta è stata quella di utilizzare i loro rendimenti medi ai fini dei suddetti grafici.
L’utilizzo delle medie dei rendimenti smussa i valori estremi: ad esempio, il massimo drawdown della media dei rendimenti generati dagli 11 modelli di ottimizzazione sarà per forza di cose minore del più alto massimo drawdown generato dal modello più rischioso.
L’approssimazione adottata è necessaria per evitare di visualizzare troppe informazioni, che avrebbero reso i grafici incomprensibili. È bene però tenere presente che i valori estremi di alcuni modelli sono più alti o più bassi di quelli delle serie storiche medie utilizzate.
Come approfondiremo nel capitolo 15, un costo basso è uno degli elementi più importanti nel perseguimento dell’efficienza di un portafoglio.
La tabella seguente riporta il TER medio di ciascun Lazy portfolio nella sua versione originale (modello “Standard”), sia in USD che in EUR, nonché il numero di ETF e l’asset allocation di ognuno.
| Lazy portfolios: asset allocation e TER medio1 | |||||
|---|---|---|---|---|---|
| Asset allocation, numero di ETF e TER medio dei Lazy portfolios in USD e in EUR | |||||
| Lazy Portfolio | Nr. ETF | TER MEDIO | Azioni | Obbligazioni | Materie prime |
| USD | |||||
| World Bond | 1 | 0.150% | 0% | 100% | 0% |
| World Stocks | 1 | 0.080% | 100% | 0% | 0% |
| Two funds 10/90 | 2 | 0.034% | 10% | 90% | 0% |
| Two funds 20/80 | 2 | 0.034% | 20% | 80% | 0% |
| Two funds 30/70 | 2 | 0.034% | 30% | 70% | 0% |
| Two funds 40/60 | 2 | 0.033% | 40% | 60% | 0% |
| Two funds 50/50 | 2 | 0.032% | 50% | 50% | 0% |
| Two funds 60/40 | 2 | 0.032% | 60% | 40% | 0% |
| Two funds 70/30 | 2 | 0.031% | 70% | 30% | 0% |
| Two funds 80/20 | 2 | 0.031% | 80% | 20% | 0% |
| Two funds 90/10 | 2 | 0.030% | 90% | 10% | 0% |
| Warren Buffett | 2 | 0.051% | 90% | 10% | 0% |
| Simple Path to Wealth | 2 | 0.031% | 75% | 25% | 0% |
| Couch Potato | 2 | 0.110% | 50% | 50% | 0% |
| Three Funds Bogleheads | 3 | 0.046% | 80% | 20% | 0% |
| Second Grader's Starter | 3 | 0.045% | 90% | 10% | 0% |
| Talmud | 3 | 0.062% | 67% | 33% | 0% |
| Margaritaville | 3 | 0.100% | 67% | 33% | 0% |
| Andrew Tobias | 3 | 0.167% | 67% | 33% | 0% |
| Gyroscopic Investing Desert | 3 | 0.139% | 30% | 60% | 10% |
| Permanent | 4 | 0.180% | 25% | 50% | 25% |
| Core Four | 4 | 0.050% | 80% | 20% | 0% |
| Bogleheads Four Funds | 4 | 0.061% | 80% | 20% | 0% |
| No Brainer | 4 | 0.082% | 75% | 25% | 0% |
| Larry | 4 | 0.228% | 30% | 70% | 0% |
| Golden Butterfly | 5 | 0.182% | 40% | 40% | 20% |
| All Weather | 5 | 0.178% | 30% | 55% | 15% |
| Ivy | 5 | 0.203% | 60% | 40% | 0% |
| Dynamic 60/40 Income | 5 | 0.250% | 60% | 40% | 0% |
| Dynamic 40/60 Income | 5 | 0.304% | 40% | 60% | 0% |
| Five Asset | 6 | 0.232% | 60% | 20% | 20% |
| David Swensen Lazy Portfolio | 6 | 0.131% | 70% | 30% | 0% |
| Coffee House | 7 | 0.066% | 60% | 40% | 0% |
| Rob Arnott | 8 | 0.190% | 30% | 60% | 10% |
| Ultimate Buy and Hold Strategy | 10 | 0.264% | 100% | 0% | 0% |
| Ultimate Buy & Hold | 12 | 0.229% | 60% | 40% | 0% |
| Dedalo Three | 3 | 0.045% | 100% | 0% | 0% |
| Dedalo Four | 4 | 0.052% | 80% | 20% | 0% |
| Dedalo Eleven | 11 | 0.205% | 80% | 20% | 0% |
| EUR | |||||
| World Bond | 1 | 0.150% | 0% | 100% | 0% |
| World Stocks | 1 | 0.450% | 100% | 0% | 0% |
| Two funds 10/90 | 2 | 0.174% | 10% | 90% | 0% |
| Two funds 20/80 | 2 | 0.168% | 20% | 80% | 0% |
| Two funds 30/70 | 2 | 0.162% | 30% | 70% | 0% |
| Two funds 40/60 | 2 | 0.156% | 40% | 60% | 0% |
| Two funds 50/50 | 2 | 0.150% | 50% | 50% | 0% |
| Two funds 60/40 | 2 | 0.144% | 60% | 40% | 0% |
| Two funds 70/30 | 2 | 0.138% | 70% | 30% | 0% |
| Two funds 80/20 | 2 | 0.132% | 80% | 20% | 0% |
| Two funds 90/10 | 2 | 0.126% | 90% | 10% | 0% |
| Warren Buffett | 2 | 0.458% | 90% | 10% | 0% |
| Simple Path to Wealth | 2 | 0.135% | 75% | 25% | 0% |
| Couch Potato | 2 | 0.105% | 50% | 50% | 0% |
| Three Funds Bogleheads | 3 | 0.201% | 80% | 20% | 0% |
| Second Grader's Starter | 3 | 0.195% | 90% | 10% | 0% |
| Talmud | 3 | 0.210% | 67% | 33% | 0% |
| Margaritaville | 3 | 0.187% | 67% | 33% | 0% |
| Andrew Tobias | 3 | 0.213% | 67% | 33% | 0% |
| Gyroscopic Investing Desert | 3 | 0.197% | 30% | 60% | 10% |
| Permanent | 4 | 0.250% | 25% | 50% | 25% |
| Core Four | 4 | 0.204% | 80% | 20% | 0% |
| Bogleheads Four Funds | 4 | 0.192% | 80% | 20% | 0% |
| No Brainer | 4 | 0.397% | 75% | 25% | 0% |
| Larry | 4 | 0.281% | 30% | 70% | 0% |
| Golden Butterfly | 5 | 0.322% | 40% | 40% | 20% |
| All Weather | 5 | 0.192% | 30% | 55% | 15% |
| Ivy | 5 | 0.266% | 60% | 40% | 0% |
| Dynamic 60/40 Income | 5 | 0.242% | 60% | 40% | 0% |
| Dynamic 40/60 Income | 5 | 0.256% | 40% | 60% | 0% |
| Five Asset | 6 | 0.261% | 60% | 20% | 20% |
| David Swensen Lazy Portfolio | 6 | 0.221% | 70% | 30% | 0% |
| Coffee House | 7 | 0.320% | 60% | 40% | 0% |
| Rob Arnott | 8 | 0.220% | 30% | 60% | 10% |
| Ultimate Buy and Hold Strategy | 10 | 0.399% | 100% | 0% | 0% |
| Ultimate Buy & Hold | 12 | 0.318% | 60% | 40% | 0% |
| Dedalo Three | 3 | 0.172% | 100% | 0% | 0% |
| Dedalo Four | 4 | 0.157% | 80% | 20% | 0% |
| Dedalo Eleven | 11 | 0.223% | 80% | 20% | 0% |
|
1 Il TER medio viene calcolato in base ai pesi "standard" di ciascun ETF (media ponderata). |
|||||
La media dei TER dei portafogli in USD è inferiore a quello dei portafogli in EUR: 0,113% contro 0,224%. Poco più della metà.
D’altra parte, gli ETF sono nati nel mercato finanziario statunitense, che è molto più sviluppato e concorrenziale di quello europeo.
In futuro, è auspicabile che il mercato degli ETF dell’area euro riduca il gap che ancora lo separa da quello statunitense in termini di costi.
Un TER medio dello 0,224% è comunque molto competitivo. Come discusso nel capitolo 6, non bisogna inoltre dimenticare che la scelta degli ETF inseriti in portafoglio non è sempre stata effettuata sulla base dei minori costi: esiste la possibilità concreta per l’investitore di abbassare ulteriormente il TER medio dei Lazy portfolios in EUR.
Lazy portfolios
Cliccando su uno dei seguenti link si aprirà la pagina relativa al Lazy portfolio scelto.
13.3.1 World Bond
13.3.2 World Stocks
13.3.3 Two funds portfolios
13.3.4 Warren Buffett
13.3.5 Simple Path to Wealth
13.3.6 Couch Potato
13.3.7 Three Funds Bogleheads
13.3.8 Second Grader's Starter
13.3.9 Talmud
13.3.10 Margaritaville
13.3.11 Andrew Tobias
13.3.12 Gyroscopic Investing Desert
13.3.13 Permanent
13.3.14 Core Four
13.3.15 Bogleheads Four Funds
13.3.16 No Brainer
13.3.17 Larry
13.3.18 Golden Butterfly
13.3.19 All Weather
13.3.20 Ivy
13.3.21 Dynamic 60/40 Income
13.3.22 Dynamic 40/60 Income
13.3.23 Five Asset
13.3.24 David Swensen Lazy Portfolio
13.3.25 Coffee House
13.3.26 Rob Arnott
13.3.27 Ultimate Buy and Hold Strategy
13.3.28 Ultimate Buy & Hold
13.3.29 Dedalo Three
13.3.30 Dedalo Four
13.3.31 Dedalo Eleven
14. Rendimenti rolling dei Lazy portfolios a 5 e 10 anni

«Se si esclude dalle attività umane tutto quanto attiene al raggiungimento del profitto, rimarrà soltanto l'arte».
Andrej Tarkovskij
L’analisi effettuata finora è stata caratterizzata dal calcolo delle misure statistiche di nostro interesse sull’interezza dei periodi scelti: 1985-2020, 2000-2020 e 2010-2020, pari a 35, 20 e 10 anni.
Un investitore potrebbe chiedersi che cosa sarebbe accaduto se avesse investito utilizzando un certo Lazy portfolio ottimizzato con uno dei modelli studiati per periodi inferiori o, perché no, di simile durata ma diversi da quelli da noi scelti: ad esempio, che rendimento sarebbe stato generato nei 10 anni che vanno dal 2005 al 2015 o dal 1996 al 2006, invece che dal 2010 al 2020?
Ovviamente, un’analisi che copra tutte le possibili durate o tutte le possibili finestre temporali di un investimento è impossibile da realizzare.
Quello che abbiamo fatto, allora, è calcolare in modalità rolling due specifiche durate – 5 e 10 anni – a partire dalla serie dei rendimenti generata dal backtest più lungo.
Dal momento che abbiamo utilizzato 11 modelli di ottimizzazione, sarebbero necessarie 11 analisi rolling a 5 anni e 11 a 10 anni per ciascun Lazy portfolio/valuta; ognuna di esse produrrebbe un set di risultati: rendimento medio, massimo, minimo e standard deviation dei rendimenti del portafoglio in USD, USD→EUR e EUR.
Il numero totale sarebbe vicino al migliaio.
Abbiamo perciò deciso di utilizzare la serie storica dei rendimenti medi degli 11 modelli, in modo da ridurre il numero di grafici visualizzati: 80 invece di 880.
I grafici conterranno 3 rappresentazioni in formato lineare dei rendimenti rolling di investimenti a 5 e 10 anni:
- La linea blu sarà quella dei rendimenti rolling dei portafogli in USD.
- La linea rossa sarà quella dei rendimenti rolling dei portafogli in USD→EUR.
- La linea verde sarà quella dei rendimenti rolling dei portafogli in EUR.
Nella parte bassa dei grafici, saranno mostrati il rendimento medio, massimo, minimo e la deviazione standard dei rendimenti dei tre portafogli.
Commenteremo soprattutto i grafici dei primi portafogli. Una volta descritte le peculiarità di questa tipologia di grafici, non sarà necessario ripetere le stesse osservazioni anche nei grafici successivi.
WORLD BOND
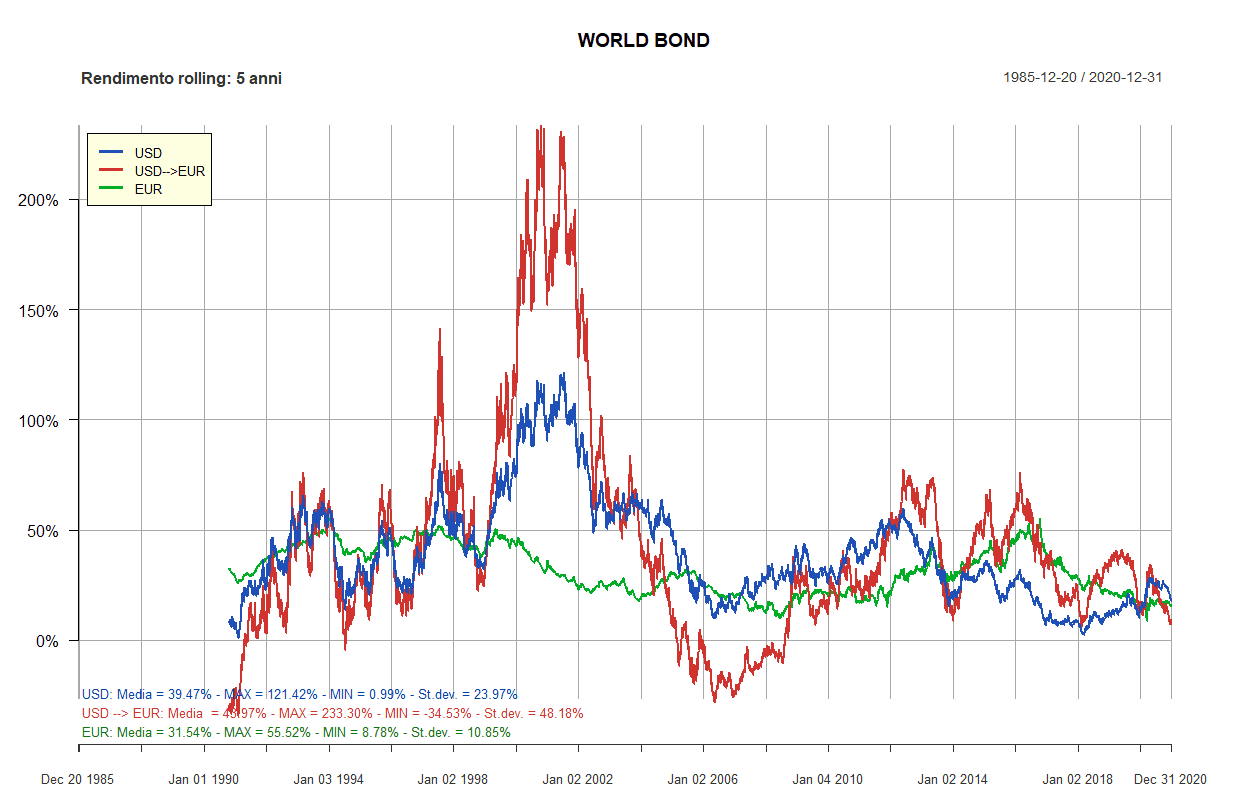
Questo grafico mostra i rendimenti rolling a 5 anni ottenuti dal World Bond Lazy portfolio.
Il grafico comincia approssimativamente all’inizio del 1991 e termina il 31 dicembre 2020:
- Il primo rendimento quinquennale è quello dell’investimento cominciato il 19 dicembre 1985 e terminato il 17 ottobre 1990.
- L’ultimo rendimento quinquennale è quello dell’investimento cominciato il 16 febbraio 2016 e terminato il 31 dicembre 2020.
È un grafico costruito su base giornaliera: contiene tutti i rendimenti a 5 anni che si sarebbero potuti ottenere iniziando l’investimento in un giorno qualsiasi del periodo compreso tra il 19 dicembre 1985 e il 16 febbraio 2016.
Per ogni portafoglio, sono stati cioè calcolati circa 7.560 rendimenti.
La linea rossa è quella che cattura subito l’occhio: parte in territorio negativo, cresce in maniera abbastanza erratica amplificando enormemente le oscillazioni della linea blu, tocca i suoi massimi nel biennio compreso tra il 2000 e il 2002, scende con violenza fino a raggiungere di nuovo valori ampiamente negativi e finisce la sua corsa – più o meno per tutto l’ultimo decennio – in un range di valori compreso tra il 10% e il 75%.
La linea rossa è quella dei rendimenti rolling dei portafogli in USD trasformati in EUR in base al tasso di cambio corrente: sono i Lazy portfolios di un investitore dell’area euro che abbia utilizzato strumenti in USD non coperti dal cambio.
La linea rossa e la linea blu sono molto diverse ma in stretta relazione tra loro, dato che la rossa è uguale alla blu trasformata dal rapporto di cambio tra dollaro ed euro.
La linea verde, invece, misura i rendimenti rolling dei portafogli in EUR che, come ormai sappiamo, sono costruiti con ETF diversi da quelli in USD.
Analizziamo i rendimenti rolling a 5 anni del World Bond in USD:
- Il rendimento medio è 39,47%: è la media dei circa 7.560 rendimenti che sono stati calcolati nel modo seguente: il primo è quello dell’investimento iniziato il 19 dicembre 1985 e terminato il 17 ottobre 1990; il secondo, quello iniziato il 20 dicembre 1985 e terminato il 18 ottobre 1990, e così via, giorno dopo giorno, fino al 7560° e ultimo investimento, iniziato il 16 febbraio 2016 e terminato il 31 dicembre 2020. Dato che ogni anno ci sono circa 252 giorni borsistici, il calcolo è presto fatto: 252 x 30 (il numero di anni compreso tra inizio 1991 e fine 2020) = 7.560.
- Il più alto di questi rendimenti è stato del 121,42%; il più basso, dello 0,99%.
- La deviazione standard dei 7.560 rendimenti calcolati è stata del 23,97%.
Sono risultati ragionevoli, con valori estremi che in un primo momento possono sembrare eccessivi: non dobbiamo però dimenticare che questa analisi copre oltre 3 decenni caratterizzati da crisi finanziarie gravi, periodi di rapida crescita economica e momenti di lateralità del mercato.
Vediamo in dettaglio i rendimenti rolling a 5 anni del World Bond in USD→EUR:
- Il rendimento medio è 43,97%.
- Il più alto di questi rendimenti è stato del 233,30%; il più basso, del −34,53%.
- La deviazione standard dei 7.560 rendimenti calcolati è stata del 48,18%.
Sono valori che fanno impressione, considerando che stiamo parlando di un portafoglio al 100% obbligazionario: sembrano completamente fuori controllo.
Il valore massimo è eccezionale e può far gola all’investitore, ma che cosa dovremmo dire di quello minimo?
Un portafoglio 100% obbligazionario è adatto a un investitore dalla bassa propensione al rischio; se così non fosse, avrebbe fatto meglio a optare per un asset allocation per lo meno bilanciata.
Un rendimento così tanto negativo per un portafoglio sulla carta molto prudente è inaccettabile: eppure, sarebbe stato proprio quello ottenuto da un investitore dell’area euro che avesse deciso di utilizzare un World Bond in USD dal cambio non coperto.
Entra in gioco anche la componente casuale: il rendimento minimo sarebbe stato un risultato molto sfortunato ma, come il grafico evidenzia, non isolato.
I rendimenti negativi della linea rossa sono numerosi e tali sono anche le occasioni in cui essa si posiziona sotto alla linea blu.
Ovviamente, è vero anche il contrario: gli investitori fortunati avrebbero potuto ottenere dei rendimenti quinquennali favolosi, ma è giusto domandarsi fino a quanto ci si vuole affidare alla fortuna in un investimento.
In ogni caso, possiamo affermare che scegliere di investire in un World Bond USD→EUR non sarebbe stata una scelta efficiente:
- Un investitore prudente, che per definizione non sarebbe stato interessato a scommettere col mercato, avrebbe dovuto utilizzare il World Bond in EUR (linea verde) o coprendo integralmente il rischio di cambio di quello in USD (linea blu).
- Un investitore mediamente o molto aggressivo avrebbe dovuto utilizzare un portafoglio più rischioso del World Bond (con una componente azionaria maggiore, quindi con più rischio di mercato, ma con meno rischio di cambio).
Una misura statistica – in particolare – rende l’idea di quanto più volatile sia un investimento dal cambio scoperto rispetto a uno in EUR o in USD dal cambio coperto: la deviazione standard dei rendimenti del World Bond in USD→EUR, che è pari a 48,18% contro il 23,97% di quella del World Bond in USD (più del doppio).
Vediamo infine i rendimenti rolling a 5 anni del World Bond EUR:
- Il rendimento medio è stato del 31,54%.
- Il più alto di questi rendimenti è stato del 55,52%; il più basso, dell’8,78%.
- La deviazione standard dei 7.560 rendimenti calcolati è stata del 10,85%.
Sono dei valori più moderati dei precedenti: nel periodo analizzato, evidentemente, il mercato obbligazionario dell’area euro è stato meno volatile di quello statunitense.
Vediamo il grafico del rendimento rolling a 10 anni:
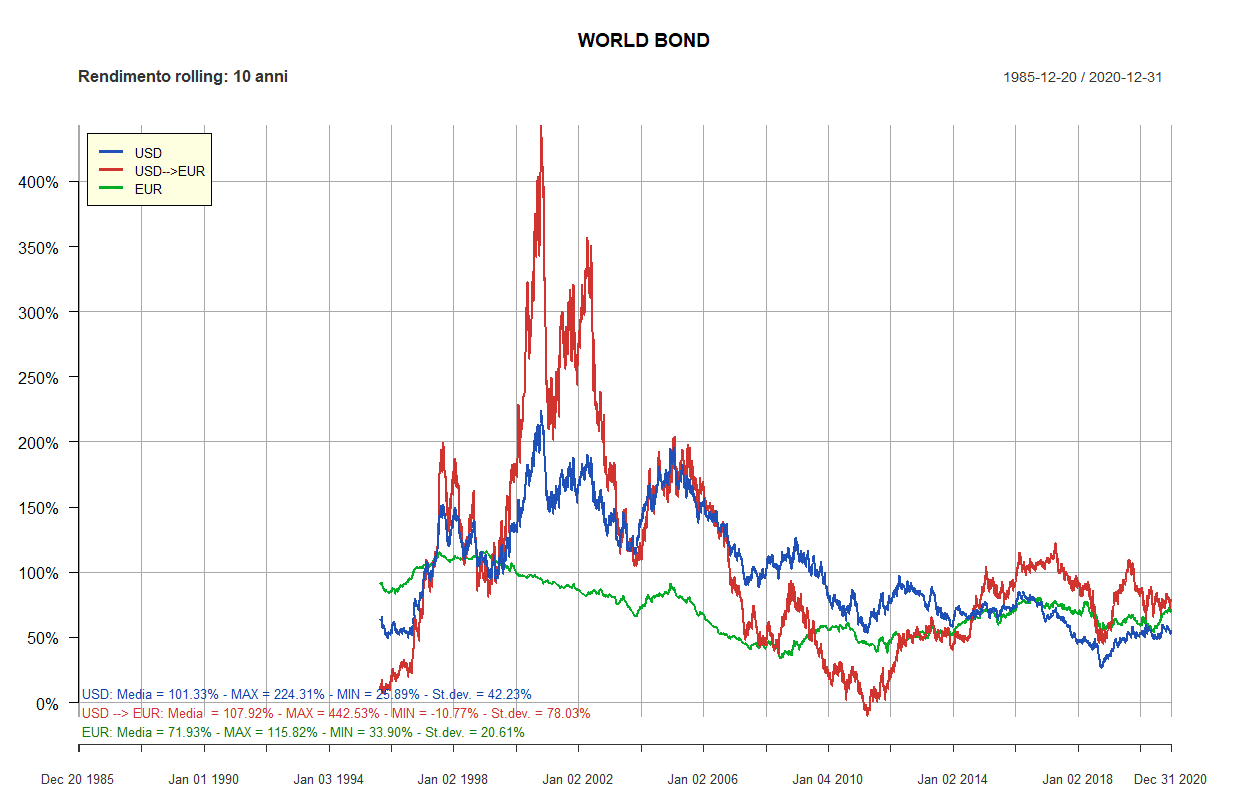
Stavolta il grafico inizia il 28 agosto 1995 e termina il 31 dicembre 2020:
- Il primo rendimento decennale è quello dell’investimento cominciato il 19 dicembre 1985 e terminato il 25 agosto 1995.
- L’ultimo rendimento decennale è quello dell’investimento cominciato il 28 marzo 2011 e terminato il 31 dicembre 2020.
Le osservazioni relative al grafico dei rendimenti rolling a 5 anni possono essere estese a questo.
La linea rossa esaspera le oscillazioni della linea blu; quella verde è molto meno volatile.
I valori medi, massimi, minimi e quelli relativi alla deviazione standard possono essere letti direttamente sul grafico.
WORLD STOCKS
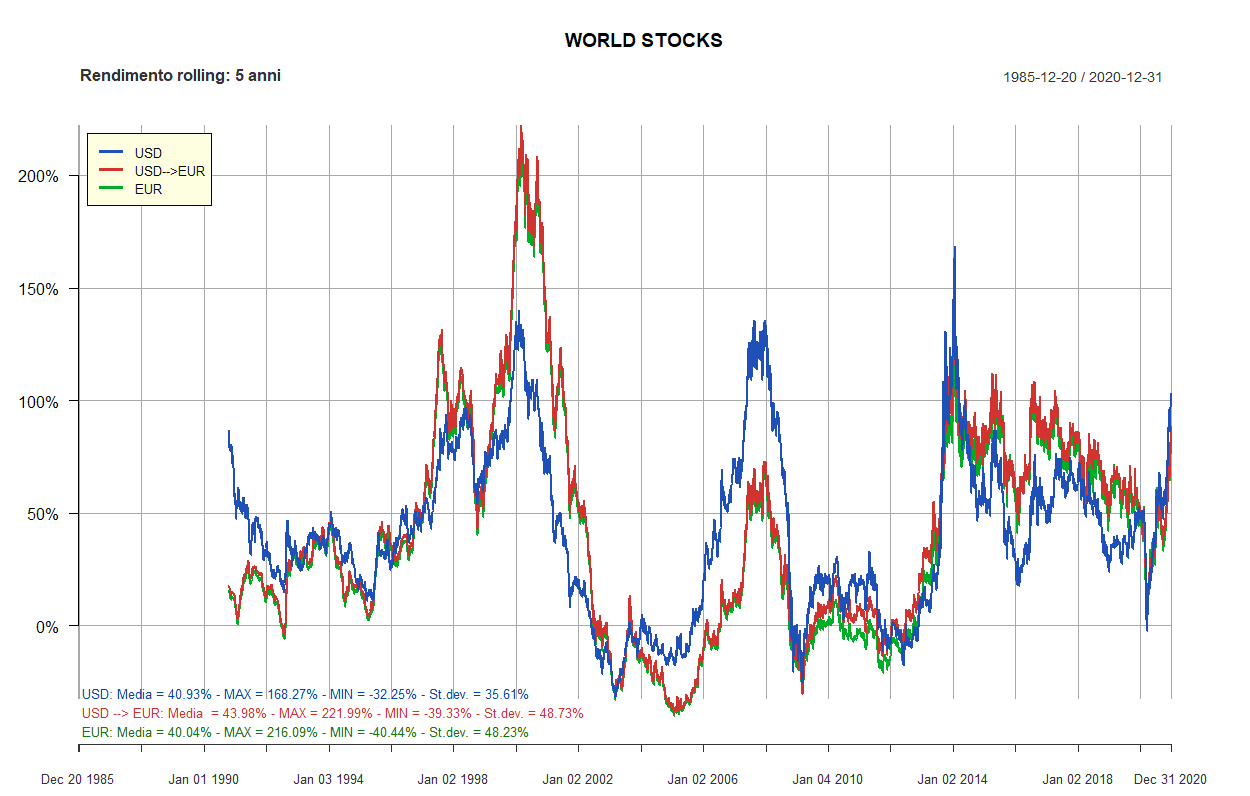
Partiamo dal grafico dei rendimenti rolling a 5 anni del World Stocks.
L’asset allocation si è adesso modificata dal 100% obbligazionario e 0% azionario al 100% azionario e 0% obbligazionario.
Accade qualcosa di apparentemente strano, ma è ciò che avevamo verificato anche nell’analisi delle equity lines e dei drawdown del capitolo 13.3.2: i rendimenti rolling del World Stocks in USD sono molto meno volatili di quelli del World Stocks in EUR. Esattamente l’opposto di ciò che era accaduto per il World Bond.
Come avevamo spiegato questo risultato?
Avevamo visto che di mezzo c’era il rapporto di cambio, dato che l’ETF utilizzato nel World Stocks in USD è il Vanguard Total World Stock (VT) e quello utilizzato nel World Stocks in EUR è il Lyxor MSCI All Country World UCITS ETF Acc EUR (ACWI).
La valuta sottostante al 60% circa è il dollaro; l’euro copre meno del 10% di entrambi gli ETF.
Tornando al grafico precedente, abbiamo che:
- La linea blu che traccia i rendimenti rolling a 5 anni del World Stocks in USD è soggetta al rischio di cambio per un 40% circa (azioni quotate in valuta diversa dal dollaro).
- La linea verde che traccia i rendimenti rolling a 5 anni del World Stocks in EUR è soggetta al rischio di cambio per oltre il 90% (azioni quotate in valuta diversa dall’euro, delle quali il 60% è il dollaro).
- La linea rossa trasforma in euro i rendimenti della linea blu: in altre parole, aggiunge il rischio di cambio tra dollaro ed euro, niente di diverso a ciò che è già implicitamente effettuato nell’ETF utilizzato dal World Stocks in EUR, che contiene già convertita in euro tutta la componente azionaria la cui valuta sottostante è il dollaro.
L’utilizzo nel World Stocks di un ETF contenente società appartenenti all’area euro avrebbe eliminato interamente il rischio di cambio con le altre valute (soprattutto il dollaro) e possiamo ipotizzare che l’eventuale linea verde del portafoglio così costruito sarebbe stata molto meno volatile e molto più vicina alla linea blu che non a quella rossa.
Vediamo il rendimento rolling a 10 anni:
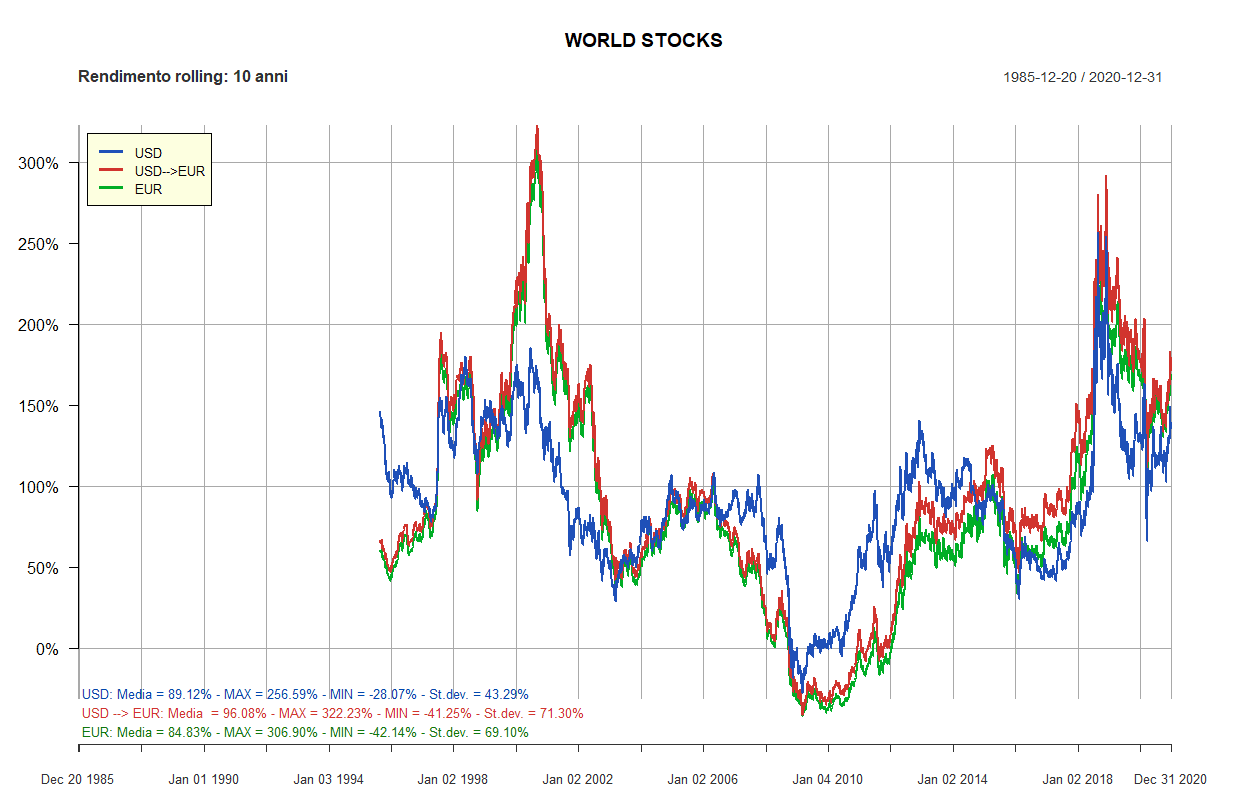
Di nuovo, le conclusioni precedenti possono essere estese ai rendimenti rolling a 10 anni.
TWO FUND 10/90
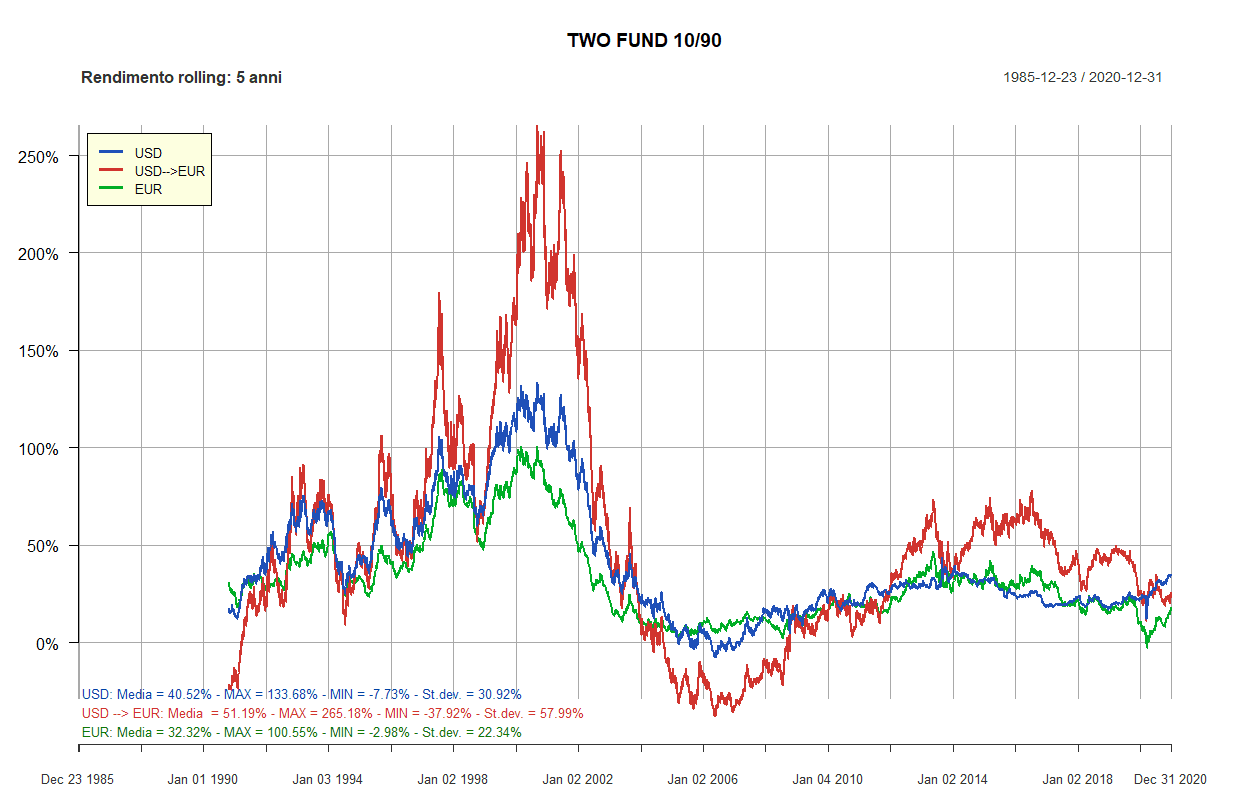
Anche nel Two funds 10/90 l’impatto del tasso di cambio USD/EUR risalta subito agli occhi: la linea rossa inasprisce le fluttuazioni di quella blu, mentre il Two funds in EUR ha un andamento molto più tranquillo.
L’ETF azionario utilizzato nel portafoglio in EUR è l’iShares Core MSCI EMU UCITS ETF EUR Acc (CSEMU), la cui valuta sottostante è l’euro. La stessa cosa vale per l’ETF obbligazionario utilizzato: è il WisdomTree EUR Aggregate Bond Enhanced Yield UCITS ETF EUR Acc (EYLD), che replica obbligazioni denominate in euro.
Possiamo concludere che, in tutti i grafici dei vari Two funds portfolios, le linee verdi saranno l’espressione dell’andamento dei mercati replicati, senza alcuna interferenza del rapporto di cambio tra euro e altre valute (in altre parole, senza rischio di cambio).
Vediamo il rendimento rolling a 10 anni:
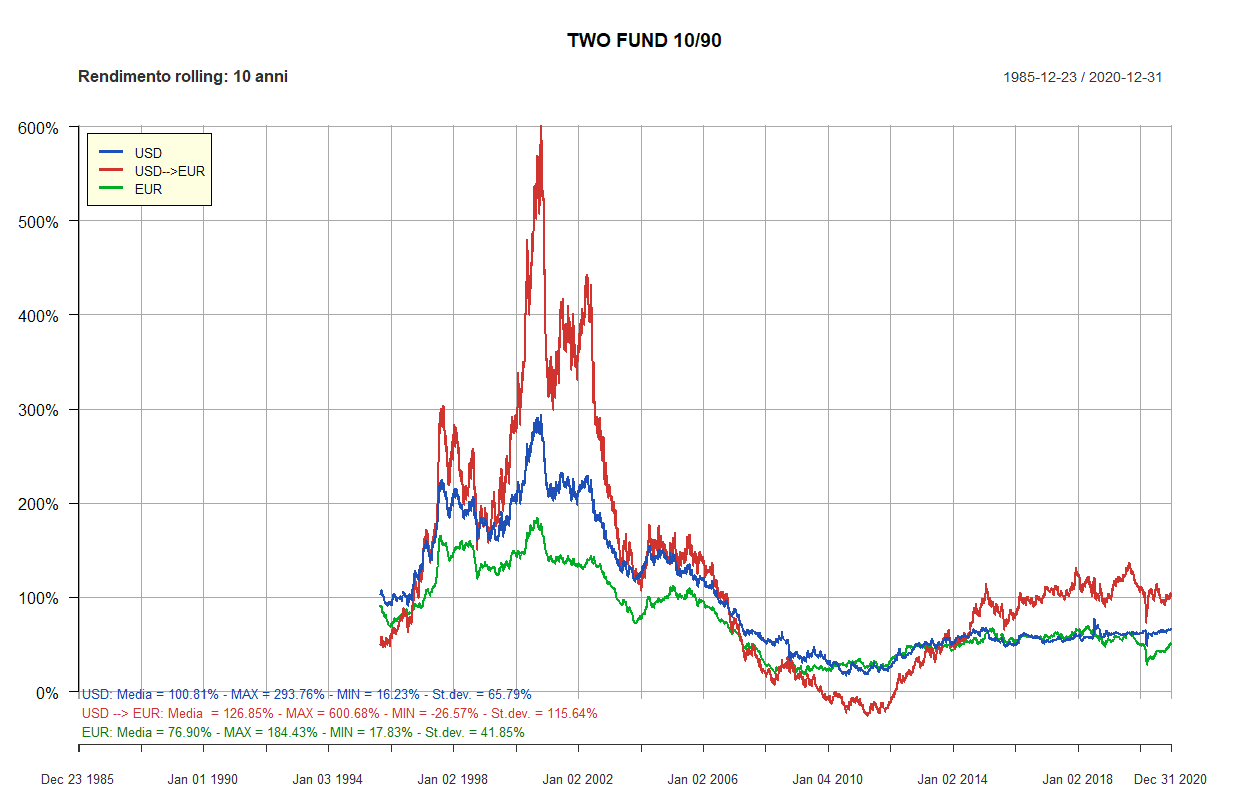
La portata del rischio di cambio è impressionante: il massimo rendimento rolling del portafoglio in USD è di quasi il 300%, mentre quello del portafoglio in USD→EUR è addirittura del 600%!
Il rovescio della medaglia, però, è che il rendimento minimo scende dal 16,23% al −26,57% e la volatilità passa dal 65,79% al 115,64%. Per un portafoglio obbligazionario al 90%, sono valori estremamente alti.
Saranno adesso visualizzati i grafici degli altri Two funds portfolios, in ordine crescente di rischiosità.
TWO FUND 20/80
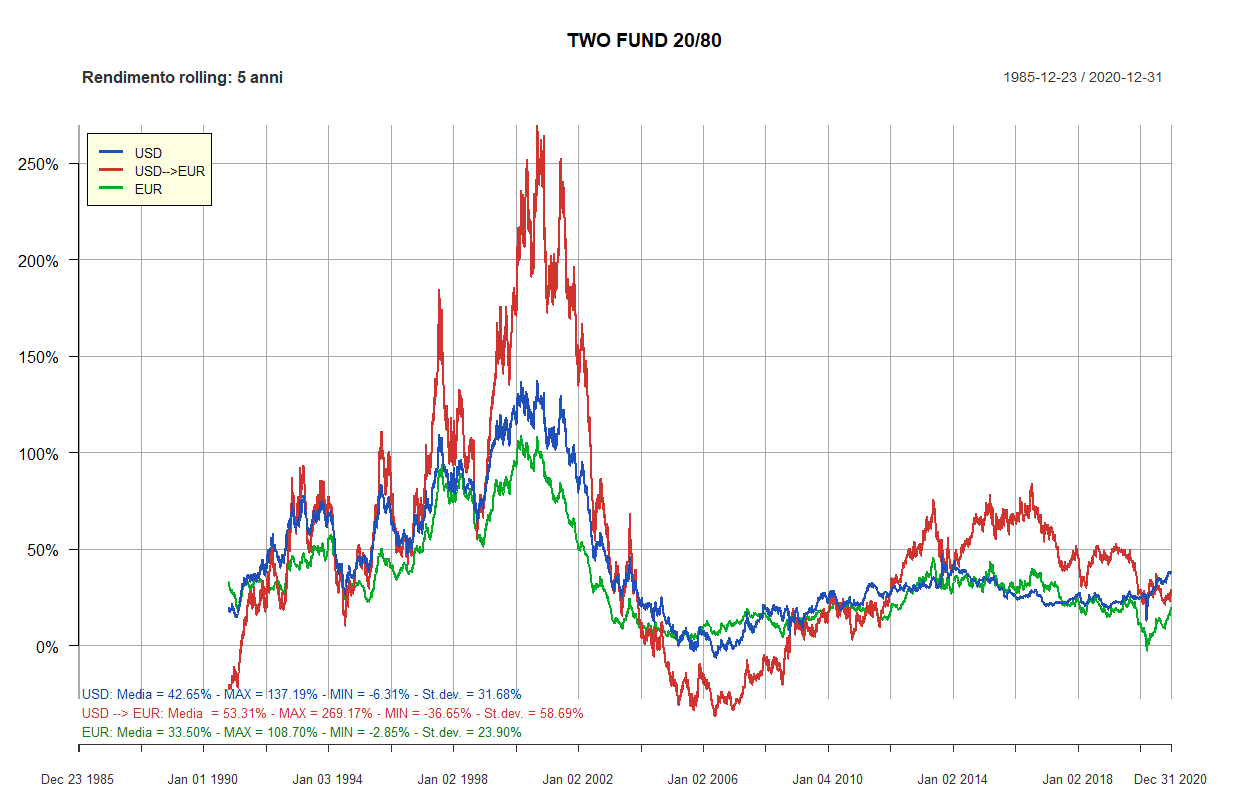
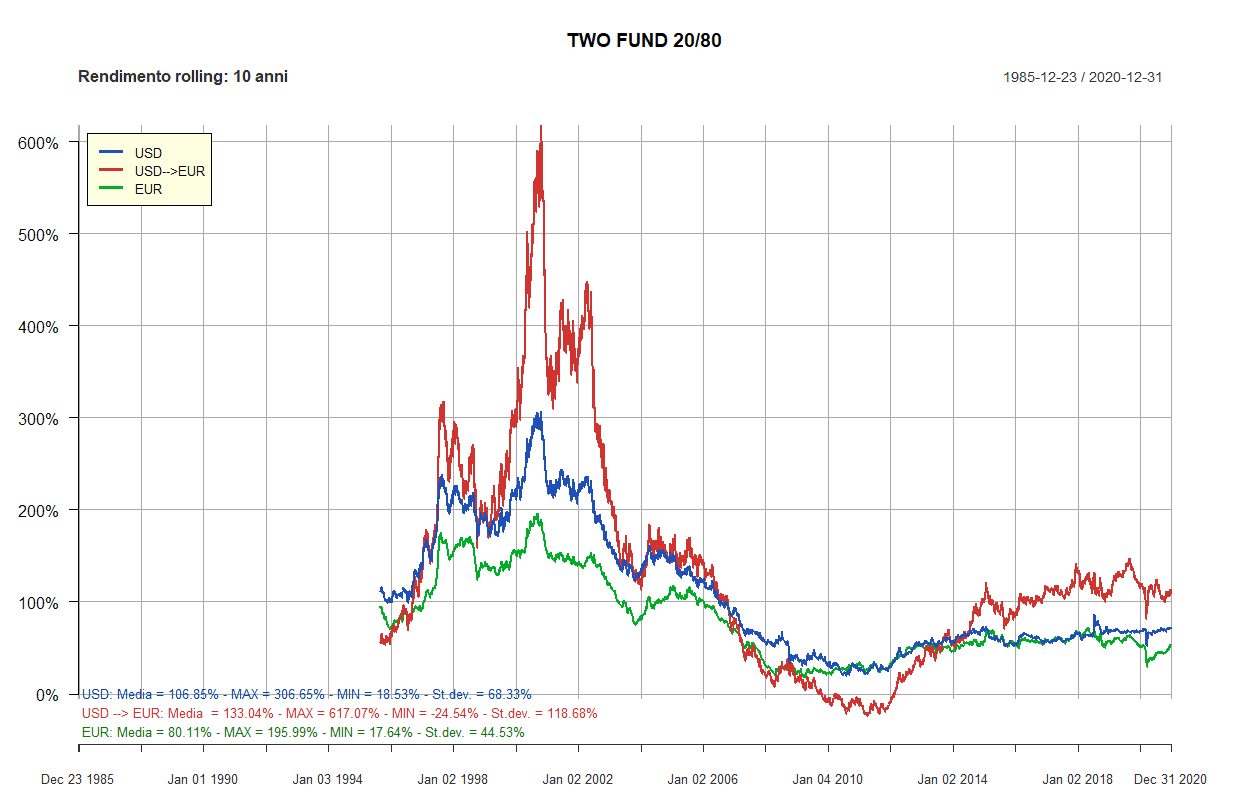
TWO FUND 30/70
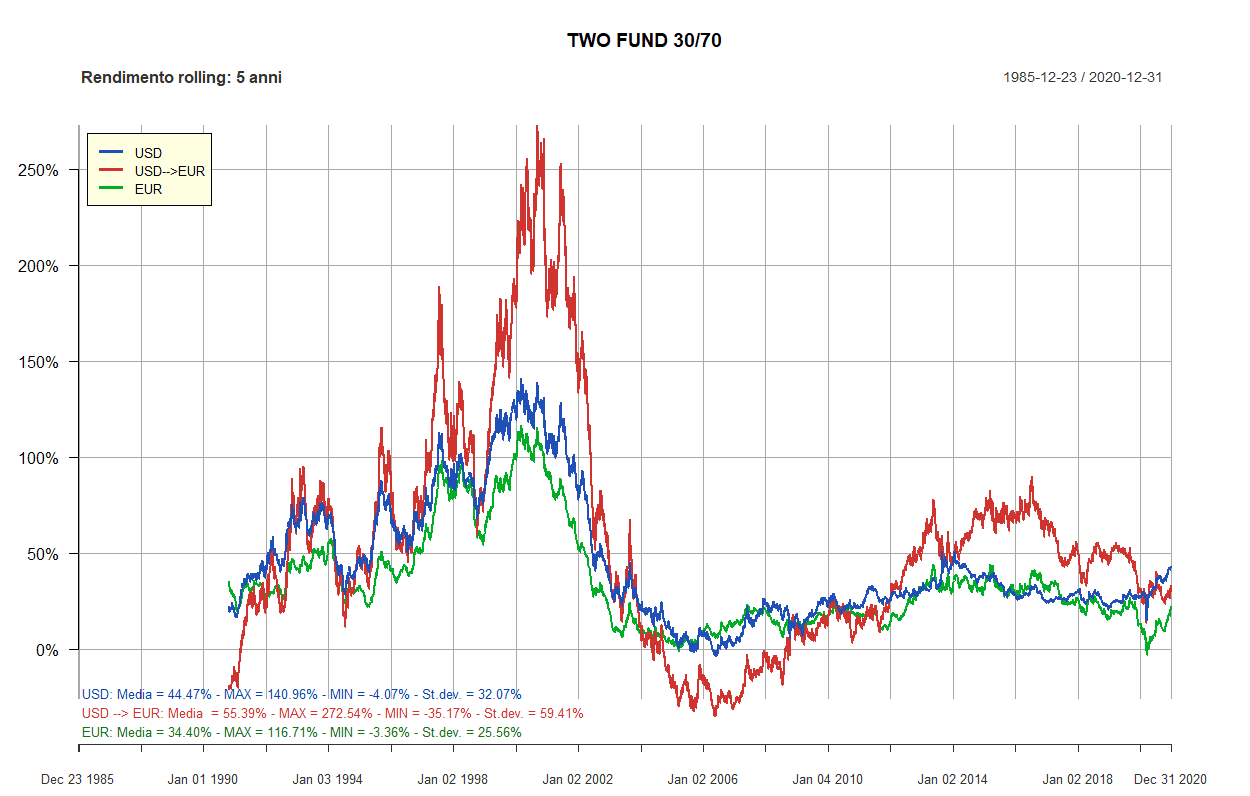
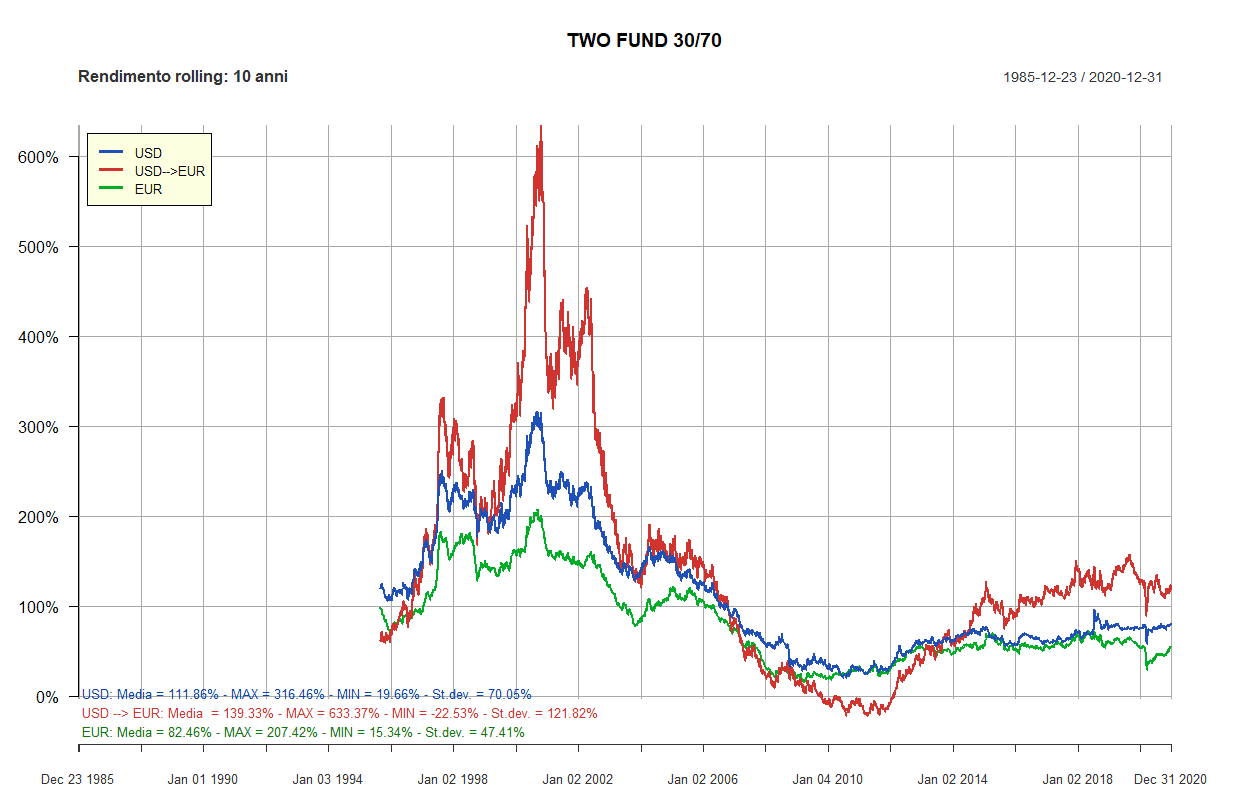
TWO FUND 40/60
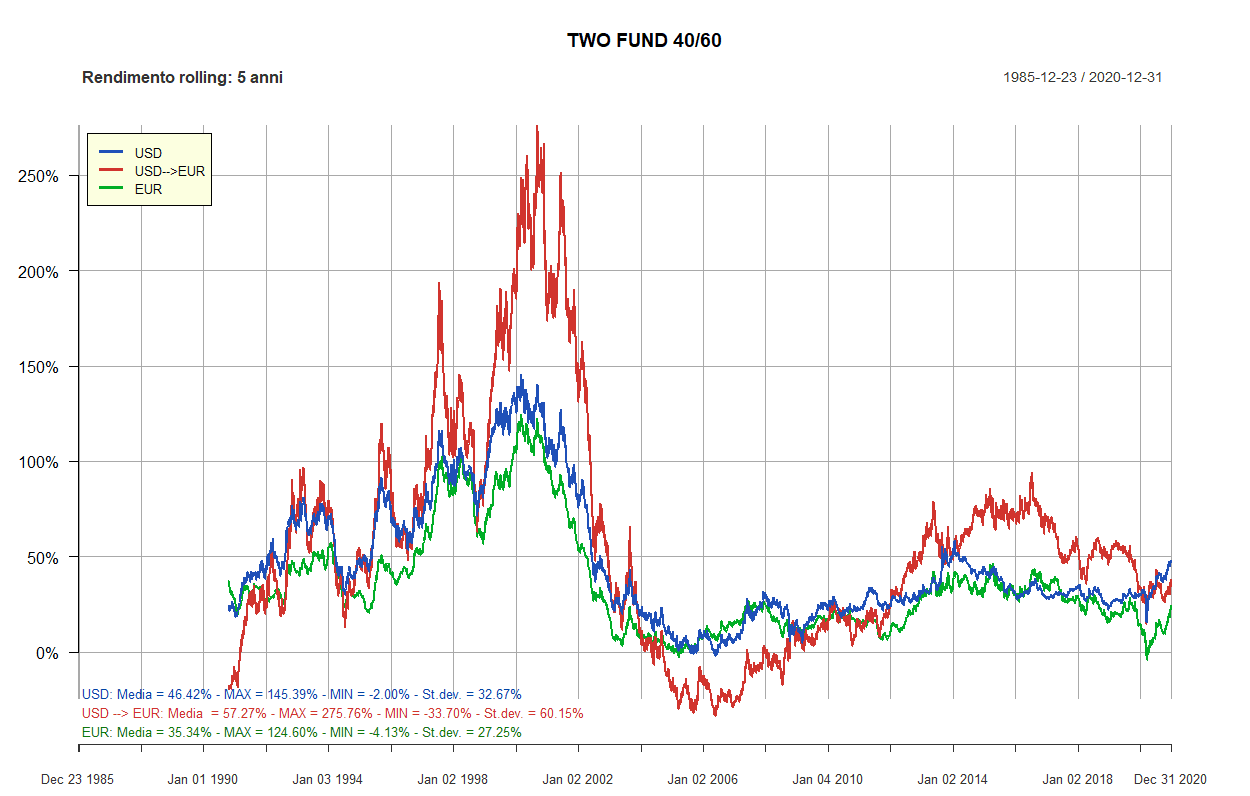
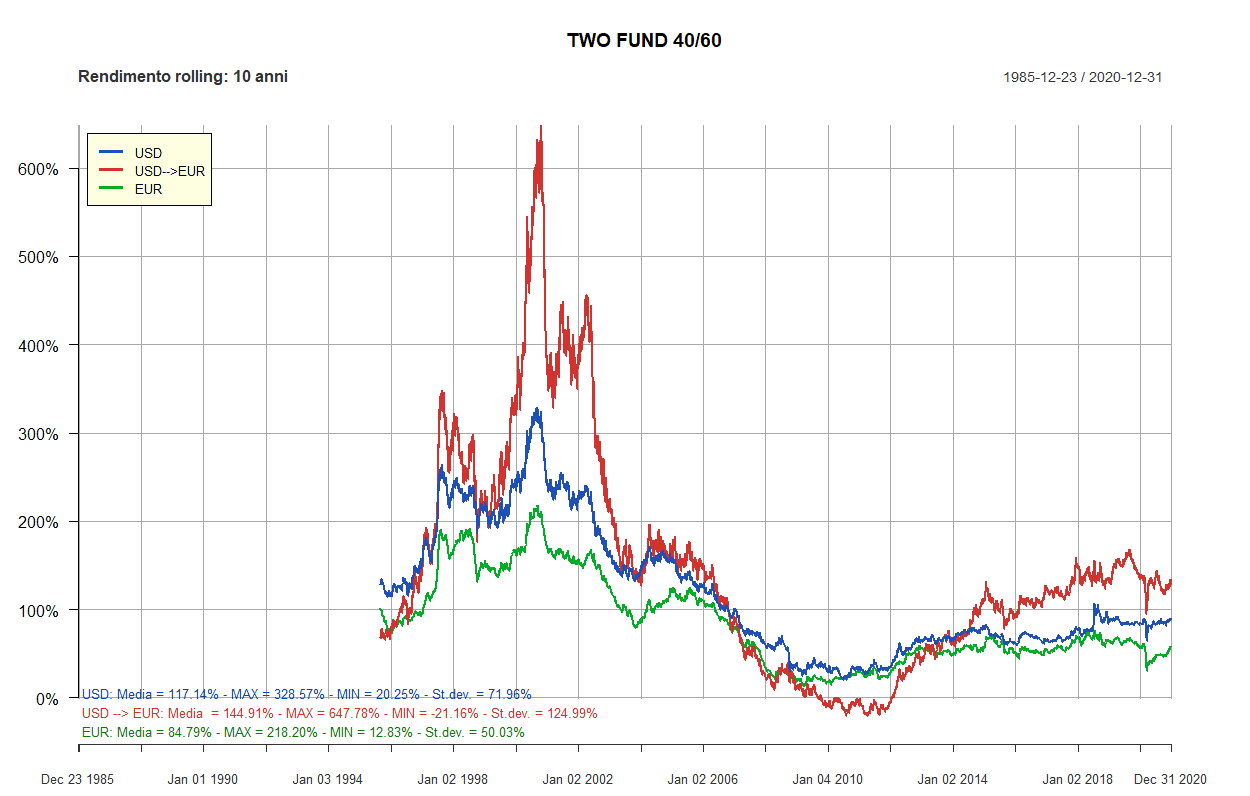
TWO FUND 50/50
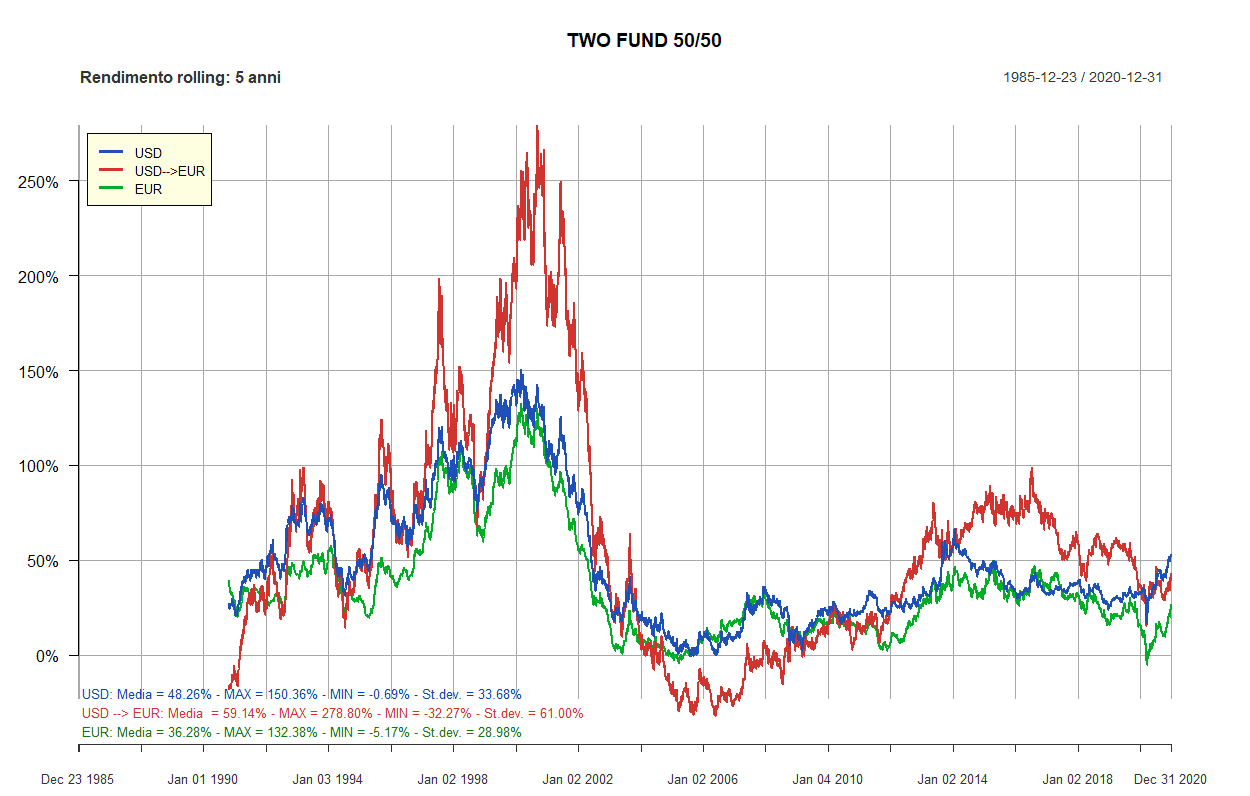
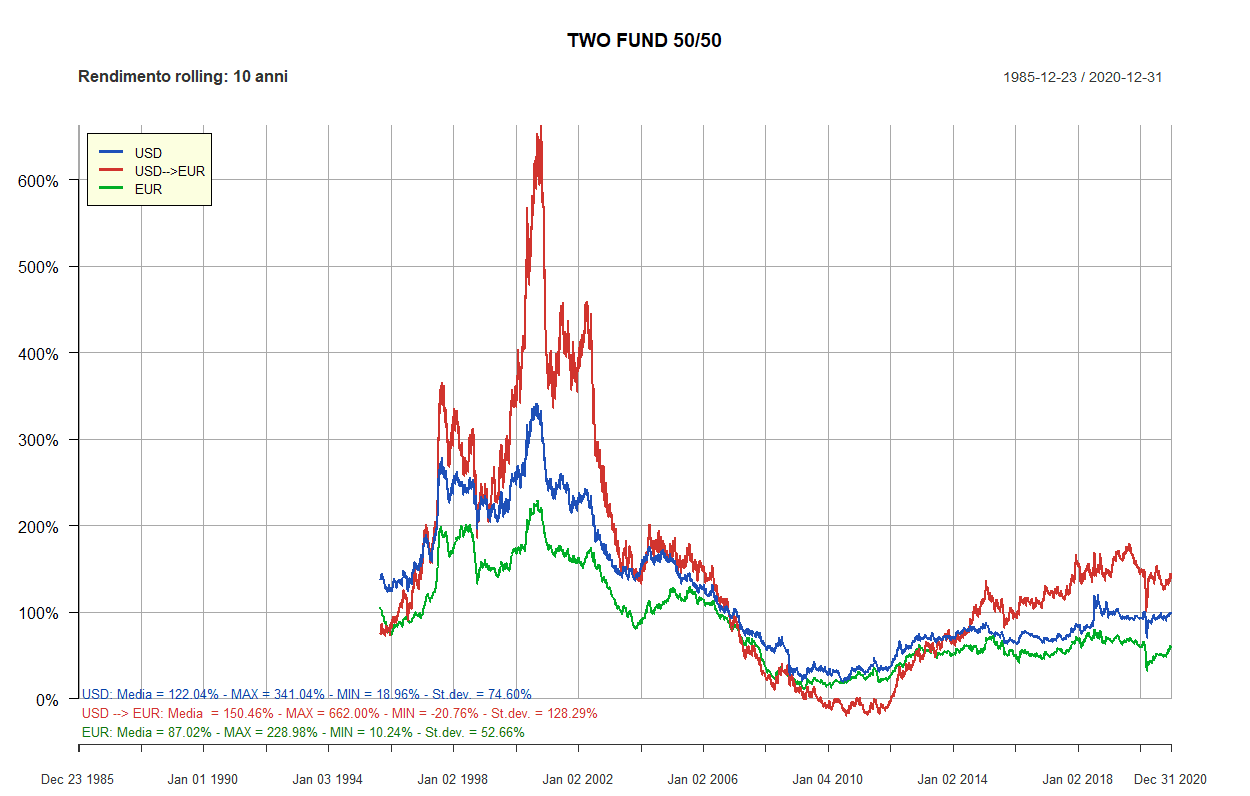
TWO FUND 60/40
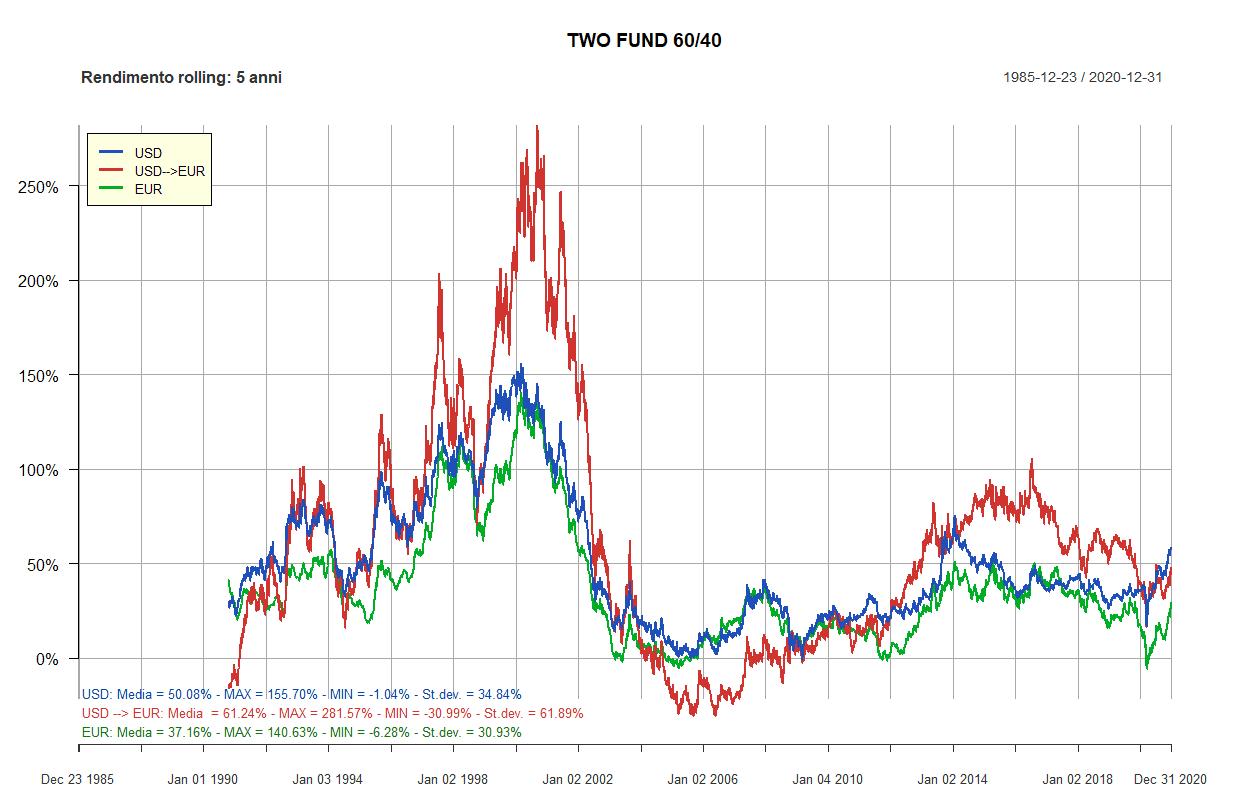
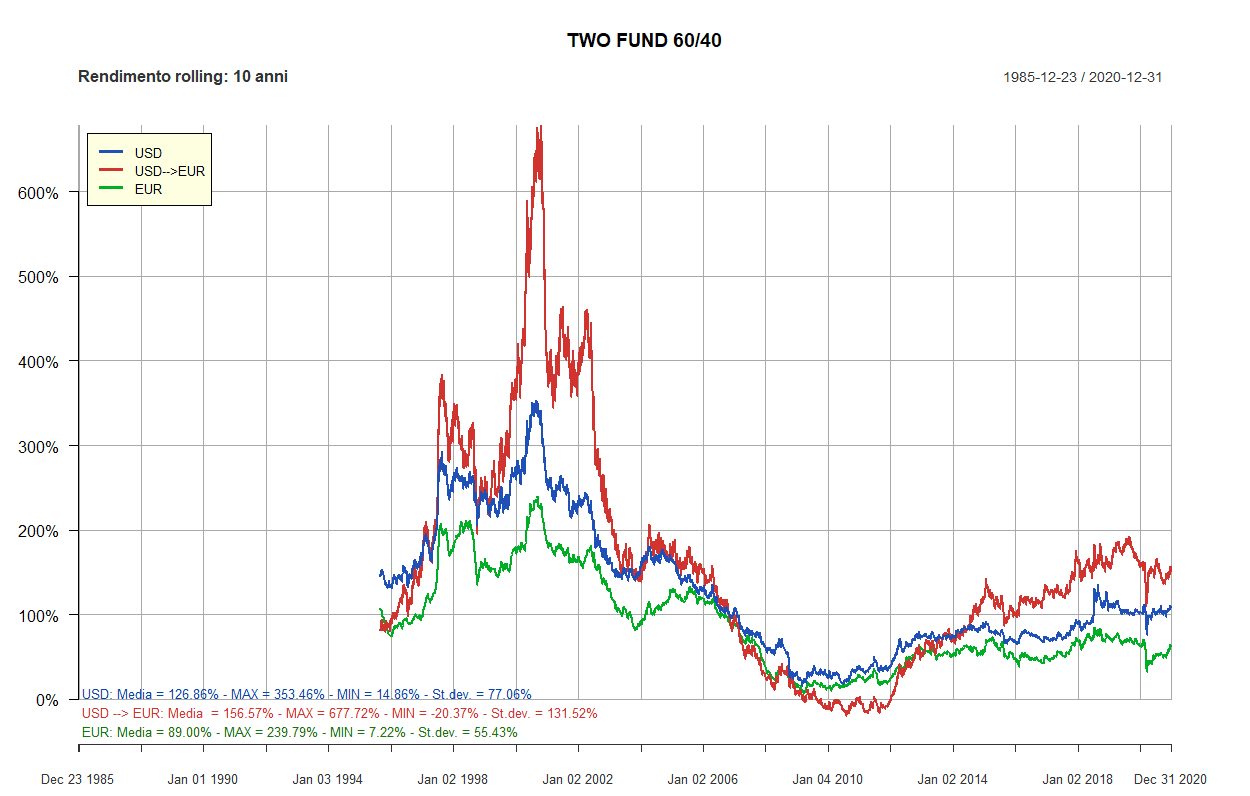
TWO FUND 70/30
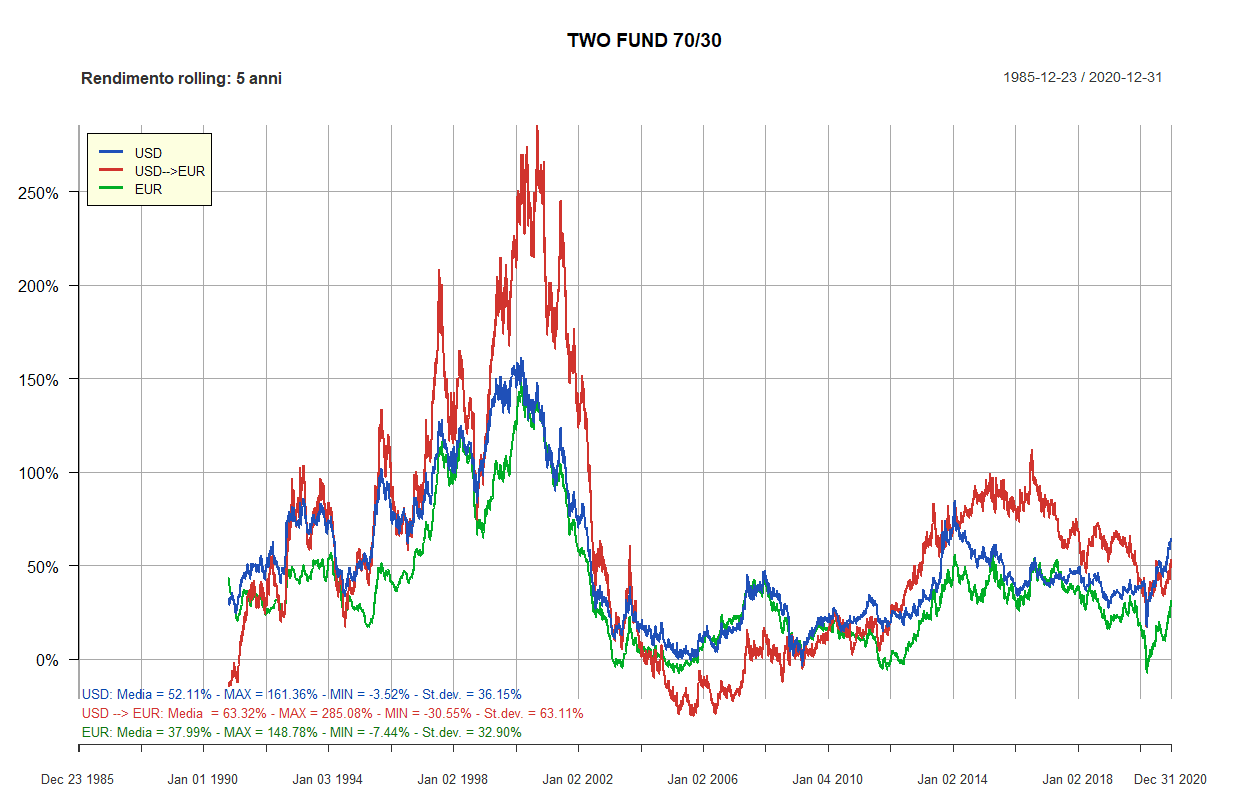
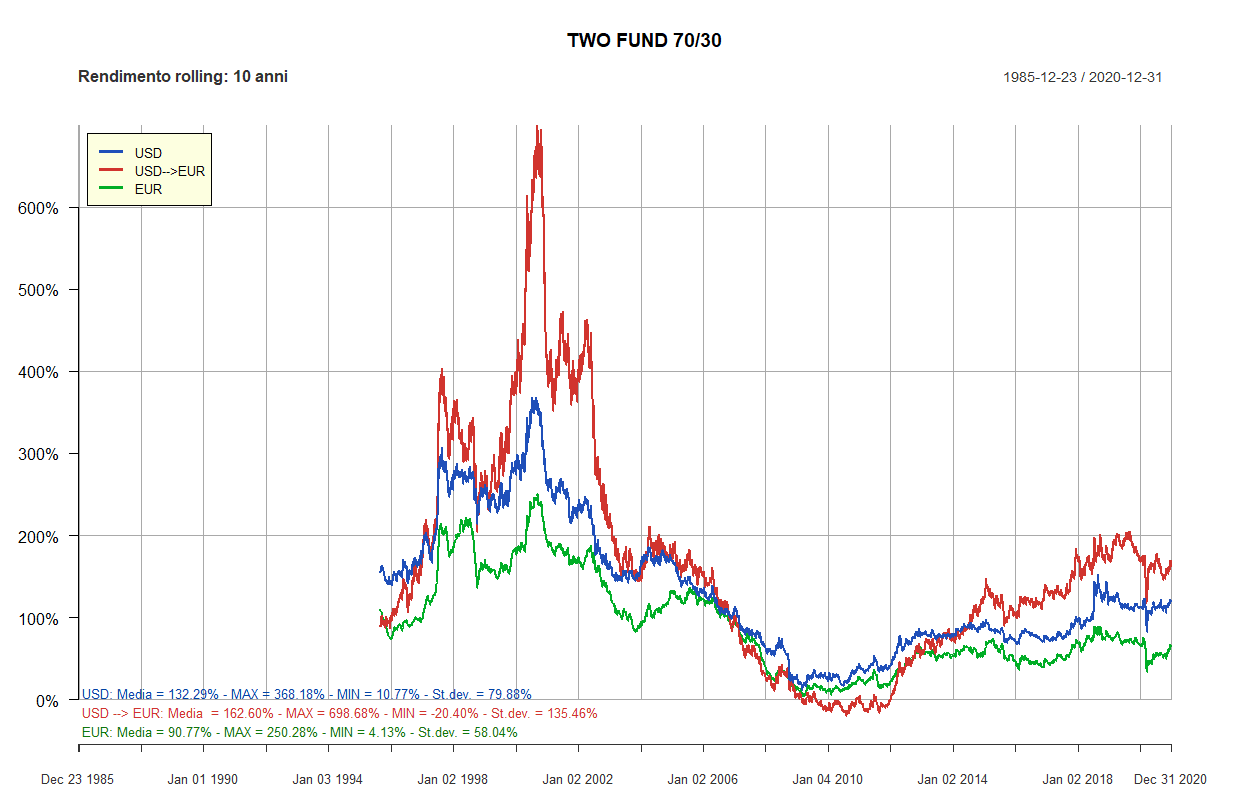
TWO FUND 80/20
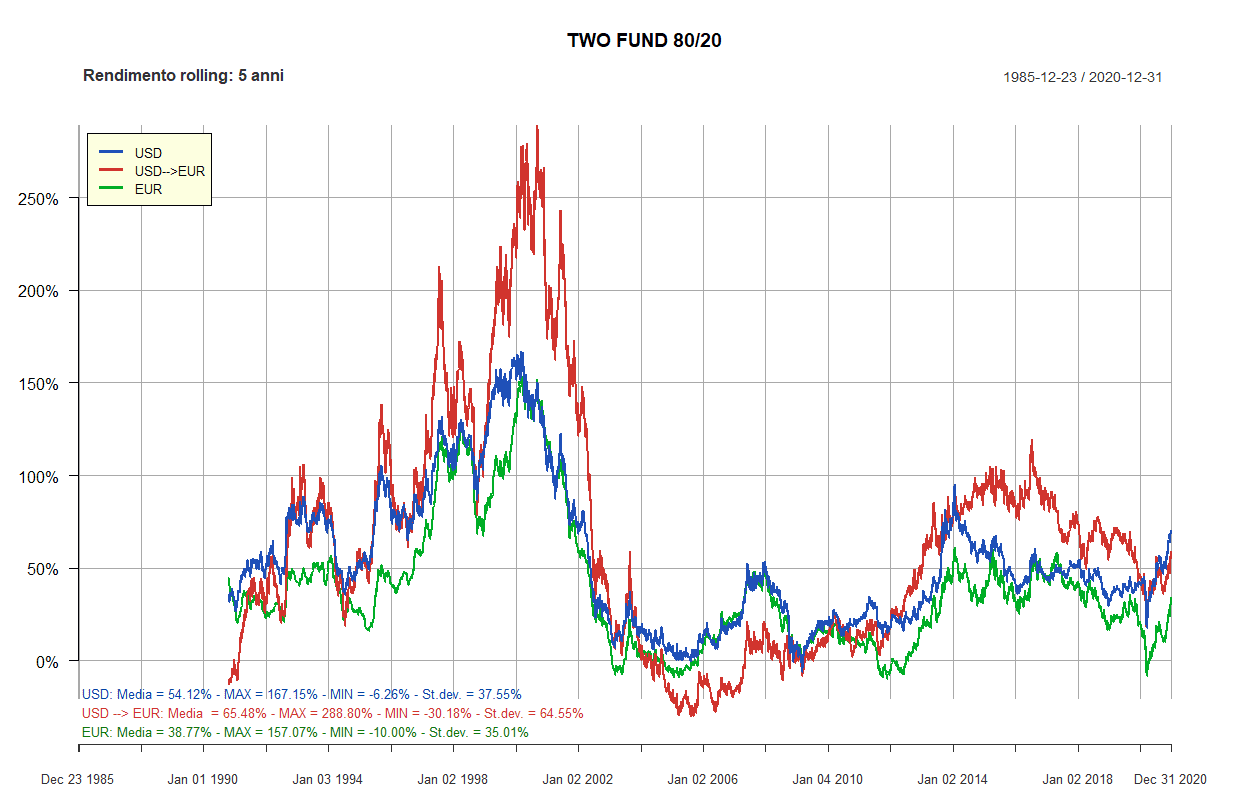
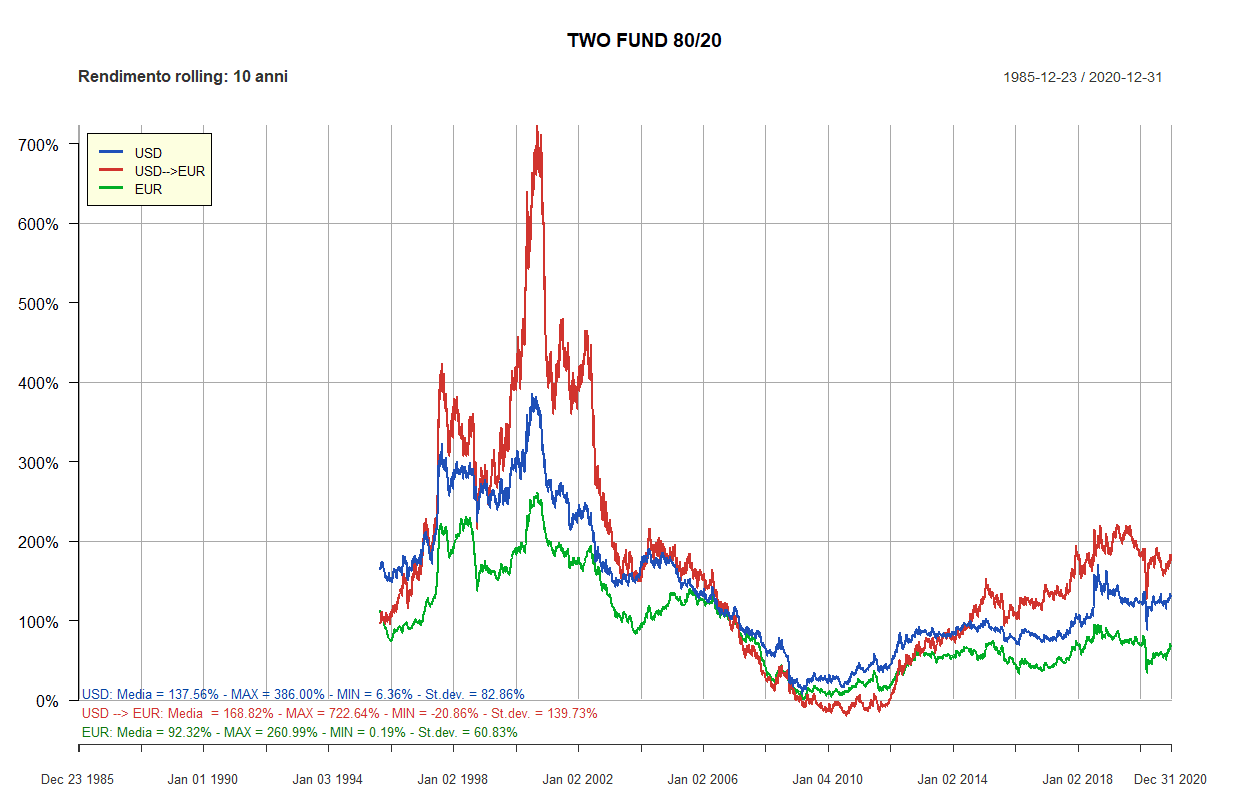
TWO FUND 90/10
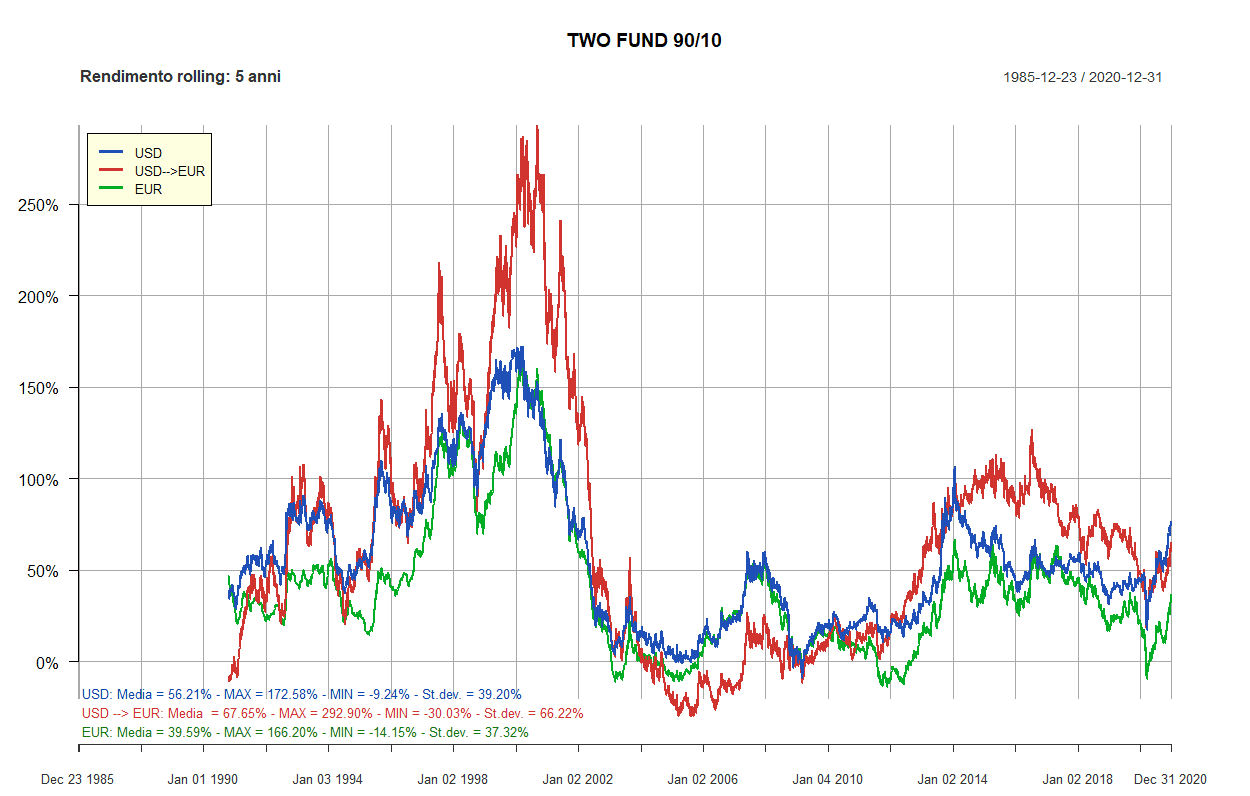
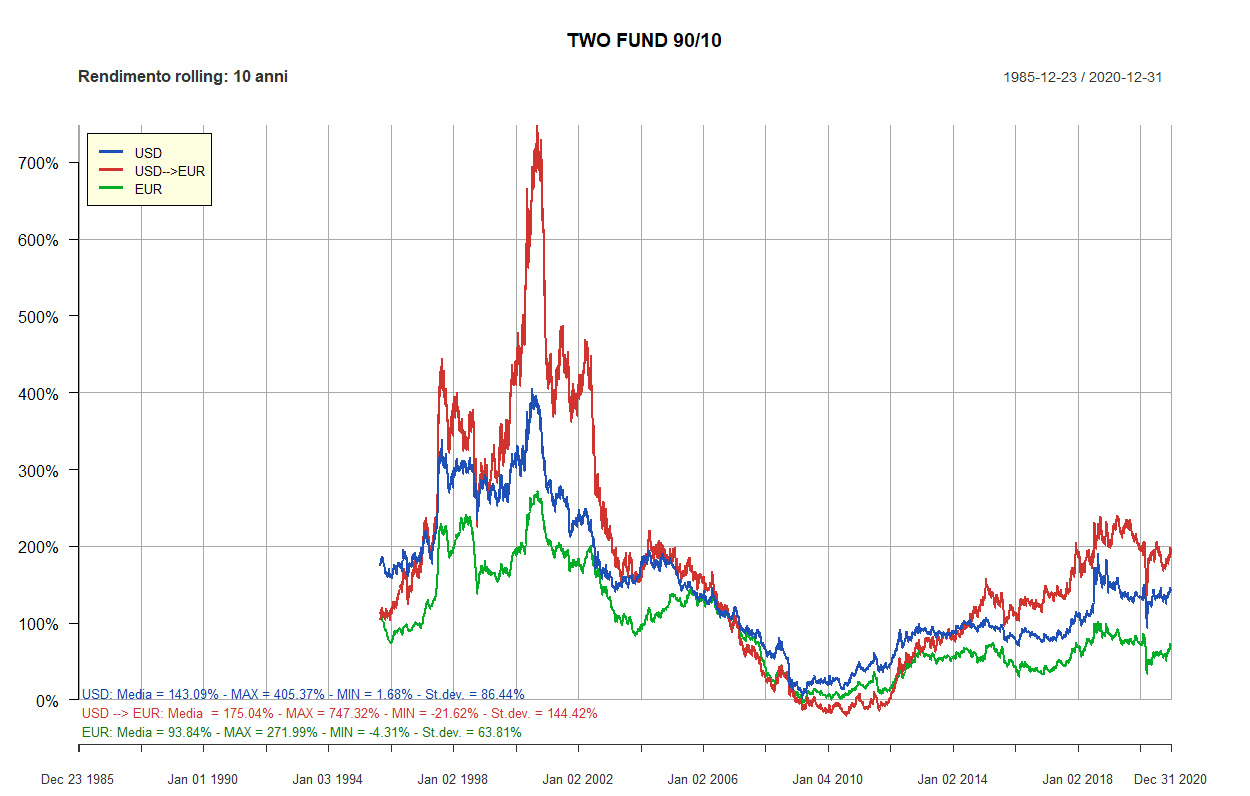
Questo è il Two funds più rischioso, essendo composto dal 90% di azionario e soltanto il 10% di obbligazionario.
È indubbio che il mercato azionario americano sia stato più redditizio di quello dell’area euro: la differenza è consistente, tant’è che i rendimenti medi rolling a 10 anni sono rispettivamente pari al 143,09% e al 93,84%.
Col senno di poi, un investitore avrebbe fatto meglio a diversificare l’investimento includendo anche il mercato americano: più volatile, ma più redditizio. L’utilizzo di un ETF hedgiato sarebbe stato consigliabile (o almeno un suo uso pari a circa la metà del peso della componente azionaria), in quanto uno non coperto avrebbe fatto crescere parecchio la volatilità dell’investimento.
Come al solito, il rischio di cambio sommato a quello di mercato aumenta la volatilità dell’investimento senza garantire un maggior rendimento atteso.
Nel periodo oggetto della nostra analisi, il rendimento rolling medio a 5 e 10 anni dei portafogli in USD→EUR è stato più alto di quello dei portafogli in USD e in EUR. Non possiamo tuttavia generalizzare questo risultato: se allungassimo il periodo dell’indagine, vedremmo probabilmente una diminuzione della differenza tra i loro rendimenti medi.
Possiamo invece essere quasi certi che l’incremento di volatilità non sarebbe stato molto diverso da quello che abbiamo ottenuto nei nostri backtest.
TWO FUND DINAMICO
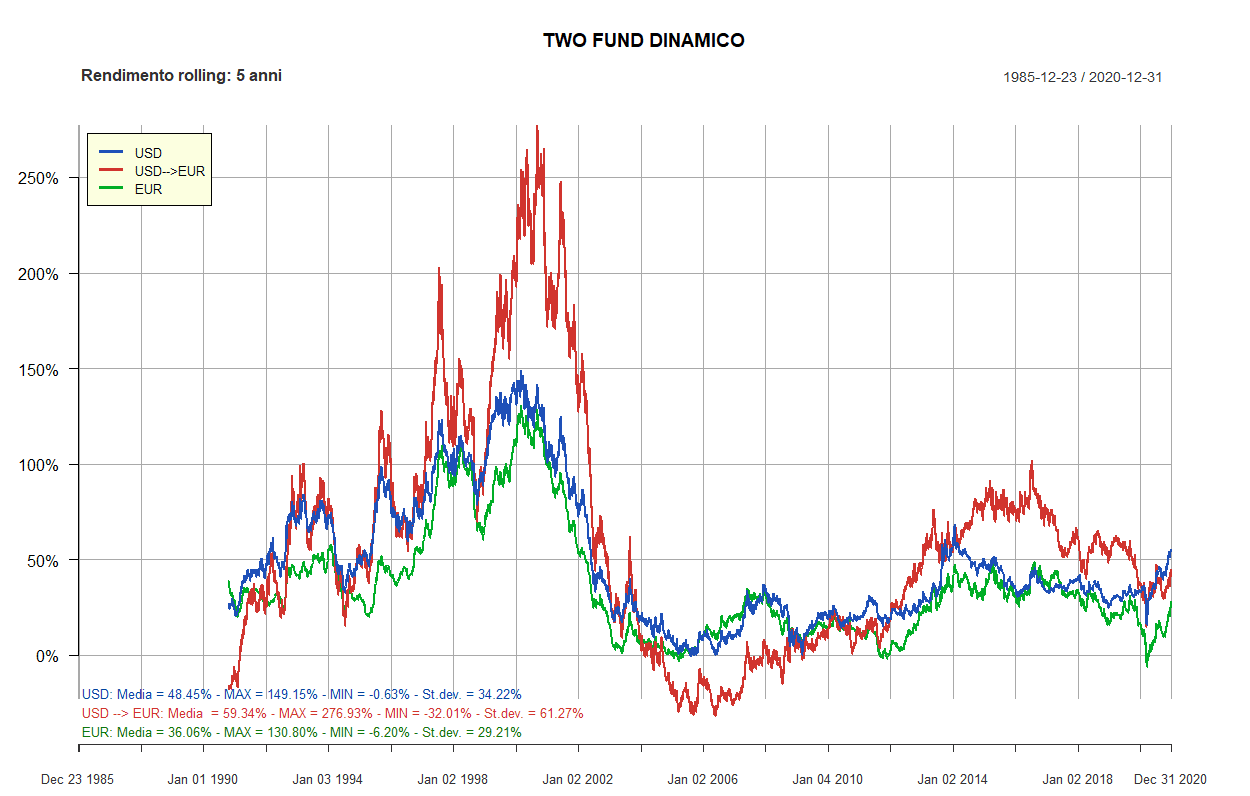
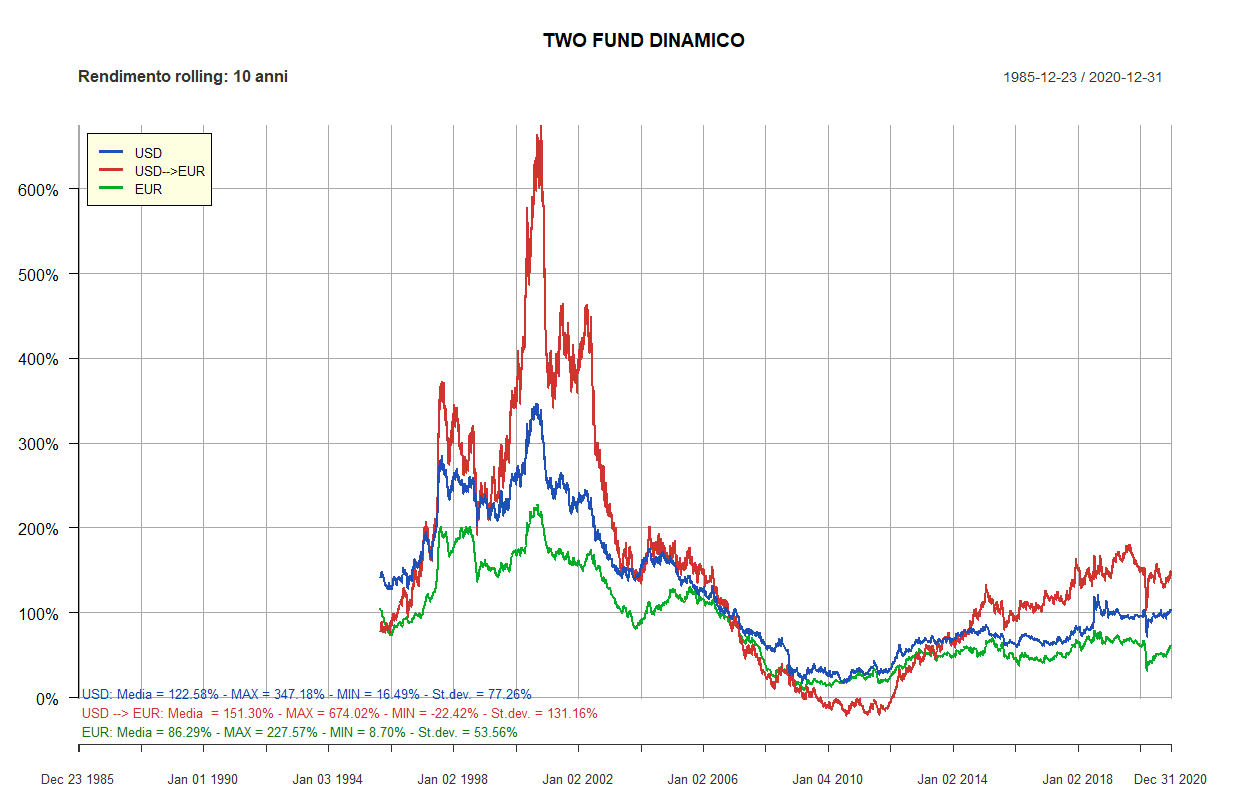
I risultati del Two funds dinamico sono molto simili a quelli del Two funds 50/50.
Il tentativo di dare dinamicità alla gestione dell’asset allocation non ha prodotto l’esito sperato.
A questo riguardo, si confermano le osservazioni riportate nel capitolo 13.3.3 subito dopo la visualizzazione delle equity lines del Two funds dinamico.
WARREN BUFFETT
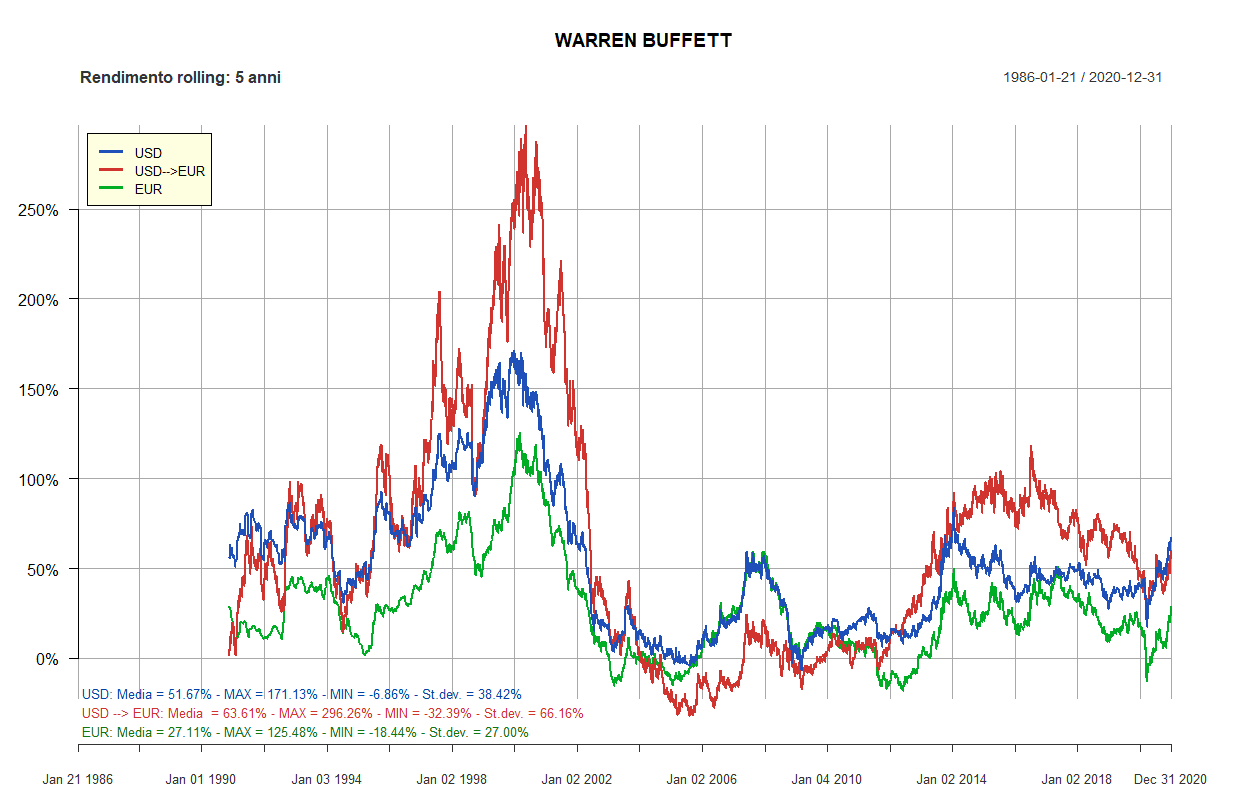
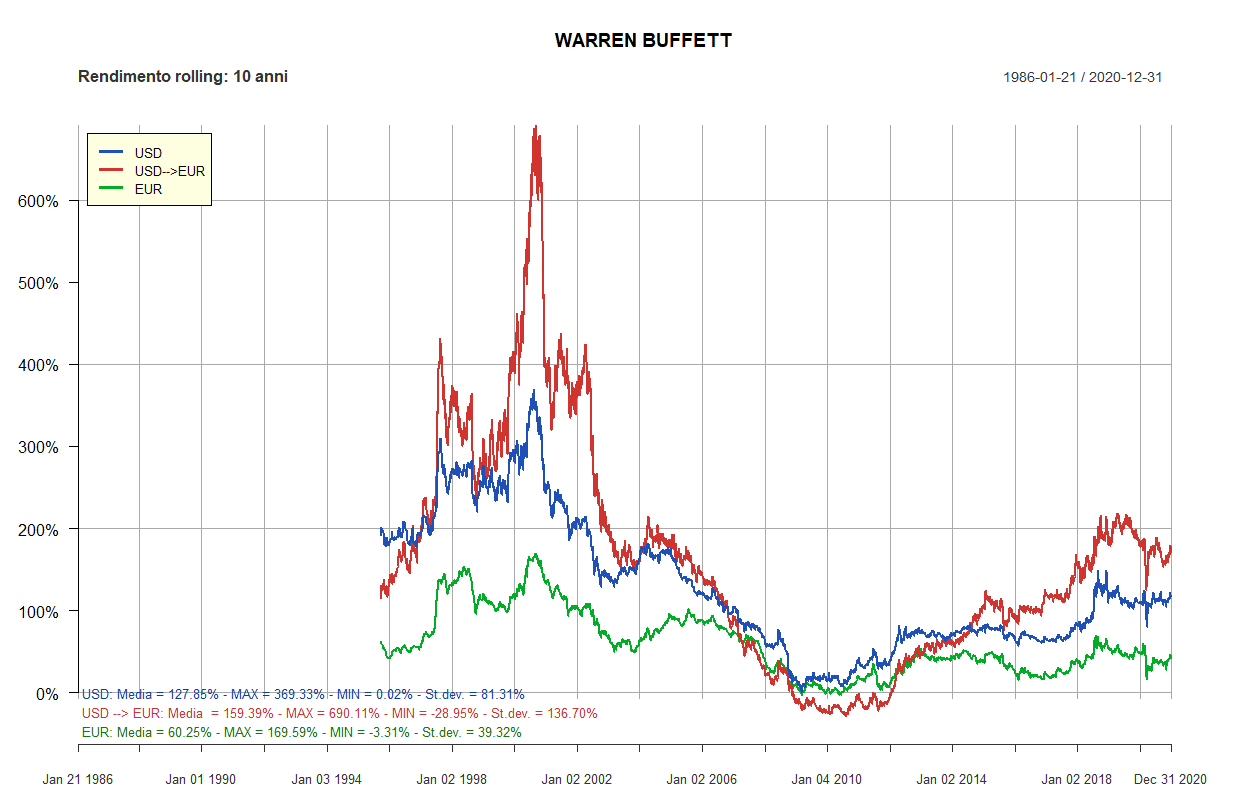
SIMPLE PATH TO WEALTH class="blu"
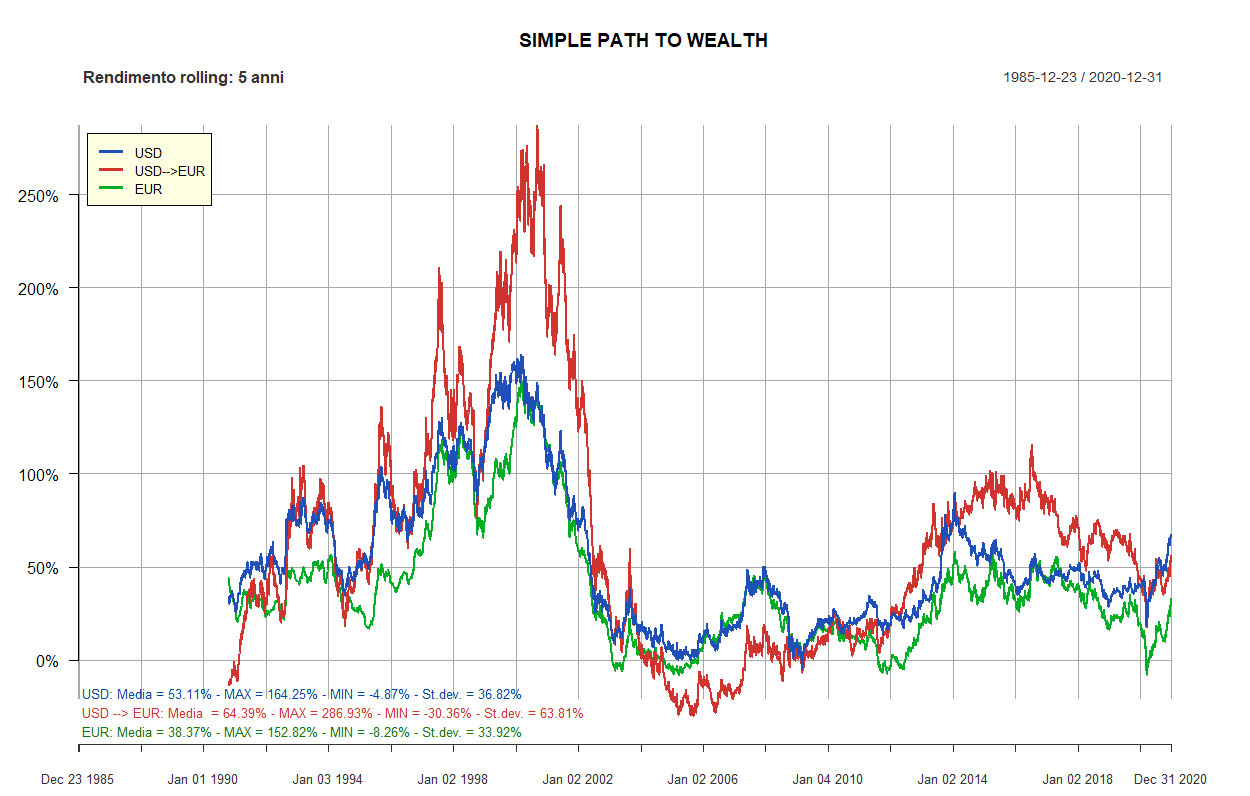
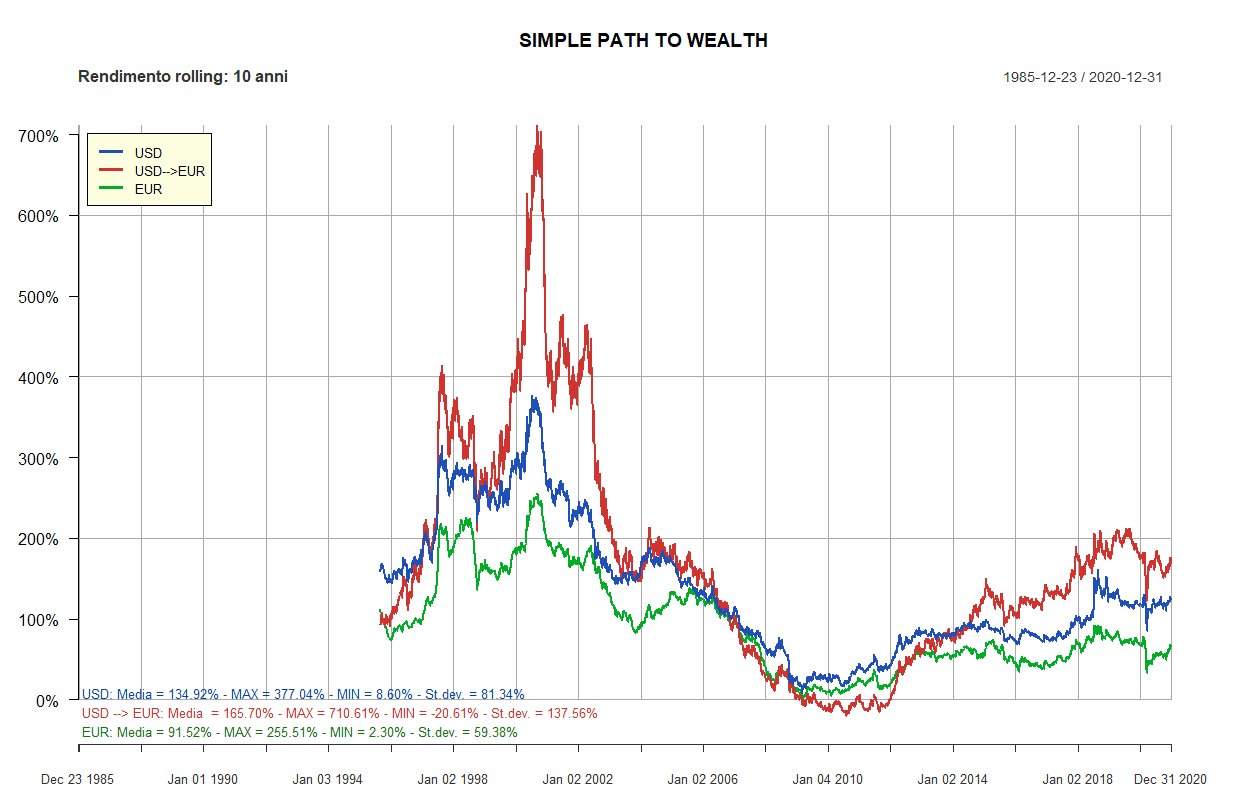
COUCH POTATO
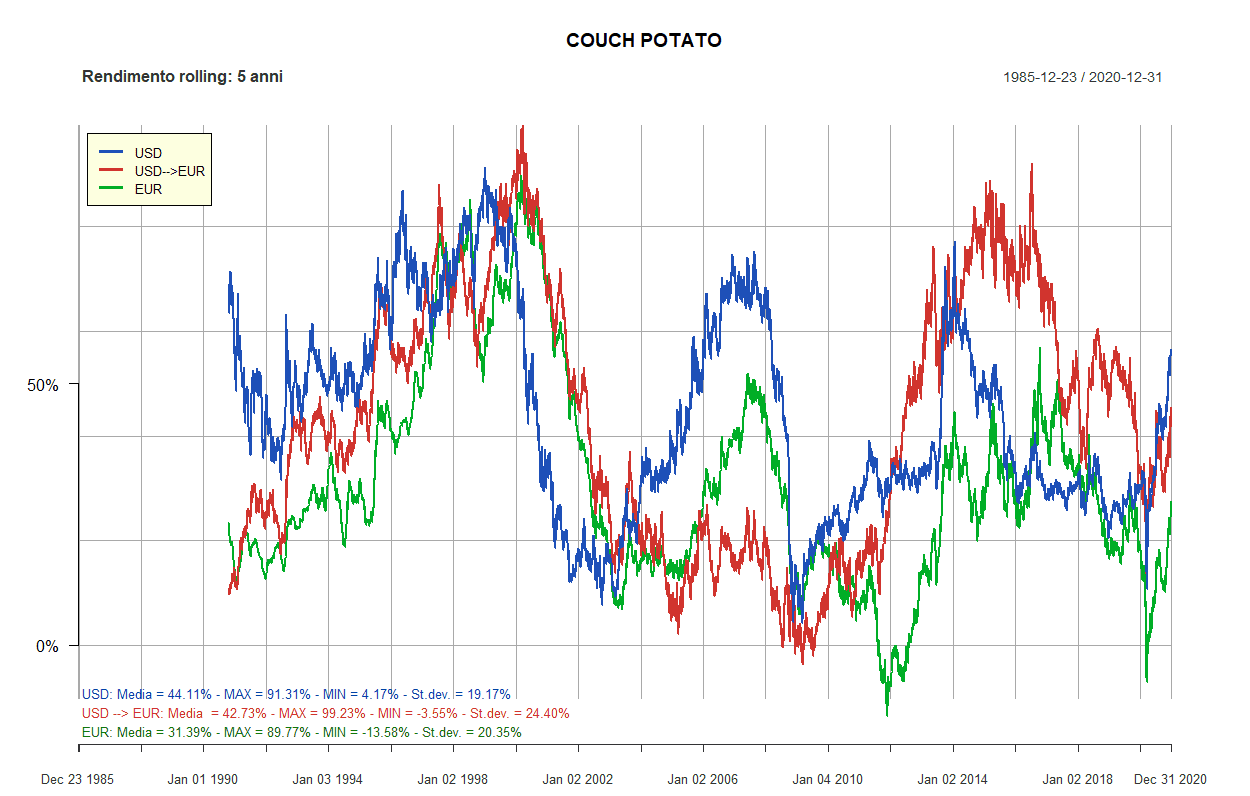
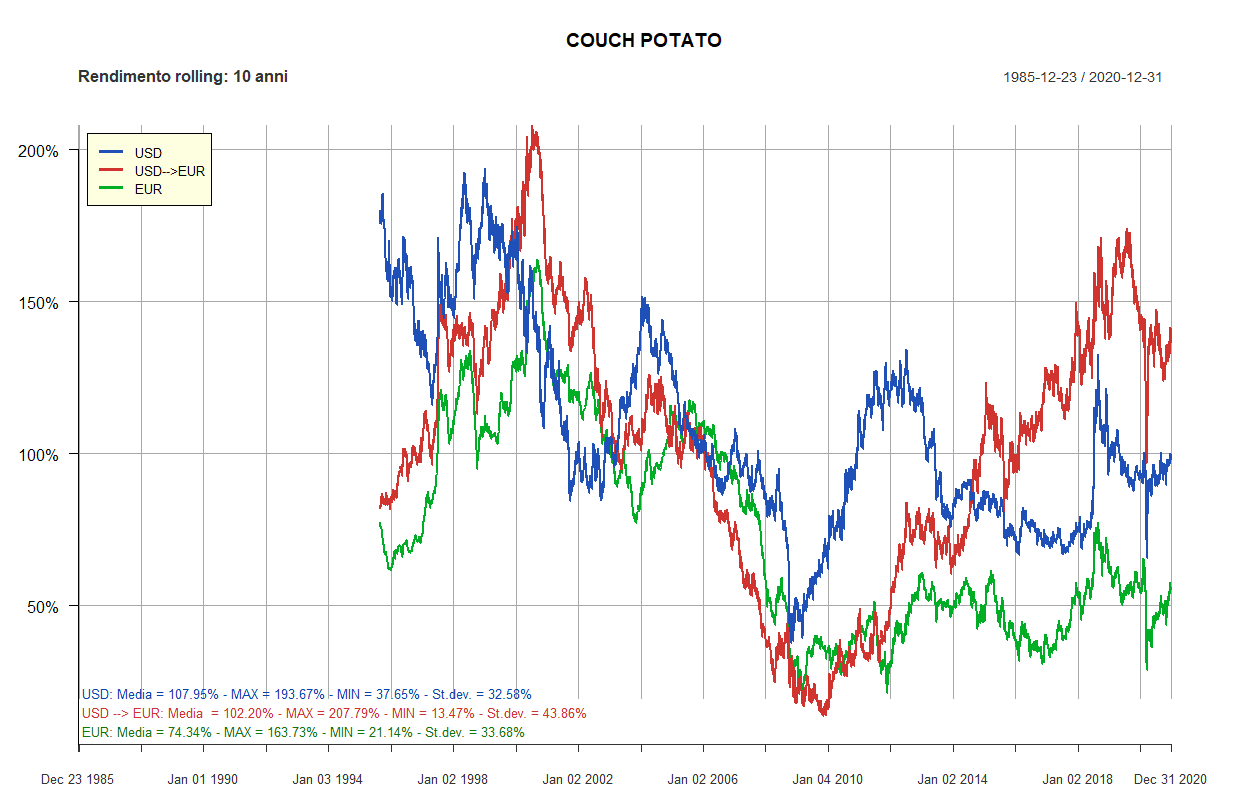
THREE FUND BOGLEHEADS
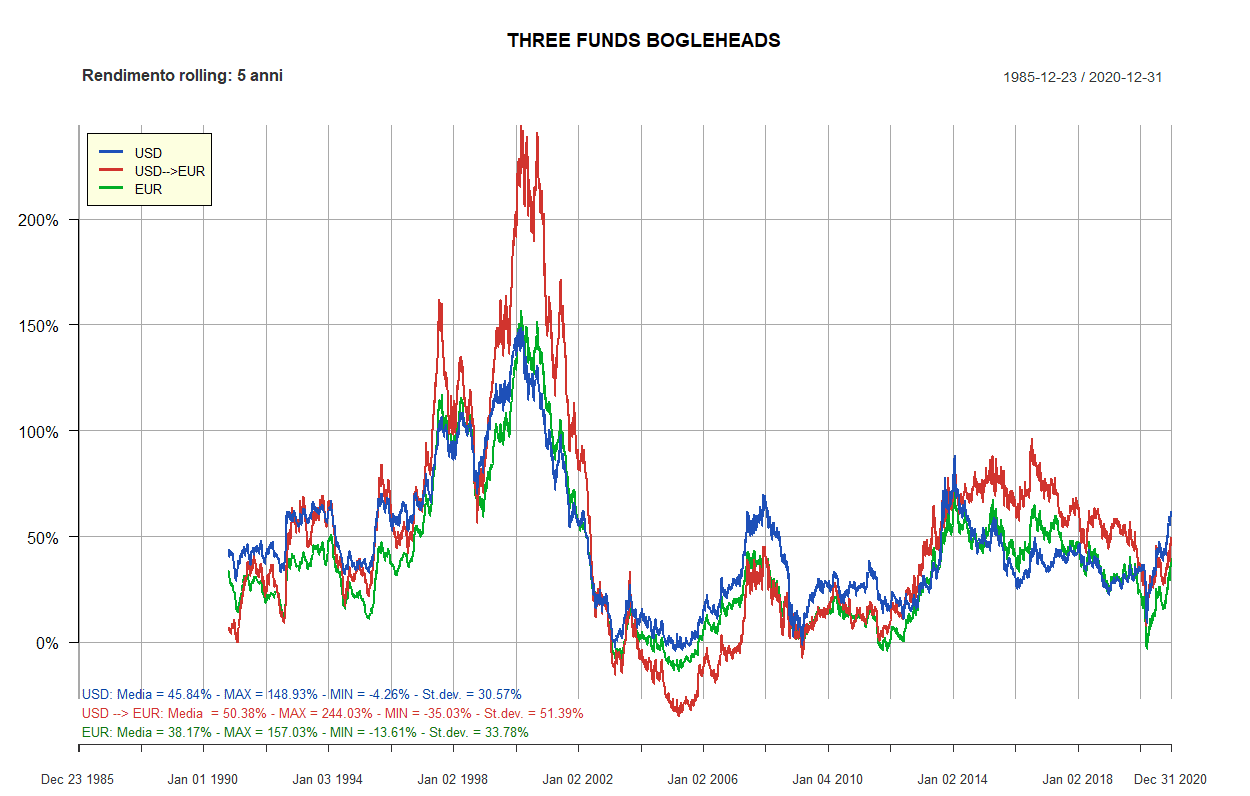
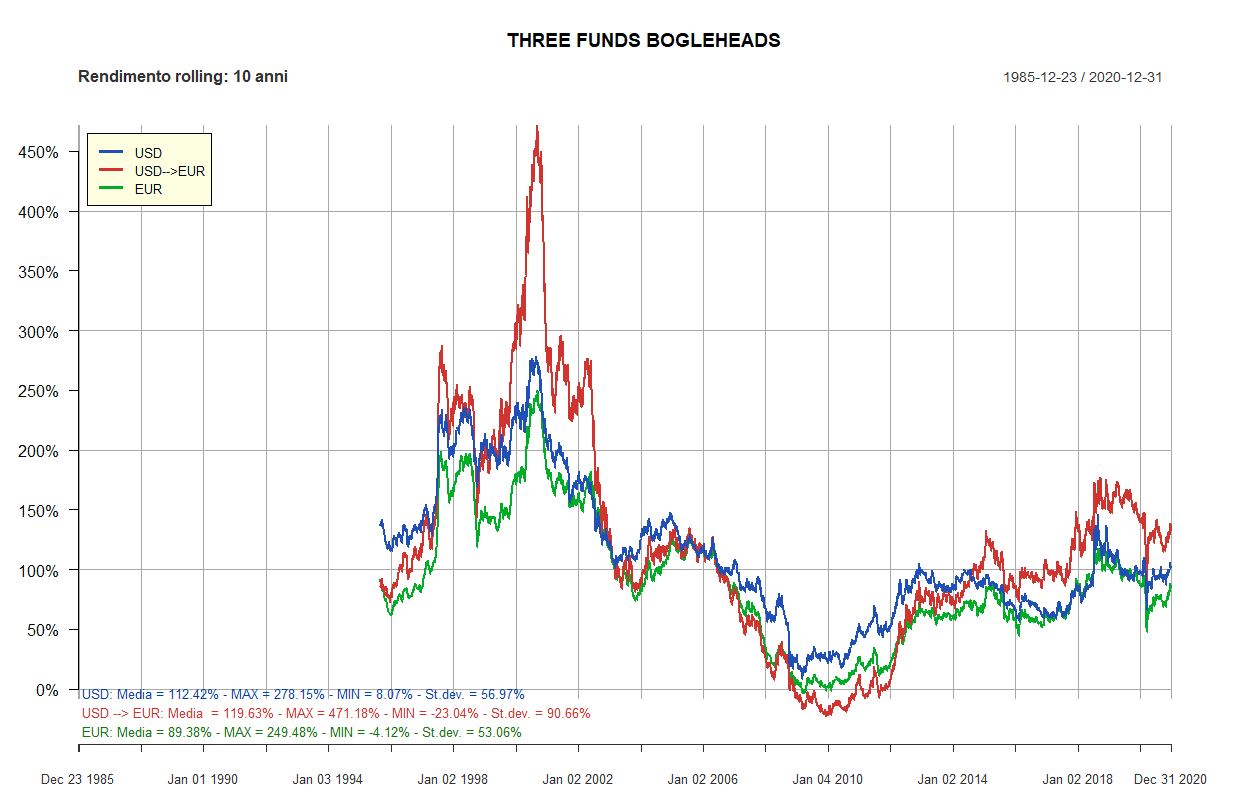
SECOND GRADER’S STARTER
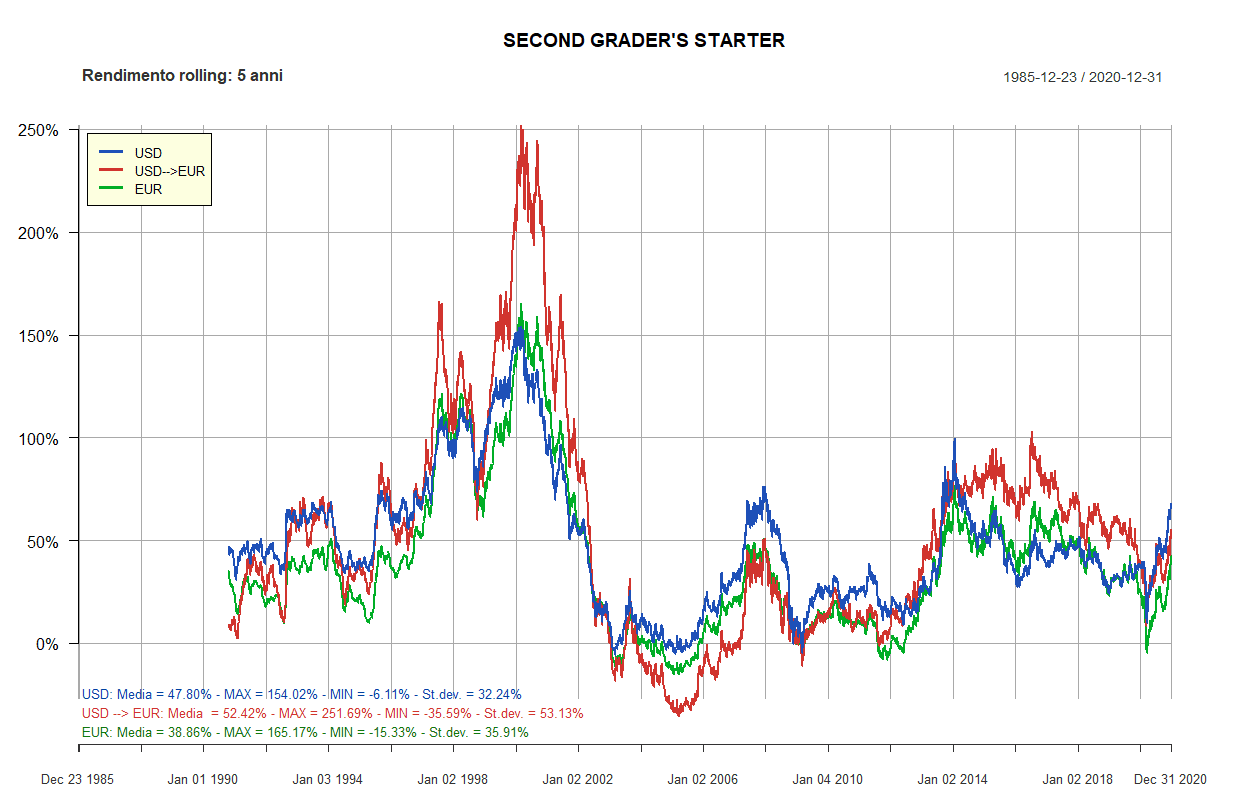
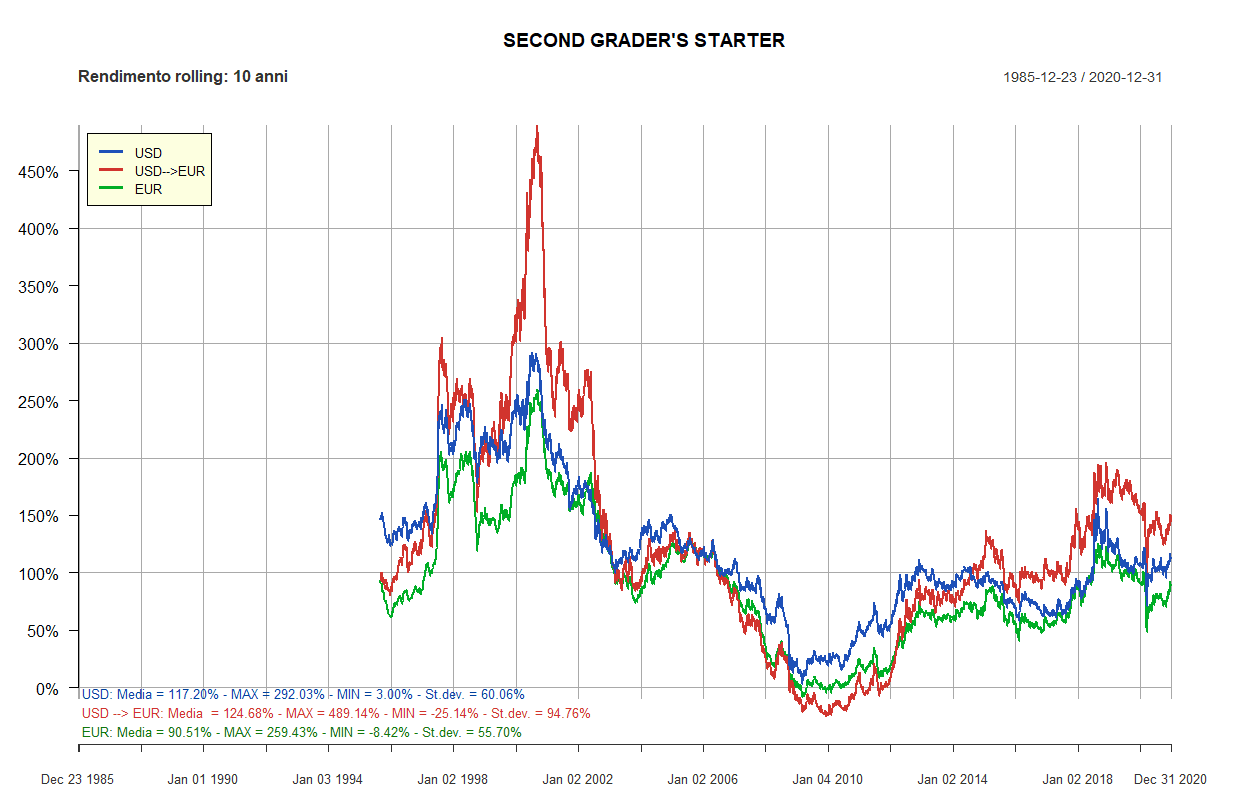
TALMUD
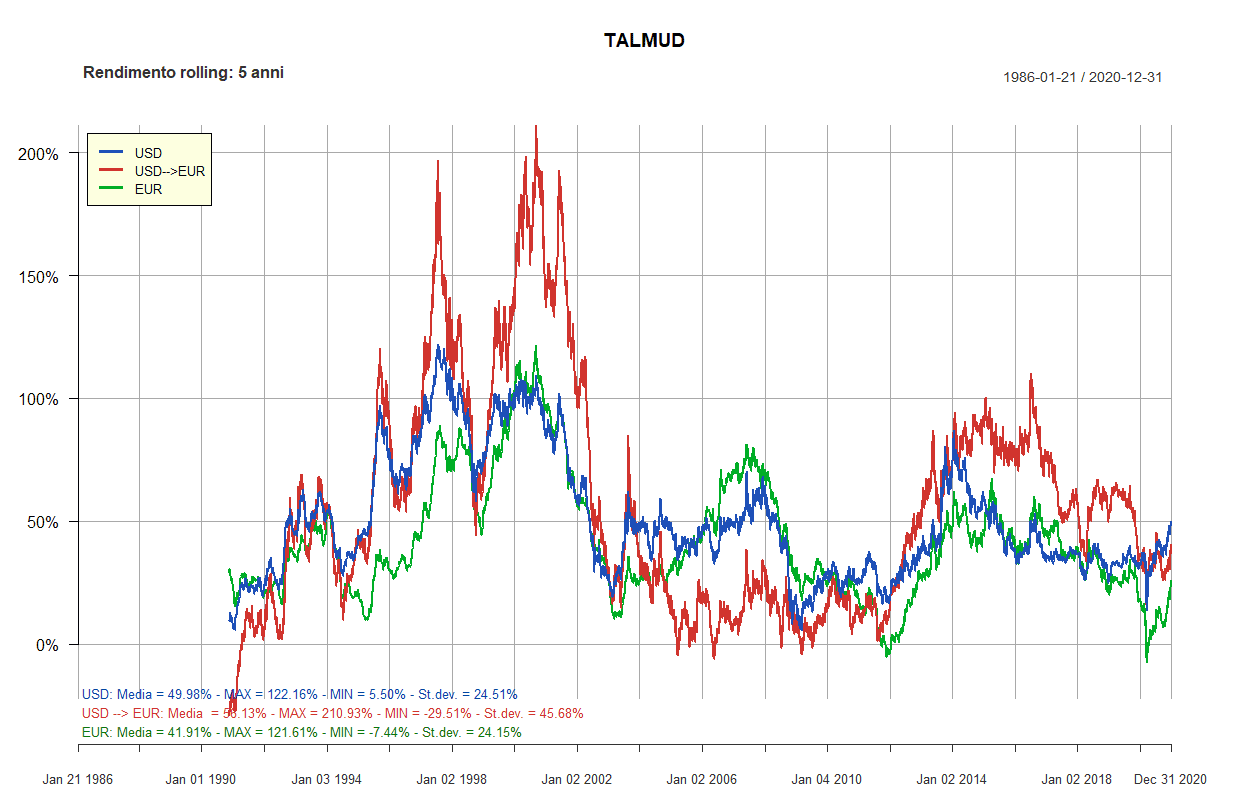
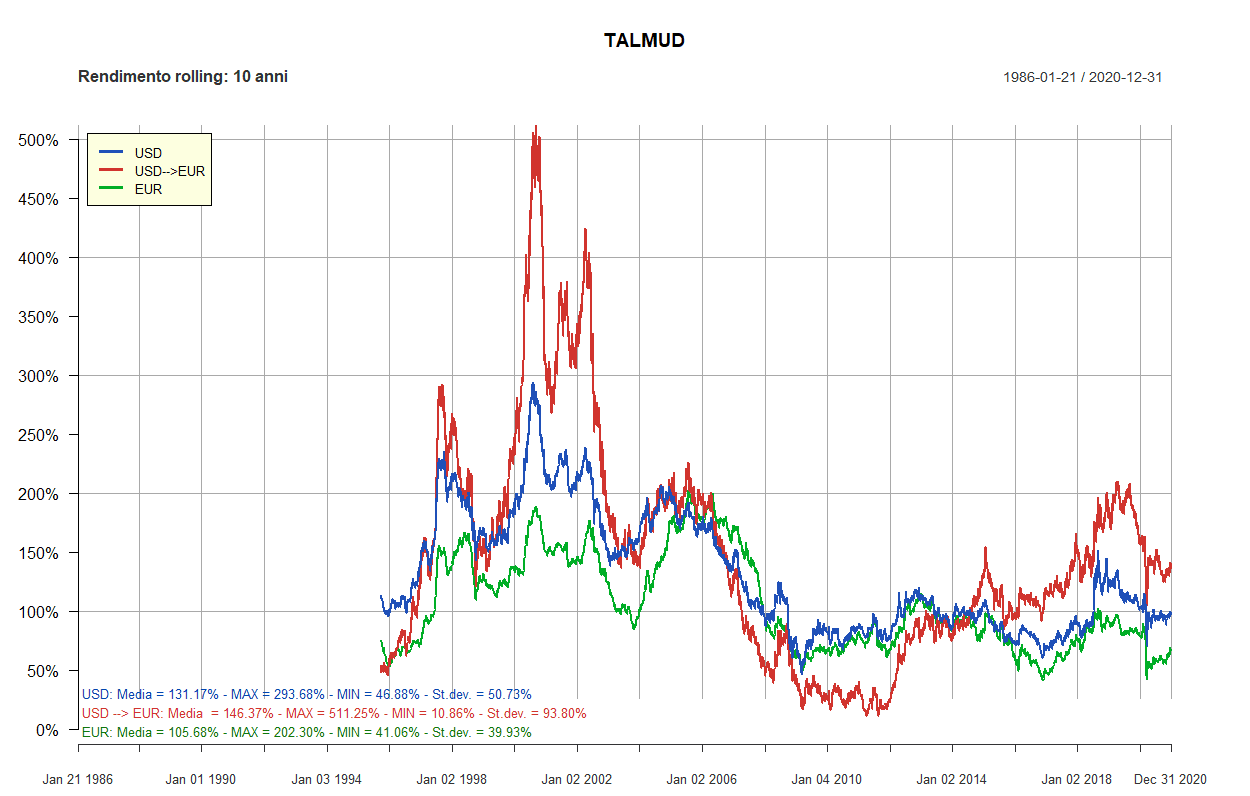
MARGARITAVILLE
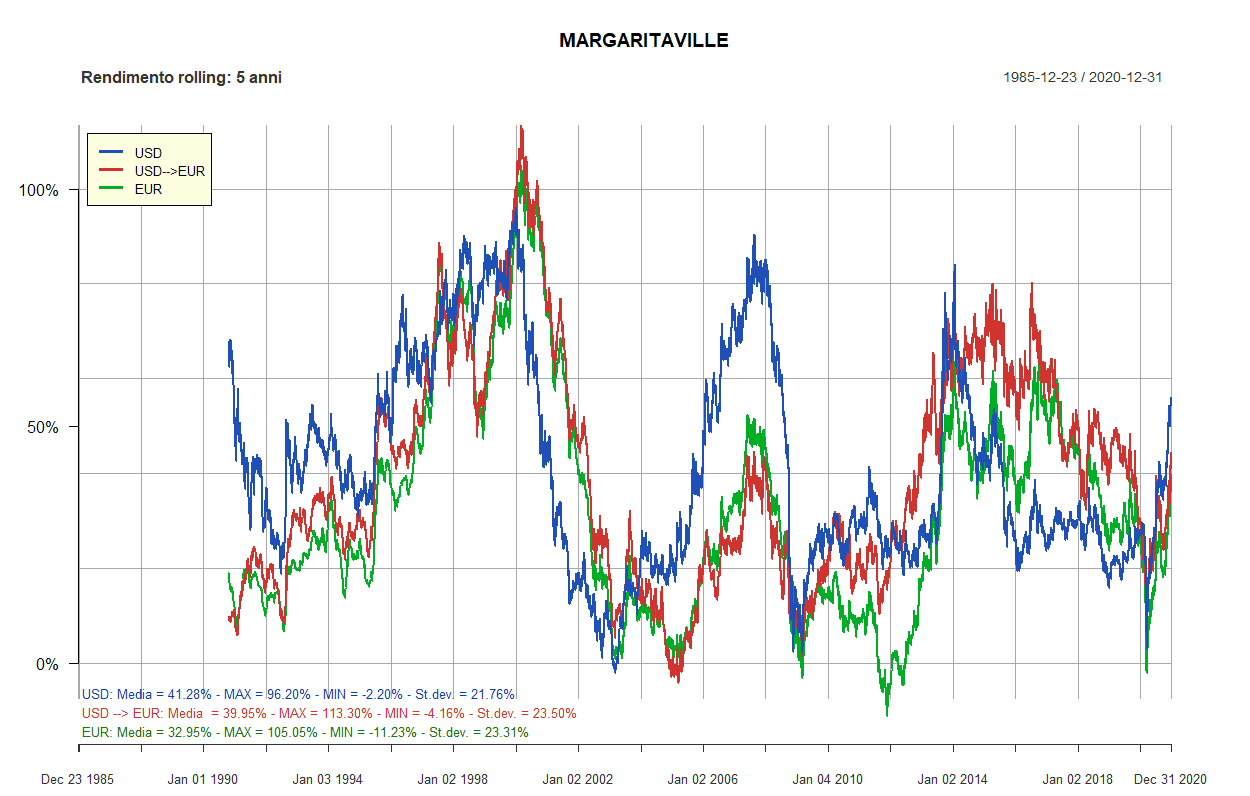
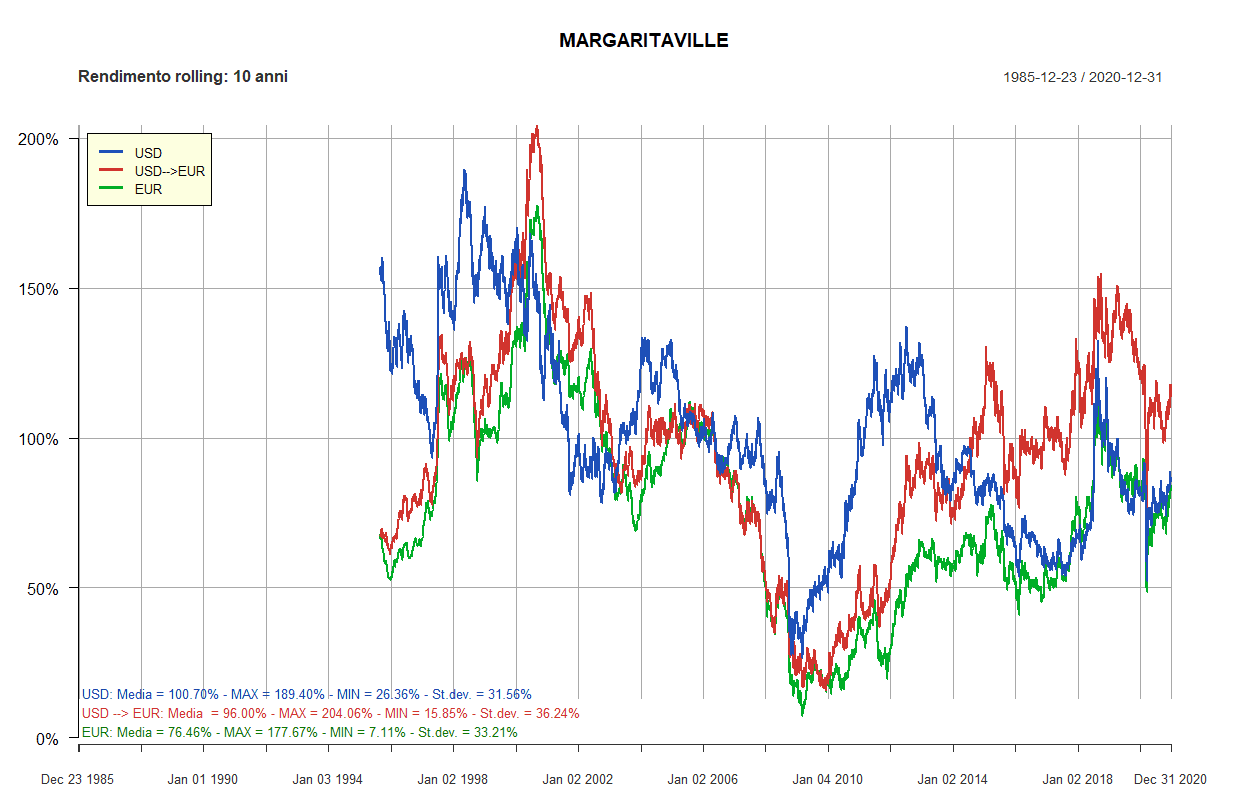
ANDREW TOBIAS
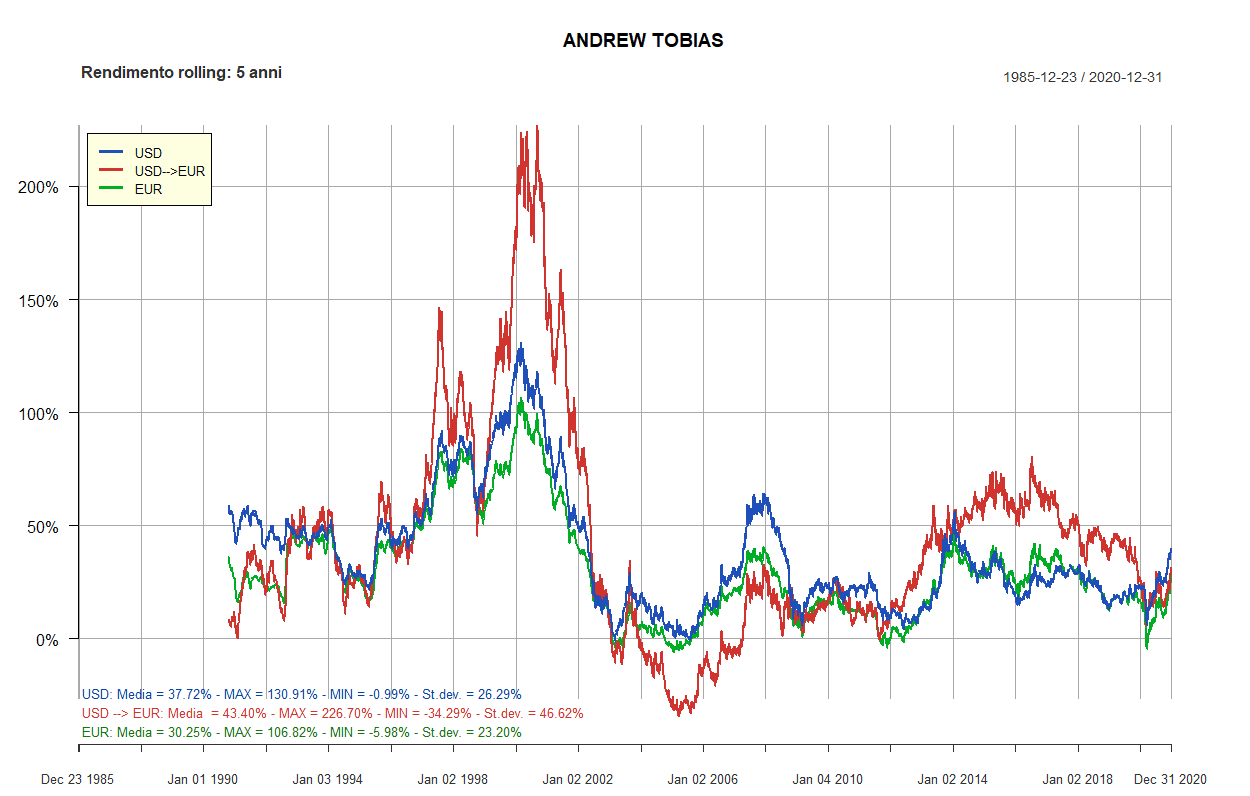
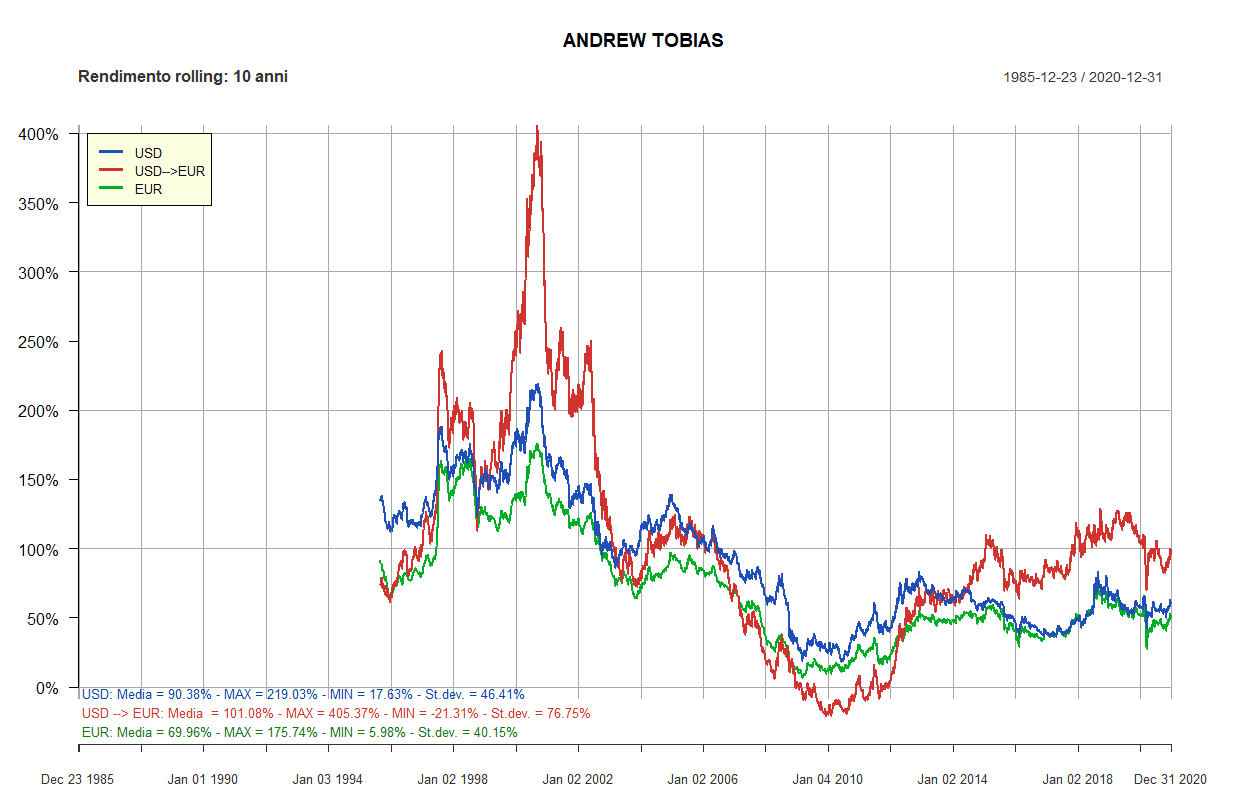
DESERT
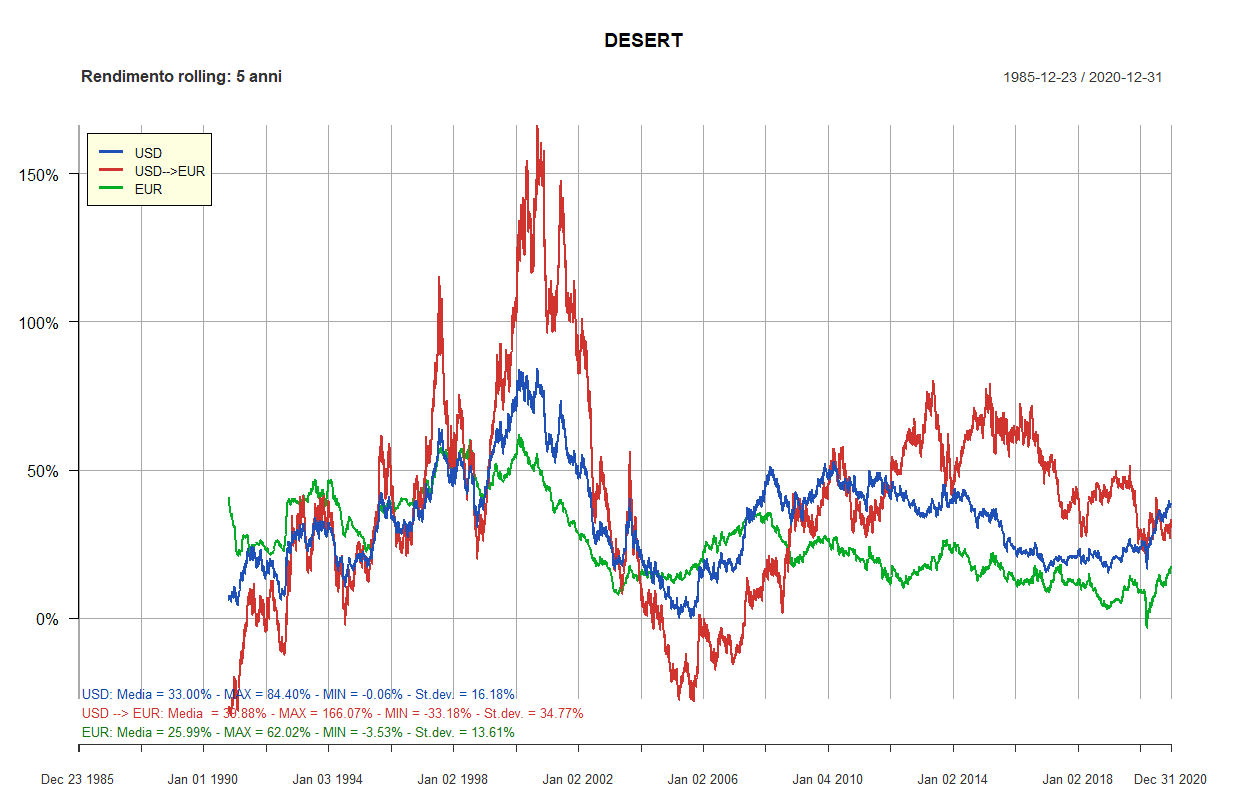
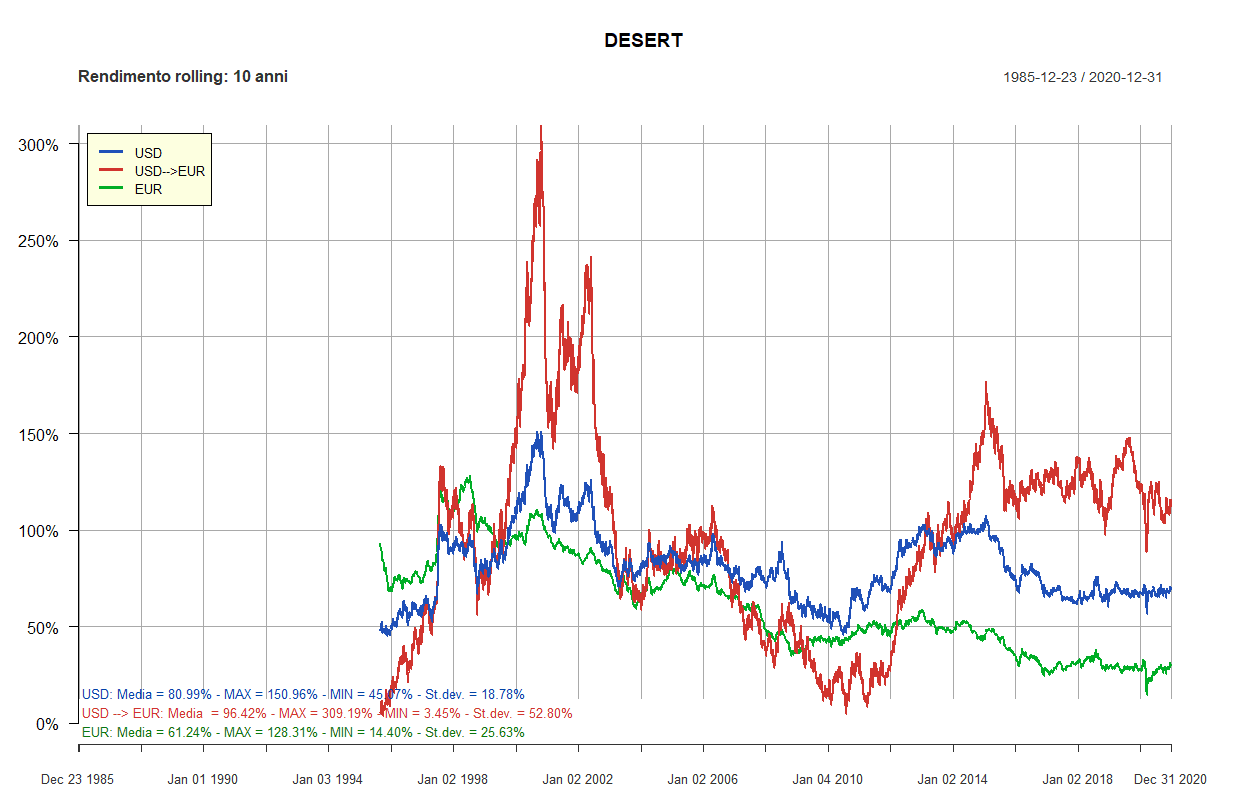
PERMANENT
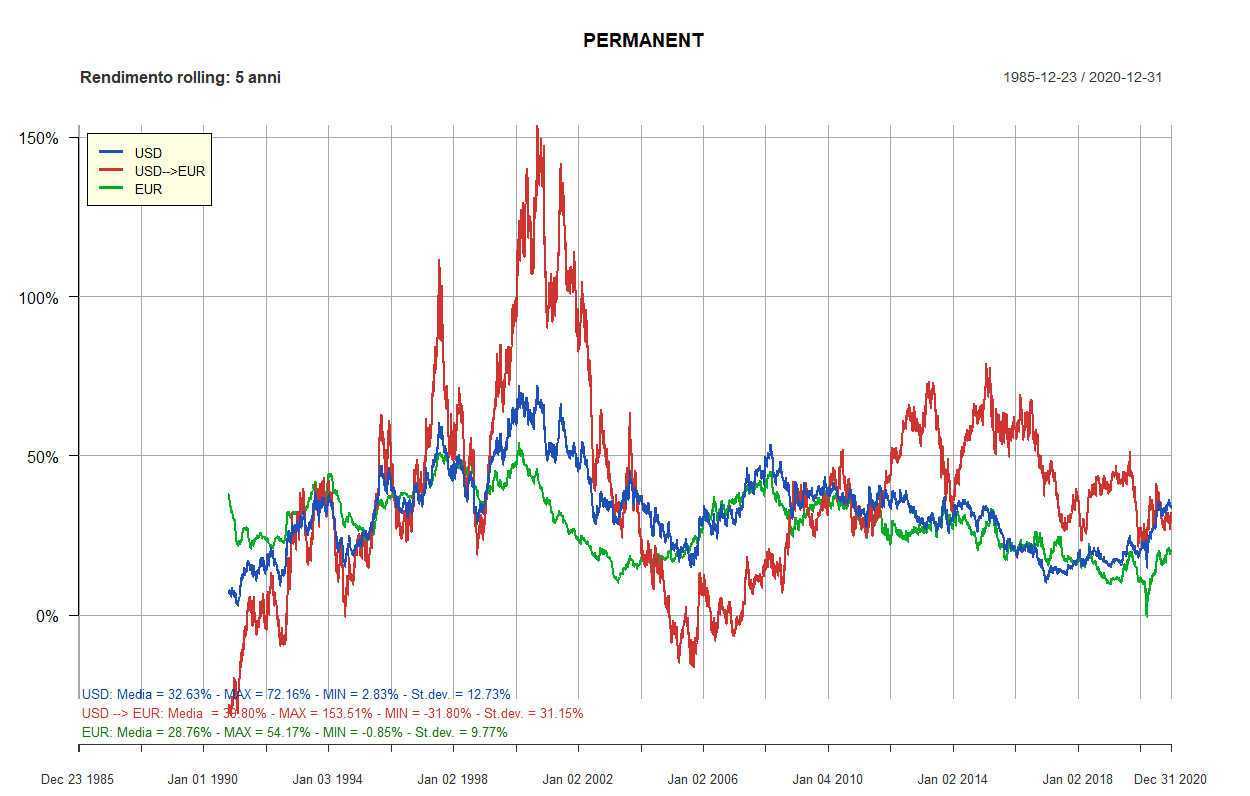
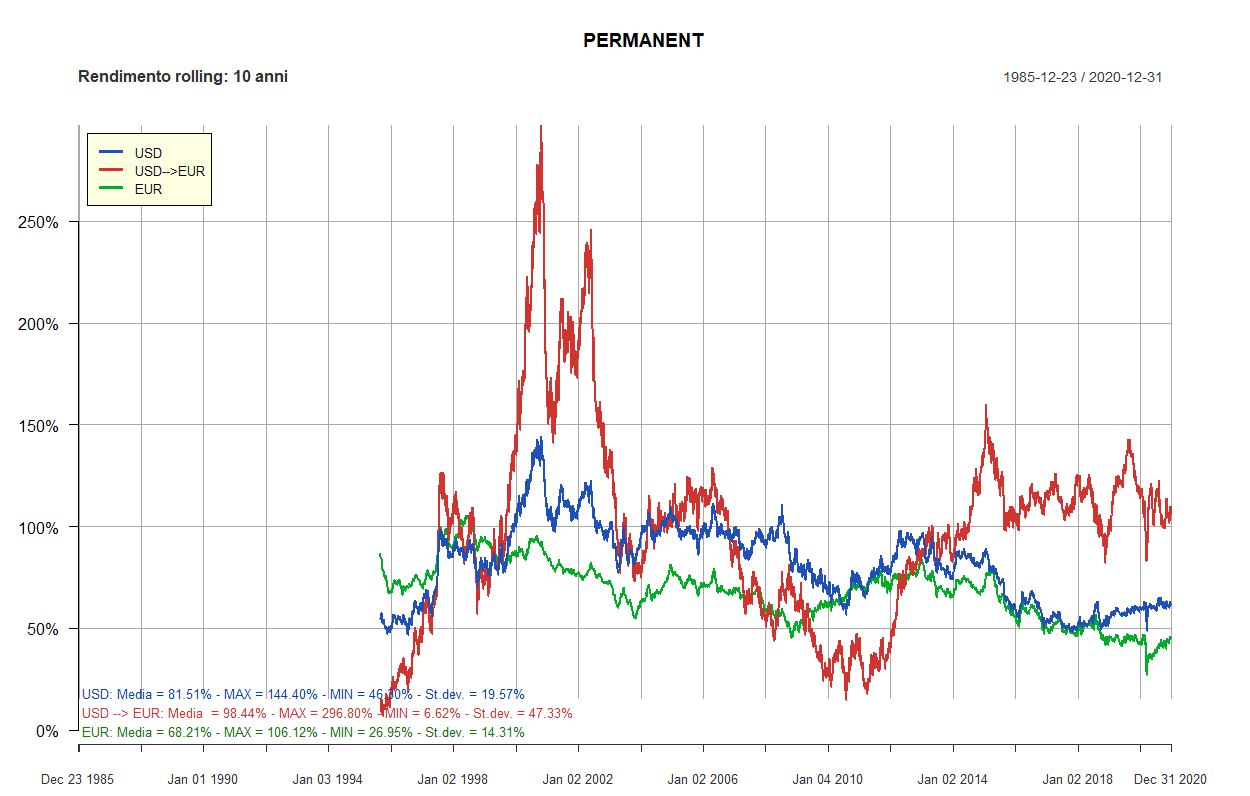
Il Permanent è un portafoglio interessante da analizzare.
Il Permanent, come abbiamo sottolineato nel capitolo 13.3.13, è uno dei portafogli più diversificati e difensivi tra quelli analizzati. Le sue caratteristiche lo rendono adatto agli investitori dalla bassa propensione al rischio.
Se il rischio di cambio è assente, la volatilità è bassa e i rendimenti medi sia a 5 anni che a 10 anni sono discreti. Le linee blu e verdi dimostrano che il Permanent ha attraversato le fasi più critiche degli ultimi 25 anni senza subire grossi scossoni.
Se, però, un investitore dell’area euro decidesse di replicare il portafoglio in USD senza coprire il cambio (linea rossa), la natura del suo investimento cambierebbe totalmente: il portafoglio prudente si trasformerebbe in aggressivo proprio a causa del rischio di cambio.
Il rendimento rolling a 10 anni medio salirebbe dall’81,51% al 98,44% (il 20,77% in più) mentre la volatilità dei rendimenti esploderebbe: dal 19,57% al 47,33%; un incremento del 161,17%!
Il Permanent portfolio in USD non hedgiato (USD→EUR) sarebbe del tutto inappropriato per un investitore prudente.
CORE FOUR
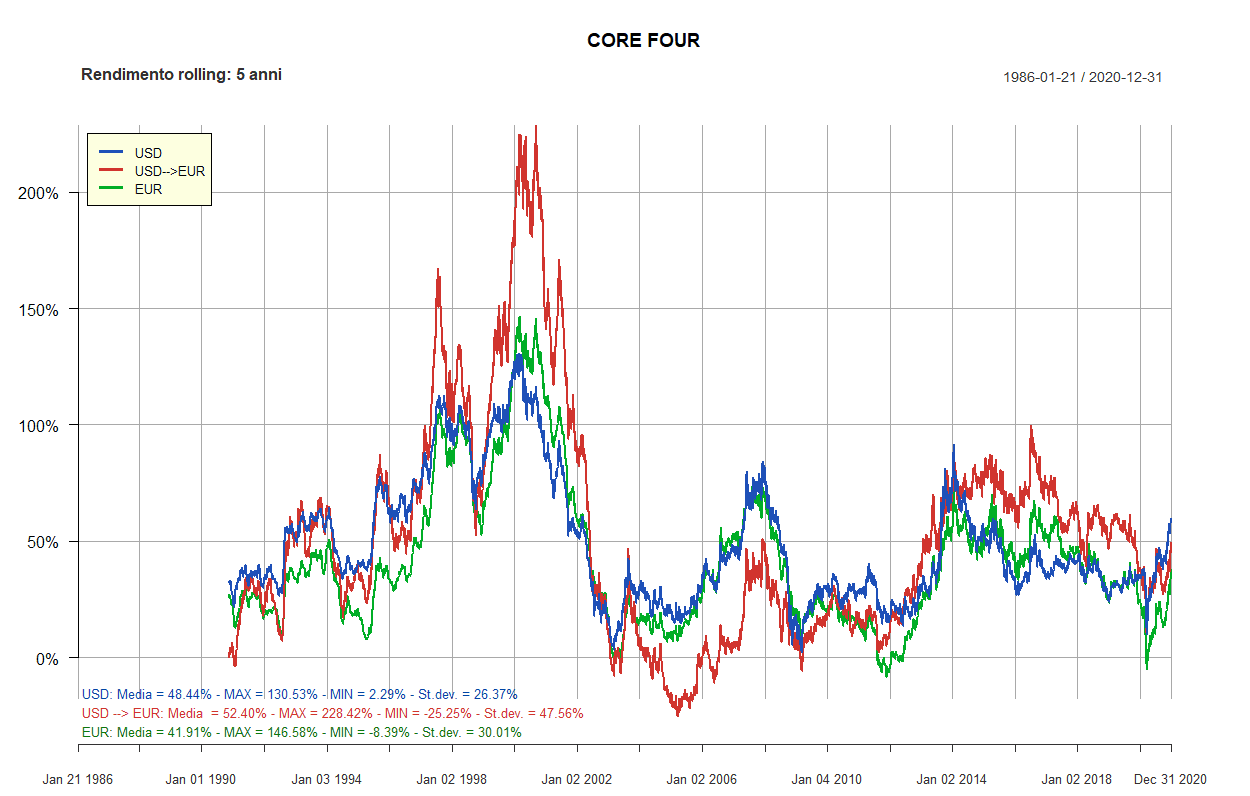
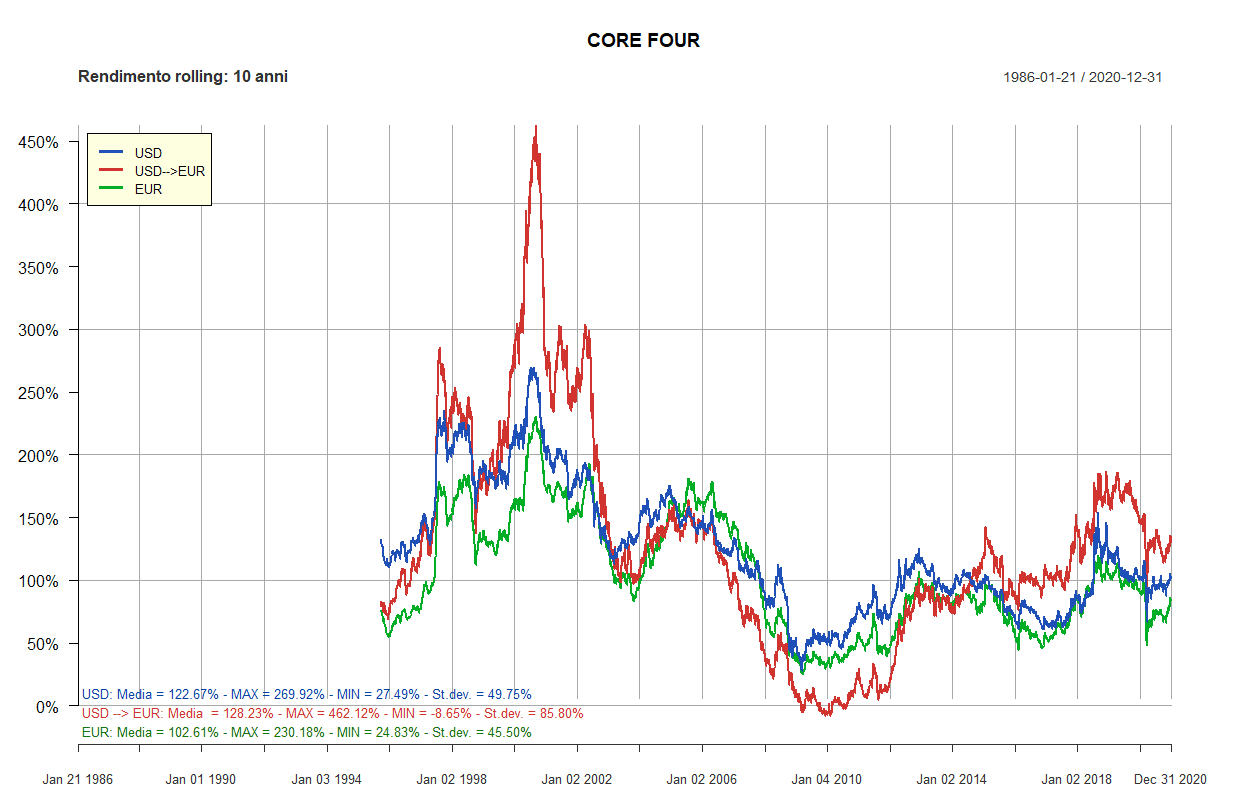
FOUR FUNDS BOGLEHEADS
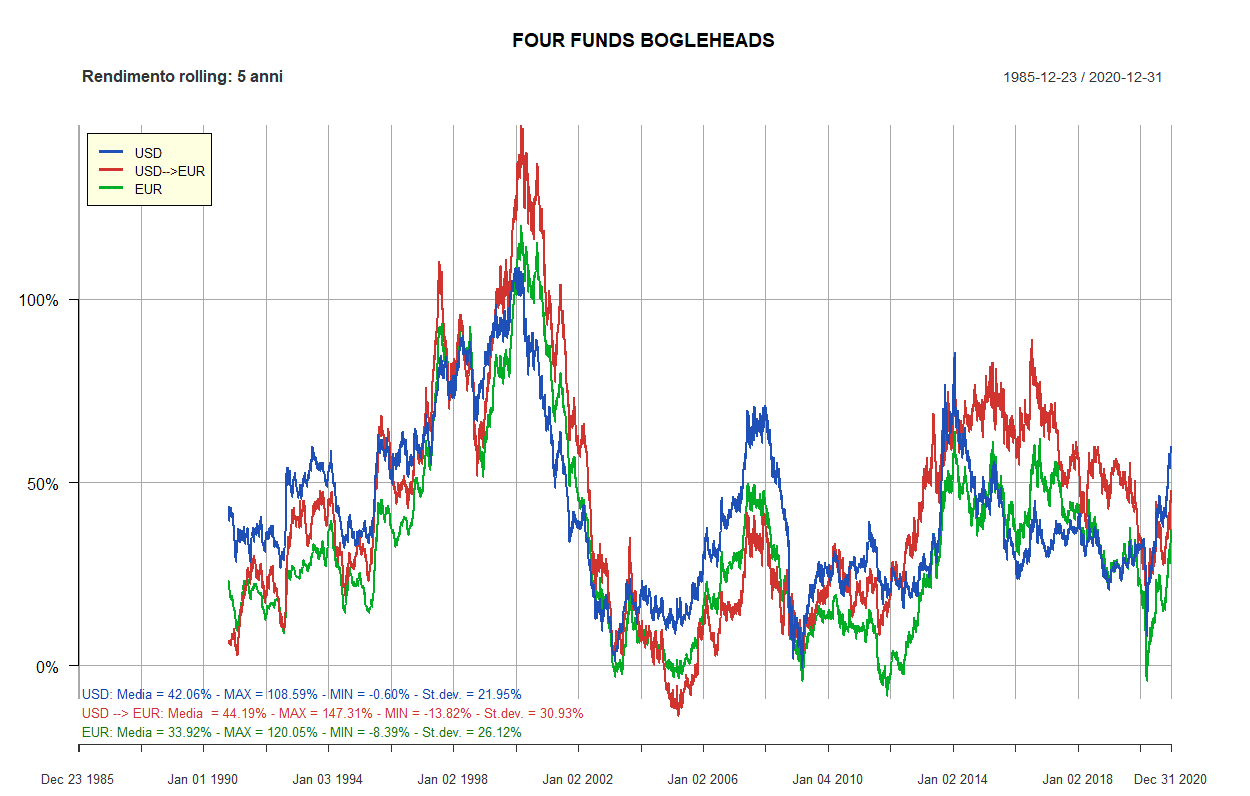
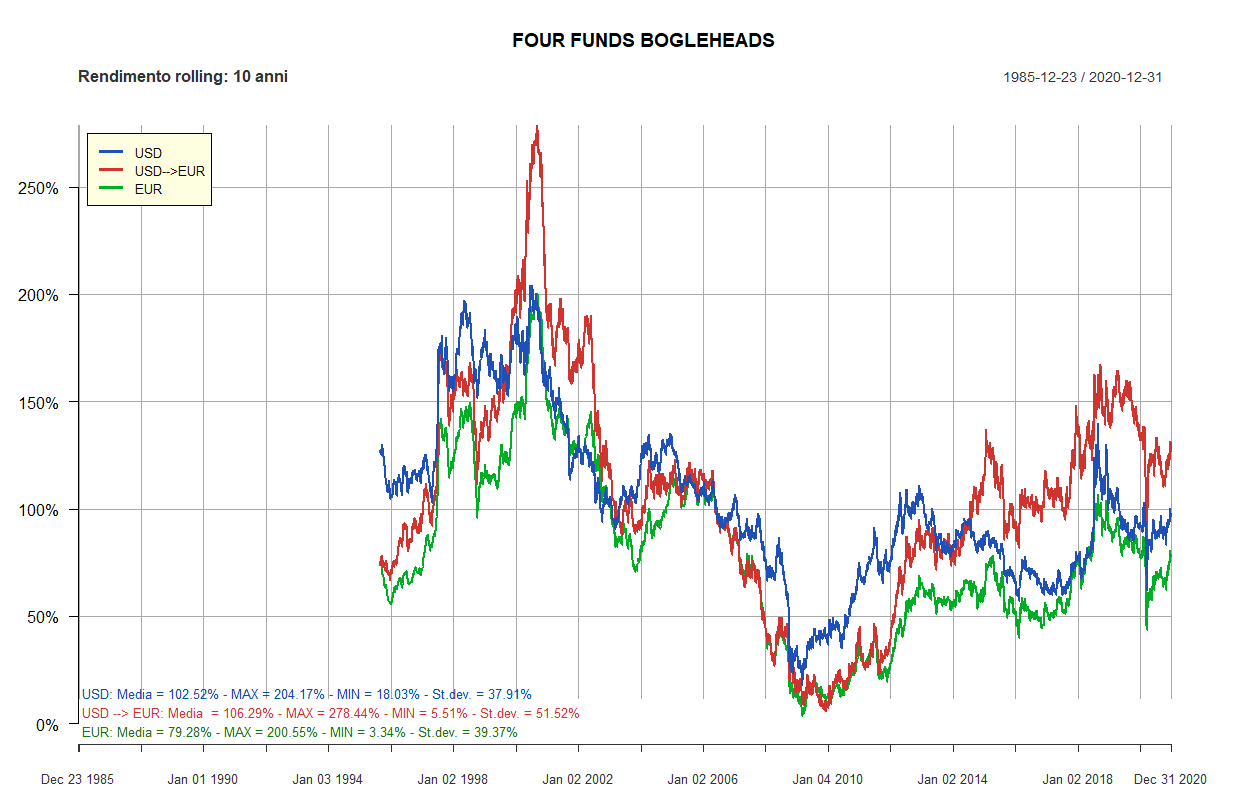
NO BRAINER
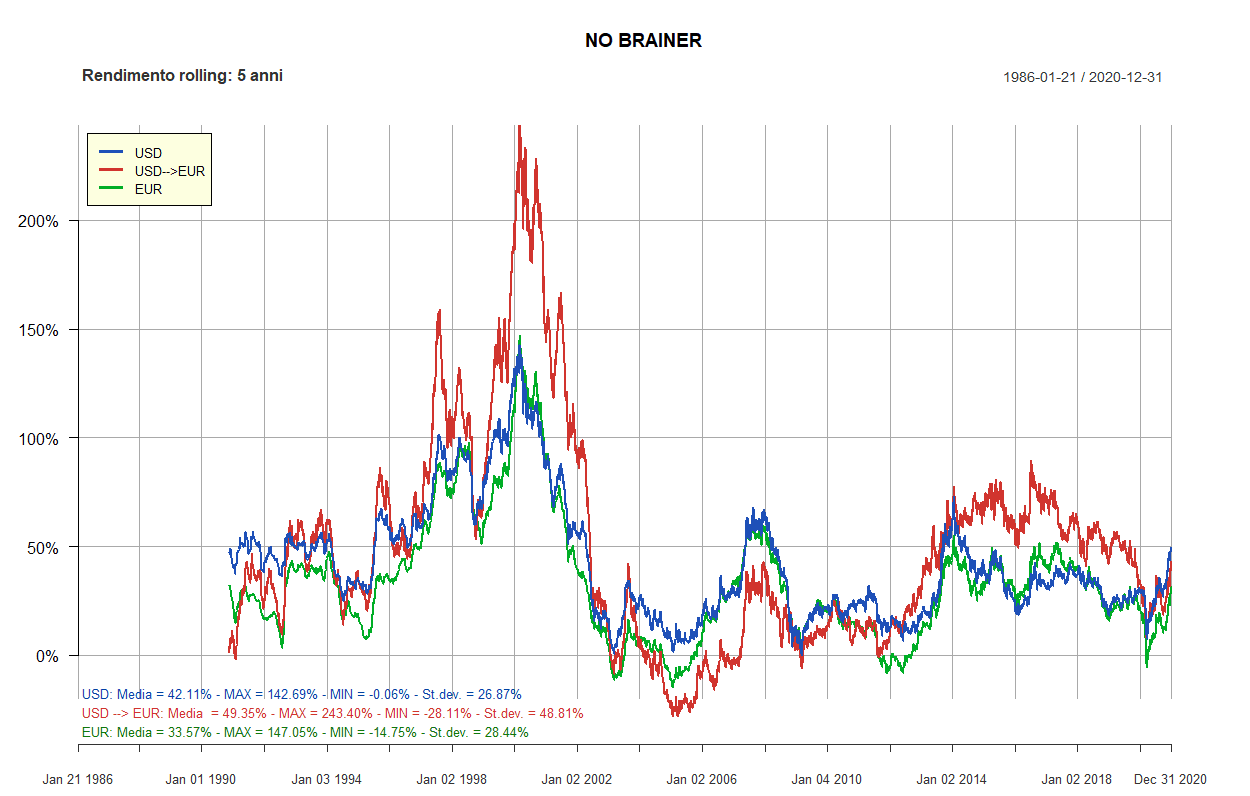
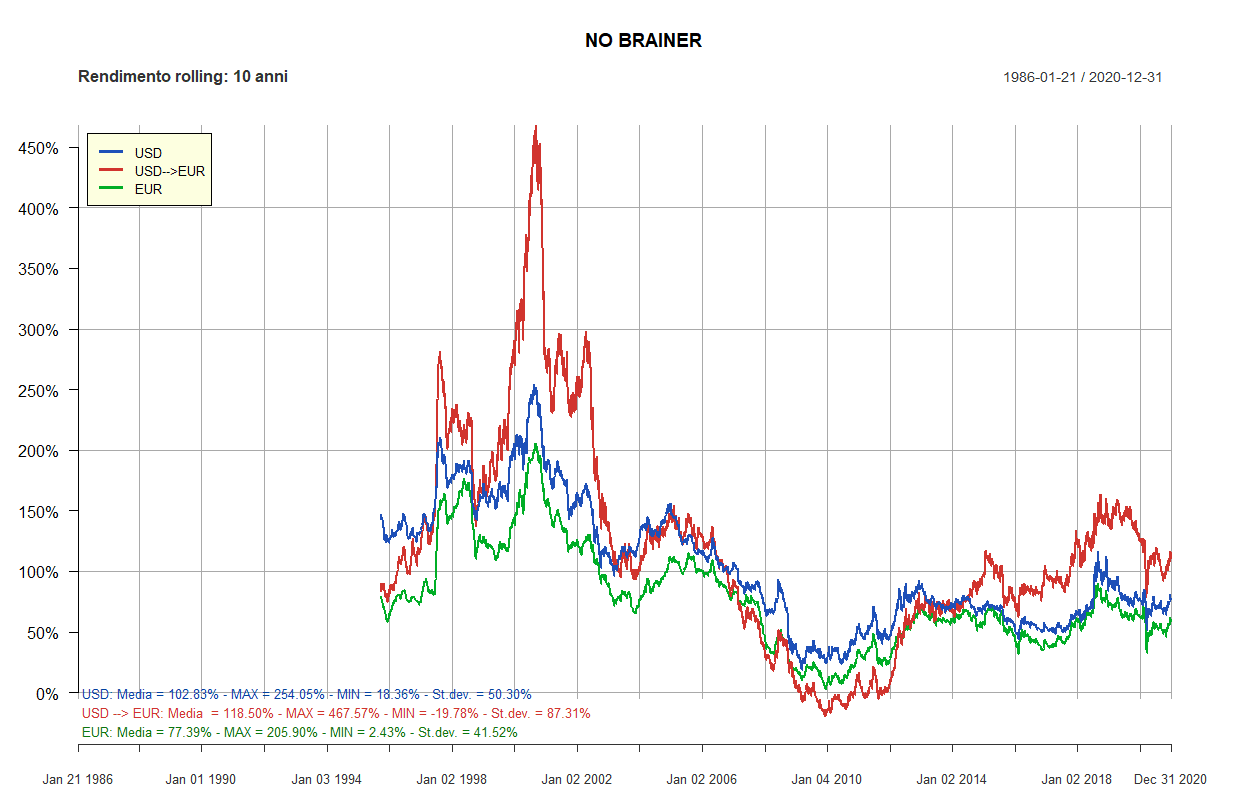
LARRY
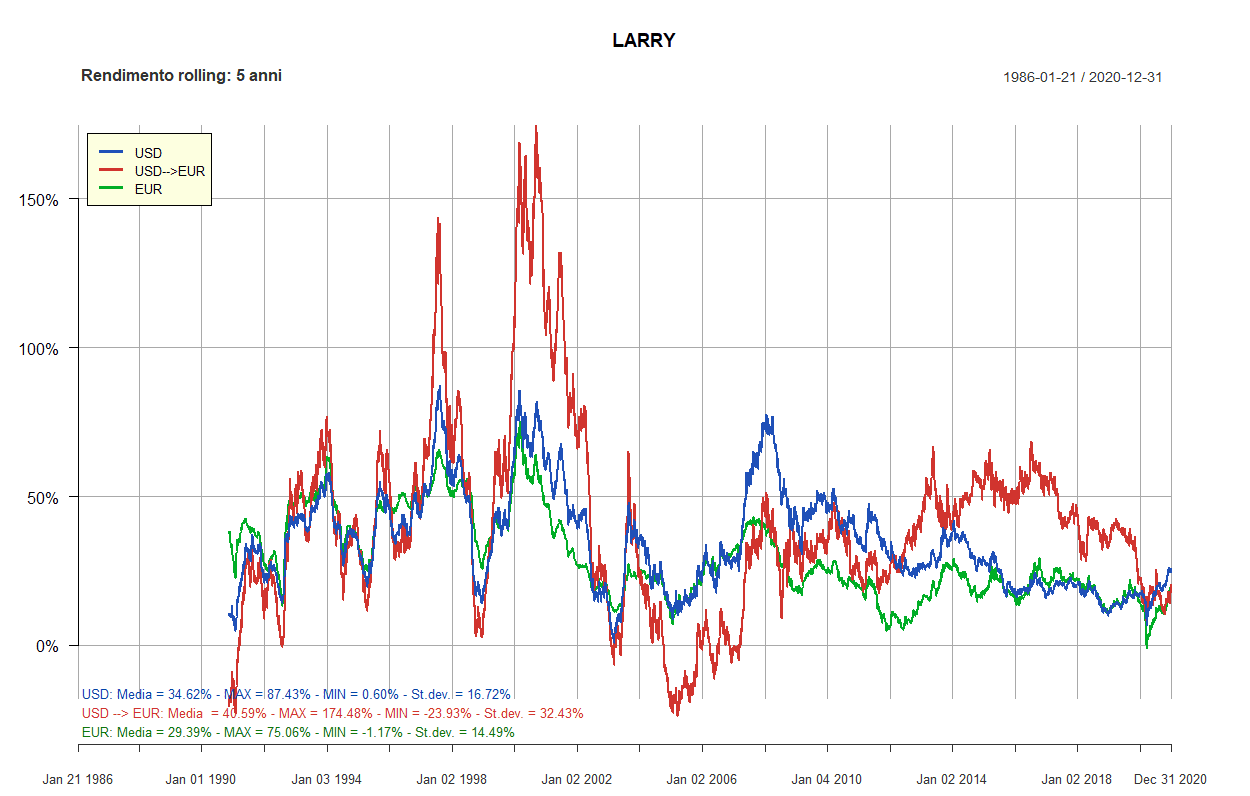
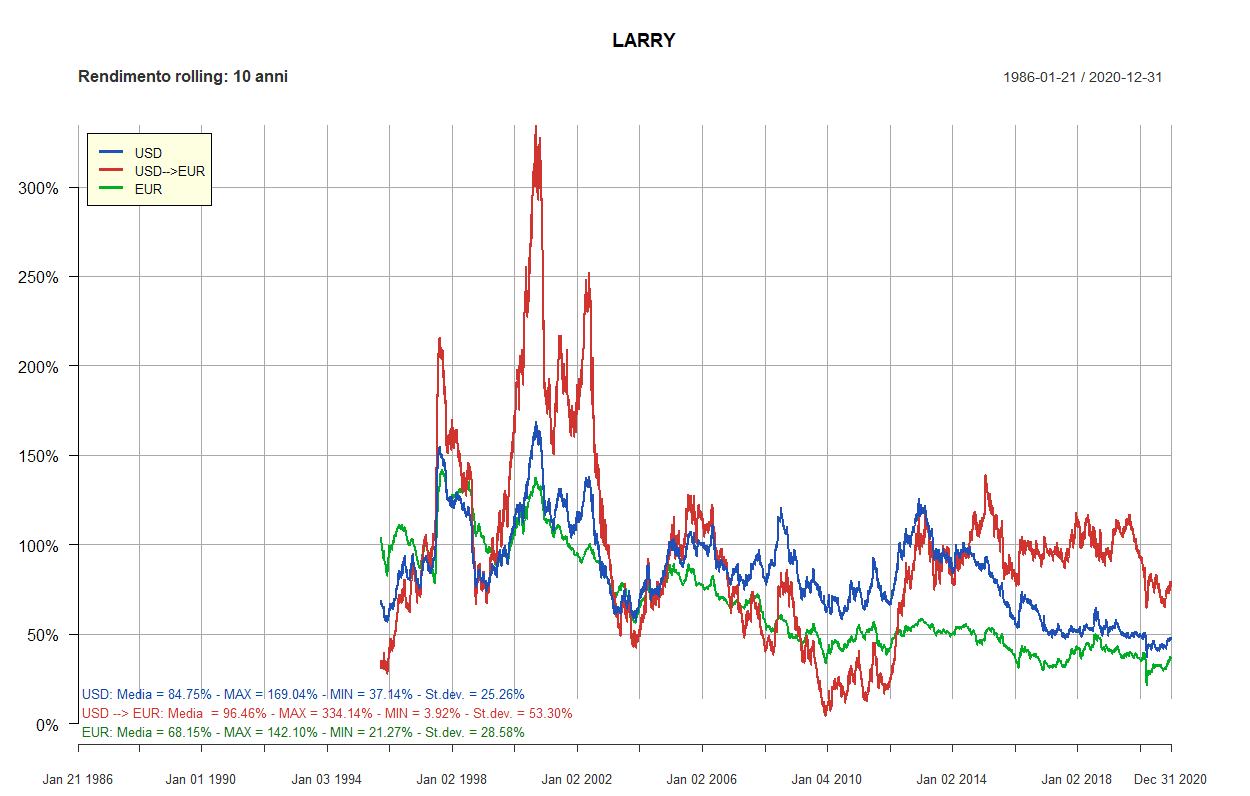
Le osservazioni fatte sul Permanent portfolio possono essere estese al Larry: è un portafoglio prudente in USD e in EUR, ma diventa un’arma pericolosa in mano a un investitore dell’area euro che volesse replicare il portafoglio in USD senza coprire adeguatamente il cambio.
GOLDEN BUTTERFLY
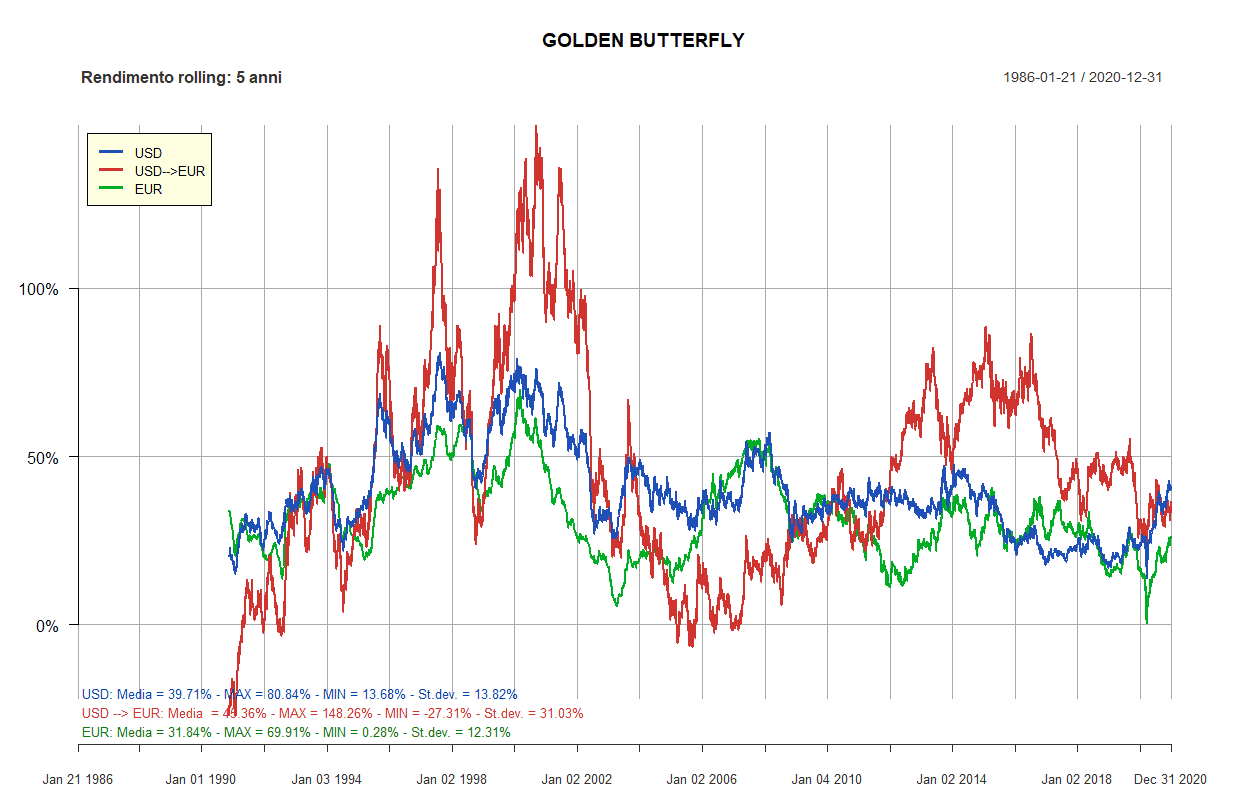
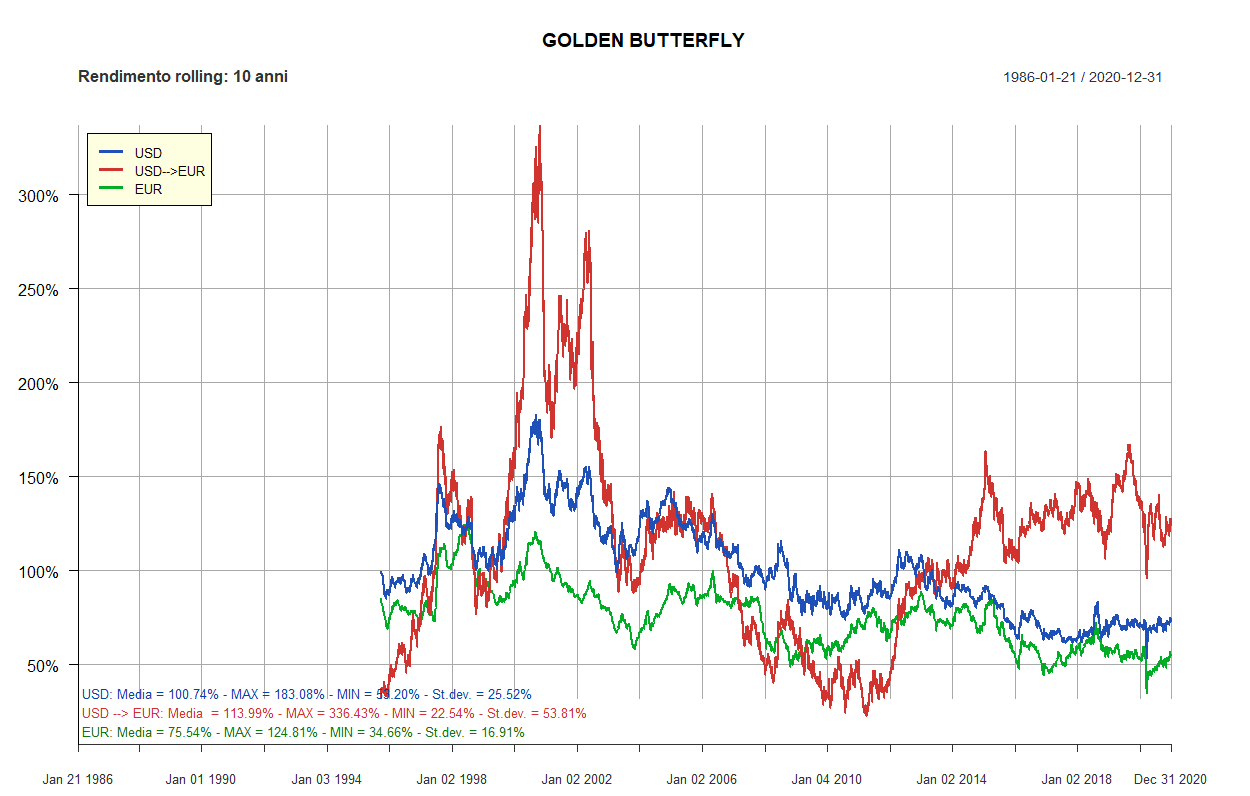
Le osservazioni fatte sul Permanent ed estese al Larry portfolio poco sopra possono essere allargate anche al Golden Butterfly: il portafoglio, naturalmente prudente sia in USD che in EUR, diventa molto rischioso se un investitore dell’area euro volesse replicare il portafoglio in USD senza coprire il cambio.
ALL WEATHER
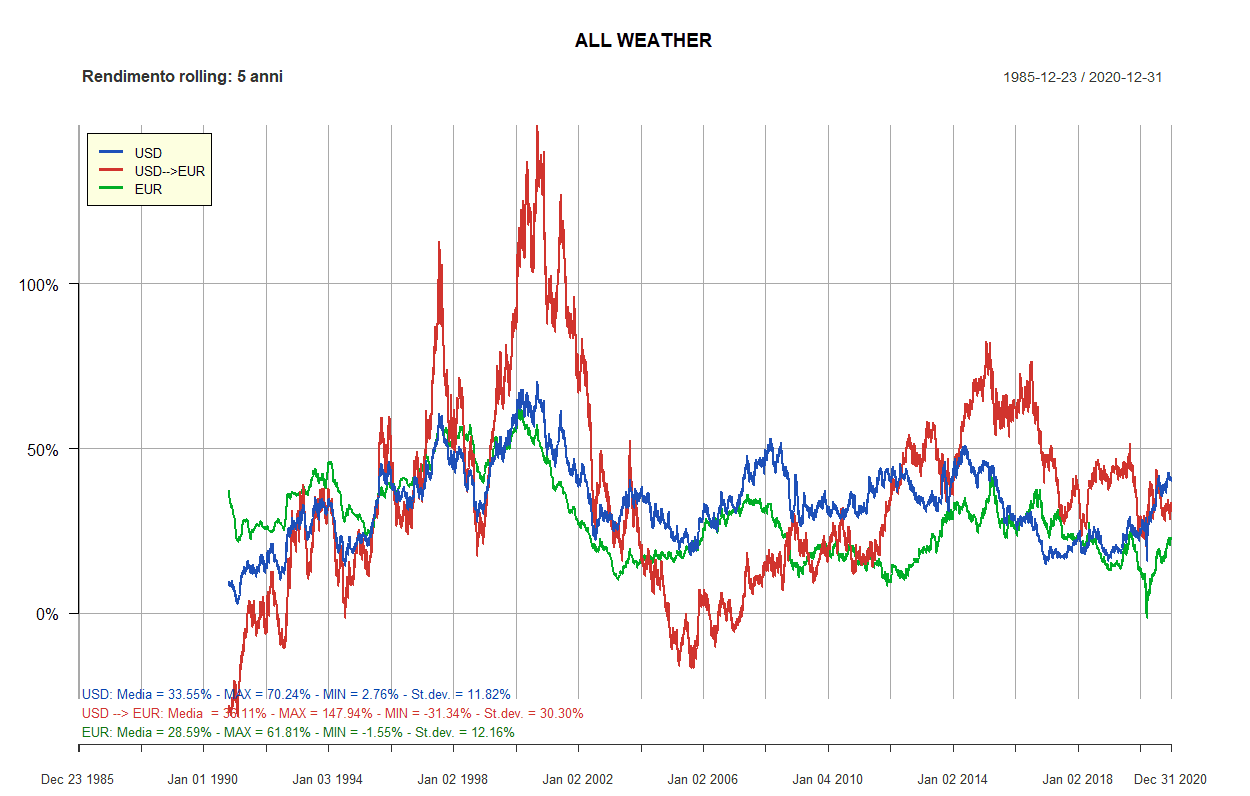
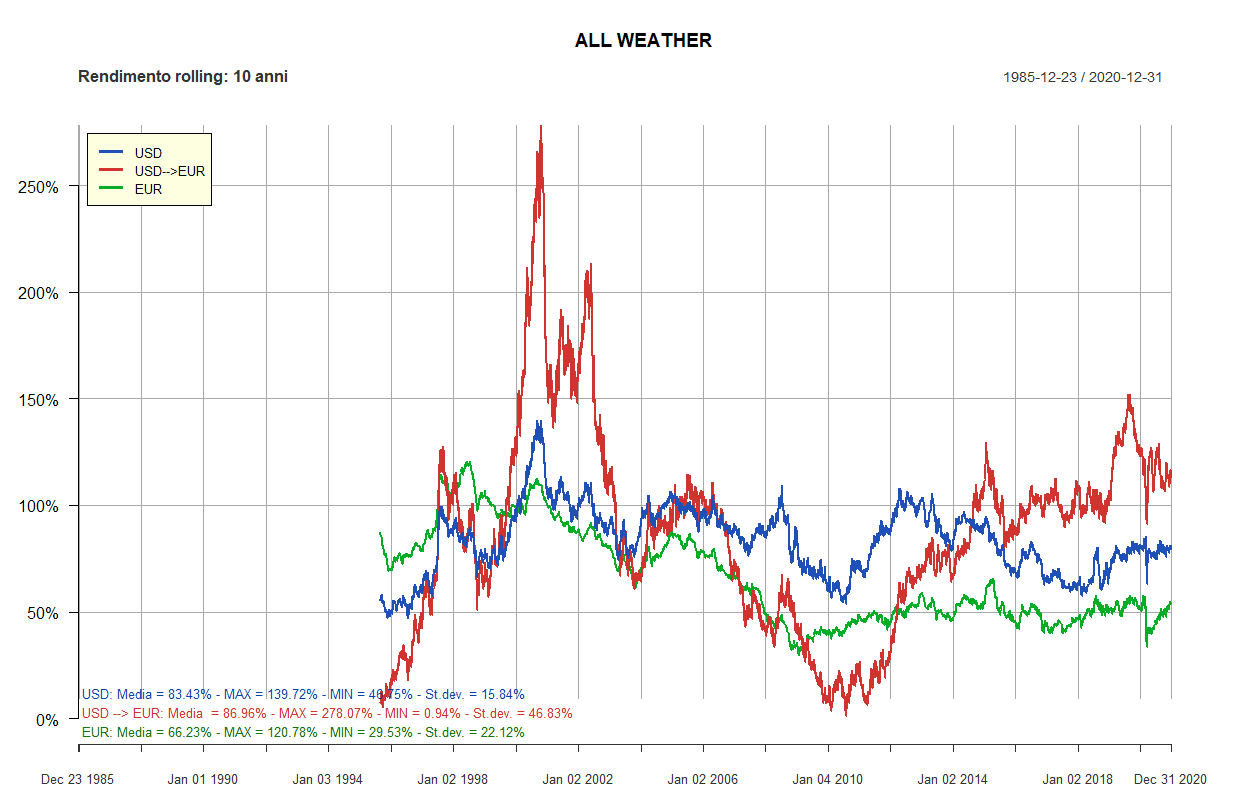
Le osservazioni fatte sul Permanent portfolio ed estese al Larry e al Golden Butterfly possono essere allargate anche all’All Weather.
IVY
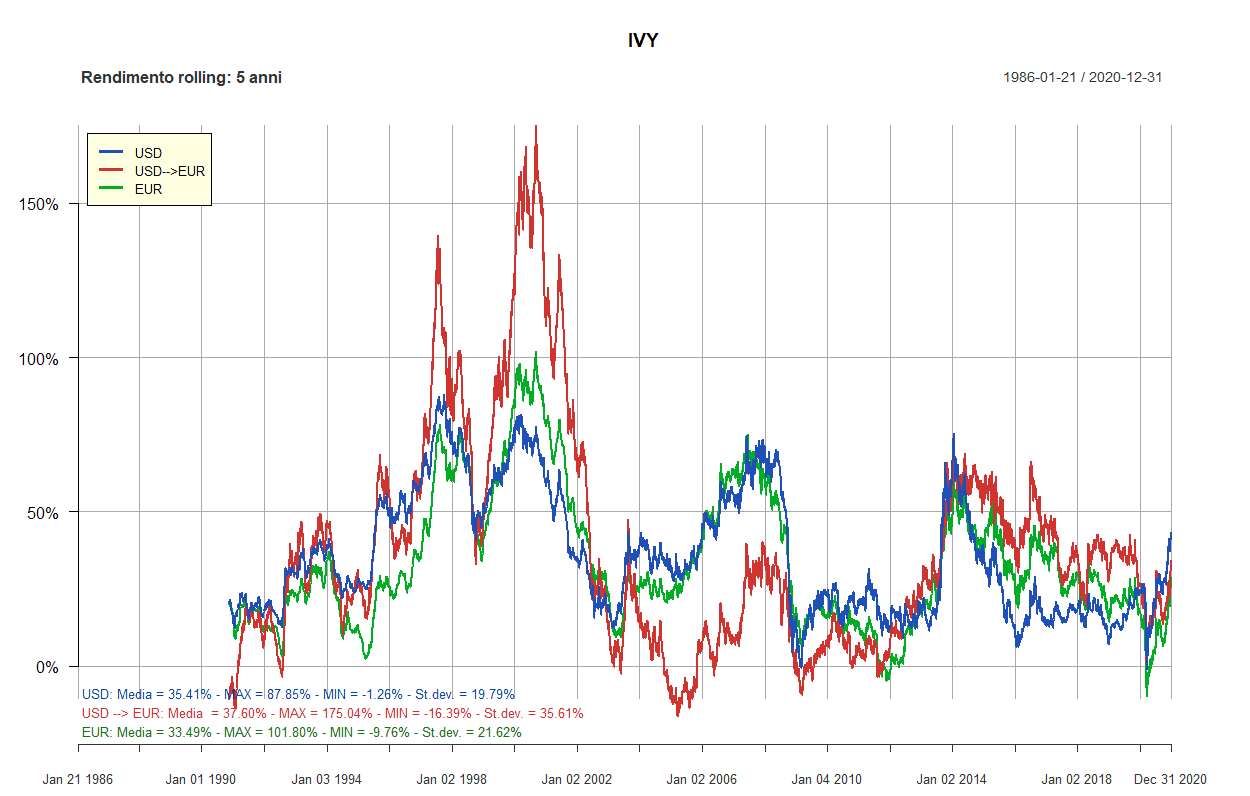
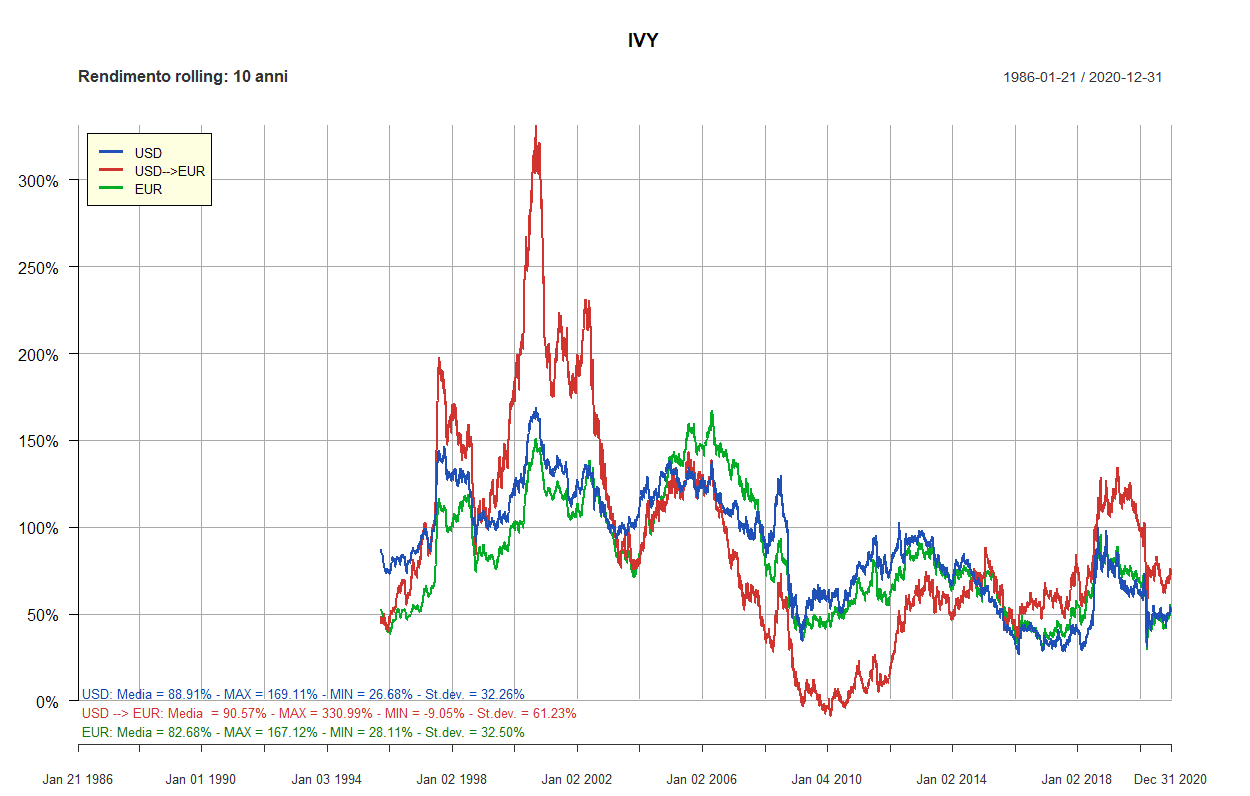
DYNAMIC 60/40 INCOME
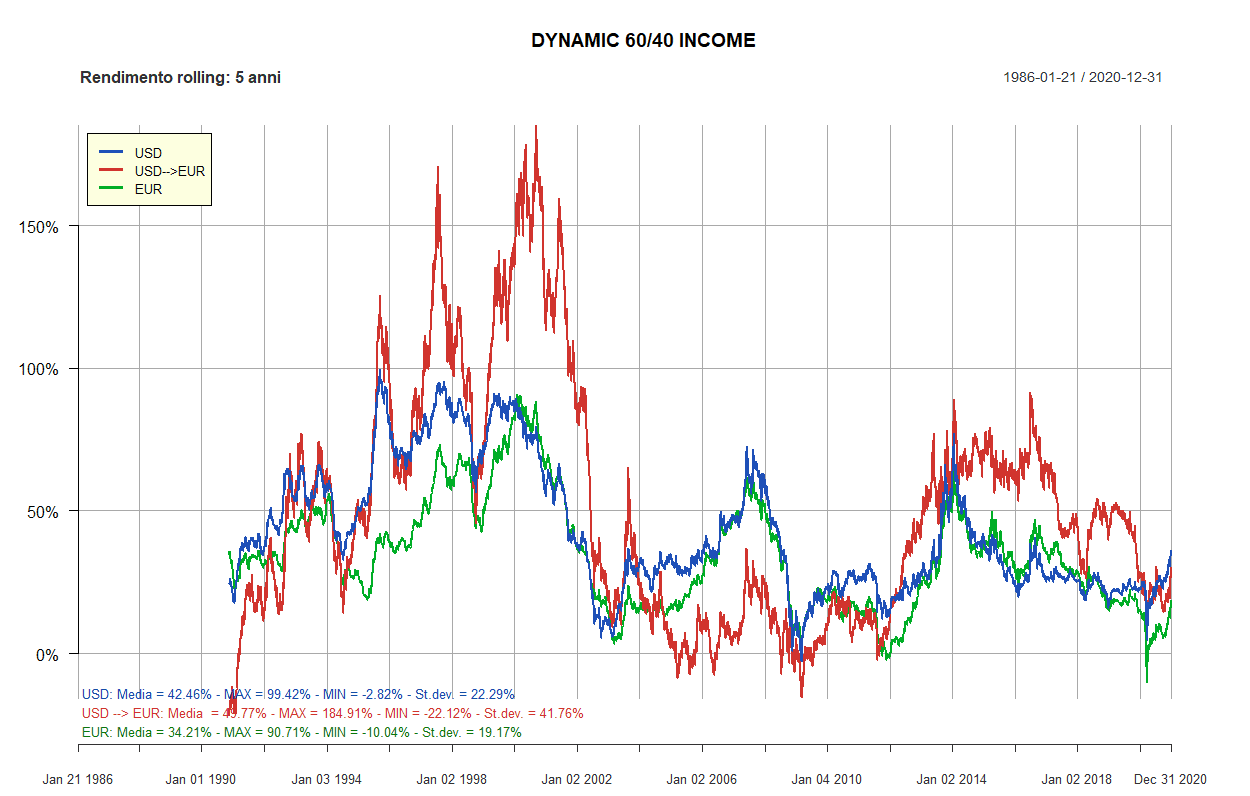
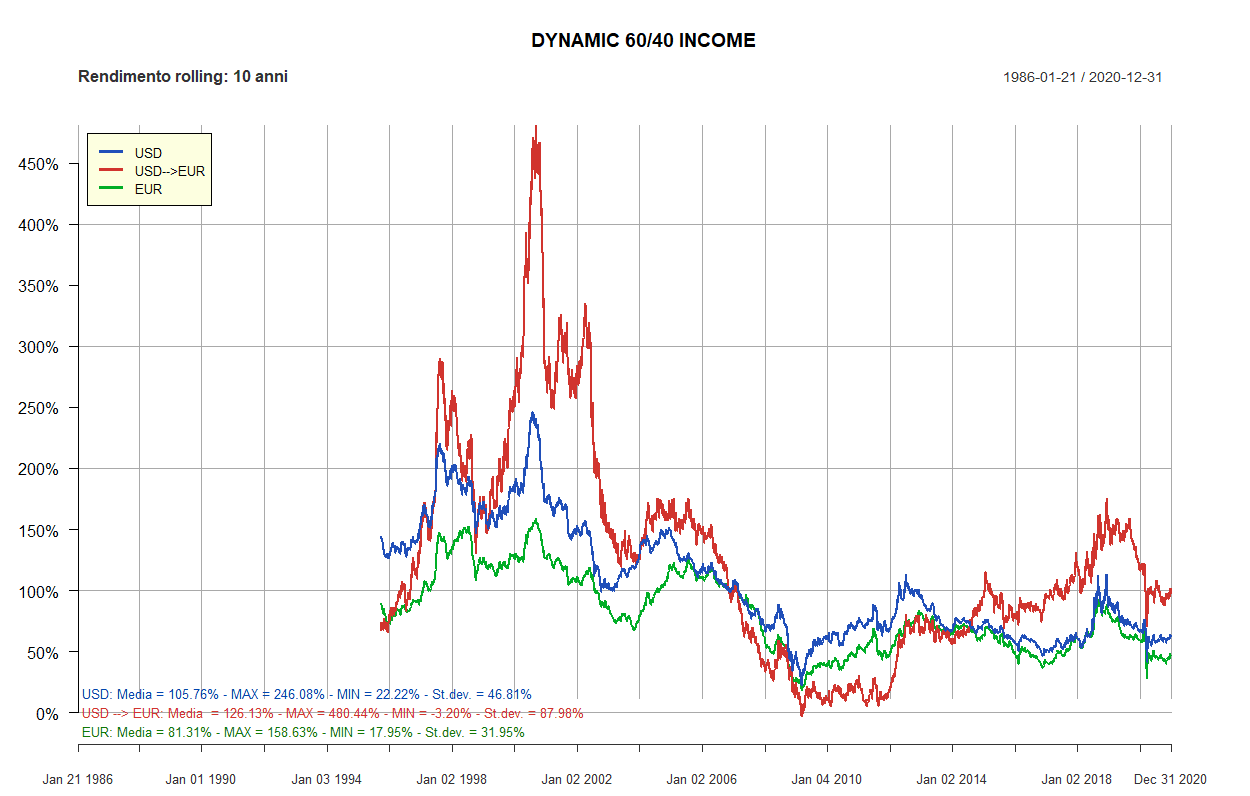
DYNAMIC 40/60 INCOME
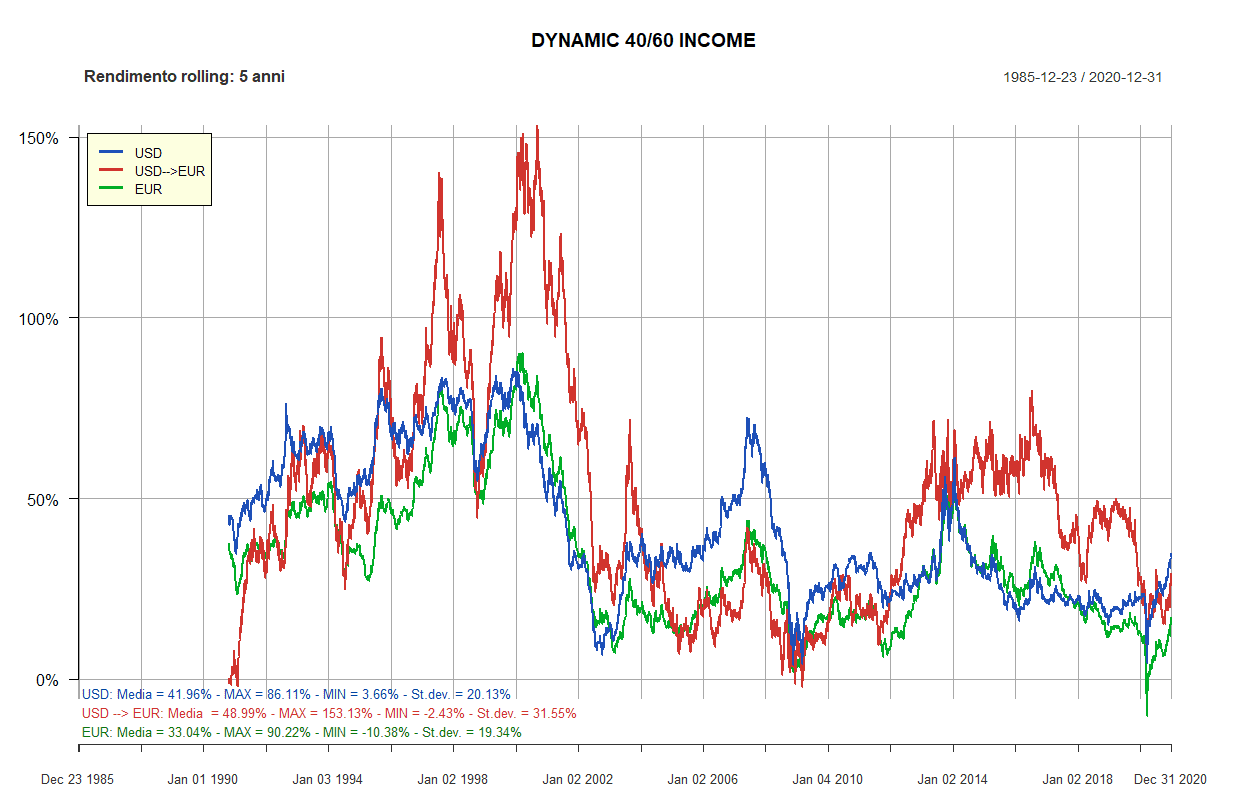
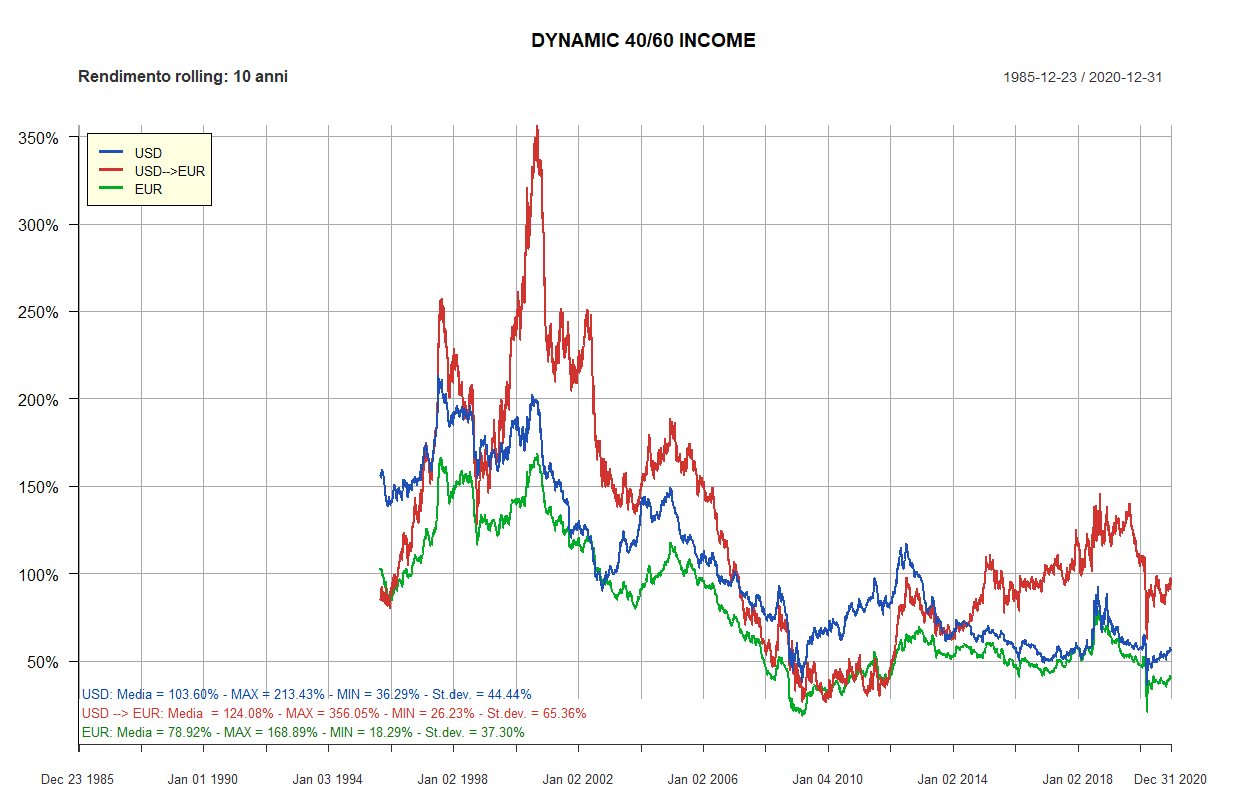
FIVE ASSET
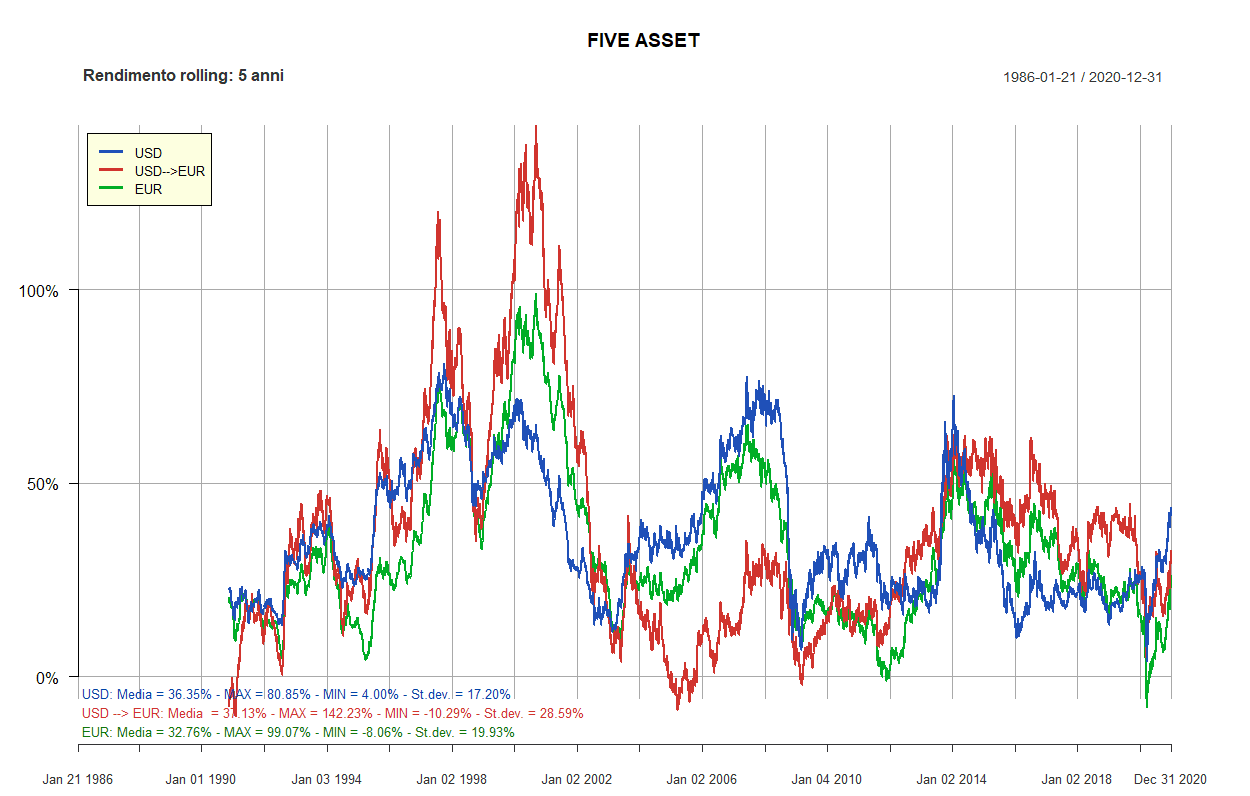
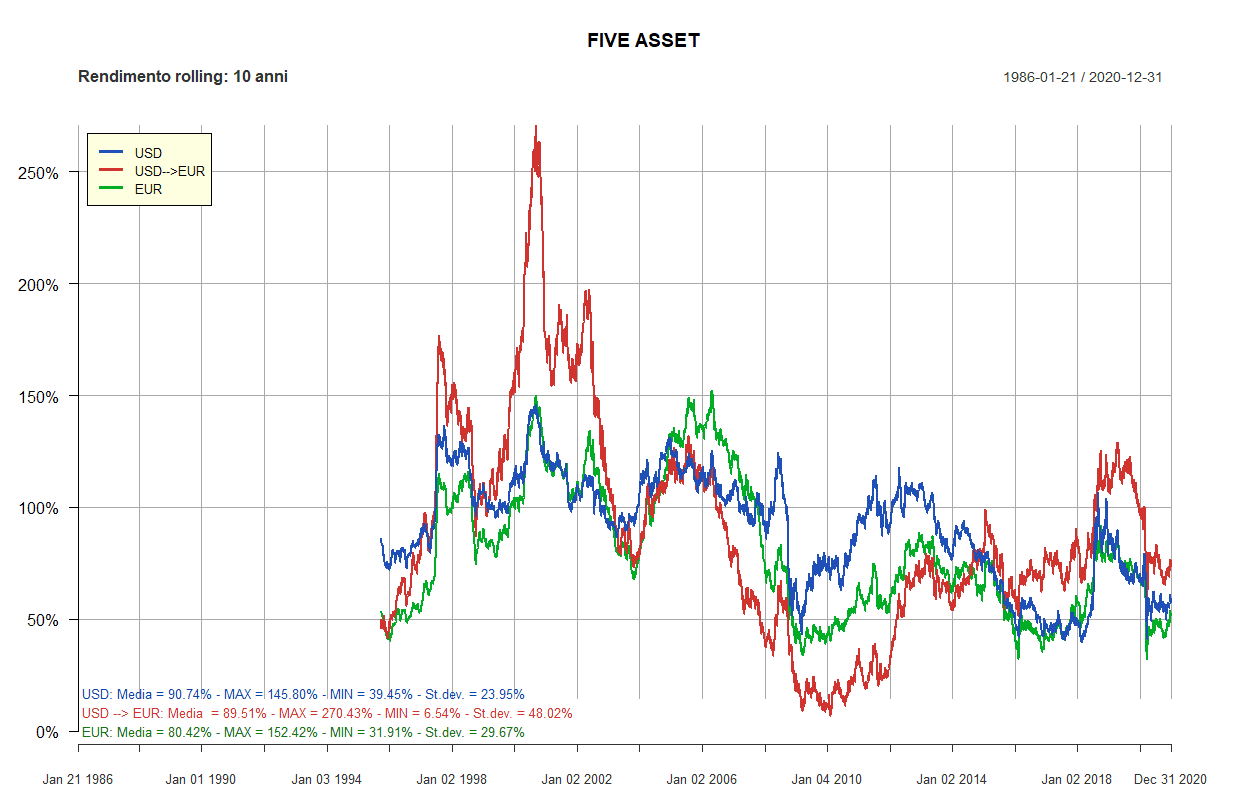
DAVID SWENSEN LAZY PORTFOLIO
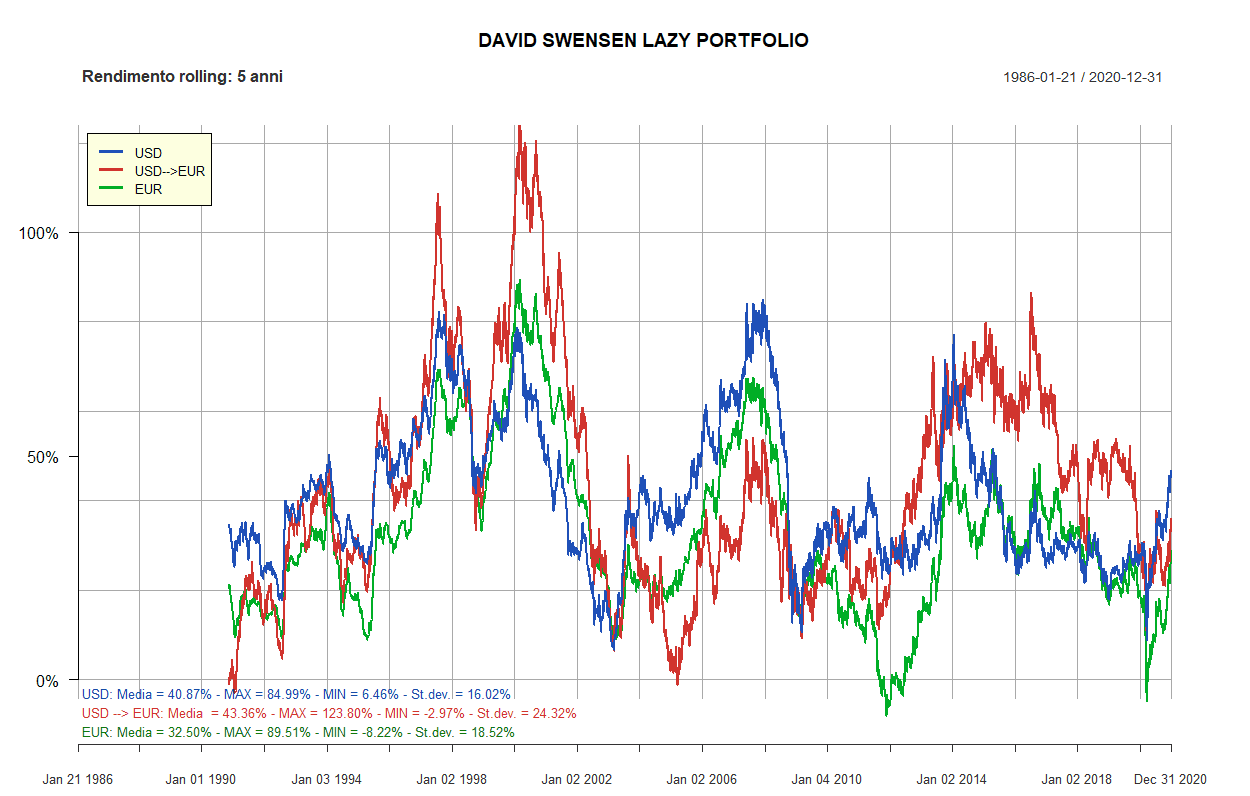
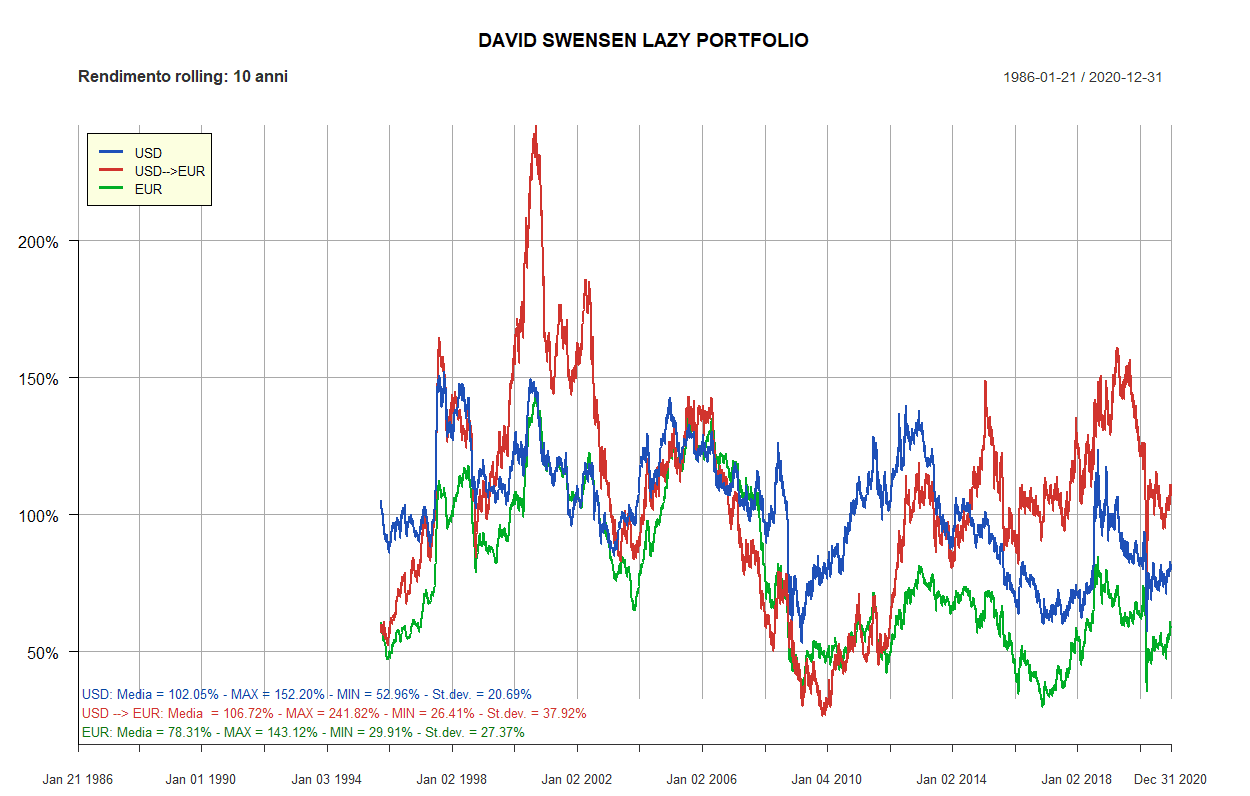
COFFEE HOUSE
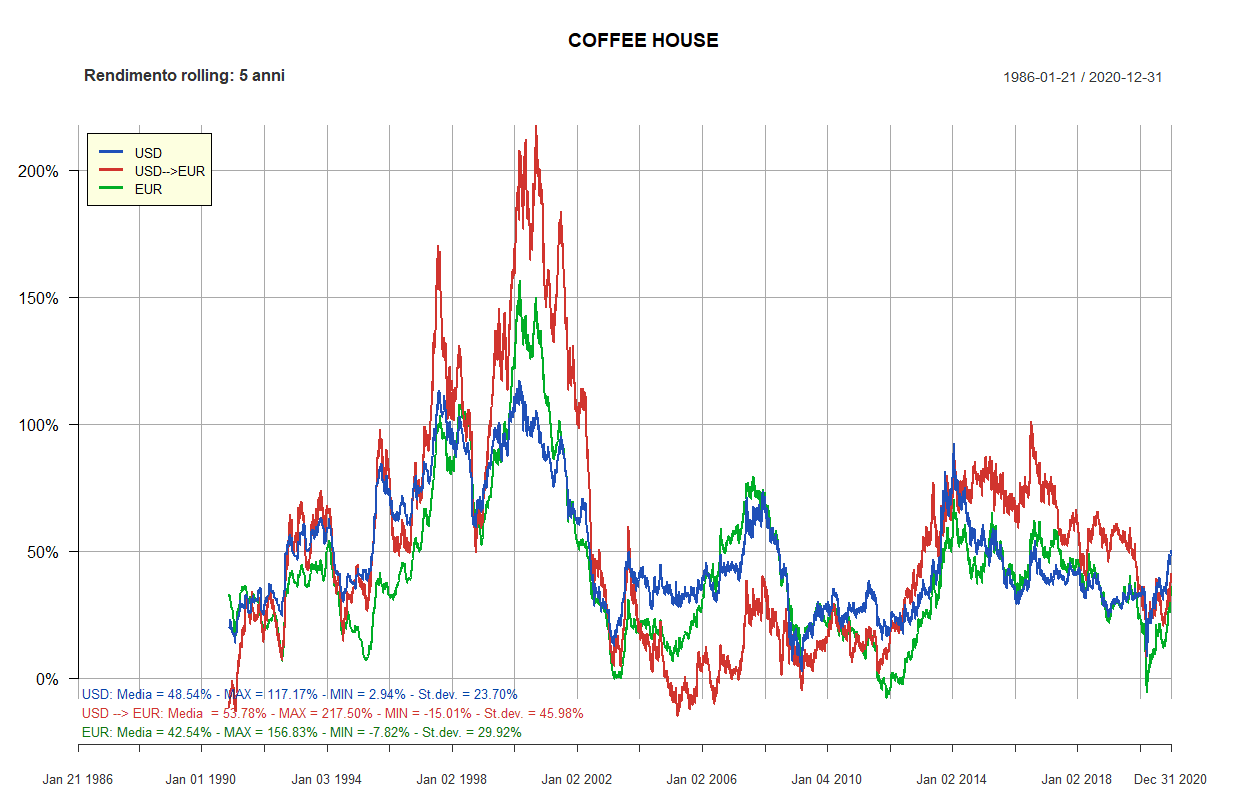
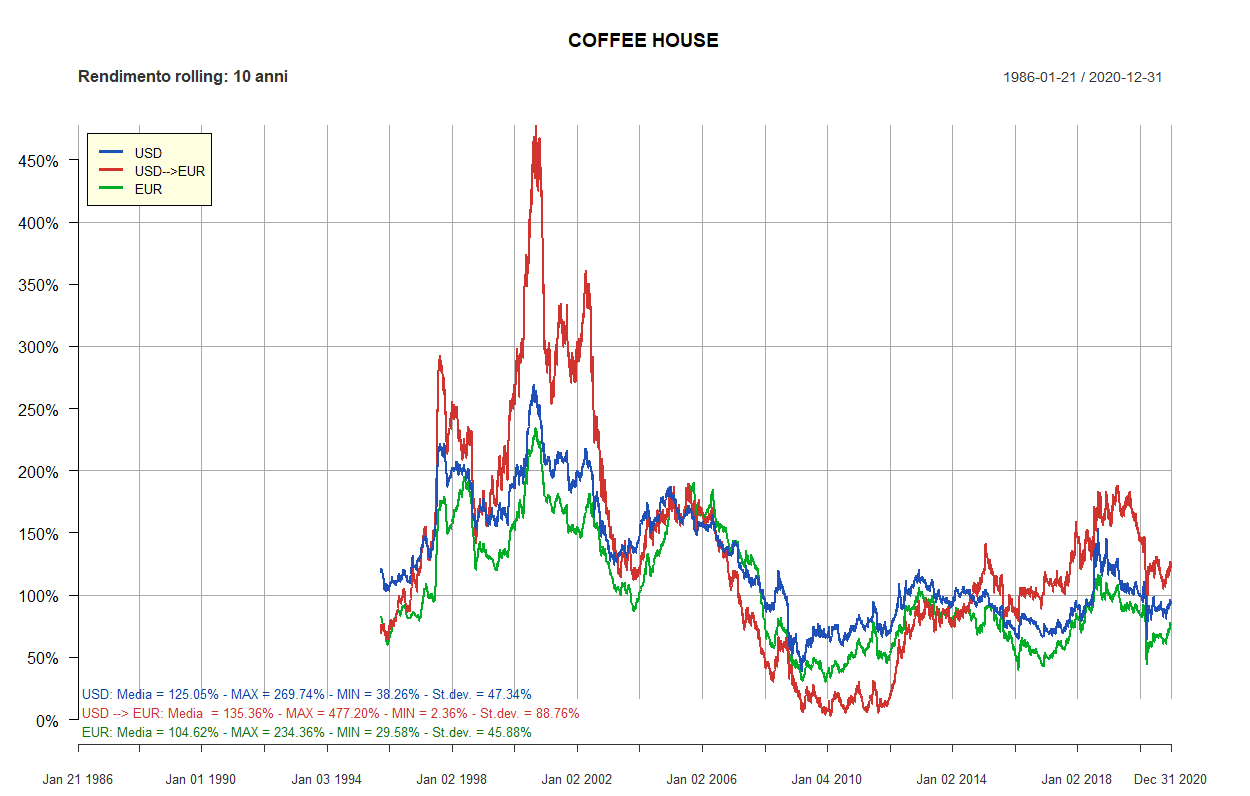
ROB ARNOTT
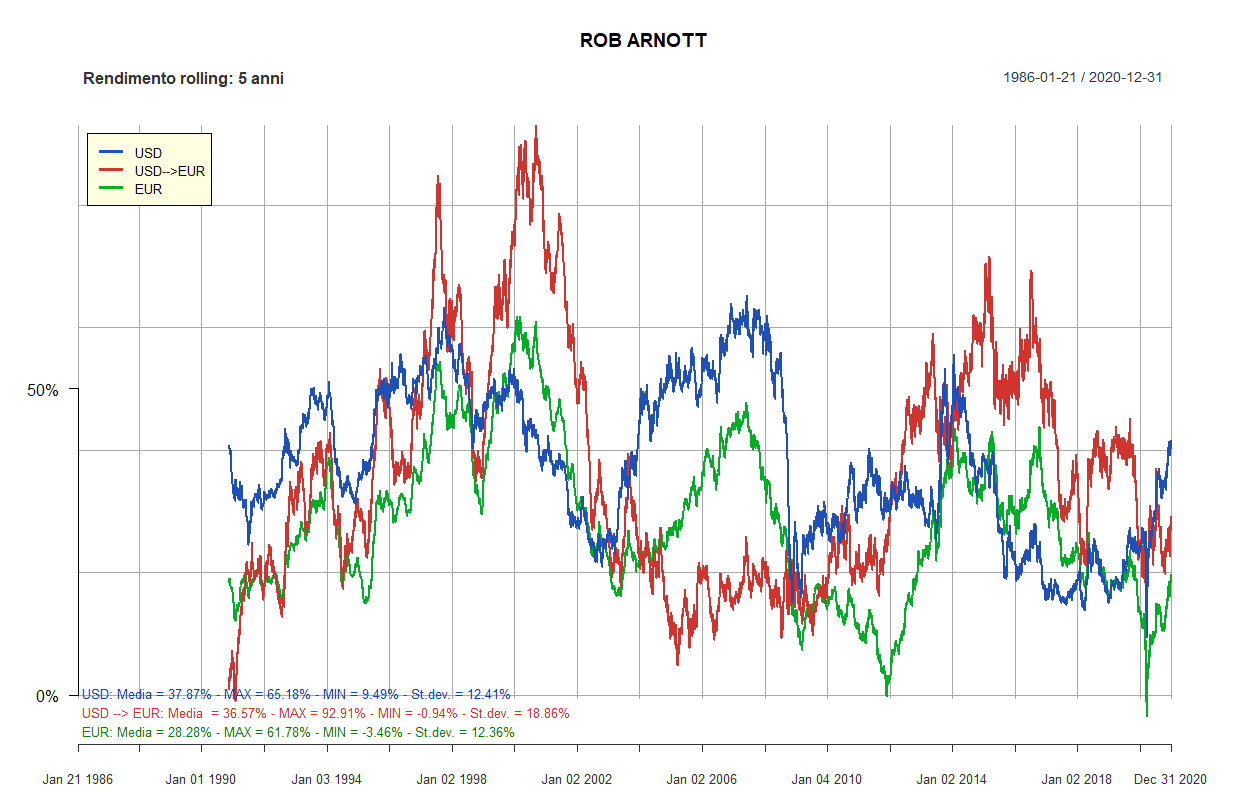
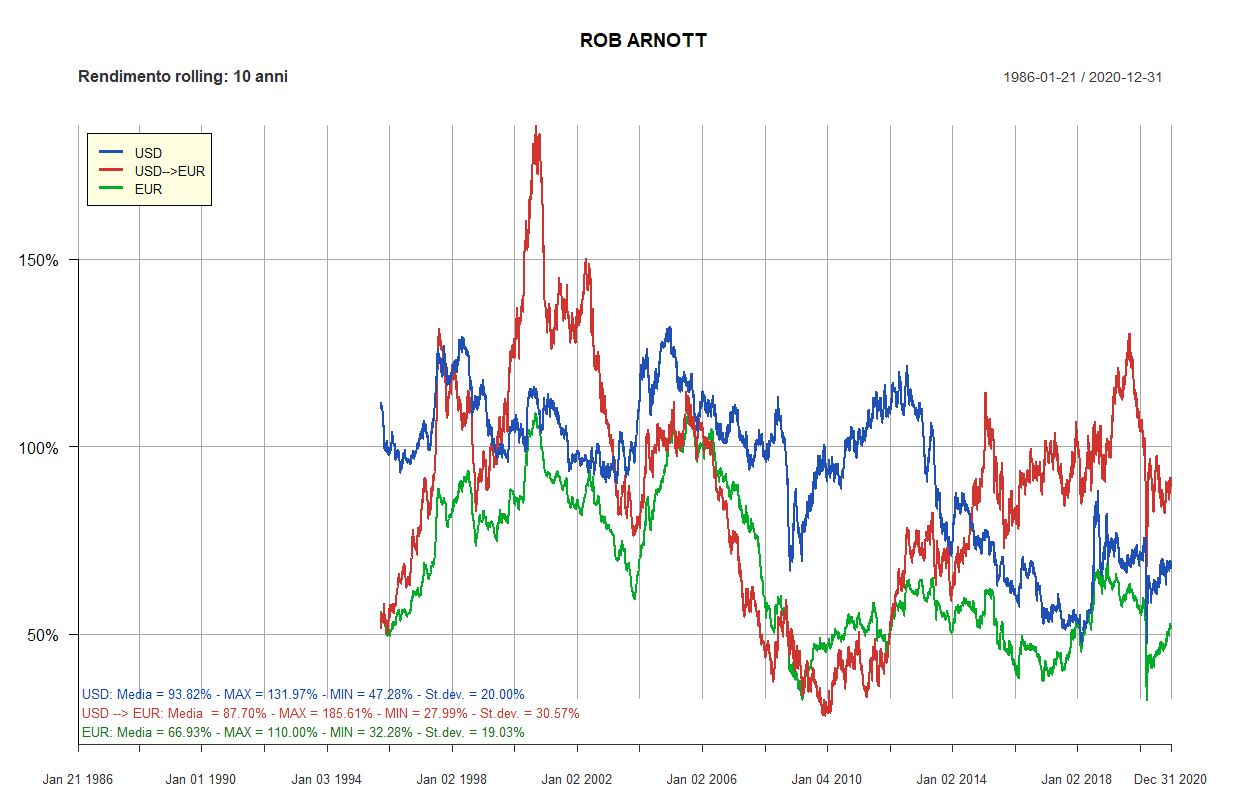
Le osservazioni fatte sui Permanent, Larry, Golden Butterfly e All Weather portfolios – ai quali rimandiamo – possono essere allargate al Rob Arnott.
ULTIMATE BUY AND HOLD STRATEGY
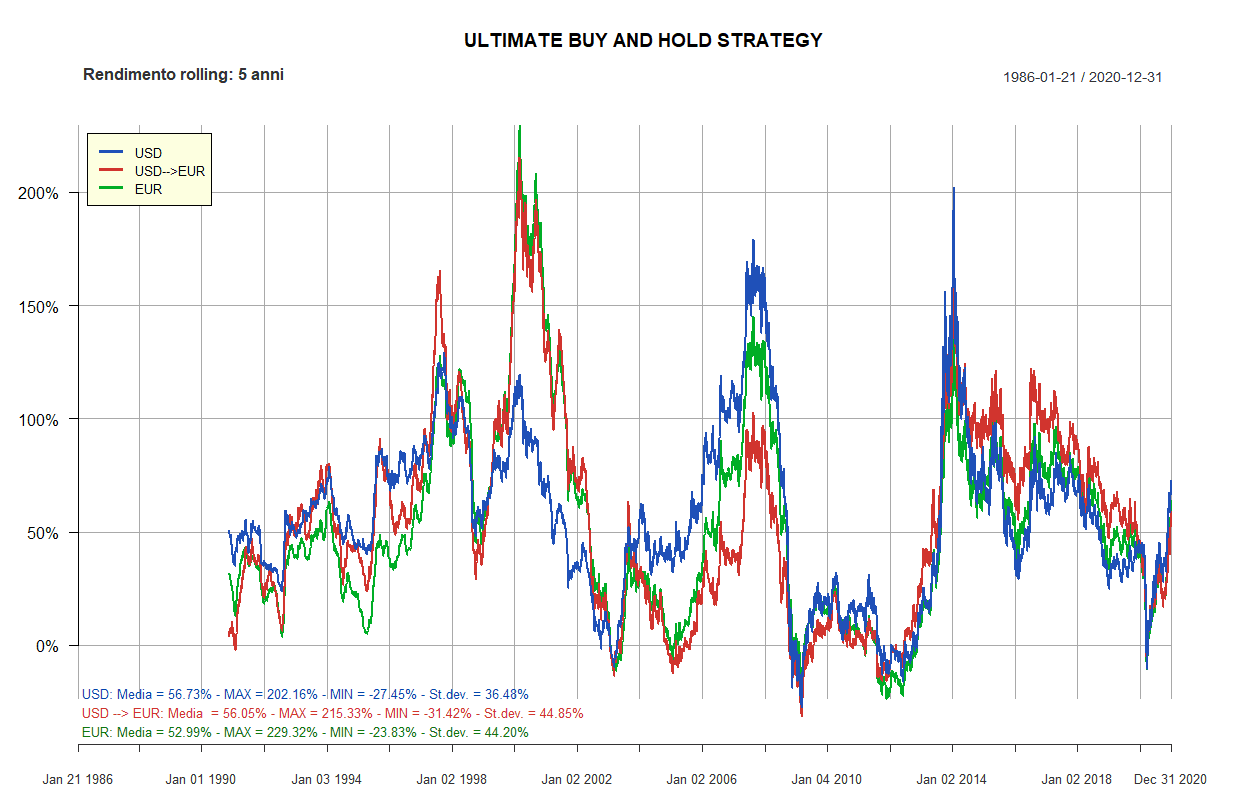
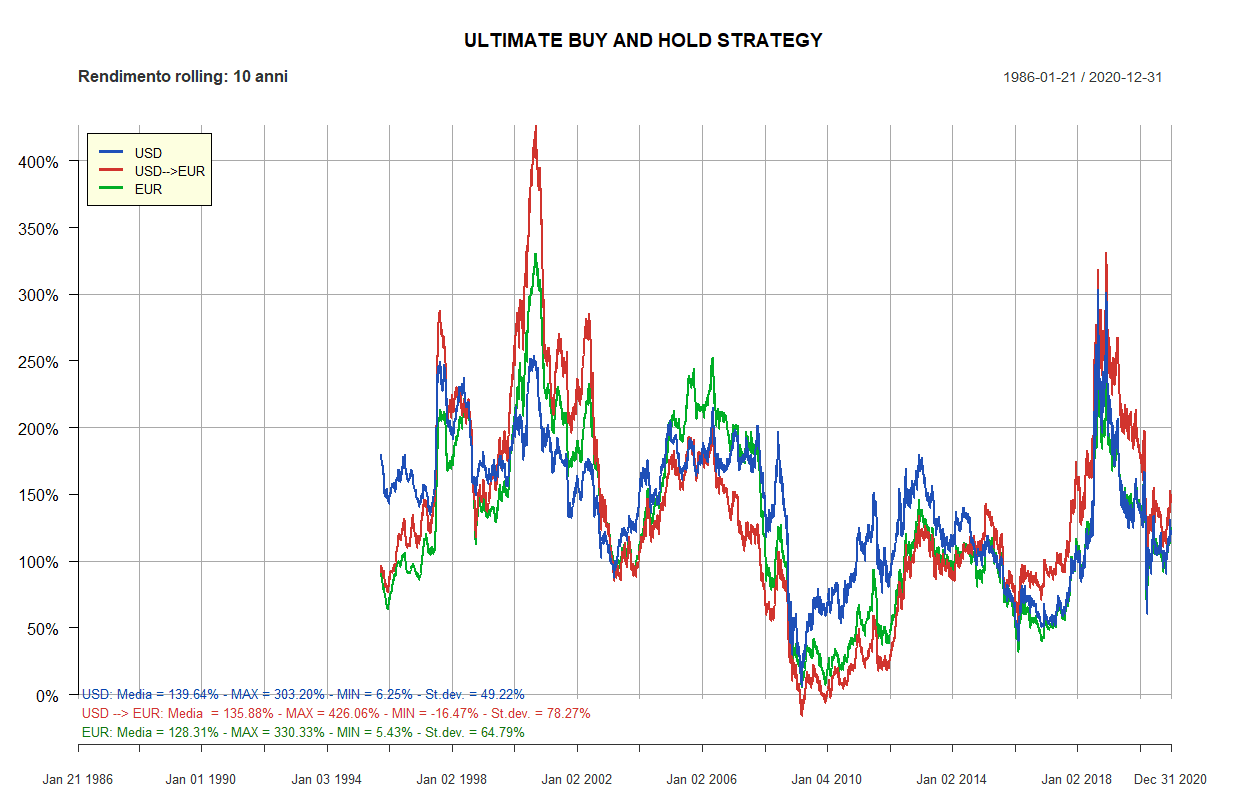
ULTIMATE BUY & HOLD
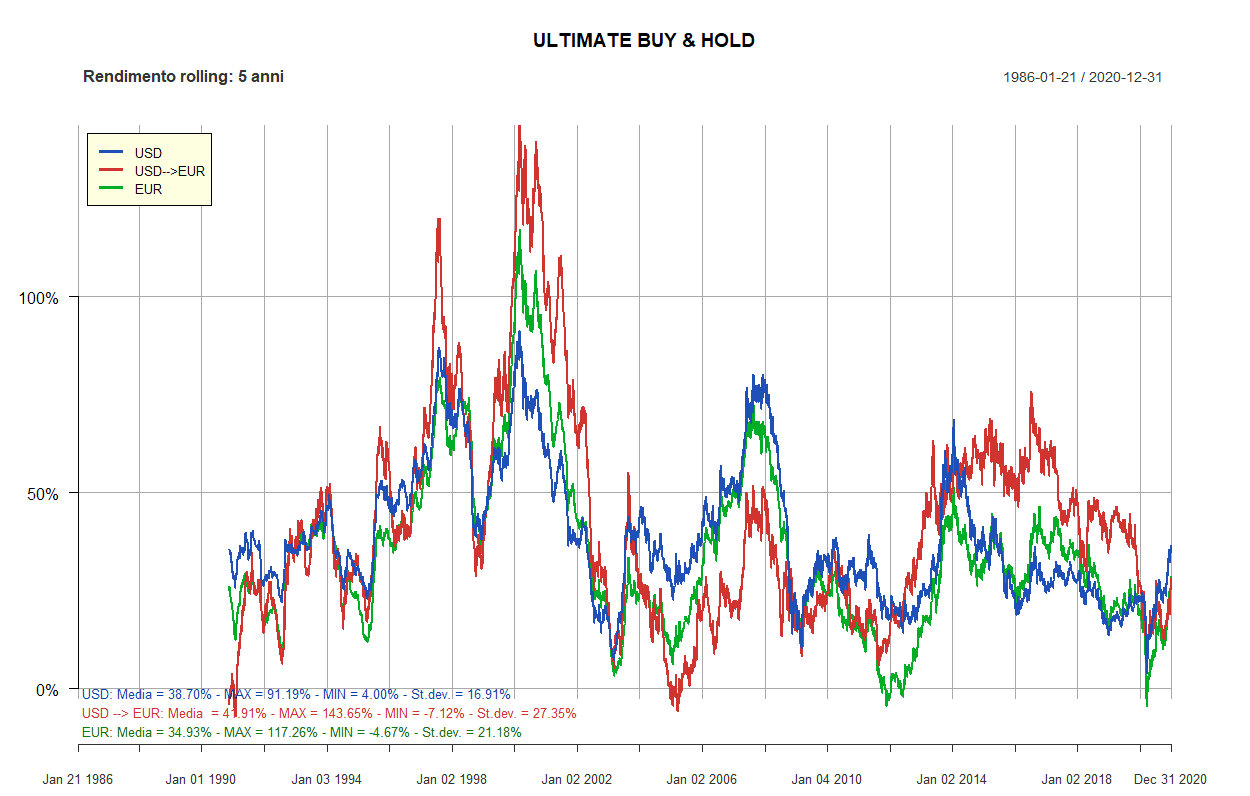
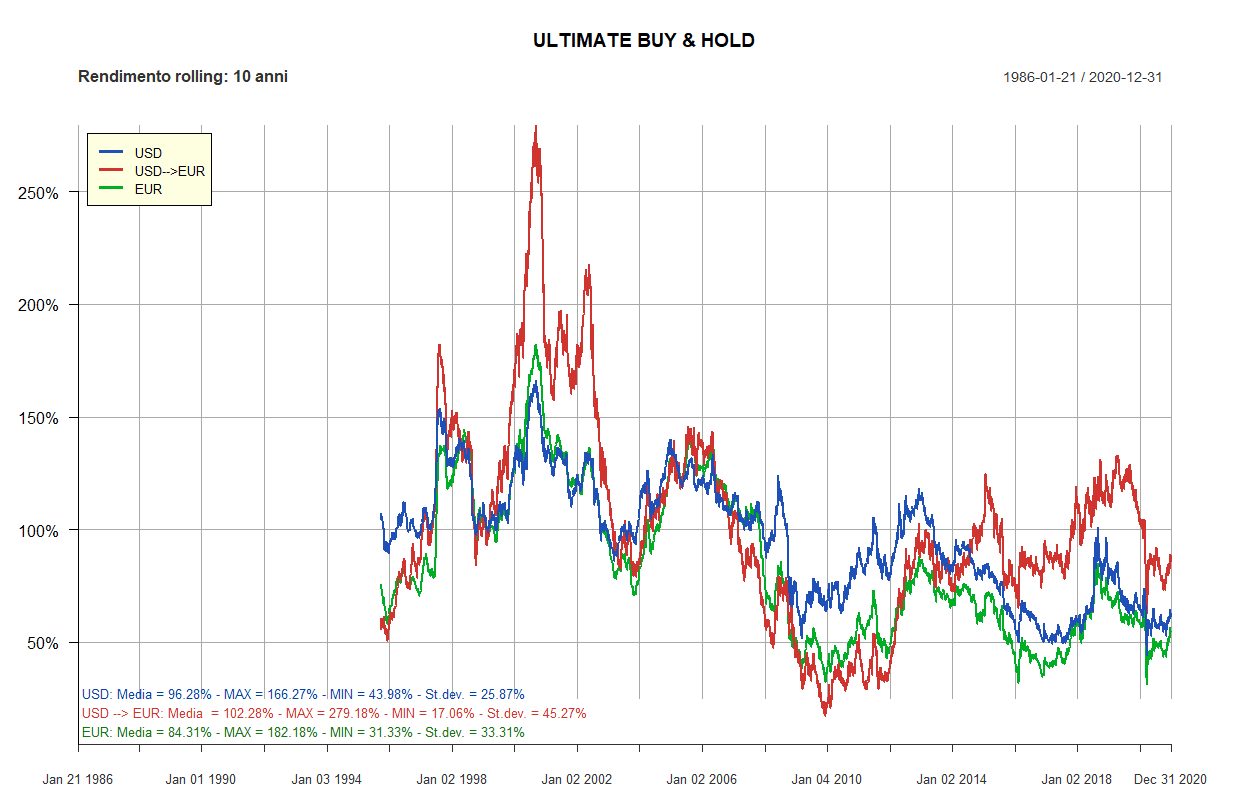
DEDALO THREE
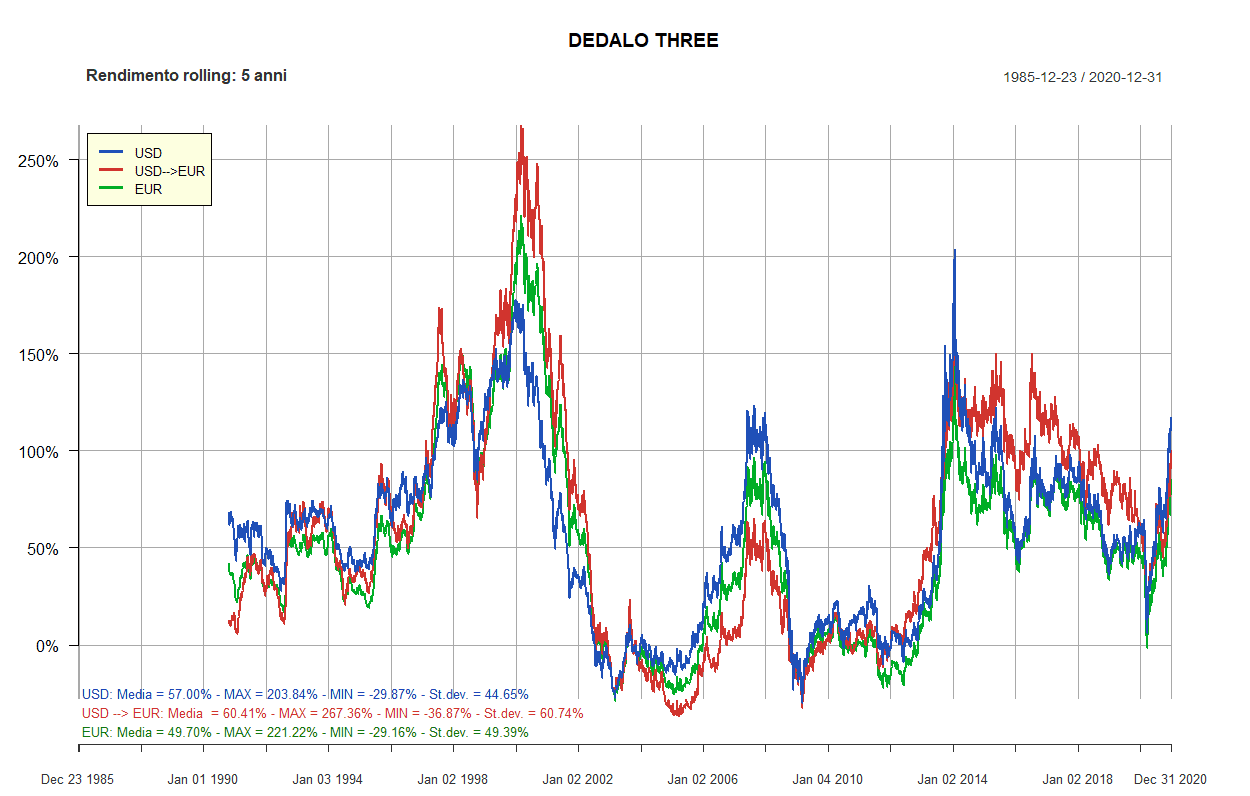
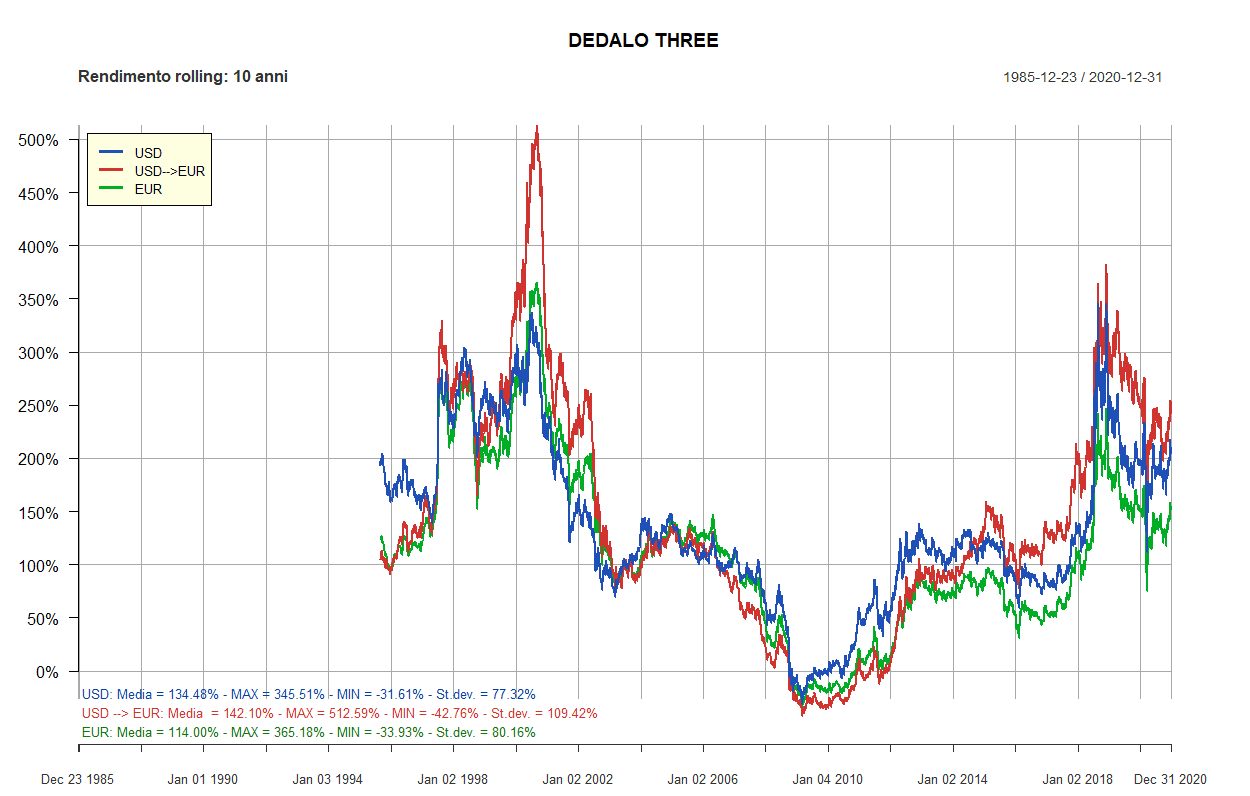
Il Dedalo Three, così come i due portafogli successivi, nasce per l’investitore dell’area euro. Non avrebbe senso, perciò, che un simile investitore utilizzasse il Dedalo Three in USD.
Il motivo per cui l’abbiamo creato e backtestato è per avere un termine di confronto anche in USD e in USD→EUR con tutti gli altri portafogli pigri.
DEDALO FOUR
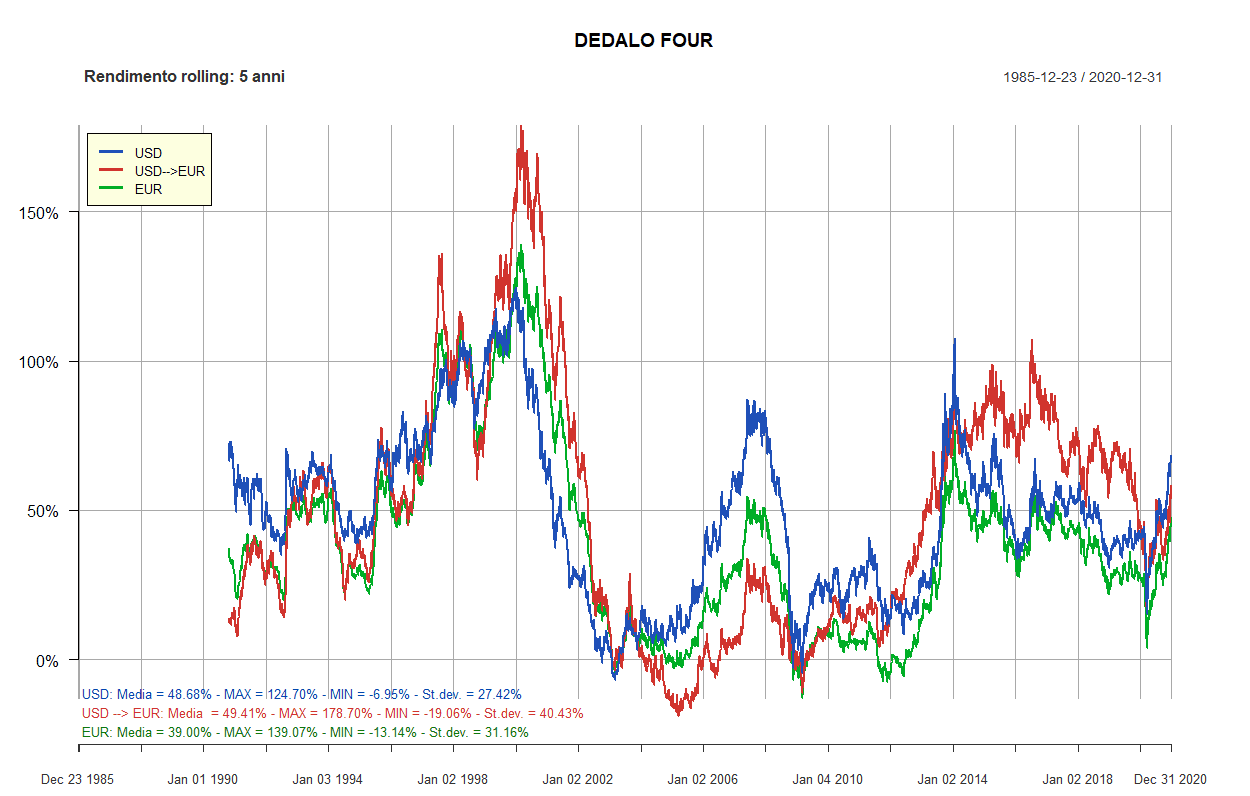
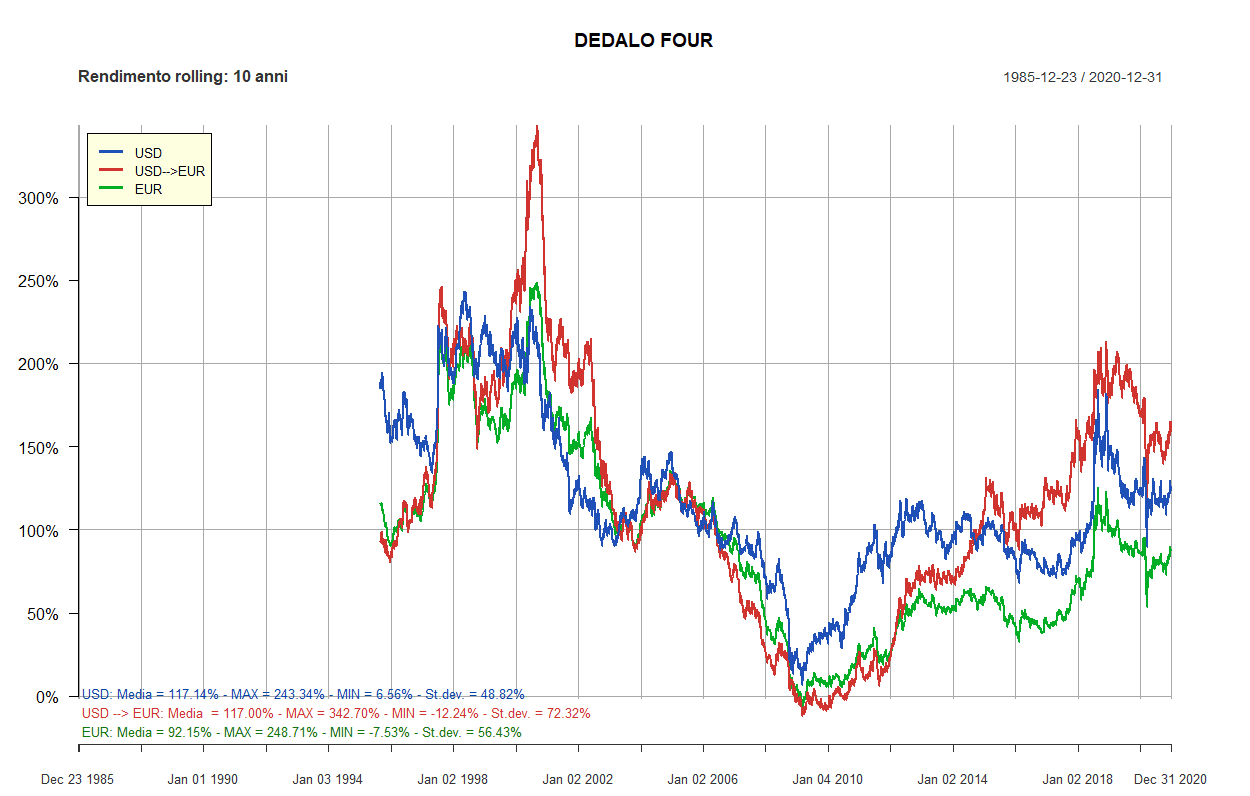
DEDALO ELEVEN
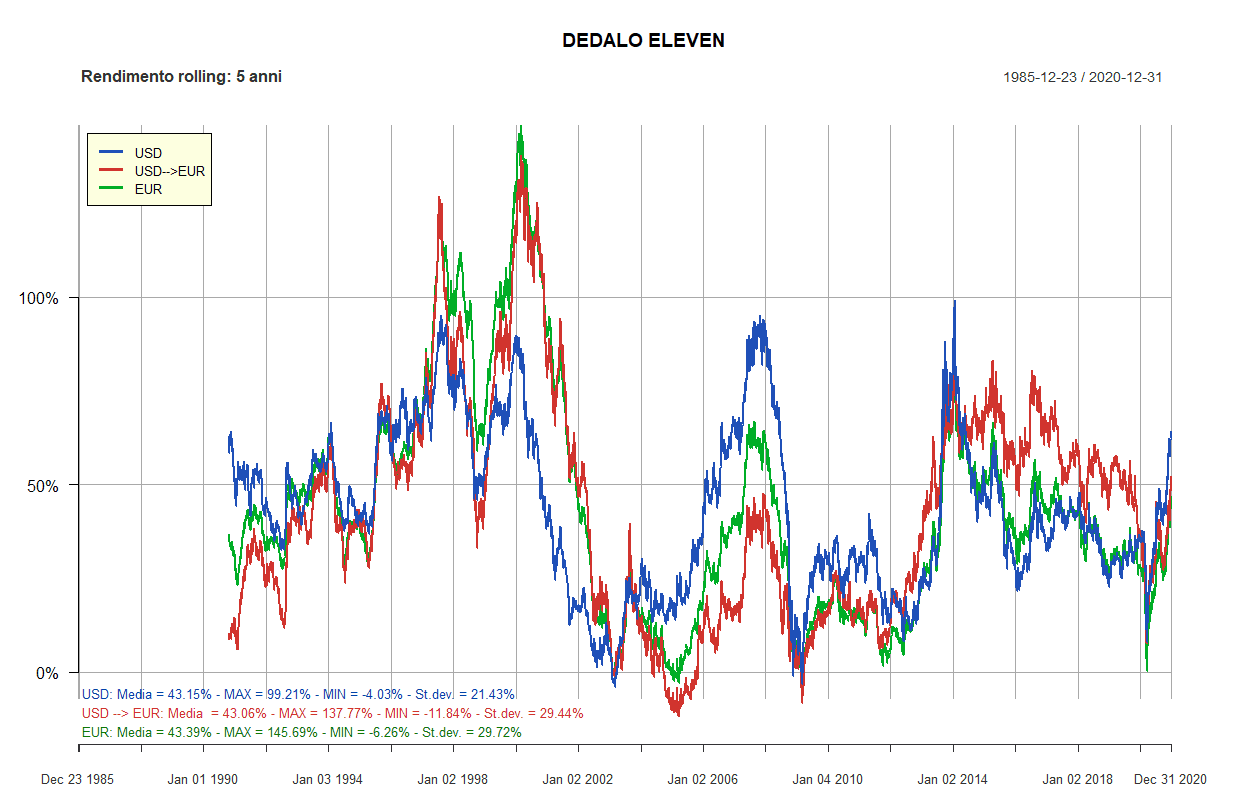
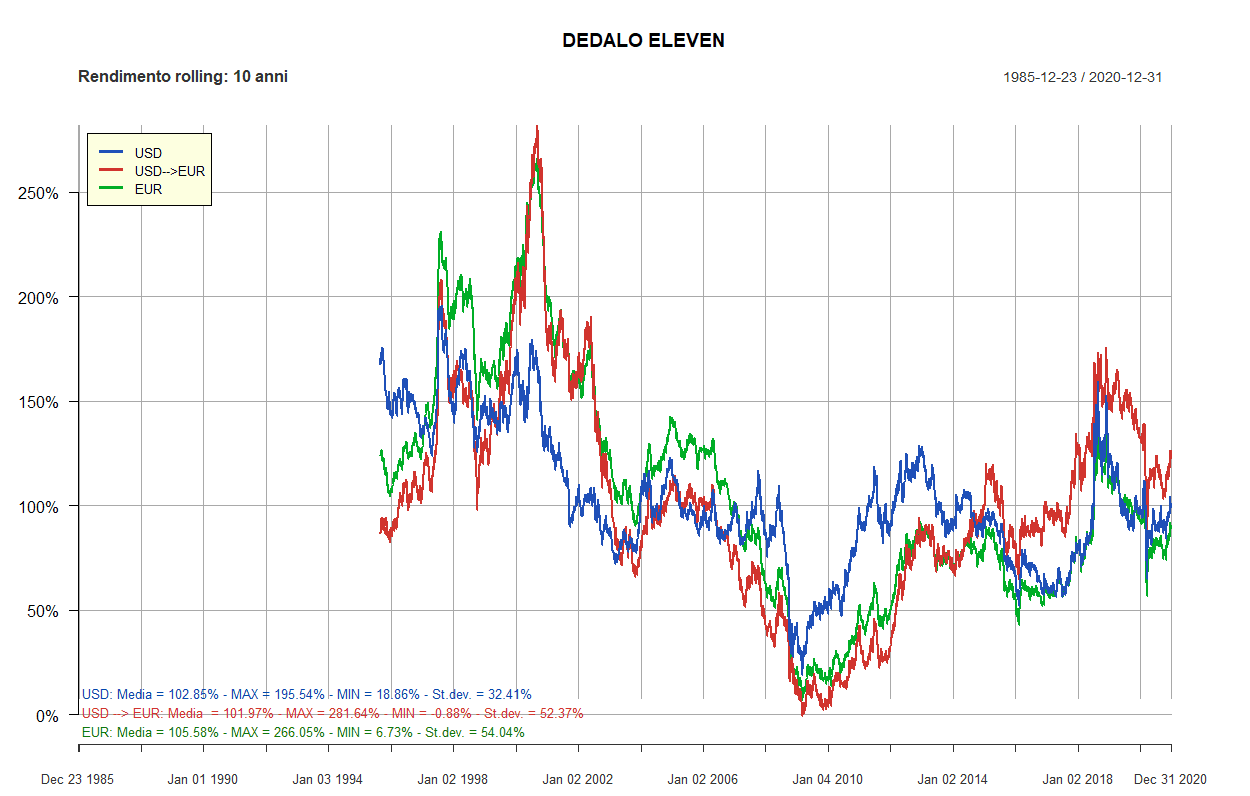
15. L’impatto del costo della consulenza finanziaria e della gestione attiva

«Investors need to understand not only the magic of compounding long-term returns, but the tyranny of compounding costs; costs that ultimately overwhelm that magic».
John Bogle
L’investitore che si avvale del supporto di un consulente finanziario deve mettere in conto il costo associato.
Le analisi condotte finora considerano soltanto il costo (TER) degli ETF: il TER è il costo minimo sostenuto da un investitore che gestisce in prima persona il proprio portafoglio finanziario.
La maggior parte degli investitori, però, preferisce avvalersi di un consulente finanziario. Esistono tre tipologie di consulenti:
- Consulenti finanziari autonomi (ex consulenti finanziari indipendenti): non guadagnano in base al tipo di strumento finanziario consigliato, ma fatturano le proprie prestazioni in uno dei due seguenti modi:
- Per ciascun cliente, in percentuale del patrimonio gestito, su base annuale.
- In base al tempo effettivo dedicato al cliente: fatturazione a tempo/oraria.
Questa tipologia di consulenti viene definita anche “Fee-Only”, dal momento che non può, per legge, ricevere alcun compenso aggiuntivo da altri intermediari finanziari come banche, SGR, SIM o compagnie assicurative.
- Consulenti finanziari abilitati all'offerta fuori sede (CFAOFS, ex promotori finanziari): in linea generale, guadagnano in base allo strumento finanziario utilizzato dai loro clienti. Più lo strumento è costoso, maggiore è il loro guadagno.
- Dipendenti bancari: le banche hanno dei budget e degli obiettivi di vendita periodici. È molto probabile che l'impiegato bancario addetto alla consulenza agli investimenti indirizzi i clienti verso gli strumenti finanziari che permettono alla banca di raggiungere il proprio budget il più velocemente possibile: spesso sono prodotti “della casa”, ovvero emessi dalla banca stessa o da una sua controllata. I loro costi sono molto elevati.
Il limite principale di una vasta parte della consulenza finanziaria è il conflitto di interessi: esso si verifica quando un consulente finanziario non mette gli interessi dei propri clienti al primo posto.
Il conflitto di interessi è un problema serio, ma non è di questo che vogliamo parlare: ci concentreremo invece sui costi associati alla consulenza finanziaria.
Con l’eccezione della consulenza autonoma con fatturazione oraria, possiamo esprimere il costo medio della consulenza con una percentuale annua che viene detratta dal patrimonio dell’investitore.
Il nostro scopo è quantificarne l’impatto: il modo migliore per farlo è quello di imputare il costo della consulenza al TER degli ETF utilizzati nelle analisi dei Lazy portfolios in USD e in EUR.
Lanceremo quindi gli stessi backtest effettuati in precedenza, aggiungendo questo maggior costo sia al TER degli ETF che agli indici da questi replicati nei periodi pre-ETF: come già descritto nel capitolo 3 – relativo all’integrazione delle serie storiche degli ETF con gli indici – ridurremo il rendimento giornaliero di ciascun ETF e di ciascun indice per la quota parte giornaliera della percentuale annuale del costo della consulenza.
Questo modo di procedere non è preciso al 100%, ma le performance calcolate nei nostri backtest saranno un’ottima approssimazione di quelle che si sarebbero realmente ottenute al netto del costo della consulenza.
Scegliere una corretta percentuale di costo è molto importante: il suo impatto complessivo non è semplicemente pari all’aliquota scelta moltiplicata per il numero di anni di durata di un backtest ma è superiore a questo, dal momento che il costo pagato è una somma che non verrà capitalizzata negli anni a venire.
Ipotizzeremo un costo annuale pari all’1%: approssimativamente, si tratta della percentuale media applicata dai consulenti finanziari autonomi ai loro clienti su base annuale (ad eccezione di quelli che utilizzano la fatturazione oraria).
I consulenti finanziari abilitati all'offerta fuori sede e gli impiegati bancari addebitano indirettamente ai loro clienti un costo quasi sicuramente superiore all’1%: non attraverso la fatturazione diretta dei loro servizi, ma in via indiretta facendoli investire attraverso strumenti finanziari a gestione attiva che hanno dei costi molto superiori a quelli degli ETF.
Uno dei più grossi problemi di questo tipo di approccio è che, spesso, i costi non vengono comunicati al cliente.
La gestione attiva prevede la figura del gestore, che si occupa della scelta degli strumenti finanziari da inserire nel fondo che amministra.
La gestione attiva ha l'obiettivo di ottenere una performance superiore a quella di un benchmark di riferimento, rappresentativo della strategia dichiarata, entro l'orizzonte temporale raccomandato.
L’idea, sulla carta, è ottima: dati alla mano, però, i fondi a gestione attiva che riescono a battere il benchmark sono una bassa percentuale del totale e la probabilità di indovinare il fondo giusto è minima.
L’alto costo della gestione attiva è la variabile principale che ne determina gli scarsi risultati in termini di rendimento.
I fondi a gestione attiva hanno, inoltre, un rischio inesistente negli ETF: il rischio gestore.
l rischio gestore è costituito da due componenti:
- In senso stretto, il rischio gestore si concretizza quando il fondo attivo è costituito da molti degli strumenti finanziari contenuti nel benchmark e il gestore effettua poche operazioni. In questo caso, l'investitore rischia di pagare un'alta commissione di gestione per un fondo attivo che assomiglia molto a uno passivo ma che, a causa dei maggiori costi, otterrà un rendimento inferiore.
- In senso più ampio, il rischio gestore si concretizza quando il fondo attivo è costituito da molti strumenti finanziari che non sono presenti nel benchmark e/o il gestore effettua molte operazioni. In questo caso, la gestione è senz'altro attiva, ma non è detto che sia una gestione di successo: l'investitore rischia di pagare un'alta commissione di gestione per un fondo attivo che, purtroppo, otterrà un rendimento inferiore a quello del benchmark.
Esistono dei casi in cui l'utilizzo di un fondo a gestione attiva può essere giustificato:
- Se si vuole investire in un mercato in cui non esistono ETF. In questo caso, la scelta è forzata.
- Se si vuole investire in un mercato considerato poco efficiente, come potrebbe ad esempio essere quello obbligazionario dei mercati emergenti: in tali mercati, sembra che la percentuale dei fondi attivi che riescono a battere il benchmark sia superiore alla media delle altre categorie.
- Quando l'utilizzo è suggerito da particolari strategie di investimento che, per funzionare meglio, necessitano anche dei fondi a gestione attiva.
Sono tutte fattispecie specifiche, dato che gli ETF coprono ormai la stragrande maggioranza dei mercati mondiali, l’inefficienza di un mercato in futuro sia tutta da dimostrare e le strategie menzionate nel terzo punto sono riservate a investitori molto esperti o professionali.
Il caso più comune di utilizzo di un fondo a gestione attiva rimane di gran lunga quello dei clienti che usufruiscono del supporto di un consulente finanziario abilitato all'offerta fuori sede o di un impiegato bancario: se è vero che l’impiegato bancario ha una retribuzione almeno in parte fissa (ma deve raggiungere dei budget), questo non vale per il consulente finanziario abilitato all'offerta fuori sede, il cui lavoro deve ovviamente essere pagato in qualche modo.
Dato che il suo guadagno deriva da una parte delle commissioni di gestione che gravano sui fondi attivi, il consulente finanziario abilitato all'offerta fuori sede non otterrebbe alcun vantaggio economico dalla vendita di un portafoglio costituito da soli ETF.
Un investitore che utilizza fondi a gestione attiva sostiene perciò un costo mediamente superiore a quello pagato da chi impiega soltanto ETF, anche nel caso in cui si avvalga del supporto di un consulente autonomo: possiamo quantificare il suo extra costo in una percentuale annua pari all’1,80%.
Ricapitolando, eseguiremo i nostri backtest altre due volte:
- La prima, addebitando un extra costo annuale dell’1%, ci permetterà di capire l’impatto sul rendimento del costo della consulenza autonoma.
- La seconda, addebitando un extra costo annuale dell’1,8%, ci permetterà di capire l’impatto sul rendimento del costo della consulenza offerta da un CFAOFS o di un impiegato bancario.
Lo scopo di questa analisi sarà, dunque, quello di confrontare il rendimento di un investimento con o senza questi costi di consulenza o di gestione: tralasceremo le altre misure statistiche anche perché le serie storiche dei rendimenti analizzati sono le stesse e il rischio rimane più o meno invariato.
I rendimenti delle tabelle seguenti sono quelli cumulati di ciascun Lazy portfolio in USD e in EUR (media degli 11 modelli di ottimizzazione).
| Commissioni di consulenza o di gestione: Rendimenti cumulati dei Lazy portfolios1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Rendimenti dei Lazy portfolios senza commissioni, con commissioni dell'1% e dell'1,8% | |||||||||
| Lazy Portfolio | 1985-2020 | 2000-2020 | 2010-2020 | ||||||
| No extra cost | +1% | +1,80% | No extra cost | +1% | +1,80% | No extra cost | +1% | +1,80% | |
| Lazy in USD | |||||||||
| World Bond | 810.89% | 535.75% | 376.81% | 164.89% | 115.78% | 83.12% | 56.11% | 40.88% | 29.77% |
| World Stocks | 1,374.35% | 929.04% | 671.77% | 241.47% | 178.15% | 136.06% | 146.47% | 122.43% | 104.90% |
| Two funds 10/90 | 920.69% | 615.89% | 441.03% | 106.91% | 68.75% | 43.29% | 69.86% | 53.45% | 41.67% |
| Two funds 20/80 | 1,018.66% | 684.01% | 492.67% | 117.97% | 77.71% | 50.92% | 76.15% | 59.13% | 46.98% |
| Two funds 30/70 | 1,125.44% | 758.62% | 547.85% | 132.89% | 89.98% | 61.24% | 85.10% | 67.22% | 54.40% |
| Two funds 40/60 | 1,259.45% | 852.14% | 618.41% | 147.58% | 101.75% | 71.31% | 95.20% | 76.35% | 62.79% |
| Two funds 50/50 | 1,402.88% | 953.47% | 695.30% | 162.70% | 114.13% | 81.81% | 105.98% | 86.13% | 71.77% |
| Two funds 60/40 | 1,563.01% | 1,064.56% | 779.49% | 181.13% | 128.98% | 94.39% | 117.52% | 96.71% | 81.52% |
| Two funds 70/30 | 1,758.55% | 1,199.23% | 880.02% | 201.32% | 144.47% | 107.56% | 130.12% | 107.85% | 91.96% |
| Two funds 80/20 | 1,974.43% | 1,349.11% | 993.05% | 221.39% | 160.58% | 121.25% | 143.68% | 120.10% | 103.24% |
| Two funds 90/10 | 2,214.90% | 1,519.26% | 1,119.27% | 242.07% | 177.29% | 135.43% | 158.15% | 133.13% | 115.15% |
| Two funds Dinamico | 1,410.83% | 959.02% | 699.47% | 161.93% | 113.50% | 81.27% | 105.53% | 85.73% | 71.40% |
| Warren Buffett | 2,075.73% | 1,498.76% | 1,182.40% | 211.21% | 165.65% | 135.83% | 137.70% | 120.75% | 110.76% |
| Simple Path to Wealth | 1,864.01% | 1,272.75% | 935.35% | 211.24% | 152.42% | 114.34% | 136.79% | 113.84% | 97.49% |
| Couch Potato | 1,541.66% | 1,053.23% | 767.77% | 305.44% | 231.91% | 182.94% | 109.43% | 89.10% | 74.26% |
| Three Funds Bogleheads | 1,412.96% | 958.83% | 693.63% | 185.14% | 132.65% | 97.66% | 110.65% | 90.19% | 75.08% |
| Second Grader's Starter | 1,582.76% | 1,076.62% | 780.87% | 202.63% | 146.42% | 109.35% | 122.72% | 101.09% | 85.16% |
| Talmud | 1,563.23% | 1,069.82% | 788.77% | 254.44% | 188.99% | 146.18% | 105.18% | 85.07% | 70.55% |
| Margaritaville | 1,313.40% | 887.72% | 641.86% | 263.19% | 197.10% | 152.73% | 95.64% | 76.71% | 62.85% |
| Andrew Tobias | 995.55% | 689.77% | 523.25% | 137.85% | 108.77% | 92.73% | 67.05% | 55.33% | 49.66% |
| Desert | 648.31% | 425.59% | 292.60% | 193.75% | 140.06% | 105.56% | 76.63% | 60.06% | 48.98% |
| Permanent | 672.72% | 442.38% | 321.13% | 213.51% | 160.66% | 125.63% | 73.36% | 57.14% | 48.25% |
| Core Four | 1,571.65% | 1,067.55% | 784.21% | 232.45% | 173.35% | 132.83% | 108.70% | 88.58% | 74.05% |
| Four Funds Bogleheads | 1,291.87% | 874.51% | 631.35% | 235.61% | 173.33% | 130.51% | 105.21% | 85.31% | 70.51% |
| No Brainer | 1,273.72% | 914.86% | 718.04% | 181.97% | 141.31% | 111.91% | 83.16% | 69.22% | 61.41% |
| Larry | 673.05% | 445.43% | 313.98% | 179.58% | 127.79% | 94.22% | 49.45% | 34.98% | 24.66% |
| Golden Butterfly | 1,099.54% | 754.70% | 551.20% | 262.22% | 202.24% | 159.19% | 85.52% | 70.06% | 59.32% |
| All Weather | 757.32% | 498.25% | 343.43% | 232.84% | 173.77% | 131.62% | 89.69% | 71.17% | 58.23% |
| Ivy | 752.24% | 499.31% | 342.61% | 149.63% | 103.55% | 73.25% | 56.20% | 41.27% | 30.47% |
| Dynamic 60/40 Income | 1,157.36% | 805.68% | 621.55% | 192.70% | 143.94% | 118.83% | 68.58% | 53.10% | 42.20% |
| Dynamic 40/60 Income | 1,166.10% | 791.96% | 574.14% | 199.10% | 148.93% | 114.40% | 61.92% | 46.51% | 36.11% |
| Five Asset | 811.69% | 542.78% | 391.09% | 195.11% | 140.44% | 103.32% | 60.69% | 45.40% | 33.69% |
| David Swensen Lazy Portfolio | 1,154.05% | 775.66% | 564.88% | 268.06% | 201.77% | 155.71% | 87.09% | 68.94% | 55.93% |
| Coffee House | 1,524.51% | 1,050.26% | 769.49% | 233.09% | 172.08% | 130.81% | 99.46% | 80.10% | 66.17% |
| Rob Arnott | 976.46% | 654.90% | 471.20% | 244.19% | 181.51% | 139.00% | 72.53% | 54.99% | 42.47% |
| Ultimate Buy and Hold Strategy | 2,219.94% | 1,532.47% | 1,126.85% | 389.20% | 299.70% | 239.25% | 135.73% | 112.52% | 95.94% |
| Ultimate Buy & Hold | 1,008.50% | 683.69% | 496.15% | 203.44% | 151.99% | 114.19% | 66.09% | 50.68% | 39.03% |
| Dedalo Three | 2,510.70% | 1,717.62% | 1,264.69% | 349.79% | 267.18% | 211.68% | 224.32% | 192.67% | 170.09% |
| Dedalo Four | 1,871.18% | 1,273.52% | 938.56% | 291.44% | 220.93% | 175.16% | 132.36% | 111.64% | 94.47% |
| Dedalo Eleven | 1,492.43% | 1,049.01% | 760.20% | 282.96% | 219.81% | 172.09% | 107.74% | 87.68% | 77.91% |
| Lazy in EUR | |||||||||
| World Bond | 582.33% | 376.23% | 257.16% | 152.83% | 105.95% | 74.79% | 70.02% | 53.43% | 41.34% |
| World Stocks | 750.33% | 493.49% | 345.11% | 120.59% | 79.68% | 52.49% | 156.16% | 131.17% | 112.95% |
| Two funds 10/90 | 607.21% | 387.49% | 264.45% | 90.66% | 55.82% | 32.72% | 42.88% | 29.02% | 19.84% |
| Two funds 20/80 | 647.43% | 416.25% | 285.62% | 92.19% | 57.06% | 33.77% | 45.64% | 31.48% | 22.11% |
| Two funds 30/70 | 680.25% | 439.23% | 303.08% | 92.63% | 57.44% | 34.11% | 48.09% | 33.69% | 24.14% |
| Two funds 40/60 | 715.01% | 461.78% | 319.52% | 92.09% | 57.12% | 33.91% | 51.04% | 36.34% | 26.58% |
| Two funds 50/50 | 749.30% | 485.56% | 337.20% | 91.58% | 56.55% | 33.34% | 53.76% | 38.80% | 28.84% |
| Two funds 60/40 | 779.31% | 506.44% | 353.43% | 90.74% | 55.86% | 32.77% | 56.30% | 41.09% | 30.95% |
| Two funds 70/30 | 805.21% | 523.75% | 366.54% | 89.25% | 54.63% | 31.71% | 58.67% | 43.22% | 32.93% |
| Two funds 80/20 | 823.89% | 536.55% | 376.08% | 87.08% | 52.86% | 30.20% | 60.88% | 45.22% | 34.76% |
| Two funds 90/10 | 839.97% | 548.20% | 384.32% | 84.31% | 50.58% | 28.26% | 62.93% | 47.04% | 36.44% |
| Two funds Dinamico | 735.89% | 476.20% | 330.19% | 94.58% | 58.99% | 35.41% | 51.79% | 37.02% | 27.20% |
| Warren Buffett | 419.45% | 270.10% | 184.95% | 59.94% | 33.22% | 14.92% | 45.37% | 30.04% | 21.32% |
| Simple Path to Wealth | 814.62% | 530.17% | 371.52% | 88.23% | 53.80% | 31.02% | 59.80% | 44.24% | 33.86% |
| Couch Potato | 576.18% | 373.88% | 256.79% | 110.86% | 68.56% | 42.81% | 51.38% | 36.52% | 25.51% |
| Three Funds Bogleheads | 805.99% | 527.55% | 369.95% | 112.42% | 73.36% | 48.41% | 82.52% | 65.28% | 52.27% |
| Second Grader's Starter | 821.46% | 535.19% | 379.14% | 109.83% | 71.22% | 46.80% | 85.45% | 67.83% | 54.69% |
| Talmud | 982.36% | 660.48% | 472.24% | 188.16% | 134.69% | 99.86% | 63.47% | 48.38% | 36.71% |
| Margaritaville | 645.83% | 417.73% | 290.11% | 135.64% | 89.71% | 61.16% | 79.32% | 61.83% | 49.02% |
| Andrew Tobias | 570.78% | 384.52% | 265.79% | 91.64% | 63.91% | 45.52% | 55.27% | 45.23% | 34.10% |
| Desert | 456.56% | 281.54% | 195.39% | 94.35% | 64.54% | 41.38% | 30.35% | 17.78% | 10.28% |
| Permanent | 564.84% | 360.54% | 250.01% | 149.76% | 108.11% | 82.32% | 47.38% | 34.94% | 24.17% |
| Core Four | 959.69% | 606.03% | 429.80% | 173.12% | 124.34% | 91.28% | 80.38% | 63.20% | 50.13% |
| Four Funds Bogleheads | 679.75% | 437.98% | 311.52% | 118.60% | 76.84% | 50.05% | 77.13% | 60.15% | 47.41% |
| No Brainer | 665.52% | 439.83% | 310.94% | 111.23% | 82.01% | 61.01% | 64.15% | 50.88% | 40.64% |
| Larry | 572.01% | 361.12% | 246.49% | 102.36% | 75.52% | 50.83% | 36.49% | 23.34% | 15.45% |
| Golden Butterfly | 693.00% | 457.54% | 325.89% | 178.63% | 131.56% | 97.11% | 57.08% | 41.76% | 31.23% |
| All Weather | 553.83% | 352.81% | 240.53% | 135.66% | 96.20% | 69.06% | 54.91% | 40.02% | 28.78% |
| Ivy | 609.34% | 401.43% | 277.53% | 156.41% | 108.67% | 77.97% | 51.21% | 36.56% | 25.25% |
| Dynamic 60/40 Income | 661.70% | 436.88% | 302.76% | 127.28% | 89.13% | 62.02% | 49.09% | 35.41% | 25.33% |
| Dynamic 40/60 Income | 630.06% | 415.14% | 294.72% | 102.06% | 65.87% | 41.55% | 43.24% | 30.25% | 19.99% |
| Five Asset | 582.29% | 377.09% | 255.44% | 136.92% | 93.52% | 64.82% | 49.82% | 34.41% | 24.28% |
| David Swensen Lazy Portfolio | 640.33% | 429.06% | 295.28% | 149.54% | 103.64% | 77.14% | 57.78% | 44.02% | 33.03% |
| Coffee House | 1,023.31% | 682.41% | 489.42% | 188.35% | 135.53% | 100.28% | 79.27% | 60.88% | 49.49% |
| Rob Arnott | 467.56% | 295.16% | 197.90% | 143.71% | 98.16% | 68.48% | 51.45% | 37.27% | 26.31% |
| Ultimate Buy and Hold Strategy | 1,590.48% | 1,082.94% | 791.60% | 264.88% | 197.05% | 152.40% | 122.38% | 99.80% | 84.35% |
| Ultimate Buy & Hold | 727.42% | 486.34% | 340.39% | 150.22% | 107.97% | 77.23% | 58.71% | 46.35% | 35.13% |
| Dedalo Three | 1,380.53% | 935.38% | 677.25% | 159.00% | 111.02% | 79.09% | 147.58% | 123.50% | 106.11% |
| Dedalo Four | 940.76% | 636.92% | 462.81% | 128.41% | 83.17% | 55.93% | 84.57% | 66.95% | 54.68% |
| Dedalo Eleven | 1,147.45% | 770.66% | 558.78% | 158.62% | 111.41% | 79.14% | 83.97% | 66.20% | 52.85% |
|
1 Rendimenti medi degli 11 modelli di ottimizzazione. |
|||||||||
L’impatto sul rendimento cumulato di un 1% e soprattutto di un 1,80% di commissioni annuali è devastante: in certi portafogli come il Two funds 90/10 e l’Ultimate Buy and Hold Strategy in USD, la differenza tra il rendimento senza commissioni e con commissioni dell’1,80% nel periodo più lungo è superiore al 1.000%!
L’1% all’anno può sembrare poco ma, ragionando invece sul rendimento cumulato di periodi più lunghi – come abbiamo fatto – le cose cambiano.
Se, poi, passiamo dalle percentuali agli euro, le proporzioni dell’impatto di questi costi assumono tutta un’altra dimensione.
Ipotizziamo un investimento di 100.000 euro: a quanto ammonta il minor guadagno?
Vediamo l’impatto all’1%:
- 18.905 dollari in meno tra il 2010 e il 2020 per i Lazy portfolios in USD e 15.679 euro in meno per quelli in EUR.
- 56.117 dollari in meno tra il 2000 e il 2020 per i Lazy portfolios in USD e 40.227 euro in meno per quelli in EUR.
- 427.225 dollari in meno tra il 1985 e il 2020 per i Lazy portfolios in USD e 257.542 euro in meno per quelli in EUR.
Questo invece è quello delle commissioni dell’1,8%:
- 32.205 dollari in meno tra il 2010 e il 2020 per i Lazy portfolios in USD e 26.931 euro in meno per quelli in EUR
- 93.636 dollari in meno tra il 2000 e il 2020 per i Lazy portfolios in USD e 67.033 euro in meno per quelli in EUR
- 672.759 dollari in meno tra il 1985 e il 2020 per i Lazy portfolios in USD e 403.290 euro in meno per quelli in EUR.
Si tratta di cifre enormi, pur essendo relative a un investimento di “soli” 100.000 euro: 100.000 euro sono una bella somma – ci mancherebbe – ma non stiamo parlando di milioni di euro.
Ovviamente, queste cifre sono tanto maggiori quanto più è lungo il periodo in cui le commissioni di consulenza o di gestione vengono pagate. Dovrebbero far riflettere anche gli investitori più scettici.
Attenzione perché sono valori medi dei 40 Lazy portfolios che abbiamo studiato: tra questi, quando l’extra costo è dell’1,8%, ce ne sono alcuni – ricordati in precedenza – che hanno generato oltre un milione di euro in meno.
La seguente tabella ci mostra le cifre esatte:
| Minori rendimenti in euro dei Lazy portfolios con commissioni dell'1% e dell'1,8%1 | ||||||
|---|---|---|---|---|---|---|
| Costo opportunità in valore assoluto (euro) dell'investimento in Lazy portfolios con commissioni di consulenza o di gestione dell'1% e dell1,80% | ||||||
| Lazy Portfolio | 1985-2020 | 2000-2020 | 2010-2020 | |||
| +1% | +1,80% | +1% | +1,80% | +1% | +1,80% | |
| Lazy in USD | ||||||
| World Bond | −275,140 | −434,080 | −49,110 | −81,770 | −15,230 | −26,340 |
| World Stocks | −445,310 | −702,580 | −63,320 | −105,410 | −24,040 | −41,570 |
| Two funds 10/90 | −304,803 | −479,662 | −38,156 | −63,619 | −16,408 | −28,189 |
| Two funds 20/80 | −334,647 | −525,993 | −40,255 | −67,047 | −17,016 | −29,165 |
| Two funds 30/70 | −366,815 | −577,581 | −42,908 | −71,648 | −17,886 | −30,701 |
| Two funds 40/60 | −407,317 | −641,045 | −45,830 | −76,274 | −18,850 | −32,406 |
| Two funds 50/50 | −449,403 | −707,574 | −48,570 | −80,891 | −19,847 | −34,208 |
| Two funds 60/40 | −498,447 | −783,520 | −52,154 | −86,740 | −20,810 | −35,995 |
| Two funds 70/30 | −559,323 | −878,533 | −56,852 | −93,763 | −22,265 | −38,155 |
| Two funds 80/20 | −625,313 | −981,378 | −60,807 | −100,134 | −23,576 | −40,442 |
| Two funds 90/10 | −695,642 | −1,095,628 | −64,784 | −106,649 | −25,019 | −43,005 |
| Two funds Dinamico | −451,806 | −711,365 | −48,427 | −80,653 | −19,804 | −34,133 |
| Warren Buffett | −576,969 | −893,329 | −45,562 | −75,378 | −16,949 | −26,945 |
| Simple Path to Wealth | −591,257 | −928,659 | −58,820 | −96,899 | −22,947 | −39,297 |
| Couch Potato | −488,433 | −773,890 | −73,533 | −122,499 | −20,339 | −35,170 |
| Three Funds Bogleheads | −454,128 | −719,334 | −52,487 | −87,480 | −20,457 | −35,573 |
| Second Grader's Starter | −506,139 | −801,895 | −56,215 | −93,280 | −21,629 | −37,559 |
| Talmud | −493,406 | −774,463 | −65,448 | −108,257 | −20,114 | −34,631 |
| Margaritaville | −425,682 | −671,542 | −66,086 | −110,451 | −18,930 | −32,783 |
| Andrew Tobias | −305,787 | −472,305 | −29,081 | −45,120 | −11,720 | −17,390 |
| Desert | −222,713 | −355,709 | −53,684 | −88,193 | −16,571 | −27,647 |
| Permanent | −230,340 | −351,595 | −52,851 | −87,880 | −16,214 | −25,105 |
| Core Four | −504,104 | −787,443 | −59,094 | −99,618 | −20,118 | −34,651 |
| Four Funds Bogleheads | −417,352 | −660,515 | −62,282 | −105,096 | −19,897 | −34,700 |
| No Brainer | −358,865 | −555,681 | −40,651 | −70,059 | −13,938 | −21,753 |
| Larry | −227,623 | −359,073 | −51,788 | −85,355 | −14,468 | −24,795 |
| Golden Butterfly | −344,839 | −548,342 | −59,980 | −103,037 | −15,463 | −26,205 |
| All Weather | −259,073 | −413,894 | −59,071 | −101,218 | −18,512 | −31,455 |
| Ivy | −252,932 | −409,632 | −46,074 | −76,377 | −14,930 | −25,729 |
| Dynamic 60/40 Income | −351,682 | −535,818 | −48,766 | −73,874 | −15,474 | −26,373 |
| Dynamic 40/60 Income | −374,146 | −591,962 | −50,169 | −84,705 | −15,404 | −25,809 |
| Five Asset | −268,912 | −420,605 | −54,665 | −91,782 | −15,285 | −27,002 |
| David Swensen Lazy Portfolio | −378,392 | −589,165 | −66,284 | −112,347 | −18,153 | −31,165 |
| Coffee House | −474,250 | −755,015 | −61,015 | −102,285 | −19,361 | −33,288 |
| Rob Arnott | −321,567 | −505,260 | −62,686 | −105,196 | −17,535 | −30,055 |
| Ultimate Buy and Hold Strategy | −687,475 | −1,093,094 | −89,498 | −149,946 | −23,206 | −39,788 |
| Ultimate Buy & Hold | −324,817 | −512,351 | −51,455 | −89,248 | −15,412 | −27,066 |
| Dedalo Three | −793,085 | −1,246,014 | −82,604 | −138,113 | −31,652 | −54,238 |
| Dedalo Four | −597,660 | −932,624 | −70,511 | −116,277 | −20,725 | −37,891 |
| Dedalo Eleven | −443,418 | −732,228 | −63,148 | −110,868 | −20,058 | −29,834 |
| Lazy in EUR | ||||||
| World Bond | −206,100 | −325,170 | −46,880 | −78,040 | −16,590 | −28,680 |
| World Stocks | −256,840 | −405,220 | −40,910 | −68,100 | −24,990 | −43,210 |
| Two funds 10/90 | −219,712 | −342,760 | −34,845 | −57,938 | −13,857 | −23,040 |
| Two funds 20/80 | −231,180 | −361,814 | −35,129 | −58,425 | −14,161 | −23,526 |
| Two funds 30/70 | −241,025 | −377,173 | −35,192 | −58,525 | −14,401 | −23,944 |
| Two funds 40/60 | −253,235 | −395,488 | −34,970 | −58,187 | −14,700 | −24,466 |
| Two funds 50/50 | −263,741 | −412,093 | −35,036 | −58,241 | −14,965 | −24,921 |
| Two funds 60/40 | −272,879 | −425,882 | −34,885 | −57,974 | −15,216 | −25,350 |
| Two funds 70/30 | −281,466 | −438,671 | −34,623 | −57,544 | −15,449 | −25,748 |
| Two funds 80/20 | −287,338 | −447,801 | −34,221 | −56,882 | −15,662 | −26,121 |
| Two funds 90/10 | −291,772 | −455,655 | −33,732 | −56,052 | −15,884 | −26,484 |
| Two funds Dinamico | −259,694 | −405,707 | −35,591 | −59,165 | −14,773 | −24,588 |
| Warren Buffett | −149,348 | −234,500 | −26,721 | −45,020 | −15,330 | −24,053 |
| Simple Path to Wealth | −284,452 | −443,108 | −34,423 | −57,210 | −15,556 | −25,939 |
| Couch Potato | −202,296 | −319,390 | −42,304 | −68,053 | −14,857 | −25,868 |
| Three Funds Bogleheads | −278,442 | −436,037 | −39,060 | −64,012 | −17,237 | −30,252 |
| Second Grader's Starter | −286,270 | −442,325 | −38,615 | −63,032 | −17,613 | −30,757 |
| Talmud | −321,889 | −510,125 | −53,461 | −88,299 | −15,089 | −26,760 |
| Margaritaville | −228,097 | −355,715 | −45,925 | −74,475 | −17,490 | −30,297 |
| Andrew Tobias | −186,260 | −304,993 | −27,728 | −46,121 | −10,045 | −21,174 |
| Desert | −175,018 | −261,162 | −29,808 | −52,965 | −12,569 | −20,074 |
| Permanent | −204,296 | −314,828 | −41,645 | −67,440 | −12,444 | −23,209 |
| Core Four | −353,664 | −529,893 | −48,778 | −81,843 | −17,176 | −30,246 |
| Four Funds Bogleheads | −241,767 | −368,234 | −41,763 | −68,545 | −16,985 | −29,719 |
| No Brainer | −225,681 | −354,572 | −29,222 | −50,222 | −13,272 | −23,510 |
| Larry | −210,896 | −325,522 | −26,841 | −51,531 | −13,158 | −21,039 |
| Golden Butterfly | −235,456 | −367,113 | −47,073 | −81,525 | −15,329 | −25,850 |
| All Weather | −201,019 | −313,297 | −39,457 | −66,594 | −14,897 | −26,134 |
| Ivy | −207,913 | −331,811 | −47,741 | −78,449 | −14,648 | −25,960 |
| Dynamic 60/40 Income | −224,828 | −358,943 | −38,150 | −65,260 | −13,679 | −23,761 |
| Dynamic 40/60 Income | −214,921 | −335,343 | −36,183 | −60,505 | −12,996 | −23,253 |
| Five Asset | −205,201 | −326,844 | −43,393 | −72,095 | −15,405 | −25,534 |
| David Swensen Lazy Portfolio | −211,274 | −345,058 | −45,900 | −72,399 | −13,754 | −24,750 |
| Coffee House | −340,902 | −533,898 | −52,813 | −88,067 | −18,385 | −29,781 |
| Rob Arnott | −172,397 | −269,654 | −45,549 | −75,233 | −14,184 | −25,144 |
| Ultimate Buy and Hold Strategy | −507,543 | −798,877 | −67,827 | −112,478 | −22,587 | −38,032 |
| Ultimate Buy & Hold | −241,074 | −387,027 | −42,249 | −72,986 | −12,365 | −23,582 |
| Dedalo Three | −445,155 | −703,284 | −47,974 | −79,905 | −24,078 | −41,470 |
| Dedalo Four | −303,848 | −477,952 | −45,240 | −72,482 | −17,616 | −29,891 |
| Dedalo Eleven | −376,787 | −588,668 | −47,211 | −79,485 | −17,766 | −31,116 |
|
1 Minori rendimenti medi in euro degli 11 modelli di ottimizzazione. |
||||||
Dove sono finiti questi soldi?
In parte, nelle tasche del consulente, della banca o della società di gestione dei fondi. E, fin qui, nessuna sorpresa.
Perché soltanto una parte e non l’intera cifra?
Perché i valori della tabella precedente rappresentano il costo opportunità delle commissioni pagate: se esse fossero state investite negli stessi portafogli, invece di essere dirottate verso gli intermediari, l’investimento avrebbe generato quelle somme in più.
Nel primo anno di vita dell’investimento, il 100% del mancato rendimento è costituito dalle commissioni. Nel secondo, circa il 96%. Nel terzo, quasi il 93% e così via fino all’ultimo anno, il 35°, dove la somma totale pagata in commissioni (poco meno di 150.000 euro) rappresenta tra il 33% e il 34% del mancato rendimento totale.
A questo punto, dovrebbe essere evidente perché l’utilizzo di strumenti finanziari economici e un costo della consulenza sostenibile siano fondamentali.
L’1% all’anno non sembra un grosso problema: nel lungo termine, però, rappresenta un costo molto alto.
Investire nei mercati finanziari con un orizzonte temporale di breve termine è possibile: nel breve, però, non si possono ottenere dei risultati di rilievo, se non rischiando moltissimo.
L’intuizione di Bogle di creare dei fondi comuni di investimento a gestione passiva e dai costi minimi (Index Funds) dimostra – ancora oggi – tutta la sua ragion d’essere.
Nel 2005, John Bogle pronunciò le frasi seguenti (il grassetto è nostro):
In investing, you get what you don't pay for. Costs matter. So intelligent investors will use low-cost index funds to build a diversified portfolio of stocks and bonds, and they will stay the course. And they won't be foolish enough to think that they can consistently outsmart the market.
Tradotta in italiano, suona più o meno così:
Investendo, ottieni ciò per cui non paghi. I costi sono importanti. È per questo che gli investitori intelligenti utilizzeranno fondi indicizzati a basso costo per costruire un portafoglio diversificato di azioni e obbligazioni e lo manterranno nel tempo. Non saranno così sciocchi da credere di poter sempre battere il mercato.
Si tratta di una conclusione sorprendente e in un certo senso paradossale, ma molto profonda. In poche parole, racchiude il messaggio che si vuole far passare in questo capitolo: a parità di tutto il resto, quanto maggiore sarà il costo di un fondo e – aggiungiamo noi – il costo della consulenza finanziaria, tanto minore sarà la sua performance netta.
Ovviamente, sarà vero anche l'opposto: pagando delle commissioni più basse, la performance netta del fondo sarà più alta, come abbiamo visto in precedenza.
16. Confronto tra fondi flessibili a gestione attiva e i Two Fund Lazy portfolios

«I can't figure out why anyone invests in active management, so asking me about hedge funds is just an extreme version of the same question. Since I think everything is appropriately priced, my advice would be to avoid high fees. So you can forget about hedge funds».
Eugene Fama
I fondi flessibili, detti anche Total Return o Absolute Return, sono un particolare tipo di fondi a gestione attiva che punta a ottenere un rendimento costante e indipendente dall’andamento dei mercati.
Il gestore ha il compito di dichiarare l’obiettivo di rischio e il rendimento del fondo che amministra; un benchmark non è di solito previsto.
La definizione di “Total” o “Absolute” return nasce proprio in opposizione a quella dei fondi a gestione attiva classici: questi ultimi hanno un benchmark che si prefiggono di battere e il loro rendimento è legato o misurato relativamente ad esso (“Relative” return).
I rendimenti dei fondi Total Return dovrebbero essere sganciati dagli andamenti dei mercati sottostanti, siano essi azionari, obbligazionari o di altro tipo.
Al gestore di un fondo Total Return viene lasciata una maggiore libertà di intervento, potendo effettuare operazioni finanziarie generalmente vietate nelle altre tipologie di fondi (ad esempio, le vendite allo scoperto).
Tra i limiti dei fondi Total Return troviamo:
- La possibilità di un rischio effettivo superiore a quello dichiarato (magari nascosto da una gestione poco comprensibile o molto complessa).
- Il costo mediamente elevato.
Abbiamo pensato di effettuare alcuni confronti tra i fondi bilanciati Total Return in euro disponibili nel nostro database e i Two funds portfolios in EUR con asset allocation simile: l’ordine seguito nella scelta dei fondi bilanciati è quello della lunghezza della serie storica disponibile.
Il primo fondo che esaminiamo è l’Anima Absolute Return A (ISIN: IT0000380763).
Nel KIID si legge che “Il Fondo è gestito attivamente senza riferimento ad alcun benchmark. Il Fondo investe principalmente in strumenti finanziari di natura azionaria e obbligazionaria denominati sia in Euro che in altre divise. In particolari situazioni di mercato il Fondo potrebbe essere investito anche totalmente in strumenti obbligazionari a breve termine o in liquidità, o anche in una sola delle asset class. Investimento in strumenti finanziari legati all’andamento delle materie prime e in strumenti finanziari derivati che abbiano ad oggetto tali strumenti nel limite del 20% del valore complessivo del Fondo. La selezione degli strumenti finanziari è effettuata in base a criteri o strategie di investimento che prevedono una allocation di portafoglio flessibile, nel rispetto di una soglia di rischio predeterminata. Con riferimento alla componente obbligazionaria, in misura significativa investimenti con merito di credito inferiore ad adeguato o privi di rating. La gestione dell’esposizione valutaria è di tipo attivo. Esposizione al rischio di cambio in misura contenuta. Il Fondo seleziona gli investimenti in base a criteri di valutazione fondamentale che tengono conto della capacità delle aziende di generare ritorni sul capitale sostenibili nel tempo e di posizionarsi strategicamente nei settori di appartenenza. Il Fondo utilizza strumenti finanziari derivati sia per finalità di copertura dei rischi sia per finalità diverse da quelle di copertura (tra cui arbitraggio)”.
Le informazioni fornite non sono molto chiare, ma possono essere sintetizzate così:
- Il fondo investe sia in azioni che in obbligazioni. Fino a un massimo del 20%, il fondo potrebbe investire su strumenti legati all’andamento delle materie prime (anche attraverso derivati).
- Il rischio di cambio è contenuto.
- La selezione degli investimenti viene effettuata in base a criteri di valutazione fondamentale.
- Il fondo può utilizzare anche strumenti derivati, sia per finalità di copertura dei rischi che per finalità speculative (tra cui eventuali arbitraggi).
Le spese correnti sono pari all’1,66% e sono previste anche commissioni legate al rendimento pari al 15% dei rendimenti del fondo eccedenti il benchmark (è previsto un High Water Mark).
Il TER e le spese correnti sono termini utilizzati spesso come sinonimi ma, in realtà, non sono la stessa cosa. Il TER è la somma tra le spese correnti e le commissioni di performance.
Le spese correnti percentuali sono calcolate come il rapporto tra il totale delle spese correnti e il valore complessivo netto del patrimonio del fondo. Esse includono le commissioni di gestione (che sono la parte più consistente del totale), le spese di revisione del bilancio, le spese di pubblicazione del valore della quota, il compenso per la banca depositaria, le spese legali e giudiziarie e le commissioni di distribuzione.
Se presenti, le spese correnti non comprendono le commissioni di ingresso e di uscita, le commissioni di performance e i costi di negoziazione dei titoli presenti in portafoglio.
Le commissioni di performance sono inesistenti negli ETF. Nei fondi a gestione attiva sono facoltative e possono essere individuate analizzando la sezione “Spese” dei KIID.
Sia questo che i successivi fondi bilanciati verranno confrontati con il Two Fund 50/50 in EUR a meno che, nel KIID, venga specificata un asset allocation differente.
Vediamo il grafico dei rendimenti cumulati:
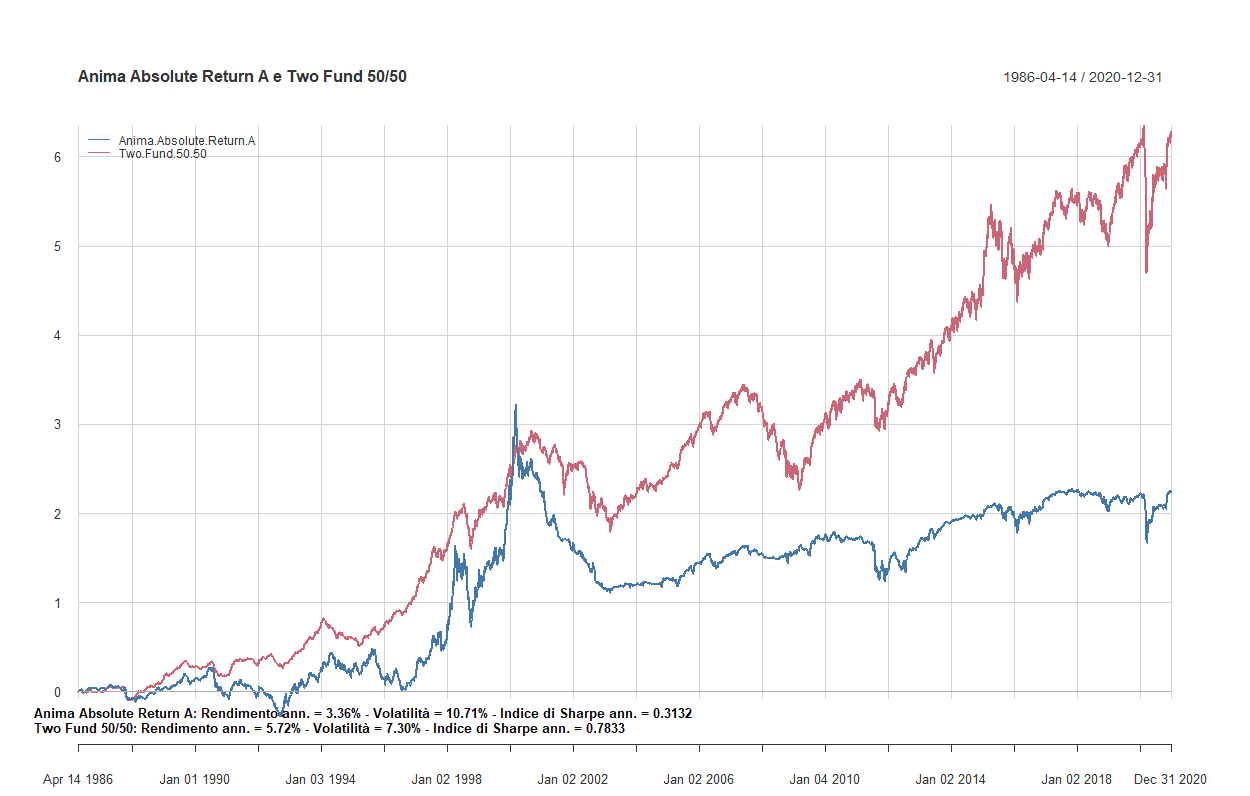
Il periodo analizzato va dal 14 aprile 1986 al 31 dicembre 2020 (data in cui sono terminate anche le nostre analisi dei Lazy portfolios).
Il grafico non ha bisogno di spiegazioni: la linea rossa è quella del Two funds 50/50 e sovrasta in maniera netta l’Anima Absolute Return.
Alcune statistiche delle performance sono visibili nella parte bassa del grafico: rendimento annualizzato, volatilità (deviazione standard annualizzata dei rendimenti) e indice di Sharpe annualizzato.
Il secondo fondo flessibile che analizziamo è il Symphonia Patrimonio Attivo (ISIN: IT0000382603).
Dal KIID otteniamo le seguenti informazioni: “È un Fondo flessibile che persegue obiettivi di rendimento assoluti su un orizzonte temporale inferiore a 3 anni con un profilo di rischio medio. Il fondo può investire in azioni fino al 70% delle proprie attività e fino al 100% in obbligazioni. Il fondo diversifica gli investimenti azionari in ambito internazionale. L’investimento in titoli obbligazionari ha ad oggetto principalmente emissioni con merito creditizio elevato (rating investment grade), ferma restando la facoltà di investire sino al 50% in titoli aventi merito creditizio inferiore o privi di rating. Lo stile di gestione è flessibile e la filosofia di investimento è focalizzata sul perseguimento di rendimenti assoluti nel medio periodo tramite la costante selezione di strumenti finanziari, rappresentativi sia di asset direzionali (azioni, obbligazioni), sia di strategie di investimento non direzionali. La scelta d’investimento sui diversi strumenti finanziari si basa sull’analisi macroeconomica per le previsioni circa l’andamento e l’evoluzione dei tassi di interesse, dei cambi nonché sull’analisi economico-finanziaria per la selezione delle società con le migliori prospettive di crescita, con attenzione particolare alle strategie industriali, alla qualità del management, alla struttura patrimoniale e al modello di business. L’analisi tecnica viene utilizzata in via complementare”.
I punti salienti sono i seguenti:
- L’investimento azionario può arrivare anche al 70% e quello obbligazionario fino al 100%.
- Il mercato di riferimento è quello internazionale (non meglio specificato).
- La strategia di investimento si basa sull’analisi macroeconomica (previsioni sui tassi di interesse e dei cambi) e sull’analisi economico-finanziaria per la selezione delle società.
- Si utilizza anche l’analisi tecnica in via complementare.
- Non è presente un benchmark di riferimento.
Le spese correnti sono pari all’1,75% e sono previste anche commissioni legate al rendimento pari al 20% dei rendimenti del fondo eccedenti l’indice di riferimento: ICE BofAML Euro Treasury Bills + 100 punti base.
Nel KIID è stato specificato che l’asset azionaria può arrivare fino al 70% del patrimonio del fondo: lo confronteremo quindi con il Two Fund 70/30 in EUR.
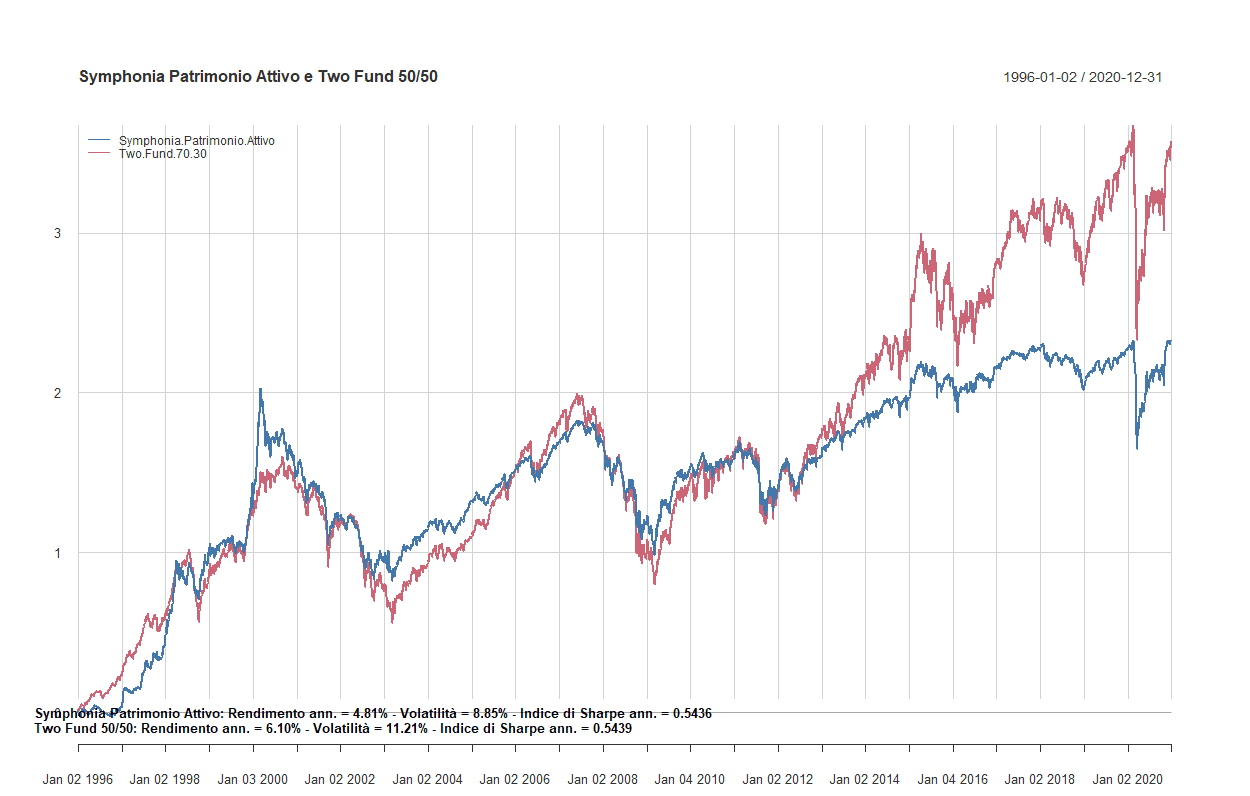
Il periodo analizzato va dal 2 gennaio 1996 al 31 dicembre 2020. È quindi molto più corto del precedente ma, comunque, superiore ai 25 anni.
Il rendimento e la volatilità del Two funds 70/30 sono stati più alti, mentre gli indici di Sharpe sono quasi identici.
Il terzo fondo è il BNP Paribas Funds Target Risk Balanced Classic, un fondo flessibile globale (ISIN: LU0089291651).
Dal KIID ricaviamo che “il Fondo è gestito in modo attivo senza fare riferimento a un indice. Il Fondo appartiene alla categoria dei fondi di fondi. Il Fondo mira ad aumentare il valore del patrimonio nel medio termine attuando una strategia di asset allocation flessibile e diversificata tra tutte le tipologie di classi di attivi, attraverso investimenti diretti o in fondi in qualunque tipo di titolo trasferibile e/o in liquidità, nonché in strumenti finanziari derivati. Il target annuale di volatilità è pari al 7,5%. Il team di gestione applica inoltre la Politica d’investimento sostenibile di BNP Paribas Asset Management, che considera criteri ambientali, sociali e di governance (ESG) negli investimenti del Fondo”.
In breve:
- Non viene specificata una percentuale di asset azionaria o obbligazionaria minima o massima.
- Si tratta di un fondo di fondi.
- Il target di volatilità è il 7,5% all’anno.
- È un fondo ESG.
Le spese correnti sono pari all’1,79% e non sono previste commissioni di performance.
Il grafico seguente misura la performance del BNP Paribas Funds Target Risk Balanced Classic e del Two Fund 50/50 in EUR.
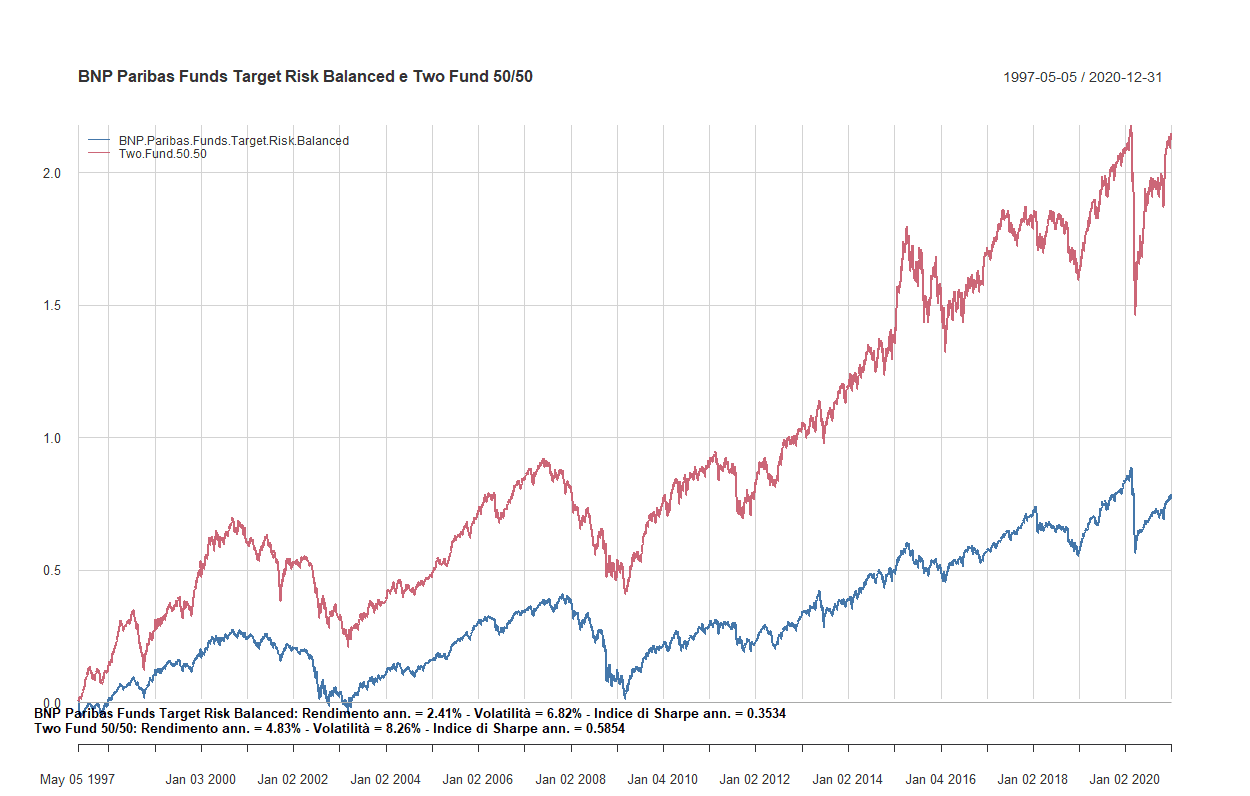
Il periodo analizzato va dal 5 maggio 1997 al 31 dicembre 2020.
Il rendimento è nettamente a favore del Two funds 50/50 e la minor volatilità del BNP Paribas non riesce a compensare il minor rendimento, tant’è che anche il suo indice di Sharpe è molto più basso di quello del Two funds.
Il quarto fondo analizzato è il Raiffeisen Bilanciato Sostenibile VTA, un bilanciato flessibile globale (ISIN: AT0000785381).
Nel KIID viene specificato che “Il Raiffeisen Bilanciato Sostenibile è un fondo misto e il suo obiettivo d’investimento è in particolare il conseguimento di una moderata crescita del capitale. Basandosi su singoli titoli (vale a dire senza prendere in considerazione la partecipazione a fondi di investimento, strumenti derivati e depositi a vista o revocabili), il Fondo investe esclusivamente in titoli e/o strumenti monetari i cui rispettivi emittenti sono catalogati come "sostenibili" in conformità a criteri sociali, ecologici ed etici. Allo stesso tempo non avviene alcun investimento in determinati settori come armamenti o biotecnologie genetiche vegetali né in imprese che violano i diritti umani e del lavoro. Una quota pari ad almeno il 51% del patrimonio del Fondo è investita direttamente in azioni (e titoli equivalenti) di società con sede legale o attività principale nell'America del nord, in Europa o in Asia e/o in obbligazioni di emittenti nordamericani, europei o asiatici. Una quota minima pari al 25% del patrimonio del Fondo è investita direttamente in azioni. Le obbligazioni e gli strumenti del mercato monetario detenuti dal Fondo possono essere emessi tra l'altro da stati, emittenti sovranazionali e/o imprese. Il Fondo è gestito in modo attivo senza relazionarsi a un parametro di riferimento”.
I punti salienti sono:
- È un fondo ESG.
- L’asset azionaria è almeno pari al 51% del patrimonio del fondo.
- Non è presente un benchmark.
Le spese correnti sono pari all’1,39% e non sono previste commissioni legate al rendimento del fondo.
Il grafico seguente misura la performance del Raiffeisen Bilanciato Sostenibile VTA e del Two Fund 50/50 in EUR.
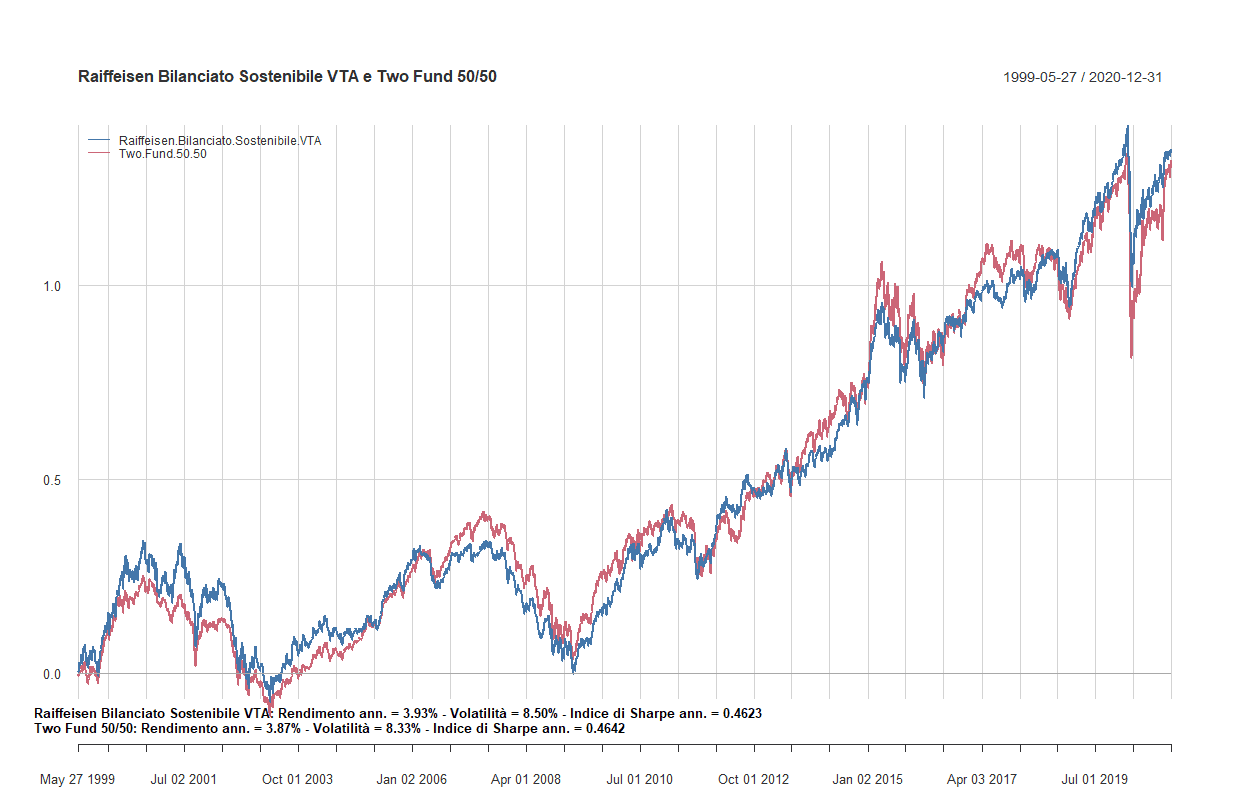
Il periodo analizzato va dal 27 maggio 1999 al 31 dicembre 2020.
Il Raiffeisen Bilanciato Sostenibile VTA è il primo dei fondi flessibili analizzati che ottiene un rendimento leggermente superiore a quello del Two funds 50/50. Quest’ultimo riesce comunque a essere un po’ meno volatile e ad avere l’indice di Sharpe appena superiore di quello del Raiffeisen.
Il quinto fondo è il GAM Multibond - Diversified Income Bond EUR B, un bilanciato obbligazionario globale (ISIN: LU0107768052).
Il KIID ci dice che “L'obiettivo del fondo consiste nel conseguire un rendimento superiore alla media nel lungo periodo, investendo nei mercati obbligazionari mondiali. A tal fine, il fondo privilegia le obbligazioni societarie e dei mercati emergenti. Le obbligazioni hanno diversi rating, in riferimento alla capacità dell'emittente di rimborsare il debito. Il Comparto investe almeno i 2/3 del patrimonio in una gamma ampiamente diversificata di obbligazioni. Il Comparto può investire il patrimonio in diverse valute, le cui fluttuazioni nei confronti della sua valuta di riferimento possono essere sottoposte a copertura. Il Comparto investe in obbligazioni a tasso fisso e variabile. Tali titoli sono emessi da società, da governi e da amministrazioni locali (di paesi industrializzati ed emergenti). È possibile investire in obbligazioni con qualsiasi scadenza, valuta e rating (capacità di rimborso del debito). Il Comparto può utilizzare strumenti finanziari complessi con finalità di copertura del patrimonio e per trarre profitto da investimenti promettenti”.
Deduciamo che:
- Il fondo investe soltanto in obbligazioni e non in azioni.
- Vengono privilegiate le obbligazioni corporate e quelle dei mercati emergenti.
- L’esposizione al cambio può essere coperta.
Più avanti, viene specificato che “Il Fondo è considerato a gestione attiva rispetto all'indice di riferimento personalizzato 30% BofA ML EMU Corp., LG Cap Index, Ex T1, UT2, LT2; 30% BofA ML EM Markets Sovereign Plus /Hedg EUR; 30% BofA ML Global High Yield Constrained Hedged; 10%, ML Euro Curr. LIBOR 3-month Const. Maturity (l'"Indice di riferimento personalizzato") in quanto si avvale dell'Indice di riferimento personalizzato nella valuta pertinente a scopo di raffronto della performance. Tuttavia, l'Indice di riferimento personalizzato non rappresenta un obiettivo di performance e non viene utilizzato per definire la composizione del portafoglio del Fondo, il quale può essere interamente investito in titoli che sono esclusi dall'Indice di riferimento personalizzato”.
Di conseguenza, il fondo non prevede un benchmark.
Le spese correnti sono pari all’1,56% e non sono previste commissioni di performance.
Il grafico seguente misura la performance del GAM Multibond - Diversified Income Bond EUR B e del World Bond in EUR (abbiamo scelto il World Bond, essendo l’unico dei Lazy portfolios composto al 100% da obbligazioni).
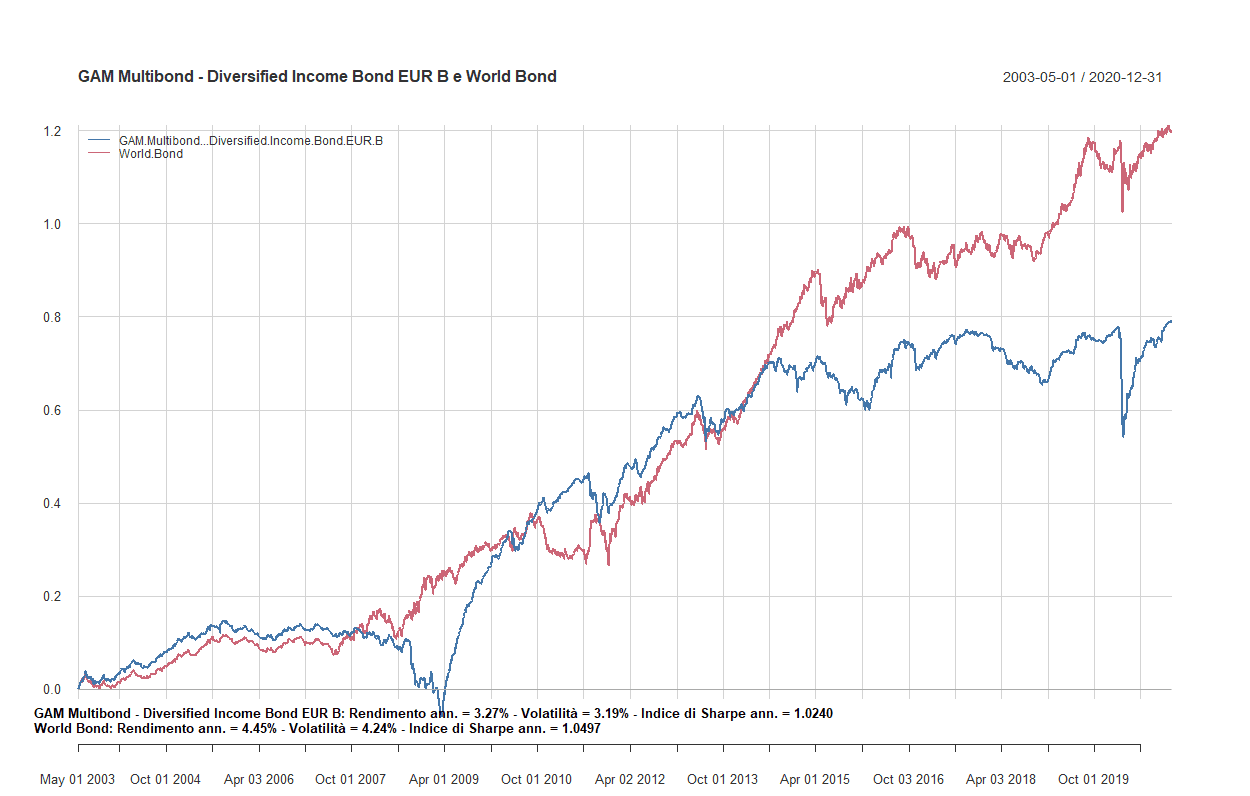
Il periodo analizzato va dal 1° maggio 2003 al 31 dicembre 2020.
Grazie a una miglior performance negli ultimi 7-8 anni, il World Bond ottiene un rendimento molto più elevato di quello del GAM Multibond - Diversified Income Bond EUR B. La volatilità del World Bond è più alta, così come – seppur di poco – l’indice di Sharpe.
Vale la pena ricordare che l’ETF sottostante al World Bond in EUR è il X710, che investe esclusivamente in obbligazioni governative dell’area euro.
Il sesto fondo è l’Invesco Global Conservative A Acc, un flessibile bilanciato globale (ISIN: LU0166421692).
Nel KIID viene specificato che “L’obiettivo del Fondo consiste nel conseguire un rendimento totale positivo durante un ciclo di mercato con una correlazione da bassa a moderata agli indici dei mercati tradizionali, cercando al contempo di limitare i livelli del calo del valore patrimoniale netto del Fondo nell'arco di un periodo di 12 mesi consecutivi. Il calo è il differenziale tra il prezzo più alto e il prezzo più basso conseguito dal Fondo nel periodo di riferimento. Il Fondo acquisirà esposizione a strumenti obbligazionari (emessi da governi o società, con un rating minimo di B- secondo l'agenzia di rating Standard & Poor’s, o rating equivalente), azioni di società, materie prime (escluse le materie prime agricole) e valute di tutto il mondo. L’asset allocation del Fondo sarà rettificata su base continuativa e in alcune circostanze il Fondo potrebbe investire fino al 100% del valore patrimoniale netto in strumenti meno rischiosi come liquidità e mezzi equivalenti, strumenti obbligazionari a breve termine e altri strumenti del mercato monetario. Il Fondo può fare un uso significativo di derivati (strumenti complessi) al fine di (i) ridurre il rischio e/o generare capitale o reddito addizionale e/o (ii) raggiungere gli obiettivi d’investimento generando livelli variabili di leva finanziaria (ossia acquisendo esposizione di mercato in misura superiore al proprio valore patrimoniale netto). Il Fondo è gestito attivamente e non è vincolato dal suo benchmark, 3 Month Euribor Index, che viene utilizzato a scopo di confronto. La sovrapposizione non è applicabile poiché il benchmark è un riferimento relativo a un tasso del mercato monetario”.
Le informazioni sono abbastanza chiare. In particolare, anche questo fondo non ha un benchmark di riferimento (quello utilizzato a scopo di confronto non vincola il gestore).
Le spese correnti sono pari all’1,38% e non sono previste commissioni di performance.
Il grafico seguente misura la performance dell’Invesco Global Conservative A Acc e del Two Fund 50/50 in EUR.
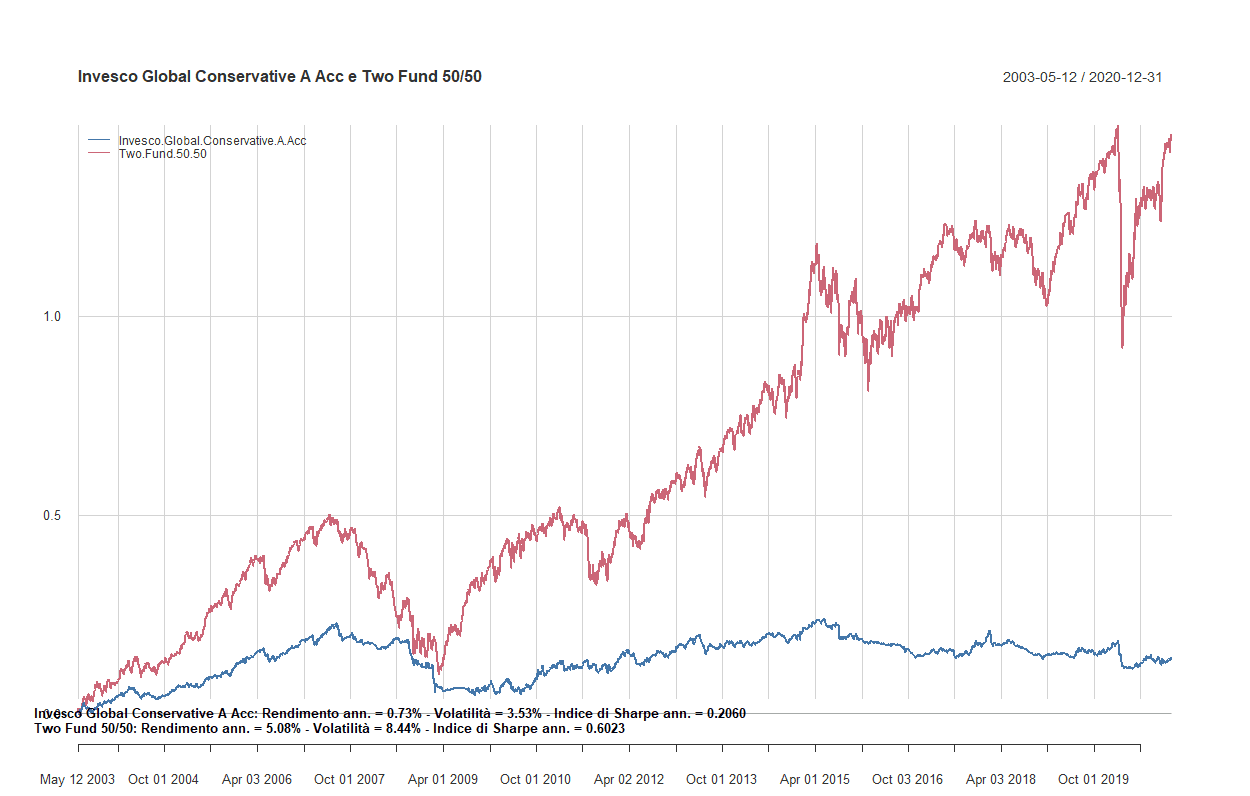
Il periodo analizzato va dal 12 maggio 2003 al 31 dicembre 2020.
Le prestazioni dell’Invesco Global Conservative A Acc sono pessime.
Il settimo fondo è il PIMCO GIS Diversified Income E Acc EUR Hedged, un flessibile obbligazionario globale hedgiato (ISIN: IE00B1Z6D669).
Nel KIID si afferma che “Il fondo è un portafoglio gestito attivamente che mira a raggiungere il proprio obiettivo d’investimento investendo principalmente in un pool diversificato di titoli e strumenti a reddito fisso (cioè prestiti che pagano un tasso d’interesse fisso o variabile) societari e dei mercati emergenti emessi da società o governi di tutto il mondo.
………
Il fondo è considerato a gestione attiva in riferimento a un insieme equamente ponderato dei seguenti tre indici: Bloomberg Barclays Global Aggregate Credit ex-Emerging Markets, ICE BofAML BB-B Rated Developed Markets High Yield Constrained Index e J.P. Morgan EMBI Global; All USD Hedged (insieme l’“Indice di riferimento”) in virtù del fatto che l’Indice di riferimento è utilizzato a fini di misurazione della duration, per calcolare l'esposizione globale del fondo usando la metodologia del VaR relativo e a fini di raffronto dei rendimenti. Alcuni titoli del fondo possono essere componenti dell’Indice di riferimento e presentare una ponderazione simile a quella del medesimo. Tuttavia, l’Indice di riferimento non è utilizzato per definire la composizione del portafoglio del fondo o come obiettivo di rendimento e il fondo può essere interamente investito in titoli che non sono componenti dell’Indice di riferimento”.
In breve:
- Si tratta di un fondo flessibile obbligazionario che investe soprattutto in obbligazioni societarie e dei mercati emergenti.
- Non ha un benchmark vincolante per la composizione del portafoglio del fondo.
Le spese correnti sono pari all’1,59% e non sono previste commissioni di performance.
Il grafico seguente misura la performance del PIMCO GIS Diversified Income E Acc EUR Hedged e del World Bond Lazy portfolio in EUR.
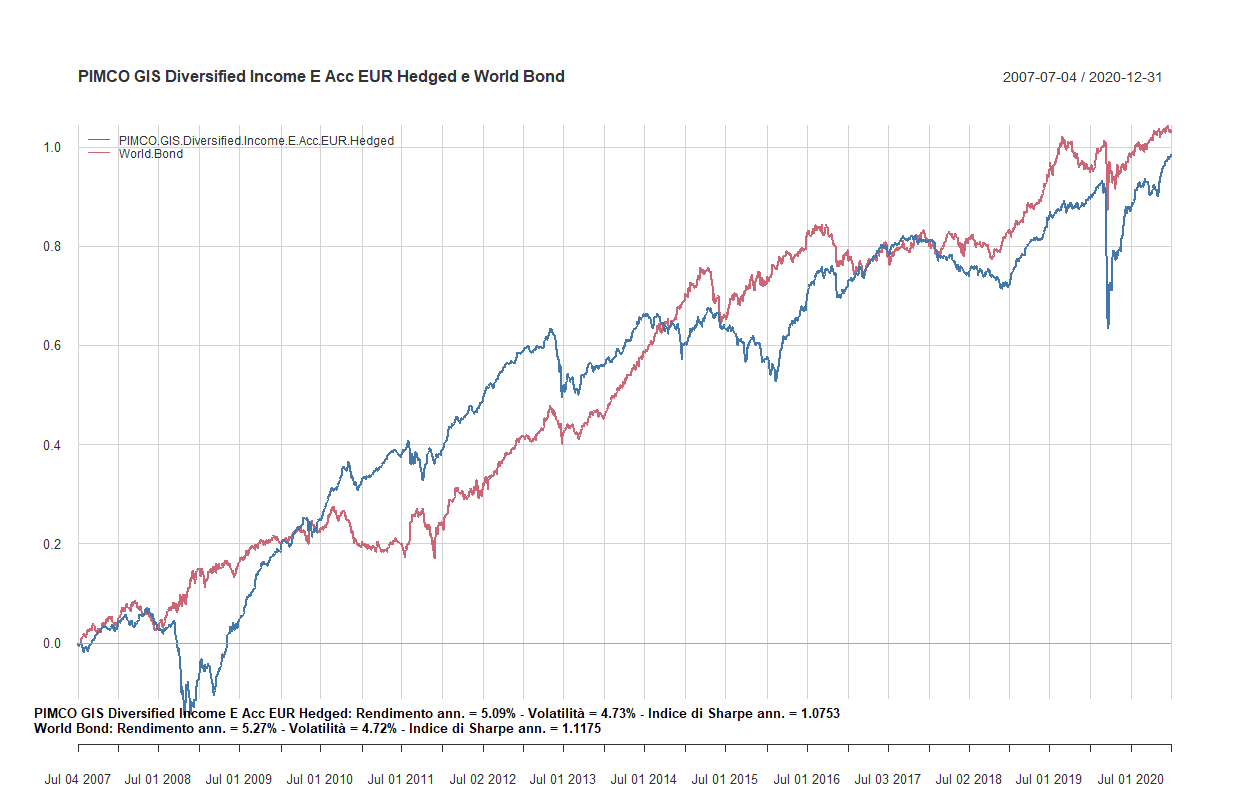
Il periodo analizzato va dal 4 luglio 2007 al 31 dicembre 2020.
Le prestazioni del PIMCO GIS Diversified Income E Acc EUR Hedged sono a tratti migliori di quelle del World Bond in EUR, ma alla fine del 2020 il Lazy portfolio aveva un leggero vantaggio in termini di rendimento, volatilità e indice di Sharpe.
L’ottavo fondo è il DNCA Invest Evolutif Class A EUR, un flessibile bilanciato globale (ISIN: LU0284394664).
Nel KIID si afferma che “Il comparto mira a realizzare un rendimento superiore rispetto all'indice composito 60% Eurostoxx 50, 30% FTSE MTS EMU GOV BOND 1-3 years, 10% EONIA, calcolato con i dividendi reinvestiti, nel periodo di investimento consigliato, proteggendo al tempo stesso il capitale nei periodi sfavorevoli attraverso una gestione opportunistica e un'allocazione flessibile degli attivi. La strategia di investimento del comparto si basa su una gestione discrezionale facendo ricorso a una politica di selezione dei titoli. La politica è interamente basata sull’analisi dei fondamentali sviluppata attraverso i principali criteri di investimento, quali la valutazione del mercato, la struttura finanziaria dell’emittente, la qualità della gestione, la posizione di mercato dell’emittente o contatti regolari con gli emittenti. La Società di gestione può utilizzare diversi metodi per rilevare i futuri rendimenti degli investimenti, per esempio i parametri di valutazione (PE, EV/EBIT, rendimento del cash-flow libero, dividend yield ecc.), la somma delle quote o i cash flow attualizzati. Il comparto investirà in azioni, obbligazioni o strumenti del mercato monetario adattando la strategia di investimento alla situazione economica ed alle aspettative del Gestore degli Investimenti. Fino al 100% del suo patrimonio netto, il comparto potrà essere esposto ad azioni di emittenti appartenenti a tutte le capitalizzazioni di mercato, senza vincoli geografici. Le azioni di emittenti con capitalizzazione al di sotto di 1 miliardo di euro non potranno superare il 10% del patrimonio netto. La quota di investimento in azioni di imprese con sede legale in paesi emergenti (compresi i paesi asiatici, ad eccezione del Giappone, o sudamericani, ecc.) potrà giungere al 20% del patrimonio netto.
………
Benchmark : Il Comparto è gestito attivamente e utilizza il benchmark per il calcolo della commissione di performance e al fine di comparare le performance. Ciò significa che Società di Gestione degli Investimenti prende decisioni d’investimento con l’intenzione di raggiungere l’obiettivo d’investimento del Comparto; tali decisioni possono riguardare la selezione delle asset class e il livello complessivo di esposizione al mercato. Il posizionamento del portafoglio del Gestore degli Investimenti non è in alcun modo vincolato dal benchmark. Lo scostamento dal benchmark può essere totale o significativo”.
I punti salienti sono i seguenti:
- L’indice composito menzionato è importante ai fini del calcolo delle commissioni di performance ma non è in alcun modo vincolante: gli indici compresi sono dell’area euro, ma il gestore può investire in tutto il mondo senza vincoli geografici.
- La strategia di selezione dei titoli si basa sull’analisi fondamentale.
Le spese correnti sono pari al 2,07% e sono previste anche commissioni legate al rendimento pari al 20% dei rendimenti del fondo eccedenti l’indice di riferimento.
Dal momento che l’indice composito che viene specificato nel KIID è azionario al 60%, confronteremo il DNCA Invest Evolutif Class A EUR con il Two funds 60/40 in EUR.
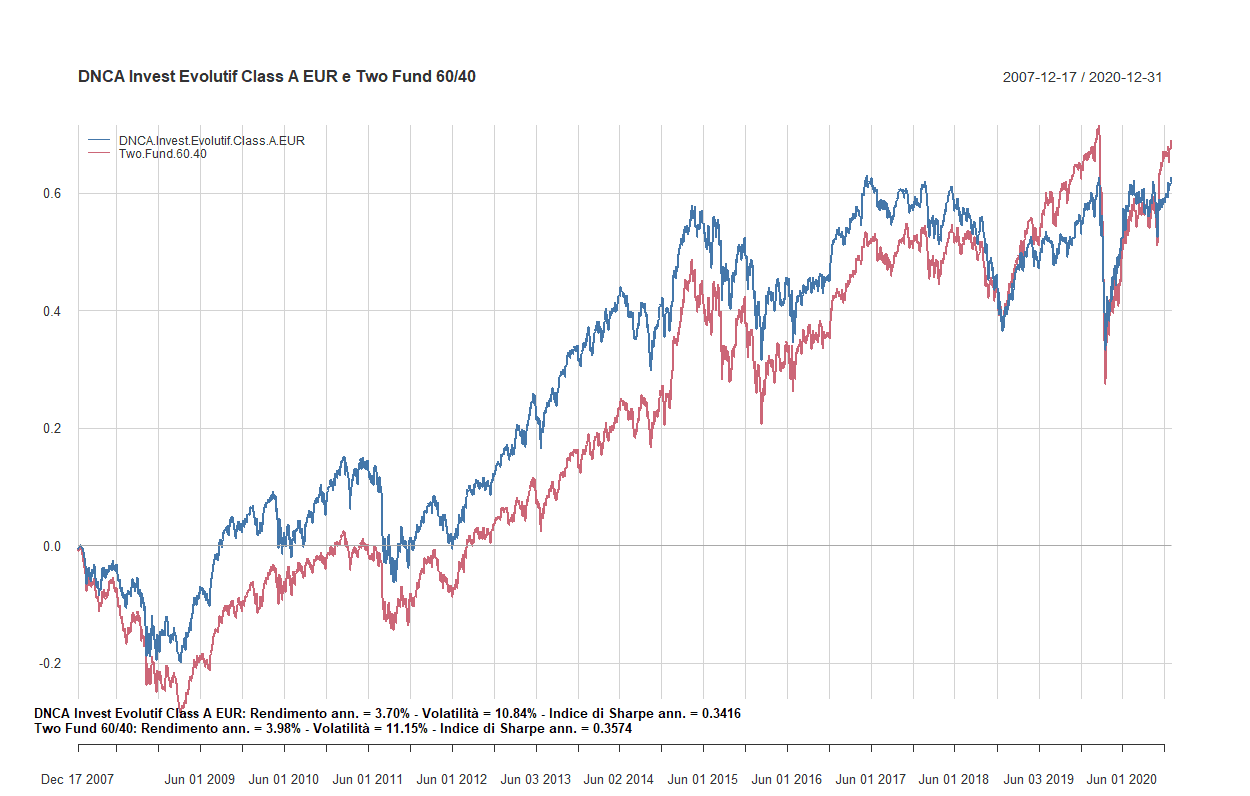
Il periodo analizzato va dal 17 dicembre 2007 al 31 dicembre 2020.
L’analisi parte poco dopo che la crisi dei subprime era scoppiata: nei primi 15 mesi i mercati azionari portano giù il Lazy portfolio e la stessa sorte, anche se con perdite inferiori, colpisce anche il DNCA Invest Evolutif Class A EUR.
Il fondo flessibile riesce a mantenere per tanti anni un certo vantaggio in termini di rendimento, che però diminuisce inesorabilmente fino al sorpasso vero e proprio del Two funds 60/40 che avviene nel corso degli ultimi mesi.
Anche le volatilità e gli indici di Sharpe sono simili.
Utilizziamo questo esempio per evidenziare un modo in cui avremmo potuto “manipolare” il confronto tra questo fondo flessibile e il Two funds 60/40.
La data di inizio è il 17 dicembre 2007 perché quello è il primo rendimento calcolato sulla base dei NAV presenti nel nostro database (la data di partenza del DNCA Invest Evolutif Class A EUR è il 13 dicembre 2007): da lì, ovviamente, parte il confronto con il Lazy portfolio.
È un confronto serrato che vede il Two funds 60/40 vincitore per pochissimo e per puro caso: se la data di fine analisi fosse stata precedente, il fondo flessibile avrebbe prevalso (il che non è un problema: ci sono sempre dei fondi a gestione attiva che fanno meglio di un Lazy portfolio dall’asset allocation simile; la difficoltà è sapere prima e non a posteriori quali siano).
Modificando la data di inizio di un paio di anni, quindi dal 17 dicembre 2007 al 17 dicembre 2009 avremmo ottenuto il risultato seguente:
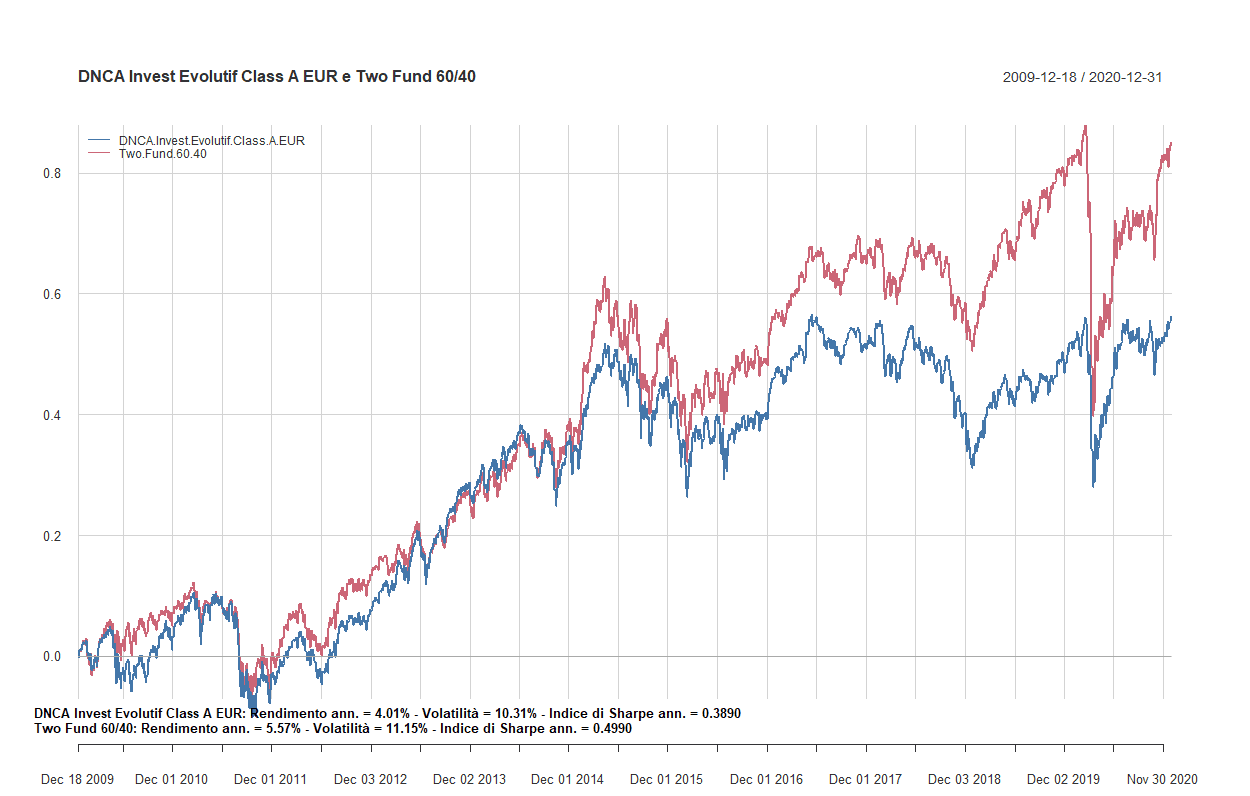
Sarebbe stata una “vittoria” più convincente del Lazy portfolio sul fondo flessibile. Ottenuta, però, manipolando la data di inizio dell’analisi: se sono disponibili due anni di dati in più, perché non utilizzarli?
Scegliendo i periodi opportuni si possono manipolare i risultati a favore dell’uno o dell’altro fondo: ecco perché si dovrebbe sempre fare attenzione e – quando possibile – verificare in prima persona i risultati delle analisi pubblicate anche in rinomati siti finanziari.
Il nono fondo è l’Eurizon MultiManager Stars Fund FCP - Private Style Total Return R, un flessibile bilanciato globale (ISIN: LU0456583508).
Nel KIID leggiamo che “il Comparto può investire fino al 100% del patrimonio netto in azioni o quote di OICVM gestiti dalla Società di Gestione, da altre società del Gruppo o da società terze. La scelta degli OICVM è effettuata attraverso processi di valutazione di natura quantitativa e qualitativa, tenuto conto della specializzazione del gestore e dello stile di gestione adottato, nonché delle caratteristiche degli strumenti finanziari sottostanti. Gli OICVM sono selezionati sulla base della qualità e della consistenza dei risultati, della trasparenza nella comunicazione, nonché della solidità del processo di investimento.
………
Il Comparto investe prevalentemente in OICVM con strategie d'investimento decorrelate o che replicano strategie di fondi speculativi ("hedge fund"). Su base accessoria, il patrimonio netto del Comparto può essere investito in qualsiasi altro strumento inclusi, ma non soltanto, strumenti finanziari di natura azionaria o correlati ad azioni, strumenti finanziari di natura obbligazionaria o correlati al debito e disponibilità liquide, compresi i depositi a termine presso istituti di credito.
………
Il Comparto è a gestione attiva senza riferimento al benchmark”.
In breve, il KIID ci dice che:
- L’asset allocation può essere anche 100% azionaria.
- Si tratta di un fondo di fondi.
- La gestione non è legata ad alcun benchmark.
Le spese correnti sono pari al 2,02% e sono previste anche commissioni legate al rendimento pari al 20% dei rendimenti del fondo eccedenti l’indice Euro OverNight Index Average capitalizzato su base giornaliera accresciuto del 3,00%.
Il fondo può investire fino al 100% in azioni ma, al momento, quasi il 50% dell’asset allocation è obbligazionaria. Lo confronteremo con il solito Two funds 50/50 in EUR:
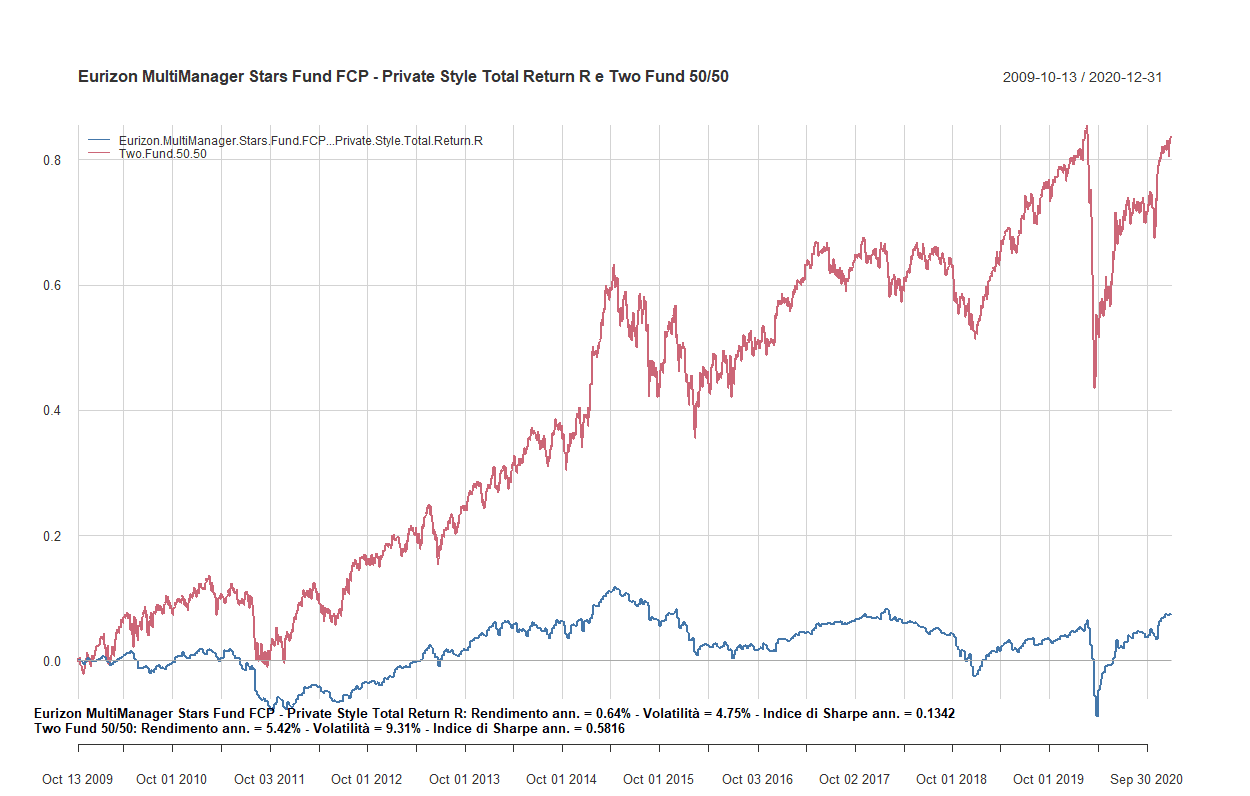
Il periodo analizzato va dal 13 ottobre 2009 al 31 dicembre 2020.
C’è poco da commentare in questo caso: la gestione dell’Eurizon MultiManager Stars Fund FCP - Private Style Total Return R è stata disastrosa.
Il decimo fondo è il BlackRock Strategic Funds - Dynamic Diversified Growth Fund D2 EUR, un flessibile bilanciato globale (ISIN: LU0586680109).
Dal KIID ricaviamo che “il Fondo punta a offrire una crescita di capitale di lungo termine e reddito sull’investimento con una bassa tolleranza verso la perdita di capitale. Il Fondo investe globalmente, sia indirettamente (attraverso altri fondi) sia direttamente, nell’intera gamma di attività aperte agli investimenti di un OICVM. Esse includono, in via non esclusiva: azioni, titoli a reddito fisso (RF) (quali obbligazioni), strumenti del mercato monetario (SMM) (ossia titoli di debito a breve scadenza), strumenti finanziari derivati (SFD), fondi, depositi e contanti. Gli strumenti finanziari derivati sono investimenti i cui prezzi si basano su una o più attività sottostanti. I titoli a reddito fisso possono essere emessi da governi, agenzie governative, società ed enti sovranazionali (per es. la Banca Internazionale per la Ricostruzione e lo Sviluppo). Il Fondo può investire nell’intera gamma di titoli a reddito fisso che possono includere investimenti con un rating creditizio relativamente basso o privi di rating. Le attività detenute dal Fondo possono essere denominate in un’ampia gamma di valute. Ai fini della gestione dell’esposizione valutaria, il consulente per gli investimenti (CI) può utilizzare tecniche di investimento (che possono includere l’utilizzo di strumenti finanziari derivati (SFD) per proteggere il valore del Fondo, per intero o in parte, o consentire al Fondo di beneficiare delle variazioni dei tassi di cambio rispetto alla valuta di denominazione del Fondo. Il CI userà gli SFD per raggiungere l’obiettivo di investimento del Fondo. Questi possono essere utilizzati per acquisire esposizione indiretta a materie prime. Una parte consistente delle attività del Fondo può essere investita in total return swap e contratti su differenze che mirano a realizzare un rendimento specificato basato su attività sottostanti, quali titoli azionari e a RF. Il Fondo è gestito in modo attivo e il CI seleziona a sua discrezione gli investimenti del Fondo e nella selezione non è vincolato da alcun indice di riferimento”.
Questi sono i punti principali:
- Il fondo può investire su strumenti finanziari di tutti i tipi, inclusi i derivati sulle materie prime.
- Il fondo può utilizzare un’ampia gamma di valute, coprendo il cambio o tentando di sfruttarlo con fini speculativi.
- La gestione non è legata ad alcun benchmark.
Le spese correnti sono pari allo 0,97% e non sono previste commissioni di performance.
Ecco il grafico del BlackRock Strategic Funds - Dynamic Diversified Growth Fund D2 EUR confrontato con il Two funds 50/50 in EUR.
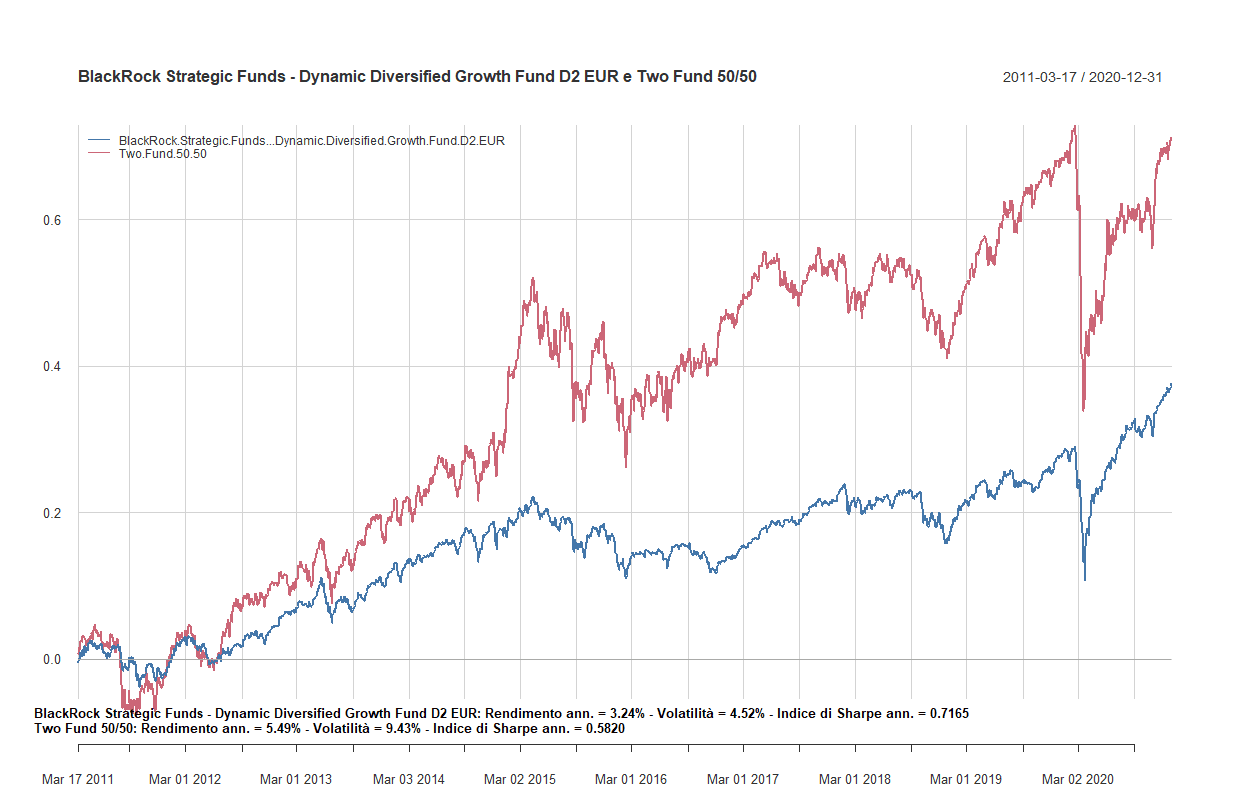
Il periodo analizzato va dal 17 marzo 2011 al 31 dicembre 2020.
Anche in questo caso non c’è molto da commentare: dopo il primo anno che è stato più o meno sugli stessi livelli, il rendimento del Two funds è cresciuto molto di più di quello del BlackRock che, essendo meno volatile, è riuscito però a ottenere un indice di Sharpe annualizzato migliore.
L’undicesimo fondo è il Lyxor Investment Funds – Flexible Allocation M (EUR), un flessibile bilanciato globale (ISIN: LU0812607454).
Il KIID ci fa sapere che “il Fondo è un OICVM attivo. L’obiettivo di investimento del Fondo consiste nel fornire un apprezzamento del capitale netto (tenendo conto di tutte le commissioni e le spese attribuibili al Fondo) superiore all’EONIA (l’“Indice di riferimento”) o al tasso del mercato monetario equivalente nella relativa valuta della Categoria di azioni, su un orizzonte da 3 a 5 anni, mantenendo il livello della volatilità annua inferiore all’8%. La maggior parte degli investimenti o delle esposizioni del Fondo non è legata all’Indice di riferimento. La strategia di investimento del Fondo può discostarsi notevolmente dall’Indice di riferimento. Il Fondo adotta un approccio basato sul rendimento assoluto al fine di generare una performance in diversi contesti di mercato. Investirà pertanto in un portafoglio diversificato di strumenti altamente liquidi. La valuta dell’azione è l’euro (EUR).
Strumenti finanziari in cui investe il Fondo: attivi idonei, tra cui, a titolo esemplificativo, azioni, obbligazioni, Exchange Traded Fund, OICVM, strumenti del mercato monetario, titoli con derivati integrati e strumenti derivati (quali future quotati, opzioni quotate, forward e swap legati ad esempio ad azioni, obbligazioni, valute, indici su materie prime e tassi di interesse).
In breve:
- Il fondo vuole limitare la volatilità annua sotto all’8%.
- Il fondo può investire su qualsiasi strumento finanziario.
- La gestione non è legata ad alcun benchmark.
Le spese correnti sono pari all’1,837% e sono previste anche commissioni di performance pari al 10% dei rendimenti del fondo eccedenti l’indice EONIA.
Ecco il grafico del Lyxor Investment Funds – Flexible Allocation M (EUR) confrontato con il Two funds 50/50 in EUR.
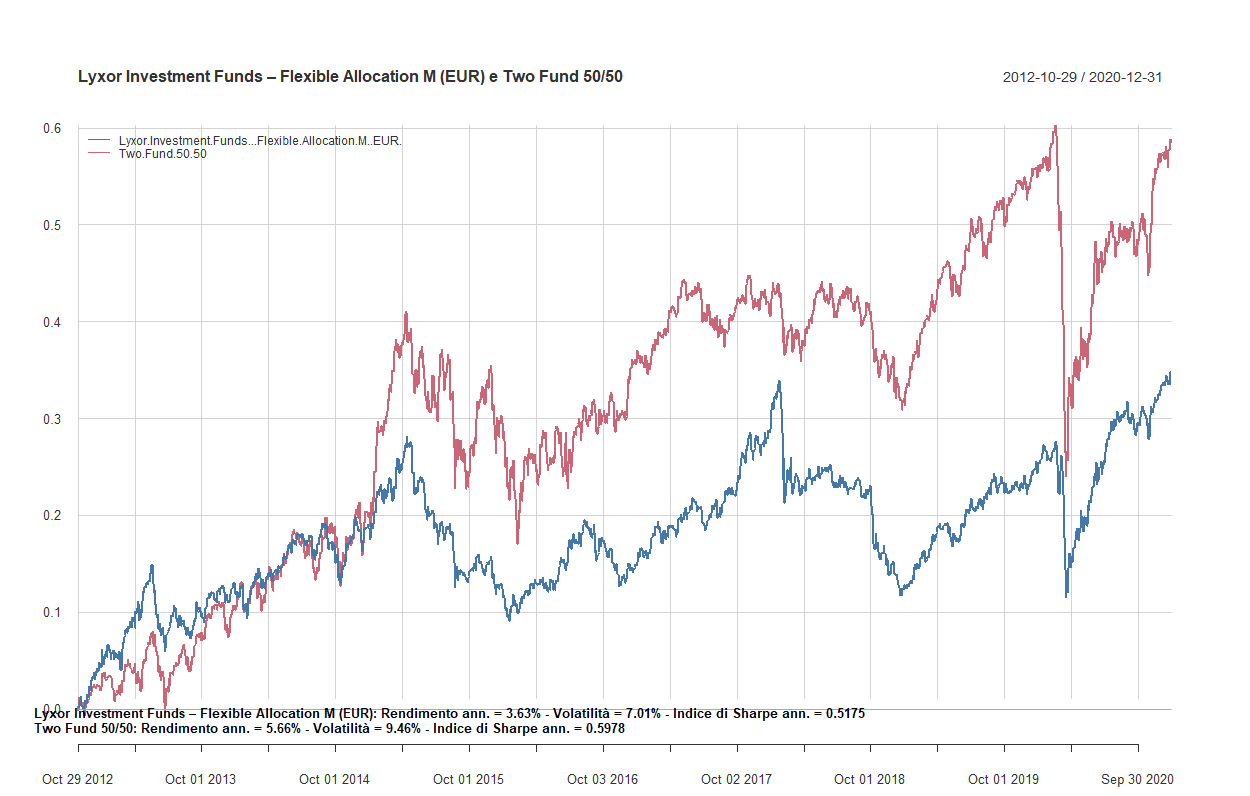
Il periodo analizzato va dal 29 ottobre 2012 al 31 dicembre 2020.
Anche stavolta il confronto è senza storia: nei primi due anni, il Lyxor si è mosso sui livelli del Two funds 50/50, ma poi ha inesorabilmente iniziato a sottoperformare.
A vantaggio del Lyxor c’è la minore volatilità che, però, non riesce a far crescere l’indice di Sharpe annualizzato ai livelli di quello del Two funds.
Potremmo continuare l’analisi per le numerose centinaia di fondi flessibili esistenti ma, come possiamo intuire, i risultati non cambierebbero granché: ogni tanto, un fondo flessibile a gestione attiva performa meglio del Two funds, ma la maggior parte delle volte è quest’ultimo a vincere il confronto, spesso con margini enormi.
Per curiosità, abbiamo lanciato l’analisi che abbiamo appena condotto su questi 11 fondi flessibili a gestione attiva su tutti i fondi flessibili presenti nel nostro database, filtrandoli in base ai seguenti criteri:
- Macrocategoria dei fondi bilanciati flessibili.
- Fondi esistenti alla data odierna (29 dicembre 2021): questo tipo di scelta, comporta un bias molto insidioso che viene definito “Survivorship bias”. In altre parole, molti fondi dalle prestazioni pessime sono stati chiusi o fusi con altri nel corso degli anni: essi non vengono analizzati e non rientrano nell’analisi, proprio perché oggi non esistono più. Un’analisi attenta, tuttavia, dovrebbe inserirli, perché altrimenti i risultati dell’analisi vengono distorti (“biased”, appunto) a favore dei fondi flessibili.
Nonostante questo, li escludiamo dal conteggio, in modo da rendere la vita più dura ai Lazy portfolios. - Fondi ad accumulazione dei proventi.
- Fondi “retail”: nella prima delle nostre analisi, evitiamo i fondi istituzionali che, se è vero che godono di spese correnti molto più basse di quelli retail, non possono essere utilizzati in forma diretta dagli investitori retail (o, almeno, non senza che vengano gravati con commissioni di altro tipo che spesso portano il costo totale a un livello superiore a quello delle spese di gestione dello stesso fondo di una classe “retail”).
Nella nostra seconda analisi, prenderemo in considerazione sia i fondi retail che gli istituzionali. - Valuta: euro.
Applicando i filtri elencati, il nostro database ha estratto 260 fondi (solo fondi retail) e 349 fondi flessibili (retail e istituzionali).
Alcune considerazioni al riguardo:
- Gli 11 fondi flessibili che abbiamo analizzato in precedenza sono inclusi tra i 260 fondi.
- Lo stesso fondo può essere disponibile in più di una classe “retail” o “istituzionale”: quando questo si verifica, tutte le classi vengono incluse nell’analisi. Potrebbe quindi succedere che la classe più economica di un fondo flessibile riesca a far meglio del Lazy portfolio, mentre la classe più cara non ci riesca.
- Nel nostro database e, quindi, nell’analisi, possono essere inclusi fondi bilanciati flessibili non negoziabili in Italia, ma soltanto in altri stati europei (Francia, Germania, Regno Unito ecc.).
- I periodi di analisi sono diversi: come abbiamo visto anche negli undici fondi flessibili esaminati in precedenza, l’analisi parte dalla data di inizio del fondo flessibile e varia da fondo a fondo. Tutte le analisi terminano invece il 31 dicembre 2020.
- La categoria scelta è quella dei fondi flessibili ma, come abbiamo visto, a volte sono inclusi in questa categoria dei fondi flessibili obbligazionari.
- Non potendo per ovvi motivi leggere i KIID di tutti i 260 fondi con lo scopo di personalizzare di volta in volta il confronto con il Lazy portfolio più simile, la nostra analisi pecca di una certa approssimazione: confronteremo allora i 260 fondi una prima volta con il Two funds 50/50 in EUR (che è quello che sarebbe comunque utilizzato nella maggior parte dei casi), una seconda volta con il Two funds 10/90 in EUR e una terza volta con il Two funds 90/10 in EUR.
Nella tabella seguente potete trovare i risultati delle nostre analisi:
| Fondi bilanciati flessibili Retail a gestione attiva e Two funds in EUR1 | ||||||
|---|---|---|---|---|---|---|
| Confronto del rendimento, volatilità e indice di Sharpe annualizzati dei fondi bilanciati flessibili e del Two Fund in EUR | ||||||
| Lazy portfolio | RENDIMENTO | VOLATILITA' | INDICE DI SHARPE | |||
| Migliori su 260 | % | Migliori su 260 | % | Migliori su 260 | % | |
| Two funds 50/50 | 234 | 90.00% | 68 | 26.15% | 196 | 75.38% |
| Two funds 10/90 | 202 | 77.69% | 193 | 74.23% | 192 | 73.85% |
| Two funds 90/10 | 234 | 90.00% | 7 | 2.69% | 129 | 49.62% |
|
1 In totale sono stati analizzati 260 fondi bilanciati flessibili RETAIL. |
||||||
Il Two funds 50/50 Lazy portfolio ottiene un rendimento più alto di quello dei fondi bilanciati flessibili su 234 dei 260 fondi analizzati (90% dei casi); il Two funds 10/90 Lazy portfolio (asset allocation 10% azionaria e 90% obbligazionaria), su 202 dei 260 fondi analizzati (77,69% dei casi) e il Two funds 90/10 di nuovo su 234 dei 260 fondi analizzati (90%).
I risultati della volatilità e degli indici di Sharpe possono essere letti direttamente nella tabella: il Two funds 50/50 e soprattutto il 90/10 sono stati nella maggior parte dei casi più volatili dei fondi flessibili e – con l’eccezione del Two funds 90/10 – hanno ottenuto indici di Sharpe più alti.
Aggiungendo anche i fondi bilanciati flessibili istituzionali, i risultati sono stati i seguenti:
| Fondi bilanciati flessibili Retail e Istituzionali a gestione attiva e Two funds in EUR1 | ||||||
|---|---|---|---|---|---|---|
| Confronto del rendimento, volatilità e indice di Sharpe annualizzati dei fondi bilanciati flessibili e del Two Fund in EUR | ||||||
| Lazy portfolio | RENDIMENTO | VOLATILITA' | INDICE DI SHARPE | |||
| Migliori su 349 | % | Migliori su 349 | % | Migliori su 349 | % | |
| Two funds 50/50 | 308 | 88.25% | 85 | 24.36% | 249 | 71.35% |
| Two funds 10/90 | 269 | 77.08% | 248 | 71.06% | 299 | 85.67% |
| Two funds 90/10 | 310 | 88.83% | 8 | 2.29% | 158 | 45.27% |
|
1 In totale sono stati analizzati 349 fondi bilanciati flessibili RETAIL e ISTITUZIONALI. |
||||||
Le percentuali di successo scendono di pochissimo e il dominio dei Lazy portfolios non sembra poter essere messo in discussione.
A questo punto, dobbiamo fare alcune precisazioni e tirare qualche conclusione:
- I fondi a gestione attiva bilanciati flessibili escono sconfitti in termini di rendimento dal confronto con 3 tipologie di Two funds Lazy portfolios: la meno rischiosa, la più rischiosa e quella a rischio medio.
- Abbiamo confrontato i fondi bilanciati flessibili con 3 tipologie di Two funds Lazy portfolios esclusivamente per semplicità: si tratta di una scelta soggettiva, logica in un certo senso, ma non è “manipolata” in alcun modo. I confronti presentati in questo capitolo sono gli unici effettuati finora. Per quanto sia possibile effettuarli con facilità, non abbiamo realizzato nessun’altra comparazione e non abbiamo intenzione di farlo in futuro (non crediamo che aggiungerebbe niente di significativo alla discussione); quantomeno, non in questo contesto.
- I rendimenti dei Two funds Lazy portfolios che abbiamo utilizzato nel confronto con i bilanciati flessibili sono quelli generati con il modello di ottimizzazione standard: in altre parole, sono i classici Lazy portfolios ribilanciati una volta all’anno. Come abbiamo visto nel capitolo 12, il modello standard è quello che, nei nostri backtest, ha ottenuto le performance peggiori.
Rimandiamo al capitolo 12 e ai capitoli precedenti per maggiori informazioni. - Nelle performance dei Two funds portfolios non sono stati inclusi i costi di transazione, di eventuali imposte pagate sul capital gain e i costi relativi allo spread/slippage.
Questi costi, nel loro insieme, potrebbero impattare i risultati ottenuti, ma crediamo che non possano cambiarli in modo sostanziale. In ogni caso, i Two funds sono composti da due soli ETF e quindi, tra tutti i Lazy portfolios, sono quelli che minimizzano i costi di transazione e di spread/slippage. - I fondi bilanciati flessibili che abbiamo analizzato hanno la libertà di investire, nella maggior parte dei casi, in ogni area geografica del mondo, di coprire o meno il cambio, di utilizzare o meno derivati con qualunque tipo di sottostante, anche le commodities.
I Two funds Lazy portfolios utilizzati sono invece costituiti da 2 ETF, uno azionario e uno obbligazionario, che investono esclusivamente nell’area euro.
La maggior sofisticazione delle strategie utilizzate dai fondi flessibili sembra non produrre i risultati sperati: le idee alla base dei Lazy portfolios – la semplicità e l’economicità – escono vincitrici da questo confronto, come John Bogle aveva già intuito mezzo secolo fa. - I fondi flessibili ottengono risultati migliori in termini di volatilità dei Two funds 50/50 e 90/10 Lazy portfolios. Un investitore prudente potrebbe essere portato a pensare che, nel suo caso, i fondi bilanciati flessibili sarebbero stati la scelta più appropriata: non è così, dal momento che sarebbe bastato scegliere un Lazy portfolio più prudente – ad esempio il Two funds 10/90 – per spostare anche la rischiosità a favore dei portafogli pigri nella maggior parte dei casi. Così facendo, si sarebbe perso qualcosa in termini di rendimento, ma il vantaggio dei Lazy portfolios è fuori discussione.
17. ETF Vanguard LifeStrategy

«Talking about ETFs is like talking about people. There are good ones, and there are bad ones».
John Bogle
Gli ETF sono strumenti finanziari pensati per replicare passivamente il mercato. Esistono ormai da diversi anni e sono sempre più conosciuti e utilizzati dagli investitori.
Il mercato degli ETF è in continua evoluzione e le società emittenti cercano sempre di proporre strumenti innovativi che riescano a soddisfare i nuovi bisogni degli investitori.
Tra questi, ci sono numerose soluzioni che riteniamo poco interessanti o che, quantomeno, devono ancora dimostrare la loro maggior efficienza nel lungo termine rispetto all’approccio classico (gli ETF Smart Beta, ad esempio).
Alcune però, hanno attirato l’attenzione del pubblico e si sono proposte come alternative ai robo-advisor e, in certi casi, alla consulenza finanziaria: lo strumento finanziario più innovativo degli ultimi anni è senz’altro la gamma di ETF denominata LifeStrategy, emessi da Vanguard.
Esistono 4 profili del LifeStrategy. La loro asset allocation è la seguente:
- LifeStrategy® 20% Equity UCITS ETF → 20% azionario, 80% obbligazionario.
- LifeStrategy® 40% Equity UCITS ETF → 40% azionario, 60% obbligazionario.
- LifeStrategy® 60% Equity UCITS ETF → 60% azionario, 40% obbligazionario.
- LifeStrategy® 80% Equity UCITS ETF → 80% azionario, 20% obbligazionario.
Gli ETF LifeStrategy sono disponibili in due modalità: a distribuzione e ad accumulazione dei proventi. Per rendere possibili i confronti con i Lazy portfolios, prenderemo in considerazione soltanto i LifeStrategy ad accumulazione o, nel caso dei LifeStrategy statunitensi che saranno esaminati in seguito, le serie storiche rettificate in funzione della distribuzione di dividendi e di eventuali frazionamenti delle quote.
Le principali caratteristiche dei Vanguard LifeStrategy sono le seguenti:
| Vanguard LifeStrategy1 | |||||
|---|---|---|---|---|---|
| TER, Ticker, ISIN, Replicazione ed Hedging dei LifeStrategy ad accumulazione dei proventi | |||||
| Nome | TER | Ticker | ISIN | Replicazione | Hedging |
| LifeStrategy® 20% Equity UCITS ETF | 0.25% | VNGA20 | IE00BMVB5K07 | Fisica (Replica totale) | Solo sulla parte obbligazionaria |
| LifeStrategy® 40% Equity UCITS ETF | 0.25% | VNGA40 | IE00BMVB5M21 | Fisica (Replica totale) | Solo sulla parte obbligazionaria |
| LifeStrategy® 60% Equity UCITS ETF | 0.25% | VNGA60 | IE00BMVB5P51 | Fisica (Replica totale) | Solo sulla parte obbligazionaria |
| LifeStrategy® 80% Equity UCITS ETF | 0.25% | VNGA80 | IE00BMVB5R75 | Fisica (Replica totale) | Solo sulla parte obbligazionaria |
|
1 I Vanguard LifeStrategy a distribuzione dei proventi non sono inclusi nella tabella. |
|||||
Il TER di tutti i LifeStrategy è pari allo 0,25%. Si tratta di un costo relativamente basso, allineato al TER medio di molti dei Lazy portfolios in EUR che abbiamo analizzato nei capitoli 13.3.1-13.3.31.
Gli ETF sottostanti non vengono gravati da ulteriori commissioni di gestione e gli unici costi non inclusi nello 0,25% sono quelli di negoziazione e lo spread bid-ask.
Per capire gli obiettivi e la politica di investimento dei LifeStrategy, vediamo che cosa riporta il loro KIID nel secondo paragrafo, comune a tutti e 4 gli ETF:
“Il Fondo persegue una strategia d'investimento a gestione attiva, in base alla quale il Gestore degli investimenti è libero di scegliere la composizione del portafoglio del Fondo e non è gestito in riferimento a un benchmark. Tuttavia, come descritto più in dettaglio di seguito, il Gestore degli investimenti gestisce il Fondo tramite allocazioni predeterminate delle attività a titoli azionari e a reddito fisso utilizzando una combinazione di schemi di investimenti collettivi sottostanti.”
È sorprendente ciò che si legge nella prima riga: “Il Fondo persegue una strategia d’investimento a gestione attiva”.
Non avevamo ripetuto fino allo sfinimento che gli ETF sono dei fondi a gestione passiva?
Qui sta la novità dei LifeStrategy: questi ETF si occupano del ribilanciamento interno periodico, in modo che i pesi della componente azionaria e obbligazionaria rimangano costanti nel tempo.
In altre parole, si tratta di una gestione attiva anomala: non è finalizzata a ottenere un rendimento più alto del benchmark (che, tra l’altro, per questi ETF non è previsto), ma a mantenere nel tempo l’asset allocation prevista.
Il grande vantaggio degli ETF LifeStrategy è, perciò, quello di evitare il ribilanciamento periodico da parte dell’investitore.
Nel terzo paragrafo, si specifica inoltre che:
Il Fondo cercherà di raggiungere il suo obiettivo di investimento acquisendo esposizione a un portafoglio diversificato composto approssimativamente per il 20% (oppure 40%-60%-80%) dal valore di titoli azionari e per l’80% (oppure 60%-40%-20%) dal valore di titoli a reddito fisso che, in base ai requisiti della Banca Centrale, sarà ottenuto prevalentemente tramite investimento diretto in titoli Exchange Traded Fund a gestione passiva ("ETF") o altri schemi di investimenti collettivi che replicano un indice (collettivamente "Fondi Target"). L'allocazione delle attività del portafoglio può essere ricostituita e ribilanciata di volta in volta a discrezione del Gestore degli investimenti. I Fondi Target in cui il Fondo investe saranno OICVM e potranno includere altri comparti di Vanguard Funds plc.
Questo paragrafo ci fa capire come i LifeStrategy siano degli ETF composti da altri ETF e si propongano di essere dei veri e propri Lazy portfolios: possono perciò essere paragonati a dei Lazy portfolios con le 4 asset allocation viste in precedenza.
I LifeStrategy sono composti da un numero di ETF compreso tra 9 (LifeStrategy 20% e LifeStrategy 40%) e 14 (LifeStrategy 80%).
Per semplicità, nelle analisi successive verranno confrontati con i Two funds Lazy portfolios 20/80, 40/60, 60/40 e 80/20.
Nella tabella seguente potete trovare la lista dei fondi Vanguard sottostanti a ciascun LifeStrategy:
| Vanguard LifeStrategy: lista dei fondi sottostanti | ||
|---|---|---|
| Composizione dell'asset azionaria e obbligazionaria | ||
| ETF sottostante | Peso | Asset |
| LifeStrategy® 20% Equity UCITS ETF | ||
| FTSE All-World UCITS ETF (USD) Accumulating | 18.62% | Azionaria |
| FTSE Developed World UCITS ETF (USD) Accumulating | 0.73% | Azionaria |
| FTSE Emerging Markets UCITS ETF (USD) Accumulating | 0.08% | Azionaria |
| Totale | 19.43% | |
| USD Treasury Bond UCITS ETF EUR Hedged Accumulating | 19.55% | Obbligazionaria |
| Global Aggregate Bond UCITS ETF EUR Hedged Accumulating | 19.29% | Obbligazionaria |
| EUR Eurozone Government Bond UCITS ETF (EUR) Accumulating | 17.17% | Obbligazionaria |
| USD Corporate Bond UCITS ETF EUR Hedged Accumulating | 16.14% | Obbligazionaria |
| EUR Corporate Bond UCITS ETF (EUR) Accumulating | 5.75% | Obbligazionaria |
| U.K. Gilt UCITS ETF EUR Hedged Accumulating | 2.67% | Obbligazionaria |
| Totale | 80.57% | |
| LifeStrategy® 40% Equity UCITS ETF | ||
| FTSE All-World UCITS ETF (USD) Accumulating | 18.80% | Azionaria |
| FTSE Developed World UCITS ETF (USD) Accumulating | 18.21% | Azionaria |
| FTSE Emerging Markets UCITS ETF (USD) Accumulating | 2.15% | Azionaria |
| Totale | 39.16% | |
| Global Aggregate Bond UCITS ETF EUR Hedged Accumulating | 19.57% | Obbligazionaria |
| USD Treasury Bond UCITS ETF EUR Hedged Accumulating | 13.24% | Obbligazionaria |
| EUR Eurozone Government Bond UCITS ETF (EUR) Accumulating | 11.54% | Obbligazionaria |
| USD Corporate Bond UCITS ETF EUR Hedged Accumulating | 10.92% | Obbligazionaria |
| EUR Corporate Bond UCITS ETF (EUR) Accumulating | 3.81% | Obbligazionaria |
| U.K. Gilt UCITS ETF EUR Hedged Accumulating | 1.76% | Obbligazionaria |
| Totale | 60.84% | |
| LifeStrategy® 60% Equity UCITS ETF | ||
| FTSE Developed World UCITS ETF (USD) Accumulating | 18.99% | Azionaria |
| FTSE All-World UCITS ETF (USD) Accumulating | 18.92% | Azionaria |
| FTSE North America UCITS ETF | 11.93% | Azionaria |
| FTSE Emerging Markets UCITS ETF (USD) Accumulating | 4.12% | Azionaria |
| FTSE Developed Europe UCITS ETF (EUR) Accumulating | 3.10% | Azionaria |
| FTSE Japan UCITS ETF (USD) Accumulating | 1.26% | Azionaria |
| FTSE Developed Asia Pacific ex Japan UCITS ETF (USD) Accumulating | 0.88% | Azionaria |
| Totale | 59.20% | |
| Global Aggregate Bond UCITS ETF EUR Hedged Accumulating | 19.70% | Obbligazionaria |
| USD Treasury Bond UCITS ETF EUR Hedged Accumulating | 6.79% | Obbligazionaria |
| EUR Eurozone Government Bond UCITS ETF (EUR) Accumulating | 5.90% | Obbligazionaria |
| USD Corporate Bond UCITS ETF EUR Hedged Accumulating | 5.59% | Obbligazionaria |
| EUR Corporate Bond UCITS ETF (EUR) Accumulating | 1.92% | Obbligazionaria |
| U.K. Gilt UCITS ETF EUR Hedged Accumulating | 0.88% | Obbligazionaria |
| Totale | 40.78% | |
| LifeStrategy® 80% Equity UCITS ETF | ||
| FTSE North America UCITS ETF | 19.42% | Azionaria |
| FTSE Developed World UCITS ETF (USD) Accumulating | 19.21% | Azionaria |
| FTSE All-World UCITS ETF (USD) Accumulating | 19.10% | Azionaria |
| FTSE Developed Europe UCITS ETF (EUR) Accumulating | 6.43% | Azionaria |
| FTSE Emerging Markets UCITS ETF (USD) Accumulating | 6.19% | Azionaria |
| S&P 500 UCITS ETF (USD) Accumulating | 4.88% | Azionaria |
| FTSE Japan UCITS ETF (USD) Accumulating | 2.55% | Azionaria |
| FTSE Developed Asia Pacific ex Japan UCITS ETF (USD) Accumulating | 1.78% | Azionaria |
| Totale | 79.56% | |
| Global Aggregate Bond UCITS ETF EUR Hedged Accumulating | 19.75% | Obbligazionaria |
| USD Treasury Bond UCITS ETF EUR Hedged Accumulating | 0.21% | Obbligazionaria |
| EUR Eurozone Government Bond UCITS ETF (EUR) Accumulating | 0.20% | Obbligazionaria |
| USD Corporate Bond UCITS ETF EUR Hedged Accumulating | 0.18% | Obbligazionaria |
| EUR Corporate Bond UCITS ETF (EUR) Accumulating | 0.07% | Obbligazionaria |
| U.K. Gilt UCITS ETF EUR Hedged Accumulating | 0.03% | Obbligazionaria |
| Totale | 20.44% | |
Le informazioni che possiamo dedurre dagli ETF che compongono ciascun LifeStrategy sono molto utili. Innanzitutto, ci permettono di capire come venga gestita ciascuna asset allocation di ogni LifeStrategy.
Ad esempio, quando l’azionario è al 20%, si tratta nella quasi totalità di azionario globale. Quando diventa il 40%, al 20% di azionario globale viene aggiunto un 18% di azionario dei soli paesi sviluppati e un 2% di azionario dei mercati emergenti.
Dalla tabella si può facilmente dedurre come varia l’azionario nei LifeStrategy 60% e 80%, così come l’obbligazionario nelle 4 asset allocation disponibili.
I LifeStrategy vengono ribilanciati periodicamente. Nel KIID si afferma che il ribilanciamento non avviene a intervalli regolari ma “di volta in volta a discrezione del Gestore degli investimenti”.
Il ribilanciamento automatico all'interno dei portafogli garantisce che il profilo di rischio desiderato venga mantenuto stabile nel lungo periodo.
Abbiamo finora elencato due grossi vantaggi degli ETF LifeStrategy:
- Il TER basso: è in linea con quello di molti Lazy portfolios in EUR.
- Il ribilanciamento automatico: è una caratteristica che i Lazy portfolios classici non hanno, dovendo essere effettuata “manualmente” una volta all’anno.
Il secondo vantaggio merita di essere sottolineato perché – oltre all’automaticità – permette all’investitore di non dover pagare imposte sul capital gain: cosa che avviene nei normali Lazy portfolios quando, per ribilanciare, si devono vendere quote di un ETF in guadagno (che avrà aumentato il suo peso in portafoglio) per acquistare quote di un ETF in perdita (che avrà invece diminuito il suo peso in portafoglio).
Passiamo adesso agli svantaggi dei LifeStrategy:
- La loro asset azionaria è statica: ciascun LifeStrategy può essere paragonato a un Lazy portfolio standard. Come avevamo visto nel capitolo 9, il modello di ottimizzazione standard era in realtà un semplice ribilanciamento, esattamente come avviene nel caso dei LifeStrategy. Per molti investitori, non è un problema: tuttavia, abbiamo visto come la strategia di ottimizzazione standard sia la meno performante in assoluto e i LifeStrategy non lasciano purtroppo spazio all’utilizzo di altri modelli di ottimizzazione.
- Il rischio di cambio dei LifeStrategy è alto: tanto maggiore è l’asset allocation azionaria, tanto maggiore è il rischio di cambio che si assume l’investitore dell’area euro.
Nel capitolo 4 e nell’analisi di ciascun Lazy portfolio nei capitoli dal 13.3.1 al 13.3.31, avevamo visto come il rischio di cambio costituisca un problema serio: l’utilizzo di strumenti finanziari pensati per un investitore americano comporta l’aggiunta del rischio di cambio a quello di mercato.
Si possono verificare 4 scenari:
- Il mercato e l’andamento del tasso di cambio sono favorevoli all’investitore dell’area euro: il rendimento finale e il rischio sostenuto sono più alti di quelli dell’investitore statunitense.
- Il mercato è favorevole ma il tasso di cambio è sfavorevole all’investitore dell’area euro: il rendimento finale può essere più alto o più basso e il rischio sostenuto è più alto di quello dell’investitore statunitense.
- Il mercato è sfavorevole ma il tasso di cambio è favorevole all’investitore dell’area euro: il rendimento finale può essere più alto o più basso mentre il rischio sostenuto è più alto di quello dell’investitore statunitense.
- Il mercato e l’andamento del tasso di cambio sono sfavorevoli all’investitore dell’area euro: il rendimento finale è più basso e il rischio sostenuto è più alto di quelli dell’investitore statunitense.
Il rendimento finale dell’investitore dell’area euro è più alto di quello dell’investitore statunitense in 1-3 casi, e peggiore negli altri 1-3. In media, il rendimento atteso è invariato.
Il rischio sostenuto dall’investitore dell’area euro è invece più alto di quello sostenuto dall’investitore statunitense in tutti e 4 i casi.
La certezza di assumersi un rischio più alto dovrebbe far riflettere l’investitore dell’area euro: non si tratta, “semplicemente”, di volatilità più alta; il rischio è più alto anche in termini di massimo drawdown, lunghezza media dei drawdown e CVaR.
Come nota positiva, riscontriamo che la parte obbligazionaria è totalmente hedgiata quando le obbligazioni sottostanti sono in valute diverse dall’euro. Il rischio di cambio sull’asset obbligazionaria è quindi assente.
In Italia, gli ETF LifeStrategy sono stati lanciati da poco: hanno fatto il loro debutto l’8 dicembre 2020. Le serie storiche dei loro rendimenti sono molto corte.
Effettueremo comunque un confronto tra i LifeStrategy e i Two funds portfolios in EUR con una simile asset allocation nel periodo compreso tra il 10 dicembre 2020 e il 21 dicembre 2021.
Ricordiamo che il Two funds portfolios in EUR è formato dagli ETF CSEMU e EYLD. L’analisi completa di questo portafoglio è stata effettuata nel capitolo 13.3.3; qui di seguito riportiamo soltanto la descrizione e le caratteristiche degli ETF che lo compongono:
| Descrizione degli ETF che compongono il Two funds portfolio | ||||
|---|---|---|---|---|
| Ticker | ISIN | Nome | Società emittente | Descrizione |
| CSEMU | IE00B53QG562 | iShares Core MSCI EMU UCITS ETF EUR (Acc) | iShares | Replica i titoli azionari ad alta e media capitalizzazione dei paesi dell'unione monetaria ed economica europea |
| EYLD | IE00BD49RB39 | WisdomTree EUR Aggregate Bond Enhanced Yield UCITS ETF EUR Acc | WisdomTree | Replica la performance di obbligazioni a tasso fisso, denominate in euro, includendo obbligazioni del tesoro, governative, societarie e cartolarizzate (Investment Grade) |
| Caratteristiche degli ETF che compongono il Two funds portfolio | |||||
|---|---|---|---|---|---|
| Ticker | TER | Replica | Hedging | PRO | CONTRO |
| CSEMU | 0.12% | Fisica (Replica totale) | No | Ampia diversificazione | Niente di rilevante |
| EYLD | 0.18% | Fisica (Campionamento) | No | Ampia diversificazione | Niente di rilevante |
Partiamo dalla visualizzazione del grafico dei NAV dei 4 ETF LifeStrategy:
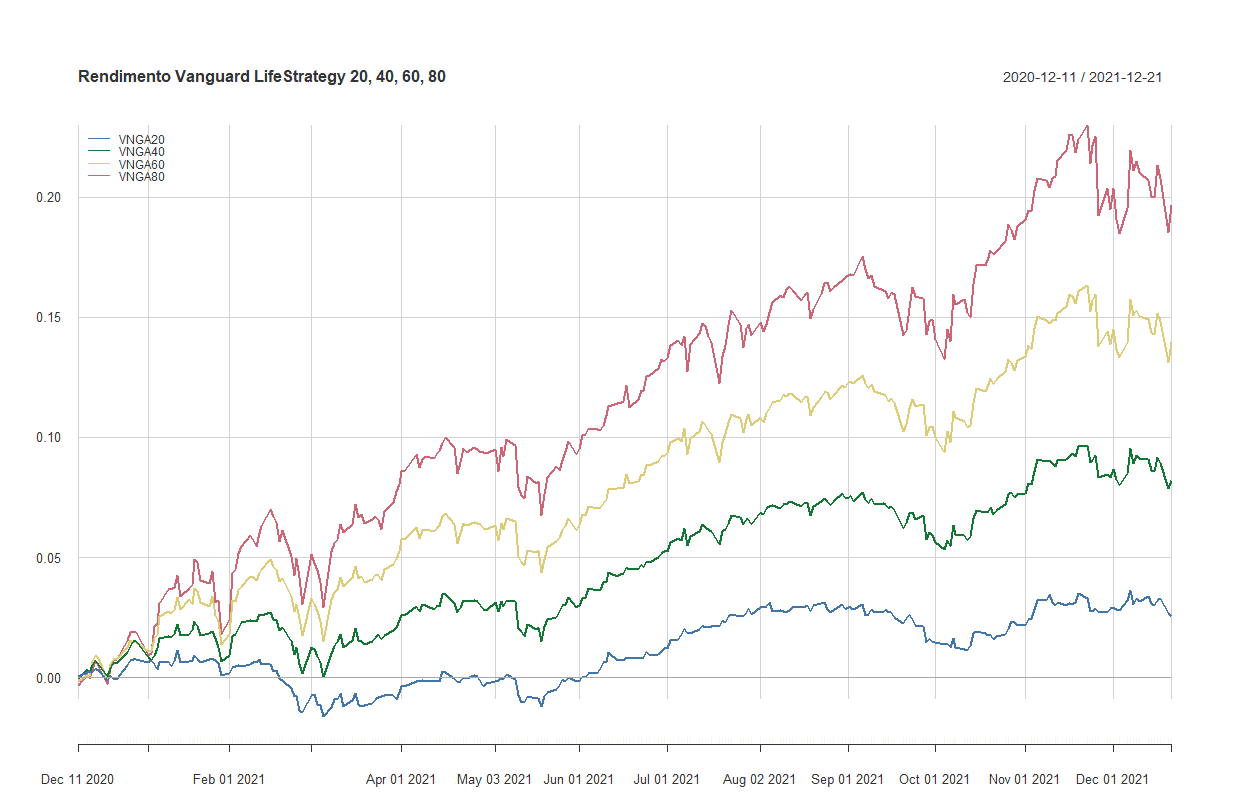
Il 2021 è stato un anno in cui i mercati azionari sono cresciuti molto: si vede bene come gli ETF con una maggiore componente azionaria abbiano ottenuto rendimenti più alti.
Quelli che seguono sono invece i rendimenti dei Two funds portfolios in EUR 20/80, 40/60, 60/40 e 80/20 nello stesso periodo di analisi:
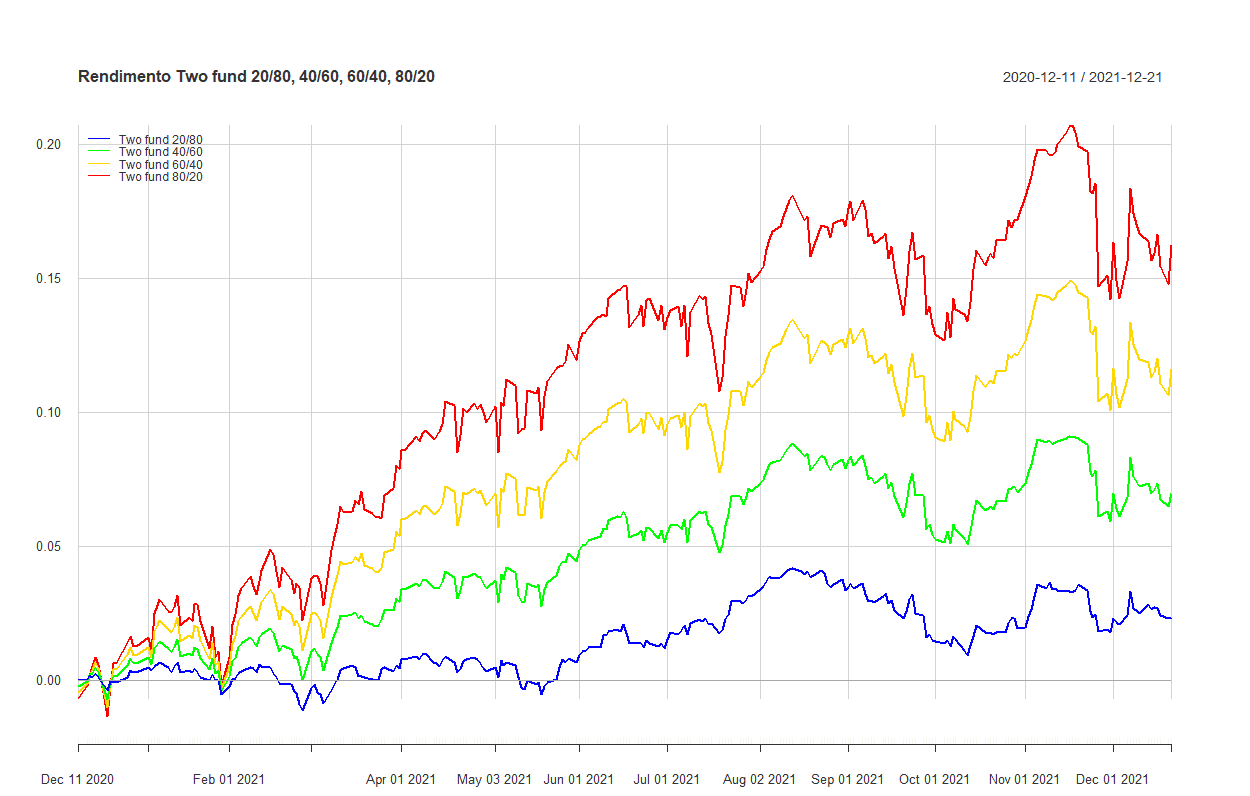
L’andamento è simile a quello dei LifeStrategy ma i rendimenti sono leggermente inferiori.
Per un confronto più diretto, riportiamo i LifeStrategy e i Two funds in uno stesso grafico:
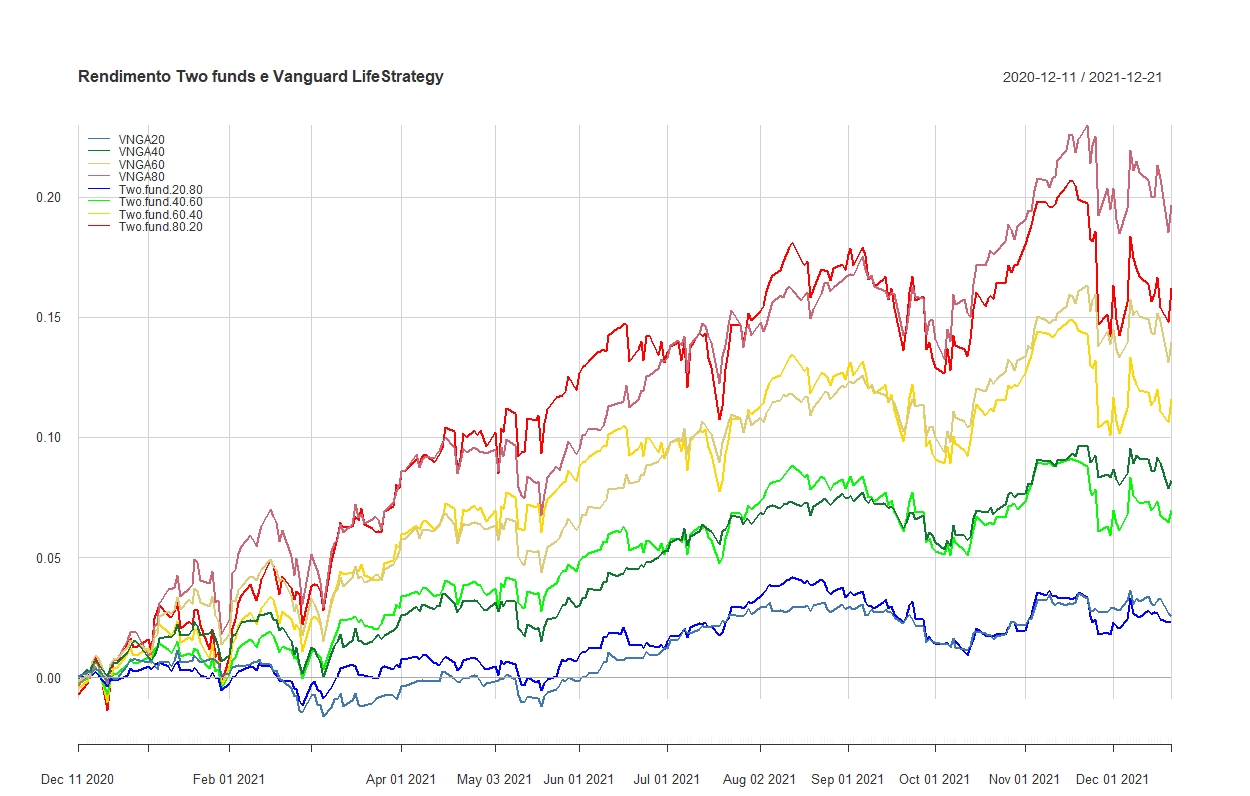
I LifeStrategy hanno generato una performance superiore a quella dei Two funds sia in termini di rendimento che di volatilità.
Questi sono i risultati ottenuti:
| Vanguard LifeStrategy e Two funds in EUR | ||||||||
|---|---|---|---|---|---|---|---|---|
| Rendimento, standard deviation e indice di Sharpe annualizzati del primo anno di vita dei LifeStrategy e del Two Fund in EUR (stesso periodo) | ||||||||
| Misura statistica | Vanguard LifeStrategy | Two funds portfolios in EUR | ||||||
| VNGA20 | VNGA40 | VNGA60 | VNGA80 | Two funds 20/80 | Two funds 40/60 | Two funds 60/40 | Two funds 80/20 | |
| Annualized Return | 2.43% | 7.77% | 13.22% | 18.60% | 2.20% | 6.60% | 10.99% | 15.36% |
| Annualized Std Dev | 3.42% | 5.06% | 7.26% | 9.87% | 3.92% | 6.17% | 8.71% | 11.24% |
| Annualized Sharpe (Rf=0%) | 0.7097 | 1.5358 | 1.8219 | 1.8847 | 0.5624 | 1.07 | 1.2608 | 1.366 |
Possiamo affermare che gli ETF LifeStrategy siano migliori dei Lazy portfolios?
La risposta è negativa. Sono strumenti finanziari diversi; ognuno con dei vantaggi e degli svantaggi.
I risultati di uno specifico anno ci dicono poco: quello che conta è il lungo termine e – nel lungo termine – i risultati della tabella soprastante potrebbero cambiare drasticamente.
Tra l’altro, il confronto che abbiamo fatto non è molto corretto, dato che abbiamo comparato i rendimenti di due portafogli che replicano mercati diversi: azionario e obbligazionario globale (LifeStrategy); azionario e obbligazionario dell’area euro (Two funds).
E il rischio di cambio che ruolo svolge? È possibile che ci abbia messo lo zampino anche stavolta?
La risposta è affermativa.
I mercati azionari globali (la parte obbligazionaria dei LifeStrategy – vale la pena ricordarlo – è totalmente hedgiata) sono composti per circa il 60% da società statunitensi e per meno del 10% da società dell’area euro: il 60% è perciò quotato in dollari e meno del 10% in euro.
Per l’investitore dell’area euro, il mercato azionario globale – laddove il cambio sia aperto, come nella parte azionaria dei LifeStrategy – comporta il rischio di cambio su oltre il 90% del sottostante. Il 60%, in particolare, è il rischio di cambio derivante dalle fluttuazioni dei tassi di cambio tra dollaro e euro.
Per l’investitore statunitense, il mercato azionario globale – laddove il cambio sia aperto – comporta il rischio di cambio su circa il 40% del sottostante. Meno del 10% è il rischio di cambio derivante dalle fluttuazioni dei tassi di cambio tra dollaro e euro.
Di conseguenza, se l’euro si rafforza nei confronti del dollaro, l’effetto sulle quotazioni dei LifeStrategy sarà negativo; se si rafforza il dollaro, invece, l’effetto sulle quotazioni dei LifeStrategy sarà positivo.
Come si è mosso il tasso di cambio nel periodo in esame?
Questo è il grafico dell’andamento del tasso di cambio tra dollaro ed euro:
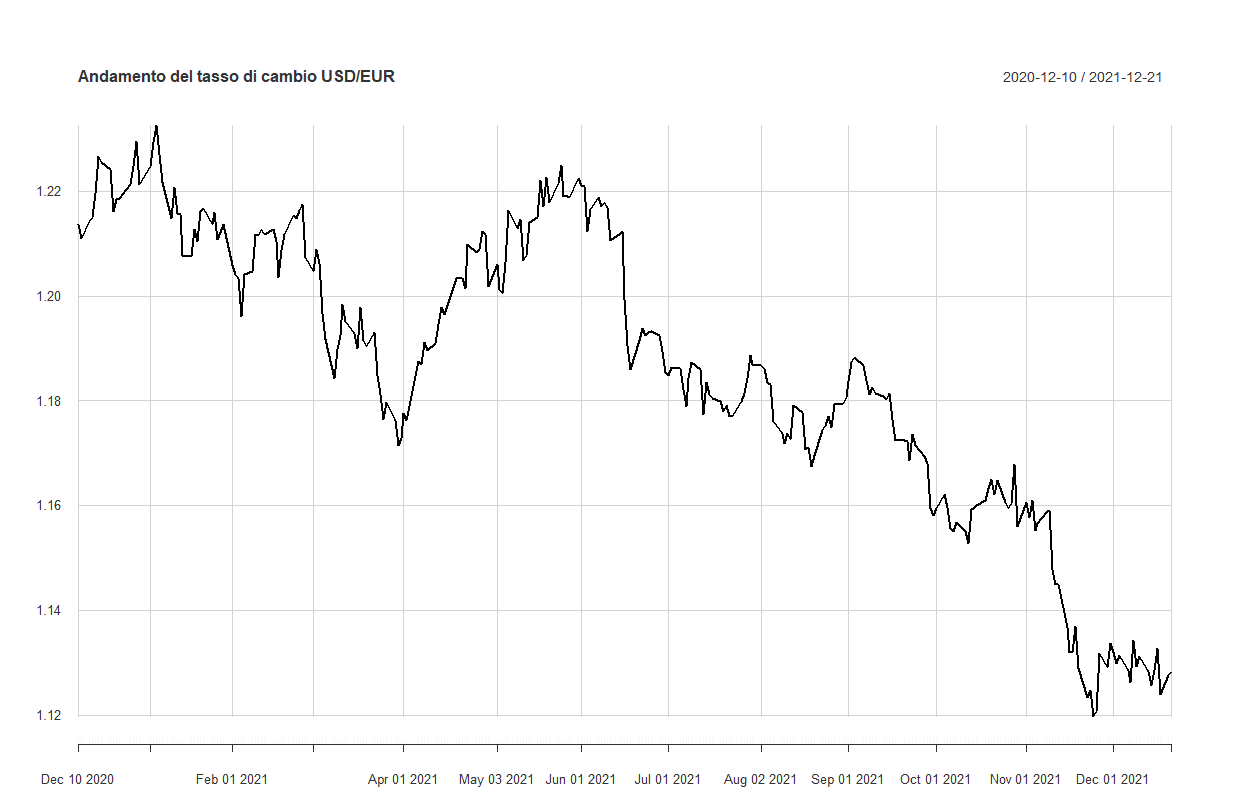
Il 10 dicembre 2020, un euro valeva poco più di 1,21 dollari; il 21 dicembre 2021, un euro valeva circa 1,125 dollari.
Nel periodo in esame, l’euro ha perso circa il 7% nei confronti del dollaro: le quotazioni dei LifeStrategy ne hanno beneficiato e il loro maggior rendimento nei confronti dei Two funds in EUR può essere almeno in parte attribuito – per l’investitore dell’area euro – all’andamento favorevole del rischio di cambio.
Sarà così anche in futuro?
Nessuno può saperlo: l’andamento futuro dei tassi di cambio è ancora meno prevedibile di quello dei mercati. I periodi favorevoli all’investitore dell’area euro si susseguiranno a quelli negativi: l’impatto sul rendimento finale è sconosciuto ma, quasi certamente, la volatilità sarà maggiore.
I sottoscrittori dei LifeStrategy hanno ottenuto delle ottime soddisfazioni nel loro primo anno di vita: il viaggio è stato abbastanza tranquillo, ma è importante che si allaccino le cinture di sicurezza perché i mercati azionari sono delle montagne russe e, in futuro, dovranno farsi trovare pronti (soprattutto chi ha investito nei LifeStrategy 60 e 80).
Gli ETF LifeStrategy sono negoziabili in Italia da poco più di un anno: negli Stati Uniti, però, esistono sotto forma di fondi comuni d’investimento a gestione passiva da quasi 30 anni; il loro lancio risale addirittura al 30 settembre 1994.
A differenza degli ETF LifeStrategy disponibili in Italia, i 4 LifeStrategy statunitensi hanno un TER diverso tra di loro:
- Vanguard LifeStrategy Income Fund (VASIX): 20% azionario, 80% obbligazionario → TER = 0,11%.
- Vanguard LifeStrategy Conservative Growth Fund (VSCGX): 40% azionario, 60% obbligazionario → TER = 0,12%.
- Vanguard LifeStrategy Moderate Growth Fund (VSMGX): 60% azionario, 40% obbligazionario → TER = 0,13%.
- Vanguard LifeStrategy Growth Fund (VASGX): 80% azionario, 20% obbligazionario → TER = 0,14%.
Tecnicamente, i LifeStrategy negoziabili sul mercato statunitense sono dei fondi di fondi; il loro costo – se si escludono le commissioni di negoziazione – è soltanto quello delle percentuali riportate sopra: sono fondi estremamente economici.
Non entreremo nel dettaglio dei fondi a gestione passiva che li costituiscono; confronteremo invece i LifeStrategy con i Two funds portfolios in USD, che abbiamo approfondito nel capitolo 13.3.3.
Vediamo il grafico dei 4 LifeStrategy nel periodo compreso tra il 30 settembre 1994 e il 31 dicembre 2020:
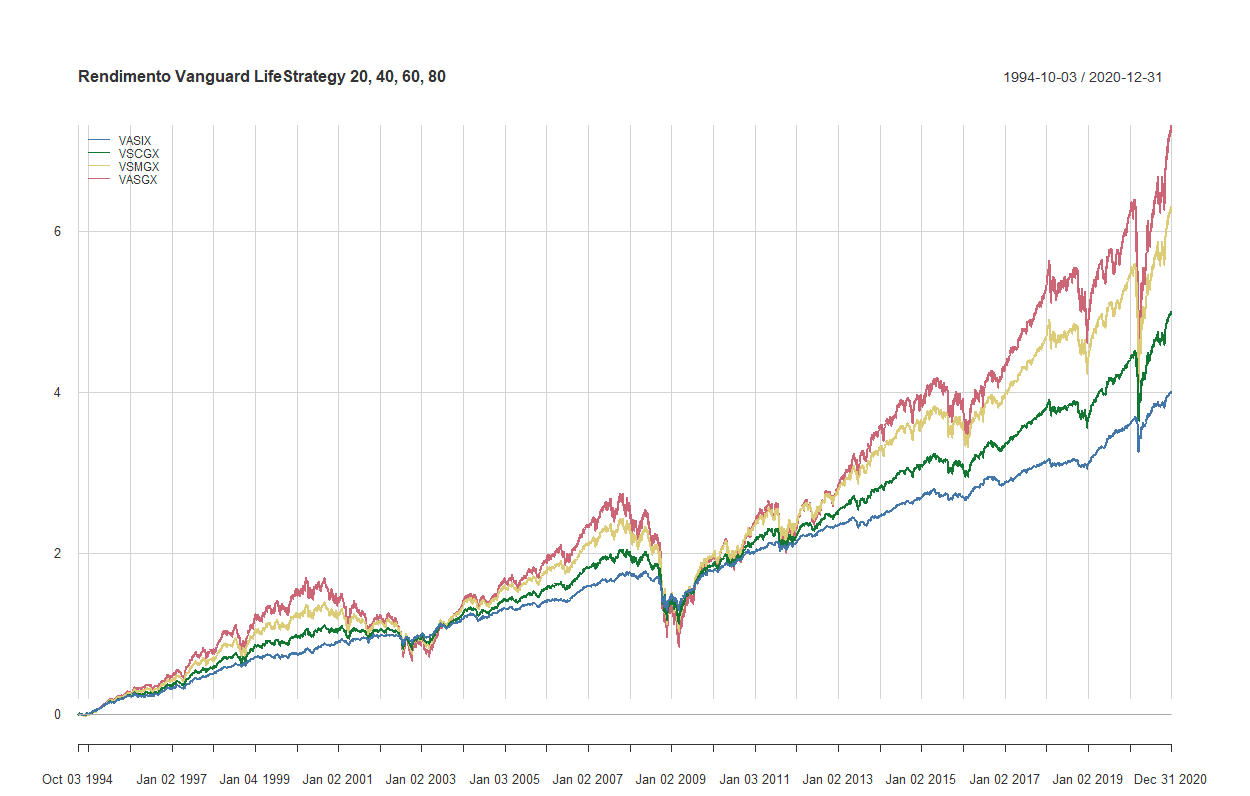
Si tratta del classico andamento del mercato azionario nel periodo in esame, con gli alti e bassi che hanno caratterizzato gli ultimi 30 anni. Si vedono bene le crisi del 2000-2003 (dotcom), del 2008-2009 (subprime), del 2020 (COVID-19) e le successive riprese del mercato.
Quelli che seguono sono invece i rendimenti dei Two funds portfolios in USD 20/80, 40/60, 60/40 e 80/20 nello stesso arco temporale:
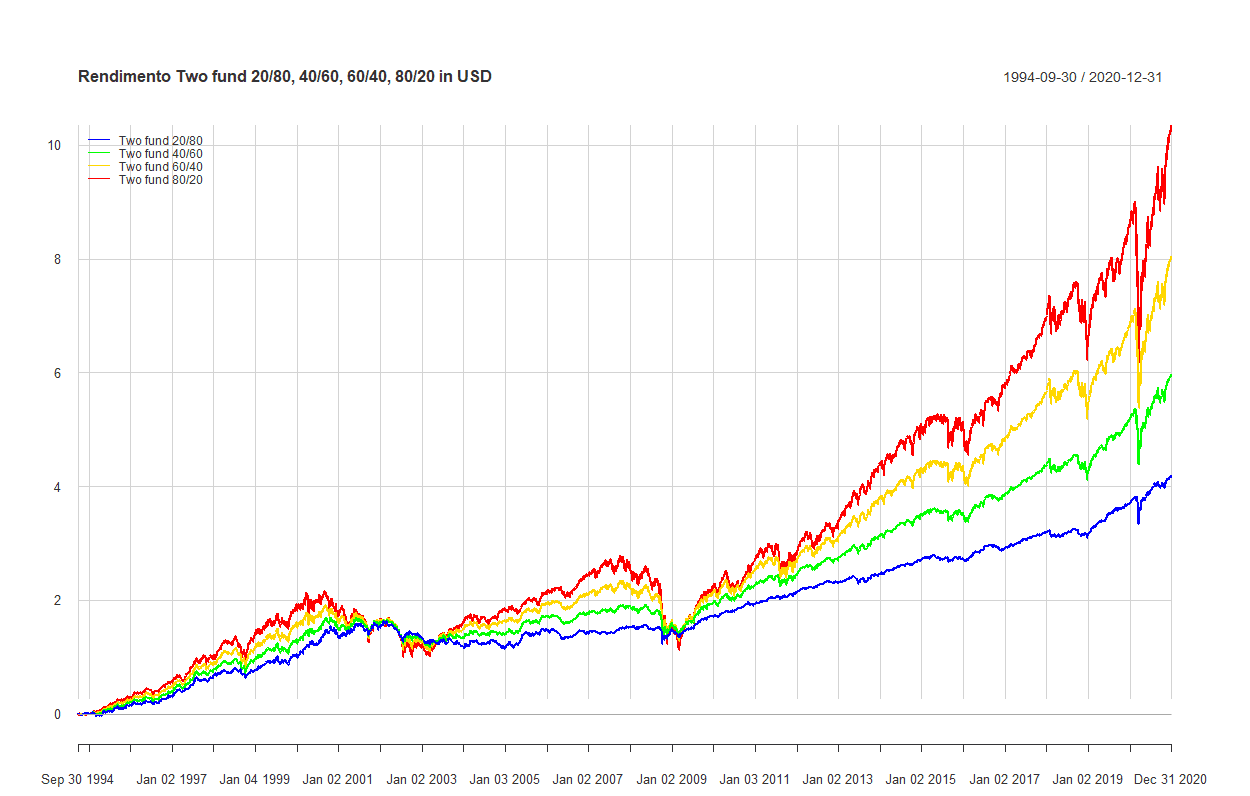
L’andamento è simile a quello dei LifeStrategy ma i rendimenti sono superiori.
Visualizziamo infine nello stesso grafico gli andamenti dei LifeStrategy e dei Two funds in USD:
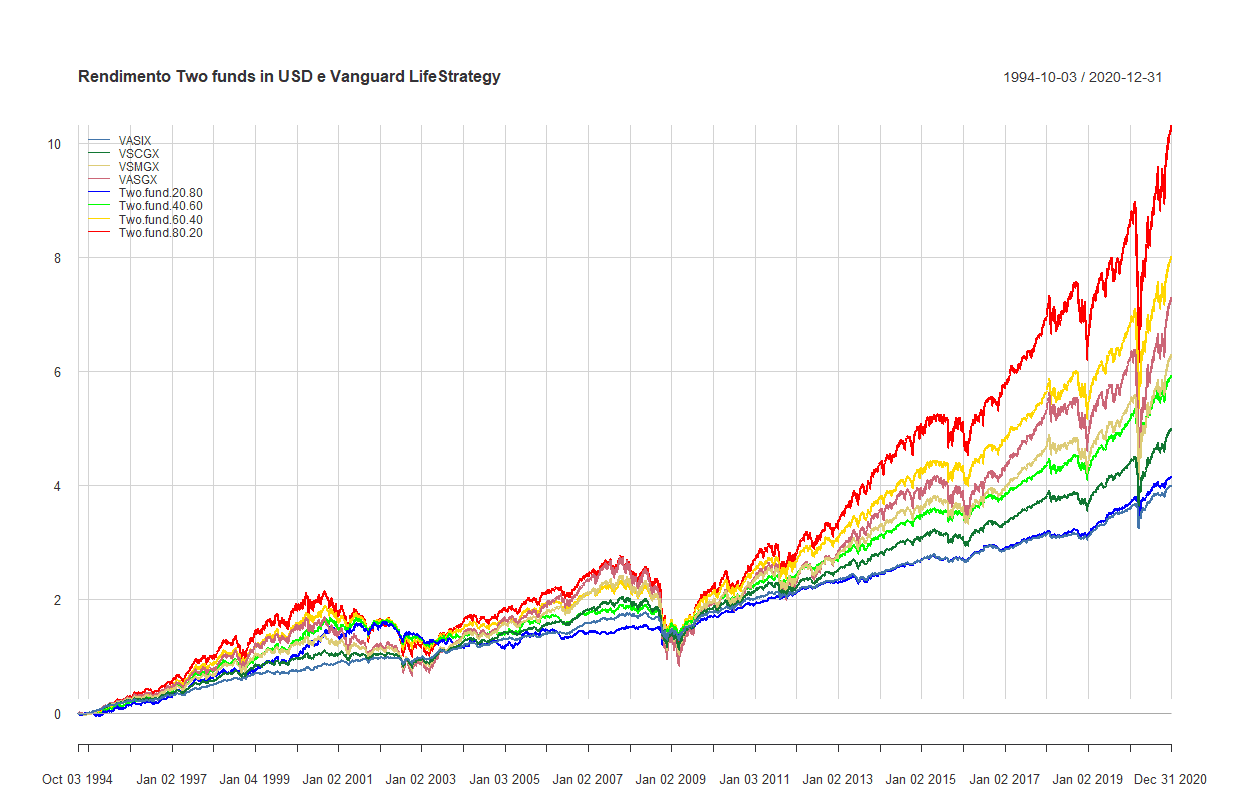
Vediamo i risultati in dettaglio:
| Vanguard LifeStrategy e Two funds in USD | ||||||||
|---|---|---|---|---|---|---|---|---|
| Rendimento, standard deviation e indice di Sharpe annualizzati dei LifeStrategy e del Two Fund in USD nello stesso periodo | ||||||||
| Misura statistica | Vanguard LifeStrategy | Two funds portfolios in EUR | ||||||
| VNGA20 | VNGA40 | VNGA60 | VNGA80 | Two funds 20/80 | Two funds 40/60 | Two funds 60/40 | Two funds 80/20 | |
| Annualized Return | 6.17% | 6.89% | 7.67% | 8.19% | 6.29% | 7.47% | 8.52% | 9.44% |
| Annualized Std Dev | 4.83% | 7.93% | 11.45% | 15.11% | 7.11% | 8.45% | 11.16% | 14.67% |
| Annualized Sharpe (Rf=0%) | 1.2773 | 0.8693 | 0.6703 | 0.5418 | 0.8851 | 0.8841 | 0.7635 | 0.6434 |
I Two funds portfolios in USD hanno generato un rendimento più elevato e, nel caso del Two funds 60/40 e dell’80/20, sono riusciti a farlo con una volatilità inferiore.
Alcune considerazioni sono necessarie:
- L’asset allocation dei LifeStrategy è globale, mentre quella dei Two funds portfolios è al 100% locale (Stati Uniti): i LifeStrategy sono più rischiosi dei Two funds portfolios perché comportano un rischio di cambio sulla parte azionaria e obbligazionaria non statunitense, pari a circa il 40% del totale.
- Questa maggior rischiosità dovrebbe essere almeno in parte mitigata dalla più ampia diversificazione del portafoglio dei LifeStrategy: la loro asset allocation è globale e ciascun LifeStrategy è composto da 5 fondi a gestione passiva contro i 2 ETF dei Two funds portfolios.
- L’asset allocation dei LifeStrategy statunitensi è cambiata nel corso degli anni:
- Il 30 settembre 2011, i fondi hanno adottato un “All-index fund portfolio”; la modifica è stata implementata nei mesi successivi.
- Il 6 febbraio 2013, Vanguard ha annunciato l’adozione di una quarta asset class: quella obbligazionaria globale (prima di allora l’asset obbligazionaria era soltanto statunitense).
- Il 26 febbraio 2015, Vanguard ha annunciato un aumento dell’asset allocation azionaria globale dal 30% al 40% dell’esposizione azionaria totale e un incremento dell’asset allocation obbligazionaria globale dal 20% al 30% dell’esposizione obbligazionaria totale. Questi cambiamenti sono stati implementati prima della fine del 2015.
I Vanguard LifeStrategy sono un’ottima soluzione di investimento: con un solo ETF (o un solo fondo a gestione passiva per gli investitori americani) si riescono a coprire tutti i mercati azionari e obbligazionari del mondo.
Le commissioni di gestione molto competitive e il ribilanciamento automatico, che riporta i pesi di ciascuna asset allocation a quelli inizialmente stabiliti, rendono i LifeStrategy strumenti finanziari appetibili soprattutto per gli investitori meno esperti o per quelli che vogliono dedicare il minor tempo possibile alla gestione del proprio portafoglio finanziario.
Esistono però delle valide alternative, soprattutto per un investitore dell’area euro. Se chi sceglie il LifeStrategy con un asset azionaria del 20% può permettersi di rischiare un po’ di più (il cambio non è coperto solo su questa parte del portafoglio), quelli che scelgono un asset azionaria dal 40% in su devono fare più attenzione.
Nei capitoli compresi tra il 13.3.1 e il 13.3.31, abbiamo visto che esistono molti Lazy portfolios in EUR dalle performance eccellenti. Crediamo che, in futuro, riescano a generare delle performance vicine o superiori a quelle dei LifeStrategy, pur essendo meno rischiosi: rischiosità che non deve essere intesa soltanto come minore volatilità, ma anche e soprattutto come massimi drawdown più contenuti e CVaR inferiori.
Infine, con i LifeStrategy non è possibile mettere in pratica una gestione dinamica – vincolata o non vincolata – mediante l’ottimizzazione periodica del portafoglio: ottimizzazione che, in base ai nostri backtest, riesce a migliorare ulteriormente le performance complessive in termini di rischio/rendimento.
18. La gestione della parte obbligazionaria e della liquidità

«Liquidity is a concern of the short-term investor and a minor matter for the long-term investor».
Peter Bernstein
Siamo in una fase storica senza precedenti. Si è sempre creduto che i tassi di interesse avessero un limite inferiore pari a zero, sotto al quale non sarebbero mai potuti scendere, dal momento che un tasso negativo avrebbe creato dei seri problemi.
Negli ultimi tempi, questa opinione è stata abbandonata e si considera che un tasso di interesse negativo sia sostenibile almeno nel breve termine: il suo limite inferiore non è più zero, ma si troverebbe adesso in territorio negativo, pur non essendo chiaro il livello al quale si posizionerebbe.
Con tassi di interesse a questi livelli, l’asset allocation obbligazionaria – che ha sempre garantito dei rendimenti nominali interessanti – non è più così attraente per un investitore:
- I tassi di interesse negativi sembrano tollerabili solo nel breve termine: dovrebbero perciò tornare a salire, posizionandosi su valori positivi.
- Una crescita dei tassi di interesse comporta automaticamente una diminuzione del prezzo dei titoli obbligazionari, che sono legati da un rapporto di proporzionalità inversa con i tassi.
La prospettiva di una crescita dei tassi di interesse tende a modificare le preferenze degli investitori: invece delle classiche obbligazioni governative, presenti tra l’altro in molti dei Lazy portfolios analizzati, la ricerca di un rendimento più alto sposta la scelta verso le obbligazioni societarie o, addirittura, verso quelle High Yield: High Yield significa letteralmente alto rendimento, ma l’alto rendimento va di pari passo con l’alto rischio.
Le obbligazioni High Yield sono quelle emesse da società o governi con minore solvibilità, quindi con un rating molto basso (inferiore al BBB) e un rischio di fallimento superiore.
Per questo motivo, vengono definite anche junk bonds (obbligazioni spazzatura).
L’asset obbligazionaria è presente in quasi tutti i Lazy portfolios: la scelta di non utilizzarla più o di trasformarla in obbligazioni High Yield sembra azzardata e proietterebbe l’investitore in una situazione ambigua, dagli sviluppi poco chiari.
I Lazy portfolios nascono con l’idea di essere mantenuti nel lungo termine: non necessariamente per i 20 o i 35 anni che abbiamo backtestato, anche se sarebbe opportuno che il periodo d’investimento non fosse troppo breve.
In un’ottica di lungo termine, le varie fasi di ogni ciclo economico – espansione, picco, recessione e punto di minimo e ripresa – possono susseguirsi anche più di una volta: avrebbe senso snaturare un portafoglio pigro e il quadro teorico che lo caratterizza solo perché l’asset obbligazionaria potrebbe attraversare un periodo di difficoltà?
Crediamo che la risposta sia negativa: rincorrere il trend del momento attraverso una gestione tattica degli asset di un Lazy portfolio è un compito difficile e impegnativo, che ha un’alta probabilità di insuccesso per più motivi:
- La gestione tattica di un portafoglio finanziario è il lavoro di un gestore di un fondo attivo: come è noto, questo compito è molto arduo anche per soggetti altamente specializzati che lo svolgono in maniera professionale e a tempo pieno; figuriamoci per l’investitore fai-da-te.
- C'è forse un equivoco di fondo associato alla funzione dell’asset obbligazionaria in un portafoglio: il suo ruolo non è quello di generare rendimento nel lungo termine; a quello, ci pensa l’azionario. La finalità della componente obbligazionaria è – in primis – quella di mitigare la volatilità del portafoglio, sfruttando sia la più bassa deviazione standard dei rendimenti obbligazionari rispetto a quelli azionari che la mancanza o la poca correlazione lineare che lega questi due asset.
La volatilità del portafoglio verrebbe quindi mitigata anche se i rendimenti obbligazionari fossero negativi: se l’investitore fosse interessato soltanto a massimizzare il suo rendimento atteso senza mitigare la volatilità del portafoglio, sarebbe allora consigliabile la scelta di un Lazy portfolio al 100% azionario. In tal caso, è bene però che l’investitore si faccia un bell’esame di coscienza e sia in grado di rispondere in maniera affermativa alla domanda seguente: sono davvero in grado di tollerare la volatilità di un portafoglio al 100% azionario?
Storicamente, i tassi di interesse nominali non sono mai stati negativi ma quelli reali sì. Il grafico seguente mostra il tasso di interesse reale calcolato come differenza tra il tasso di interesse nominale del Treasury bill a un anno e il tasso di inflazione statunitense tra il 1° gennaio 1871 e il 15 dicembre del 2021:
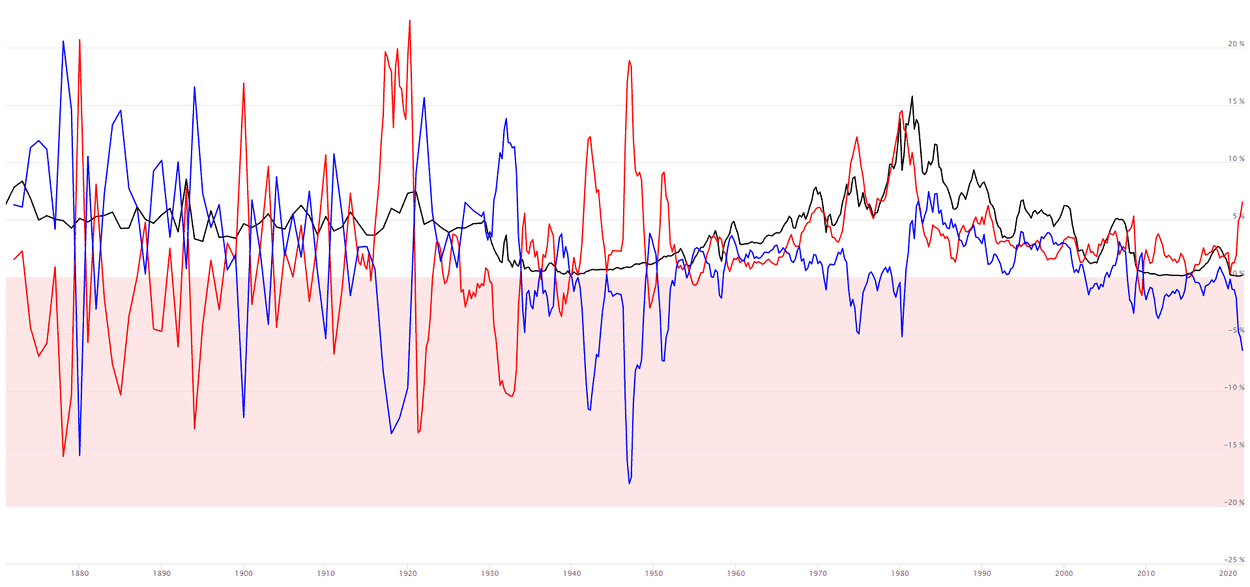
La linea nera è il tasso di interesse nominale del Treasury Bond a un anno; la linea rossa è il tasso di inflazione e la linea blu è il tasso di interesse reale.
Il numero di volte in cui il tasso di interesse reale è stato negativo è alto. La situazione in cui ci troviamo, almeno per quanto riguarda il mercato statunitense, non è qualcosa di mai visto prima.
Chi, nonostante tutto, volesse evitare a tutti i costi gli ETF obbligazionari, potrebbe sostituirli con la liquidità: la parte riservata al comparto obbligazionario sarebbe perciò mantenuta liquida, possibilmente su un conto deposito non vincolato.
Questa scelta comporta l’abbandono di ogni velleità di ottenere un rendimento positivo dal comparto obbligazionario, in cambio della sicurezza di non ottenerne uno negativo e di avere un asset finanziario – la liquidità – a volatilità nulla e non correlato linearmente con la parte azionaria del portafoglio.
Se la cifra da mantenere liquida supera i 100.000 euro, si va incontro a un altro problema: i conti correnti e i conti deposito sono garantiti dal Fondo interbancario di tutela dei depositi per le banche (FITD) e dal Fondo di garanzia dei depositanti (FGD) per le banche di credito cooperativo fino a 100.000 euro.
Per somme superiori, l’investitore si assume un rischio non da poco perché, in caso di insolvenza della banca, non è detto che riuscirebbe ad avere indietro il suo denaro.
Tenere la liquidità ferma su un conto corrente non è il massimo: si legge ovunque come essa costituisca un costo, a maggior ragione in un periodo di inflazione crescente.
In questo caso, però, essa farebbe parte di una strategia più ampia: sostituendo l’asset obbligazionaria di un Lazy portfolios, questa liquidità avrebbe uno scopo ben preciso. Non si tratterebbe, insomma, di una risorsa improduttiva.
La liquidità potrebbe essere inoltre investita gradualmente al verificarsi di determinate condizioni di mercato.
Una possibile strategia potrebbe essere la seguente:
- Al momento della sottoscrizione degli ETF del Lazy portfolio scelto, la cui parte obbligazionaria viene sostituita dalla liquidità, si prende nota del valore del NAV o dei NAV degli ETF obbligazionari che costituiscono il Lazy portfolio (quelli che sarebbero stati pagati in caso di investimento “classico” in quel portafoglio pigro).
- Ipotizziamo un caso semplice, con un singolo ETF obbligazionario in portafoglio sostituito dalla liquidità: il primo 20% della liquidità viene investito in quell’ETF nel momento in cui il suo valore scende del −2,5%; il secondo 20%, al raggiungimento del −5%; il terzo, del −7,5% e così via fino all’ultimo quinto di liquidità, che viene investito al −12,5%.
Queste percentuali sono esemplificative: dovrebbero essere modificate in base all’importo da investire (se fosse una somma esigua, potrebbero bastare un paio di soglie di entrata) e alla volatilità del sottostante (un ETF obbligazionario monetario non raggiungerà quasi mai il −12,5% e si potrebbe pensare a 5 soglie a partire dal −1% o −1,5%; un ETF High Yield è molto più volatile e le soglie potrebbero essere ampliate a intervalli del −5% o del −7,5%).
L’ingresso sul mercato nel momento in cui il trend è discendente ha dei vantaggi e degli svantaggi.
Vantaggi:
- Si pagano le quote degli ETF obbligazionari meno di quanto sarebbero costate investendo a tempo zero (al momento della sottoscrizione della componente azionaria).
- Se si teme un imminente rialzo dei tassi, l’idea di non investire nell’asset obbligazionaria fin da subito e di farlo quando i prezzi saranno più bassi offre un supporto psicologico all’investitore che, altrimenti, rischierebbe di rimanere liquido con il 100% della somma destinata all’investimento.
Svantaggi:
- Serve tempo per verificare, almeno una volta alla settimana o al mese, il prezzo dell’ETF, per capire se la soglia di ingresso sia stata raggiunta.
- Le diminuzioni dei valori dei NAV potrebbero avvenire in concomitanza con le crisi finanziarie. Quando c’è una crisi finanziaria, tutti i notiziari descrivono scenari catastrofici che diffondono il panico tra gli investitori: quello, però, è proprio il momento in cui l’investitore dovrebbe entrare nel mercato. Non è facile; servono nervi saldi e molta determinazione.
- Non è detto che le soglie di perdita prestabilite vengano raggiunte dagli ETF: la liquidità potrebbe perciò rimanere tale fino alla fine dell’investimento.
Questa strategia è utilizzabile su tutti gli ETF che compongono un Lazy portfolio o sui soli ETF azionari (o che replicano l’oro o un paniere di commodities): non è però consigliabile farlo, dal momento che almeno la parte azionaria del portafoglio dovrebbe iniziare a generare una performance positiva il prima possibile e il ritardo accumulato nell’attesa del raggiungimento delle soglie potrebbe causare una perdita di rendimento anche di molto superiore a quella ottenuta dal ribasso dei NAV degli ETF.
19. La scelta del Lazy portfolio

«The enemy of a good plan is the dream of a perfect plan».
Carl von Clausewitz
Nonostante la mole di informazioni fornite, un investitore potrebbe avere ancora delle difficoltà nella scelta del Lazy Portfolio più adatto a soddisfare le sue esigenze.
Giunti a questo punto, dovrebbe essere chiaro che non esiste il portafoglio pigro migliore in assoluto: ogni persona ha degli obiettivi di investimento diversi e una propensione al rischio diversa; il portafoglio migliore per qualcuno potrebbe non esserlo per altri.
La scelta del Lazy portfolio – o di un portafoglio finanziario in generale – è una delle fasi più delicate e importanti del processo di investimento: se si sbagliasse il portafoglio, le conseguenze potrebbero essere gravi:
- Disinvestimento anticipato.
- Rendimento inferiore alle aspettative o a quello potenzialmente ottenibile in funzione della propensione al rischio dell’investitore.
- Stress psicologico superiore alle aspettative o a quello potenzialmente sostenibile in funzione della propensione al rischio dell’investitore.
Non è questo il contesto per esaminare in profondità tutte le fasi del processo di investimento o proporre un test di autovalutazione psicologica o della propria propensione al rischio: ci limiteremo a dare qualche indicazione su come scegliere il Lazy portfolio, anche perché si presuppone, come abbiamo visto nel capitolo 11, che i Lazy portfolios siano un’ottima soluzione soprattutto per gli investitori evoluti che gestiscono in prima persona i loro portafogli finanziari.
A fini meramente illustrativi, un possibile percorso, in via generale, per individuare un esempio di portafoglio coerente tra quelli esaminati in questo studio è il seguente:
- Comprendere bene i pro e i contro di ciascun Lazy portfolio, nonché le differenze tra loro esistenti: la lettura dei capitoli dal 13.3.1 al 13.3.31 dovrebbe permettere di ottenere questo risultato.
- Identificare la propria propensione al rischio. Per un investitore inesperto è un compito molto difficile: non ha mai sperimentato le sensazioni che si provano quando i mercati finanziari attraversano una grave crisi e il valore corrente del proprio portafoglio è molto inferiore a quello di partenza.
In una situazione del genere, le conoscenze teoriche non sono di alcun aiuto. Come valutare la propensione al rischio è un argomento vasto, che sconfina nella psicologia e non può essere affrontato in questo contesto: partiamo dal presupposto che un investitore intenzionato a seguire l’approccio dei Lazy portfolios sia in grado di valutare correttamente la propria propensione al rischio. - Individuare nel modo più dettagliato possibile le caratteristiche dell’investimento che si vuole effettuare, rispondendo alle seguenti domande:
- Qual è l’intenzione del mio investimento?
- Che somma posso investire e che capitale voglio generare? In quanto tempo?
- La logica conseguenza del punto precedente sarà la definizione dell’orizzonte temporale d’investimento: a volte, sarà in funzione dell’obiettivo prefissato (ad esempio, la costruzione di una pensione integrativa o l’accumulo del capitale necessario per far studiare un figlio all’università una volta raggiunti i 18 anni); altre volte, sarò io a sceglierlo nei limiti del possibile (se, ad esempio, voglio acquistare un appartamento e per raggiungere la somma necessaria all’acquisto devo raddoppiare il mio capitale, sarebbe assurdo fissarsi un orizzonte temporale di un paio di anni).
In merito al secondo punto, può essere utile riprendere la distinzione tra propensione al rischio in senso assoluto e relativo, già incontrata nel capitolo 11: la propensione al rischio in senso assoluto mi aiuta a scegliere il tipo di portafoglio; quella in senso relativo, il tipo di ottimizzazione.
Partiamo dal presupposto che un investitore abbia identificato la propria propensione al rischio assoluta e relativa. Per semplicità, le suddividiamo in bassa, media e alta: unendo queste due informazioni si crea una matrice della propensione al rischio con 9 possibili profili:
Matrice della propensione al rischio
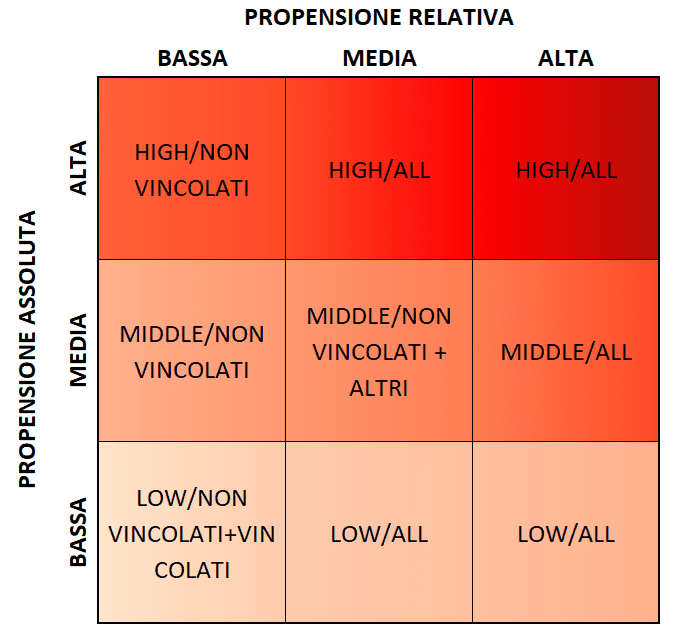
Più lo sfondo è rosso scuro, più alto è il rischio che l’investitore è in grado di assumersi.
Quello che è scritto all’interno di ogni cella della matrice è il nome del gruppo dei Lazy portfolios (propensione assoluta) e dei modelli di ottimizzazione (propensione relativa) dal quale l’investitore può selezionare il portafoglio e il relativo modello in base alla prima delle due heatmaps che seguono:
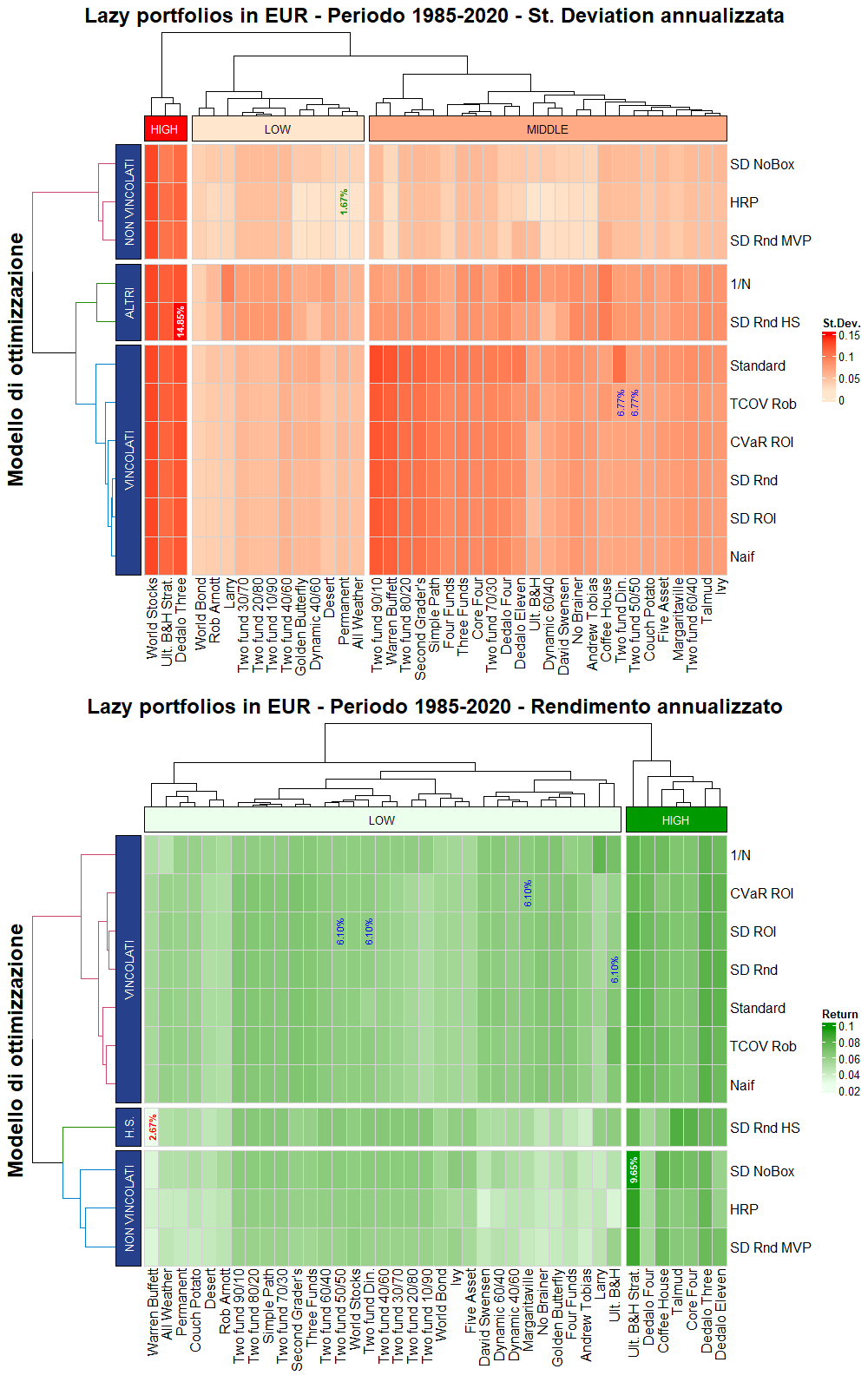
La prima heatmap è quella della deviazione standard annualizzata dei Lazy portfolios in EUR relativi ai backtest della durata più lunga (1985-2020). La seconda heatmap è quella dei rendimenti annualizzati degli stessi portafogli.
Nella heatmap della deviazione standard, l’investitore può verificare quali siano i portafogli che corrispondono alla sua propensione al rischio assoluta e relativa, individuabili nella matrice della propensione al rischio vista in precedenza.
Supponiamo di avere una propensione al rischio assoluta bassa e una propensione al rischio relativa media: in corrispondenza della cella della matrice della propensione al rischio che unisce queste due propensioni al rischio si legge “LOW/ALL”.
“LOW” è il gruppo di Lazy portfolios meno rischiosi in senso assoluto; come si può vedere nella prima heatmap, esso comprende i seguenti portafogli:
- World Bond
- Rob Arnott
- Larry
- Two funds 10/90
- Two funds 20/80
- Two funds 30/70
- Two funds 40/60
- Golden Butterfly
- Dynamic 40/60
- Desert
- Permanent
- All Weather
Effettivamente, tra i Lazy portfolios analizzati questi sono i meno rischiosi. Nello stesso tempo, la rischiosità può variare molto anche all’interno di questo gruppo di portafogli: anche senza scomodare le performance di ciascuno di essi, si intuisce subito che il Two funds 10/90 sarà meno rischioso del Two funds 40/60; il World Bond sarà meno rischioso del Dynamic 40/60 ecc.
“ALL” non è il nome di un gruppo di modelli di ottimizzazione: sta a indicare che un investitore dalla propensione al rischio relativa media potrà selezionare uno qualsiasi dei modelli di ottimizzazione a disposizione.
Alcune considerazioni su cui vale la pena riflettere sono le seguenti:
- Il World Bond Lazy portfolio è composto da un singolo ETF e la sua scelta risolve in partenza il problema dell’individuazione di un modello di ottimizzazione.
- Anche se tutti i modelli sono selezionabili, si può notare che:
- Quelli appartenenti al gruppo “ALTRI” sono i più rischiosi, dal momento che le celle della matrice sono colorate di un rosso un po’ più intenso delle altre.
- Nel gruppo dei “NON VINCOLATI”, invece, i due modelli meno rischiosi sono – come sempre – l’HRP e lo SD Rnd MVP.
- Poche differenze sono presenti tra i modelli “VINCOLATI”, con l’eccezione del modello “Standard” che sembra dimostrarsi più rischioso di tutti gli altri modelli appartenenti allo stesso cluster.
- La combinazione Lazy portfolio/modello di ottimizzazione con la più bassa volatilità è Permanent Lazy portfolio/modello HRP: nella heatmap è riportato in verde il valore 1,67% in corrispondenza della cella che li unisce.
Dopo aver fatto tutte le considerazioni del caso, supponiamo di aver scelto il Two funds 20/80 Lazy portfolio ottimizzato con il modello vincolato CVaR ROI: possiamo adesso verificare, nella heatmap successiva, a quanto corrisponda il rendimento annualizzato generato storicamente da quel Lazy portfolio e dal modello che vorremmo utilizzare.
Il verde poco pronunciato ci dà subito l’idea che non sia molto alto: il valore preciso lo possiamo trovare nella tabella dei risultati del Two funds 20/80 in EUR, visionabile nel capitolo 13.3.3, ed è pari al 5,35%.
Il 5,35% non è male ma va confrontato con la somma che voglio generare (e in quanto tempo), come indicato nel terzo dei quattro passaggi precedenti: se, ad esempio, il mio obiettivo era quello di raddoppiare il capitale in 10 anni, avrò una bassa probabilità di raggiungerlo, dato che il rendimento generato dal 5,35% capitalizzato per 10 anni è pari a circa il 68%.
In questo caso, posso teoricamente muovermi in due direzioni:
- Rivedendo il mio orizzonte temporale: se potesse essere allungato, il mio obiettivo potrebbe essere raggiunto in 13/14 anni (ovviamente più l’orizzonte temporale è lungo, più alta sarà la probabilità di raggiungere il mio obiettivo di investimento).
- Optando per un modello di ottimizzazione o, addirittura, un Lazy portfolio più rischioso che, in passato, abbia generato un rendimento annualizzato superiore: è una strada percorribile ma si sconsiglia di seguirla, perché c’è il serio pericolo di scegliere una combinazione Lazy portfolio/modello di ottimizzazione che non sarà psicologicamente tollerabile (il rischio di un disinvestimento anticipato per eccessivo stress è dietro l’angolo).
Se proprio si vuole andare in questa direzione, è meglio modificare il modello di ottimizzazione, e soltanto in seconda battuta, il Lazy portfolio inizialmente selezionato, facendo comunque attenzione a sceglierne uno appartenente allo stesso gruppo di rischiosità (nel nostro esempio, il gruppo “LOW”).
Non si dovrebbe in alcun modo optare per un Lazy portfolio appartenente a un gruppo di portafogli più rischiosi.
Come effettuare la scelta iniziale tra tutti i Lazy portfolios del gruppo?
Non c’è una regola precisa: se si conoscono bene i portafogli e, già in partenza, si hanno delle preferenze che sono incluse tra le opzioni disponibili, la scelta è conseguente.
È probabile, però, che questo non avvenga. Selezionare il Lazy portfolio più corretto al raggiungimento dell’obiettivo dell’investimento ma che sia anche appropriato alla personalità dell’investitore non è un’operazione semplice e deve essere valutata attentamente: oltre alla procedura descritta in precedenza, un ulteriore aiuto potrebbe arrivare dalla consultazione delle altre heatmaps del capitolo 12.3 e da tutte le misure statistiche presentate nei capitoli dedicati a ciascun Lazy portfolio (capitoli 13.3.1-13.3.31).
Se non si riesce a identificare un singolo portafoglio tra una rosa di candidati composta da poche unità, si consiglia infine di rileggere e approfondire le caratteristiche di ciascuno di essi nei suddetti capitoli, fin quando non si hanno le idee chiare: la formula magica che riesce ad associare a ogni soggetto il Lazy portfolio più adatto purtroppo non esiste ed è compito dell’investitore – in primis – fare tutto il possibile per portare a termine nel migliore dei modi questa fondamentale fase del processo di investimento.
Terminiamo il capitolo con alcune considerazioni:
- Le misure statistiche che abbiamo calcolato sono relative al passato: non è assolutamente detto che, in futuro, si raggiungano gli stessi rendimenti o non vengano superati i valori massimi registrati nelle misure di rischio come la deviazione standard, il massimo drawdown o il CVaR.
Non deve essere mai dimenticato il classico disclaimer che si legge in tutti i siti finanziari e nella contrattualistica di tutti gli strumenti finanziari: i rendimenti passati non sono indicativi di quelli futuri. - Si deve fare particolare attenzione ai modelli di ottimizzazione non vincolati: i pesi delle asset allocation suggerite possono infatti discostarsi molto da quelli standard di ciascun Lazy portfolio.
In particolare, il modello SD NoBox – pur essendo risultato il migliore nelle classifiche pubblicate nel capitolo 12.2 – potrebbe essere rischioso in determinati periodi; degli altri tre, due modelli (HRP e SD Rnd MVP) sono generalmente più conservativi, come descritto nei capitoli 8 e 9; l’altro (Boudt Rnd HS) è imprevedibile e molto rischioso.
Questa procedura di scelta del Lazy portfolio è abbastanza approssimativa ed è soltanto un modo per aiutare l’investitore nella scelta del portafoglio pigro che, potenzialmente, manterrà per molti anni o decenni a venire: di nuovo, questo passaggio è fondamentale e non deve essere completato in modo affrettato o senza capire a fondo ciò che si sta facendo.
Prendetevi il giusto tempo per capire. Il tempo per capire non sarà mai tempo perso. I mercati finanziari non chiudono domani.
Entrare sul mercato oggi, o tra un mese o due, non cambierà di molto il rendimento finale del vostro investimento.
Potrebbe però fare la differenza tra riuscire a completarlo o interromperlo prematuramente: questo sì che avrà un impatto enorme sul rendimento finale.
20. Conclusioni

«Il pensiero è indefinito in entrambe le direzioni: non conosce conclusioni ultime, né princìpi primi».
Nicolás Gómez Dávila
Concludiamo questo lavoro sui Lazy portfolios così come l’avevamo iniziato: riflettendo sul fatto che, mentre nella società attuale la pigrizia è una caratteristica che sminuisce l’essere umano, negli investimenti finanziari l’approccio pigro è una vera e propria filosofia di investimento.
Purtroppo, in Italia i Lazy portfolios sono ancora poco conosciuti e utilizzati.
Le convinzioni sbagliate in materia di investimenti finanziari sono molte diffuse tra gli investitori e, forse, anche tra molti consulenti finanziari.
Il conflitto di interessi è un problema di cui abbiamo già accennato, ma non è il solo motivo per cui i consulenti consigliano strumenti finanziari costosi: la causa è da ricercarsi anche nella bassa qualità della consulenza finanziaria.
Uno studio del 2018, pubblicato nell’articolo The Misguided Beliefs of Financial Advisors ("Le convinzioni sbagliate dei Consulenti Finanziari"), ha analizzato i comportamenti di 4.407 consulenti finanziari canadesi tra gennaio 1999 e dicembre 2013.
Le informazioni relative ai loro conti personali e a quelli dei loro clienti sono state diffuse da due società appartenenti al Canadian Mutual Fund Dealers (MFDs) che, complessivamente, gestiscono circa il 5% di tutti gli asset del settore.
Di questi 4.407 consulenti, l’indagine si è concentrata sui 3.276 che detenevano il proprio portafoglio d'investimento presso le stesse società di consulenza per cui lavoravano e su 488.263 clienti attivi (non necessariamente in modo continuativo) di età compresa tra 32 e 67 anni nell'arco dei 15 anni analizzati.
La conclusione della ricerca è sorprendente: i consulenti finanziari gestiscono i loro investimenti in linea con ciò che raccomandano ai loro clienti. Dato che, come lo studio dimostra, sia i consulenti che i loro clienti hanno generato un alpha annuale netto del −3%, i risultati ottenuti sono innanzitutto l'espressione dell'utilizzo di strumenti finanziari costosi come i fondi a gestione attiva sia da parte dei consulenti che dei loro clienti.
In altre parole, la qualità della consulenza è bassa non o non soltanto a causa del conflitto di interessi, ma soprattutto per colpa di alcune convinzioni sbagliate in materia di investimenti, ancora molto radicate negli stessi consulenti finanziari:
- Active management: i consulenti finanziari raccomandano soprattutto costosi fondi a gestione attiva perché sono convinti che la gestione attiva sia superiore a quella passiva. La dimostrazione ce la fornisce il fatto che loro stessi utilizzano la gestione attiva per i propri investimenti. Ma c'è di più: viene esclusa la possibilità che il vero scopo sia quello di generare fiducia nei clienti, magari mostrando loro i portafogli utilizzati per convincerli a fare lo stesso. Anche quando i consulenti cessano di essere tali, infatti, continuano a far uso degli stessi costosi strumenti finanziari.
- Underdiversification: sia i portafogli dei consulenti finanziari che quelli dei loro clienti sono poco diversificati.
- Return chasing: sia i consulenti che i loro clienti utilizzano strategie di investimento finalizzate all'ottenimento di rendimenti più alti di quelli del mercato: switchano in continuazione i fondi meno performanti con quelli dai rendimenti più alti.
Il return chasing non è altro che una forma di market timing.
Se è vero che la realtà canadese di 10-20 anni fa potrebbe essere diversa da quella italiana odierna, il problema del conflitto di interessi e della scarsa cultura finanziaria è molto vivo ancora oggi.
Di certo, i rendimenti medi degli investitori italiani (e non solo) sono di alcuni punti percentuali inferiori a quelli del mercato e, secondo le ultime statistiche disponibili per il mercato statunitense, il gap tra il rendimento dell’investitore medio nel mercato azionario e quello del mercato è aumentato nella prima metà del 2021.
Studi simili vengono portati avanti da DALBAR, Inc. dal 1984 e uno di questi ci dice che tra il 1° gennaio 1998 e il 31 dicembre 2017 il rendimento dell’investitore medio nel mercato azionario è stato del 5,29%; quello dell’indice S&P 500, del 7,20%.
In Italia, è probabile che le cose non siano andate e non vadano affatto meglio.
Utilizzando i Lazy portfolios, gli investitori avrebbero ottenuto gli stessi rendimenti del mercato: lo sola differenza sarebbe stata ascrivibile alle (basse) spese correnti degli ETF.
Non è azzardato affermare che i pochi soggetti che hanno utilizzato questo approccio di investimento abbiano con molta probabilità ottenuto dei rendimenti superiori a quelli della stragrande maggioranza degli investitori.
I Lazy portfolios sono una strategia di investimento passiva, ma non per questo non richiedono una profonda analisi e una lunga serie di decisioni – tutte molto importanti – che l’investitore deve prendere prima di iniziare il proprio investimento:
- Quanto voglio rischiare? In quali percentuali di azionario e di obbligazionario devo dividere il mio portafoglio?
- Voglio aggiungere l’oro o altre commodities al mio portafoglio? Se sì, perché? Quali sono i vantaggi e quali sono i rischi? Se no, perché?
- Quanto rischio valutario voglio assumermi? Che percentuale del mio portafoglio voglio investire senza coprire il cambio? Perché?
- Se sono già in possesso della liquidità da investire, preferisco investirla in un’unica soluzione o attraverso un Piano di Accumulo del Capitale a rate costanti (Cost Averaging) o Value Averaging?
- Se non sono già in possesso della liquidità da investire, è opportuno che risparmi e investa mensilmente una quota delle mie entrate? Se sì, perché e in che percentuale? Se no, perché?
- In base ai miei obiettivi d’investimento, preferisco utilizzare strumenti finanziari ad accumulazione o a distribuzione dei proventi? Perché?
- Quanti strumenti finanziari voglio inserire nel mio portafoglio? Perché non di più o di meno?
- Ogni quanto tempo voglio ribilanciare il portafoglio? Preferisco ribilanciare soltanto quando uno o più ETF raggiungono determinate soglie di rendimento? Perché?
- Che modello di ottimizzazione dei pesi voglio utilizzare? Preferisco un modello statico o uno dinamico? Per quale ragione?
- Perché il mio investimento ha la potenzialità di generare un rendimento? Di quale entità e in quanto tempo?
- Quali sono le possibili conseguenze di un disinvestimento anticipato?
- Se decido di utilizzare un approccio di investimento pigro, quale Lazy portfolio preferisco e perché?
- Voglio dedicare una piccola percentuale del mio capitale a investimenti alternativi o particolarmente speculativi come le criptovalute? Se sì, perché? Quali sono i rischi che mi assumo? Se no, perché?
- È bene che inizi a investire subito o è meglio aspettare un momento più favorevole?
- Con quale frequenza devo controllare l’andamento del mio investimento?
- Qual è l’ammontare del fondo di liquidità che, per sicurezza, devo costituire prima di investire? Perché non di più o di meno?
- Se ho dei debiti o un mutuo, vale la pena rimborsarli – magari parzialmente – con la liquidità che ho a disposizione invece di investirla?
- Mi sento in grado di rispondere a tutte queste domande oppure ho bisogno del supporto di un consulente finanziario?
- In quest’ultimo caso, da che tipo di consulente finanziario voglio farmi assistere e quale modalità di pagamento preferisco utilizzare? Perché?
Tutte queste domande sono fondamentali e non esistono risposte facili, scontate o valide per tutti gli investitori.
Eliminare lo stock picking e il market timing non implica, come alcuni credono, l’assenza di scelte soggettive nel processo di investimento.
La scelta di un approccio passivo e di un Lazy portfolio adatto alle proprie esigenze è solo un primo passo – per quanto molto importante – in direzione di una semplificazione del processo di investimento.
21. Bibliografia

«I libri sono l’alimento della giovinezza e la gioia della vecchiaia».
Marco Tullio Cicerone
Alexander, Market Risk Analysis, Volume II: Practical Financial Econometrics, Wiley, 2008.
Arnott, Hsu, West, The Fundamental Index: A Better Way to Invest, Wiley, 2008.
Babylonian Talmud, Tractate Baba Mezi'a, Baba Mezi'a 42a.
Benartzi, Thaler, Naive Diversification Strategies in Defined Contribution Saving Plans, The American Economic Review, Vol. 91, no. 1, 2001, pp. 79-98.
Bennett, Custom Moment and Objective Functions, April 18, 2015.
Bernstein, The Intelligent Asset Allocator: How to Build Your Portfolio to Maximize Returns and Minimize Risk, McGraw-Hill Education, 2017.
Boudt, Lu, Peeters, Higher Order Comoments of Multifactor Models and Asset Allocation, Finance Research Letters, 13, 2014, pp. 225-233.
Browne, Fail-Safe Investing: Lifelong Financial Security in 30 Minutes, St. Martin's Press, 1999.
Burns, Random Portfolios for Performance Measurement, in Kontoghiorghes, Gatu (Editors), Optimisation, Econometric and Financial Analysis, Springer, 2010, pp. 227-249.
Canova, Modelling and forecasting exchange rates with a Bayesian time-varying coefficient model, Journal of Economic Dynamics and Control, 17, 1993, pp. 233-261.
Collins, The Simple Path to Wealth, CreateSpace Independent Publishing Platform; 1st edition (2016).
Dalbar, Inc., 2017 Quantitative Analysis of Investor Behavior report.
Dalbar, Inc., 2021 mid-year update, Quantitative Analysis of Investor Behavior report.
Demiguel, Garlappi, Uppal, Optimal Versus Naive Diversification: How Inefficient is the 1/N Portfolio Strategy?, Review of Financial Studies, Vol. 22, Issue 5, 2009, pp. 1915-1953.
Duchin, Levy, Markowitz Versus the Talmudic Portfolio Diversification Strategies, Journal of Portfolio Management, Winter 2009, pp. 71-44, pubblicato in versione più ampia in Guerard, Handbook of Portfolio Construction, pp. 97-123.
Engel, Mark, West, Exchange rate models are not as bad as you think, NBER Macroeconomics Annual 2007, Volume 22, pp. 381-441, National Bureau of Economic Research, Inc.
Escobar, Mitterreiter, Saunders, Seco, Zagst, Market Crises and the 1/N Asset-Allocation Strategy, Journal of Investment Strategy, Vol. 2, 2013, pp. 1-23.
Faber, The Ivy Portfolio: How to Invest Like the Top Endowments and Avoid Bear Markets, Wiley, 2013.
Gibson, Asset Allocation: Balancing Financial Risk, McGraw-Hill Education; 5th edition (2013).
Hauptmann, Zagst, Hoppenkamps, Min, Ramsauer, Forecasting market turbulence using regime-switching models, Financial Markets and Portfolio Management, Vol. 28, 2014, pp. 139-164.
Hsu, Han, Wu, Cao, Asset allocation strategies, data snooping, and the 1/N rule, Journal of Banking & Finance, Vol. 97, 2018, pp. 257-269.
Kilian, Taylor, Why is so difficult to beat the random walk forecast of exchange rates?, European Central Bank, Working Paper No. 88, November 2001.
Kremnitzer, Comparing Active and Passive Fund Management in Emerging Markets, Senior Honors Thesis, Spring 2012, Economics Department, University of California, Berkeley.
Kritzman, Page, Turkington, In Defense of Optimization: The Fallacy of 1/ N, Financial Analysts Journal, Vol. 66, no. 2, 2010, pp. 31-39.
Lam, Fung, Yu, Comparing Forecast Performance of Exchange Rate Models, Hong Kong Monetary Authority, Working Paper 08/2008, June 2008.
Linnainmaa, Melzer, Previtero, The Misguided Beliefs of Financial Advisors, May 16, 2018, Kelley School of Business, Research Paper No. 18-9.
Lopez de Prado, Advances in Financial Machine Learning, Wiley (2018).
Lopez de Prado, Machine Learning for Asset Managers, Cambridge University Press (2020).
Mankiw, It May Be Time for the Fed to Go Negative, April 18, 2009.
Marçal, Hadad Junior, Is It Possible to Beat the Random Walk Model in Exchange Rate Forecasting? More Evidence for Brazilian Case, March 3, 2015.
Markowitz, Portfolio Selection, The Journal of Finance, Vol. 7, No. 1, 1952, pp. 77-91.
McLaren, Five reasons to use an active fund manager in emerging markets, 1 July 2020.
Meese, Rogoff, Empirical exchange rate models of the seventies: Do they fit out of sample?, Journal of International Economics, Volume 14, Issues 1-2, February 1983, pp. 3-24.
Merriman, Buck, Financial Fitness Forever: 5 Steps to More Money, Less Risk, and More Peace of Mind, McGraw-Hill Education, 2012.
Merriman, Live It Up Without Outliving Your Money! Getting the Most from Your Investments in Retirement, Wiley, 2008.
Meucci, Fully flexible views: Theory and practice, Journal of Risk, Vol.21, No.10, October 2008, pp. 97-102.
Moosa, Burns, The unbeatable random walk in exchange rate forecasting: Reality or myth?, Journal of Macroeconomics, 40, 2014, pp. 69-81.
Peterson, Carl, Boudt, Bennett, Varon, Yollin, Douglas Martin, Package ‘PortfolioAnalytics’, February 6, 2020.
Rashid, Do exchange rates follow random walks? An application of Variance-Ration Test, Pakistan Economic and Social Review, Volume XLIV, No. 1, Summer 2006, pp. 57-79.
Ripley, Venables, Bates, Hornik, Gebhardt, Firth, Package ‘MASS’, September 9, 2020.
Rossi, Exchange Rate Predictability, Journal of Economic Literature, Vol. 51, No. 4, December 2013, pp. 1063-1119.
Ruppert, Matteson, Statistics and Data Analysis for Financial Engineering, Springer; 2nd ed., 2015.
Schulthies, The Coffeehouse Investor: How to Build Wealth, Ignore Wall Street, and Get On with Your Life, Portfolio, 2013.
Slater, The Vanguard Experiment: John Bogle's Quest to Transform the Mutual Fund Industry, McGraw-Hill Education, 1996.
Swedroe, Grogan, Reducing the Risk of Black Swans: Using the Science of Investing to Capture Returns with Less Volatility, Buckingham (2018 edition).
Swedroe, The Only Guide to a Winning Investment Strategy You'll Ever Need, St. Martin’s Press, Revised edition (2005).
Swensen, Pioneering Portfolio Management: An Unconventional Approach to Institutional Investment, Free Press, Revised and updated edition (2009).
Swensen, Unconventional Success: A Fundamental Approach to Personal Investment, Free Press (2005).
Tenreyro, Let’s talk about negative rates, Speech at the UWE Bristol webinar, 2021.
Tobias, The Only Investment Guide You’ll Ever Need, Mariner Books, 2016.
Tu, Zhou, Markowitz Meets Talmud: A Combination of Sophisticated and Naïve Diversification Strategies, Journal of Financial Economics, Vol. 99, Issue 1, January 2011, pp. 204-215.
VanEck, The Case for Active Management in Emerging Markets, March 2017.
Zani, Cerioli, Analisi dei dati e data mining per le decisioni aziendali, Giuffré, 2007.
Il Percorso intermedio continua con l'articolo:


