Causal Factor Investing
- Information
- Strategie di investimento
- Prima pubblicazione: 11 Gennaio 2026 Stampa
«Meno comprendiamo un fenomeno, più variabili cerchiamo per spiegarlo».
Russell L. Ackoff
Questo articolo fa parte del Percorso avanzato, pensato per investitori già esperti e professionisti che vogliono approfondire gli sviluppi teorici e le applicazioni pratiche della finanza moderna. In fondo alla pagina, troverai il link al prossimo articolo del percorso.
Negli ultimi decenni, nella finanza quantitativa e più in generale nel mondo degli investimenti si è affermata una strategia nota come factor investing.
Il suo obiettivo è quello di individuare fattori sistematici – come ad esempio value, momentum o size – in grado di spiegare i rendimenti degli asset e, potenzialmente, di generare una performance superiore rispetto al mercato.
Questa indagine, condotta in modo quasi ossessivo, ha dato origine a una tale proliferazione di presunti fattori che l’economista John Cochrane, con una celebre metafora, l’ha definita Factor zoo.
Nel saggio Causal Factor Investing: Can Factor Investing Become Scientific?, Marcos López De Prado riprende e affina questa immagine con una provocazione ancora più incisiva, parlando di un bestiario dei fattori: mentre uno zoo raccoglie creature reali, un bestiario medievale mescolava senza distinzione animali autentici e figure mitologiche come chimere, grifoni e arpie.
Secondo De Prado, gran parte della letteratura sul factor investing potrebbe basarsi su illusioni statistiche, miraggi nati da una persistente confusione tra correlazione e causalità.
L’intento del suo lavoro è promuovere una vera maturazione epistemologica della disciplina, trasformandola da un approccio prevalentemente descrittivo e fenomenologico a una scienza fondata sui principi dell’inferenza causale.
L'autore invita a compiere un salto di qualità intellettuale: distinguere i fattori autentici da quelli immaginari e costruire strategie d’investimento basate su fondamenta scientifiche.
Questo articolo ha uno scopo essenzialmente divulgativo: presentare e discutere i contenuti principali di Causal Factor Investing di Marcos López De Prado, un lavoro che considero fondamentale e profondamente innovativo nel dibattito contemporaneo sul factor investing.
Credo sia opportuna una breve avvertenza per i lettori: l'articolo è piuttosto lungo e richiede un certo impegno. Chi fosse interessato principalmente alla discussione sul factor investing può iniziare la lettura dal quarto capitolo, dove il tema entra nel vivo.
Detto questo, una lettura completa e non affrettata resta fortemente consigliata: molti passaggi, soprattutto quelli legati all’inferenza causale, non sono immediati e richiedono una certa gradualità.
Per chi conosce già l’argomento e ha maturato una posizione sul factor investing, la lettura potrebbe risultare scomoda. In questo caso, l’impegno richiesto può essere persino maggiore, perché alcune tesi mettono in discussione convinzioni consolidate.
Prima di addentrarci nel contenuto, è infine doveroso chiarire un aspetto metodologico: tutto il merito dell’analisi presentata in questo articolo è del Prof. Marcos López De Prado o di altri autori citati. Gli eventuali errori di interpretazione o di traduzione delle loro idee sono, invece, da imputare esclusivamente al sottoscritto.
Ogni commento o analisi non direttamente riconducibile al pensiero di De Prado sarà opportunamente segnalato. In particolare, le mie riflessioni personali sono concentrate nel settimo capitolo.
Indice
- Associazione vs causalità
- Isolare causa ed effetto nei dati finanziari
- L'equivoco della causalità in econometria
- La causalità nel factor investing
- Mettere alla prova l'econometria con esperimenti controllati
- Le conclusioni di De Prado
- Causal Factor Investing: riflessioni personali
1. Associazione vs causalità
In questo capitolo, esploreremo i fondamenti della distinzione tra associazione e causalità, indispensabile per una corretta lettura dei dati e per la costruzione di strategie di investimento più solide.
Un celebre aforisma dell'economista statunitense Thomas Sowell ricorda che "Uno dei primi concetti insegnati nei manuali introduttivi di statistica è che la correlazione non implica causalità. Ed è anche uno dei primi che viene dimenticato".
Il monito “la correlazione non implica causalità” rappresenta uno dei fondamenti della statistica: eppure, la finanza quantitativa lo ha spesso disatteso.
Per comprendere appieno la portata di questo errore, è necessario chiarire in modo formale la differenza tra questi due concetti.
Due variabili, \(X\) e \(Y\), sono associate quando la conoscenza di una fornisce informazioni sulla probabilità che si verifichi l’altra. In termini matematici, ciò avviene quando la probabilità congiunta che si verifichino \(X\) e \(Y\) non coincide con il prodotto delle loro probabilità individuali:
\begin{equation}
P(X, Y) \ne P(X) \cdot P(Y)
\end{equation}
Partiamo dalla definizione di indipendenza per capire il perché.
Due variabili casuali, \(X\) e \(Y\), si dicono indipendenti se la conoscenza di una non cambia la probabilità di osservare l'altra.
In tal caso, la probabilità congiunta si scompone nel prodotto delle probabilità individuali:
\begin{equation}
P(X, Y) = P(X) \cdot P(Y)
\end{equation}
Quando due eventi sono indipendenti, il verificarsi di \(X\) è completamente scollegato dal verificarsi di \(Y.\)
Di conseguenza, se la conoscenza di \(X\) ci permette, anche solo in parte, di prevedere \(Y\), allora \(X\) e \(Y\) non sono indipendenti. In questo caso, \(P(X,Y) \neq P(X)\cdot P(Y).\)
Un esempio classico, citato proprio da De Prado, è la relazione osservata tra le vendite di gelati \((X)\) e il numero di annegamenti \((Y)\) nel corso dell’anno.
Nei periodi in cui le vendite di gelati aumentano, si registra anche un numero più elevato di annegamenti. Si tratta di una semplice associazione, rilevata tramite l’osservazione passiva dei dati.
Immaginiamo di raccogliere i seguenti dati su 100 giorni:
| Numero di giorni | Fa caldo (Z) | Vendite gelato (X) | Annegamenti (Y) |
|---|---|---|---|
| 60 | Sì | Alte | Sì |
| 40 | No | Basse | No |
Calcoliamo ora le probabilità:
\begin{equation}
P(X = \text{Alte}) = \frac{60}{100} = 0,6 \qquad P(Y = \text{Sì}) = \frac{60}{100} = 0,6
\end{equation}
Se \(X\) e \(Y\) fossero indipendenti, la probabilità congiunta sarebbe pari al prodotto delle probabilità marginali:
\begin{equation}
P(X = \text{Alte},\ Y = \text{Sì}) = P(X = \text{Alte}) \cdot P(Y = \text{Sì}) = 0,6 \times 0,6 = 0,36
\end{equation}
Nei dati, osserviamo invece che in 60 giorni su 100, quando le vendite di gelati sono alte, si verifica anche un annegamento, per cui:
\begin{equation}
P(X = \text{Alte},\ Y = \text{Sì}) = 0,6
\end{equation}
E, poiché 0,6 ≠ 0,36, i due eventi non sono indipendenti, ma associati: sapere che le vendite di gelato sono alte aumenta la probabilità di osservare un annegamento.
La causalità si colloca invece su un piano concettuale completamente diverso. Non descrive ciò che accade simultaneamente, ma ciò che accadrebbe se intervenissimo attivamente sul sistema.
Per formalizzare questa idea, il pioniere dell’inferenza causale Judea Pearl ha introdotto uno strumento teorico di grande utilità: il do-operator.
L’espressione \(do(X = x)\) non indica l’osservazione passiva di \(X\) che assume un certo valore, ma rappresenta l’azione di imporre quel valore, indipendentemente dalle sue cause naturali.
In questo senso, una variabile \(X\) è causa di \(Y\) se, e solo se, un intervento su \(X\) modifica la probabilità di \(Y\):
\begin{equation}
P(Y \mid do(X = x)) \ne P(Y)
\end{equation}
Applicando questo principio al nostro esempio, la distinzione appare evidente: se un’autorità sanitaria imponesse il divieto di vendere gelati, ovvero \(do(Vendite Gelato=0)\), nessuno si aspetterebbe una riduzione del numero di annegamenti.
La relazione tra i due fenomeni non è causale: si tratta di una correlazione spuria, generata dalla presenza di una terza variabile nascosta, un confounder (confondente), che in questo caso è la stagione calda \((Z).\)
È infatti il caldo a determinare, in modo indipendente, sia l’aumento delle vendite di gelati sia la maggiore frequentazione di spiagge e piscine, da cui deriva un rischio più elevato di annegamenti.
Per rappresentare e comprendere le relazioni tra variabili, l’inferenza causale si serve di strumenti grafici noti come Directed Acyclic Graphs (DAGs), o grafi causali.
In queste mappe concettuali, le variabili sono rappresentate come nodi, collegati da frecce orientate che indicano la presenza e la direzione di una relazione causale.
Nel nostro esempio, il grafo causale mostrerebbe una freccia che parte dal Caldo \((Z)\) e punta sia verso le vendite di gelato \((X)\) che verso gli annegamenti \((Y).\) Non vi sarebbe invece alcuna freccia da \(X\) a \(Y\), perché l’aumento delle vendite di gelato non causa direttamente gli annegamenti: entrambi i fenomeni sono semplicemente influenzati dalla temperatura elevata.
L’intervento \(do(X=x)\) viene rappresentato graficamente eliminando tutte le frecce entranti nel nodo \(X\), in modo che \(X\) non sia più influenzato dalle sue cause originarie, ma assuma il valore stabilito esclusivamente dall’intervento.
Una volta reciso il collegamento tra \(Z\) e \(X\), scompare ogni percorso che collega \(X\) a \(Y\), rendendo evidente – in modo intuitivo e immediato – l’assenza di un nesso causale tra i due eventi.
In termini formali, l’intervento si esprime come:
\begin{equation}
P(Y \mid do(X = x)) = P(Y)
\end{equation}
Una volta imposto il valore di \(X\), la probabilità di \(Y\) rimane invariata: non esiste dunque una relazione causale tra \(X\) e \(Y.\)
Il quadro teorico evidenzia la fragilità intrinseca del factor investing tradizionale: fondandosi esclusivamente su dati osservativi, non è in grado di distinguere una relazione realmente causale da una semplice correlazione spuria, destinata a svanire non appena cambiano le condizioni ambientali o i regimi di mercato.
Un nuovo metodo scientifico per l’investimento
Come può un investitore passare dalla semplice osservazione di un pattern statistico alla comprensione di un meccanismo causale?
Marcos López De Prado propone di adottare un approccio rigoroso, articolato in tre fasi, che ricalca il metodo della scoperta scientifica.
1. LA FASE FENOMENOLOGICA
Il percorso inizia con la fase fenomenologica, quella della pura osservazione.
In questa fase, il ricercatore individua un’anomalia o un pattern ricorrente che sembra contraddire teorie consolidate come, ad esempio, l’ipotesi dei mercati efficienti.
Si potrebbe osservare, in via ipotetica, che un marcato squilibrio tra ordini di acquisto e di vendita (order flow imbalance) tenda a precedere un allargamento del bid-ask spread e un aumento della volatilità.
Questo primo passo si fonda su un ragionamento induttivo: "Poiché è accaduto così in passato, presumo che accadrà di nuovo".
Ed è proprio a questo livello che gran parte della ricerca finanziaria tende a fermarsi: alla semplice constatazione di un’associazione empirica, senza compiere il salto verso l’identificazione del meccanismo causale sottostante.
2. LA FASE TEORICA
Il secondo passo rappresenta il vero salto qualitativo: la costruzione di una teoria causale. In questa fase, si passa dalla semplice descrizione alla formulazione di un meccanismo esplicativo testabile, capace di rendere conto del fenomeno osservato.
Non ci si limita più a dire che “\(X\) e \(Y\) sono associati”, ma si avanza un’ipotesi strutturata del tipo:
\begin{equation}
X \longrightarrow M \longrightarrow Y
\end{equation}
ovvero, “\(X\) causa \(Y\) attraverso un meccanismo intermedio \(M.\)”
Questo tipo di inferenza è abduttiva: un termine poco comune ma che indica semplicemente il processo con cui, partendo dall’osservazione, si formula l’ipotesi più plausibile tra quelle possibili.
Nel nostro esempio, De Prado suggerisce di far riferimento alla teoria PIN (Probability of Informed Trading), che propone una narrazione causale coerente e verificabile:
- i trader informati generano uno squilibrio negli ordini (order flow imbalance);
- tale squilibrio comporta delle perdite per i market maker;
- i market maker, per proteggersi, allargano il proprio bid-ask spread;
- uno spread più ampio riduce la liquidità del mercato, aumentando la volatilità.
Una teoria, per essere scientifica, deve essere falsificabile: deve cioè generare previsioni specifiche che possano essere smentite dai dati.
Come ricordava il fisico Wolfgang Pauli, infatti, una teoria che non rischia mai di essere confutata non è nemmeno sbagliata: è sterile dal punto di vista scientifico.
3. LA FASE DI FALSIFICAZIONE
Il terzo momento è quello della falsificazione, cuore pulsante del metodo scientifico.
In questa fase, la comunità di ricerca – operando in modo indipendente – tenta attivamente di confutare la teoria proposta, in linea con l’idea, resa celebre da Karl Popper, che una teoria sia scientifica solo se espone sé stessa al rischio di essere smentita dai dati.
Il ragionamento segue la logica del modus tollens, formalmente esprimibile come:
\begin{equation}
A \Rightarrow B, \quad \neg B \Rightarrow \neg A
\end{equation}
cioè: “Se la teoria \(A\) implica necessariamente la conseguenza \(B,\) e \(B\) non si verifica, allora \(A\) deve essere rigettata o profondamente rivista”.
Per testare la teoria PIN, è possibile adottare diverse strategie: condurre un esperimento controllato quando le condizioni lo consentono, sfruttare un esperimento naturale, cioè un evento esogeno che generi flussi di ordini casuali, oppure verificare le previsioni più rischiose della teoria, quelle che difficilmente potrebbero confermarsi per semplice coincidenza.
Un esempio di questo terzo approccio riguarda i modelli derivati dalla teoria PIN, come il VPIN, che segnalarono un crescente rischio di crisi di liquidità poco prima del Flash Crash del 2010.
Si tratta di un’evidenza empirica rilevante, per quanto non definitiva, che mostra come una teoria causale ben formulata possa produrre previsioni sorprendentemente efficaci in contesti reali.
Questo esempio non intende dimostrare in modo conclusivo la validità della teoria PIN, ma illustrare in che modo il metodo scientifico – osservazione, formulazione di un meccanismo causale e tentativi di confutazione – possa essere applicato allo studio dei mercati finanziari.
È proprio questa impostazione a segnare un cambio di paradigma rispetto al factor investing tradizionale, come evidenziato nella tabella seguente:
| Caratteristica | Factor Investing Tradizionale | Causal Factor Investing |
|---|---|---|
| Obiettivo principale | Identificare associazioni statistiche (correlazioni) tra fattori e rendimenti. | Identificare meccanismi causali che spiegano i rendimenti. |
| Logica dominante | Induzione (“funzionerà perché ha funzionato in passato”). | Deduzione e abduzione (“funzionerà perché il meccanismo causale è stato testato”). |
| Strumenti chiave | Regressione, backtesting, analisi statistica su dati osservativi. | Inferenza causale, grafi causali (DAG), do-operator, esperimenti reali o naturali. |
| Risultato | Un “bestiario” di fattori, molti dei quali spuri e instabili. | Un insieme selezionato di teorie robuste e falsificabili. |
| Vulnerabilità | Elevata sensibilità a data mining, overfitting e cambiamenti di regime. | Maggiore robustezza strutturale grazie alla comprensione dei meccanismi sottostanti. |
L’approccio del Causal Factor Investing rappresenta una rivoluzione epistemologica nella finanza quantitativa, che reinterpreta l’attività d’investimento alla luce dei principi del metodo scientifico.
La sua adozione non è però priva di ostacoli, dato che richiede:
- Competenze interdisciplinari che vadano oltre la statistica classica.
- Dati di qualità, adatti alla verifica di ipotesi causali.
- Un deciso abbandono della mentalità orientata al puro backtesting.
I vantaggi potenziali sono però considerevoli. Le strategie fondate su meccanismi causali compresi e verificati sono più robuste, trasparenti e meno esposte ai rischi del data mining.
Il messaggio che si vuole trasmettere agli investitori è il seguente: affidarsi a un fattore senza testarne la logica causale equivale a navigare a vista, sperando che il vento non cambi mai direzione.
Il contributo di Marcos López De Prado ci invita dunque a porre domande più profonde e a costruire risposte più solide, per realizzare portafogli che siano il risultato di una decisione consapevole e scientificamente fondata sul funzionamento reale dei mercati.
2. Isolare causa ed effetto nei dati finanziari
Nel complesso mondo degli investimenti, come in molte altre sfere decisionali, tendiamo a dare per scontato che se compio una determinata azione, mi aspetto un determinato risultato.
Ma siamo certi che questo legame sia robusto?
Molte volte, ciò che consideriamo una relazione di causa ed effetto è solo una coincidenza, un riflesso statistico generato da variabili nascoste.
Distinguere tra correlazione e causalità rappresenta il nucleo dell’inferenza causale, la disciplina che fornisce strumenti logici e statistici per andare oltre le apparenze e individuare i veri fattori che regolano i sistemi complessi.
De Prado esamina attentamente questa problematica, offrendo una guida metodologica per orientarsi tra le insidie dei dati osservazionali.
L’obiettivo è comprendere se e quando un fenomeno ne causa un altro, un passaggio essenziale per sviluppare strategie di investimento solide, basate su una comprensione causale e approfondita delle dinamiche dei mercati finanziari.
Il problema fondamentale dell’inferenza causale
Per comprendere ciò che è in gioco nell’analisi causale, è utile partire dal suo obiettivo ideale: ciò che il ricercatore intende stimare è l’Average Treatment Effect (ATE), ossia l’effetto causale medio che un "trattamento" \(X\) esercita su un "risultato" \(Y.\)
In altri termini, si vuole determinare cosa accadrebbe, in media, se fosse possibile applicare un determinato intervento a un’intera popolazione e confrontare l’esito con quello che si osserverebbe in assenza dello stesso intervento.
Grazie all’introduzione del do-operator da parte di Judea Pearl, che consente di rappresentare formalmente un intervento attivo sul sistema, l’Average Treatment Effect può essere descritto come la differenza tra due scenari ipotetici: nel primo, tutta la popolazione riceve il trattamento \(x_1;\) nel secondo, riceve invece \(x_0,\) ossia la condizione in cui il trattamento non viene applicato.
In termini matematici, l’ATE è dato dalla differenza tra il valore atteso di \(Y\) quando si interviene imponendo \(X=x_1,\) e il valore atteso di \(Y\) quando si impone \(X=x_0.\)
\begin{equation}
ATE = E[Y \mid do(X = x_1)] - E[Y \mid do(X = x_0)]
\end{equation}
Il problema è che, nel mondo reale, questi due scenari non possono verificarsi contemporaneamente: questo avviene perché si dispone quasi esclusivamente di dati osservazionali, in cui i gruppi si formano spontaneamente senza un intervento controllato.
Di conseguenza, invece dell’ATE, ciò che si osserva è soltanto la differenza tra le medie dei gruppi che, per ragioni indipendenti dalla volontà del ricercatore, hanno ricevuto o meno il trattamento.
De Prado mostra che la differenza osservata nei dati non coincide con l’effetto causale puro, ma può essere scomposta in due componenti: l’ATT (Average Treatment effect on the Treated), cioè l’effetto del trattamento su chi lo ha ricevuto, e l’SSB, il Self-Selection Bias.
Quest’ultimo rappresenta la distorsione che nasce dal fatto che i gruppi “trattati” e “non trattati” non sono equivalenti fin dall’inizio: differiscono per caratteristiche che, se ignorate, falsano la stima dell’effetto causale.
Per esempio, se gli individui che scelgono spontaneamente un trattamento sono, in media, più motivati o più istruiti degli altri, una parte del risultato attribuito al trattamento rifletterà in realtà queste differenze pregresse, non l’effetto del trattamento stesso.
Con questa distinzione in mente, possiamo formalizzare la scomposizione della differenza osservata:
\begin{equation}
\text{Differenza Osservata} = ATT + SSB
\end{equation}
L'ATT è la componente di reale interesse nell’analisi causale. La seconda componente, l’SSB (Self-Selection Bias), è ciò che impedisce di misurarlo correttamente.
Come già anticipato, questo termine si riferisce alle differenze preesistenti tra i due gruppi: differenze che non sono dovute al trattamento, ma a fattori che influenzano sia la probabilità di ricevere \(X,\) sia l’esito \(Y.\)
In sostanza, l’SSB quantifica quanto i gruppi fossero già diversi fin dall’inizio.
Per comprendere appieno questo concetto, è necessario introdurre la nozione di controfattuale, cioè lo scenario alternativo che, per definizione, non possiamo osservare.
Il nucleo dell’inferenza causale sta proprio in questa impossibilità: non possiamo sapere cosa sarebbe accaduto agli individui che hanno ricevuto il trattamento se non lo avessero ricevuto.
È come voler osservare due universi paralleli, in cui la stessa persona vive simultaneamente due condizioni diverse: poiché questo scenario è impossibile, siamo costretti a confrontare gruppi diversi di individui.
Se, però, questi gruppi differiscono già prima del trattamento, nasce il Self-Selection Bias. L’esempio delle vendite di gelato e degli annegamenti rende particolarmente chiaro questo concetto.
La forte correlazione osservata tra le due variabili non riflette un effetto causale del consumo di gelato (l’ATT è praticamente nullo), ma è spiegata quasi interamente da un SSB elevato dovuto alla presenza di un confounder, cioè di un fattore confondente: il clima caldo \((Z).\)
È infatti il caldo a determinare sia l’aumento delle vendite di gelato \((X)\) che una maggiore frequentazione di spiagge e piscine \((Y),\) generando così un’associazione spuria tra le due variabili.
L’inferenza causale si configura quindi come l’arte – e la scienza – di identificare, stimare e correggere il Self-Selection Bias.
Una volta chiarito il ruolo del Self-Selection Bias, resta da capire come neutralizzarlo per isolare la relazione causale.
De Prado non propone una soluzione unica, ma un insieme di strategie organizzate in una gerarchia basata sulla solidità delle assunzioni e sulla loro applicabilità nei contesti reali.
Le tre vie per isolare la causalità
Ciascuna delle strategie che seguono presenta punti di forza, limiti e condizioni di applicabilità. Considerate nel loro insieme, queste soluzioni forniscono strumenti per stimare l’effetto causale in modo più affidabile.
1. STUDI INTERVENTISTICI: i Randomized Controlled Trial (studi controllati randomizzati)
La via più immediata per eliminare il Self-Selection Bias consiste nello stabilire a priori chi riceve il trattamento.
È questo il principio alla base degli studi interventistici, il cui modello di riferimento è il Randomized Controlled Trial (RCT), molto diffuso in ambito medico.
L’idea è abbastanza intuitiva: invece di limitarsi a osservare gruppi che si formano spontaneamente, il ricercatore li crea assegnando i partecipanti in modo casuale al gruppo di trattamento o a quello di controllo.
La randomizzazione funziona come una sorta di “livella statistica”: quando il campione è abbastanza grande, rende i due gruppi simili in media per tutte le caratteristiche, sia quelle visibili sia quelle che non possiamo misurare.
Proprio questa simmetria permette di attribuire eventuali differenze negli esiti esclusivamente al trattamento, isolandone così l’effetto causale.
Da un punto di vista matematico, la randomizzazione elimina le differenze preesistenti tra i gruppi. In termini di scomposizione dell’effetto osservato, ciò significa che il Self-Selection Bias (SSB) tende a scomparire:
\begin{equation}
SSB \longrightarrow 0
\end{equation}
Di conseguenza, la differenza osservata tra i due gruppi diventa una stima diretta e non distorta dell’effetto causale medio (ATE):
\begin{equation}
ATE = E[Y \mid do(X = x_1)] - E[Y \mid do(X = x_0)]
\end{equation}
Purtroppo, questo criterio ideale è difficilmente applicabile in ambito finanziario.
I Randomized Controlled Trial, infatti, sono quasi sempre impraticabili: non sarebbe etico assegnare a un gruppo di investitori strategie potenzialmente rischiose, né sarebbe economicamente o logisticamente possibile randomizzare interventi su larga scala, come una politica monetaria.
2. ESPERIMENTI NATURALI: una fonte di quasi-randomizzazione
Quando non è possibile applicare una randomizzazione diretta, la seconda possibilità consiste nell’individuare situazioni in cui è il contesto stesso a produrre una sorta di randomizzazione naturale.
È questo il principio degli esperimenti naturali (o quasi-esperimenti), che sfruttano eventi o regole esterne – come ad esempio modifiche normative o circostanze casuali – in grado di creare due gruppi comparabili.
Questo tipo di approccio richiede un’attenta analisi del contesto: occorre riconoscere quei casi in cui un evento esogeno o una decisione amministrativa ha suddiviso la popolazione in gruppi che, almeno in media, sono simili in tutto tranne che per il trattamento ricevuto.
Tra i metodi più utilizzati in questo ambito rientrano:
- Regression Discontinuity Design (RDD): sfrutta l’esistenza di una soglia oggettiva (ad esempio, un punteggio minimo per ottenere un beneficio) per confrontare individui appena sopra e appena sotto la soglia. Questi due gruppi sono considerati, in media, simili in tutto tranne che per il trattamento.
- Difference-in-Differences (DiD): confronta l’evoluzione nel tempo di un gruppo che riceve il trattamento con quella di un gruppo di controllo simile, assumendo che, in assenza del trattamento, i due gruppi avrebbero seguito un andamento parallelo.
Si tratta di strumenti molto validi, ma entrambi si fondano su un presupposto non sempre facile da verificare direttamente: l’idea che l’assegnazione al trattamento sia as if random, cioè “come se” fosse avvenuta in modo casuale.
3. INTERVENTI SIMULATI: i grafi causali (DAG) come mappa delle relazioni causali
Quando non si dispone né di un Randomized Controlled Trial né di un esperimento naturale affidabile – la situazione più comune in finanza e nelle scienze sociali, dove i dati emergono da scelte individuali e da processi non controllabili – si ricorre alla terza via: gli interventi simulati basati sui grafi causali.
Qui la randomizzazione non viene cercata nei dati, ma la si introduce in modo formale, costruendo un modello esplicito delle relazioni causali attraverso un grafo causale (DAG), cioè un grafo orientato e privo di cicli.
In un grafo causale:
- I nodi rappresentano le variabili coinvolte.
- Le frecce indicano la direzione delle relazioni causali ipotizzate.
Vediamo un semplice esempio:
\begin{equation}
X \longrightarrow Y
\end{equation}
In questo schema, \(X\) è interpretato come la causa e \(Y\) come l’effetto. La freccia indica una relazione causale direzionale: un cambiamento in \(X\) può produrre un cambiamento in \(Y,\) mentre non vale il contrario.
Rappresentare la relazione in questo modo significa dichiarare apertamente quale meccanismo causale si sta assumendo, invece di lasciarlo implicito nei risultati statistici.
Una volta esplicitate le ipotesi nel grafo causale, è possibile applicare il do-calculus: un insieme di regole che permette di analizzare la struttura causale del grafo e calcolare l’effetto di un intervento simulato.
L’obiettivo è quello di chiudere tutti i percorsi spuri (backdoor paths, generati da variabili esterne al rapporto causale) e mantenere aperti soltanto i percorsi causali validi.
Per farlo, è essenziale distinguere tre tipi di variabili:
- Confounder (variabile confondente): influenza sia il trattamento \(X\) sia l’esito \(Y,\) creando un’associazione spuria tra le due variabili. Un classico esempio è, di nuovo, il caldo, che aumenta sia le vendite di gelati sia la frequentazione di spiagge e piscine e, indirettamente, il numero di annegamenti.
- Mediator (mediatore): si trova sul percorso causale tra \(X\) e \(Y,\) trasmettendo l’effetto di \(X\) su \(Y\) (ad esempio, \(X \longrightarrow Z \longrightarrow Y\)). Controllare per il mediatore significa bloccare quel percorso, ottenendo una stima dell’effetto causale che esclude proprio la parte di effetto che si vuole misurare.
- Collider (variabile di collisione): riceve due frecce da variabili diverse (ad esempio, \(X \longrightarrow Z \longleftarrow Y\)). Un collider chiude il percorso tra \(X\) e \(Y\) in un grafo causale. In assenza di interventi, impedisce qualsiasi flusso informativo tra le due variabili. Il problema nasce quando si “condiziona” sul collider, cioè quando si filtrano o analizzano i dati in base al suo valore. In questo caso il percorso si apre artificialmente e può comparire una correlazione inesistente.
Un esempio classico di collider bias riguarda il mondo del cinema. Nella popolazione, bellezza e talento sono indipendenti.
Eppure, se consideriamo soltanto gli attori famosi, la situazione cambia. La fama, infatti, può essere raggiunta sia grazie alla bellezza sia grazie al talento: è quindi un collider, perché riceve due frecce in un grafo causale:
\begin{equation}
Bellezza \longrightarrow Fama \longleftarrow Talento
\end{equation}
Se consideriamo solo gli attori famosi (cioè se condizioniamo sulla fama), accade che:
- Chi è diventato famoso pur non essendo particolarmente bello, deve aver compensato con molto talento.
- Chi è diventato famoso pur avendo poco talento, deve aver compensato con una bellezza sopra la media.
Il risultato è un’associazione negativa tra bellezza e talento che non esiste nella popolazione generale: nasce un legame apparente, creato non da un meccanismo causale, ma dal criterio stesso con cui abbiamo selezionato i dati.
Il collider bias è un errore insidioso e difficile da individuare, perché può introdurre correlazioni inesistenti anche quando i dati sembrano ben strutturati.
All’interno di questo quadro, il do-calculus mette a disposizione diverse tecniche per stimare effetti causali anche utilizzando dati puramente osservazionali. Tra le principali, abbiamo:
- Backdoor adjustment: consiste nel "chiudere" i percorsi causali indiretti tra due variabili controllando per le cause comuni (i confounder noti), così da isolare il legame causale diretto tra \(X\) e \(Y.\)
Esempio: per stimare l’effetto dell’attività fisica sulla salute cardiovascolare è necessario controllare per l’età, che influisce su entrambe le variabili. - Front-door adjustment: sfrutta una variabile intermedia (mediatore) osservabile per stimare un effetto causale anche quando esistono confounder (cause comuni) non osservabili.
Esempio: per stimare l’effetto del fumo sul rischio di cancro ai polmoni, la quantità di catrame nei polmoni può fungere da mediatore: dipende solo dal fumo e permette di ricostruire l’effetto complessivo anche in presenza di confounder nascosti (predisposizione genetica, stato socio-economico, stile di vita, condizioni lavorative e così via). - Variabili strumentali: si utilizza una variabile esterna che influenza il trattamento \(X\) ma non l’esito finale \(Y\) se non attraverso il trattamento stesso, così da sfruttare una variazione "quasi causale" di \(X\) per stimarne l'effetto causale.
Esempio: la distanza da un centro di formazione può fungere da variabile strumentale perché influisce sulla probabilità di partecipare a un certo corso: a parità di caratteristiche personali, chi vive più vicino tende a iscriversi più facilmente, mentre per chi vive lontano la partecipazione è meno probabile. Questa differenza nella partecipazione è determinata da un fattore esterno e non da una scelta legata al reddito futuro. Poiché la distanza, di per sé, non incide direttamente sul reddito, la variazione “quasi causale” nella partecipazione al corso permette di stimare in modo più affidabile l’effetto causale della formazione sul reddito.
Dal punto di vista formale, questi metodi consentono di eliminare il Self-Selection Bias (SSB) e di stimare l’effetto causale anche in assenza di dati sperimentali, purché le ipotesi alla base del modello causale siano corrette.
Valutazione e implicazioni pratiche: il prezzo della conoscenza
I metodi presentati permettono di affrontare il Self-Selection Bias in modo rigoroso, ma non senza compromessi.
I Randomized Controlled Trial devono la loro forza alla randomizzazione, che riduce drasticamente le ipotesi necessarie. Gli interventi simulati, invece, dipendono interamente dalla correttezza del grafo causale ipotizzato: si tratta di un’assunzione sostanziale, perché un modello causale impreciso porta inevitabilmente a conclusioni errate.
Si profila così un trade-off tra la solidità delle evidenze e il peso delle assunzioni richieste:
- I Randomized Controlled Trial sono molto affidabili, ma trovano scarsa applicazione in ambito finanziario.
- Gli interventi simulati sono più flessibili e utilizzabili, ma si basano su ipotesi esplicite sulla struttura causale dei dati.
In altre parole, il prezzo da pagare per fare inferenza causale senza ricorrere a esperimenti reali è la trasparenza: occorre dichiarare apertamente le proprie ipotesi – di norma tramite un grafo causale (DAG) – e riconoscere che la solidità delle conclusioni dipende direttamente dalla correttezza di tali ipotesi.
Per chi opera nei mercati, le implicazioni sono notevoli. Anche una comprensione solo concettuale di questi meccanismi aiuta a evitare interpretazioni fuorvianti e favorisce il passaggio da una mentalità centrata sulla predizione a una focalizzata sulla comprensione dei processi che generano i dati.
Di fronte a una correlazione elevata, l'analista attento dovrebbe sempre domandarsi:
- Esiste un fattore nascosto – un confounder \(Z\) – che può spiegare il legame osservato?
- Sto, magari senza accorgermene, creando un’illusione statistica “condizionando” su un collider?
Adottare questa prospettiva causale può trasformare il modo in cui si interpretano le informazioni e si prendono decisioni. È un percorso che richiede rigore, spirito critico e la disponibilità a rendere esplicite le proprie assunzioni.
Il beneficio, però, è una comprensione più strutturata e affidabile a supporto di decisioni più consapevoli ed efficaci.
3. L'equivoco della causalità in econometria
Nonostante sia ben noto che correlazione e causalità non sono la stessa cosa, la prassi econometrica più diffusa – quella insegnata nei manuali e applicata quotidianamente – continua a operare in un’area di incertezza permanente.
Il quinto capitolo di Causal Factor Investing, intitolato Causality in Econometrics, è particolarmente illuminante in questo senso.
La critica che viene mossa è che molta econometria contemporanea produca stime associative formalmente corrette, che nella pratica vengono caricate di un significato causale non esplicitato, generando un cortocircuito logico che mette in dubbio la solidità delle conclusioni ottenute.
Il capitolo si apre con un’affermazione volutamente provocatoria, sulla scia delle conclusioni di uno studio di Chen e Pearl: molti manuali di economia trascurano i più recenti standard dell’analisi causale e, talvolta, negano esplicitamente che i modelli econometrici abbiano un significato causale.
Secondo De Prado, questa ambiguità è alla radice di numerosi fraintendimenti che caratterizzano buona parte della ricerca economica, in particolare nei campi dell’asset pricing e del factor investing.
La freccia nascosta nella regressione OLS
Il primo e più evidente esempio di questa confusione riguarda lo strumento probabilmente più utilizzato in econometria: la regressione ai minimi quadrati (OLS).
A prima vista, una regressione sembra descrivere un’associazione simmetrica tra due variabili, \(X\) e \(Y.\) Se ciò fosse vero, invertendo le variabili e stimando un modello in cui \(X\) viene spiegato da \(Y,\) ci si aspetterebbe di ottenere coefficienti coerenti con quelli del modello originale.
Ad esempio, se stimiamo:
\begin{equation}
Y_t = \beta_0 + \beta_1 X_t + \varepsilon_t
\end{equation}
e, successivamente:
\begin{equation}
X_t = \gamma_0 + \gamma_1 Y_t + \zeta_t
\end{equation}
dovremmo attenderci che il coefficiente \(γ_1\) sia l'inverso di \(β_1.\)
In realtà, chiunque abbia provato a invertire le variabili in un’analisi OLS sa bene che questa simmetria non si verifica.
Questa incoerenza matematica è un segnale d’allarme: mostra che, contrariamente a quanto si insegna, la regressione OLS non è uno strumento neutrale.
Già nel momento in cui si scrive \(Y=f(X),\) si introduce implicitamente una direzione: si traccia una freccia causale da \(X\) a \(Y.\) Questa assunzione diventa ancora più evidente osservando il ruolo del termine di errore \(\varepsilon.\)
Nel modello OLS, la condizione fondamentale per ottenere una stima non distorta di \(β_1\) è l'esogeneità, espressa come:
\begin{equation}
E[\varepsilon \mid X] = 0
\end{equation}
Questa condizione viene spesso interpretata, in modo riduttivo, come “l’errore non è correlato con \(X\)”. In una prospettiva causale, però, il suo significato è molto più vincolante.
Con il termine esogeneità si assume infatti che il termine di errore \(\varepsilon\) – che raccoglie tutte le determinanti di \(Y\) non incluse nel modello – sia indipendente dalla variabile \(X,\) considerata come possibile causa.
In altri termini, si sta postulando che non esistano fattori non osservati che influenzino simultaneamente sia \(X\) che \(Y.\)
L'esogeneità, quindi, è un’ipotesi causale sostanziale: equivale a supporre che \(X\) sia stato assegnato in modo "quasi casuale" rispetto a tutte le altre cause di \(Y.\) Si tratta di un presupposto che, nei dati economici osservazionali, raramente trova riscontro.
Se invece l’obiettivo fosse semplicemente descrivere un’associazione simmetrica tra due variabili, bisognerebbe ricorrere a metodi alternativi come la regressione ortogonale o la regressione di Deming, che ammettono errori su entrambe le variabili.
Il nodo della questione è che lo strumento principale dell’econometria incorpora un'inclinazione causale fin dalla sua stessa formulazione: caratteristica che viene di rado esplicitata.
Nella formazione degli economisti, l’uso di strumenti causali moderni come i grafi causali o il do-calculus di Pearl è molto trascurato.
Di conseguenza, la scelta delle variabili da includere in un modello finisce talvolta per essere affidata a procedure automatiche prive di un reale fondamento teorico, come la selezione stepwise.
Con questa espressione si indicano metodi che aggiungono o rimuovono variabili dal modello in modo iterativo, sulla base di criteri puramente statistici – ad esempio il miglioramento dell’\(R^2,\) la riduzione di un criterio informativo o la significatività dei coefficienti – senza fare riferimento a una teoria sul funzionamento causale del fenomeno studiato.
Questi metodi reagiscono più alle peculiarità contingenti dei dati che a una struttura causale ben definita, con il risultato di modelli fragili e facilmente soggetti a distorsioni.
La mancanza di una prospettiva causale nella fase di costruzione del modello conduce a un secondo problema, forse ancora più insidioso: l’ambiguità nell’interpretazione dei risultati.
Se il modello incorpora un’ipotesi causale non dichiarata, come vanno interpretati i coefficienti stimati?
L’ambiguità del coefficiente beta: associazione o causa?
Questa confusione si manifesta in maniera evidente quando si interpreta il coefficiente di regressione, il celebre \(\beta.\)
Qual è il significato di questo valore?
Esistono due interpretazioni della condizione di esogeneità, molto diverse tra loro e raramente esplicitate:
- Esogeneità implicita (interpretazione associativa). In questo caso, l’errore \(\varepsilon\) viene definito come la differenza tra il valore osservato \(Y\) e la previsione basata su \(X.\) Con questa definizione, la condizione \(E[\varepsilon \mid X] = 0\) risulta automaticamente soddisfatta: è una tautologia matematica. In questo contesto, \(\beta\) non ha alcun significato causale: è semplicemente la pendenza della retta di regressione, cioè una misura di un’associazione lineare. Non risponde alla domanda fondamentale: “Cosa accadrebbe a \(Y\) se modificassi attivamente \(X\)?”
Questa è l’interpretazione prudente, generalmente riportata nei manuali. - Esogeneità esplicita (interpretazione causale). Qui non si definisce l’errore a posteriori: si assume a priori che il modello \(Y = X\beta + \varepsilon\) descriva una relazione causale. L'errore \(\varepsilon\) raccoglie tutte le altre cause di \(Y\) e si assume che queste siano indipendenti da \(X.\)
Si tratta di un’ipotesi forte sulla struttura del sistema: solo se è valida, \(\beta\) può essere interpretato come un vero effetto causale. In tal caso, \(\beta\) misura la variazione attesa di \(Y\) in seguito a una variazione unitaria di \(X,\) mantenendo costanti tutte le altre influenze.
È la formalizzazione del famoso principio del ceteris paribus, espressa come:
\begin{equation}
\beta = \frac{\partial E[Y \mid \text{do}(X)]}{\partial x}
\end{equation}
Il problema, come osserva De Prado riprendendo un’intuizione di Haavelmo – vincitore del premio Nobel per l'Economia nel 1989 – è che gli economisti si trovano in una posizione contraddittoria.
La teoria insegnata loro si concentra principalmente sull’interpretazione debole e associativa del coefficiente \(\beta;\) nella pratica, però, \(\beta\) viene spesso trattato come un indicatore causale: ad esempio, per proporre politiche economiche o delineare strategie di investimento.
Si finisce così per utilizzare modelli che presuppongono una direzione causale implicita, interpretando i risultati come se riflettessero veri rapporti di causa-effetto, mentre la formazione teorica tende a ricondurli a semplici associazioni statistiche.
Questa ambiguità di fondo genera il rischio di arrivare a conclusioni fuorvianti e di basare decisioni operative su presupposti non adeguatamente giustificati.
Le implicazioni pratiche sono notevoli: un coefficiente \(\beta\) che riflette una pura associazione osservata nel passato può essere utile per la previsione in contesti relativamente stabili; risulta però del tutto inadeguato quando si tratta di valutare l’effetto di una nuova politica economica o di una nuova strategia di investimento, che costituiscono veri e propri interventi sul sistema.
Per affrontare questo tipo di valutazioni è necessario disporre di un \(\beta\) realmente causale. La sua stima impone di affrontare in modo esplicito – e di motivare – l’assunzione di esogeneità, un passaggio che nella pratica viene quasi sempre trascurato.
Il caso della “causalità” di Granger: un nome improprio
L’ambiguità interpretativa si estende anche ad altri strumenti molto utilizzati nell'analisi delle serie storiche, come la cosiddetta "causalità” di Granger.
Questo test, ampiamente diffuso in finanza, verifica se i valori passati di una variabile \(X\) aiutino a prevedere i valori attuali di una variabile \(Y,\) anche dopo aver considerato i valori passati di \(Y.\)
Se ciò accade, si dice che “\(X\) Granger-causa \(Y\)”.
Il testo non esita a definire la causalità di Granger un misnomer, cioè un nome improprio e potenzialmente fuorviante. Diversi sono infatti i problemi che si manifestano quando questo strumento viene interpretato in senso causale:
- La precedenza temporale non implica causalità. Il semplice fatto che un evento preceda un altro non garantisce un rapporto causale. L’esempio classico è il canto del gallo che precede e “prevede” il sorgere del sole, ma non ne è la causa: far tacere il gallo non impedirà al sole di sorgere. Allo stesso modo, il test di Granger non misura l’effetto di un intervento su \(X.\)
- Vulnerabilità ai confounder. Se esiste una variabile nascosta \(Z\) che influenza sia \(X\) che \(Y,\) il test di Granger può rilevare una relazione che sembra causale ma non lo è affatto.
- Problemi di specificazione. La scelta del numero di ritardi da includere nel modello è, di solito, arbitraria e può modificare radicalmente i risultati.
- Assunzione di linearità. Il test presuppone che la relazione tra le variabili sia lineare, una condizione che raramente descrive fedelmente i fenomeni reali.
Di conseguenza, la causalità di Granger misura la predittività sequenziale, non la causalità in senso proprio: indica se \(X\) sia utile per prevedere \(Y,\) ma non se rappresenta la sua causa.
Ciononostante, nella figura sottostante, riportata anche da De Prado, si può apprezzare il grande numero di citazioni dell’articolo originale di Granger, con un massimo di 2.392 nel 2022:
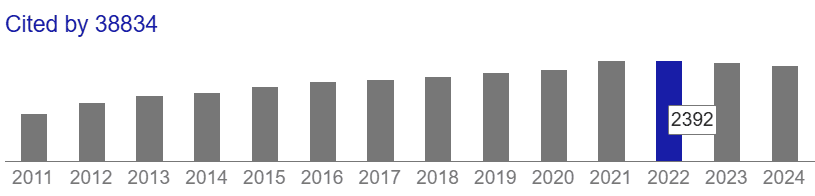
Numero di citazioni dell'articolo di Granger "Investigating Causal Relations by Econometric Models and Cross-Spectral Methods". Fonte: Google Scholar (visitato il 12 dicembre 2025)
Il test di Granger continua a essere largamente utilizzato, spesso in modo improprio, anche nella letteratura sul factor investing.
La sua popolarità rivela quanto sia ancora diffusa la confusione tra prevedibilità e causalità. È uno strumento comodo, perché algoritmico e semplice da applicare, ma evita di porsi la domanda più importante: qual è il meccanismo che collega \(X\) e \(Y?\)
In assenza di una risposta a questo interrogativo, i risultati del test restano un esercizio statistico, privo di un reale contenuto esplicativo.
Un futuro più rigoroso: la rivoluzione della credibilità
Nonostante la severità della critica, il capitolo non si chiude con un tono pessimistico: viene infatti riconosciuto il ruolo di quegli economisti che, in controtendenza, hanno introdotto un approccio causale più solido nelle scienze sociali.
De Prado cita le variabili strumentali di P.G. Wright (1928), Haavelmo sul significato del coefficiente \(\beta\) (1944), fino agli autori contemporanei come Joshua Angrist, Guido Imbens e David Card, tutti premi Nobel per l'Economia nel 2021.
Questi studiosi hanno promosso l’uso di esperimenti naturali, regression discontinuity design e altre metodologie concepite per avvicinarsi, per quanto possibile, alla logica dell’esperimento controllato. Da questo filone di ricerca ha preso forma la cosiddetta “rivoluzione della credibilità” in economia.
Nonostante questi progressi, rimane un nodo irrisolto: ambiti come l’asset pricing e il factor investing sembrano ancora estranei a questo approccio più rigoroso.
In queste discipline si fa ancora ampio ricorso a correlazioni, associazioni e test come quello di Granger, senza chiedersi: “\(X\) causa davvero \(Y\)?”
De Prado richiama anche il celebre articolo di Leamer del 1983, Let’s Take the Con Out of Econometrics – dove con allude all’inganno, spesso involontario, di presentare come causali risultati che sono in realtà solo associativi – per ricordare quanto sia persistente, in finanza, l’errore di confondere correlazione e causalità.
Il messaggio conclusivo è un invito a cambiare paradigma. La matematica stessa dei modelli econometrici contiene assunzioni causali implicite: ignorarle significa costruire teorie su basi fragili o, peggio, prendere decisioni d’investimento fondate su relazioni puramente statistiche e prive di un fondamento causale.
Occorre quindi ribaltare l’ordine delle operazioni: prima, definire la struttura causale del fenomeno – anche mediante un grafo che ne rappresenti le relazioni – e, solo dopo, scegliere il modello statistico più adatto a stimare l’effetto causale che si intende analizzare.
È la teoria causale che deve guidare l’analisi empirica, non il contrario.
Questa è l’essenza dell’inferenza causale moderna: un approccio che, pur ancora poco diffuso nella pratica finanziaria, rappresenta la via più solida per costruire una conoscenza credibile.
4. La causalità nel factor investing
Dopo aver evidenziato le ambiguità causali che permeano l’econometria, Marcos López De Prado arriva al fulcro della sua tesi nel sesto capitolo, Causality in Factor Investing.
In queste pagine, mostra come la persistente confusione tra associazione e causalità abbia prodotto una disciplina dalle fondamenta fragili, segnata da numerose false scoperte.
Il capitolo aiuta anche a capire perché molte strategie di factor investing, pur apparendo solide nei backtest, finiscano per deludere nella pratica.
L’analisi invita a ripensare sia il modo in cui le strategie vengono costruite, sia le ragioni per cui le si considera efficaci.
Le assunzioni causali implicite del factor investing
Il factor investing si basa sull’idea di ottenere esposizione a caratteristiche misurabili (i cosiddetti “fattori”) ritenute in grado di spiegare i rendimenti.
Tuttavia, come osserva De Prado, questa pratica – pur affondando le radici nella letteratura accademica sull’asset pricing – incorpora un significato causale che raramente viene dichiarato o giustificato.
In molti casi, i ricercatori non dichiarano le assunzioni causali che orientano le loro scelte modellistiche. Eppure queste assunzioni, consapevoli o meno, sono sempre presenti.
De Prado individua almeno quattro modi in cui il “contenuto causale” di una strategia factor-based diventa evidente:
- La scelta del modello. Optare per una regressione OLS per modellare i rendimenti \(Y\) in funzione di un fattore \(X\) – invece di ricorrere a tecniche di machine learning più efficaci in termini di previsione – rivela un intento preciso: prevedere \(Y,\) ma anche isolare e quantificare l’impatto di \(X.\) È una scelta che presuppone implicitamente una struttura causale del tipo \(X \longrightarrow Y.\)
- La priorità all’interpretazione. I ricercatori di fattori preferiscono stimatori non distorti, come l’OLS (in presenza delle opportune condizioni), rispetto a modelli predittivi più performanti ma meno interpretabili (come le reti neurali) o a modelli che accettano un po’ di bias per ridurre la varianza (come Ridge o LASSO).
Questa preferenza per la “purezza” del coefficiente \(\beta\) mostra che l’obiettivo principale è stimare un effetto causale, non costruire il modello predittivo più accurato. - L'enfasi sul test di ipotesi. Attribuire centralità ai p-value e alla verifica dell’ipotesi nulla \(H_0 : \beta = 0\) contro l’alternativa \(H_1 : \beta \neq 0\) è tipico di chi intende affermare un legame causale.
Chi fosse interessato unicamente alla previsione valuterebbe invece la rilevanza di una variabile attraverso metriche di tipo associativo, come la riduzione dell’errore di previsione, senza basarsi sull’esito di un test di significatività. - La costruzione dei portafogli. Gli investitori che adottano una strategia fattoriale costruiscono portafogli per ottenere un’esposizione “pura” a un singolo fattore \(X\) (per esempio, long su titoli value e short su titoli growth), con l'obiettivo di isolare e sfruttare una relazione ritenuta causale tra quel fattore e i rendimenti.
Un investitore orientato esclusivamente alla previsione seguirebbe invece una logica diversa. Utilizzerebbe il modello per stimare i rendimenti attesi complessivi dei singoli titoli e costruirebbe il portafoglio direttamente sulla base di tali previsioni, senza preoccuparsi di separare o interpretare il contributo delle singole variabili. In questo caso, ciò che conta è l’accuratezza predittiva finale del modello, non l’identificazione dell’effetto di un fattore specifico.
Un esempio può aiutare a capire meglio questa differenza. Si consideri un modello che utilizza più variabili – come value, momentum e volatilità – per stimare i rendimenti azionari.
L’investitore fattoriale, convinto che il fattore value abbia un ruolo causale, costruisce un portafoglio che privilegia sistematicamente le azioni value e penalizza quelle growth, anche se nel breve periodo alcune azioni growth presentano previsioni di rendimento più elevate. L’obiettivo è quello di mantenere un’esposizione coerente a un fattore che si ritiene remunerato nel tempo.
L’investitore orientato alla previsione, al contrario, utilizza lo stesso modello per ordinare i titoli in base al rendimento atteso complessivo e acquista semplicemente quelli con le previsioni migliori, indipendentemente dal fatto che tali previsioni derivino dal value, dal momentum o da una combinazione delle variabili. In questo caso, il portafoglio riflette una previsione, non una specifica ipotesi causale.
La distinzione è sostanziale: nel primo approccio si investe sulla base di una causa presunta; nel secondo, sulla base di una previsione, senza che a quest’ultima sia attribuito un significato causale.
L’intero impianto del factor investing – dalla scelta del modello all’interpretazione dei risultati, fino all’allocazione del capitale – riflette l’intento di stimare e sfruttare un effetto causale di \(X\) su \(Y.\)
Il problema principale è che questa intenzione causale rimane quasi sempre implicita e, soprattutto, non viene giustificata in modo esplicito.
Di rado i ricercatori chiariscono il grafo causale che sostiene le loro analisi, privando così la comunità scientifica della possibilità di discutere, valutare o confutare le assunzioni di base.
Così facendo, si opera in una sorta di vuoto teorico, in cui la matematica econometrica viene applicata in modo meccanico, senza una reale riflessione sulla coerenza tra il modello e la realtà che si intende descrivere.
Questa dissonanza tra la pratica e la teoria dichiarata rappresenta la radice di un problema strutturale: se non si è disposti a esplicitare e motivare le premesse causali di un modello, come si può avere fiducia nei risultati che produce?
È qui che affonda le sue radici la difficoltà del factor investing nel generare risultati robusti e capaci di superare la prova del tempo.
L’illusione delle spiegazioni economiche e i due tipi di “falso”
Numerosi articoli sul factor investing propongono spiegazioni economiche che appaiono plausibili per giustificare i fattori individuati.
Un esempio ricorrente nella letteratura è l’interpretazione del premio del fattore value come compenso per una maggiore esposizione a rischi di distress o di deterioramento delle condizioni economico-finanziarie dell’impresa.
Secondo De Prado, però, queste spiegazioni raramente raggiungono lo status di vere teorie scientifiche.
Mancano infatti di tre elementi fondamentali:
- Non esplicitano un meccanismo causale preciso e falsificabile.
- Non descrivono l’esperimento ideale che permetterebbe di testarlo.
- Non indicano un metodo per stimare l’effetto causale dai dati osservazionali quando un esperimento diretto non è realizzabile.
Questa carenza di rigore scientifico alimenta la proliferazione di fattori spuri, che De Prado suddivide in due categorie, ciascuna con origini e conseguenze differenti.
La comprensione di tale distinzione è essenziale, perché i due tipi di errore richiedono rimedi completamente diversi.
Spuriosità di tipo A: scambiare rumore per segnale
Si tratta dell’errore più noto, tipico delle pratiche di data mining. Si verifica quando un ricercatore, dopo numerosi tentativi, interpreta una fluttuazione casuale (rumore) come un vero pattern statistico (segnale).
Le cause principali sono il p-hacking – la ricerca selettiva di specificazioni che producano p-value significativi – e l’overfitting nei backtest, cioè la costruzione di strategie perfettamente adattate al passato ma prive di reale capacità predittiva.
Questo errore genera falsi positivi: illusioni statistiche destinate a dissolversi man mano che si accumulano nuovi dati. Fortunatamente, l'errore può essere contenuto applicando procedure rigorose di aggiustamento per test multipli.
Spuriosità di tipo B: scambiare associazione per causalità
Si tratta dell’errore più sottile e, secondo De Prado, anche il più insidioso. Si verifica quando il ricercatore individua un’associazione statistica reale e persistente, ma la interpreta erroneamente come una relazione causale.
A differenza dell’errore di tipo A, qui l’associazione esiste davvero e, con l’aumentare della dimensione campionaria, la significatività si rafforza, consolidando la convinzione del ricercatore.
Purtroppo, tale associazione non deriva da un legame diretto \(X \longrightarrow Y,\) ma da una struttura causale più complessa, spesso determinata da variabili omesse.
La spuriosità di tipo B non può essere corretta con aggiustamenti statistici: richiede un’integrazione di conoscenze extra-statistiche, ovvero una teoria ben fondata e la costruzione di un grafo causale appropriato.
È proprio questo il problema più serio del factor investing, perché dà origine a modelli che appaiono solidi sul piano statistico ma sono, in realtà, concettualmente fragili.
Una volta individuata la spuriosità di tipo B come il vero avversario, l’analisi si sposta sulle sue cause operative: se l’errore nasce da una discrepanza tra il modello statistico e la struttura causale del fenomeno, in che modo i ricercatori finiscono per specificare i modelli in modo scorretto?
I "peccati capitali" della modellazione: under-controlling e over-controlling
La spuriosità di tipo B nasce quasi sempre da una specificazione errata del modello, cioè dall’inclusione o dall'esclusione impropria di alcune variabili.
L’analisi causale moderna, grazie ai grafi, ha messo in evidenza i due peccati capitali nella scelta delle variabili di controllo, entrambi con conseguenze potenzialmente gravi.
1. Under-controlling: l’omissione di un confounder
È l’errore più intuitivo: non includere nel modello una variabile \(Z\) che rappresenta una causa comune sia del fattore \(X\) sia dei rendimenti \(Y\) (un confounder).
Omettere questa variabile genera una stima distorta dell’effetto di \(X\) su \(Y,\) poiché il coefficiente \(\beta\) finisce per riflettere non solo l’effetto causale reale, ma anche l’associazione spuria indotta da \(Z.\)
De Prado mostra come questa omissione possa avere due effetti negativi per l’investitore:
- Errata attribuzione della performance. L’investitore crede di essere esposto solo al rischio del fattore \(X,\) ma in realtà assume anche il rischio legato al confounder nascosto \(Z.\) La performance attribuita al fattore è quindi in parte, o del tutto, generata da variabili non considerate.
- Apparente instabilità dei premi al rischio. Anche se i veri premi al rischio di \(X\) e \(Z\) sono stabili, la covarianza tra le due variabili può cambiare nel tempo. Questo fa sembrare instabile il premio al rischio di \(X,\) inducendo l’investitore a credere che il mercato stia cambiando, quando in realtà il problema dipende da una specificazione errata del modello. Si tratta spesso di una spiegazione più parsimoniosa dell’instabilità dei fattori rispetto alle narrazioni che richiamano mutamenti nei fondamentali o nel comportamento degli investitori.
2. Over-controlling: l’inclusione di una variabile proibita
Si tratta di un errore meno intuitivo, messo in evidenza proprio dall’analisi causale moderna.
La saggezza convenzionale sostiene che aggiungere una variabile irrilevante a un modello sia sostanzialmente innocuo: nella peggiore delle ipotesi, riduce la precisione delle stime.
In realtà, i grafi causali mostrano che includere la variabile sbagliata può essere dannoso quanto omettere quella giusta.
I principali casi di over-controlling sono:
- Controllare per un mediatore. Quando l’effetto di \(X\) su \(Y\) passa attraverso una variabile intermedia \(Z\) (struttura \(X \longrightarrow Z \longrightarrow Y\)), includere \(Z\) come variabile di controllo blocca in parte, o del tutto, il percorso causale. Il risultato è una sottostima dell’effetto totale di \(X\) su \(Y,\) perché si rimuove proprio il meccanismo attraverso cui l’effetto si trasmette.
- Controllare per un collider. È uno degli errori più seri, come sottolinea Pearl. Un collider è una variabile sulla quale convergono due frecce (\(X \longrightarrow Z \longleftarrow Y\)). Di per sé, un collider interrompe il passaggio di informazione tra \(X\) e \(Y;\) tuttavia, condizionare su di esso – cioè selezionare o analizzare i dati in base al suo valore – apre un percorso spurio e introduce una correlazione artificiale che distorce le stime.
Senza un’analisi esplicita del grafo causale, è impossibile stabilire quali variabili vadano incluse e quali, invece, escluse dal modello.
La pratica, ancora molto diffusa, di aggiungere variabili unicamente in base al loro potere esplicativo – la cosiddetta specification searching – è rischiosa, perché mescola la fase di scoperta della struttura causale con quella di stima dell’effetto, aumentando la probabilità di produrre modelli mal specificati.
A questo punto, De Prado introduce uno schema concettuale che consente di mettere ordine tra le diverse forme di evidenza impiegate nella ricerca finanziaria.
Questo perché non tutte le evidenze hanno lo stesso valore scientifico, soprattutto quando l’obiettivo è comprendere relazioni di causa ed effetto.
Nel capitolo Hierarchy of Evidence, l’autore propone una classificazione dei principali approcci utilizzati in finanza, ordinandoli in base al loro rigore metodologico e alla solidità delle conclusioni che consentono di trarre:
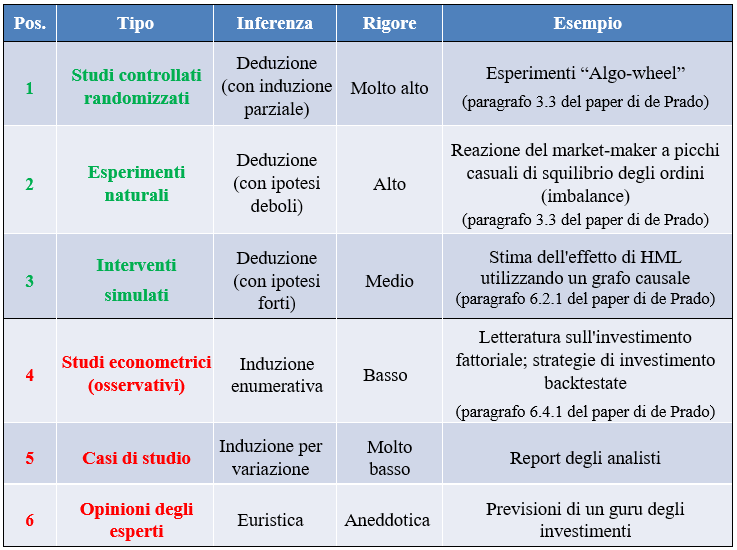
Gerarchia delle evidenze nella ricerca finanziaria (M.L. de Prado, Causal Factor Investing: can Factor Investing become scientific?, Cambridge University Press, 2023, p. 50. La traduzione in italiano è nostra)
La tabella mostra una vera e propria gerarchia delle evidenze, ispirata a quella utilizzata in medicina e in altre scienze empiriche.
In cima alla graduatoria si trovano gli esperimenti controllati randomizzati (Randomized Controlled Trial), che rappresentano lo standard più elevato per l’inferenza causale: la randomizzazione permette di isolare l’effetto di una variabile riducendo al minimo il Self-Selection Bias.
Come abbiamo già avuto modo di dire, in finanza questi esperimenti sono raramente realizzabili.
Subito sotto compaiono gli esperimenti naturali, in cui eventi esterni e non controllati dagli agenti economici generano variazioni “quasi casuali”. Anche in questo caso, il rigore rimane elevato, purché le assunzioni siano credibili.
Un livello intermedio è occupato dagli interventi simulati, basati su grafi causali e modelli strutturali. Qui l’inferenza rimane di tipo deduttivo, ma la solidità delle conclusioni dipende in modo diretto dalla correttezza delle ipotesi causali adottate.
Scendendo nella gerarchia si incontrano gli studi econometrici osservazionali, tipici della letteratura sul factor investing. Pur essendo molto diffusi, questi approcci si basano su inferenze induttive e presentano un grado di rigore decisamente inferiore quando vengono interpretati in chiave causale.
Alla base della piramide si collocano infine i casi di studio (case study) e le opinioni degli esperti, utili come spunti esplorativi ma privi di alcun valore scientifico.
Fino ad oggi, gran parte della ricerca sui fattori opera stabilmente nei livelli più bassi di questa gerarchia, pur traendo conclusioni che presuppongono un livello di evidenza ben più elevato.
È proprio questo scarto tra metodo utilizzato e interpretazione dei risultati a rendere fragile l’intero impianto del factor investing tradizionale.
Conclusione: verso una scienza dell’investimento
L’incoerenza logica del factor investing ha mantenuto la disciplina in una fase ancora “fenomenologica”, in cui si accettano affermazioni spurie senza un adeguato vaglio scientifico.
Da qui nasce una distanza profonda tra le convinzioni, talvolta granitiche, di molti studiosi e le performance insoddisfacenti osservate dagli investitori.
Il capitolo si chiude richiamando la performance storicamente deludente di un importante indice multi-factor – il Bloomberg-Goldman Sachs Asset Management US Equity Multi-Factor Index – a dimostrazione del fatto che molte strategie, una volta considerati i costi, non hanno mantenuto le promesse:
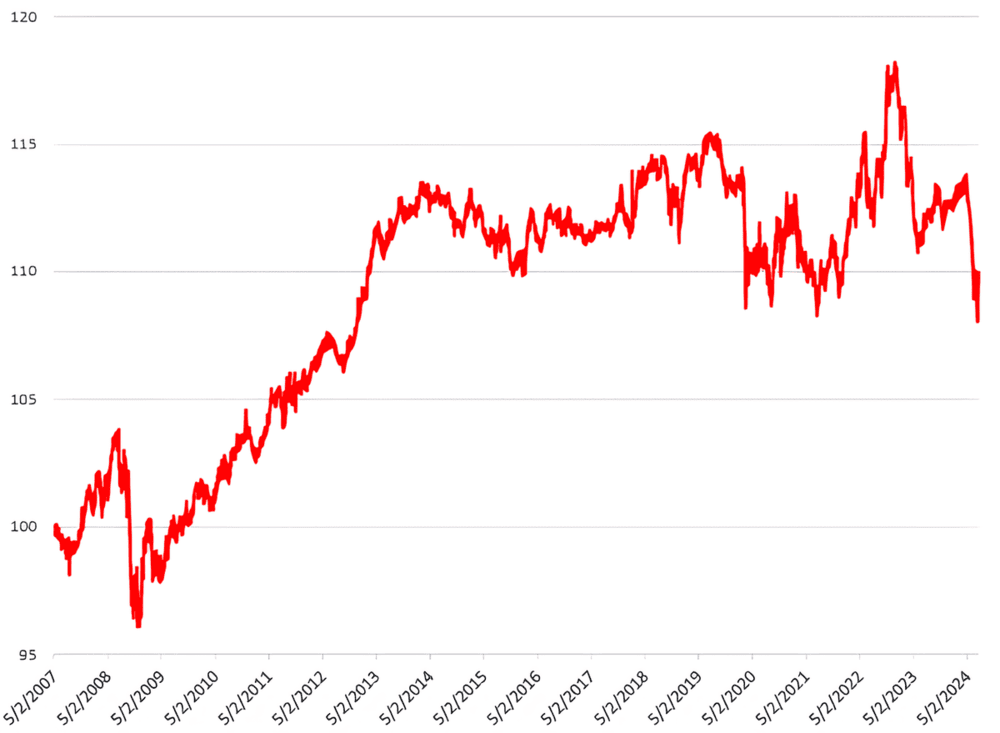
Bloomberg-Goldman Sachs Asset Management US Equity Multi-Factor Index (approx. 2007-2024)
L'andamento del grafico non è quindi un’anomalia, ma la conseguenza di tutto quanto è stato detto fin qui: quando manca una comprensione causale dei fenomeni, anche i risultati più convincenti sul passato faticano a reggere alla prova del tempo.
5. Mettere alla prova l'econometria con esperimenti controllati
Dopo aver costruito un solido impianto teorico sulla necessità di un approccio causale al factor investing, Marcos López De Prado dedica il settimo capitolo, Monte Carlo Experiments, a una verifica empirica controllata.
Qui la teoria cede il passo al laboratorio: attraverso una serie di esperimenti, l’autore mostra come le procedure econometriche standard, applicate a strutture causali note ma ignorate, conducano sistematicamente a conclusioni errate.
Questo capitolo funziona come un banco di prova: generando dati da mondi in cui la verità causale è interamente nota, De Prado mette in evidenza come e perché i modelli econometrici tradizionali falliscano, scambiando associazione per causalità e producendo scoperte spurie di tipo B.
L’obiettivo è mostrare che, anche di fronte a strutture causali elementari, l’econometria applicata in modo “ateorico” è destinata a sbagliare.
Per farlo, vengono analizzate tre configurazioni causali fondamentali: la forchetta (fork), il collider e la catena (chain).
Ognuno di questi esperimenti illustra un principio chiave dell’inferenza causale e mostra, in modo concreto, un errore ricorrente nella pratica econometrica.
Il Caso della Forchetta: Il Pericolo del Confounder Omesso
La prima struttura analizzata è la “forchetta” (fork), così chiamata perché una singola variabile \(Z\) si biforca in due rami causali, influenzando sia \(X\) che \(Y.\) Si tratta del caso classico di un confounder.
In questo scenario, \(Z\) agisce come causa comune delle due variabili osservate \(X\) e \(Y.\) Non esiste alcun legame causale diretto tra \(X\) e \(Y:\) l’associazione osservata nasce unicamente dal fatto che entrambe le variabili sono influenzate da una terza causa, invisibile ma determinante.
È probabilmente la fonte più frequente di correlazioni spurie nella pratica: due fenomeni che si muovono insieme non perché uno influenzi l’altro, ma perché rispondono alla stessa dinamica sottostante.
La struttura a forchetta (confounder)
La struttura causale di base è una forchetta, in cui una variabile \(Z\) agisce come causa comune sia di \(X\) che di \(Y,\) generando un percorso backdoor tra le due variabili:
\begin{equation}
Y \longleftarrow Z \longrightarrow X
\end{equation}
Questo percorso induce un’associazione statistica tra \(X\) e \(Y\) che non ha natura causale.
Se il confounder \(Z\) viene incluso nel modello, ossia se si controlla per \(Z,\) il percorso backdoor viene bloccato. \(X\) e \(Y\) risultano indipendenti in senso condizionale:
\begin{equation}
X \;\perp\!\!\!\perp\; Y \mid Z
\end{equation}
L’associazione spuria scompare, rivelando correttamente l’assenza di un legame causale diretto tra \(X\) e \(Y.\)
Per illustrare questo scenario, De Prado costruisce un semplice esperimento:
- Genera 5.000 osservazioni in cui \(Z\) è una variabile casuale, mentre sia \(X\) che \(Y\) sono definiti come \(Z\) più un termine di rumore. Per costruzione, \(X\) non causa \(Y.\)
- Simula il comportamento di un ricercatore che, ignorando la vera struttura causale, stima una regressione OLS di \(Y\) su \(X:\)
\begin{equation}
Y = \alpha + \beta X + \varepsilon
\end{equation}
Il risultato è un coefficiente \(\beta\) di circa 0,5, con p-value vicino a zero. Secondo i criteri econometrici tradizionali, il ricercatore concluderebbe – con grande sicurezza – che \(X\) ha un effetto statisticamente significativo su \(Y,\) interpretandolo erroneamente come causale.
Eppure, conoscendo la struttura reale del sistema, sappiamo che si tratta di una tipica scoperta spuria di tipo B: l’associazione è reale, ma la conclusione causale è falsa. L’omissione del confounder \(Z\) (under-controlling) ha prodotto un falso positivo.
L’esperimento non si ferma qui: viene mostrato anche come correggere l'errore.
3. Il ricercatore, questa volta, specifica il modello in modo appropriato, includendo \(Z\) come variabile di controllo:
\begin{equation}
Y = \alpha + \beta X + \gamma Z + \varepsilon
\end{equation}
Il risultato cambia completamente:
- La nuova stima di \(\beta\) è prossima a zero e non è statisticamente significativa.
- Il coefficiente \(\gamma,\) associato a \(Z,\) si avvicina a 1 ed è altamente significativo dal punto di vista statistico.
Una volta controllato il confounder, il bias scompare e il modello rivela correttamente l’assenza di un rapporto causale tra \(X\) e \(Y.\)
Questo esperimento evidenzia quanto sia pericoloso omettere variabili rilevanti e quanto una specificazione guidata dalla struttura causale sia indispensabile.
L’esperimento sulla forchetta ci consegna un primo importante insegnamento: ignorare le cause comuni porta a vedere legami causali dove non esistono.
Ma cosa accade se, nel tentativo di essere più precisi, inseriamo nel modello variabili che non andrebbero considerate?
Il prossimo esperimento mostra come le buone intenzioni possano condurre a risultati ancora peggiori.
Il Caso del collider: Il peccato mortale del controllo eccessivo
La seconda struttura considerata il collider, talvolta indicato nella letteratura come immorality.
In questo scenario, \(X\) e \(Y\) sono due cause indipendenti di una terza variabile \(Z.\) Nella popolazione generale, \(X\) e \(Y\) non mostrano alcuna associazione.
Il problema nasce quando un ricercatore decide di controllare per \(Z.\)
La struttura del collider
La struttura causale considerata è un collider, in cui due variabili \(X\) e \(Y\) sono cause indipendenti di una terza variabile \(Z.\) In questa configurazione non esiste alcun percorso causale che colleghi direttamente \(X\) e \(Y,\) e le due variabili risultano quindi non associate nella popolazione:
\begin{equation}
X \longrightarrow Z \longleftarrow Y
\end{equation}
Si verifica un paradosso quando si decide di controllare per \(Z.\) Condizionando sul collider, si apre artificialmente un percorso non causale tra \(X\) e \(Y,\) inducendo un’associazione spuria che non riflette alcun legame reale tra le due variabili.
È l’equivalente di tentare di inferire una relazione tra due cause osservando unicamente il loro effetto.
Questo scenario è particolarmente insidioso perché contraddice una convinzione diffusa in econometria: l'idea che controllare per un numero maggiore di variabili migliori sempre la qualità dell’analisi. In presenza di un collider, accade esattamente il contrario.
L’esperimento di De Prado mostra quanto questo principio possa essere fuorviante:
- Genera dati in cui \(X\) e \(Y\) sono variabili casuali indipendenti, mentre \(Z\) è definita come la loro somma più un termine di rumore. Per costruzione, \(X\) e \(Y\) non hanno alcun legame.
- Simula il comportamento di un ricercatore che, ritenendo erroneamente che \(Z\) sia un confounder, la include nel modello di regressione:
Modello errato (con collider):
\begin{equation}
Y = \alpha + \beta X + \gamma Z + \varepsilon
\end{equation}
Anche in questo caso il risultato è un falso positivo: il coefficiente \(\beta\) risulta negativo e statisticamente significativo.
Un ricercatore inesperto sarebbe portato a concludere che \(X\) eserciti un effetto negativo su \(Y,\) ma sappiamo che si tratterebbe di una scoperta spuria di tipo B, generata dall’errore di over-controlling: includendo il collider, si introduce artificialmente una correlazione che nel sistema reale non esiste.
La soluzione, in questo caso, consiste nel fare meno, non di più. Specificando correttamente il modello ed escludendo il collider \(Z,\) si ottiene:
\begin{equation}
Y = \alpha + \beta X + \varepsilon
\end{equation}
In questa formulazione, il coefficiente \(\beta\) risulta, come previsto, prossimo a zero e privo di significatività statistica.
Questo esperimento fa capire come la scelta delle variabili di controllo non possa basarsi sull’intuizione o su procedure automatiche, ma deve derivare da un'ipotesi precisa sulla struttura causale.
Senza una mappa esplicita – un grafo causale – si rischia di creare relazioni spurie dal nulla.
È particolarmente istruttivo, come sottolinea De Prado, che il modello errato (quello che include il collider) presenti un \(R^2\) più elevato: un ricercatore guidato esclusivamente dal potere esplicativo del modello sarebbe inevitabilmente tratto in inganno.
Abbiamo visto i rischi derivanti dall’omissione di una variabile rilevante (il confounder) e all’inclusione di una variabile proibita (il collider).
Ma cosa accade quando una variabile si trova “nel mezzo”, cioè lungo il percorso causale stesso?
Il Caso della catena: Il dilemma del mediatore
La terza struttura analizzata è la catena causale, che rappresenta un caso di mediazione. In questo contesto, l’effetto di \(X\) su \(Y\) non è diretto, ma passa interamente attraverso una variabile intermedia \(Z.\) La struttura causale è:
\begin{equation}
X \longrightarrow Z \longrightarrow Y
\end{equation}
Esiste quindi un vero legame causale tra \(X\) e \(Y,\) ma di natura indiretta: \(X\) influenza \(Y\) solo attraverso il suo impatto su \(Z.\)
Controllare per un mediatore è un errore di over-controlling: significa bloccare proprio il percorso causale che si intende stimare, producendo un falso negativo, cioè portando a concludere che l’effetto non esista, quando in realtà è presente.
De Prado propone tuttavia un esperimento più articolato, che mette in luce un rischio ancora più insidioso: la fallacia della mediazione.
Questa si verifica quando il mediatore \(Z\) è a sua volta influenzato da una variabile esterna \(W,\) che agisce da confounder. Si tratta di una configurazione frequente nei sistemi complessi, in cui i percorsi causali raramente sono lineari e isolati.
In questo scenario più realistico, un ricercatore che controlla per il mediatore \(Z:\)
- Blocca il percorso causale genuino.
- Apre un percorso backdoor spurio attraverso il confounder \(W.\)
Il risultato è una stima del coefficiente \(\beta\) non soltanto errata, ma potenzialmente di segno opposto rispetto all'effetto reale.
L’esperimento mostra proprio questo esito: il coefficiente stimato \(\beta\) risulta negativo e statisticamente significativo, nonostante tutti i legami causali presenti nel sistema siano positivi.
È una situazione analoga al celebre paradosso di Simpson, in cui una tendenza osservata all’interno dei gruppi si inverte quando i dati vengono aggregati.
Ancora una volta, la soluzione risiede in una corretta specificazione del modello, guidata da un’analisi esplicita del grafo causale.
In questo caso, sarebbe bastato riconoscere la struttura per evitare di controllare il mediatore \(Z,\) scongiurando così l’inversione del segno e la conseguente conclusione fuorviante.
Un'altra spiegazione per i celebri fattori di fama-french
Sulla base delle evidenze raccolte tramite gli esperimenti Monte Carlo, De Prado conclude il capitolo applicando questa nuova lente critica ai modelli più influenti della finanza moderna: i modelli a tre e a cinque fattori di Fama e French.
Secondo l’autore, molti risultati di questi lavori storici sono probabilmente spuri, sia di tipo A (riconducibili a pratiche di p-hacking) sia, soprattutto, di tipo B, ossia dovuti all’errata interpretazione di semplici associazioni come relazioni causali.
Le principali criticità individuate sono tre:
- Specification-searching. I modelli Fama-French sarebbero stati selezionati principalmente per la loro capacità esplicativa, senza il supporto di un grafo causale che giustificasse la scelta delle variabili incluse.
- Under-controlling. I modelli ignorano confounder rilevanti, come variabili macroeconomiche (ciclo economico, inflazione) e fattori tecnici come il momentum, noto per essere correlato con il value.
- Over-controlling (potenziale). L’inclusione del fattore value (book-to-market) potrebbe introdurre un errore da collider. Se i rendimenti azionari e la dimensione di un’azienda sono indipendenti, ma entrambi influenzano il book-to-market, controllare per il value può generare una correlazione spuria tra rendimenti e size, offrendo una possibile spiegazione del comportamento anomalo spesso osservato nel fattore size.
De Prado propone quindi un possibile grafo causale in cui i risultati dei modelli Fama-French risultano distorti sia dalla presenza di confounder sia da effetti di collider.
Pur trattandosi di un’ipotesi, l’autore sottolinea che l'onere della prova spetta a chi afferma l’esistenza di un fattore: è necessario rendere esplicite le proprie assunzioni causali, chiarire il meccanismo che si intende misurare e motivare la scelta delle variabili di controllo.
In sintesi, molti risultati dei modelli Fama-French e degli innumerevoli studi che ne hanno replicato l’impostazione sono probabilmente spuri.
Non per malafede, ovviamente, ma perché gli strumenti econometrici tradizionali vengono applicati in assenza di un quadro causale chiaro, esponendo la ricerca agli stessi errori evidenziati dagli esperimenti discussi in precedenza.
Del resto, questo era l’obiettivo del capitolo: mostrare che, senza una teoria e una mappa causale, i dati non “parlano da soli” e possono facilmente condurre a conclusioni sbagliate.
6. Le conclusioni di De Prado
Giunto alla fine del suo percorso, Marcos López De Prado sintetizza i risultati della sua analisi. La sua tesi è che il factor investing, nella sua formulazione tradizionale, non ha mantenuto le promesse che lo avevano accompagnato.
Sul piano accademico, si è progressivamente ridotto a un esercizio di data mining, dando origine a una proliferazione di scoperte spurie sia di tipo A (rumore interpretato come segnale, overfitting nei backtest), sia di tipo B (associazioni erroneamente interpretate come relazioni causali).
Sul piano applicativo, è stato presentato come una metodologia scientificamente fondata, ma non è riuscita a produrre in modo sistematico quei rendimenti statisticamente significativi che venivano attribuiti ai fattori.
Chiarita la natura del problema, De Prado indica anche un possibile percorso evolutivo, delineando i principi di una nuova disciplina: il Causal Factor Investing.
Si tratta di un invito a ripensare il modo in cui i fattori vengono studiati e utilizzati, abbandonando l’approccio puramente associativo in favore di un quadro causale esplicito, capace di spiegare perché una strategia dovrebbe funzionare, e non soltanto se ha funzionato in passato.
Le ragioni per cui il Factor Investing è una black box (scatola nera)
La diagnosi di De Prado è che il factor investing si è progressivamente trasformato in una scatola nera a causa di una profonda incoerenza logica.
Gran parte della letteratura sui fattori ignora il contenuto causale implicito nei modelli utilizzati. Gli autori giustificano le loro scelte esclusivamente in termini associativi ma poi, nella fase applicativa, costruiscono portafogli e interpretano i risultati come se riflettessero autentici rapporti di causa-effetto.
Questa doppia lettura metodologica ha delle gravi conseguenze. In assenza di una teoria causale chiara e falsificabile, diventa infatti impossibile sottoporre a verifica la validità di un fattore.
Un backtest, per quanto sofisticato, rimane un esercizio associativo sul passato: è vulnerabile all’overfitting e non può né confermare né confutare un meccanismo causale.
Quando una strategia fattoriale smette di funzionare, come è accaduto al value tra il 2017 e il 2022, diventa difficile fornire una risposta convincente alla domanda: perché?
Se non si comprende il motivo per cui una strategia avrebbe dovuto funzionare in origine, non è possibile spiegare nemmeno perché abbia cessato di farlo.
In questo vuoto interpretativo, molti asset manager ricorrono a ragionamenti induttivi (“ha funzionato per anni, quindi tornerà a funzionare”), ignorando le stesse avvertenze che rivolgono ai clienti: le performance passate non sono indicative di quelle future.
Secondo De Prado, questo approccio è del tutto inadeguato, soprattutto per gli investitori istituzionali – fondi pensione, fondi sovrani, compagnie assicurative – che gestiscono risparmi collettivi e non possono permettersi di adottare strategie prive di trasparenza.
La domanda “perché?” dovrebbe essere inquadrata come un vero e proprio obbligo fiduciario. Non saper rispondere equivale ad ammettere di non comprendere a fondo il prodotto offerto, trasformando l’investimento in un atto di fede anziché in una decisione basata su conoscenze solide.
Una volta messe in luce le lacune dell’approccio tradizionale, De Prado apre a una prospettiva più costruttiva: mostra come un paradigma causale possa offrire nuove opportunità nella gestione del rischio e della performance, che finora sono rimaste inesplorate.
I benefici di un approccio causale
Adottare un approccio causale potrebbe portare dei benefici concreti per gli investitori. De Prado ne individua almeno otto, che delineano il profilo di una strategia d’investimento più solida, trasparente e coerente nel tempo.
1. Efficienza
I modelli causali permettono una corretta attribuzione del rischio e della performance. Diventa così possibile distinguere tra rischi remunerati dal mercato (ad esempio, un autentico premio per il rischio di fallimento) e rischi non remunerati, come l’esposizione involontaria a un confounder macroeconomico. Ne deriva la possibilità di costruire portafogli più efficienti, focalizzati sui primi e meno esposti ai secondi.
2. Interpretabilità
Una teoria causale rende la strategia comprensibile e difendibile. Gli investitori istituzionali possono spiegare ai propri stakeholder perché i risultati si discostano dalle attese, mantenendo la fiducia anche nei periodi difficili. Invece di limitarsi a constatare che “il fattore value sta sottoperformando”, diventa possibile spiegare, ad esempio, che “il legame tra basso prezzo e valore intrinseco è temporaneamente influenzato da una correlazione con il momentum, un rischio che viene monitorato attivamente”.
3. Trasparenza
Un grafo causale rende esplicite le assunzioni alla base del modello. La strategia smette di essere una scatola nera e diventa un insieme di ipotesi dichiarate e falsificabili, che possono essere discusse, criticate e migliorate.
4. Riproducibilità
Un'impostazione causale riduce la probabilità di scoperte spurie:
- Limita le false scoperte di tipo A, perché circoscrive la ricerca a ipotesi teoricamente plausibili.
- Riduce le false scoperte di tipo B, perché richiede di motivare la persistenza del fenomeno attraverso un meccanismo strutturale.
5. Robustezza
Le strategie puramente associative sono fragili: funzionano finché l’intera struttura sottostante rimane stabile, una condizione che spesso non si verifica. Le strategie causali, invece, restano valide finché il nesso causa-effetto rimane intatto, risultando più affidabili nel tempo e meno sensibili ai cambiamenti di regime.
6. Estrapolabilità
Solo una strategia basata su una teoria causale può affrontare, e talvolta sfruttare, eventi rari e inattesi. Conoscere le condizioni che attivano un meccanismo permette di anticipare o mitigare gli effetti dei cosiddetti “cigni neri”.
7. Monitorabilità
La validità di un meccanismo causale può essere direttamente monitorata. Invece di attendere che una rottura strutturale emerga dai risultati ex post, è possibile osservare in tempo reale le variabili chiave del meccanismo e intervenire prima che le perdite si materializzino.
8. Migliorabilità
Le teorie causali, a differenza delle semplici relazioni statistiche, possono essere progressivamente affinate con l'aumentare della comprensione del fenomeno. Una strategia causale può evolvere, rafforzarsi e adattarsi nel tempo.
La via da seguire: una collaborazione per il futuro
Come può realizzarsi questa trasformazione?
De Prado individua nella forte influenza degli interessi commerciali sulla ricerca accademica uno dei principali ostacoli.
Gli studi puramente associativi sono infatti più rapidi ed economici da produrre e alimentano un’industria multimiliardaria, creando un incentivo sistemico a perpetuarne l’utilizzo.
Per spezzare questo circolo vizioso, l’autore propone una soluzione: favorire una collaborazione strutturata tra accademici impegnati in una ricerca rigorosa e investitori istituzionali non commerciali, come fondi sovrani o endowment universitari.
Questi soggetti, non condizionati da pressioni di natura commerciale, perseguono obiettivi allineati con quelli dei loro beneficiari finali e si trovano dunque in una posizione ideale per sostenere un approccio più scientifico.
La nuova disciplina del Causal Factor Investing dovrebbe caratterizzarsi per l’adozione di strumenti avanzati, come quelli sviluppati nell’ambito della scoperta causale e del do-calculus, utili a investigare le reali fonti di rischio e rendimento.
La crescente disponibilità di dati alternativi apre inoltre possibilità inedite per condurre esperimenti naturali e forme innovative di inferenza causale, fino a poco tempo fa difficilmente praticabili.
In definitiva, l’appello di De Prado è finalizzato a elevare gli standard della ricerca e della pratica negli investimenti: adottare un approccio causale significa adempiere ai propri doveri fiduciari con un livello di trasparenza e solidità che soltanto un metodo realmente scientifico può garantire.
Per raggiungere questo ambizioso obiettivo e assistere all’alba di una nuova fase dell’investimento quantitativo, la comunità del factor investing deve però prima risvegliarsi dal suo "sonno associazionista”.
Il messaggio finale è che la finanza quantitativa, per evolvere, deve tornare a porsi domande più profonde: invece di chiedersi semplicemente che cosa funziona nei dati, dovrebbe interrogarsi su quale meccanismo rende possibile ciò che osserviamo.
È in questo cambio di prospettiva che risiede il potenziale di una disciplina capace di connettere in modo più maturo la ricerca scientifica e la pratica professionale.
Resta però aperta una questione essenziale: quanto è realistico immaginare che il factor investing, così come lo conosciamo, riesca a intraprendere questo percorso?
L'opera di De Prado indica la strada da percorrere: resta da capire se l'industria finanziaria saprà – o vorrà – seguirla.
È su questo punto che si concentra il capitolo successivo, nel quale offrirò il mio punto di vista su ciò che, a mio giudizio, attende il factor investing nel futuro.
7. Causal Factor Investing: riflessioni personali
Arrivato a questo punto, mi sembra utile condividere alcune impressioni su Causal Factor Investing di Marcos López De Prado.
I capitoli precedenti hanno ricostruito il suo impianto e le sue argomentazioni. Qui, invece, voglio fissare alcune conclusioni personali: valutazioni, dubbi e conseguenze pratiche che, a mio giudizio, seguono naturalmente da questo lavoro.
1. Un libro da Premio Nobel
Si tratta di un lavoro che, per profondità e portata innovativa, potrebbe valere al suo autore un Premio Nobel. L’opera rimette in discussione mezzo secolo di pratiche consolidate nella teoria finanziaria e interroga il criterio con cui, per decenni, abbiamo stabilito cosa potesse essere considerato un “risultato scientifico”.
La finanza quantitativa ha generato una letteratura sterminata; proprio per questo, un’opera che sposta l’attenzione dalla quantità delle evidenze al loro valore conoscitivo finisce per incidere in modo enorme.
Se definisco questo libro da Nobel, è perché tale è il mio giudizio sulla sua portata intellettuale. De Prado obbliga il lettore a confrontarsi con una domanda che in finanza viene spesso aggirata o attenuata attraverso formulazioni prudenti: che cosa stiamo misurando quando stimiamo un modello?
Se la risposta resta incerta, l’intera architettura che ne discende – test, regressioni, portafogli, backtest – finisce per poggiare su basi fragili.
2. L'econometria "classica" e la causalità implicita
Una parte importante del libro è dedicata all’econometria così come viene comunemente insegnata e praticata.
L’aspetto che ho trovato più rilevante è che l’econometria associativa può essere formalmente impeccabile e, allo stesso tempo, indurre di fatto a letture causali, perché il linguaggio utilizzato e l’uso che se ne fa spingono naturalmente in quella direzione.
Quando stimiamo una regressione e interpretiamo un coefficiente come se rappresentasse l’effetto di un intervento, stiamo già assumendo una particolare visione del mondo: diamo per scontate l’esogeneità, l’assenza di variabili omesse rilevanti, la mancata presenza di collider condizionati, la stabilità della struttura causale su orizzonti operativi non banali.
In molti contesti finanziari, ipotesi di questo tipo sono poco robuste per costruzione: i dati sono osservazionali, le variabili spesso endogene, i regimi mutano e le regole e le metriche che guidano le decisioni finiscono per modificare il sistema osservato.
Nonostante gli anni trascorsi a studiare statistica, per me si è trattata di una vera e propria rivelazione di natura metodologica.
Questo lavoro aiuta a rimettere ordine tra due piani che nella pratica vengono spesso sovrapposti: il piano del calcolo, quasi sempre molto rigoroso, e quello dell’interpretazione, che diventa scivoloso non appena entra in gioco la causalità.
Ed è proprio qui che si manifesta uno degli aspetti più scomodi del libro: molte conclusioni operative poggiano su un salto interpretativo che resta sottinteso e raramente viene reso esplicito.
3. La promessa del causal factor investing è reale, ma ritengo difficile una sua adozione diffusa
Il Causal Factor Investing, inteso come prospettiva metodologica, è molto convincente: richiede una mappa causale esplicita, impone interrogativi più stringenti, rende discutibili le assunzioni e crea le condizioni per parlare di falsificabilità in un ambito che spesso si fonda su conferme retrospettive.
Come standard epistemico, lo considero un avanzamento netto rispetto al livello attuale.
La mia valutazione sulle prospettive future della disciplina resta tuttavia prudente. Intravedo una difficoltà strutturale: un approccio causale aumenta i costi e restringe lo spazio commerciale delle narrazioni semplici, quelle che "si vendono bene", perché impone di chiarire le condizioni che renderebbero falsa una tesi.
La falsificabilità è un vantaggio sul piano scientifico, ma comporta anche un rischio reputazionale ed economico. Questa tensione, da sola, aiuta a spiegare molte resistenze.
C’è poi una seconda difficoltà. In finanza e nelle scienze sociali, la causalità è particolarmente sensibile al contesto: basta un cambiamento di regime, una trasformazione istituzionale o una modifica nel comportamento degli operatori perché un meccanismo ritenuto valido perda efficacia o ne cambi addirittura il segno.
Ciò rende più complesso costruire teorie causali stabili che siano anche sfruttabili operativamente su orizzonti lunghi: una spiegazione causale può essere corretta e più robusta di una relazione associativa, pur restando difficile da trasformare in una strategia replicabile su larga scala.
4. Se i “fattori” pubblici deludono, torna una vecchia domanda: qual è l'eredità del CAPM?
Quando si mette in dubbio l’affidabilità del factor investing tradizionale, ritengo quasi inevitabile questa domanda: e se l’unico fattore robusto fosse il rendimento di mercato stesso?
A livello concettuale, questa ipotesi riconduce al Capital Asset Pricing Model (CAPM) e al suo nucleo teorico.
La mia rivalutazione del CAPM non riguarda la sua capacità di prevedere i rendimenti futuri in modo operativamente utile. Su questo punto resto scettico: il CAPM non è un modello previsionale.
La rivalutazione riguarda piuttosto il suo messaggio generale: la possibilità di battere il mercato in modo sistematico, stabile e replicabile tende a essere molto limitata, soprattutto quando ci si muove entro il perimetro delle informazioni pubbliche, delle strategie trasparenti e dei vincoli tipici dell’investitore istituzionale o del retail evoluto.
Aggiungo una precisazione per evitare equivoci: anche il beta “non funziona” in molte finestre temporali e secondo diverse metriche.
Ciò non invalida necessariamente l’intuizione di fondo in una prospettiva lunga e dinamica: il rischio di mercato può continuare a rappresentare una forza dominante nel rendimento atteso, pur senza manifestarsi attraverso una relazione lineare e stabile nel breve periodo.
A mio avviso, questo rende il CAPM ancora competitivo come cornice di disciplina intellettuale, capace di ridimensionare le ambizioni di extra-rendimento sistematico.
Gli unici ambiti in cui vedo eccezioni più credibili sono quelli legati alle microstrutture, all’esecuzione, all’informazione privata, alla capacità tecnologica e ai dati difficilmente accessibili.
Si tratta di terreni che richiedono risorse, competenze e condizioni molto diverse da quelle implicate dal factor investing “pubblico”. Sono anche contesti poco adatti alla piena divulgazione perché il vantaggio, quando esiste, tende a essere – e a rimanere – di natura proprietaria.
5. Possibile che nessuno se ne sia accorto per almeno tre decenni?
A una prima lettura, l’impianto proposto da Marcos López de Prado può apparire eccessivo: il problema è così diffuso? Il disallineamento tra associazione e causalità è davvero così pervasivo? E perché nessuno se ne è accorto prima?
A me, invece, la costruzione di De Prado sembra molto plausibile per una ragione piuttosto semplice: l’associazione è più facile, meno costosa, più rapida e meno rischiosa della causalità.
Un modello associativo non richiede una teoria falsificabile: richiede una specificazione statistica ben costruita e una narrazione verosimile.
Una teoria causale, invece, richiede qualcosa in più dei numeri: impone una struttura che possa essere messa alla prova, contestata e, se necessario, smentita.
Questa dinamica non riguarda solo la finanza. Coinvolge molti ambiti in cui modelli previsionali e test statistici occupano una posizione centrale.
Il risultato è un ecosistema in cui la produzione di evidenza è abbondante, mentre l'evidenza realmente robusta resta una merce piuttosto rara.
Il punto forse più interessante è che gli strumenti concettuali dell’inferenza causale moderna sono disponibili da tempo: la loro adozione rimane limitata perché più complessa e più costosa e, soprattutto, perché riduce lo spazio dell’ambiguità interpretativa, un aspetto che considero fondamentale.
6. Il lavoro di De Prado è scomodo, sia per il mondo accademico che per l'industria finanziaria
Sul versante accademico, l’adozione di standard causali più rigorosi comporta un costo reputazionale: significa ammettere che una parte rilevante della letteratura, pur tecnicamente sofisticata, risulti epistemicamente debole.
Molti risultati richiederebbero una riclassificazione: da presunte relazioni strutturali a risultati che descrivono regolarità valide solo in contesti specifici.
È una prospettiva difficile da accettare per chi ha costruito carriera, ricerca e riconoscimento su quel tipo di evidenza.
Sul versante industriale, il costo è più direttamente economico: esistono fondi a gestione attiva, ETF, strategie sistematiche e un intero linguaggio commerciale costruito attorno ai fattori. Esistono forti interessi nel mantenere in vita quel framework, anche quando i risultati sono deboli.
Un cambio di paradigma pone subito un problema pratico: occorre disporre di alternative implementabili. Ed è tutt’altro che evidente che tali alternative siano già disponibili.
Il Causal Factor Investing, allo stato attuale, appare ancora pionieristico e oneroso; richiede risorse, dati, lavoro teorico e una cultura statistica diversa da quella oggi dominante.
7. La gerarchia delle evidenze come criterio di giudizio
Tra gli strumenti concettuali proposti da De Prado, la gerarchia delle evidenze occupa una posizione particolare: introduce un criterio di giudizio che distingue le forme di evidenza per rigore e forza esplicativa.
Proprio per questo, le sue implicazioni vanno oltre il piano metodologico e toccano direttamente il modo in cui la letteratura viene valutata e presentata.
La diretta conseguenza è che una parte rilevante della produzione finanziaria finisce nelle fasce più basse della scala.
La classificazione può essere discutibile nei dettagli, ma risulta difficile metterne in discussione l’intuizione di fondo: in un ambiente in cui individui e istituzioni hanno interesse a presentare evidenza debole come se fosse solida, una gerarchia di questo tipo introduce un elemento di attrito, se non addirittura di imbarazzo.
Ed è proprio per questo che la considero preziosa: crea una forma di reality check, un sano richiamo alla realtà.
8. Implicazioni pratiche
Da queste considerazioni derivano alcune regole di prudenza che, almeno per me, diventano imprescindibili.
- Una regressione lineare non "spiega" niente, indipendentemente dalla narrazione che la accompagna: è un riassunto numerico di una relazione nei dati, il cui contenuto causale va argomentato e sostenuto.
- Una strategia deve poggiare su un meccanismo dichiarabile, che includa anche le ipotesi sotto le quali smetterebbe di essere valido.
- La robustezza non coincide con la significatività: un p-value basso può convivere con un errore causale ampio.
- Il backtest è un punto di partenza, non di arrivo: può servire come primo controllo descrittivo, ma non come fondamento teorico.
Queste regole rendono più difficile raccontarsi favole finanziarie ben confezionate.
9. Una conclusione senza soluzioni facili
Sul piano scientifico, considero il lavoro di Marcos López de Prado una pietra miliare: alza lo standard, riduce l’ambiguità e rende finalmente discutibili assunzioni che prima restavano nascoste.
Sul piano industriale e accademico, considero invece probabile una risposta lenta e difensiva: la causalità ha un costo e rende più rischioso vendere certezze o sfornare paper scientifici in serie.
La finanza quantitativa ha comunque bisogno di criteri più severi per distinguere ciò che descrive da ciò che spiega: in assenza di teorie causali solide e falsificabili, la promessa di un extra-rendimento costante resta poco più di un sogno.
Di conseguenza, quando questa promessa viene addirittura presentata come sistematica, impone un livello di sospetto ancora maggiore.
È una conclusione scomoda, ma intellettualmente inevitabile.
Il libro Causal Factor Investing è disponibile a questo indirizzo.
Di factor investing avevamo già parlato in un articolo più breve, disponibile qui.
Il Percorso avanzato continua con l'articolo:


